Sonic Eddy Model of the Turbulent Boundary Layer

Abstract

The effects of Mach number on the skin friction and velocity fluctuations of the turbulent boundary layer are considered through a sonic eddy model. Originally proposed for free shear flows, the model assumes that the eddies responsible for momentum transfer have a rotation Mach number of unity, with the entrainment rate limited by acoustic signaling. Under this assumption, the model predicts that the skin friction coefficient should go as the inverse Mach number in a regime where the Mach number is larger than unity but smaller than the square root of the Reynolds number. The velocity fluctuations normalized by the friction velocity should be the inverse square root of the Mach number in the same regime. Turbulent transport is controlled by acoustic signaling. The density field adjusts itself such that the Reynolds stresses correspond to the momentum transport. In contrast, the conventional van Driest–Morkovin view is that the Mach number effects are due to density variations directly. A new experiment or simulation is proposed to test this model using different gases in an incompressible boundary layer, following the example of Brown and Roshko in the free shear layer.

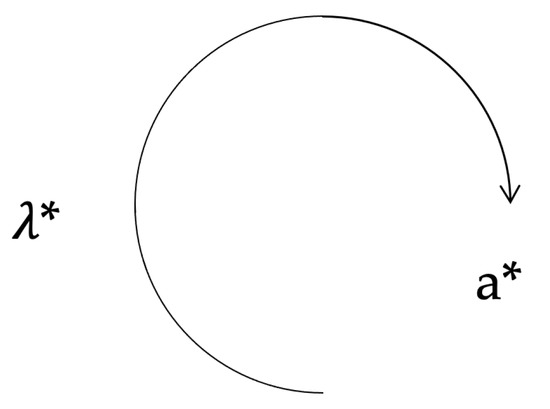
1. Introduction

It has long been known that the skin friction in a turbulent boundary layer declines with increasing Reynolds and Mach numbers. Prandtl’s universal law of skin friction describes the Reynolds number effect for incompressible flow. Not so clear is the physical mechanism for the effect of the Mach number.

Mach number plays a confusing dual role, affecting both the density through the energy equation and the acoustic signaling speed [1]. In a perfect gas, it is difficult to distinguish the physical mechanism controlling compressible turbulence.

In this short communication, a heuristic model for compressible turbulence is pursued. It assumes that Mach number effects on turbulence are solely attributable to acoustic signaling rather than to changes in density. This approach contrasts with the prevailing view that density changes are important [2,3]. In order to apply this model to the boundary layer, it is instructive to first consider the case of free shear flows.

A simple model [4] of compressible turbulent entrainment makes two assumptions:

(i)

an eddy must complete a rotation to do anything, such as entrain or transport momentum, and

(ii)

entrainment is an intrinsically non-steady process.

Consider the implications of these two assumptions in a fluid with a relatively low speed of sound compared to the speed of the turbulent motions. The information that a non-steady event has occurred on one side of a vortex propagates across the diameter of the vortex at the local speed of sound. For relatively low speed of sound, this process takes a finite amount of time. If the propagation time is greater than the rotation period of the vortex, then the information concerning the non-steady event will not reach the opposite side of the eddy within the critical time window for influencing the dynamics of the vortex. So, the non-steady event can have no effect on the dynamics. As far as that vortex is concerned, the non-steady event might as well never have happened. The vortex can neither entrain mass nor transport momentum. From a dynamical viewpoint, the vortex is inert.

The eddy Mach number is defined as an eddy’s rotational speed divided by the local average speed of sound. The factor of pi is suppressed, both for simplicity and to avoid implying a precision in the vortex rotation angle required for momentum transport that is unwarranted. In addition, there may be a large uncertainty in the local speed of sound. All eddies with an eddy Mach number greater than unity rotate too fast for signal propagation across their diameter during the time interval that matters, one rotation period. They are impotent.

There is a special, distinguished eddy size. The acoustic signaling time across its diameter is just equal to one eddy rotation period. Such a “sonic” eddy has a rotational Mach number of unity. In a Kolmogorov spectrum, all eddies smaller than the sonic eddy have rotational Mach numbers less than unity, so their dynamics are essentially incompressible, i.e., unconstrained by a finite signaling speed. Since it is the largest active eddy, the sonic eddy determines the rates of entrainment and momentum transport.

The sonic eddy concept is consistent with the underlying instability that drives the basic turbulence. First defined by [5], the convective Mach number is essentially the eddy Mach number of the largest vortices.

The original model asserted that the spreading angle for the free shear layer would undergo a sudden decrease as the Mach number increased through M = 1. However, this is inconsistent with the smooth and progressive decrease in the size of the sonic eddy with increasing Mach number, as noted by [1]. So, the original model should be amended. According to this revision, the spreading angle of the shear layer in this regime varies inversely with the size of the sonic eddy, i.e., inversely with Mach number. Figure 1 is a sketch of a log–log diagram of the normalized spreading angle of a shear layer as a function of Mach number.

There are three transitions between different regimes. The first occurs when the size of the sonic eddy equals the largest possible vortex size, at M = 1. The sonic eddy becomes as small as the smallest possible eddy, the Kolmogorov microscale, when the Mach number is equal to the square root of the Reynolds number, as described in [4]. The third transition occurs at M = Re, when the sonic eddy equals the mean free path of the gas.

2. Materials and Methods

Let us now apply this model to the boundary layer. For an equilibrium, self-similar flow, the skin friction is equal to the rate of momentum flux removal from the outer, wake flow. Using the standard wake approximation, the wake momentum defect is proportional to ρUΔU, where ρ is the fluid density, U is the freestream speed, and ΔU is the characteristic velocity defect in the wake. Thus, the skin friction coefficient $c_{fi}$ for incompressible flow is

$$c_{fi}=\mathrm{const}.\frac{\Delta \mathrm{U}}{\mathrm{U}}$$

(1)

The amplitude of the velocity fluctuations u′ should be proportional to the velocity defect DU. Thus,

$$c_{fi}=\mathrm{const}.\frac{\Delta \mathrm{U}}{\mathrm{U}}=\mathrm{const}.\frac{u^{\prime }}{\mathrm{U}}$$

(2)

If the turbulence is compressible (M > 1), then according to this model, momentum is essentially transferred only by those eddies whose rotational Mach number is unity. Thus, the effective value of the velocity defect as far as momentum transfer is concerned is an average speed of sound $a_{*}$instead of ΔU. Consequently, at a fixed Reynolds number, the skin friction coefficient $c_f$is proportional to the inverse Mach number,

$$c_f=\frac{\mathrm{const}.}{\mathrm{M}}$$

(3)

Additionally,

$$c_f=\frac{u_{\tau }^2}{{\mathrm{U}}^2}$$

(4)

where $u_{\tau }$is the friction velocity, and a factor of two is suppressed for simplicity. Replacing DU by the local average speed of sound $a_{*}$, it follows from Equations (1)–(4) that

$$\frac{u^{\prime }}{\mathrm{U}}=\frac{u^{\prime }}{u_{\tau }}{c}_f^{1/2}=\frac{\mathrm{const}.}{\mathrm{M}}$$

(5)

and thus

$$\frac{u^{\prime }}{u_{\tau }}=\mathrm{const}. \frac{u_{\tau }}{\mathrm{U}}=\mathrm{const}. {\mathrm{M}}^{-1/2}$$

(6)

According to the model, this expression should be valid for Mach numbers between unity and the square root of the Reynolds number, at which point the sonic eddy has shrunk to the Kolmogorov microscale, the smallest possible eddy size.

In combination with the velocity field, the density field must be consistent with the Reynolds stresses. Even if acoustic signaling completely controls the momentum transport, as assumed in the sonic eddy model, the van Driest–Morkovin density scaling still works. The subtle distinction is that the density field is a consequence of the signaling. Mach number controls the signaling, which, in turn, controls the transport and hence the density field. A single, unified physics is presumed for all vortices, no matter their proximity to a wall.

In contrast, the van Driest–Morkovin view implies that the density field influences the vortex dynamics near a wall but not away from a wall. Somehow, there is one type of physics for a vortex near a wall, and another type for a vortex away from a wall. This raises awkward questions: At what distance from the wall is there a transition between the two types of physics? How does a vortex know this?

3. Discussion

3.1. Comparison with Experiment and DNS

3.1.1. Skin Friction

The skin friction and streamwise velocity fluctuations as a function of Mach number for an adiabatic wall have been measured and computed by [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].

Due to experimental challenges in supersonic flow, particularly with measuring velocity fluctuations, direct numerical simulations offer some relative advantages. The DNS results of [28,29] are particularly informative and remarkable. The only fundamental disadvantage of DNS is its limitation to modest Reynolds numbers.

Figure 2 is a plot of skin friction normalized by its incompressible value as a function of freestream Mach number, here labeled Ma [30]. The curved dashed line is van Driest–Morkovin scaling, and the straight dashed line is the sonic eddy model, assuming a constant speed of sound. The open circles are measurements from [11,12,13,14,15,16,17,18,19,20], the blue squares are from [28], and the green triangles are non-adiabatic cases from [29]. The latter two are at constant Reynolds number. Density scaling closely correlates with the DNS results.

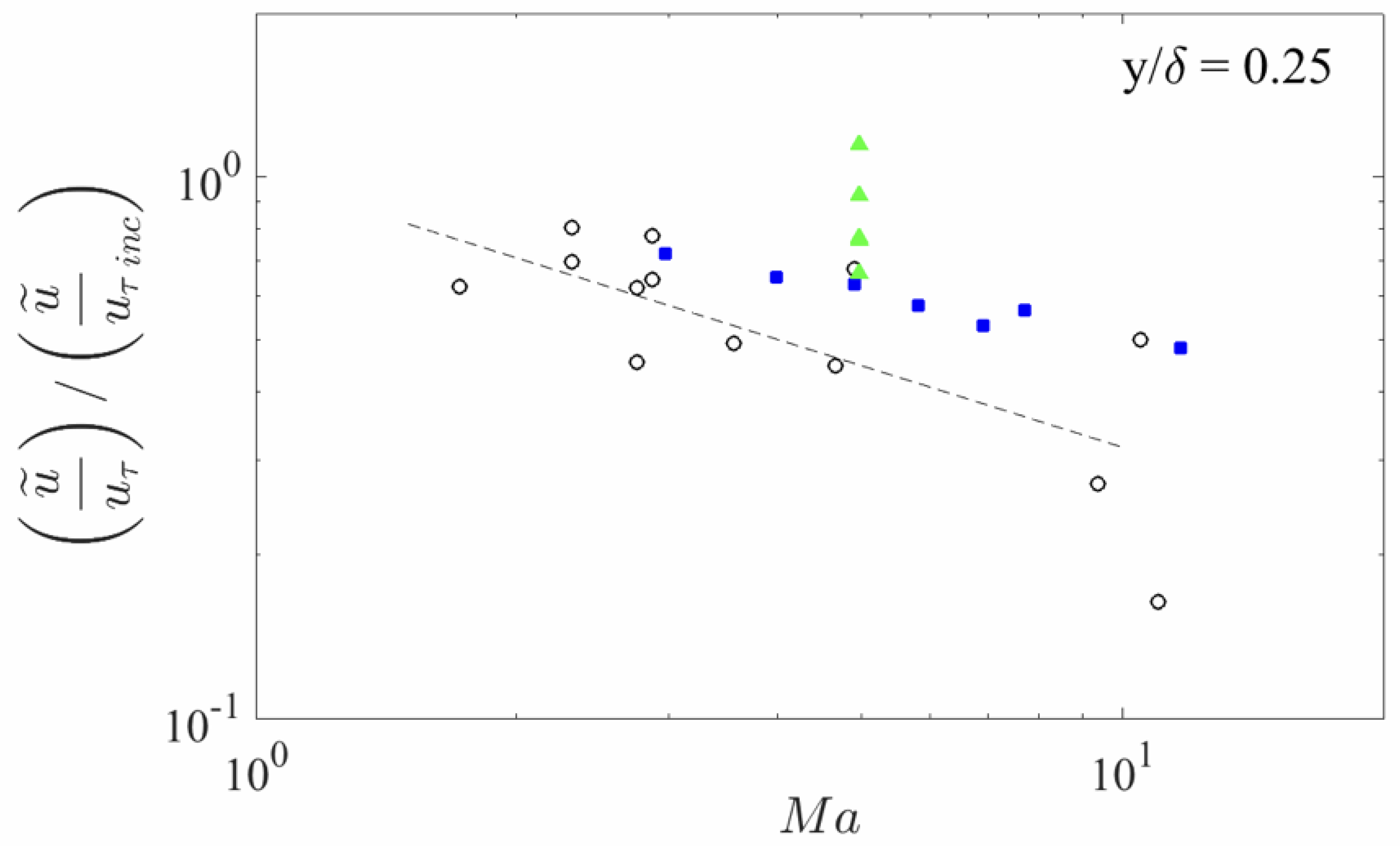
3.1.2. Velocity Fluctuations

Figure 3 is a plot of the streamwise velocity fluctuations as a function of freestream Mach number at a height of 25% of the boundary layer thickness, with the same symbols as in Figure 2. The dashed line has a slope of minus one half, as predicted by the model. Note that the speed of sound is the freestream value, rather than the more appropriate local one. The comparisons may improve if the local rather than the freestream speed of sound is utilized.

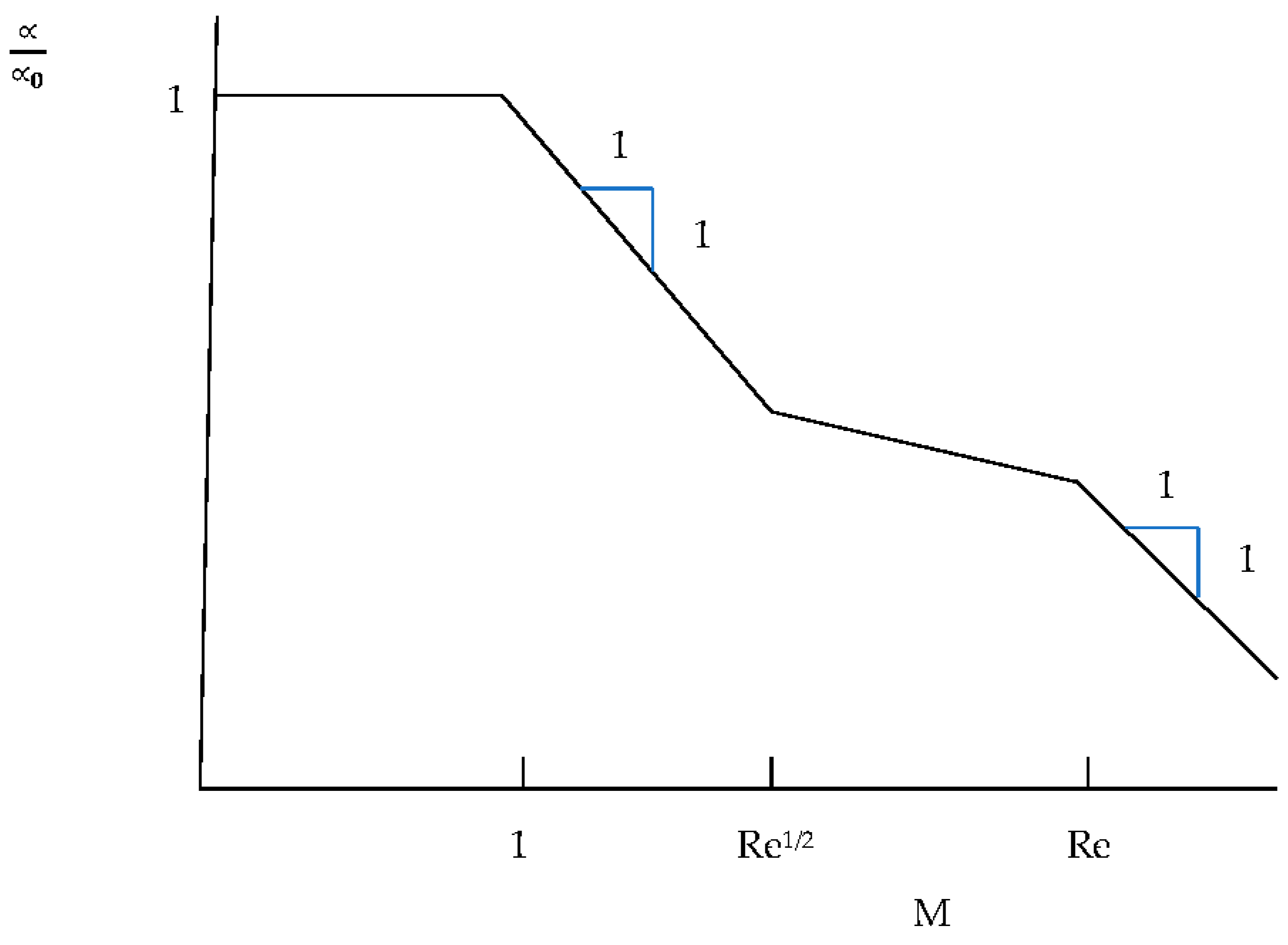
3.1.3. Growth Rate

Mach number has only a weak effect on growth rate of the boundary layer [31]. The rate of growth increases by about 20% as the Mach number increases from 1.7 to 5. This may be consistent with a diffusive growth rate controlled by an eddy viscosity equal to the product of the local speed of sound and the size of the sonic eddy. The eddy viscosity of sonic eddies can account for the peculiar behavior of the hypersonic wake, where the visible growth rate vanishes for hundreds of effective body diameters downstream of the body [4]. Density ratio effects are too weak to account for it.

3.1.4. Eddy Celerity

When the freestream Mach number is about 3, the eddy speed divided by the freestream speed of sound, $a_{\infty }$, is typically about 0.3 less than that of the freestream Mach number [17]. Assuming, for simplicity, that an eddy accommodates a speed difference across it symmetrically, the speed difference between the freestream and the eddy would be half of the total speed difference across the eddy. Therefore, the change in flow speed across these eddies normalized by $a_{\infty }$ is about 0.6, a number reasonably close to the value of unity assumed in this model. A further refinement would normalize by the local speed of sound.

The integral scale in a Mach three-boundary layer was about one-third of the layer thickness [24], consistent with the model. A neighboring shear layer at a lower value of convective Mach number was observed with the same dual-wire probe to have an integral scale much larger, comparable to the shear layer thickness. Consequently, this probe technique was capable of resolving the difference in scales [25].

At a freestream Mach number of 7.2, the eddy celerity normalized by the free stream speed of sound is about 1.4 less that the freestream Mach number [26]. Consequently, the speed difference across that eddy normalized by the freestream speed of sound is about three, apparently too large to be consistent with the model. However, normalization by the local rather than the freestream speed of sound would lower this number.

3.1.5. Topology

The large-scale structure of the turbulence in the incompressible free shear layer is two-dimensional [32]. The model implies that all compressible turbulence must have a three-dimensional structure, because the signaling speed limits the coherence length of the eddies to the size of the sonic eddy. There must be a topological transformation in the large-scale structure of the free shear layer at a Mach number of about unity, from two-dimensional to three-dimensional. Such a transformation has been observed [33,34]. This topological transformation is accompanied by a change in growth rate, as described above [4].

In contrast, the incompressible boundary layer is already three-dimensional, so no topological transformation is necessary at M = 1. However, the correlation distance would be expected to shrink with increasing Mach number, along with the shrinking size of the sonic eddy. This is supported by the velocity iso-correlations in [28].

3.2. Proposed New Experiment or Simulation

To clearly distinguish between the effects of density from those of signaling, a new experiment or direct numerical simulation is required. Following the strategy of [32] for the free shear layer, a new experiment or simulation would directly measure the effect of density ratio in an incompressible boundary layer. Helium and air flows would form an incompressible boundary layer with a strong density gradient. According to the sonic eddy model, the density gradient would have little effect on the vortex dynamics, as modeled by [35]. In the free shear layer, for example, a change in density ratio by a factor of 49 only changes the spreading angle by a factor of 2 [32]. In contrast, according to the van Driest–Morkovin viewpoint, the density ratio in both free and wall flows would have a large effect.

4. Conclusions

Using the same physical arguments as for free shear flows, the effect of Mach number on momentum transport in a boundary layer has been modeled. The central idea is that an eddy must communicate with itself during one rotation in order to transport momentum. In general, the largest active eddy controls the transport. In a compressible flow, the finite acoustic signaling speed limits the size of the largest active eddy to one with an eddy Mach number of unity, the sonic eddy.

The present model contrasts with the conventional approach that attributes the effect of Mach number on the boundary layer to density ratio effects. Since density ratio effects are known to be relatively weak in the free shear layer, it is natural to expect the same physics to apply to all turbulent vortices, including those in wall flows. If so, then Mach number affects momentum transport through the speed of sound rather than the square root of the specific total energy $\surd h_0$. Due to the confusing dual role of Mach number in compressible turbulence, a new experiment or numerical simulation is proposed to distinguish between signaling and density effect.