Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows
Abstract
1. Introduction
2. Wavelet-Filtered Navier–Stokes Equations
2.1. Wavelet Threshold Filtering
2.2. Filtered Governing Equations
2.3. Closure Modeling
2.4. Adaptive Wavelet Collocation Method
- (i)
- given a known solution at the current computational grid, say , the associated wavelet coefficients are computed through forward wavelet transform;
- (ii)
- the mask consisting of the AWC points associated with the retained wavelets (with coefficients for which the moduli are above the prescribed threshold) is created;
- (iii)
- the extended mask is generated by adding the AWC points corresponding to adjacent wavelets (for which the coefficients can potentially become significant during the next time step); and
- (iv)
- the recursive reconstruction check procedure is performed on the extended mask , ensuring that all the ancestry points, necessary to perform the forward wavelet transform on the updated computational grid , are present.
2.5. Homogeneous Turbulence Simulation
3. Hierarchical Adaptive Eddy-Capturing Approach
Combined Wavelet-Collocation/Volume-Penalization Method
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DNS | Direct Numerical Simulation |
| LES | Large-Eddy Simulation |
| SGS | Sub-Grid Scale |
| HIT | Homogeneous Isotropic Turbulence |
| WA-LES | Wavelet-based Adaptive Large-Eddy Simulation |
| WTF | Wavelet Threshold Filtering |
| WA-DNS | Wavelet-based Adaptive Direct Numerical Simulation |
| CVS | Coherent Vortex Simulation |
| LDKM | Localized Dynamic Kinetic-energy Model |
| AWC | Adaptive Wavelet Collocation |
| CFL | Courant–Friedrich–Lewy |
| FD | Finite Difference |
| GDM | Global Dynamic Model |
| WA-URANS | Wavelet-based Adaptive Unsteady Reynolds-Averaged Navier–Stokes |
| WA-DDES | Wavelet-based Adaptive Delayed Detached Eddy Simulation |
References
- Jimenez, J.; Wray, A.; Saffman, P.; Rogallo, R. The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 1993, 225, 65–90. [Google Scholar] [CrossRef]
- De Stefano, G.; Goldstein, D.E.; Vasilyev, O.V. On the role of subgrid-scale coherent modes in large-eddy simulation. J. Fluid Mech. 2005, 525, 263–274. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. “Perfect” modeling framework for dynamic SGS model testing in large eddy simulation. Theor. Comput. Fluid Dyn. 2004, 18, 27–41. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V.; Goldstein, D.E. A-priori dynamic test for deterministic/stochastic modeling in large-eddy simulation of turbulent flow. Comput. Phys. Commun. 2005, 169, 10–13. [Google Scholar] [CrossRef]
- Vincent, A.; Meneguzzi, M. The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 1991, 225, 1–20. [Google Scholar] [CrossRef]
- Sweldens, W. The lifting scheme: A construction of second generation wavelets. SIAM J. Math. Anal. 1998, 29, 511–546. [Google Scholar] [CrossRef]
- Donoho, D.L. Interpolating Wavelet Transforms; Technical Report 3; Preprint; Department of Statistics, Stanford University: Stanford, CA, USA, 1992. [Google Scholar]
- De Stefano, G.; Denaro, F.M.; Riccardi, G. High-order filtering for control volume flow simulation. Int. J. Numer. Methods Fluids 2001, 37, 797–835. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Sharp cutoff versus smooth filtering in large eddy simulation. Phys. Fluids 2002, 14, 362–369. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. A fully adaptive wavelet based approach to homogeneous turbulence simulation. J. Fluid Mech. 2012, 695, 149–172. [Google Scholar] [CrossRef]
- De Stefano, G.; Brown-Dymkoski, E.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation of supersonic channel flow. J. Fluid Mech. 2020, 901, A13. [Google Scholar] [CrossRef]
- Pope, S. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 1–24. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V.; Goldstein, D.E. Localized dynamic kinetic-energy-based models for stochastic coherent adaptive large eddy simulation. Phys. Fluids 2008, 20, 045102. [Google Scholar] [CrossRef]
- Ghosal, S.; Lund, T.S.; Moin, P.; Akselvoll, K. A dynamic localization model for large-eddy simulation of turbulent flows. J. Fluid Mech. 1995, 286, 229. [Google Scholar] [CrossRef]
- Carati, D.; Ghosal, S.; Moin, P. On the representation of backscatter in dynamic localization models. Phys. Fluids 1995, 7, 606–616. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; De Stefano, G.; Goldstein, D.E.; Kevlahan, N.K.R. Lagrangian dynamic SGS model for stochastic coherent adaptive large eddy simulation. J. Turbul. 2008, 9, 1–11. [Google Scholar] [CrossRef]
- Meneveau, C.; Lund, T.S.; Cabot, W.H. A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; Bowman, C. Second generation wavelet collocation method for the solution of partial differential equations. J. Comput. Phys. 2000, 165, 660–693. [Google Scholar] [CrossRef]
- Vasilyev, O.V. Solving multi-dimensional evolution problems with localized structures using second generation wavelets. Int. J. Comput. Fluid Dyn. 2003, 17, 151–168. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen differenzengleichungen der mathematischen physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; Kevlahan, N.K.R. An adaptive multilevel wavelet collocation method for elliptic problems. J. Comput. Phys. 2005, 206, 412–431. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation with explicit filtering. J. Comput. Phys. 2013, 238, 240–254. [Google Scholar] [CrossRef]
- Fröhlich, J.; Schneider, K. An adaptive wavelet Galerkin algorithm for one-dimensional and 2-dimensional flame computations. Eur. J. Mech. B Fluids 1994, 13, 439–471. [Google Scholar]
- Nejadmalayeri, A.; Vezolainen, A.; Brown-Dymkoski, E.; Vasilyev, O.V. Parallel adaptive wavelet collocation method for PDEs. J. Comput. Phys. 2015, 298, 237–253. [Google Scholar] [CrossRef]
- Brown-Dymkoski, E.; Vasilyev, O.V. Adaptive-anisotropic wavelet collocation method on general curvilinear coordinate systems. J. Comput. Phys. 2017, 333, 414–426. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Stochastic coherent adaptive large eddy simulation of forced isotropic turbulence. J. Fluid Mech. 2010, 646, 453–470. [Google Scholar] [CrossRef]
- Goldstein, D.E.; Vasilyev, O.V.; Kevlahan, N.K.R. CVS and SCALES simulation of 3-D isotropic turbulence. J. Turbul. 2005, 6, 1–20. [Google Scholar] [CrossRef]
- Nejadmalayeri, A.; Vezolainen, A.; Vasilyev, O.V. Reynolds number scaling of coherent vortex simulation and stochastic coherent adaptive large eddy simulation. Phys. Fluids 2013, 25, 110823. [Google Scholar] [CrossRef]
- Farge, M.; Schneider, K.; Kevlahan, N.K.R. Non-gaussianity and coherent vortex simulation for two-dimensional turbulence using an adaptive orthogonal wavelet basis. Phys. Fluids 1999, 11, 2187–2201. [Google Scholar] [CrossRef]
- Farge, M.; Pellegrino, G.; Schneider, K. Coherent vortex extraction in 3d turbulent flows using orthogonal wavelets. Phys. Rev. Lett. 2001, 87, 054501. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L.; Johnstone, I.M. Ideal Spatial Adaptation via Wavelet Shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Schneider, K.; Farge, M.; Pellegrino, G.; Rogers, M. Coherent vortex simulation of three-dimensional turbulent mixing layers using orthogonal wavelets. J. Fluid Mech. 2005, 534, 39–66. [Google Scholar] [CrossRef]
- Geurts, B.J.; Frohlich, J. A framework for predicting accuracy limitations in large-eddy simulation. Phys. Fluids 2002, 14, L41–L44. [Google Scholar] [CrossRef]
- Nejadmalayeri, A.; Vezolainen, A.; De Stefano, G.; Vasilyev, O.V. Fully adaptive turbulence simulations based on Lagrangian spatio-temporally varying wavelet thresholding. J. Fluid Mech. 2014, 749, 794–817. [Google Scholar] [CrossRef]
- Angot, P.; Bruneau, C.H.; Fabrie, P. A penalization method to take into account obstacles in viscous flows. Numer. Math. 1999, 81, 497–520. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder. J. Fluid Mech. 2014, 748, 433–456. [Google Scholar] [CrossRef]
- De Stefano, G.; Nejadmalayeri, A.; Vasilyev, O.V. Wall-resolved wavelet-based adaptive large-eddy simulation of bluff-body flows with variable thresholding. J. Fluid Mech. 2016, 788, 303–336. [Google Scholar] [CrossRef]
- Carbou, G.; Fabrie, P. Boundary layer for a penalization method for viscous incompressible flow. Adv. Differ. Equ. 2003, 8, 1409–1532. [Google Scholar]
- Sohankar, A.; Norberg, C.; Davidson, L. Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 1999, 11, 288–306. [Google Scholar] [CrossRef]
- Brun, C.; Aubrun, S.; Goossens, T.; Ravier, P. Coherent structures and their frequency signature in the separated shear layer on the sides of a square cylinder. Flow Turbul. Combust. 2008, 81, 97–114. [Google Scholar] [CrossRef]
- Luo, S.C.; Chew, Y.T.; Ng, Y.T. Characteristics of square cylinder wake transition flows. Phys. Fluids 2003, 15, 2549–2559. [Google Scholar] [CrossRef]
- Lyn, D.A.; Rodi, W. The flapping shear layer formed by flow separation from the forward of a square cylinder. J. Fluid Mech. 1994, 267, 353–376. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V.; Brown-Dymkoski, E. Wavelet-based adaptive unsteady Reynolds-averaged turbulence modelling of external flows. J. Fluid Mech. 2018, 837, 765–787. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-averaged Navier-Stokes computations of wall-bounded internal and external compressible turbulent flows. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. AIAA Paper 2018–0545. [Google Scholar]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-Averaged Navier-Stokes simulations of wall-bounded compressible turbulent flows. AIAA J. 2020, 58, 1529–1549. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; Hussaini, M.Y. Wavelet-based adaptive delayed detached eddy simulations for wall-bounded compressible turbulent flows. J. Fluid Mech. 2019, 873, 1116–1157. [Google Scholar] [CrossRef]
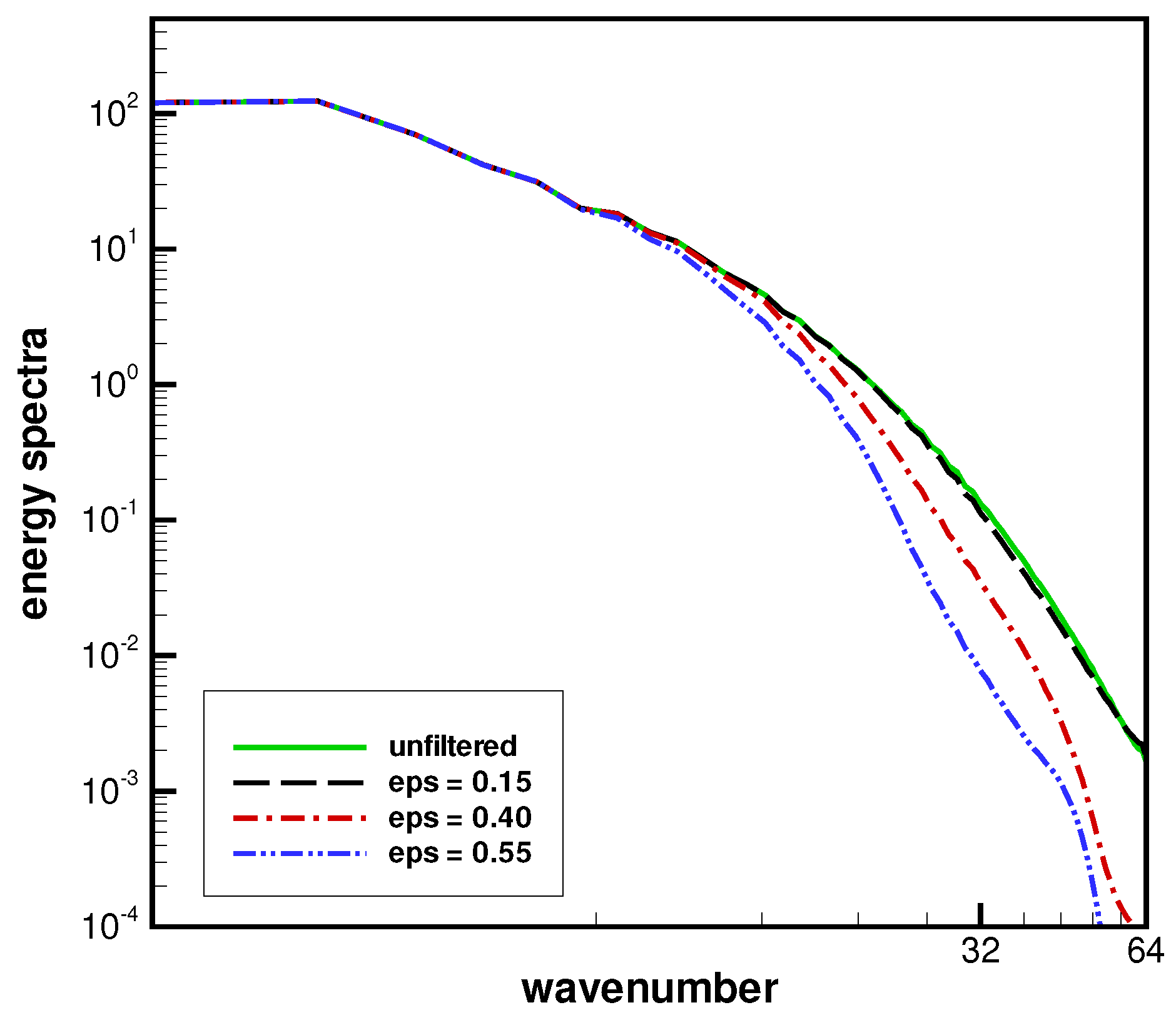
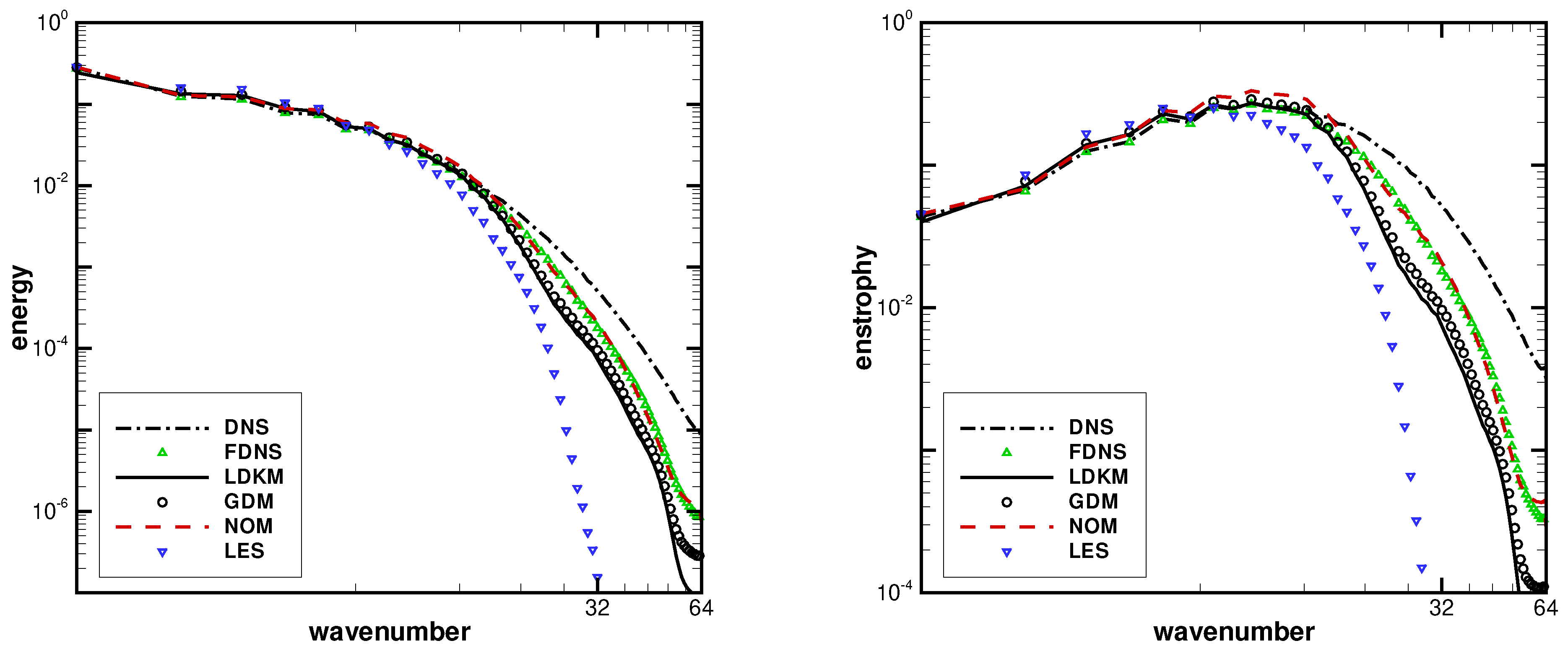
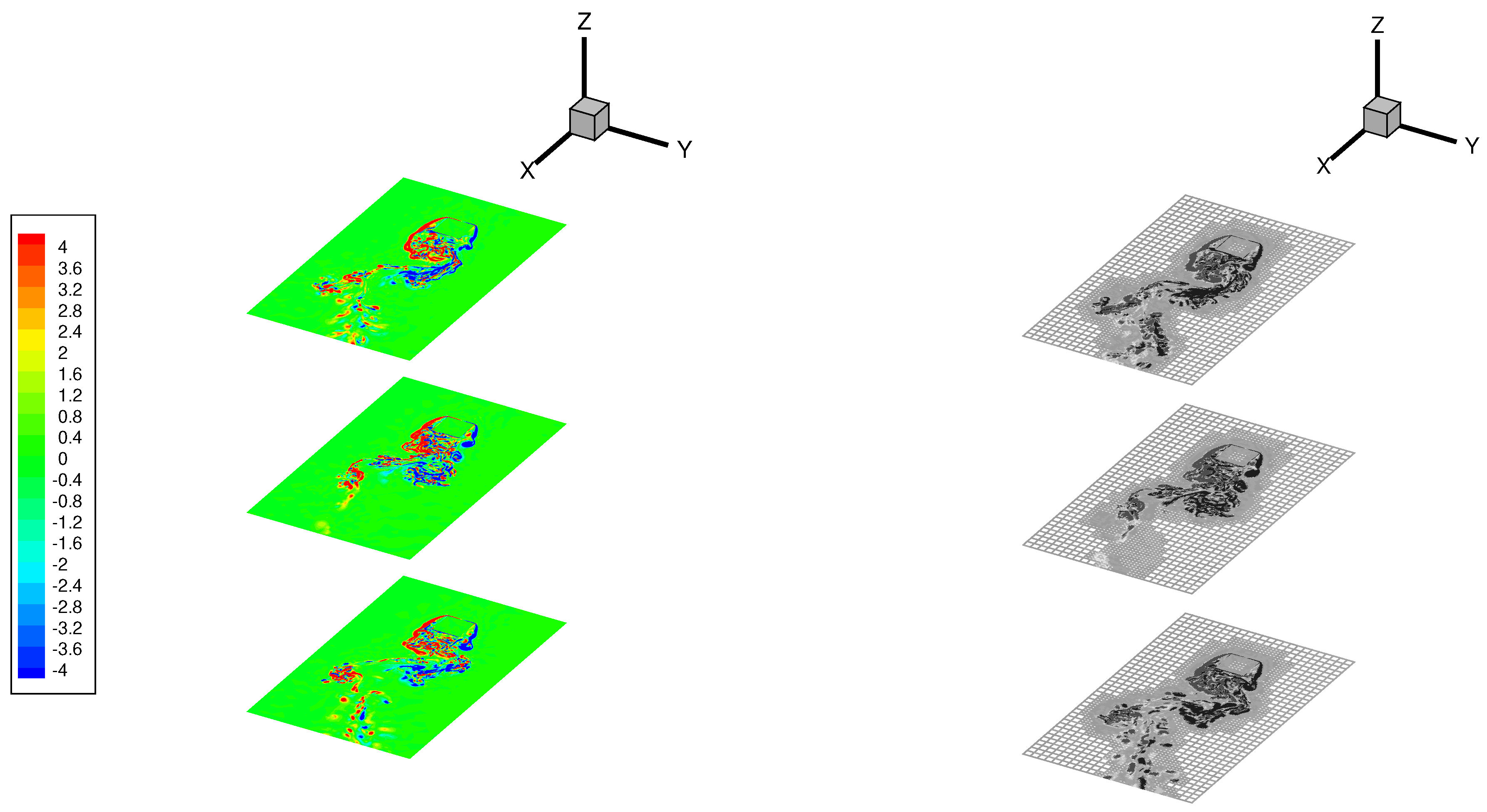

| Threshold | Wavelets | Energy | Enstrophy |
|---|---|---|---|
| 0.55 | 0.15% | 95.08% | 60.06% |
| 0.40 | 0.46% | 98.11% | 77.08% |
| 0.15 | 5.07% | 99.88% | 97.53% |
| 0.05 | 12.50% | 99.99% | 99.98% |
| Study | |||||
|---|---|---|---|---|---|
| WA-DNS [36] | 4 | 200 | 1.57 | ||
| DNS [39] | 6 | 5.56 | 200 | 1.39 | |
| Experimental [41] | − | − | 200 | − | |
| WA-LES [37] | 4 | 2000 | |||
| LES [40] | 4 | 2000 | |||
| Experimental [42] | 7 | 2.1 |
| 1.57 | |||||
| 1.60 | |||||
| 1.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Stefano, G.; Vasilyev, O.V. Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows. Fluids 2021, 6, 83. https://doi.org/10.3390/fluids6020083
De Stefano G, Vasilyev OV. Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows. Fluids. 2021; 6(2):83. https://doi.org/10.3390/fluids6020083
Chicago/Turabian StyleDe Stefano, Giuliano, and Oleg V. Vasilyev. 2021. "Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows" Fluids 6, no. 2: 83. https://doi.org/10.3390/fluids6020083
APA StyleDe Stefano, G., & Vasilyev, O. V. (2021). Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows. Fluids, 6(2), 83. https://doi.org/10.3390/fluids6020083







