Geometry and Flow Properties Affect the Phase Shift between Pressure and Shear Stress Waves in Blood Vessels
Abstract
1. Introduction
2. Physical Model
2.1. Physical Ingredients
2.2. Dimensionless Groups
3. Numerical Model
4. Validation
5. Results and Discussion
5.1. Study Cases
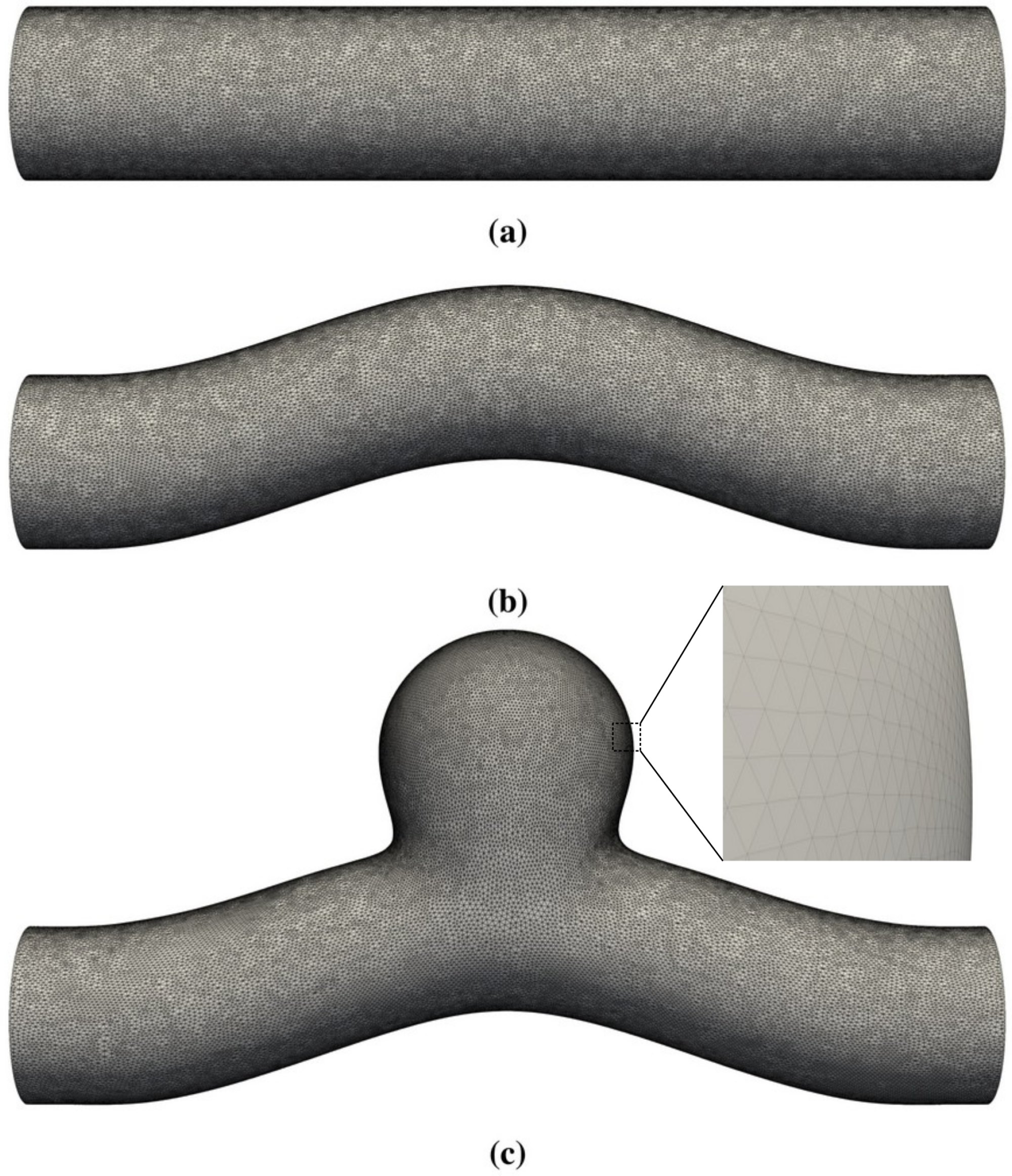
- First, we focused on the effect of flow. We performed the simulations of sinusoidal flow through a curved tube without an aneurysm (Figure 1b). We varied the flow properties in two ways:
- (a)
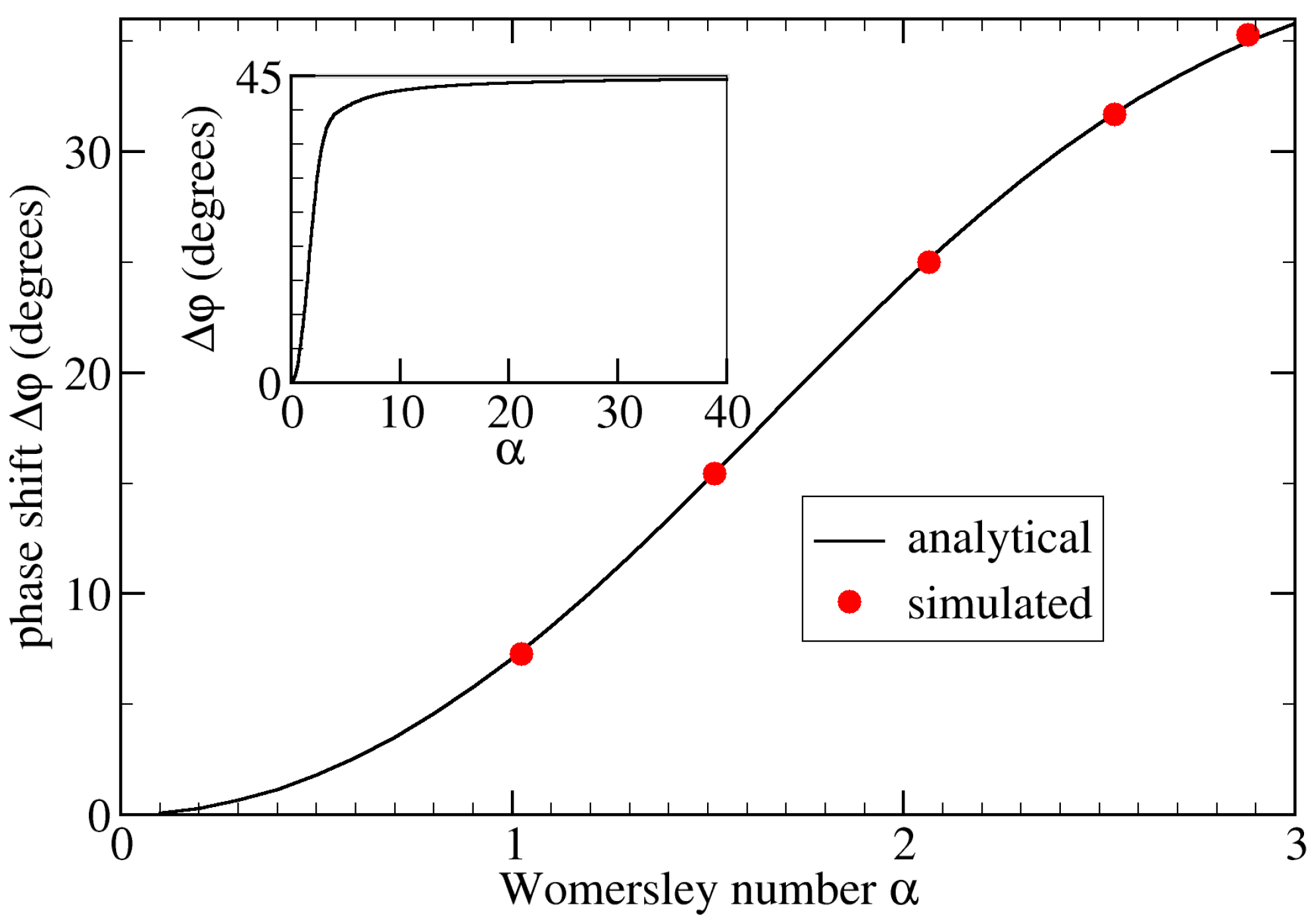
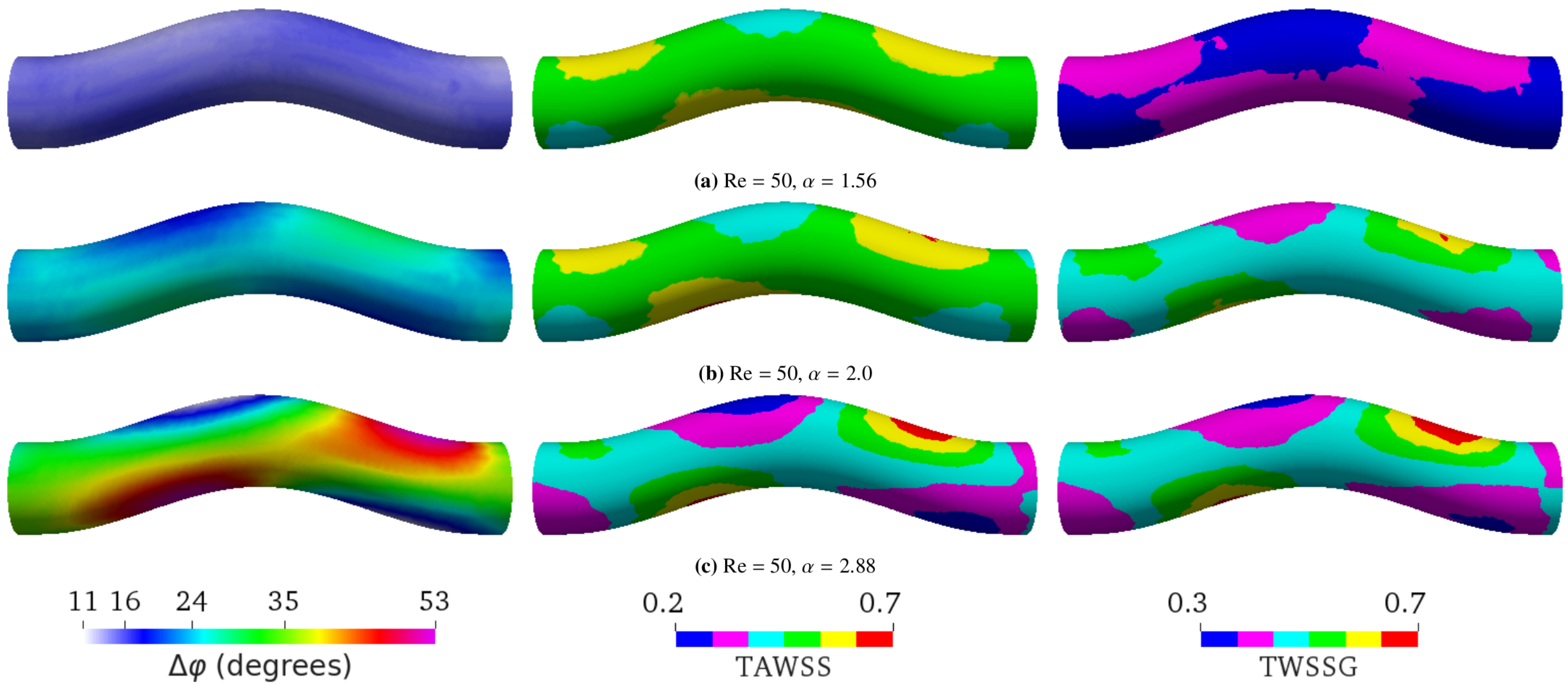
- Varying the Womersley number while keeping the Reynolds number Re fixed. This was achieved by changing the period T: , 2.0, and 2.88 for s, 1.6 s, and 0.8 s, respectively (see Figure 4). Note that the average flow speed (and thus Re) depends on . Therefore, one also needs to change the pressure drop to maintain a given value of Re;
- (b)
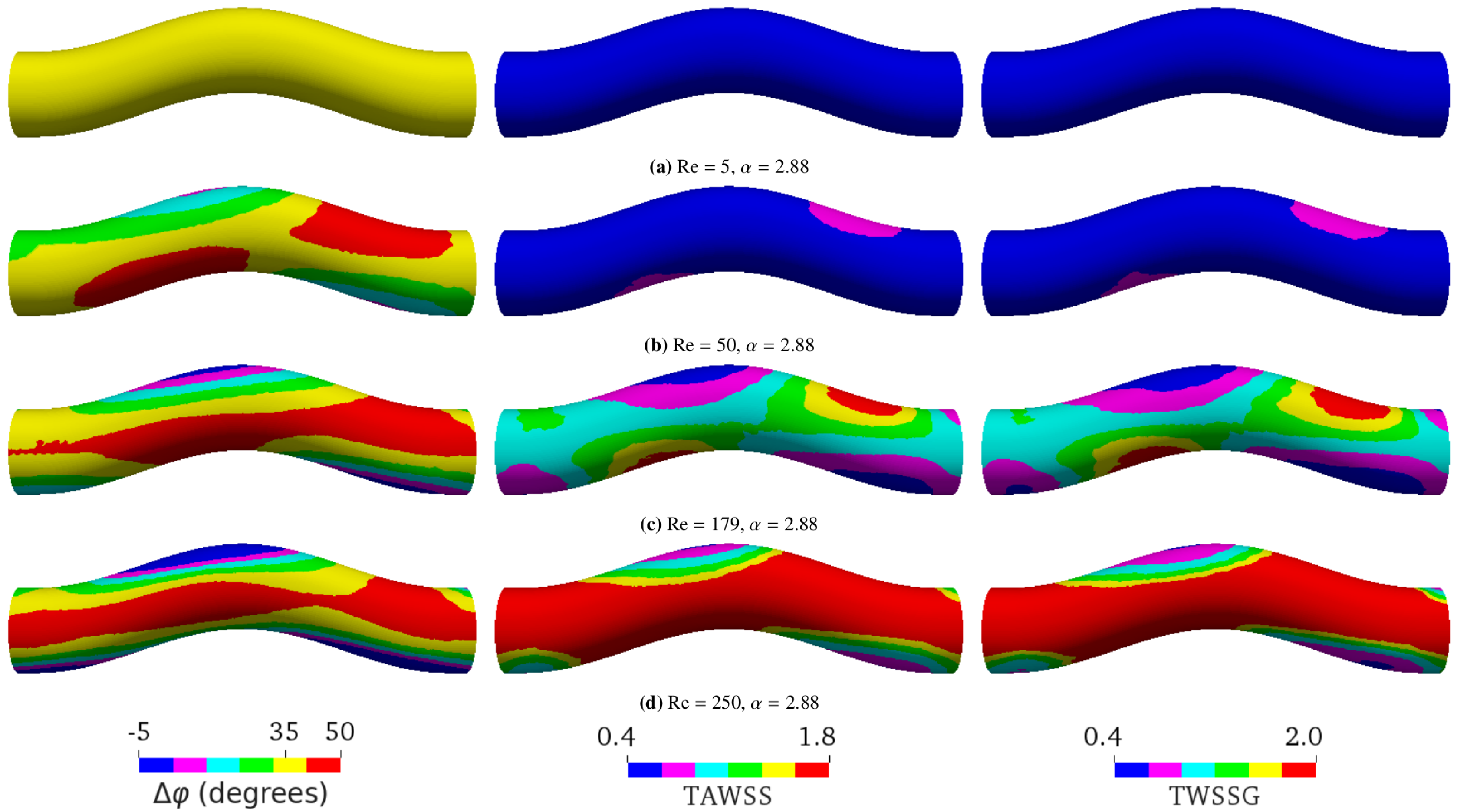
- Varying only Re by altering the flow speed via the amplitude of the pressure gradient: Re = 5, 50, 179, or 250 as a result of changing the average flow velocity to 0.00475 m/s, 0.0475 m/s, 0.17 m/s, or 0.2375 m/s, respectively (see Figure 5);
5.2. Varying Flow Properties in a Curved Tube without Aneurysm
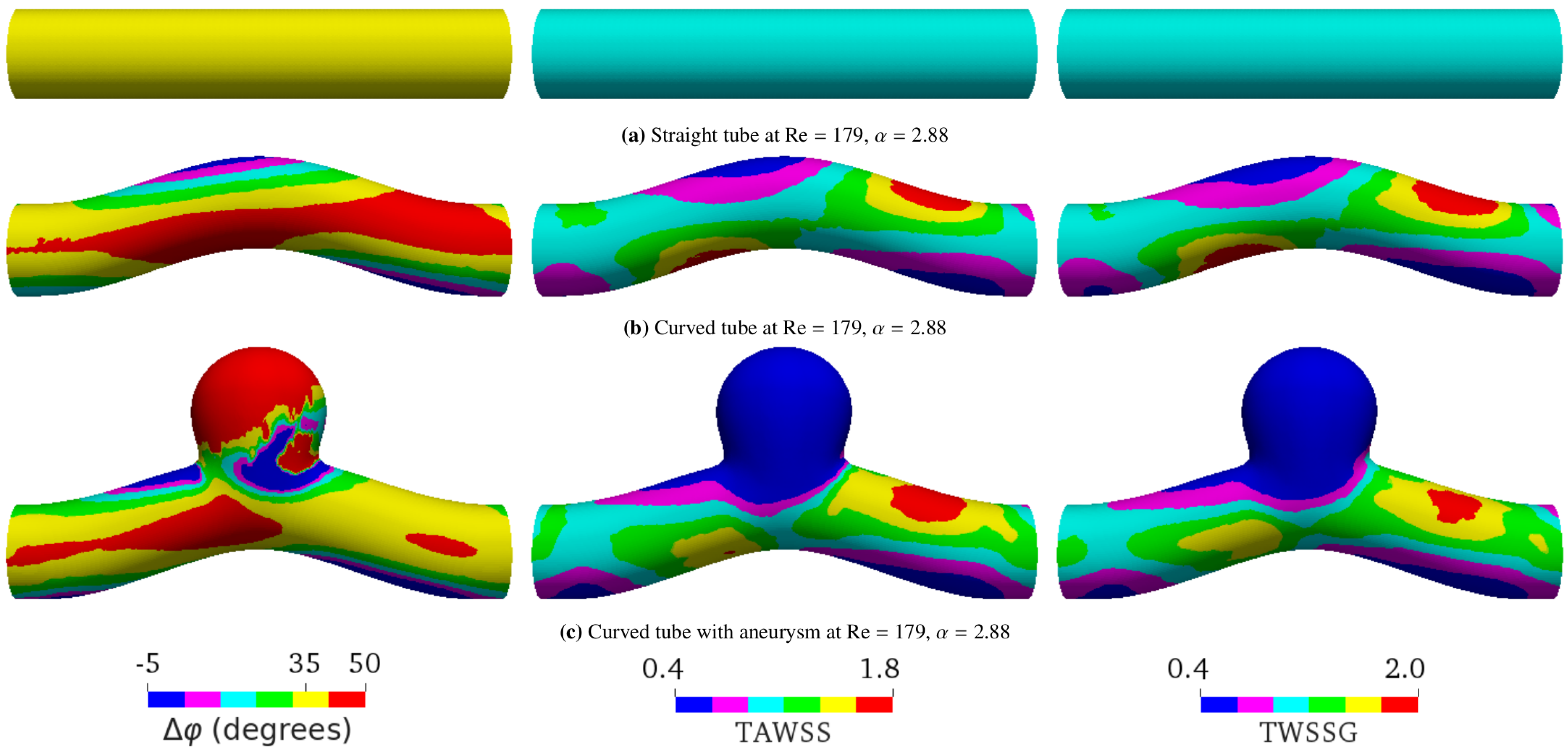
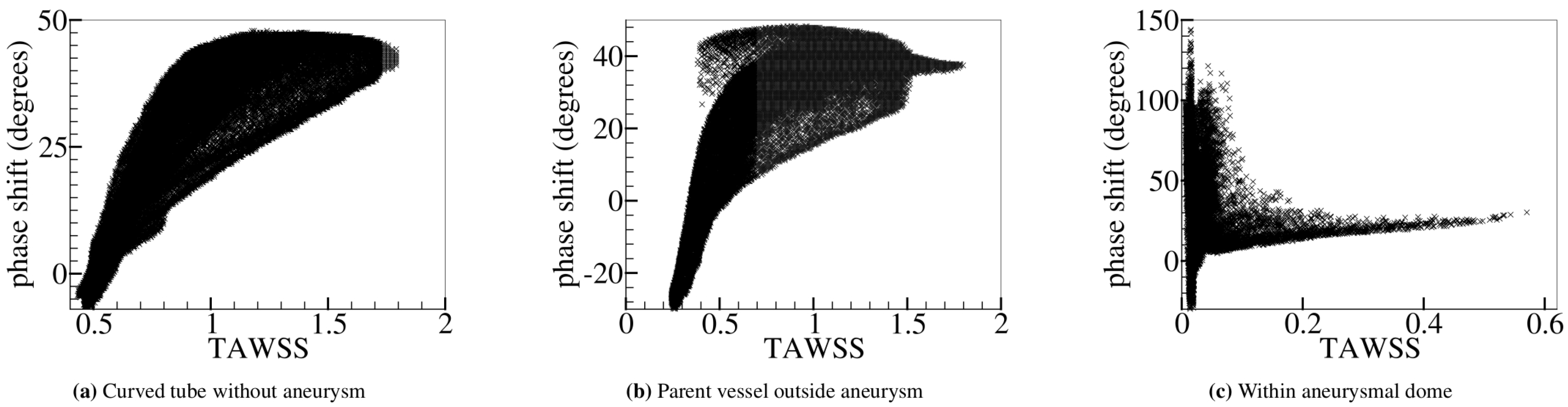
5.3. Curved Tube with Aneurysm
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Time Scales
References
- World Health Organization, Regional Office for Europe. Global atlas on Cardiovascular Disease Prevention and Control: Published by the World Health Organization in Collaboration with the World Heart Federation and the World Stroke Organization; World Health Organization, Regional Office for Europe: Copenhagen, Denmark, 2011; 155p. [Google Scholar]
- Tateshima, S.; Tanishita, K.; Omura, H.; Sayre, J.; Villablanca, J.; Martin, N.; Vinuela, F. Intra-aneurysmal hemodynamics in a large middle cerebral artery aneurysm with wall atherosclerosis. Surg. Neurol. 2008, 70, 454–462. [Google Scholar] [CrossRef]
- Yang, J.; Cui, C.; Wu, C. Cerebrovascular hemodynamics in patients with cerebral arteriosclerosis. Neural Regen. Res. 2011, 6, 2532–2536. [Google Scholar]
- Sugiyama, S.; Niizuma, K.; Nakayama, T.; Shimizu, H.; Endo, H.; Inoue, T.; Fujimura, M.; Ohta, M.; Takahashi, A.; Tominaga, T. Relative residence time prolongation in intracranial aneurysms: A possible association with atherosclerosis. Neurosurgery 2013, 73, 767–776. [Google Scholar] [CrossRef]
- Bae, H.; Choi, J.; Kim, B.; Lee, K.; Shin, Y. Predictors of Atherosclerotic Change in Unruptured Intracranial Aneurysms and Parent Arteries During Clipping. World Neurosurg. 2019, 130, e338–e343. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, K.; Gotlieb, A. The role of shear stress in the pathogenesis of atherosclerosis. Lab. Investig. 2005, 85, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Chiu, J.J.; Usami, S.; Chien, S. Vascular endothelial responses to altered shear stress: Pathologic implications for atherosclerosis. Ann. Med. 2009, 41, 19–28. [Google Scholar] [CrossRef]
- Evans, P.; Kwak, B. Biomechanical factors in cardiovascular disease. Cardiovasc. Res. 2013, 99, 229–231. [Google Scholar] [CrossRef]
- Steinman, D.; Thomas, J.; Ladak, H.; Milner, J.; Rutt, B.; Spence, J. Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI. Magn. Reson. Med. 2002, 47, 149–159. [Google Scholar] [CrossRef]
- Joshi, A.; Leask, R.; Myers, J.; Ojha, M.; Butany, J.; Ethier, C. Intimal thickness is not associated with wall shear stress patterns in the human right coronary artery. Arterioscler. Thromb. Vasc. Biol. 2004, 24, 2408–2413. [Google Scholar] [CrossRef]
- Torii, R.; Wood, N.; Hadjiloizou, N.; Dowsey, A.; Wright, A.; Hughes, A.; Davies, J.; Francis, D.; Mayet, J.; Yang, G.; et al. Stress phase angle depicts differences in coronary artery hemodynamics due to changes in flow and geometry after percutaneous coronary intervention. Am. J. Physiol. Heart Circ. Physiol. 2009, 296, H765–H776. [Google Scholar] [CrossRef]
- Tarbell, J.; Shi, Z.; Dunn, J.; Jo, H. Fluid Mechanics, Arterial Disease, and Gene Expression. Annu. Rev. Fluid Mech. 2014, 46, 591–614. [Google Scholar] [CrossRef]
- Al-Rawi, M.; Al-Jumaily, A.; Lowe, A. Stress Phase Angle for Non-Invasive Diagnosis of Cardiovascular Diseases. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Proceedings (IMECE), Vancouver, BC, Canada, 12–18 November 2010; Volume 2, pp. 747–749. [Google Scholar] [CrossRef]
- Qiu, Y.; Tarbell, J. Interaction between wall shear stress and circumferential strain affects endothelial cell biochemical production. J. Vasc. Res. 2000, 37, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Makris, G.; Nicolaides, A.; Xu, X.; Geroulakos, G. Introduction to the biomechanics of carotid plaque pathogenesis and rupture: Review of the clinical evidence. Br. J. Radiol. 2010, 83, 729–735. [Google Scholar] [CrossRef]
- Sadeghi, M.; Shirani, E.; Tafazzoli-Shadpour, M.; Samaee, M. The effects of stenosis severity on the hemodynamic parameters-assessment of the correlation between stress phase angle and wall shear stress. J. Biomech. 2011, 44, 2614–2626. [Google Scholar] [CrossRef]
- Qiu, Y.; Tarbell, J. Numerical simulation of pulsatile flow in a compliant curved tube model of a coronary artery. J. Biomech. Eng. 2000, 122, 77–85. [Google Scholar] [CrossRef]
- Tada, S.; Tarbell, J. A Computational Study of Flow in a Compliant Carotid Bifurcation-Stress Phase Angle Correlation with Shear Stress. Ann. Biomed. Eng. 2005, 33, 1202–1212. [Google Scholar] [CrossRef] [PubMed]
- Dancu, M.; Tarbell, J. Large Negative Stress Phase Angle (SPA) attenuates nitric oxide production in bovine aortic endothelial cells. J. Biomech. Eng. 2006, 128, 329–334. [Google Scholar] [CrossRef]
- Samaee, M.; Tafazzoli-Shadpour, M.; Alavi, H. Coupling of shear-circumferential stress pulses investigation through stress phase angle in FSI models of stenotic artery using experimental data. Med. Biol. Eng. Comput. 2017, 55, 1147–1162. [Google Scholar] [CrossRef] [PubMed]
- Maul, T.; Chew, D.; Nieponice, A.; Vorp, D. Mechanical stimuli differentially control stem cell behavior: Morphology, proliferation, and differentiation. Biomech. Model. Mechanobiol. 2011, 10, 939–953. [Google Scholar] [CrossRef]
- Owatverot, T.; Oswald, S.; Chen, Y.; Wille, J.; Yin, F. Effect of combined cyclic stretch and fluid shear stress on endothelial cell morphological responses. J. Biomech. Eng. 2005, 127, 374. [Google Scholar] [CrossRef]
- Tada, S.; Dong, C.; Tarbell, J. Effect of the Stress Phase Angle on the Strain Energy Density of the Endothelial Plasma Membrane. Biophys. J. 2007, 93, 3026–3033. [Google Scholar] [CrossRef]
- Shojaei, S.; Tafazzoli-Shadpour, M.; Shokrgozar, M.; Haghighipour, N.; Jahromi, F. Stress phase angle regulates differentiation of human adipose-derived stem cells toward endothelial phenotype. Prog. Biomater. 2018, 7, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Amaya, R.; Pierides, A.; Tarbell, J. The Interaction between Fluid Wall Shear Stress and Solid Circumferential Strain Affects Endothelial Gene Expression. PLoS ONE 2015, 10, e0129952. [Google Scholar] [CrossRef]
- Amaya, R.; Cancel, L.; Tarbell, J. Interaction between the Stress Phase Angle (SPA) and the Oscillatory Shear Index (OSI) Affects Endothelial Cell Gene Expression. PLoS ONE 2016, 11, e0166569. [Google Scholar] [CrossRef]
- Hahn, C.; Schwartz, M. Mechanotransduction in vascular physiology and atherogenesis. Nat. Rev. Mol. Cell Biol. 2009, 10, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Harloff, A.; Nussbaumer, A.; Bauer, S.; Stalder, A.; Frydrychowicz, A.; Weiller, C.; Hennig, J.; Markl, M. In vivo assessment of wall shear stress in the atherosclerotic aorta using flow-sensitive 4D MRI. Magn. Reson. Med. 2010, 63, 1529–1536. [Google Scholar] [CrossRef]
- Hoogendoorn, A.; Kok, A.M.; Hartman, E.M.J.; de Nisco, G.; Casadonte, L.; Chiastra, C.; Coenen, A.; Korteland, S.A.; Van der Heiden, K.; Gijsen, F.J.H.; et al. Multidirectional wall shear stress promotes advanced coronary plaque development: Comparing five shear stress metrics. Cardiovasc. Res. 2019, 116, 1136–1146. [Google Scholar] [CrossRef] [PubMed]
- Gaudio, L.; Veltri, P.; De Rosa, S.; Indolfi, C.; Fragomeni, G. Model and Application to Support the Coronary Artery Diseases (CAD): Development and Testing. Interdiscip. Sci. Comput. Life Sci. 2020, 12, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Ojha, M. Wall shear stress temporal gradient and anastomotic intimal hyperplasia. Circ Res. 1994, 74, 1227–1231. [Google Scholar] [CrossRef] [PubMed]
- White, C.; Haidekker, M.; Bao, X.; Frangos, J. Temporal Gradients in Shear, but Not Spatial Gradients, Stimulate Endothelial Cell Proliferation. Circulation 2001, 103, 2508–2513. [Google Scholar] [CrossRef] [PubMed]
- Younis, H.; Kaazempur-Mofrad, M.; Chan, R.; Isasi, A.; Hinton, D.; Chau, A.; Kim, L.; Kamm, R. Hemodynamics and wall mechanics in human carotid bifurcation and its consequences for atherogenesis: Investigation of interindividual variation. Biomech. Model. Mechanobiol. 2004, 3, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi Ardakani, V.; Tu, X.; Gambaruto, A.M.; Velho, I.; Tiago, J.; Sequeira, A.; Pereira, R. Near-Wall Flow in Cerebral Aneurysms. Fluids 2019, 4, 89. [Google Scholar] [CrossRef]
- Carvalho, V.; Carneiro, F.; Ferreira, A.C.; Gama, V.; Teixeira, J.C.; Teixeira, S. Numerical Study of the Unsteady Flow in Simplified and Realistic Iliac Bifurcation Models. Fluids 2021, 6, 284. [Google Scholar] [CrossRef]
- Krüger, T.; Gross, M.; Raabe, D.; Varnik, F. Crossover from tumbling to tank-treading-like motion in dense simulated suspensions of red blood cells. Soft Matter 2013, 9, 9008–9015. [Google Scholar] [CrossRef]
- Pasculli, A. Viscosity Variability Impact on 2D Laminar and Turbulent Poiseuille Velocity Profiles; Characteristic-Based Split (CBS) Stabilization. In Proceedings of the 2018 5th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Corfu, Greece, 25–27 August 2018; Volume 1, pp. 128–134. [Google Scholar] [CrossRef]
- Warriner, R.; Johnston, K.; Cobbold, R. A viscoelastic model of arterial wall motion in pulsatile flow: Implications for Doppler ultrasound clutter assessment. Physiol. Meas. 2008, 29, 157–179. [Google Scholar] [CrossRef] [PubMed]
- Okada, K.; Yamaguchi, R. Structure of pulsatile flow in a model of elastic cerebral aneurysm. J. Biorheol. 2011, 25, 1–7. [Google Scholar] [CrossRef]
- Lee, C.; Zhang, Y.; Takao, H.; Murayama, Y.; Qian, Y. A fluid-structure interaction study using patient-specific ruptured and unruptured aneurysm: The effect of aneurysm morphology, hypertension and elasticity. J. Biomech. 2013, 46, 2402–2410. [Google Scholar] [CrossRef]
- Yamaguchi, R.; Tanaka, G.; Liu, H. Effect of Elasticity on Flow Characteristics Inside Intracranial Aneurysms. Int. J. Neurol. Neurother. 2016, 3, 049. [Google Scholar] [CrossRef]
- Diehl, R.; Linde, D.; Lücke, D.; Berlit, P. Phase relationship between cerebral blood flow velocity and blood pressure: A clinical test of autoregulation. Stroke 1995, 26, 1801–1804. [Google Scholar] [CrossRef]
- Niu, L.; Meng, L.; Xu, L.; Liu, J.; Wang, Q.; Xiao, Y.; Qian, M.; Zheng, H. Stress phase angle depicts differences in arterial stiffness: Phantom and in vivo study. Phys. Med. Biol. 2015, 60, 4281–4294. [Google Scholar] [CrossRef]
- He, X.; Ku, D. Pulsatile flow in the human left coronary artery bifurcation: Average conditions. J. Biomech. Eng. 1996, 118, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Lallemand, P.; Luo, L. Theory of the Lattice Boltzmann Method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Peskin, C.S. The Immersed Boundary Method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Krüger, T.; Varnik, F.; Raabe, D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 2011, 61, 3485–3505. [Google Scholar] [CrossRef]
- Gross, M.; Krüger, T.; Varnik, F. Fluctuations and diffusion in sheared athermal suspensions of deformable particles. EPL (Europhys. Lett.) 2014, 108, 68006. [Google Scholar] [CrossRef][Green Version]
- Gross, M.; Krüger, T.; Varnik, F. Rheology of dense suspensions of elastic capsules: Normal stresses, yield stress, jamming and confinement effects. Soft Matter 2014, 10, 4360–4372. [Google Scholar] [CrossRef]
- Wang, H.; Krüger, T.; Varnik, F. Effects of size and elasticity on the relation between flow velocity and wall shear stress in side-wall aneurysms: A lattice Boltzmann-based computer simulation study. PLoS ONE 2020, 15, e0227770. [Google Scholar] [CrossRef]
- Zhang, J.; Kwok, D. Pressure boundary condition of the lattice Boltzmann method for fully developed periodic flows. Phys. Rev. E 2006, 73, 047702. [Google Scholar] [CrossRef]
- Uchida, S. The pulsating viscous flow superposed on the steady laminar motion of incompressible fluid in a circular pipe. J. Appl. Math. Phys. (ZAMP) 1956, 7, 403–422. [Google Scholar] [CrossRef]
- Womersley, J. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- Dean, W. The streamline motion of fluid in a curved pipe. Philos. Mag. 1928, 5, 673–695. [Google Scholar] [CrossRef]

| T | |||
|---|---|---|---|
| 1.02 | 262,492 | 0.012 | |
| 1.52 | 119,314 | 0.012 | |
| 2.06 | 64,494 | 0.012 | |
| 2.54 | 153,393 | 0.0033 | |
| 2.88 | 119,409 | 0.0033 |
| Physical | Simulation | ||
|---|---|---|---|
| Variable | Units | Units | |
| Radius | R | 2.0 mm | 22.9 |
| Viscosity | 4 mPa s | 0.0033 | |
| Density | 1.055 g/cm3 | 1.0 | |
| Period | T | 0.8 s | 119,409 |
| Pressure gradient | 1357 Pa/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Krüger, T.; Varnik, F. Geometry and Flow Properties Affect the Phase Shift between Pressure and Shear Stress Waves in Blood Vessels. Fluids 2021, 6, 378. https://doi.org/10.3390/fluids6110378
Wang H, Krüger T, Varnik F. Geometry and Flow Properties Affect the Phase Shift between Pressure and Shear Stress Waves in Blood Vessels. Fluids. 2021; 6(11):378. https://doi.org/10.3390/fluids6110378
Chicago/Turabian StyleWang, Haifeng, Timm Krüger, and Fathollah Varnik. 2021. "Geometry and Flow Properties Affect the Phase Shift between Pressure and Shear Stress Waves in Blood Vessels" Fluids 6, no. 11: 378. https://doi.org/10.3390/fluids6110378
APA StyleWang, H., Krüger, T., & Varnik, F. (2021). Geometry and Flow Properties Affect the Phase Shift between Pressure and Shear Stress Waves in Blood Vessels. Fluids, 6(11), 378. https://doi.org/10.3390/fluids6110378






