Abstract
Continuous interest in space journeys opens the research fields, which might be useful in non-terrestrial conditions. Due to the lack of the gravitational force, there will be a need to force the flow for mixing or heat transfer. Strong magnetic field offers the conditions, which can help to obtain the flow. In light of this origin, presented paper discusses the dually modified Graetz-Brinkman problem. The modifications were related to the presence of the magnetic field influencing the flow and asymmetrical thermal boundary condition. Dimensionless numerical analysis was performed, and two dimensionless numbers (magnetic Grashof number and magnetic Richardson number) were defined for paramagnetic fluid flow. The results revealed the heat transfer enhancement due to the strong magnetic field influence accompanied by possible but not essential flow structure modifications. On the other hand, the flow structure changes can be utilized to prevent the solid particles’ sedimentation. The explanation of the heat transfer enhancement including energy budget and vorticity distribution was presented.
1. Introduction
The heat transfer enhancement methods are divided into passive and active ones. Utilization of passive methods always requires interference with the existing system geometry or material properties. However, this approach is usually justified economically because the costs are mostly carried at the initial stage. On the other hand, active methods require an additional and regularly supplied energy source in order to improve system performance, therefore they are less welcomed, but in the reasonable cases, the operational costs do not matter.
Thermo-magnetic convection of weakly magnetic fluids is an example of active method application, which requires an energy transported by electric current. The state-of-the-art dedicated solutions still seem to be impaired by this fact and are practically excluded from the engineering applications. However, the field that combines both the solution for large power supply problem and the need for significant heat transfer enhancement, can be easily determined. In the time of space race restarted again, the utilization of the strong magnetic field reveals itself as a useful approach.
The first papers considering the possibility of heat transfer enhancement for the natural convection phenomenon of weakly magnetic (para- and dia-magnetic) fluids appeared in the early 1990s’ []. The numerical approach for dia- [] and para-magnetic [] materials’ thermo-magnetic convection was presented about 10 years later. These two papers also contained the derivation of dimensionless conservation equations dedicated to the problem of thermo-magnetic convection. After that, numerical and experimental comparisons were presented, i.e., in References [,,].
The studies dedicated to the thermo-magnetic convection phenomena have expanded since then, combined with different branches of science, and reached new methodologies. The combination of active (magnetic field) and passive (addition of nanoparticles) heat transfer enhancement methods was reported in References [,]. The studies considering thermo-magnetic convection in rectangular cavities of various aspect ratios were presented in Reference []. In Reference [], the application of the Lattice-Boltzmann method for thermo-magnetic convection mathematical description was proposed. The presentation of the passive magnetic heat transfer enhancement method, thermo-magnetic convection under no gravity conditions and the magnetic damping effect on the sloshing of liquid paramagnetic substances were studied in References [,,] and Reference []. The issue of resonant enhancement in an enclosure filled with paramagnetic fluid due to the time-periodic magnetizing force was presented in Reference []. The authors of Reference [] presented the application example of the cooling system driven by waste heat and permanent magnets only.
An overview of the investigations mentioned in the previous paragraph leads to the conclusion that the researchers focused mostly on the topic of thermo-magnetic convection in the closed cavities, with no artificially driven flow. The topic of forced convection of paramagnetic fluid under the influence of a strong magnetic field was firstly presented by Ozoe []. He was followed by the authors, who undertook his work, in References [,].
The presented paper is dedicated to the modified Graetz-Brinkman (G-B) problem [] and provides further information considering heat transfer and flow structure modifications due to the strong magnetic field in forced convection of paramagnetic fluid. The dimensionless mathematical model of the defined problem was discussed. Its construction led to a formulation of two dimensionless numbers (namely magnetic Grashof number and magnetic Richardson number) for paramagnetic fluid flow. These parameters play an essential role in the description of the discussed phenomena. The studies are aimed not only at the heat transfer intensification, but also possible interference in the flow structure. That is why the asymmetrical boundary conditions were applied. In reality, the non-symmetrical flow structure can prevent sedimentation of some solid particles carried by the flow, for example when considering the nanofluid flow. The explanation of the heat transfer enhancement occurrence is presented with the usage of energy budget and distribution of the magnetically modified vorticity.
2. Materials and Methods
2.1. Mathematical Model
2.1.1. Important Dimensionless Parameters
The following formula describes Reynolds (Re) number:
where: —reference velocity (average inlet velocity) (m/s), —pipe diameter (m), and —kinematic viscosity (m2/s).
The Prandtl number was represented by the following expression:
where: —thermal diffusivity (m2/s).
The Grashof number definition took the form:
where: —gravitational acceleration (m/s2), —thermal expansion coefficient (1/K), —heated wall temperature (K), and —inlet fluid temperature (K).
The magnetic Grashof number (for which derivation is presented later on) was defined as:
where: —reference density (kg/m3), —reference temperature ( (K), —reference volumetric magnetic susceptibility (-), —magnetic induction in the center of the coil () (T), —electrical current (A), —coil diameter (m), and —magnetic permeability of the vacuum (H/m).
The Richardson number formula was utilized in the following form:
The magnetic Richardson number formula could be written as:
The following definition described the Nusselt number:
where: —convective heat transfer coefficient ( (W/(m2K)), —area weighted value of the heat flux over heated wall small axial subsection (W/m2), —fluid bulk temperature (K), and —thermal conductivity (W/(mK)).
The process of local heat transfer coefficient calculation value was as follows: (1) Calculation of the bulk fluid temperature () over cross-section at the XY plane (perpendicular to pipe axis), (2) calculation of the heat flux value (q) over corresponding heated wall small axial subsection, and (3) its substitution into . In practice, the area where the heat flux was calculated was the thin half-rings located around the subsequent XY cross-sections.
2.1.2. Dimensionless Conservation Equations
The following assumptions were included in the mathematical model:
- -
- Stationary flow,
- -
- Three-dimensional flow,
- -
- Laminar flow,
- -
- Incompressible flow,
- -
- No additional mass or energy sources,
- -
- The thermo-magnetic force was treated as the body force,
- -
- Constant values of thermo-physical properties,
- -
- Paramagnetic and electrically non-conductive fluid.
Taking into account the above-mentioned assumptions, the dimensionless mass conservation equation could be presented as follows:
The following equation presents the dimensional momentum conservation equation for the studied phenomena:
The necessary dimensionless variables are presented as follows:
where: —dimensionless flow velocity vector (-), —dimensionless pressure (-), —dimensionless temperature (-), —dimensionless density (-), —dimensionless magnetic induction vector (-), —flow velocity vector (m/s), —reference velocity ( (m/s), —pressure (Pa), —reference pressure ( (Pa), —fluid density (kg/m3), —magnetic induction vector (T), —dimensionless density (-), N—dimensionless kinematic viscosity (-), —reference kinematic viscosity (m2/s), —dimensionless thermal expansion coefficient (-), —reference thermal expansion coefficient (1/K), G—dimensionless gravitational acceleration (-), and —reference gravitational acceleration (m/s2).
Substituting into Equation (9) gives:
After basic transformations:
The dimensionless momentum conservation equation took the form of:
Taking into consideration constant values of viscosity, thermal expansion coefficient, gravitational acceleration, and density, the final form of the dimensionless conservation equation is presented as follows:
Considering the low value of pyromagnetic coefficient and the previous assumptions, the dimensionless energy conservation equation was formulated as:
2.1.3. Biot-Savart Law
In order to calculate dimensionless magnetic induction distribution, the Biot-Savart law in the following form was utilized []:
where: —infinitely small element of the coil (m), and r—position vector (m).
2.1.4. Energy Budget
According to Equation (15), the energy budget included two terms: convective and diffusive ones. The convective term equation was as follows:
while the diffusive term could be presented as follows:
2.2. The Studied Case
The dually modified G-B problem was the subject of the presented work. The studied case schematic view is presented in Figure 1. The geometry consisted of a straight circular channel oriented horizontally. Its wall was divided in halves, creating the inlet adiabatic zone and outlet isothermally heated zone. The wall of the second zone was also divided, creating the top heating wall and bottom heating wall. Division of the isothermally heated wall provided the possibility of applying the asymmetrical thermal boundary condition, which was the first classical G-B problem modification. The second modification referred to the presence of a single circular magnetic coil located around the junction between adiabatic and heated parts. The coil generated the magnetic field for the studied system. The flow was considered as laminar and fully developed at the inlet.

Figure 1.
The studied case with characteristic dimensionless parameters.
The following boundary conditions were applied:
- At the inlet: ; ,
- At the outlet: ,At the heated wall: ; ,
- At the adiabatic wall: ; ,
- In the center of the magnetic coil: .
Six cases of various material properties (represented by Prandtl number) and heating configuration (top, bottom) were studied. The flow characteristic was considered as laminar at Re = 200. The fluid was characterized by Pr = 0.7 (Prandtl number value for air), Pr = 10 (Prandtl number value for water with addition of the paramagnetic salt), and Pr = 100 (Prandtl number value for engine oil). Fluid magnetic properties and magnetic field strength were determined by Rim (Rim = 5). The gravitational buoyancy effect was considered low and represented by Ri (Ri = 0.025). The exemplary dimensional system and fluid properties are listed in Table 1.

Table 1.
Exemplary dimensional system and fluid properties for Pr = 0.7 (air) and Rim = 5.
2.3. Numerical Approach
A structured grid (Figure 2) containing 380,250 hexahedral cells was constructed. The minimum cell volume was set to 8.242648 × 10−7 m3, while the maximum value was 9.190577 × 10−5 m3, which gave the mean cell volume equal to 4.122598 × 10−5 m3. A two-step validation method was utilized in order to perform a grid sensitivity study. At the first step, several grid setups varying in radial division were compared to the analytical solution for a developed laminar flow velocity profile. The initial mesh for the second validation step was chosen on this basis. The second step was performed for the grids divided radially into 66 (basic grid from the previous step), 106, and 131 elements, and based on the comparison between velocity profiles obtained in the strong magnetic field environment. Finally, the grid divided radially into 106 elements was chosen as the further grid concentration, provided there were no significant changes in the velocity distribution (<<1%).
Figure 2.
The details of constructed mesh: (a) axial cross-section, (b) radial cross-section, (c) close-up of the pipe center.
The numerical computations were performed with the utilization of Ansys Fluent software (ACK Cyfronet AGH, Krakow, Poland). The solver was set to pressure-based segregated algorithm. The momentum and energy equations were solved with the usage of second-order upwind discretization schemes. The second-order scheme was utilized to solve the pressure equation. The built-in solver abilities were supplemented with number of user-defined functions and functionalities to obtain, i.e., dimensionless approach, magnetic force distribution, energy budget, or Nusselt number distribution (Figure 3).
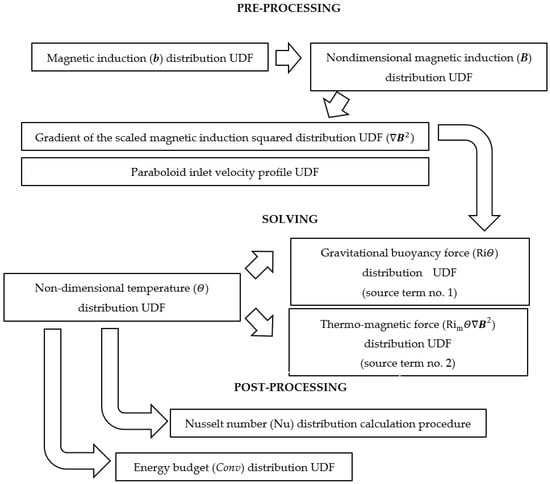
Figure 3.
User-defined functions implementation scheme.
3. Results and Discussion
Figure 4 presents dimensionless temperature distribution in the axial cross-section of the studied geometry. On each diagram, information about the fluid, heating zone configuration, presence of magnetic force, and value of Richardson number is shown. Additionally, four cross-sections, namely: 0.3, 0.7, 1.2, and 1.9, are indicated. They will be described later on. The difference between the results obtained for a case with the strong magnetic field influence and without it can be clearly seen only for a fluid characterized by Prandtl number value Pr = 0.7 (Figure 4a,b). The results obtained for the rest of the studied parameters (Figure 4c–f) characterized by Prandtl number values Pr = 10 and Pr = 100 showed no differences.
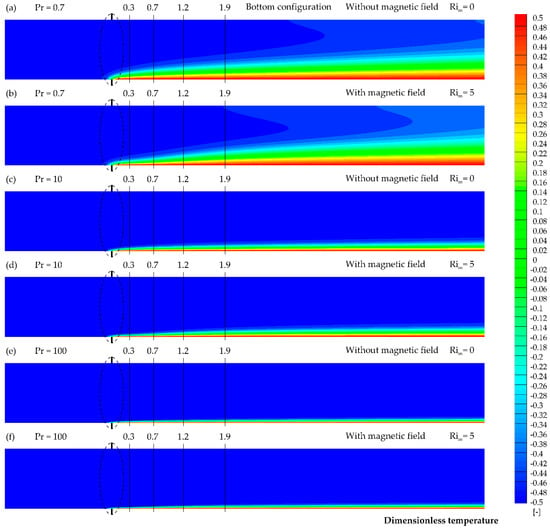
Figure 4.
Dimensionless temperature distribution in the axial cross-section for bottom configuration: (a) Pr = 0.7 and Rim = 0, (b) Pr = 0.7 and Rim = 5, (c) Pr = 10 and Rim = 0, (d) Pr = 10 and Rim = 5, (e) Pr = 100 and Rim = 0, (f) Pr = 100 and Rim = 5.
Figure 5 and Figure 6 present velocity fields under the strong magnetic field influence obtained for the bottom and top heating configurations. The flow in the first case (Pr = 0.7) visibly responded to the additional magnetic force effect. The flow structure lost its symmetry (Figure 5 and Figure 6a,d) and was attracted to the heated side of the wall. The small acceleration zone was observed between z = 0.7 and z = 1.2, in the vicinity of the heated area. However, the value of this acceleration is local in nature and did not exceed the maximal initial flow velocity. The magnetic force presented in the discussed results acted as a slowing down force. The low-velocity area near the adiabatic part of the wall was enlarged due to the fluid stream shifting towards the heated part. However, the flow asymmetrical structure was limited to the vertical direction. The horizontal cross-sections (Figure 5 and Figure 6b,c) showed symmetry of the velocity field with respect to the YZ plane. What is more, the structures obtained for the cross-section located in the XZ (horizontal) (Figure 5 and Figure 6b) plane and for the cross-section parallel and below to this plane (Figure 5 and Figure 6b) were similar to the M-shaped flow structure presented in References [,].
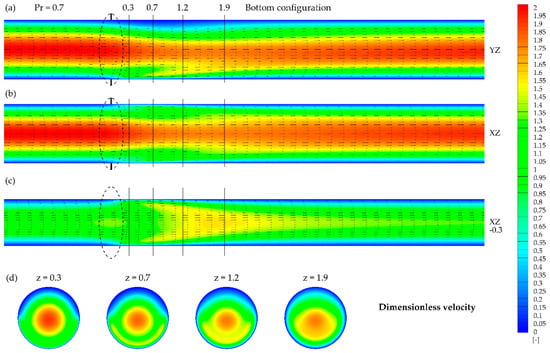
Figure 5.
Dimensionless velocity contours and vectors obtained for Pr = 0.7 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
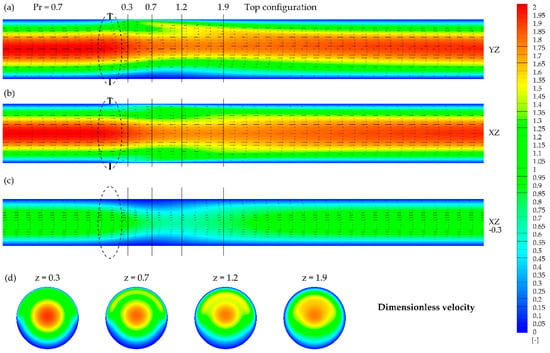
Figure 6.
Dimensionless velocity contours and vectors obtained for Pr = 0.7 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
Increasing the value of the Prandtl number up to Pr = 10 led to a significant reduction of visible magnetic field interference with the flow structure (Figure 7 and Figure 8). The fluid stream was slightly shifted towards the heated wall, which can be seen on the axial cross-sections (Figure 7 and Figure 8a). Additionally, a narrowing of the hydrodynamic boundary layer might be observed between the cross-sections z = 0.3 and z = 1.2 (Figure 7 and Figure 8b–d).
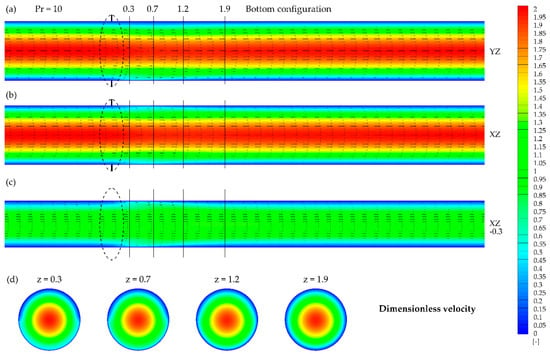
Figure 7.
Dimensionless velocity contours and vectors obtained for Pr = 10 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
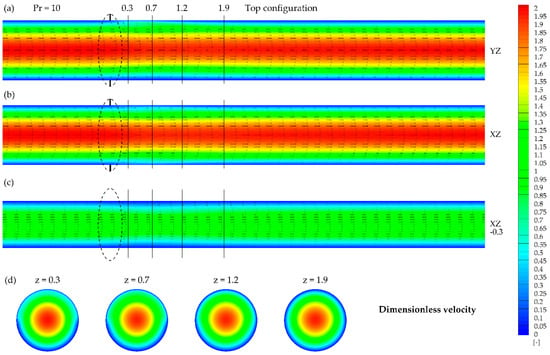
Figure 8.
Dimensionless velocity contours and vectors obtained for Pr = 10 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
Figure 9 and Figure 10 show results obtained for the fluid characterized by Pr = 100. The velocity field seemed to be intact by the presence of the magnetic field and preserved its paraboloid shape. Nevertheless, the heat transfer in this case was influenced, which will be discussed further.
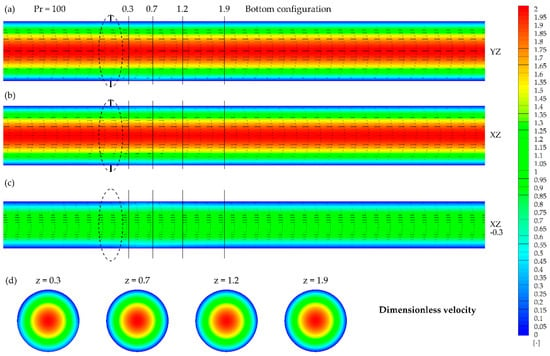
Figure 9.
Dimensionless velocity contours and vectors obtained for Pr = 100 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
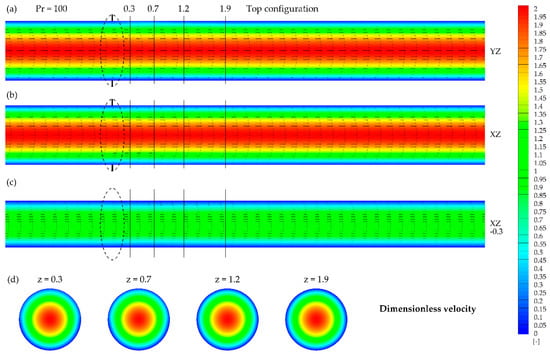
Figure 10.
Dimensionless velocity contours and vectors obtained for Pr = 100 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
Velocity fields, obtained for each Prandtl number value considering bottom and top configurations, mirrored each other with respect to the XZ plane with the slight discrepancies between them. These discrepancies (Figure 5 and Figure 6a) are considered to be an effect of gravitational buoyancy force impact.
An influence of the strong magnetic field on the heat transfer and its enhancement is exhibited in Figure 11. For every studied case, a local increase of Nusselt number value was observed for the flows in the magnetic field with respect to the flows without it. The area affected by this influence was always located between approximately z = 0 and z = 2. From the global point of view, this local change led to an increase in the heat transfer rate. Table 2 presents the percentage increase in average Nusselt number value for the corresponding cases (with and without the magnetic field). The values obtained for bottom and top configurations were slightly different for Pr = 0.7 and Pr = 10, but without a clear tendency. This subject requires further studies. Increase in the Nusselt number value varied from about 24% for Pr = 0.7 to 9% for Pr = 100.
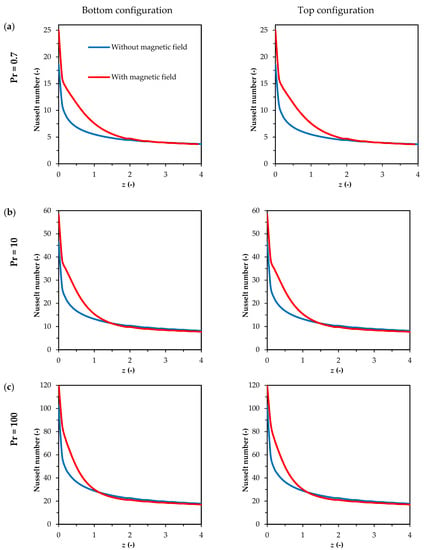
Figure 11.
Nusselt number distribution for the cases without and with the magnetic field influence for: (a) Pr = 0.7, (b) Pr = 10, (c) Pr = 100.

Table 2.
Percentage increase in average Nusselt number value for the studied cases.
Energy budget calculated for the four cross-sections perpendicular to the flow axis (corresponding with the cross-sections shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) is presented in Figure 12. The budget was reduced to distribution of the convective term as it is equal to the diffusive term (see Equations (15), (17), and (18)). Distribution of the convective term influenced by the magnetic field was wider than distribution obtained for the case without the magnetic field. This tendency was observed for every studied case. However, increasing the distance from the magnetic field source (located at z = 0) reduced these disproportions. Difference between the maximum energy term values (obtained for Pr = 0.7) for the cases with and without magnetic field at the subsequent cross-sections are: 103% at z = 0.3 (Figure 12a), 72% at z = 0.7 (Figure 12b), 28% at z = 1.2 (Figure 12c), and 4% at z = 1.9 (Figure 12d). Energy budget explains the increase in Nusselt number for the flows under an influence of the strong magnetic field through increasing convective term value. This increment is strictly connected to the velocity and temperature field maldistribution due to the magnetic field effect (Equation (17)).
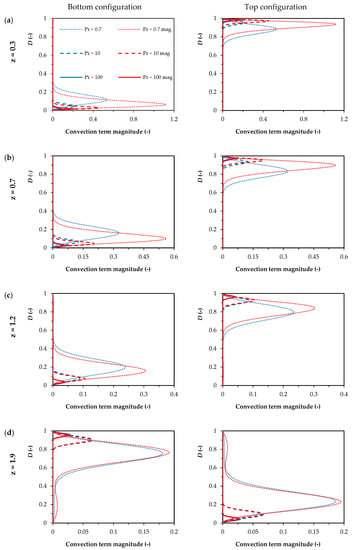
Figure 12.
Energy budget calculated for the radial cross-sections located at: (a) z = 0.3, (b) z = 0.7, (c) z = 1.2, (d) z = 1.9.
Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 present the dimensionless vorticity magnitude ( distribution for the studied cases in the cross-sections discussed previously (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10). The possible explanation for the increase in Nusselt number value despite the lack of interference of the magnetizing force with flow structure (Figure 9 and Figure 10) for Prandtl number value Pr = 100 is presented in Figure 17 and Figure 18, where the local change in vorticity near the heated wall can be observed. In all of the studied cases, the magnetic field might be considered as a vortex generator, which leads to the heat transfer enhancement. The vorticity distribution strongly depends on the Prandtl number value, similar to the velocity distribution.
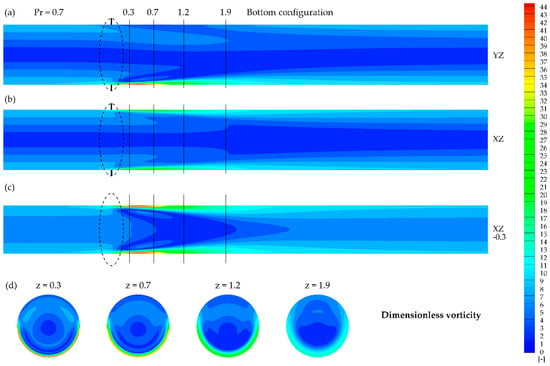
Figure 13.
Dimensionless vorticity contours obtained for Pr = 0.7 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
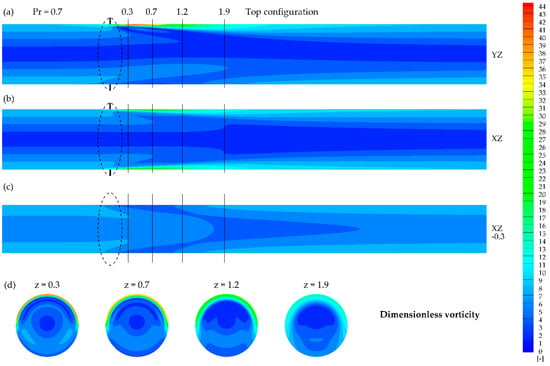
Figure 14.
Dimensionless vorticity contours obtained for Pr = 0.7 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
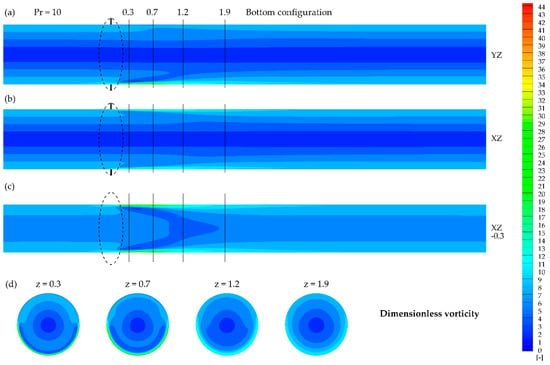
Figure 15.
Dimensionless vorticity contours obtained for Pr = 10 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
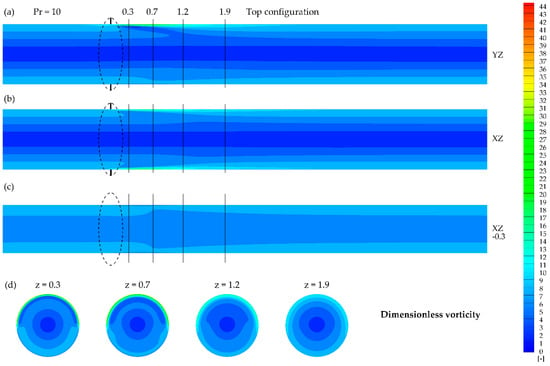
Figure 16.
Dimensionless vorticity contours obtained for Pr = 10 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
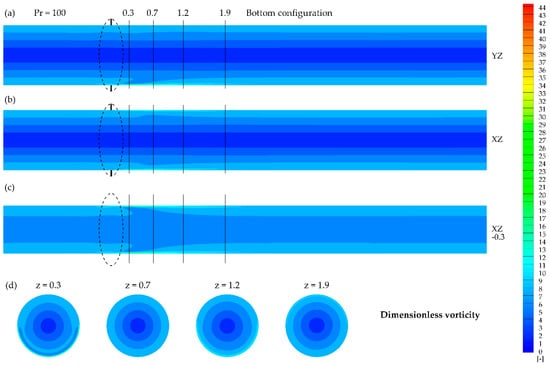
Figure 17.
Dimensionless vorticity contours obtained for Pr = 100 and bottom configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
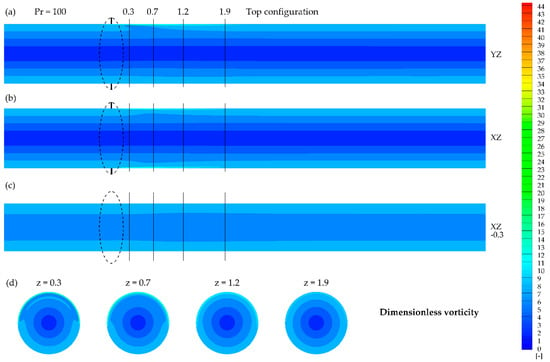
Figure 18.
Dimensionless vorticity contours obtained for Pr = 100 and top configuration in the presence of the magnetic field at: (a) YZ plane, (b) XZ plane, (c) XZ plane (y = −0.3), (d) XY planes at given z.
4. Conclusions
The dimensionless mathematical model for the given problem was proposed. It included formulation of two dimensionless parameters (namely magnetic Grashof and magnetic Richardson number), which are crucial for the simplification of the presented considerations and proper classification of magnetically altered flow of paramagnetic fluids in the future.
The presented results confirmed the magnetic field ability to enhance heat transfer also for the forced convection problems with asymmetrical thermal boundary condition. Magnetic field influence increased the Nusselt number value by the percentage of 9–24% (Table 2) depending on the fluid properties represented by the Prandtl number (0.7, 10, 100). For lower Prandtl number values, the higher ratio between the average Nusselt number for the cases with and without magnetic field was obtained. However, even for the Pr = 100, the heat transfer enhancement must be considered as at least interesting. The presented energy budget (Figure 12) explained the heat transfer enhancement with the increased value of convective term in the energy equation for the cases subjected to the strong magnetic field. What is more, the magnetic field enhanced the heat transfer despite the small (Pr = 10, Figure 7 and Figure 8) or even not clearly visible (Pr = 100, Figure 9 and Figure 10) interference with the flow structure, which can be explained by the still observed change in vorticity distribution (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18). This last conclusion seems to be useful in terms of heat transfer enhancement, while preserving the existing flow structure. However, when considering the reduction of sedimentation, only the flow with low Prandtl number value can be taken into account. In such case, the asymmetrical conditions might be helpful for nanofluid flow, where sediments can gather and throttle the flow.
Author Contributions
Conceptualization, E.F.-W. and L.P.; methodology, E.F.-W., L.P. and S.G.; software, L.P. and S.G.; validation, E.F.-W., L.P. and S.G.; formal analysis, L.P.; investigation, L.P.; resources, E.F.-W. and L.P.; data curation, L.P. and S.G.; writing—original draft preparation, E.F.-W. and L.P.; writing—review and editing, E.F.-W. and L.P.; visualization, L.P.; supervision, E.F.-W.; project administration, E.F.-W. and L.P.; funding acquisition, L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Polish Ministry of Science and Higher Education, Grant AGH No. 16.16.210.476.
Acknowledgments
This research was supported by the PL-Grid Infrastructure.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin symbols | |
| dimensionless magnetic induction vector ( ) (-) | |
| magnetic induction vector (T) | |
| Conv | convective term of energy equation (-) |
| D | dimensionless diameter (-) |
| diameter (m) | |
| Diff | diffusive term of energy equation (-) |
| infinitely small element of the coil (m) | |
| G | dimensionless gravitational acceleration (-) |
| gravitational acceleration (m/s2) | |
| Grashof number (-) | |
| convective heat transfer coefficient (W/(m2K)) | |
| electrical current (A) | |
| thermal conductivity (W/(mK)) | |
| dimensionless pipe length ( (-) | |
| pipe length (m) | |
| Nu | Nusselt number (-) |
| dimensionless pressure () (-) | |
| pressure (Pa) | |
| Prandtl number (-) | |
| q | heat flux magnitude (W/m2) |
| r | position vector (m) |
| Reynolds number (-) | |
| Ri | Richardson number (-) |
| T | temperature (K) |
| dimensionless flow velocity vector (, ) (-) | |
| flow velocity vector (m/s) | |
| u | velocity magnitude (m/s) |
| y | dimensionless radial distance (y-coordinate) (-) |
| dimensionless axial distance (z-coordinate) (-) | |
| Greek symbols | |
| thermal diffusivity (m2/s) | |
| thermal expansion coefficient (1/K) | |
| dimensionless thermal expansion coefficient (-) | |
| dimensionless temperature ( ) (-) | |
| N | dimensionless kinematic viscosity (-) |
| magnetic permeability (H/m) | |
| fluid kinematic viscosity (m2/s) | |
| density (kg/m3) | |
| dimensionless density () (-) | |
| volumetric magnetic susceptibility (-) | |
| dimensionless vorticity magnitude () (-) | |
| vorticity magnitude (1/s) | |
| Subscripts | |
| 0 | reference value |
| b | bulk |
| C | cold (inlet) fluid |
| center | center |
| coil | coil |
| f | fluid |
| H | heated (hot) wall |
| m | magnetic |
| max | maximal |
| n | normal |
| p | pipe |
| v | vacuum |
References
- Braithwaite, D.; Beaugnon, E.; Tournier, R. Magnetically controlled convection in a paramagnetic fluid. Nature 1991, 354, 134–136. [Google Scholar] [CrossRef]
- Tagawa, T.; Ujihara, A.; Ozoe, H. Numerical computation for Rayleigh–Benard convection of water in a magnetic field. Int. J. Heat Mass Transf. 2003, 46, 4097–4104. [Google Scholar] [CrossRef]
- Tagawa, T.; Shigemitsu, R.; Ozoe, H. Magnetizing force modeled and numerically solved for natural convection of air in a cubic enclosure: Effect of the direction of the magnetic field. Int. J. Heat Mass Transf. 2002, 45, 267–277. [Google Scholar] [CrossRef]
- Fornalik-Wajs, E.; Filar, P.; Wajs, J.; Roszko, A.; Pleskacz, L.; Ozoe, H. Flow structure, heat transfer and scaling analysis in the case of thermo-magnetic convection in a differentially heated cylindrical enclosure. In Proceedings of the Journal of Physics: Conference Series, Krakow, Poland, 15–18 June 2014; Volume 530. [Google Scholar]
- Wrobel, W.A.; Fornalik-Wajs, E.; Szmyd, J.S. Analysis of the influence of a strong magnetic field gradient on convection process of paramagnetic fluid in the annulus between horizontal concentric cylinders. J. Phys. Conf. Ser. 2012, 395, 012124. [Google Scholar] [CrossRef]
- Kenjereš, S.; Fornalik-Wajs, E.; Wrobel, W.; Szmyd, J.S. Inversion of flow and heat transfer of the paramagnetic fluid in a differentially heated cube. Int. J. Heat Mass Transf. 2020, 151, 119407. [Google Scholar] [CrossRef]
- Fornalik-Wajs, E.; Roszko, A.; Donizak, J.; Kraszewska, A. Comparison of the experimental and numerical analyses of silver nanofluid under influence of strong magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 3139–3162. [Google Scholar] [CrossRef]
- Fornalik-Wajs, E.; Roszko, A.; Donizak, J. Nanofluid flow driven by thermal and magnetic forces–Experimental and numerical studies. Energy 2020, 201, 117658. [Google Scholar] [CrossRef]
- Kraszewska, A.; Pyrda, L.; Donizak, J. Experimental analysis of enclosure aspect ratio influence on thermo-magnetic convection heat transfer. J. Phys. Conf. Ser. 2016, 745, 032153. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, H.; Ling, X. Lattice Boltzmann method for thermomagnetic convection and entropy generation of paramagnetic fluid in porous enclosure under magnetic quadrupole field. Int. J. Heat Mass Transf. 2018, 127, 224–236. [Google Scholar] [CrossRef]
- Wada, K.; Kaneda, M.; Suga, K. Rayleigh-Bénard convection of paramagnetic liquid under a magnetic field from permanent magnets. Symmetry 2020, 12, 341. [Google Scholar] [CrossRef]
- Kaneda, M.; Fujiwara, H.; Wada, K.; Suga, K. Natural convection of paramagnetic fluid along a vertical heated wall under a magnetic field from a single permanent magnet. J. Magn. Magn. Mater. 2020, 502, 166574. [Google Scholar] [CrossRef]
- Song, K.; Wu, S.; Tagawa, T.; Shi, W.; Zhao, S. Thermomagnetic convection of paramagnetic gas in an enclosure under no gravity condition. Fluids 2019, 4, 49. [Google Scholar] [CrossRef]
- Furuichi, Y.; Tagawa, T. Numerical study of the magnetic damping effect on the sloshing of liquid oxygen in a propellant tank. Fluids 2020, 5, 88. [Google Scholar] [CrossRef]
- He, W.; Qin, G.; Wen, X.; Lin, J.; Jia, C. Resonant enhancement of thermomagnetic convection of paramagnetic fluid in an enclosure due to time-periodic magnetizing force. Numer. Heat Transf. Part A Appl. 2020, 78, 1–17. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Automatic cooling by means of thermomagnetic phenomenon of magnetic nanofluid in a toroidal loop. Appl. Therm. Eng. 2016, 107, 700–708. [Google Scholar] [CrossRef]
- Ozoe, H. Magnetothermal wind tunnel. In Magnetic Convection, 1st ed.; Imperial College Press: London, UK, 2005; pp. 193–204. ISBN 10: 1-86094-578-3. [Google Scholar]
- Pleskacz, L.; Fornalik-Wajs, E. Low Reynolds number flow’s heat transfer influenced by strong magnetic field. J. Phys. Conf. Ser. 2016, 745, 032156. [Google Scholar] [CrossRef]
- Pleskacz, Ł.; Fornalik-Wajs, E. Identification of the structures for low Reynolds number flow in the strong magnetic field. Fluids 2019, 4, 36. [Google Scholar] [CrossRef]
- Graetz, L. Ueber die Wärmeleitungsfähigkeit von Flüssigkeiten. Ann. Phys. 1882, 254, 79–94. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).