Towards the Understanding of Humpback Whale Tubercles: Linear Stability Analysis of a Wavy Flat Plate
Abstract
1. Introduction
2. Materials and Methods
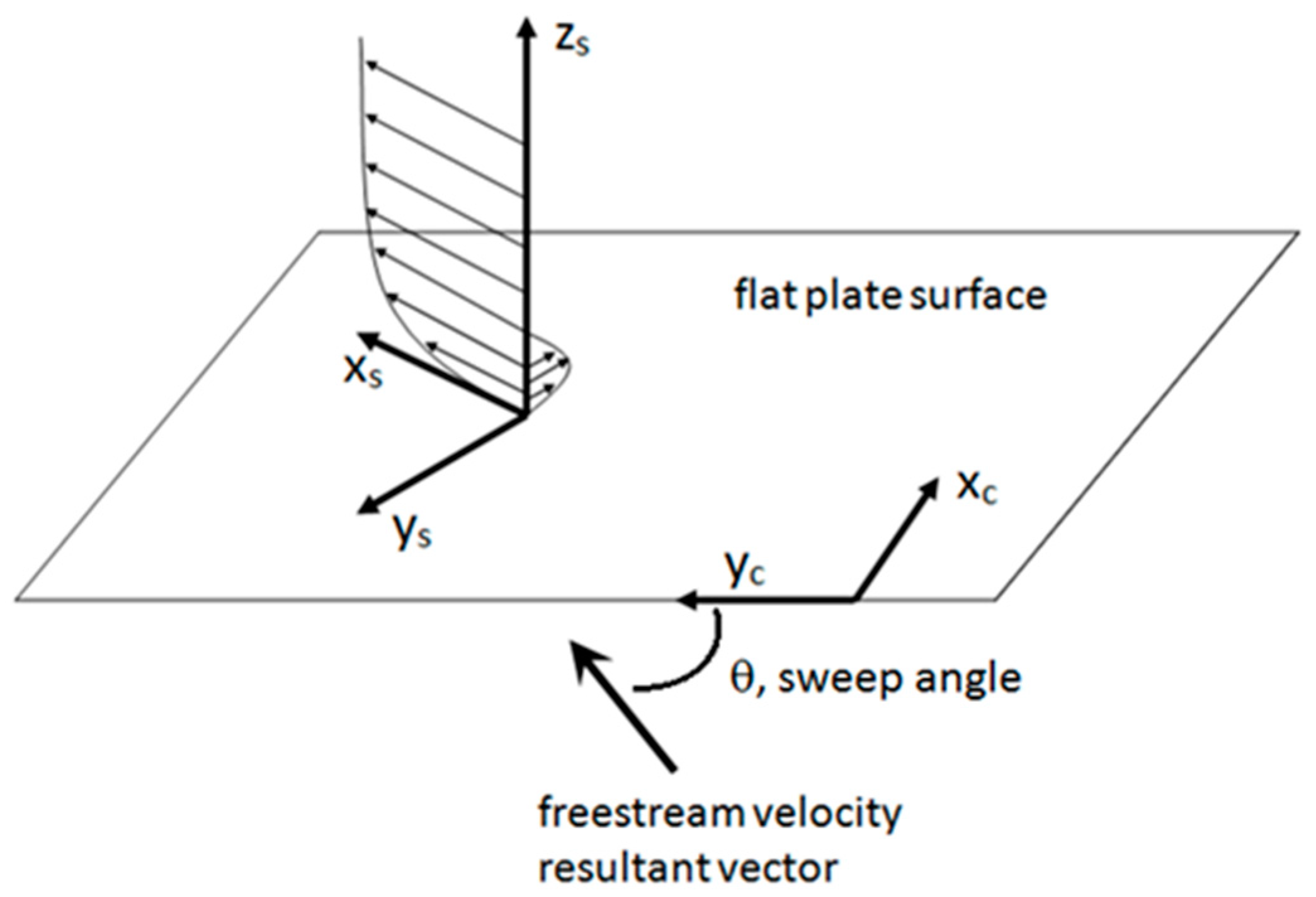
2.1. Geometry
2.2. Linear Stability Equations
2.3. Base Flow Models
3. Results
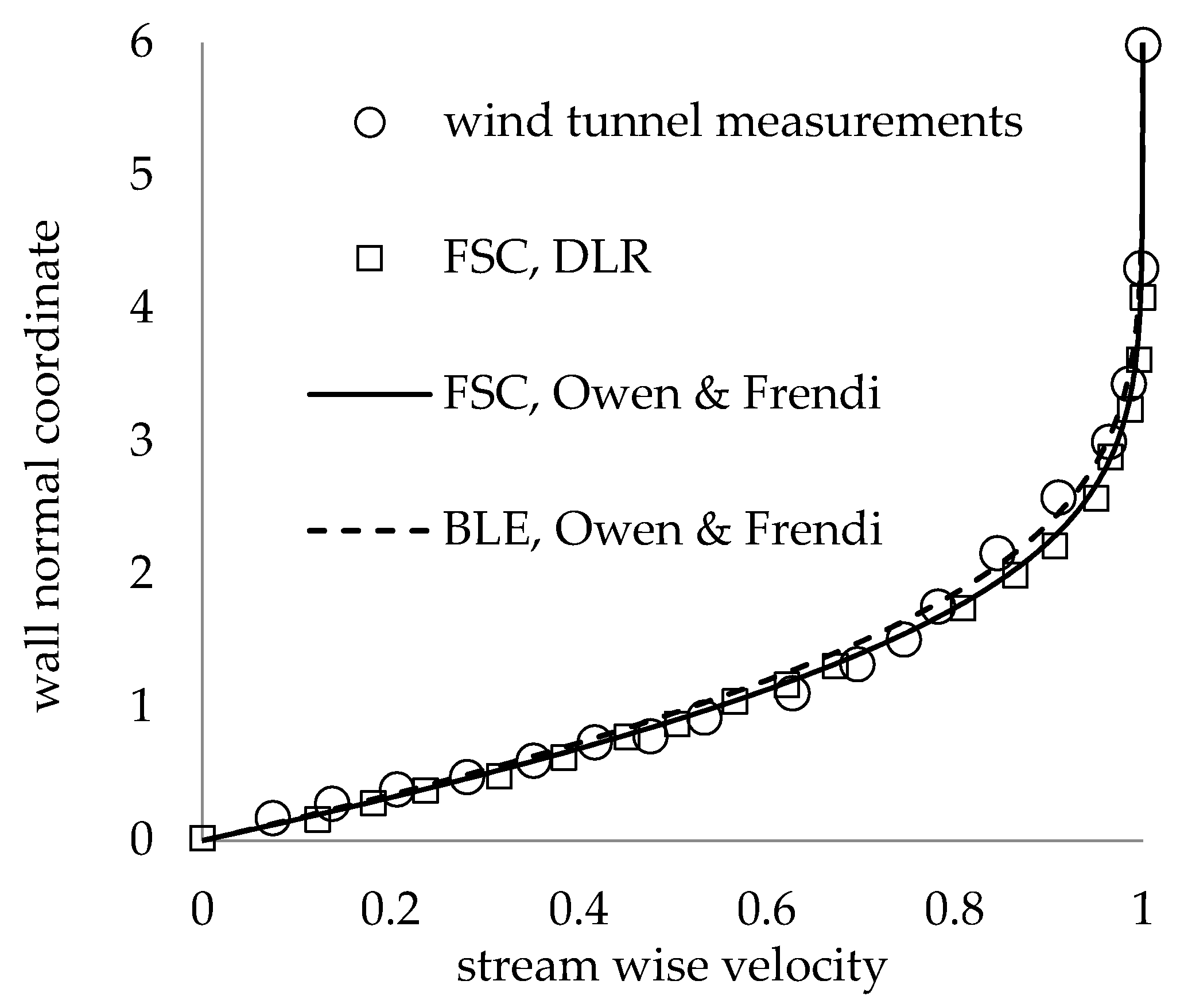
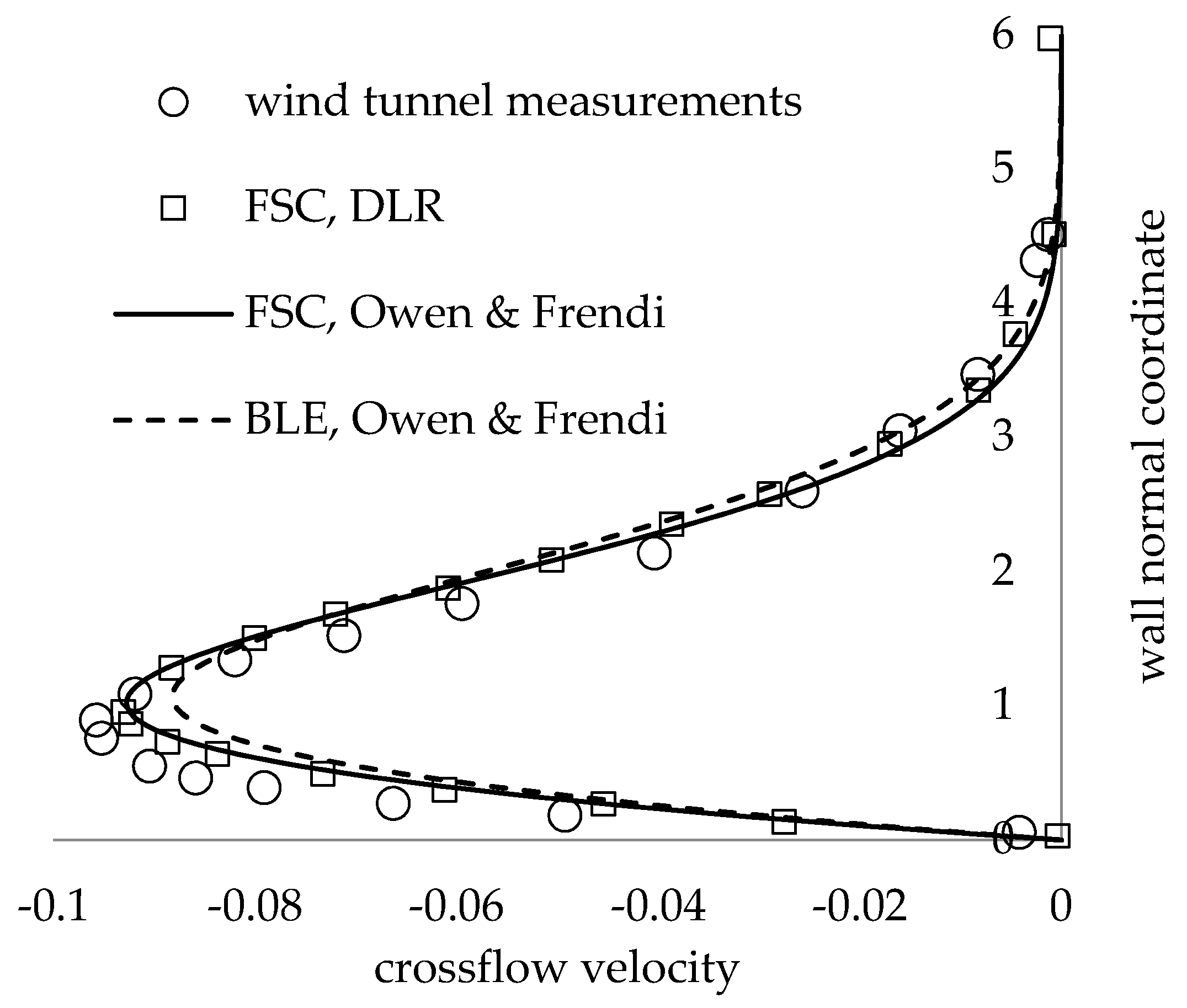
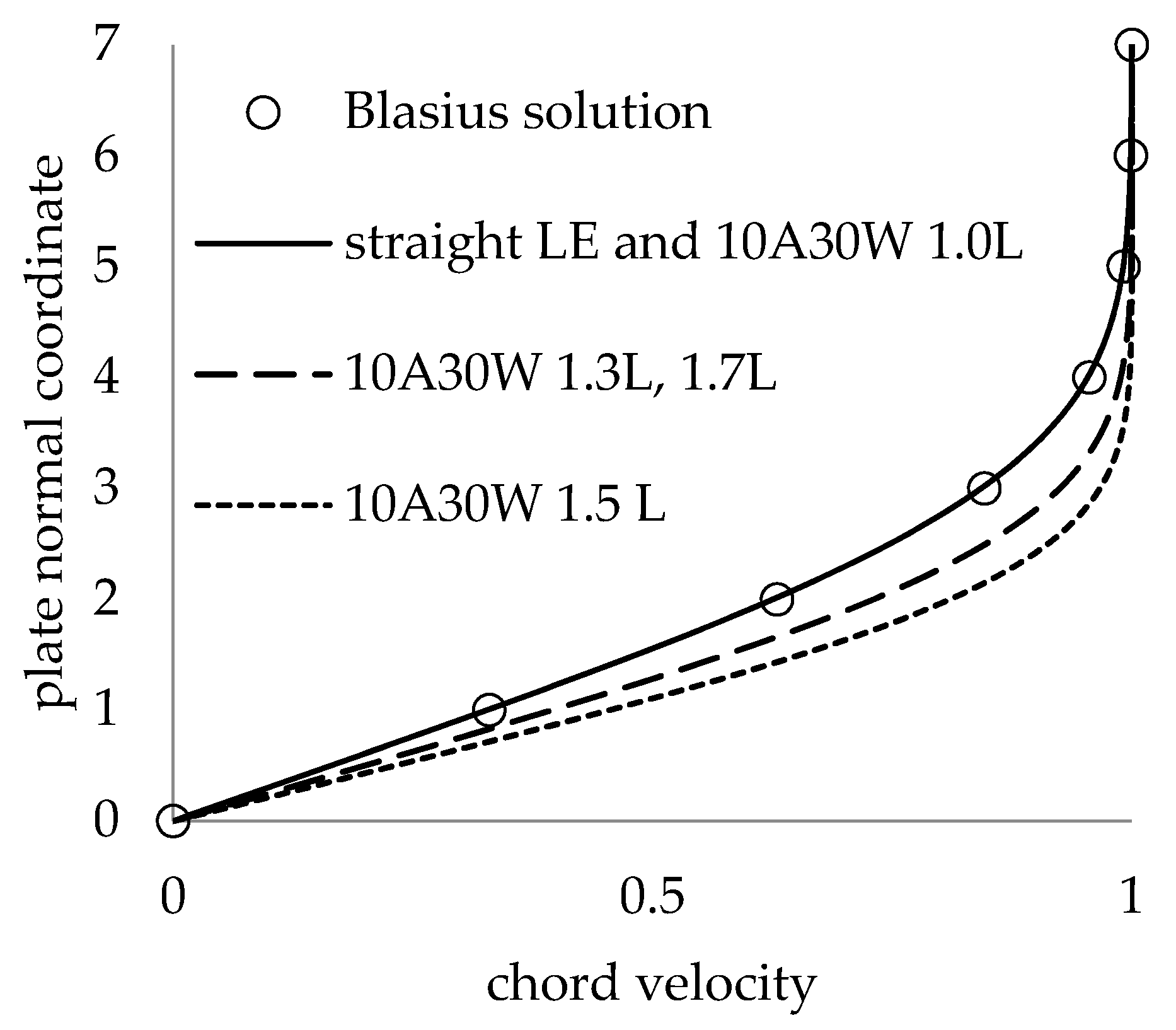
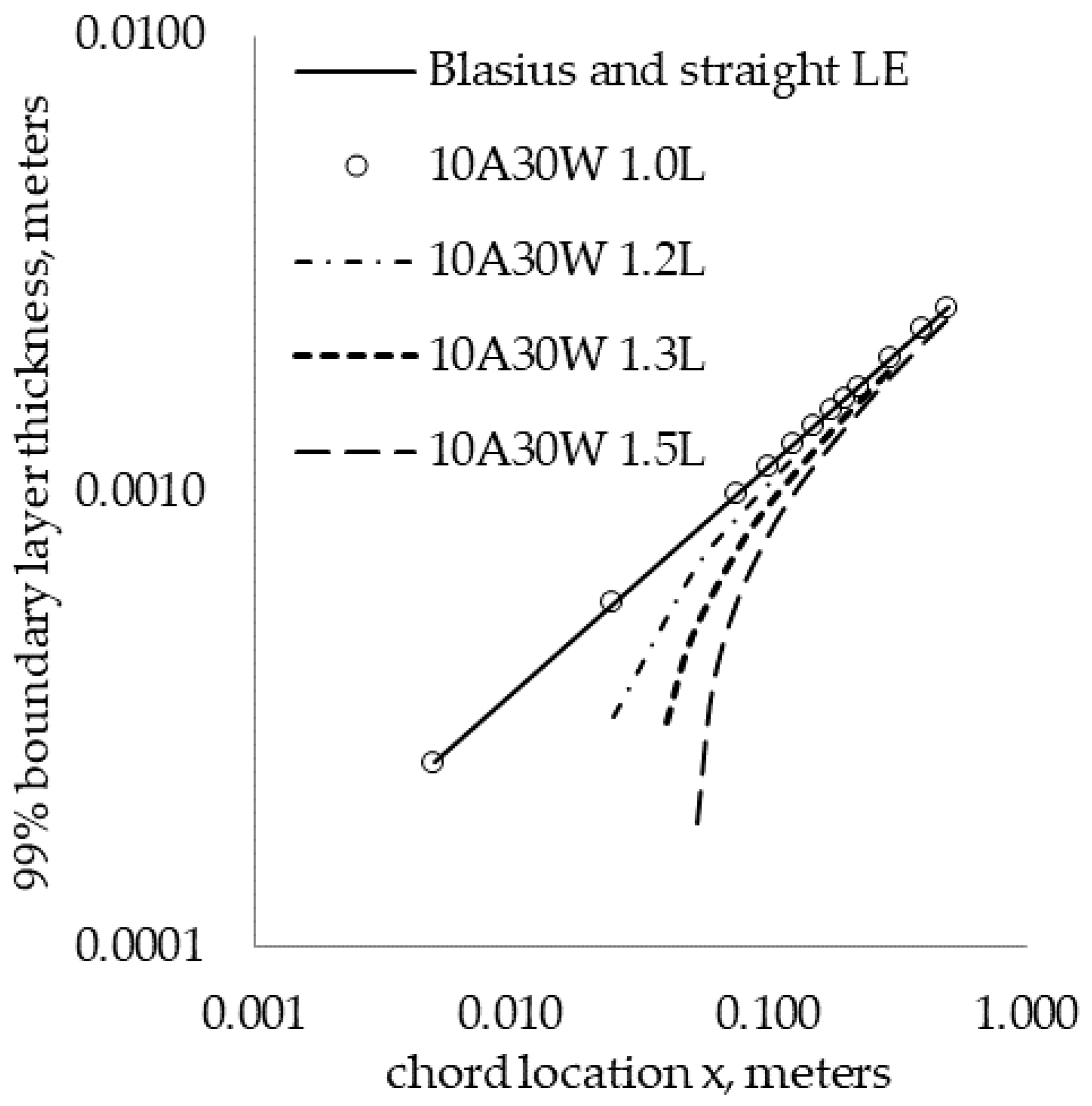
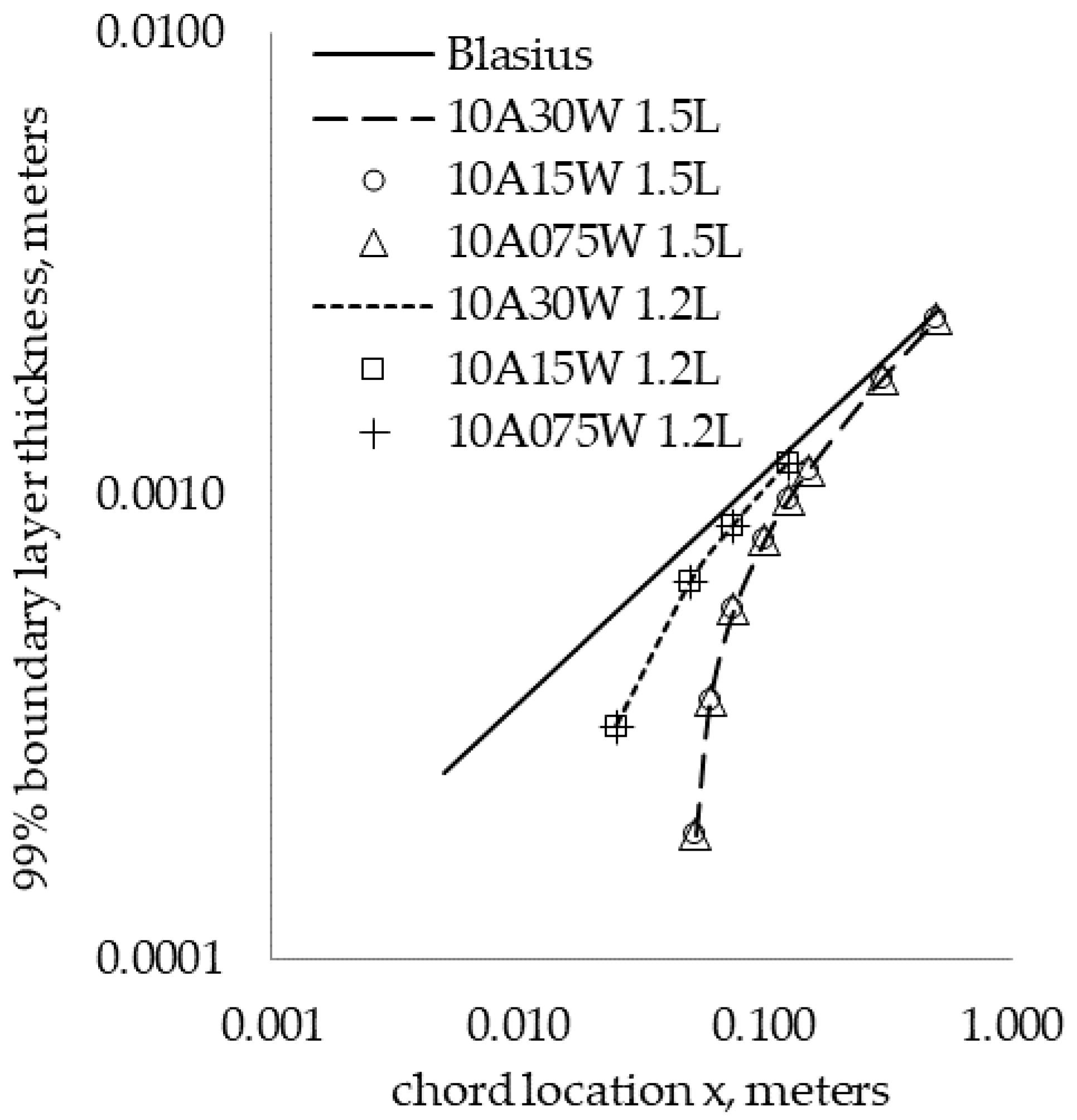
3.1. Base Flow Validation
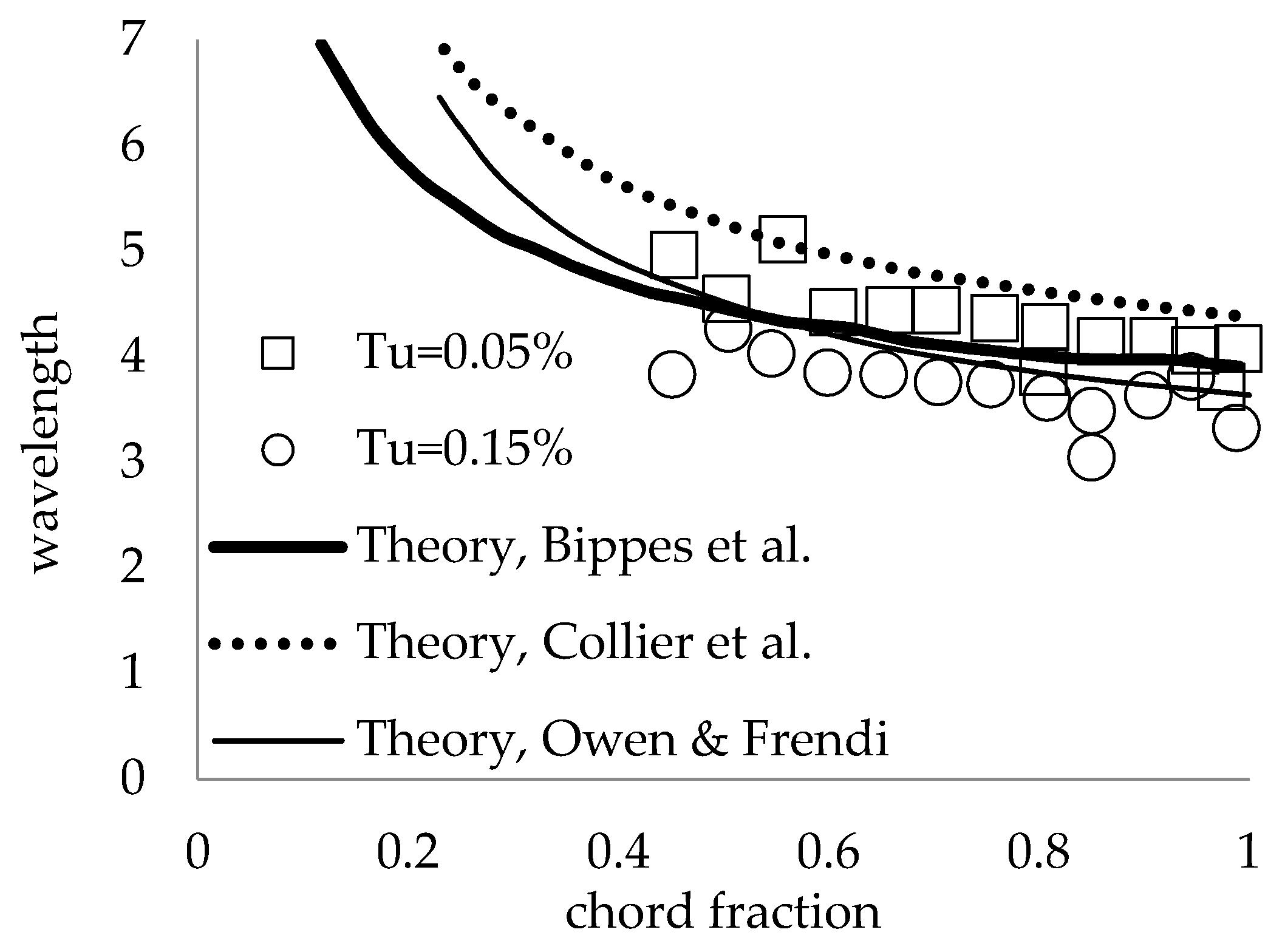
3.2. Stability Validation
3.3. Zero-Sweep Flat Plate—Base Flow and Stability
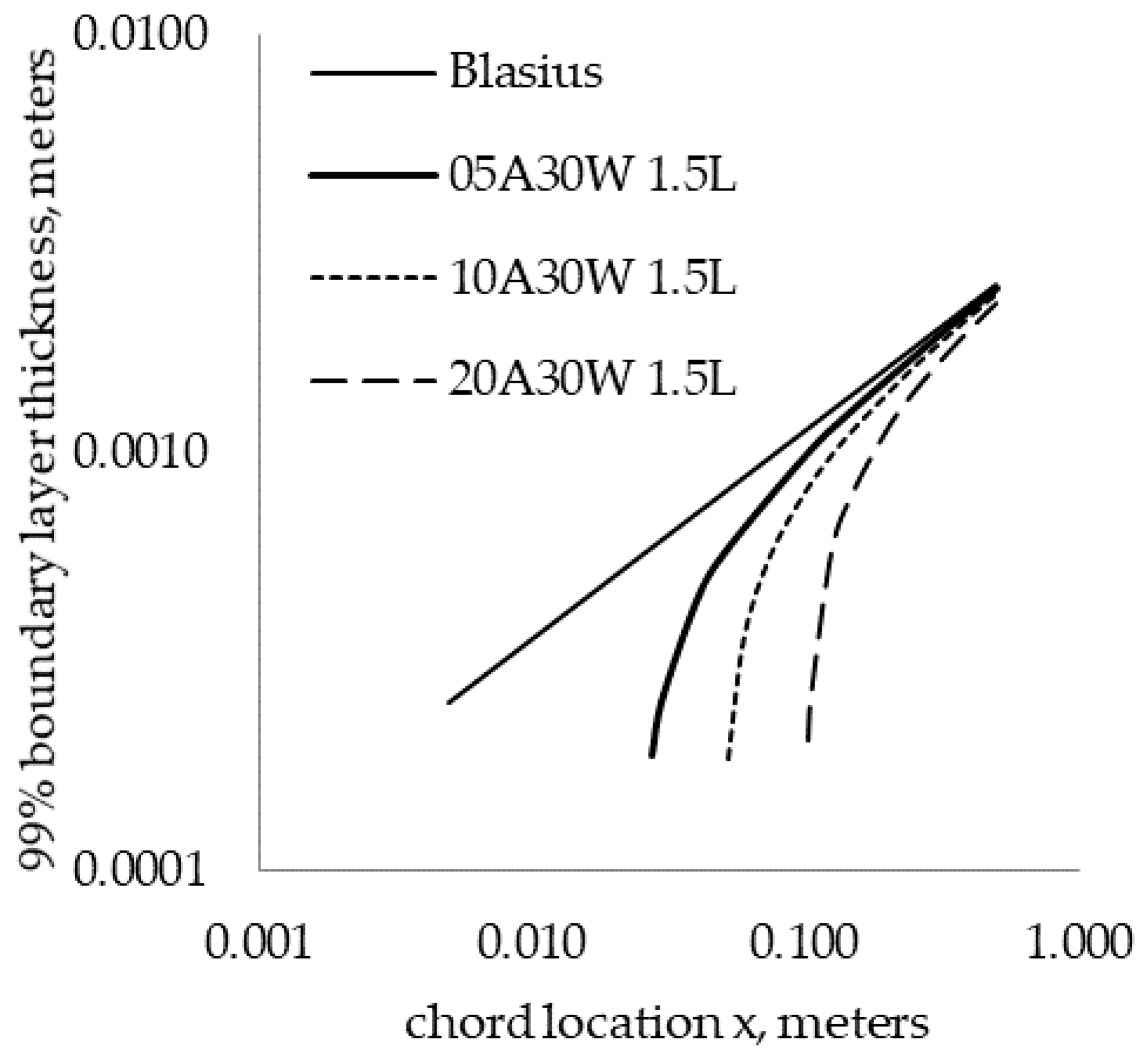
3.3.1. Base Flow
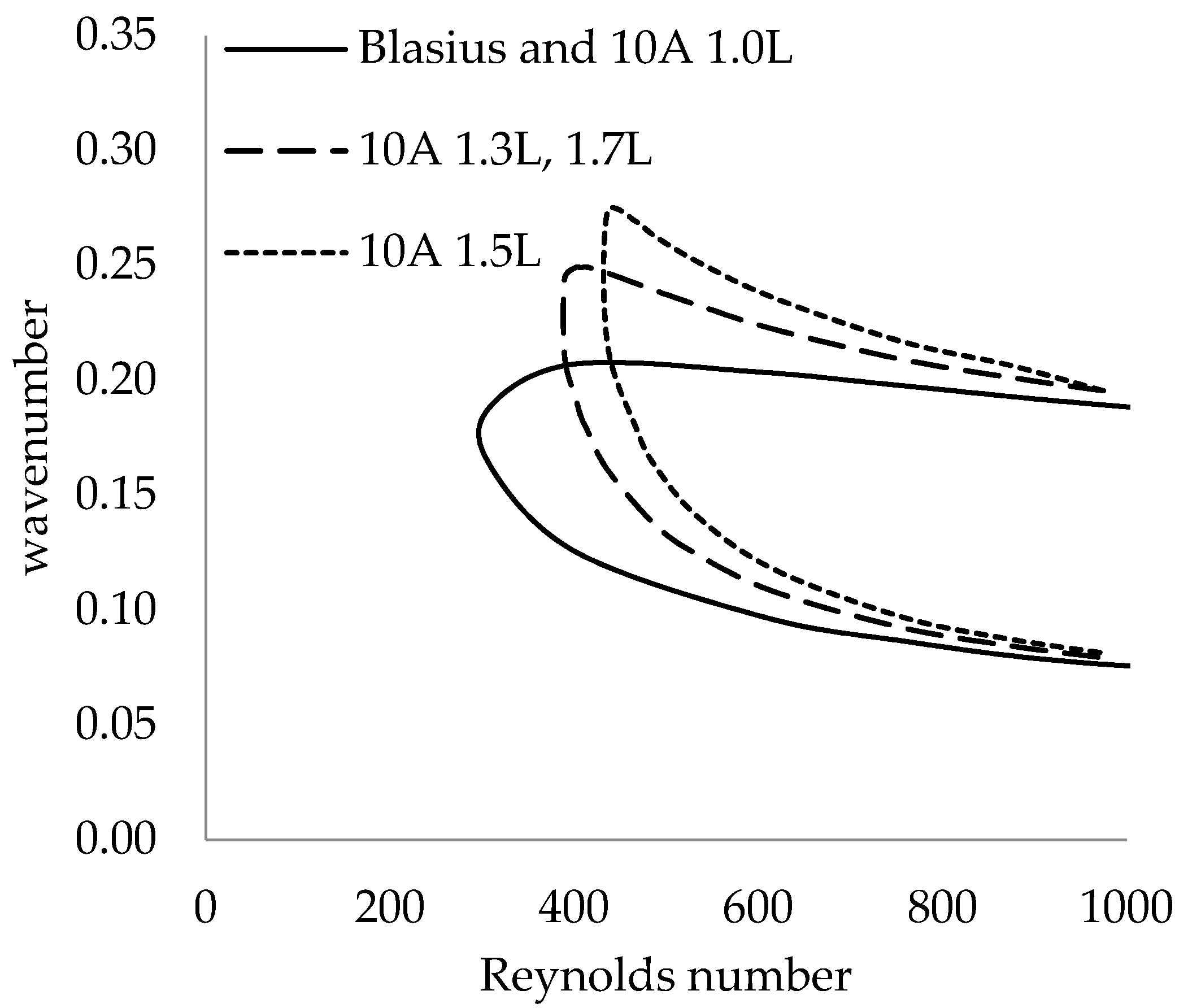
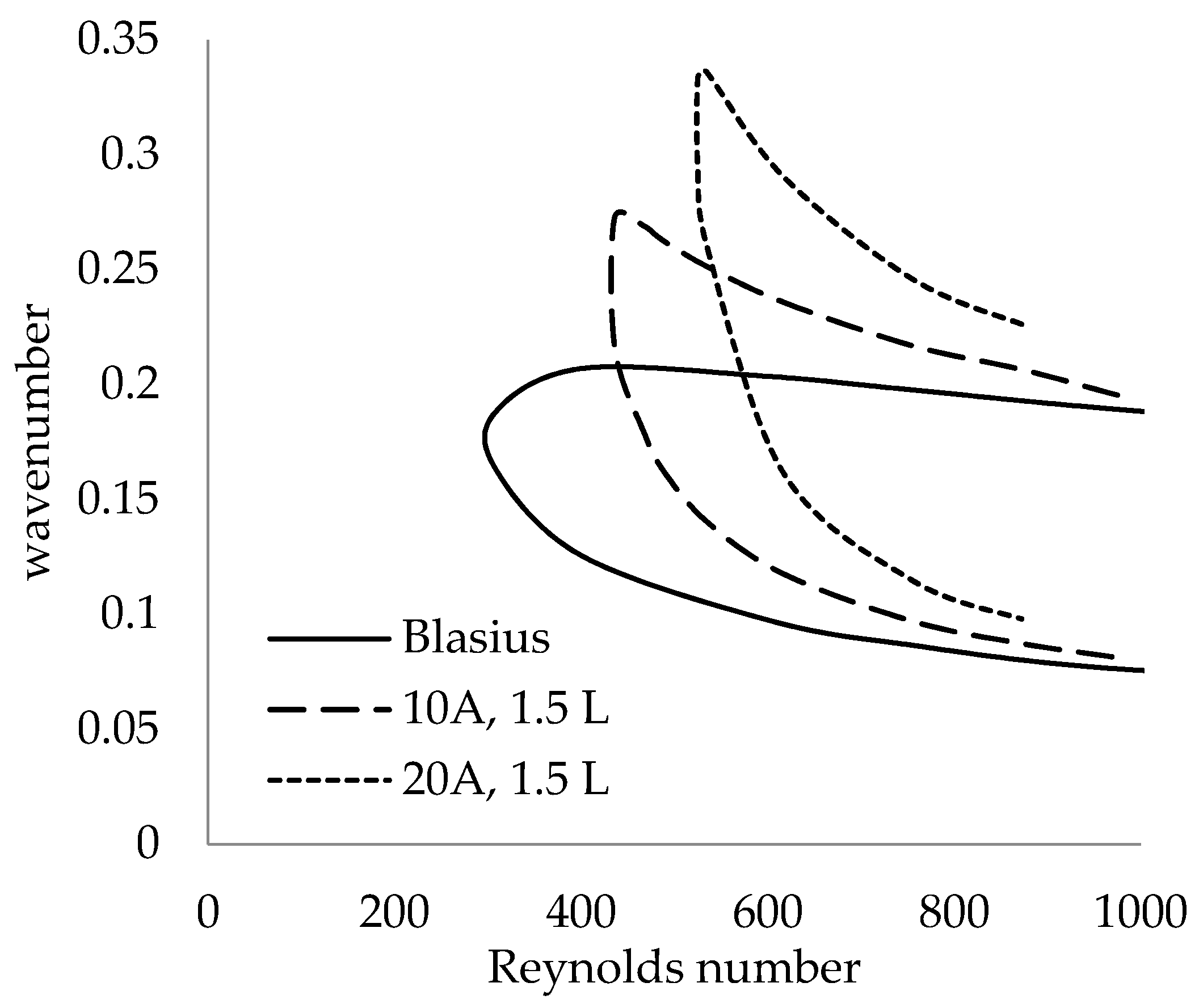
3.3.2. Stability
3.4. Swept Flat Plate—Base Flow and Stability
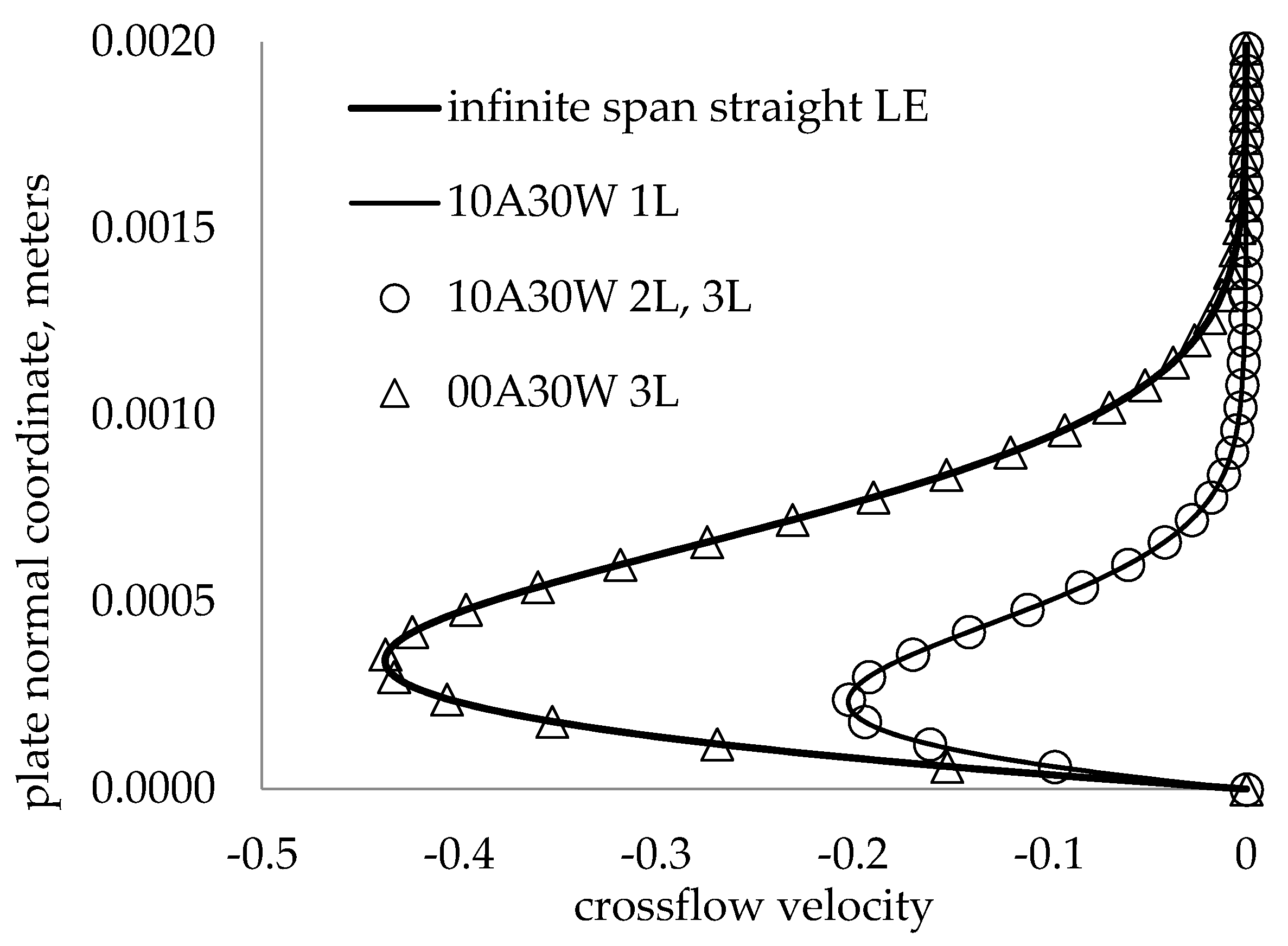
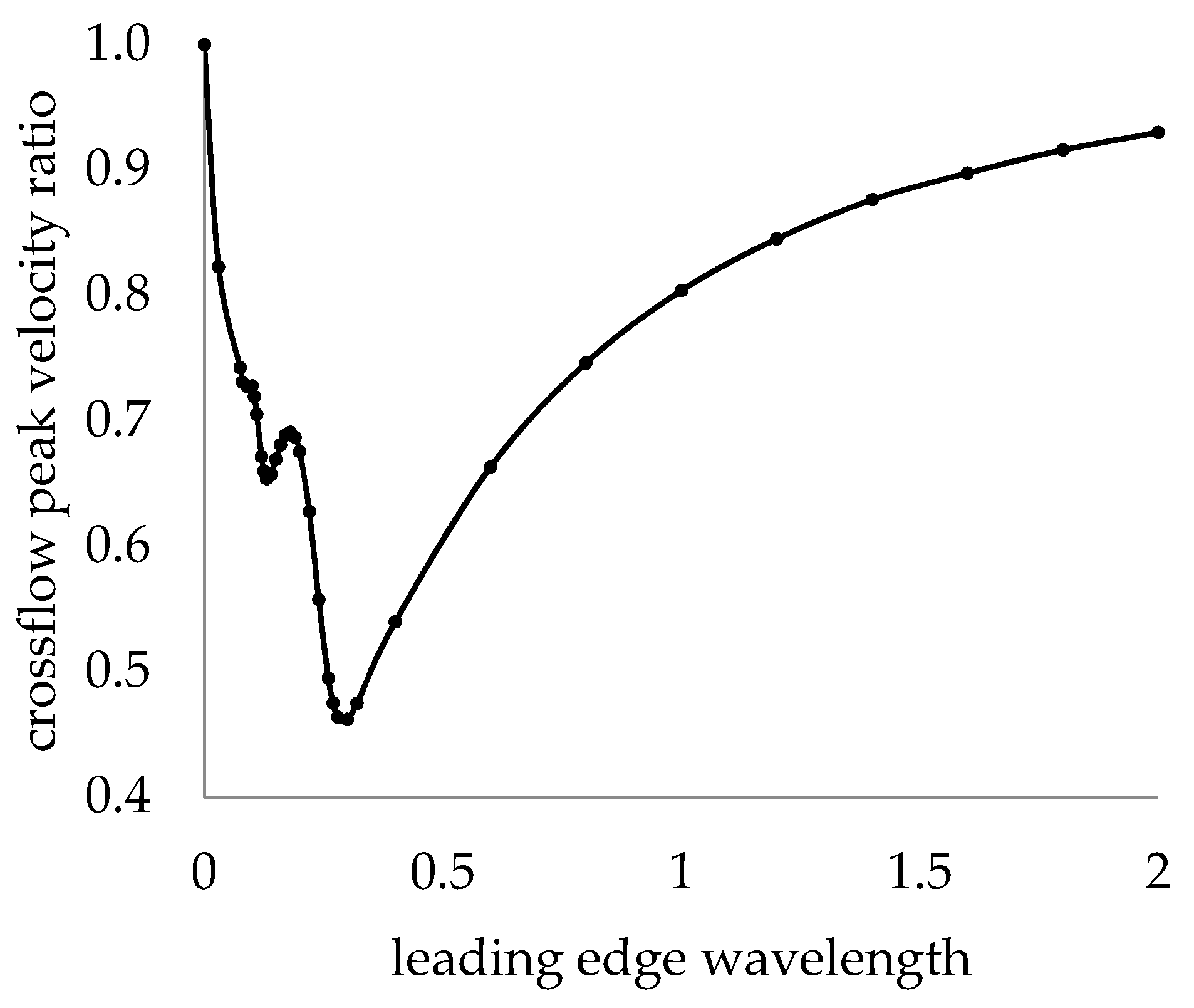
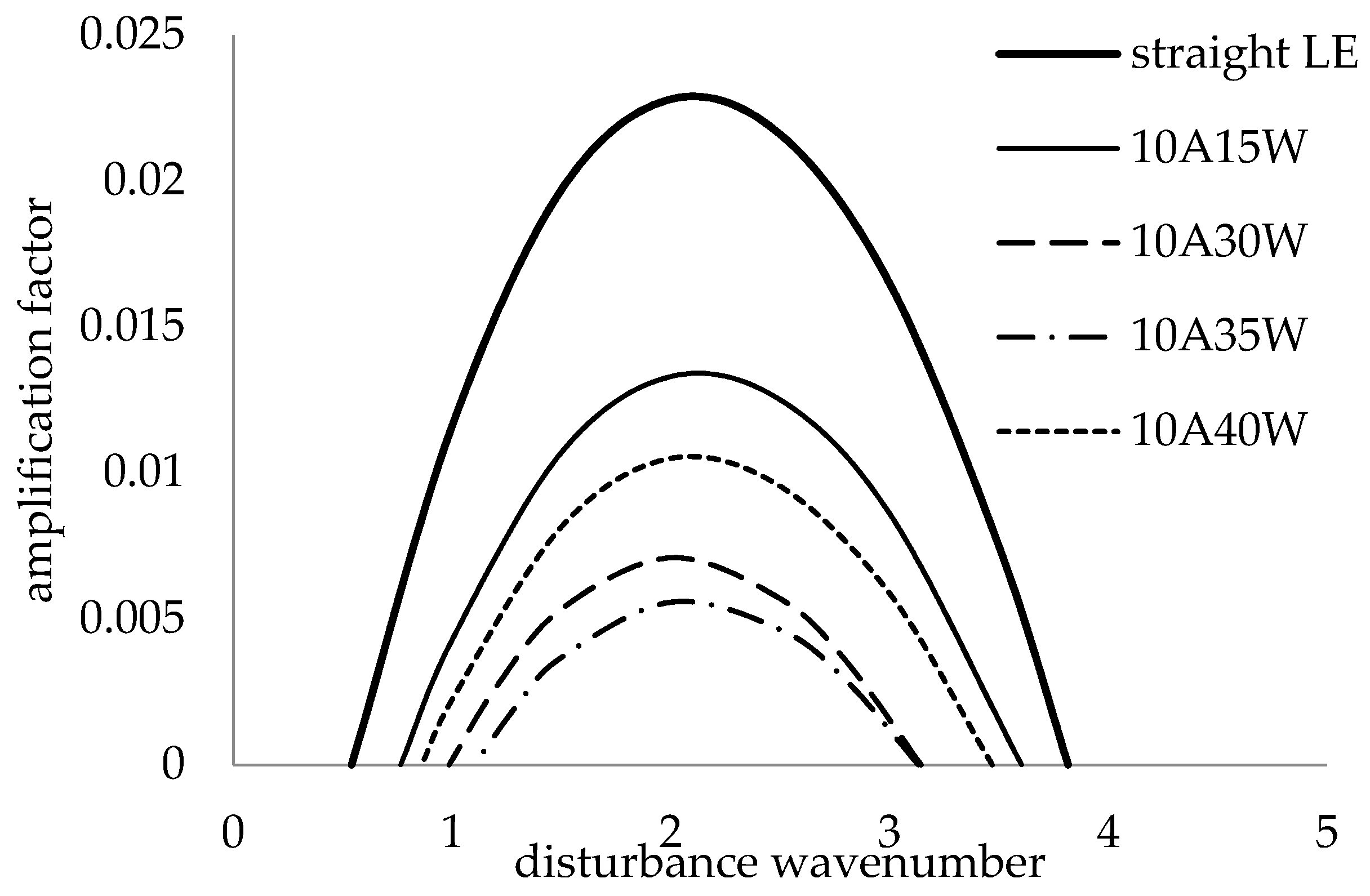
3.4.1. Local Analysis
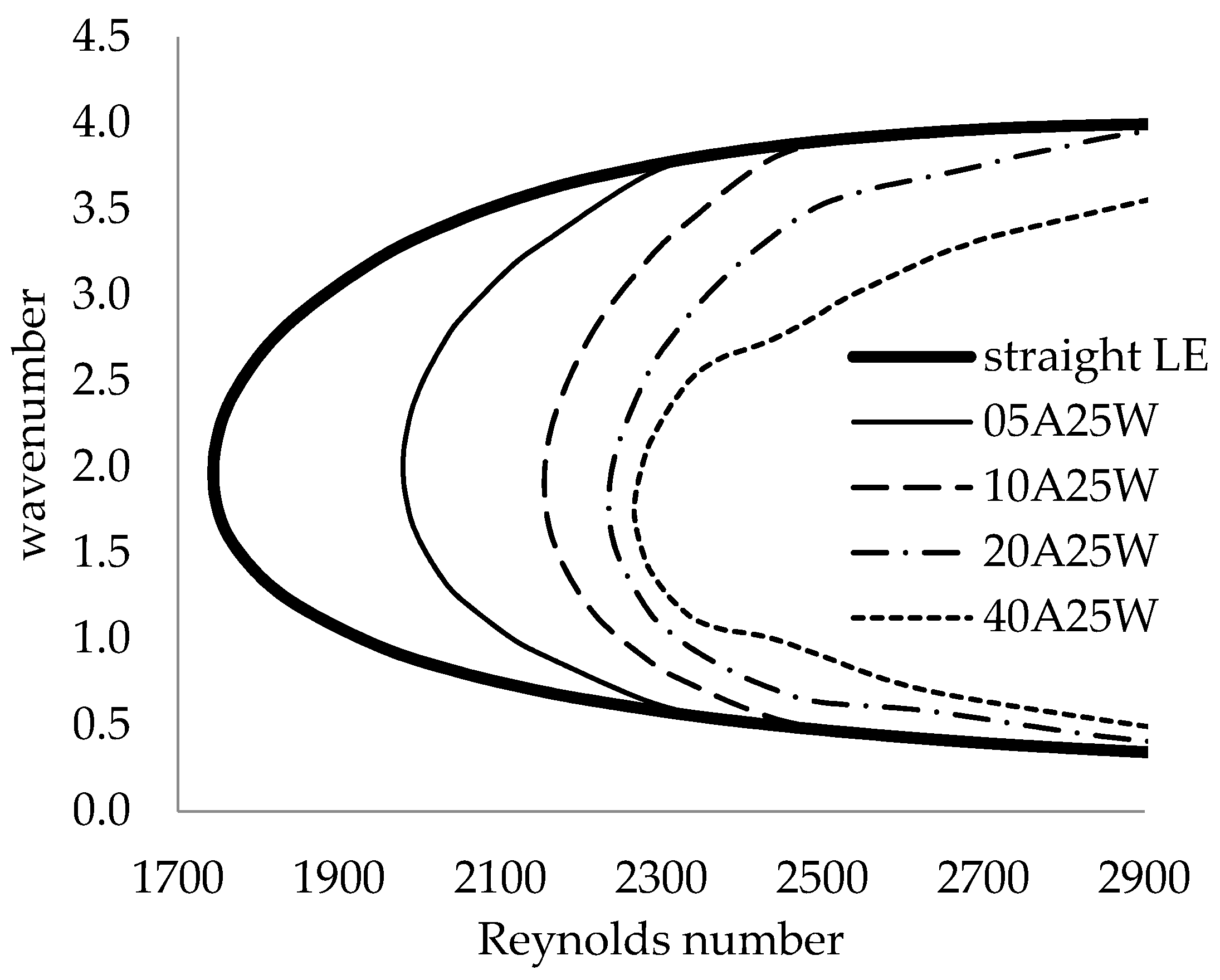
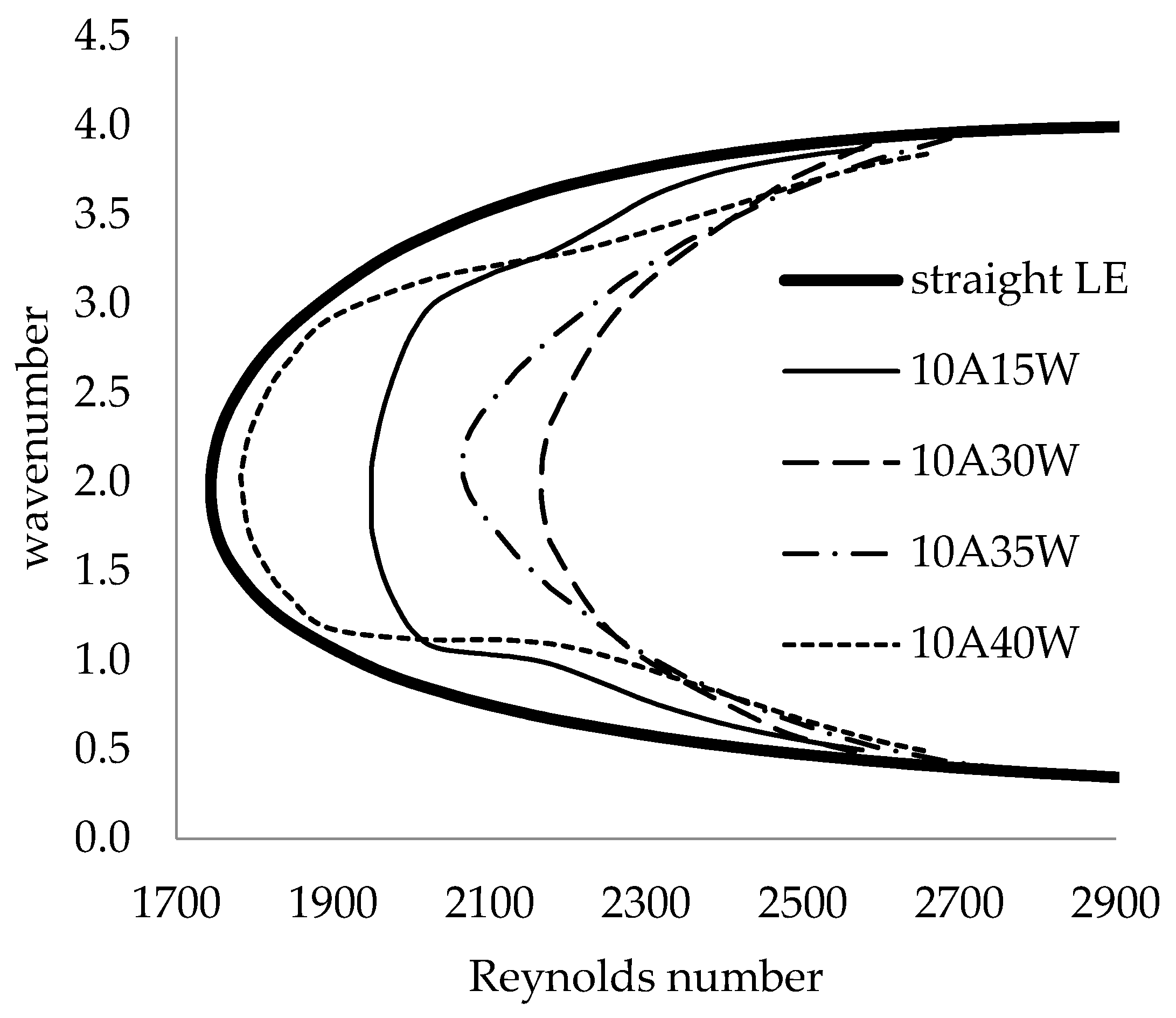
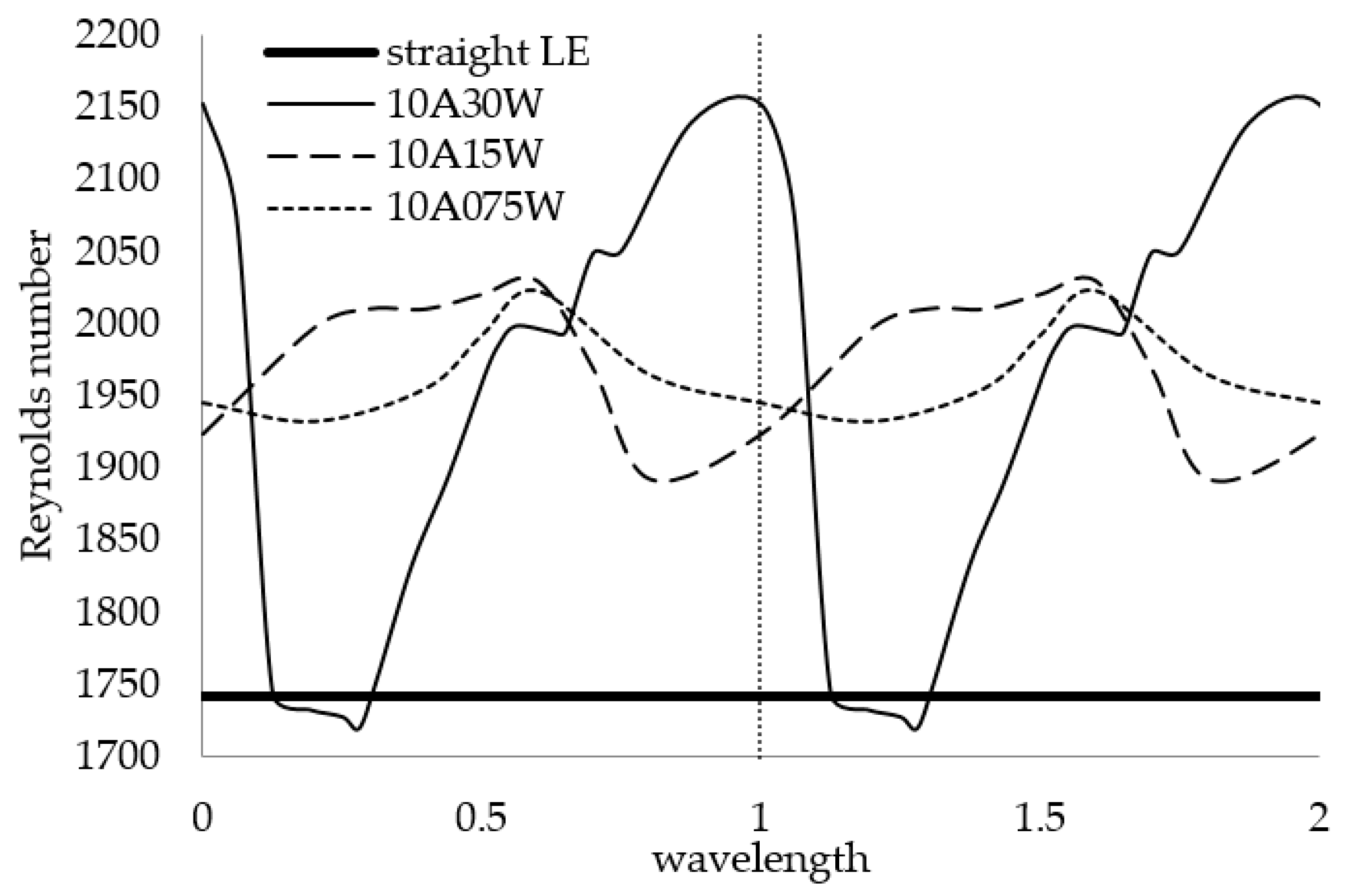
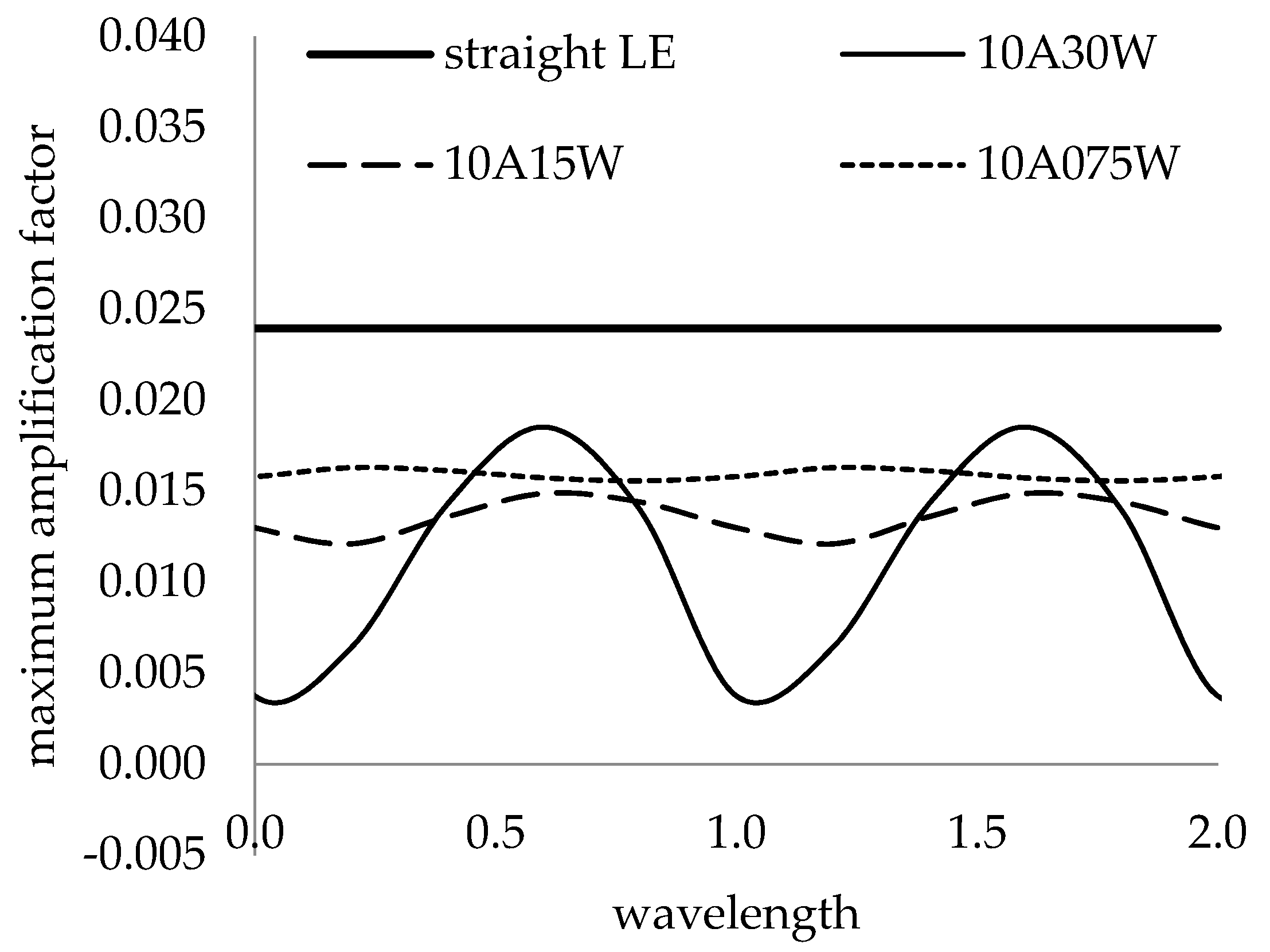
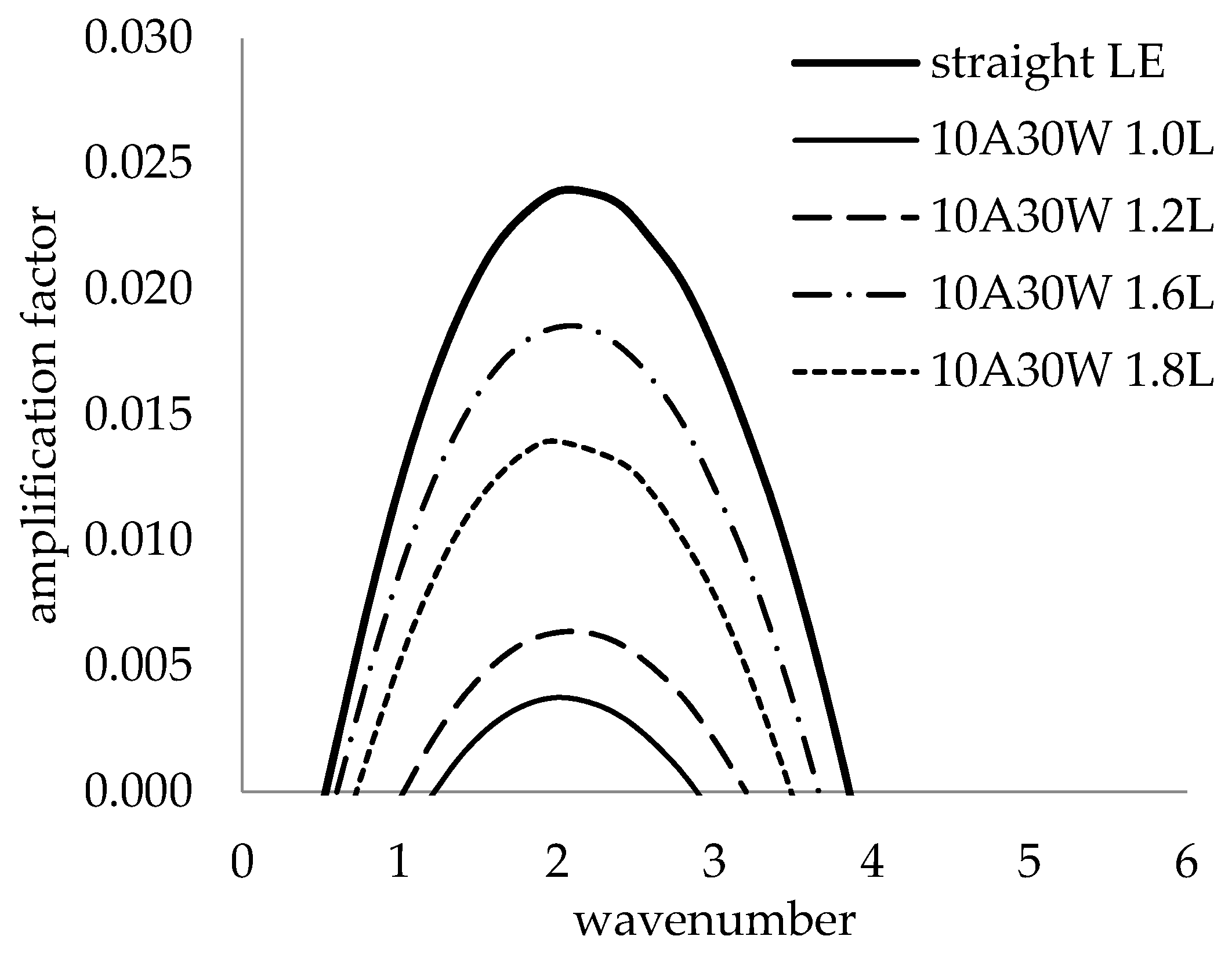
3.4.2. Global Analysis
4. Discussion
5. Conclusions
- The wavy leading edge increased the critical Reynolds number for both swept and un-swept plates.
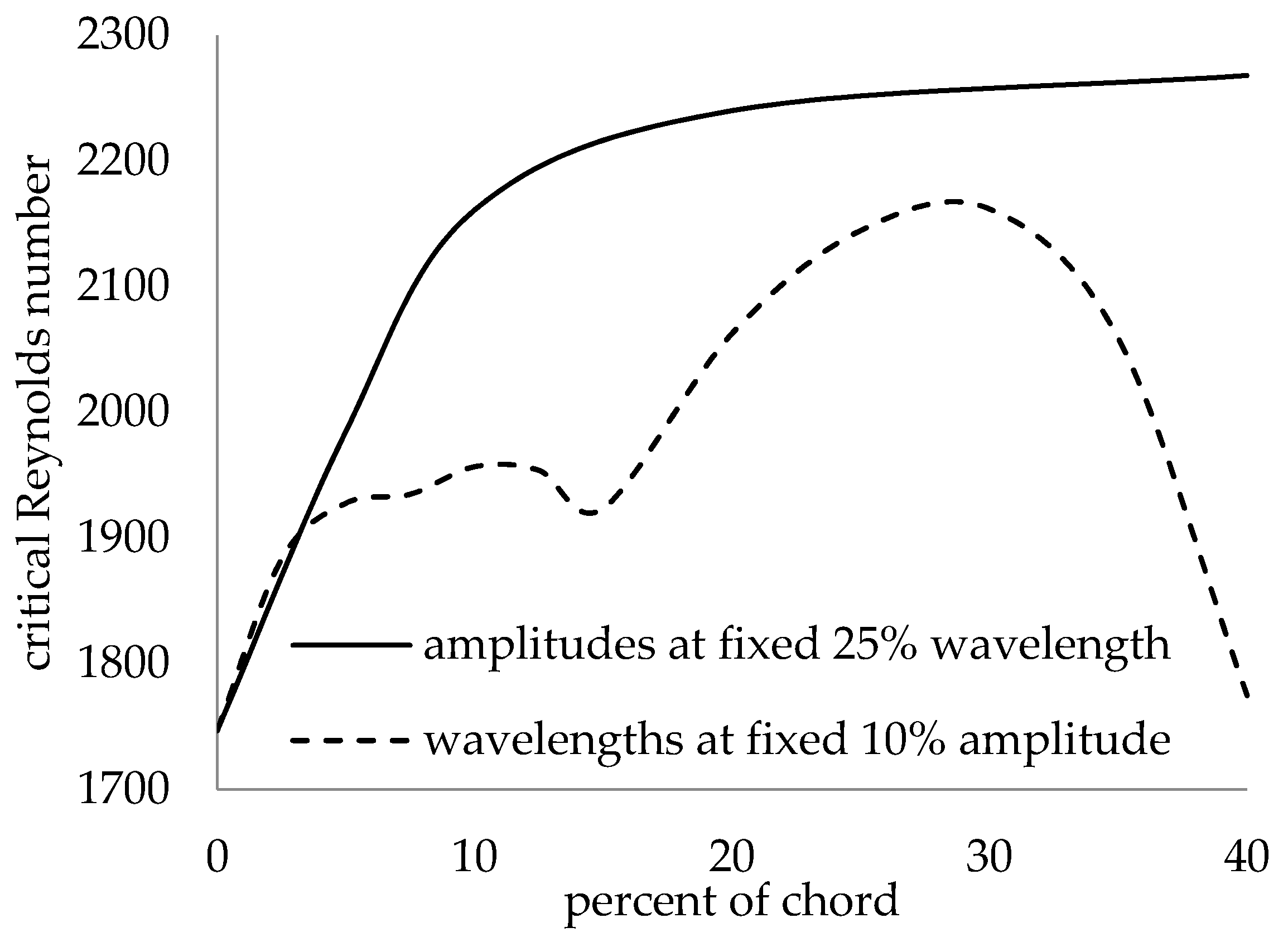
- For the un-swept plate, increasing the leading-edge amplitude increased the critical Reynolds number, while changing the leading-edge wavelength had no effect on the mean flow.
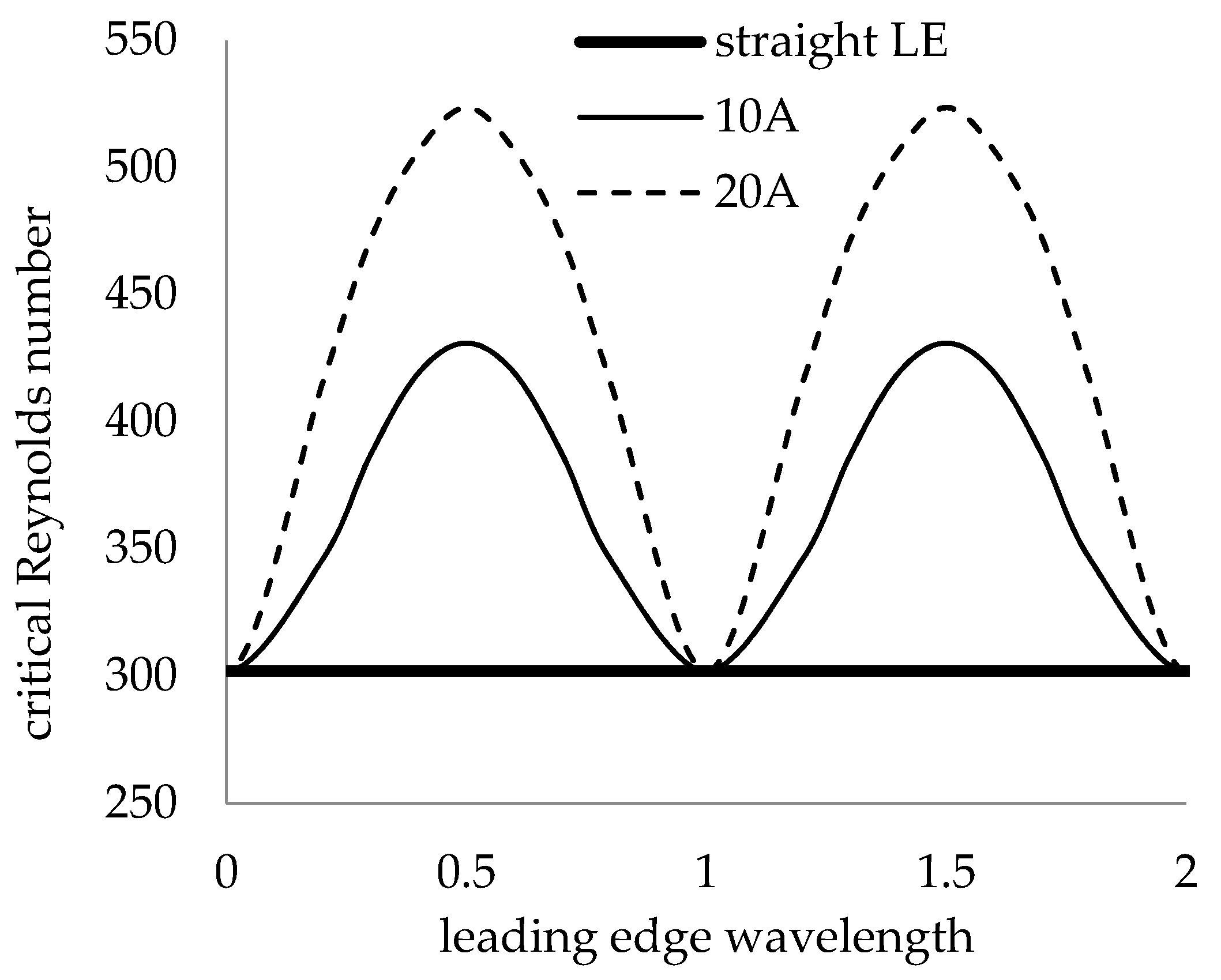
- For the swept plate, a local analysis at the leading-edge peak showed that increasing the leading-edge amplitude increased the critical Reynolds number asymptotically, while the leading-edge wavelength required optimization.
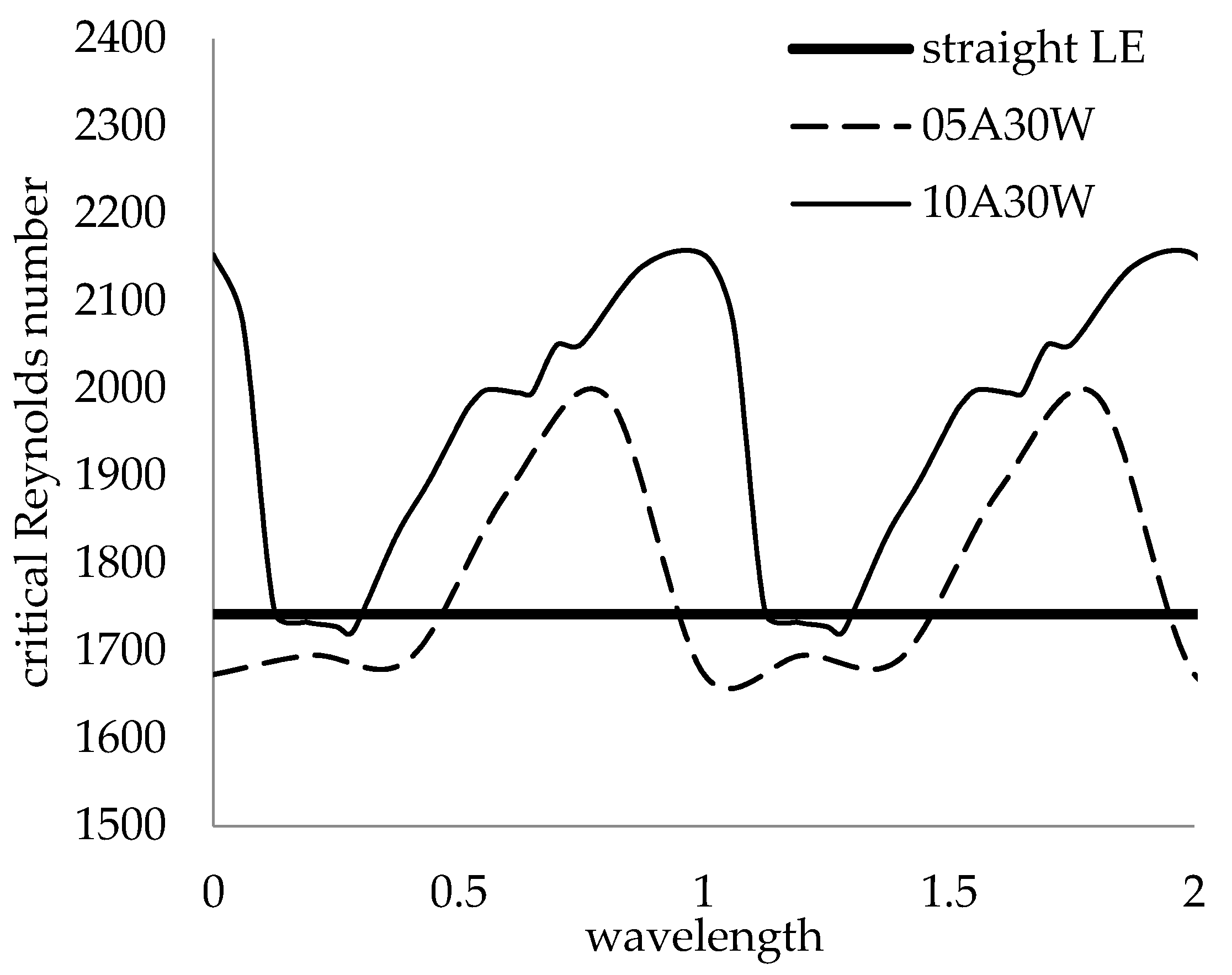
- The global stability analysis performed across the span of the swept plate showed that smaller leading-edge wavelengths produced relatively constant critical Reynolds number profiles that were larger than those of the straight leading edge, while larger leading-edge wavelengths produced oscillating critical Reynolds number profiles.
- It was also found that the most amplified wavenumber was not affected by the wavy leading-edge geometry and hence independent of the waviness.
Author Contributions
Funding
Conflicts of Interest
References
- Bushnell, D.M.; Moore, K.J. Drag reduction in nature. Annu. Rev. Fluid Mech. 1991, 23, 65–79. [Google Scholar] [CrossRef]
- Fish, F.E.; Battle, J.M. Hydrodynamic design of the humpback whale flipper. J. Morphol. 1995, 225, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Miklosovic, D.S.; Murray, M.M.; Howle, L.E.; Fish, F.E. Leading edge tubercles delay stall on humpback whale flippers. Phys. Fluids 2004, 16, L39–L42. [Google Scholar] [CrossRef]
- Johari, H.; Henoch, C.; Custodio, D.; Levshin, A. Effects of leading-edge protuberances on airfoil performance. AIAA J. 2007, 45, 2634–2642. [Google Scholar] [CrossRef]
- Van Nierop, E.; Alben, S.; Brenner, M. How bumps on whale flippers delay stall: An aerodynamic model. Phys. Rev. Lett. 2008, 100, 054502. [Google Scholar] [CrossRef]
- Hansen, K.L.; Kelso, R.M.; Dally, B.B. Performance variations of leading-edge tubercles for distinct airfoil profiles. AIAA J. 2011, 49, 185–194. [Google Scholar] [CrossRef]
- Favier, J.; Pinelli, A.; Piomelli, U. Control of the separated flow around an airfoil using a wavy leading edge inspired by humpback whale flippers. CR MEC 2012, 340, 107–114. [Google Scholar] [CrossRef]
- Hansen, K.; Kelso, R.; Doolan, C. Reduction of flow induced airfoil tonal noise using leading edge sinusoidal modifications. Acoust. Aust. 2012, 40, 172–177. [Google Scholar]
- Zhang, M.; Frendi, A. Effect of airfoil leading edge waviness on flow structures and noise. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1821–1842. [Google Scholar] [CrossRef]
- Biedermann, T.M.; Czeckay, P. Effect of inflow conditions on the noise reduction through leading edge serrations. AIAA J. 2019, 57, 4104–4141xx. [Google Scholar] [CrossRef]
- Lord Rayleigh, F.R.S. On the stability, or instability, of certain fluid motions. Sci. Pap. 1880, 1, 474. [Google Scholar] [CrossRef]
- Orr, W.M. The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part II: A viscous liquid. Proc. R. Ir. Academy Sect. A Math. Phys. Sci. 1907, 27, 69–138. [Google Scholar]
- Sommerfeld, A. Ein beitrag zur hydrodynamischen erklarung der turbulenten flussigkeitsbewegung. In Proceedings of the 4th International Mathematical Congress, Rome, Italy, 6–11 April 1908; Volume 2, pp. 116–124. [Google Scholar]
- Prandtl, L. On the motion of fluids of very small viscosity. In Proceedings of the Third International Mathematical Congress, Heidelberg, Germany, 8–13 August 1904. [Google Scholar]
- Blasius, H. Grenzschichten in flussigkeiten mit kleiner reibung. Z. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Prandtl, L. Bemerkungen uber die enstehung der turbulenz. ZAMM 1921, 1, 431–436. [Google Scholar] [CrossRef]
- Tollmien, W. Uber die Entstehung der Turbulenz. Nachr. Ges. Wiss. Gott. Math. Phys. Kl. 1928, 1929, 21–44. [Google Scholar]
- Schlichting, H. Berechnung der anfachung kleiner storungen bie der plattenstromung. ZAMM 1933, 13, 171–174. [Google Scholar]
- Schubauer, G.B.; Skramstad, H.K. Laminar boundary layer oscillations and transitions on a flat plate. J. Aero. Sci. 1947, 14, 69–76. [Google Scholar] [CrossRef]
- Squire, H.B. On the stability of the three dimensional disturbances of viscous flow between parallel walls. Proc. Roy. Soc. Lond. 1933, A142, 621. [Google Scholar]
- Kaplan, R.E. The Stability of Laminar Incompressible, Boundary Layers in the Presence of Compliant Boundaries. Mass. Inst. Tech. 1964. ASRL TR 116-1. Available online: file:///C:/Users/MDPI/AppData/Local/Temp/34181048-MIT.pdf (accessed on 18 November 2020).
- Jordinson, R. The flat plate boundary layer. Part 1. Numerical integration of the Orr-Sommerfeld equation. J. Fluid Mech. 1970, 43, 801–811. [Google Scholar] [CrossRef]
- Mack, L. A numerical study of the temporal eigenvalue spectrum of the Blasius boundary sayer. J. Fluid Mech 1976, 73, 497–520. [Google Scholar] [CrossRef]
- Grosch, C.E.; Orszag, S.A. Numerical solution of problems in unbounded regions: Coordinate transforms. J. Comput. Phys. 1977, 25, 273–296. [Google Scholar] [CrossRef]
- Itoh, N. A Power Series method for the Numerical Treatment of the Orr-Sommerfeld Equation. Trans. Jpn. Soc. Aero Space Sci. 1974, 17, 65–75. [Google Scholar]
- Ng, B.S.; Reid, W.H. An initial value method for eigenvalue problems using compound matrices. J. Comput. Phys. 1979, 30, 125–136. [Google Scholar] [CrossRef]
- Josslin, R.D.; Streett, C.L. The role of stationary cross-flow vortices in boundary-layer transition on swept wings. Phys. Fluids 1994, 6, 3442–3452. [Google Scholar] [CrossRef]
- Malik, M.R.; Li, F.; Choudhari, M.M.; Chang, C.L. Secondary instability of crossflow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 1999, 399, 85–115. [Google Scholar] [CrossRef]
- Balachandar, S.; Streett, C.L.; Malik, M.R. Secondary instability in rotating disk flow. J. Fluid Mech. 1992, 242, 323–347. [Google Scholar] [CrossRef]
- Gregory, N.; Stuart, J.T.; Walker, W.S. On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. Roy. Soc. A 1955, 248, 155–199. [Google Scholar]
- Malik, M.R.; Wilkinson, S.P.; Orszag, S.A. Instability and transition in rotating disk flow. Aiaa J. 1981, 19, 1131–1138. [Google Scholar] [CrossRef]
- Mack, L.M. Boundary-Layer Linear Stability Theory. AGARD Report No. 709. 1984. Part 3. Available online: https://apps.dtic.mil/sti/pdfs/ADP004046.pdf (accessed on 18 November 2020).
- Nitschke-Kowsky, P.; Bippes, H. Instability and transition of a three-dimensional boundary layer on a swept flat plate. Phys. Fluids 1988, 31, 786–795. [Google Scholar] [CrossRef]
- Falkner, V.M.; Skan, S.W. Some approximate solutions of the boundary-layer equations. Philos. Mag. 1931, 12, 865. [Google Scholar] [CrossRef]
- Hartree, D.R. On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer. Proc. Camb. Philos. Soc. 1937, 33, 223. [Google Scholar] [CrossRef]
- Cooke, J.C. The boundary layer of a class of infinite yawed cylinders. Proc. Camb. Philos. Soc. 1950, 46, 645. [Google Scholar] [CrossRef]
- Malik, M.R.; Orszag, S.A. Linear stability analysis of three-dimensional compressible boundary layers. J. Sci. Comput. 1987, 2, 77–97. [Google Scholar] [CrossRef]
- Arnal, D.; Coustols, E.; Juillen, J.C. Experimental and theoretical study of transition phenomena on an infinite swept wing. Rech. Aerosp. 1984, 4, 39. [Google Scholar]
- Bippes, H.; Muller, B.; Wagner, M. Measurements and Stability Calculations of the Disturbance Growth in an Unstable Three-Dimensional Boundary Layer. Phys. Fluids A Fluid Dyn. 1991, 3, 2371–2377. [Google Scholar] [CrossRef]
- Bippes, H. Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability. Prog. Aerosp. Sci. 1999, 35, 363–412. [Google Scholar] [CrossRef]
- Saric, W.S.; Reed, H.L.; White, E.B. Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 2003, 35, 413–440. [Google Scholar] [CrossRef]
- Saric, W.S.; Carpenter, A.L.; Reed, H.L. Passive control of transition in three-dimensional boundary layers, with emphasis on discrete roughness elements. Phil. Trans. R. Soc. A 2011, 369, 1352–1364. [Google Scholar] [CrossRef]
- Musleh, A.A.; Frendi, A. On the effects of a flexible structure on boundary layer stability and transition. J. Fluids Eng. 2011, 133, 071103. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002; p. 95. [Google Scholar]
- Fischer, T.M.; Dallmann, U. Primary and secondary stability analysis of a three-dimensional boundary-layer flow. Phys. Fluids A 1991, 3, 2378–2391. [Google Scholar] [CrossRef]
- Collier, F.S., Jr.; Muller, B.; Bippes, H. The stability of a three-dimensional laminar boundary layer on a swept flat plate. In Proceedings of the 21st Fluid Dynamics, Plasma Dynamics, and Lasers Conference, Seattle, WA, USA, 18–20 June 1990. AIAA 90-1447. [Google Scholar] [CrossRef]



| Author | Grid Points | cR | ci |
|---|---|---|---|
| Owen and Frendi | 250 | 0.364 060 89 | 0.007 981 84 |
| Owen and Frendi | 500 | 0.364 111 13 | 0.007 962 72 |
| Owen and Frendi | 1000 | 0.364 123 10 | 0.007 959 96 |
| Grosch and Orszag | 32 (spectral) | 0.364 122 86 | 0.007 959 72 |
| R | cR Owen & Frendi | ci Owen & Frendi | cR Mack | ci Mack |
|---|---|---|---|---|
| 580 | 0.3641 | 0.0080 | 0.3641 | 0.0080 |
| 1000 | 0.3383 | 0.0048 | 0.3383 | 0.0048 |
| 2000 | 0.3089 | −0.0164 | 0.3089 | −0.0166 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owen, M.; Frendi, A. Towards the Understanding of Humpback Whale Tubercles: Linear Stability Analysis of a Wavy Flat Plate. Fluids 2020, 5, 212. https://doi.org/10.3390/fluids5040212
Owen M, Frendi A. Towards the Understanding of Humpback Whale Tubercles: Linear Stability Analysis of a Wavy Flat Plate. Fluids. 2020; 5(4):212. https://doi.org/10.3390/fluids5040212
Chicago/Turabian StyleOwen, Miles, and Abdelkader Frendi. 2020. "Towards the Understanding of Humpback Whale Tubercles: Linear Stability Analysis of a Wavy Flat Plate" Fluids 5, no. 4: 212. https://doi.org/10.3390/fluids5040212
APA StyleOwen, M., & Frendi, A. (2020). Towards the Understanding of Humpback Whale Tubercles: Linear Stability Analysis of a Wavy Flat Plate. Fluids, 5(4), 212. https://doi.org/10.3390/fluids5040212





