Investigating the Formation of Submesoscale Structures along Mesoscale Fronts and Estimating Kinematic Quantities Using Lagrangian Drifters
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. CARTHE Drifter
2.1.2. Marine X-Band Radar Velocities
2.1.3. SST Data
2.1.4. CTD Data
2.2. Methods
2.2.1. Velocity Reconstruction with Gaussian Process Regression
2.2.2. Optimization of Hyperparameters
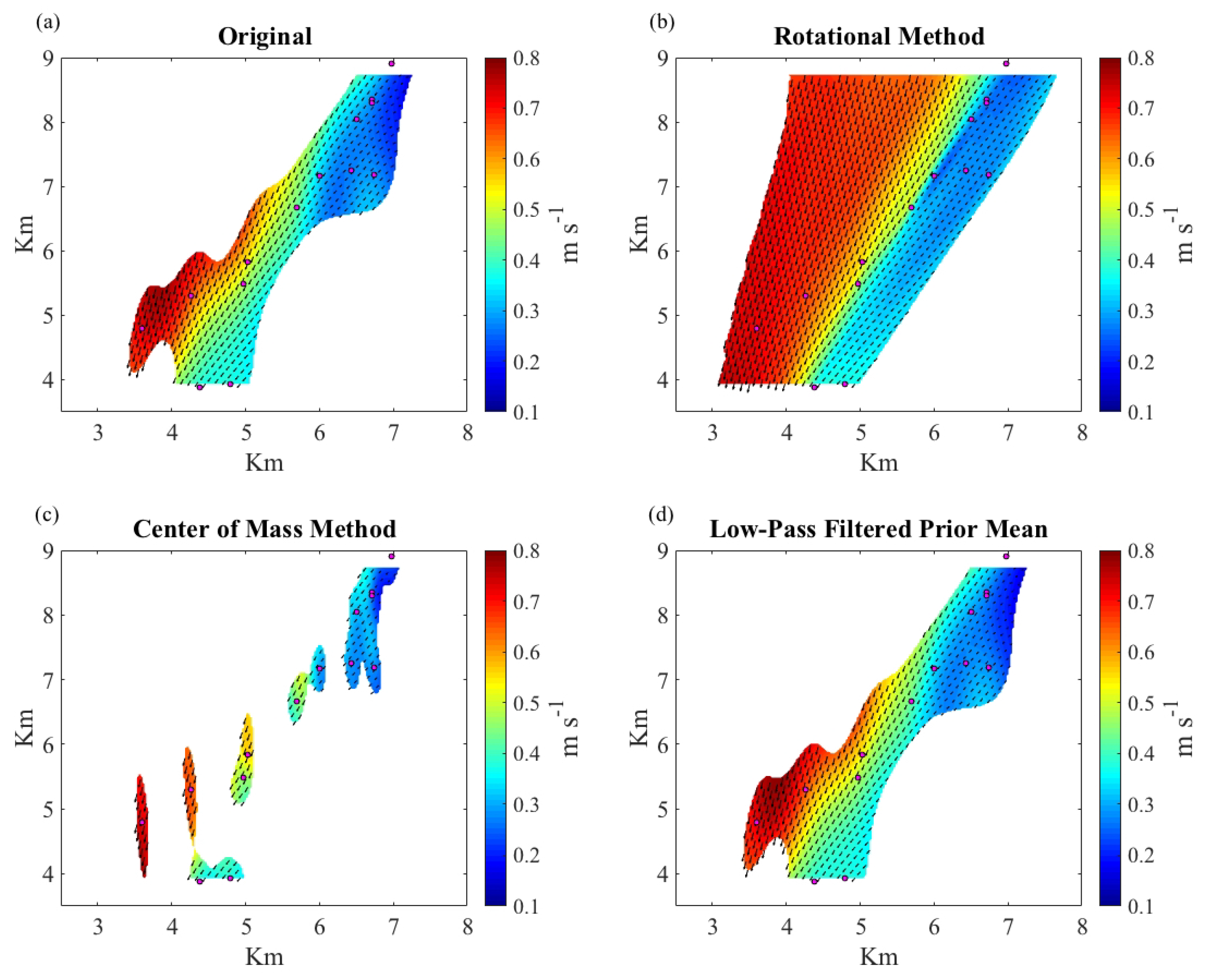
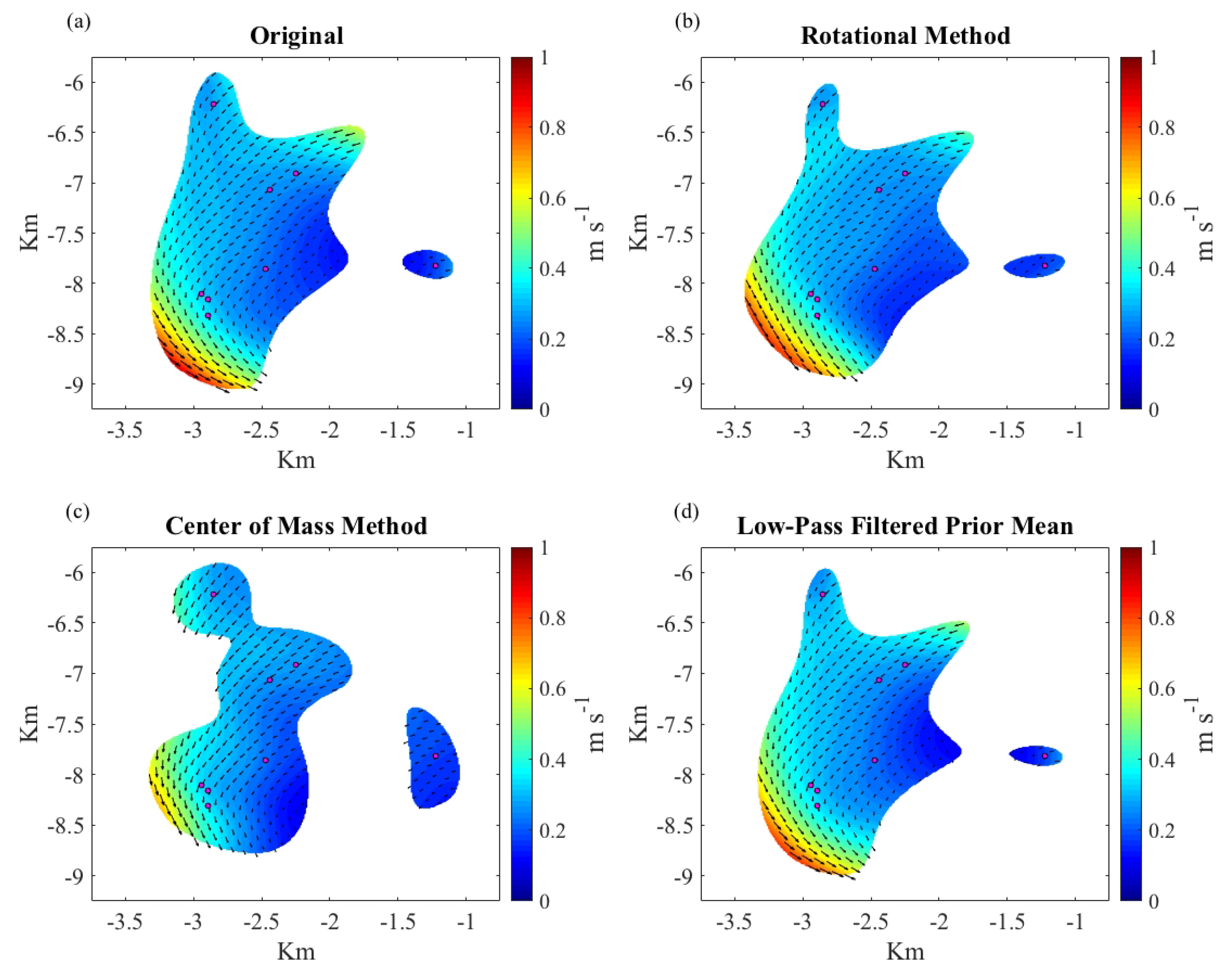
2.2.3. Variations of the GPR Framework
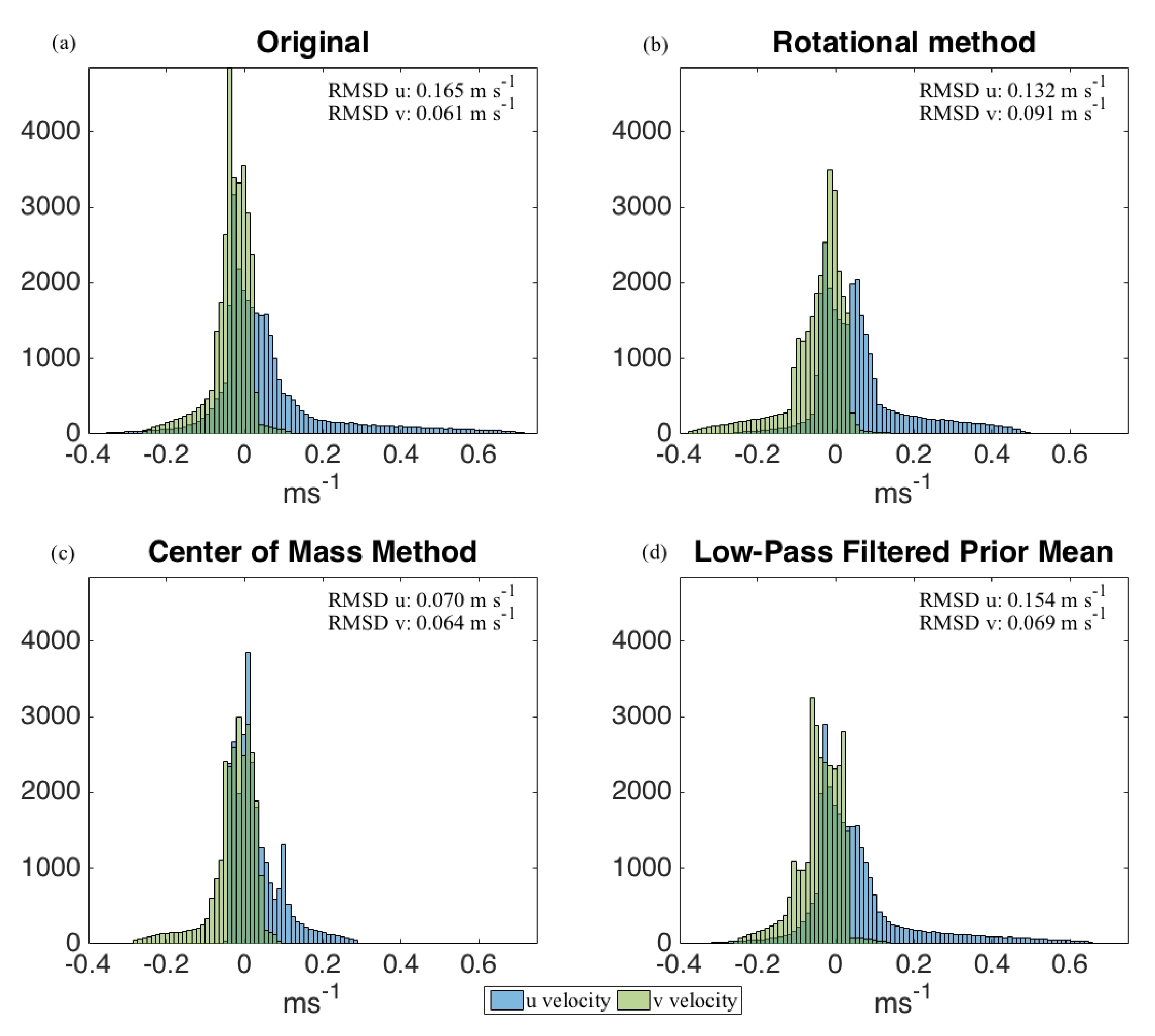
2.2.4. Velocity Validation with X-Band Velocity Fields
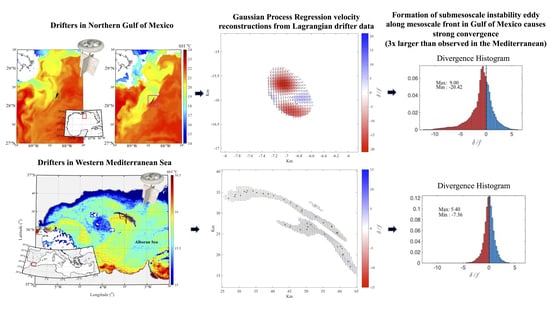
3. Results
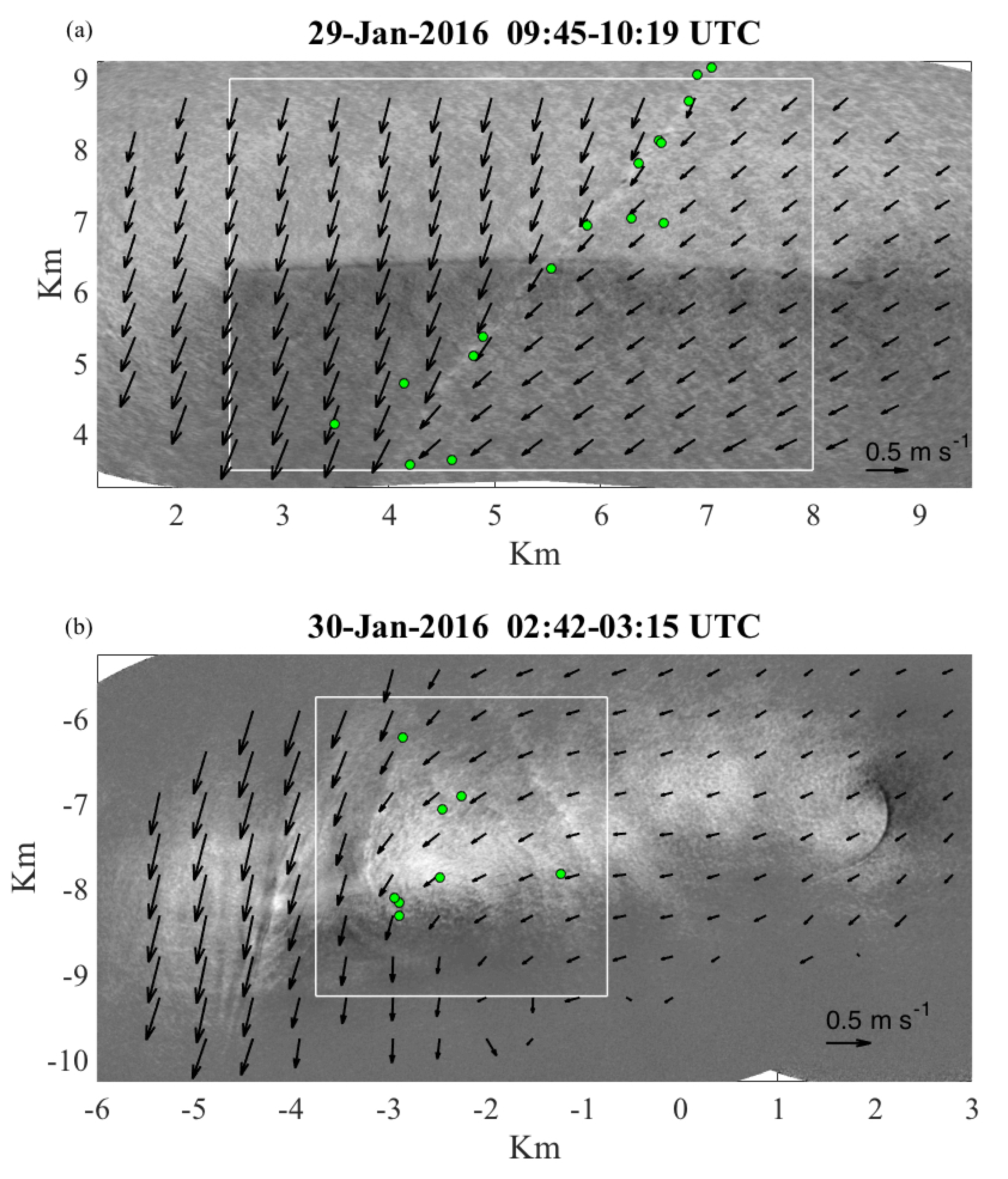
3.1. Comparison of GPR and Marine Radar Velocities in the Gulf of Mexico
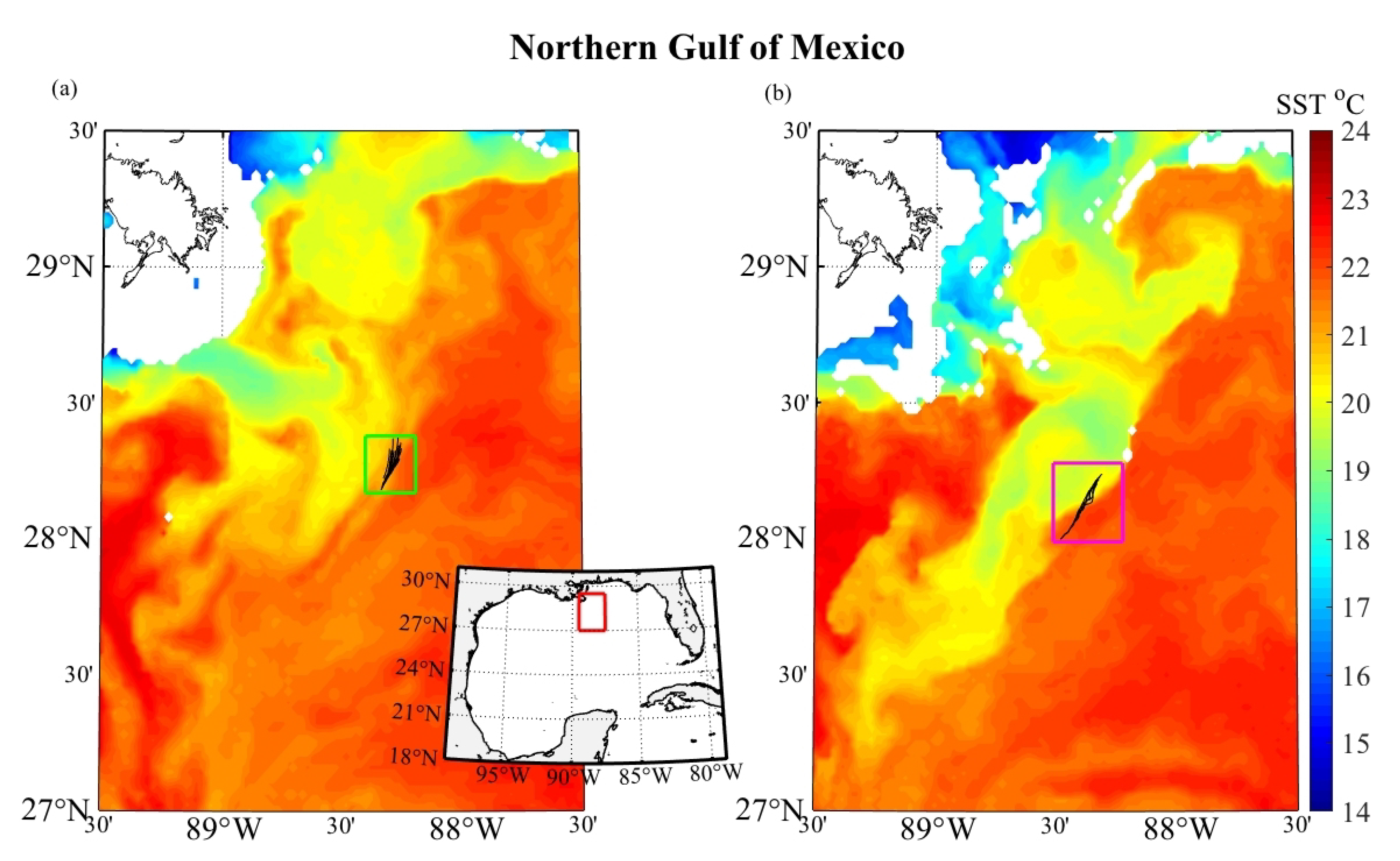
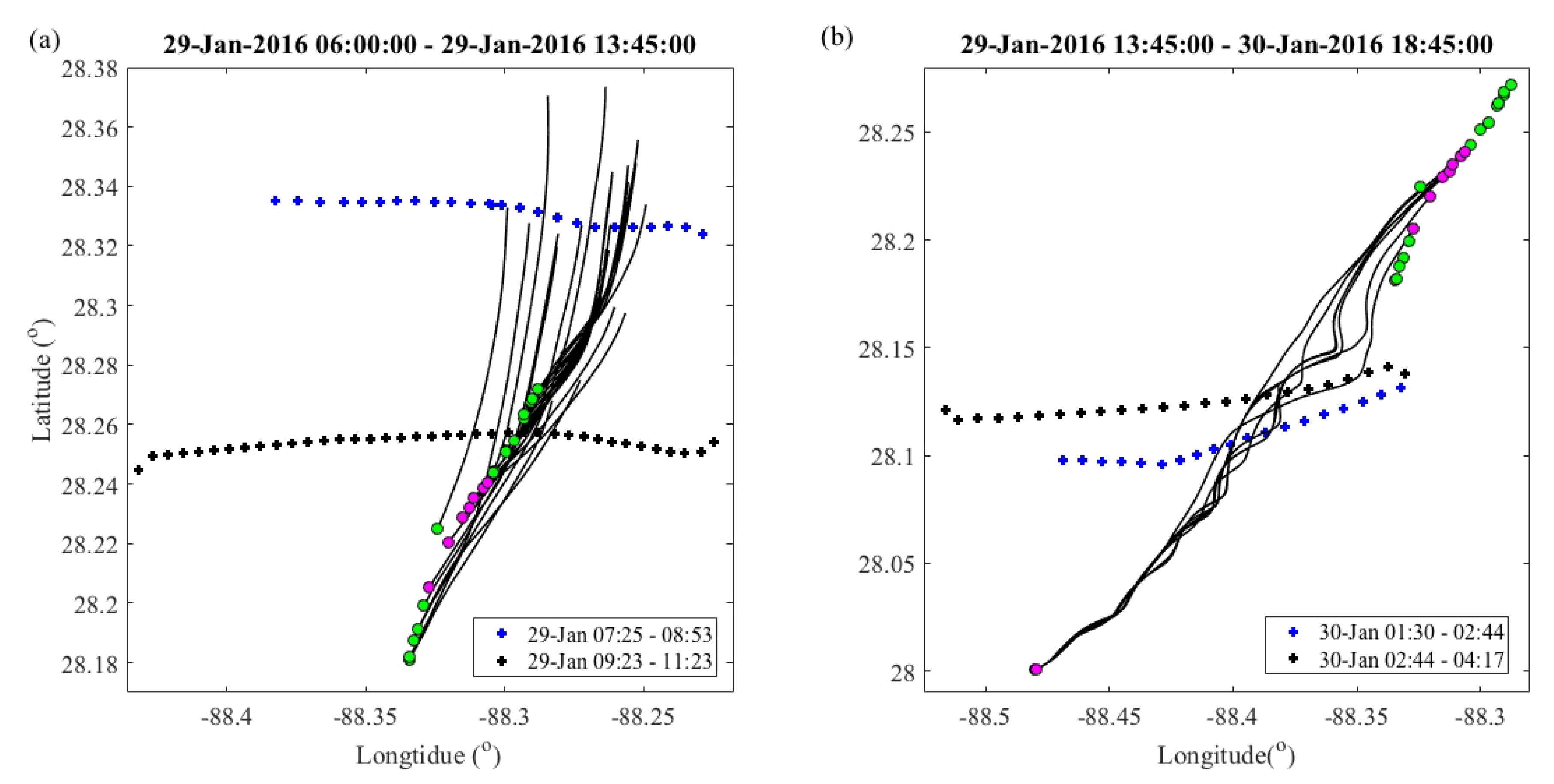
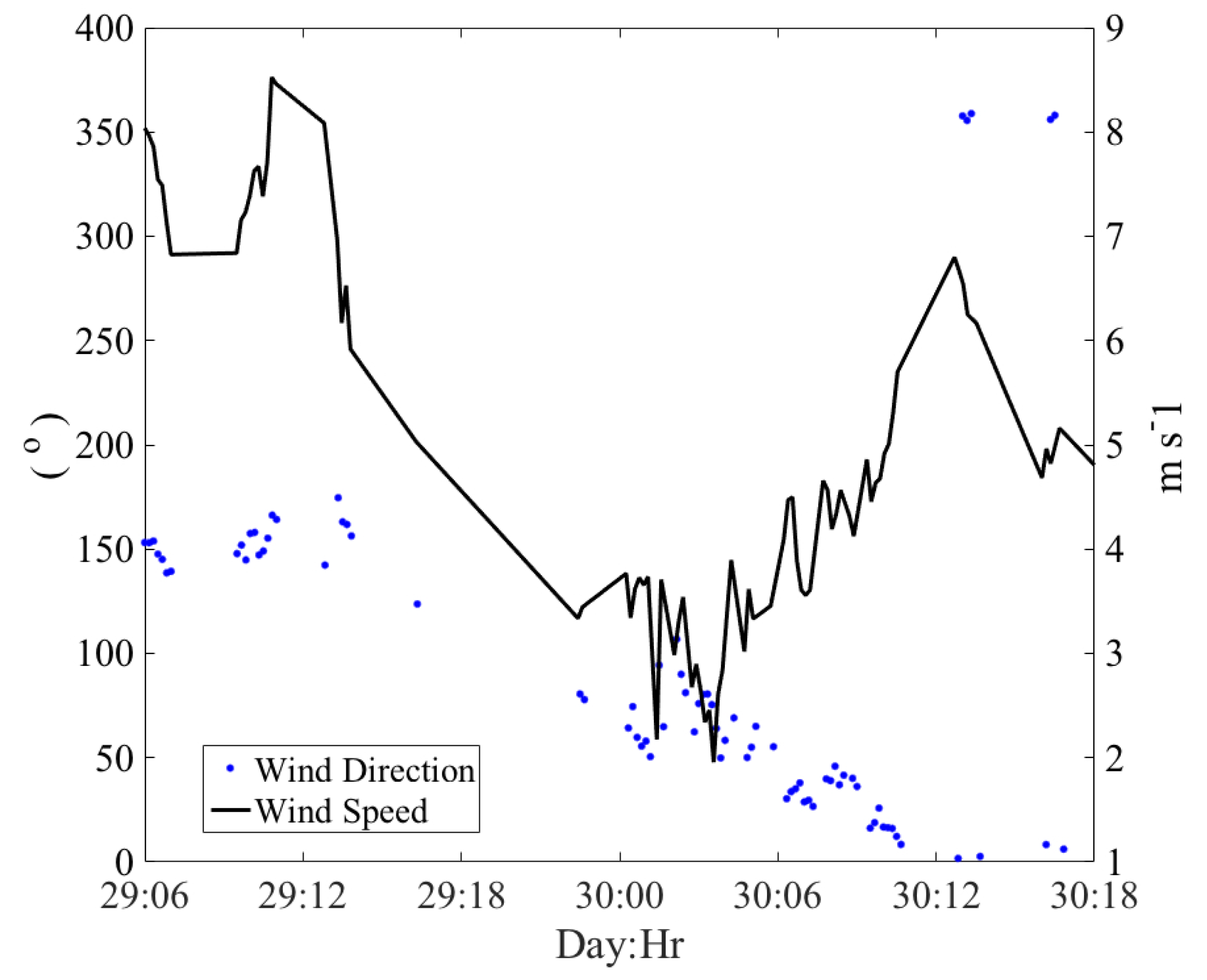
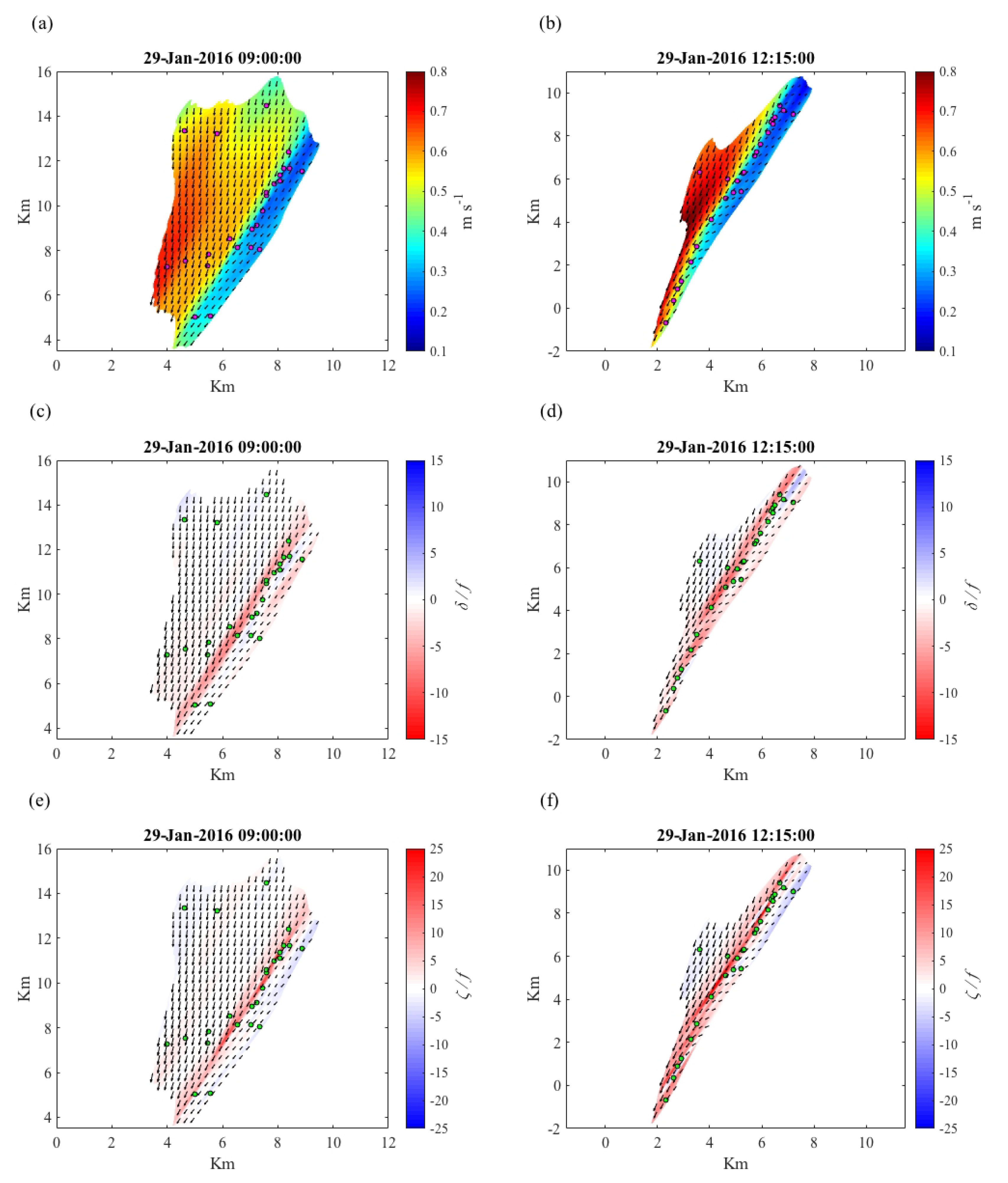
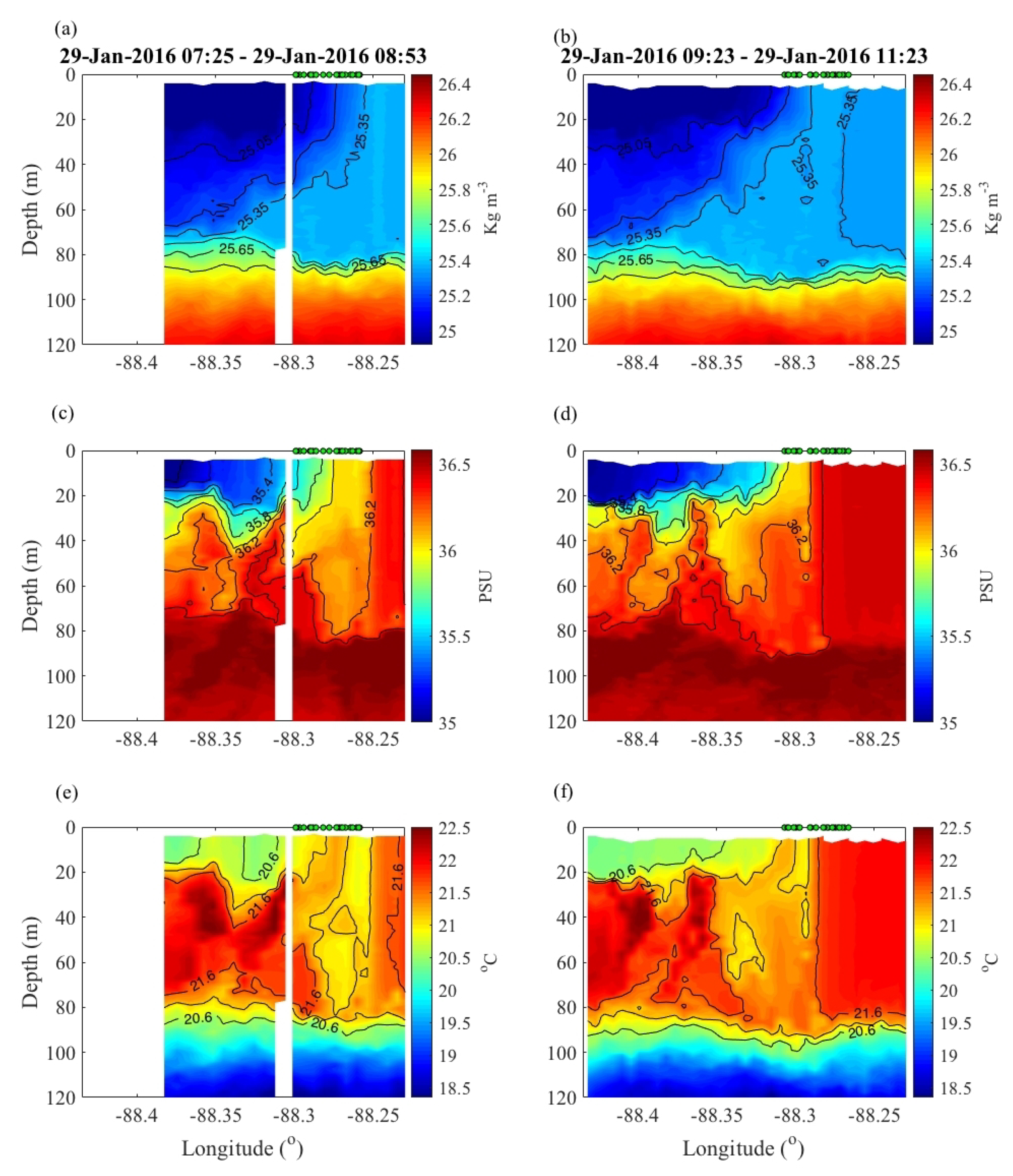
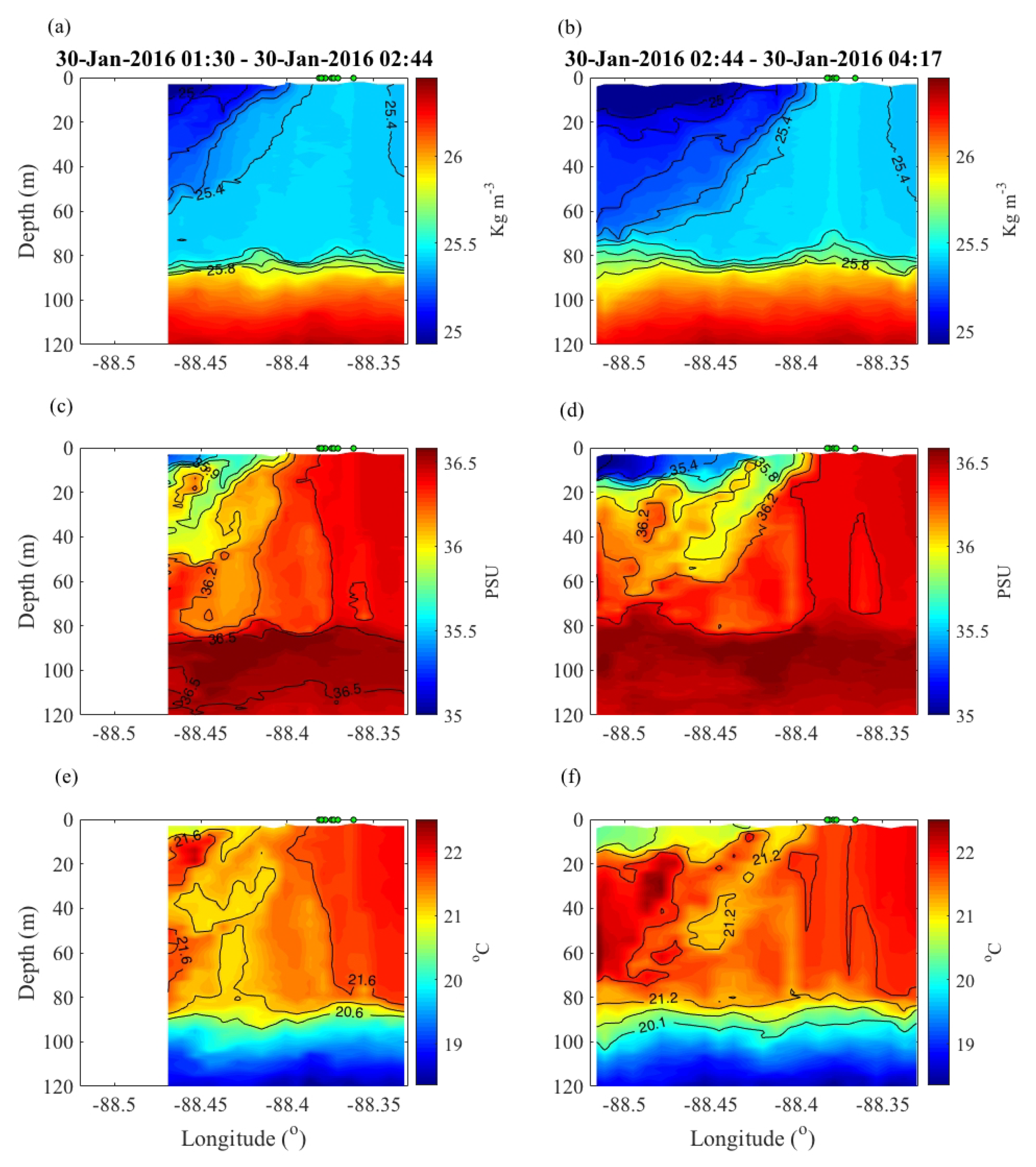
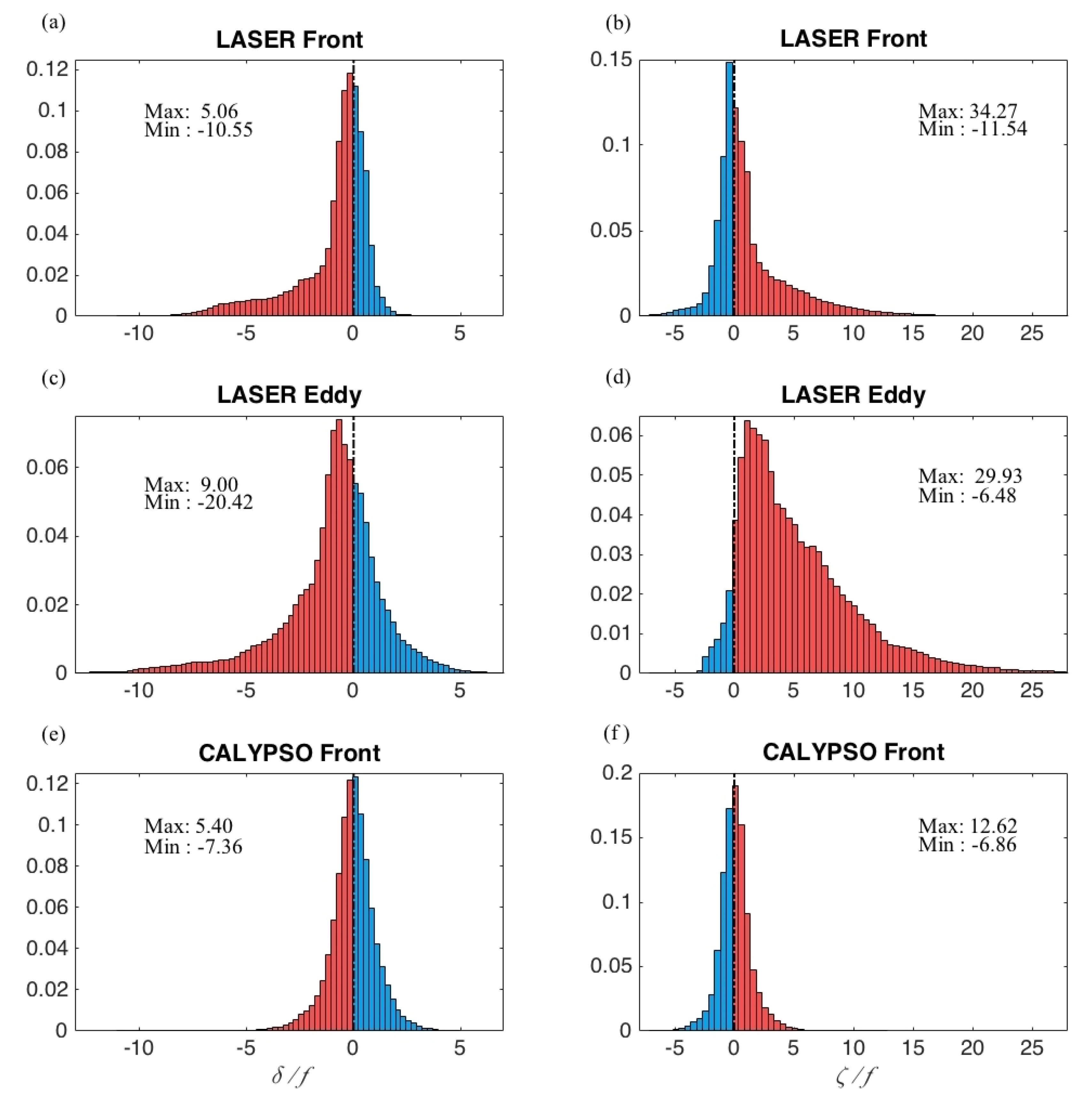
3.2. Mesoscale Front in Gulf of Mexico: Correlation Scales, Kinematics, and CTD Transects
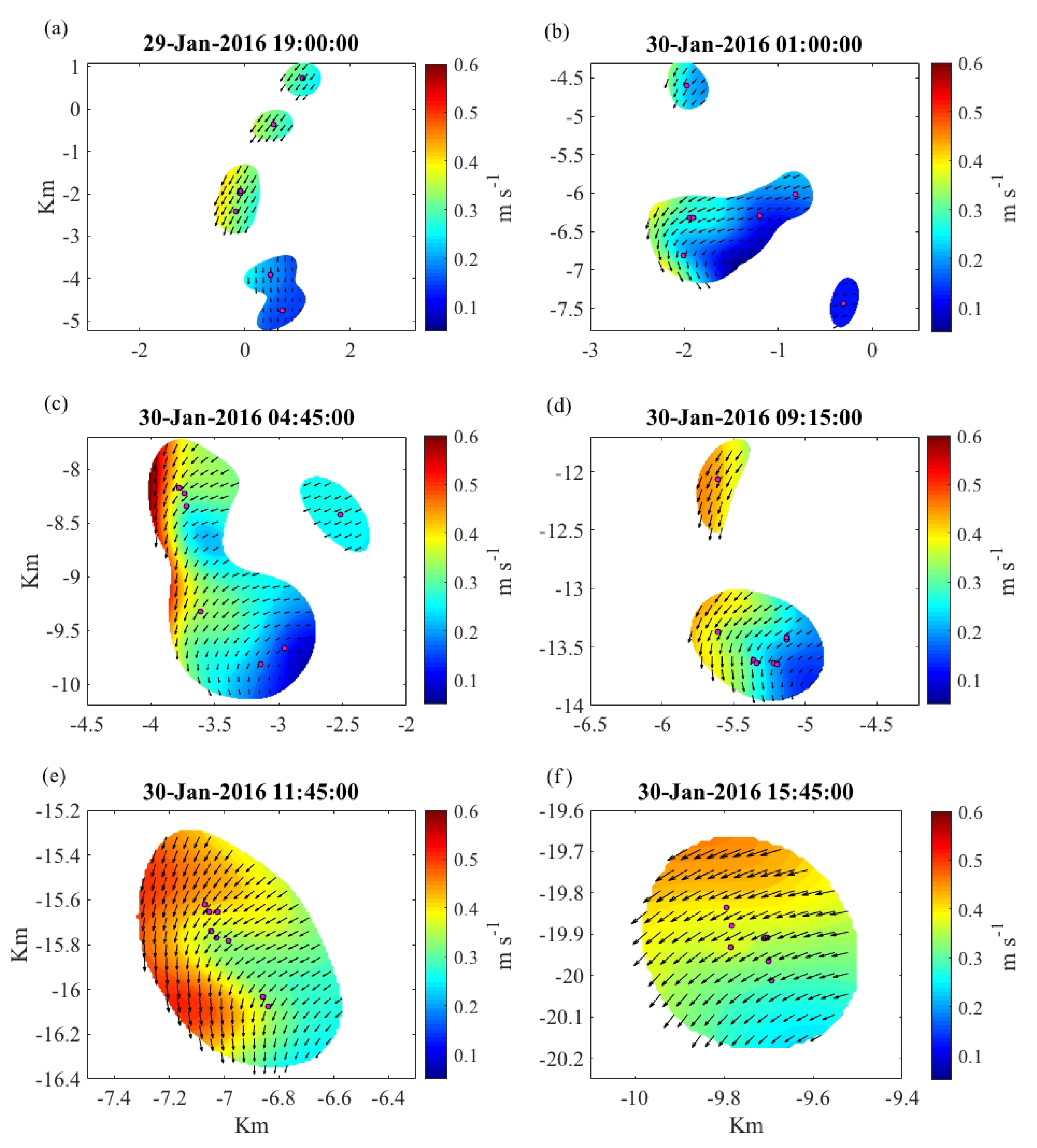
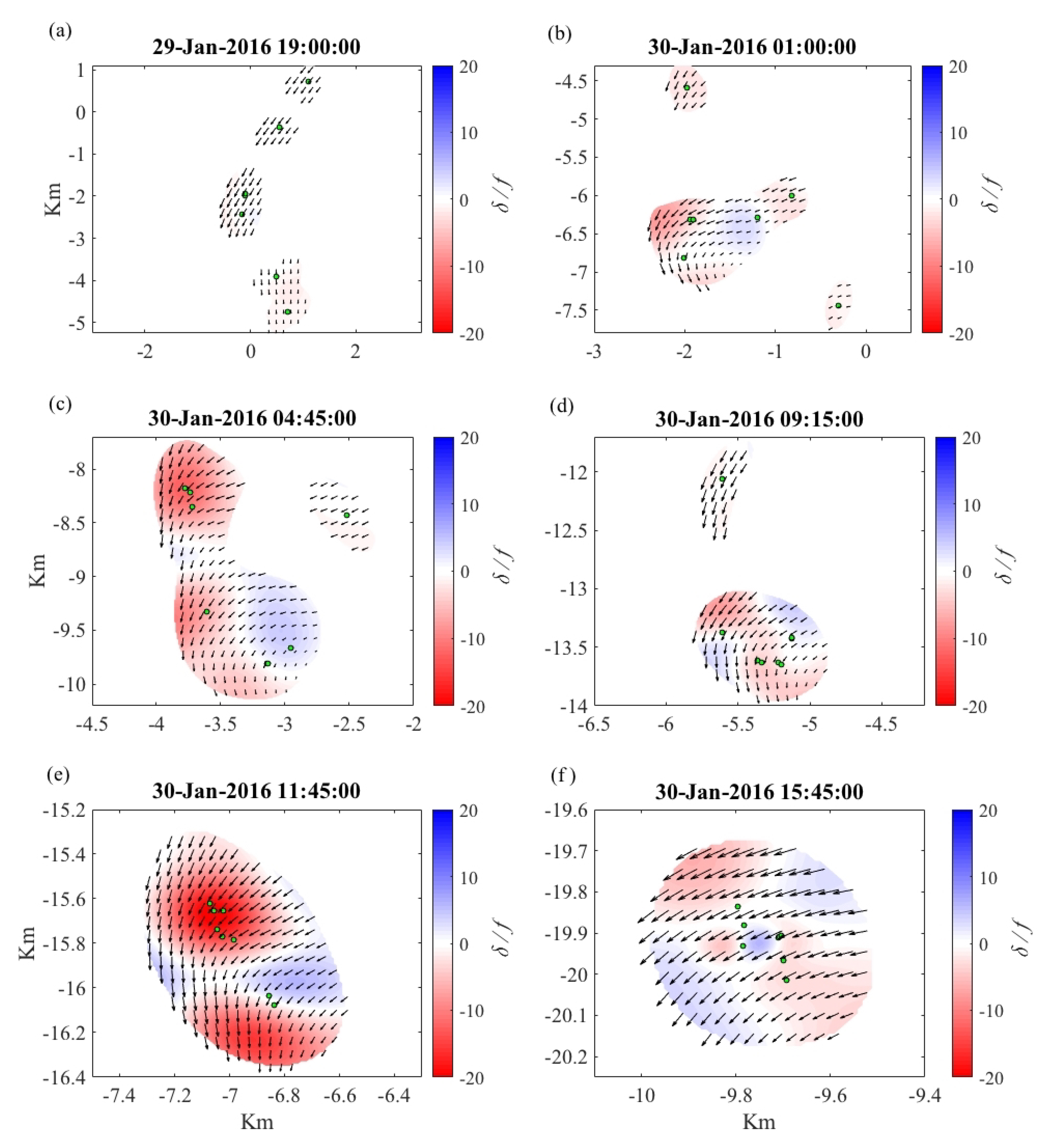
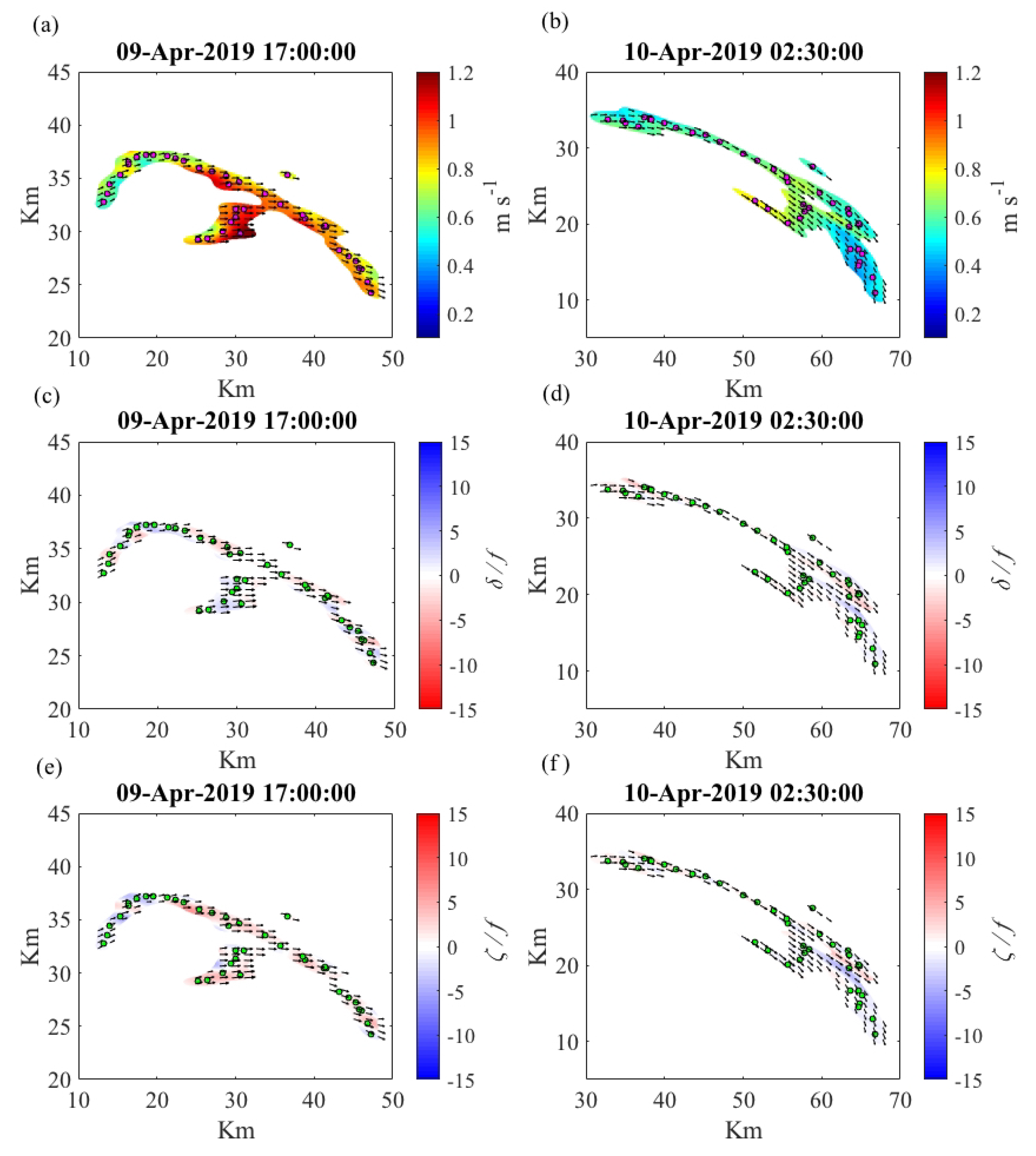
3.3. Submesoscale Eddy: Correlation Scales, Kinematics, and CTD Transects
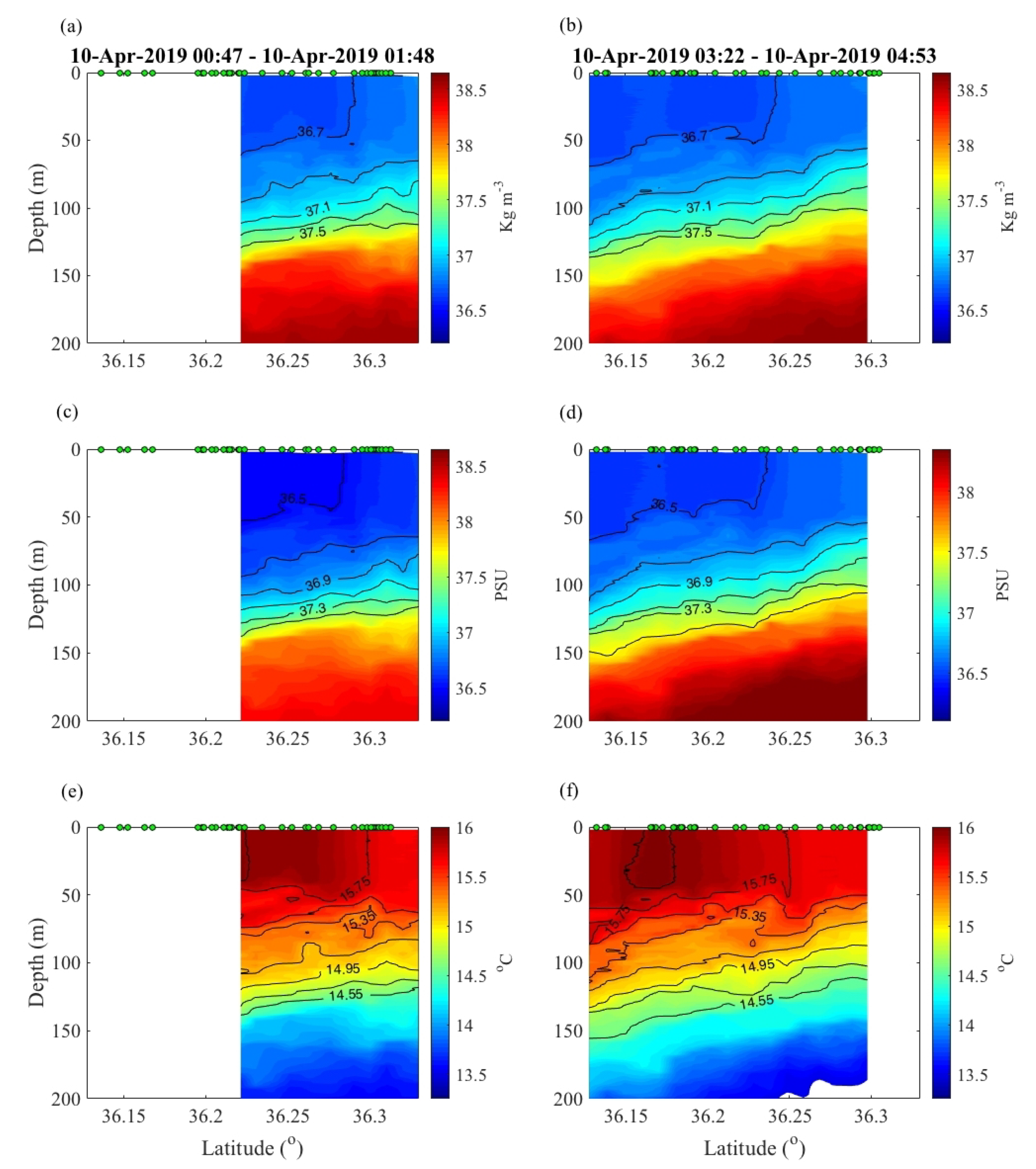
3.4. Comparison to Mesoscale Front in the Mediterranean
3.5. Vertical Velocities
4. Discussion
4.1. X-Band and GPR Velocities in the Gulf of Mexico
4.2. Gulf of Mexico vs. Mediterranean Flow Features
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boccaletti, G.; Ferrari, R.; Fox-Kemper, B. Mixed layer instabilities and restratification. J. Phys. Oceanogr. 2007, 37, 2228–2250. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current system. Part I: Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 2008, 38, 29–43. [Google Scholar] [CrossRef]
- Poje, A.C.; Özgökmen, T.M.; Lipphardt, B.L.; Haus, B.K.; Ryan, E.H.; Haza, A.C.; Jacobs, G.A.; Reniers, A.J.; Olascoaga, M.J.; Novelli, G.; et al. Submesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Natl. Acad. Sci. USA 2014, 111, 12693–12698. [Google Scholar] [CrossRef] [PubMed]
- Özgökmen, T.M.; Poje, A.C.; Fischer, P.F.; Childs, H.; Krishnan, H.; Garth, C.; Haza, A.C.; Ryan, E. On multi-scale dispersion under the influence of surface mixed layer instabilities and deep flows. Ocean Model. 2012, 56, 16–30. [Google Scholar] [CrossRef]
- D’Asaro, E.A.; Shcherbina, A.Y.; Klymak, J.M.; Molemaker, J.; Novelli, G.; Guigand, C.M.; Haza, A.C.; Haus, B.K.; Ryan, E.H.; Jacobs, G.A.; et al. Ocean convergence and the dispersion of flotsam. Proc. Natl. Acad. Sci. USA 2018, 115, 1162–1167. [Google Scholar] [CrossRef] [PubMed]
- Thomas, L.; Ferrari, R. Friction, frontogenesis, and the stratification of the surface mixed layer. J. Phys. Oceanogr. 2008, 38, 2501–2518. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Ohlmann, J.C.; Molemaker, M.J.; Baschek, B.; Holt, B.; Marmorino, G.; Smith, G. Drifter observations of submesoscale flow kinematics in the coastal ocean. Geophys. Res. Lett. 2017, 44, 330–337. [Google Scholar] [CrossRef]
- Mahadevan, A.; Tandon, A. An analysis of mechanisms for submesoscale vertical motion at ocean fronts. Ocean Model. 2006, 14, 241–256. [Google Scholar] [CrossRef]
- Calil, P.H.; Richards, K.J. Transient upwelling hot spots in the oligotrophic North Pacific. J. Geophys. Res. Ocean. 2010, 115, C02003. [Google Scholar] [CrossRef]
- Lévy, M.; Ferrari, R.; Franks, P.J.; Martin, A.P.; Rivière, P. Bringing physics to life at the submesoscale. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Molemaker, M.J.; McWilliams, J.C.; Capet, X. Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 2010, 654, 35–63. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current system. Part II: Frontal processes. J. Phys. Oceanogr. 2008, 38, 44–64. [Google Scholar] [CrossRef]
- D’Asaro, E.; Lee, C.; Rainville, L.; Harcourt, R.; Thomas, L. Enhanced turbulence and energy dissipation at ocean fronts. Science 2011, 332, 318–322. [Google Scholar] [CrossRef] [PubMed]
- Scully-Power, P. Navy oceanographer shuttle observations STS 41-G mission report. NUSC Tech. 1986, 7611, 117. [Google Scholar]
- Munk, W.; Armi, L.; Fischer, K.; Zachariasen, F. Spirals on the sea. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2000, 456, 1217–1280. [Google Scholar] [CrossRef]
- Flament, P.; Armi, L. The shear, convergence, and thermohaline structure of a front. J. Phys. Oceanogr. 2000, 30, 51–66. [Google Scholar] [CrossRef]
- Shcherbina, A.Y.; D’Asaro, E.A.; Lee, C.M.; Klymak, J.M.; Molemaker, M.J.; McWilliams, J.C. Statistics of vertical vorticity, divergence, and strain in a developed submesoscale turbulence field. Geophys. Res. Lett. 2013, 40, 4706–4711. [Google Scholar] [CrossRef]
- Sheres, D.; Kenyon, K.E.; Bernstein, R.L.; Beardsley, R.C. Large horizontal surface velocity shears in the ocean obtained from images of refracting swell and in situ moored current data. J. Geophys. Res. 1985, 90, 4943. [Google Scholar] [CrossRef]
- Lund, B.; Haus, B.K.; Horstmann, J.; Graber, H.C.; Carrasco, R.; Laxague, N.J.; Novelli, G.; Guigand, C.M.; Özgökmen, T.M. Near-surface current mapping by shipboard marine X-band radar: A validation. J. Atmos. Ocean. Technol. 2018, 35, 1077–1090. [Google Scholar] [CrossRef]
- Rascle, N.; Molemaker, J.; Marié, L.; Nouguier, F.; Chapron, B.; Lund, B.; Mouche, A. Intense deformation field at oceanic front inferred from directional sea surface roughness observations. Geophys. Res. Lett. 2017, 44, 5599–5608. [Google Scholar] [CrossRef]
- Berta, M.; Griffa, A.; Özgökmen, T.M.; Poje, A.C. Submesoscale evolution of surface drifter triads in the Gulf of Mexico. Geophys. Res. Lett. 2016, 43, 11751–11759. [Google Scholar] [CrossRef]
- Gonçalves, R.C.; Iskandarani, M.; Özgökmen, T.; Thacker, W.C. Reconstruction of Submesoscale Velocity Field from Surface Drifters. J. Phys. Oceanogr. 2019, 49, 941–958. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [PubMed]
- Thacker, W.C.; Iskandarani, M.; Gonçalves, R.C.; Srinivasan, A.; Knio, O.M. Pragmatic aspects of uncertainty propagation: A conceptual review. Ocean Model. 2015, 95, 25–36. [Google Scholar] [CrossRef]
- Iskandarani, M.; Wang, S.; Srinivasan, A.; Carlisle Thacker, W.; Winokur, J.; Knio, O.M. An overview of uncertainty quantification techniques with application to oceanic and oil-spill simulations. J. Geophys. Res. Ocean. 2016, 121, 2789–2808. [Google Scholar] [CrossRef]
- Haza, A.C.; D’Asaro, E.; Chang, H.; Chen, S.; Curcic, M.; Guigand, C.; Huntley, H.S.; Jacobs, G.; Novelli, G.; Özgökmen, T.M.; et al. Drogue-loss detection for surface drifters during the Lagrangian Submesoscale Experiment (LASER). J. Atmos. Ocean. Technol. 2018, 35, 705–725. [Google Scholar] [CrossRef]
- Novelli, G.; Guigand, C.M.; Cousin, C.; Ryan, E.H.; Laxague, N.J.; Dai, H.; Haus, B.K.; Özgökmen, T.M. A biodegradable surface drifter for ocean sampling on a massive scale. J. Atmos. Ocean. Technol. 2017, 34, 2509–2532. [Google Scholar] [CrossRef]
- Klymak, J.M.; Crawford, W.; Alford, M.H.; Mackinnon, J.A.; Pinkel, R. Along-isopycnal variability of spice in the North Pacific. J. Geophys. Res. C Ocean. 2015, 120, 2287–2307. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Brett, G.; Pratt, L.; Rypina, I.; Sanchez-Garrido, J. The Western Alboran Gyre: An analysis of its properties and its exchange with surrounding water. J. Phys. Oceanogr. 2020. submitted. [Google Scholar]
- Rypina, I.I.; Pratt, L.J.; Pullen, J.; Levin, J.; Gordon, A.L. Chaotic advection in an archipelago. J. Phys. Oceanogr. 2010, 40, 1988–2006. [Google Scholar] [CrossRef]
- Laxague, N.J.; Özgökmen, T.M.; Haus, B.K.; Novelli, G.; Shcherbina, A.; Sutherland, P.; Guigand, C.M.; Lund, B.; Mehta, S.; Alday, M.; et al. Observations of Near-Surface Current Shear Help Describe Oceanic Oil and Plastic Transport. Geophys. Res. Lett. 2018, 45, 245–249. [Google Scholar] [CrossRef]
- Lodise, J.; Özgökmen, T.; Griffa, A.; Berta, M. Vertical structure of ocean surface currents under high winds from massive arrays of drifters. Ocean Sci. 2019, 15, 1627–1651. [Google Scholar] [CrossRef]
- Flexas, M.M.; Gomis, D.; Ruiz, S.; Pascual, A.; León, P. In situ and satellite observations of the eastward migration of the Western Alboran Sea Gyre. Prog. Oceanogr. 2006, 70, 486–509. [Google Scholar] [CrossRef]
- Rudnick, D.L. Intensive surveys of the Azores front: 2. Inferring the geostrophic and vertical velocity fields. J. Geophys. Res. C Ocean. 1996, 101, 16291–16303. [Google Scholar] [CrossRef]
Sample Availability: Raw, processed drifter trajectory data and drogue classification for the Gulf of Mexico are publicly available through the Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC) under https://data.gulfresearchinitiative.org/data/R4.x265.000:0027 (last access: 25 September 2017; D’Asaro et al., 2016), https://data.gulfresearchinitiative.org/data/R4.x265.237:0001 (last access: 25 September 2017; D’Asaro et al., 2017), and https://data.gulfresearchinitiative.org/data/R4.x265.000:0044 (last access: 25 September 2017; Haza et al., 2017), respectively. The moving vessel profiler CTD data can also be found under https://data.gulfresearchinitiative.org/data/R4.x265.000:0028 (last access: 28 June 2017; Klymak et al., 2016). Data associated with the CALYPSO 2019 experiment, Aviso SST products produced by Collecte Localisation Satellites (CLS) with support from CNES, as well as Aqua-MODIS SST data are available upon request. |




| Hyperparameter | u | v |
|---|---|---|
| (m s) | 0.029 | 0.029 |
| (h) | 0.53 | 1.33 |
| (km Cross-front) | 0.07 | 0.23 |
| (km Along-front) | 0.63 | 1.46 |
| (m s) | 0.343 | 0.153 |
| (h) | 4.23 | 2.82 |
| (km Cross-front) | 0.77 | 1.6 |
| (km Along-front) | 5.85 | 5.23 |
| (m s) | 0.012 | 0.011 |
| Time Period | Velocity | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Component | (m s) | (h) | (km) | (km) | (m s) | (h) | (km) | (km) | (m s) | |
| 29 January 12:00–29 January 19:45 | u | 0.022 | 0.70 | 0.27 | 0.28 | 0.063 | 5.36 | 2.29 | 2.46 | 0.002 |
| v | 0.039 | 0.77 | 0.37 | 0.14 | 0.130 | 7.51 | 1.39 | 0.53 | 0.007 | |
| 29 January 18:00–30 January 01:45 | u | 0.057 | 1.26 | 0.42 | 0.38 | 0.074 | 2669 | 2.53 | 3.27 | 0.001 |
| v | 0.040 | 1.26 | 0.80 | 0.55 | 0.184 | 17,550 | 12.48 | 1.03 | 0.005 | |
| 30 January 00:00–30 January 07:45 | u | 0.057 | 1.48 | 0.38 | 0.33 | 0.161 | 10,273 | 1.10 | 1.30 | 0.005 |
| v | 0.067 | 1.21 | 0.40 | 0.33 | 0.187 | 6.27 | 2334 | 0.36 | 0.004 | |
| 30 January 06:00–30 January 13:45 | u | 0.049 | 0.74 | 0.25 | 0.21 | 0.075 | 10.77 | 0.39 | 0.35 | 0.005 |
| v | 0.037 | 0.57 | 0.16 | 0.18 | 0.157 | 8652 | 6837 | 0.57 | 0.003 | |
| 30 January 11:00–30 January 18:45 ** | u | 0.001 | 0.54 | 0.03 | 0.05 | 0.097 | 2.77 | 0.29 | 0.23 | 0.003 |
| v | 0.047 | 0.96 | 0.13 | 0.13 | 0.129 | 2121 | 1.91 | 0.36 | 0.007 |
| Time Period | Velocity | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Component | (m s) | (h) | (km) | (km) | (m s) | (h) | (km) | (km) | (m s) | |
| 09 April 15:00–09 April 22:45 | u | 0.097 | 0.72 | 0.75 | 1.87 | 0.426 | 5.69 | 12.06 | 18.64 | 0.001 |
| v | 0.067 | 0.72 | 0.58 | 2.25 | 0.242 | 6.71 | 18.28 | 12.12 | 0.001 | |
| 09 April 21:00–10 April 04:45 | u | 0.064 | 1.10 | 0.57 | 2.48 | 0.627 | 7.02 | 15.23 | 12.06 | 0.008 |
| v | 0.052 | 1.00 | 0.56 | 2.48 | 0.250 | 4.26 | 10.44 | 22.01 | 0.005 |
| Flow Feature | (m s) | (m) | |
|---|---|---|---|
| GoM Mesoscale Front | −0.029 | 40 | -10.55 |
| GoM Submesoscale Eddy | −0.056 | 40 | −20.42 |
| Med Mesoscale Front | −0.0270 | 50 | −7.36 |
| Reference | Max | Max | Instrument | Method |
|---|---|---|---|---|
| Shcherbina et al. (2013) | 2 | 3 | ADCP | Dual ship transects |
| Lund et al. (2018) | 5 | 5 | X-band Radar | Backscatter intensity |
| D’Asaro et al. (2018) | 6 | 8 | CARTHE Drifters | Cluster ellipses |
| Ohlmann et al. (2017) | 10 * | 10 | Microstar drifters | Linear least squares |
| Gonçalves et al. (2019) | 8 | 13 | CARTHE Drifters | GPR |
| Current work(Med Sea Front) | 7 | 13 | CARTHE Drifters | GPR rotational |
| Current work(Gulf of Mexico Front) | 11 | 34 | CARTHE Drifters | GPR rotational |
| Current work(Gulf of Mexico Eddy) | 20 | 30 | CARTHE Drifters | GPR center of mass |
| Rascle et al. (2017) ** | 45–80 | 45–80 | Visible camera via aeroplane | Sea surface roughness |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lodise, J.; Özgökmen, T.; Gonçalves, R.C.; Iskandarani, M.; Lund, B.; Horstmann, J.; Poulain, P.-M.; Klymak, J.; Ryan, E.H.; Guigand, C. Investigating the Formation of Submesoscale Structures along Mesoscale Fronts and Estimating Kinematic Quantities Using Lagrangian Drifters. Fluids 2020, 5, 159. https://doi.org/10.3390/fluids5030159
Lodise J, Özgökmen T, Gonçalves RC, Iskandarani M, Lund B, Horstmann J, Poulain P-M, Klymak J, Ryan EH, Guigand C. Investigating the Formation of Submesoscale Structures along Mesoscale Fronts and Estimating Kinematic Quantities Using Lagrangian Drifters. Fluids. 2020; 5(3):159. https://doi.org/10.3390/fluids5030159
Chicago/Turabian StyleLodise, John, Tamay Özgökmen, Rafael C. Gonçalves, Mohamed Iskandarani, Björn Lund, Jochen Horstmann, Pierre-Marie Poulain, Jody Klymak, Edward H. Ryan, and Cedric Guigand. 2020. "Investigating the Formation of Submesoscale Structures along Mesoscale Fronts and Estimating Kinematic Quantities Using Lagrangian Drifters" Fluids 5, no. 3: 159. https://doi.org/10.3390/fluids5030159
APA StyleLodise, J., Özgökmen, T., Gonçalves, R. C., Iskandarani, M., Lund, B., Horstmann, J., Poulain, P.-M., Klymak, J., Ryan, E. H., & Guigand, C. (2020). Investigating the Formation of Submesoscale Structures along Mesoscale Fronts and Estimating Kinematic Quantities Using Lagrangian Drifters. Fluids, 5(3), 159. https://doi.org/10.3390/fluids5030159