Abstract
A fully coupled pressure-based algorithm and finite-volume framework for the simulation of the acoustic cavitation of bubbles in polytropic gas-liquid systems is proposed. The algorithm is based on a conservative finite-volume discretization with collocated variable arrangement, in which the discretized governing equations are solved in a single linear system of equations for pressure and velocity. Density is described by the polytropic Noble-Abel stiffened-gas model and the interface between the interacting bulk phases is captured by a state-of-the-art algebraic Volume-of-Fluid (VOF) method. The new numerical algorithm is validated using representative test-cases of the interaction of acoustic waves with the gas-liquid interface as well as pressure-driven bubble dynamics in infinite and confined domains, showing excellent agreement of the results obtained with the proposed algorithm compared to linear acoustic theory, the Gilmore model and high-fidelity experiments.
1. Introduction
Acoustic cavitation describes the pressure-driven behavior of bubbles in a liquid environment, where an externally introduced change in pressure, e.g., by an ultrasound transducer or through laser-induced optical breakdown, causes a radial bubble motion that can range from moderate bubble oscillations to a strong inertial bubble collapse that emits shock waves in the liquid, concentrating large amounts of acoustic energy [1]. In many engineering applications, ranging from fast-running ship propellers to artificial heart valves, hydrodynamic cavitation, where the pressure difference is induced by an acceleration of the flow, is associated with considerable negative effects on its environment and is, therefore, undesirable. Acoustic cavitation, however, was found to be useful for a large number of engineering applications, including ultrasonic cleaning [2], for ultrasonic contrast agents in medical imaging [3], to actuated microbubbles that act as micropumps [4], and to facilitate self-organization of microbubbles into crystals and arrays [5].
Since Lord Rayleigh first derived a model for the pressure-driven collapse of an empty cavity in an incompressible liquid in 1917 [6], substantial research efforts have been dedicated to understanding and mathematically describing the pressure-driven behavior of bubbles [1,7]. Plesset [8] extended the model of Rayleigh to account for the gas phase inside the bubble, which led to the famous Rayleigh-Plesset (RP) equation, a second-order differential equation, which has since been extended to include liquid compressibility [9,10], among other mechanisms. The RP equation and its subsequent extensions have been the basis for most subsequent research on cavitation. However, RP equations are based on strongly simplifying assumptions: the bubble is spherical and the gas density is assumed to be much smaller than the liquid density. Alleviating these limitations requires computation of the fully resolved flow field and interface dynamics of the gas-liquid system, by solving the full set of governing conservation laws describing the behavior of two-phase flows using appropriate numerical methods, such as finite-volume or finite-element methods. Such numerical methods have been recently applied to study a broad range of cavitation phenomena, including laser-induced cavitation bubbles [11,12], the bubble-collapse-driven penetration of a biomaterial surrogate [13], shock-driven bubble collapse [14,15] or the dynamics of cavitation bubbles in viscoelastic media [16].
Describing the interacting fluids by a polytropic equation of state is a popular choice when modeling the pressure-driven behavior of bubbles [7,12]. In a polytropic fluid, the density is a function of only the pressure p, as defined by the polytropic relationship, given for an ideal gas as , where is the polytropic exponent and is a fluid-dependent constant. From a mathematical and numerical viewpoint, the most appealing feature of flows of polytropic fluids is that pressure does not depend on temperature and the energy equation becomes redundant, simplifying the mathematical analysis of these flows as well as the design and implementation of the associated numerical methods. Describing the gas inside bubbles as a polytropic fluid is one of the founding assumptions of the RP equation [17] and using polytropic fluid models has been demonstrated to be suitable even for the prediction of complex bubble behavior, such as wall-bounded cavitation [12].
Pressure-based algorithms, in which the density is described by a suitable equation of state and the continuity equation serves as an equation for pressure, are particularly suited to model acoustic cavitation, due to the broad range of Mach numbers occurring in cavitating gas-liquid systems. To this end, an important aspect of pressure-based algorithms is that changes in pressure are finite in all Mach number regimes and that the vanishing density differences at low Mach numbers do not present a problem [18]. Pressure-based algorithms for compressible and incompressible flows are traditionally founded on a predictor-corrector procedure, e.g., projection methods [19,20] or the SIMPLE method [21]. Previously proposed pressure-based finite-volume algorithms using polytropic fluid models dedicated to the prediction of bubble dynamics and cavitation are also founded on such segregated algorithms [12,22,23]. Over the past decade, research efforts dedicated to pressure-based algorithms have increasingly focused on fully coupled methods [18,24,25,26,27,28,29], whereby the discretized governing equations are solved simultaneously in a single system of equations, which have been shown to yield performance benefits for incompressible flows [24] and an improved stability for two-phase flows [26]. Furthermore, fully coupled algorithms do not require any form of underrelaxation to reach a converged solution, even for compressible flows with strong shocks [29], contrary to segregated pressure-based algorithms. Recent work by Denner and co-workers [15,30] has demonstrated the utility of fully coupled pressure-based algorithms for interfacial flows at all Mach numbers, including bubble dynamics and collapse. Despite the demonstrated versatility, robustness and increasing maturity of fully coupled pressure-based algorithms, such an algorithm has not yet been proposed for two-phase flows of polytropic fluids.
In this article, a novel fully coupled pressure-based algorithm for the prediction of acoustic cavitation is proposed, based on a conservative finite-volume framework and a Volume-of-Fluid (VOF) method to represent the interacting bulk phases. The discretized continuity and momentum equations are solved simultaneously in a single linear system of equations for pressure and velocity, with density defined based on pressure by a polytropic fluid model. Each term of the linearized and discretized governing equations makes an implicit contribution to pressure and/or velocity, leading to a robust pressure-velocity coupling. The proposed numerical framework is validated by representative test-cases, including the propagation of acoustic waves, as well as the Rayleigh collapse and the wall-bounded cavitation of a bubble.
The governing equations are presented in Section 2, the polytropic closure model is presented in Section 3, the numerical framework is described in Section 4 and the interface treatment is presented in Section 5. The results of the various test-cases considered to validate the numerical framework are presented in Section 6. The article is concluded and summarized in Section 7.
2. Governing Equations
The conservation laws governing the flow of a polytropic fluid are the conservation of mass
and the conservation of momentum
where t is the time, is the velocity vector, p is the pressure and is the density. The stress tensor for the considered Newtonian fluids is given as
where is the dynamic viscosity.
The Volume-of-Fluid (VOF) method [31] is applied to distinguish the interacting bulk phases and model the motion of the fluid interface. Both bulk phases are represented by an indicator function , with
where is the computational domain, where and are the subdomains occupied by fluids a and b, respectively. Neglecting mass transfer between the bulk phases, the fluid interface propagates with the flow and, therefore, the material derivative of is
In the interest of clarity but without loss of generality, surface tension and gravity are neglected in the following, to focus on the novel aspects of the proposed algorithm. However, the extension of the proposed algorithm to include surface tension and gravity is straightforward, following the work of Denner and van Wachem [26].
3. Polytropic Closure
The governing Equations (1) and (2) are closed by defining the density based on pressure, using the Noble–Abel stiffened-gas (NASG) model [32]. The NASG model combines the Noble–Abel gas model (also often called co-volume gas model) [33] and the stiffened-gas model [34] to obtain a simple gas model that accounts for molecular repulsion and attraction. The thermal equation of state of the NASG model is defined as [32]
where is the heat capacity ratio, is the specific isochoric heat capacity, is the specific isobaric heat capacity, is the specific volume, b is the co-volume and is a pressure constant that accounts for the attraction between molecules. Based on the isentropic relationship for such an NASG fluid [32], a polytropic fluid model can be derived as
where and is the polytropic exponent, from which the density follows as
The polytropic constant K is defined based on the predefined reference density and the predefined reference pressure as
The polytropic NASG model reduces to the polytropic description of an ideal-gas model for , , of a Noble-Abel gas model for , , and of a stiffened-gas model for and .
4. Numerical Framework
The proposed numerical framework is predicated on a fully coupled pressure-based algorithm with a conservative finite-volume discretization of the governing equations and a collocated variable arrangement [18], with a spatial and temporal convergence that is consistent with the employed second-order schemes [18,30]. The momentum-weighted interpolation used to define the fluxes at cell faces is the only source of numerical dissipation, leading to a small error in kinetic energy that converges with third order under mesh refinement [18,35]. The numerical framework presented in the following assumes a rectilinear mesh, without skewness or non-orthogonality. Corrections for mesh skewness and non-orthogonality may be included in the presented discretization following the work of Denner et al. [18].
4.1. Finite-Volume Discretization
The BDF2 scheme, also known as Second-Order Backward Euler scheme, is used to discretize the transient terms of the governing equations, which is defined for the transient term of a general fluid variable, , at cell P as [18]
with , where V is the volume of the mesh cell, is the current time-step and is the previous time-step. The superscripts and denote the values of the previous and previous-previous time-level, respectively. For consistency, the transient terms of both the continuity Equation (1) and the momentum Equation (2) are discretized with the same scheme.
Applying the divergence theorem and the midpoint rule, the advection terms of the governing equations are discretized as
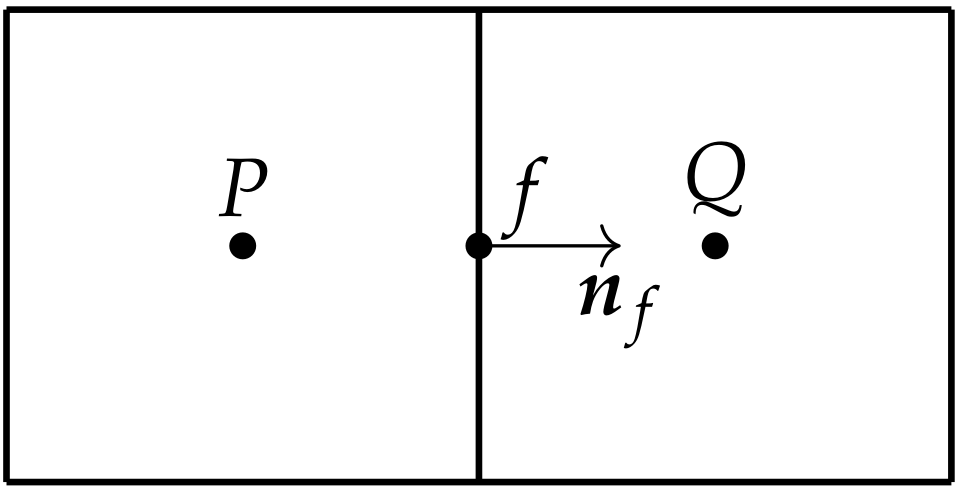
where subscript f denotes the mesh face shared by cell P and its neighbor cell Q, as illustrated in Figure 1, is the advecting velocity at face f, presented in detail in Section 4.2, is the area of mesh face f and is the unit normal vector of face f, which points out of cell P. The advected variable is interpolated using a TVD formulation, given as [36]
where and are the values of the advected variable at the upwind and downwind cells, respectively, is the position of the center of the upwind cell U, is the position of the center of face f, is the distance between the cell centers adjacent to face f, and is the flux limiter.
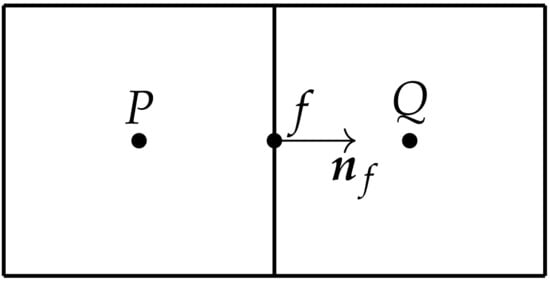
Figure 1.
Illustration of mesh cell P and its neighbor cell Q, with their shared face f and its unit normal vector (pointing out of cell P).
Applying the divergence theorem, the viscous stress term of the momentum Equation (2) is given as
where denotes linear interpolation from the adjacent cell centers and is the face viscosity determined by harmonic interpolation from the adjacent cell centers. The face-centered gradient of the primary velocity component, , is discretized as
4.2. Advecting Velocity
The advecting velocity, , is discretized based on a momentum-weighted interpolation (MWI) [37]. The MWI provides a robust coupling between pressure and velocity for flows at low Mach numbers [35] and avoids pressure-velocity decoupling as a result of the applied collocated variable arrangement. The advecting velocity at face f is given as [35]
where the face density is determined by harmonic interpolation from the cell centers adjacent to face f. The coefficient is defined based on the applied time-step as well as the velocity coefficients associated with the advection and shear stress terms of the discretized momentum equations [35]. The density weighting applied to the cell-centered pressure gradient has been shown to yield robust results for flows with large and abrupt changes in density [35], demonstrated for incompressible interfacial flows with a density ratio of up to [26,38]. The transient term of Equation (15) is critical for a correct representation of pressure waves and ensures that the MWI is time-step independent [35].
4.3. Discretized Governing Equations
Applying the discretization schemes described above, the discretized continuity Equation (1) is given at cell P as
and the discretized momentum Equation (2) are given at cell P as
where superscript n is the iteration counter of the nonlinear iterations conducted to solve the discretized governing equations in each time-step, see Section 4.4. To this end, superscript denotes the solution that is sought implicitly and superscript stands for the most recent available solution. A Newton linearization is applied to linearize both governing equations [29]. The linearization of the advection term of the continuity equation as well as the transient term of the momentum equations is defined as
and the linearization of the advection term of the momentum equations is defined as
where , and are generic fluid variables. This linearization facilitates an implicit treatment of all terms in the governing equations that depend on pressure and velocity, which has previously been shown to improve the stability and performance of the solution algorithm for flows in all Mach number regimes [29,39,40]. It also provides the implicit pressure-velocity coupling necessary to robustly predict flows with low Mach numbers.
The implicit treatment of the density at cell centers is given by reformulating Equation (8) as an implicit function of the cell-centered pressure, given as
and the implicit treatment of the advecting velocity is given by the semi-implicit formulation
4.4. Solution Procedure
The linear system of discretized governing equations, , is solved simultaneously for the pressure p and the velocity vector . Considering a three-dimensional computational mesh with N cells, this linear system of equations then follows as
where are the coefficient submatrices of size , where denotes the conserved quantity and denotes the primary solution variable associated with a given governing equation. The subvectors with length N contain the solution of the primary solution variable and the subvectors with length N contain all contributions from boundary conditions, previous nonlinear iterations as well as previous time-levels. The solution procedure conducts nonlinear iterations to solve the system of discretized Equations (22), in which (22) is preconditioned by the Block-Jacobi preconditioner and then solved using the BiCGSTAB solver of the software library PETSc [41,42,43], as discussed in detail by Denner et al. [18].
5. Interface Treatment
The discretized governing equations are extended to interfacial flows using an interface advection method (see Section 5.1) in conjunction with an appropriate definition of the fluid properties (see Section 5.2). In order to represent the two interacting fluids discretely, the indicator function translates into a color function , defined for cell P as
5.1. Interface Advection
To advect the fluid interface between two fluids, Equation (5) is integrated in each cell, which gives the following transport equation for the color function , Equation (23),
which is discretized using an algebraic VOF method [30]. Discretizing the transient term using the Crank–Nicolson scheme, the semi-discretized form of Equation (24) is given as
where is the applied VOF time-step. The same advecting velocity that is used for all advection terms of the discretized governing equations is applied to advect the color function. The face value is discretized using the CICSAM scheme [44], which accounts for the available flux volume as well as the orientation of the interface. To retain a sharp interface, a relatively small time-step is used, satisfying a Courant number of , and a dual time-stepping method [45] is applied for a better computational performance. The time-step applied to solve the VOF advection equation is generally smaller than the time-step applied to solve Equation (22). The fluid time-step , thus, has to be an integer multiple of the VOF time-step to ensure a consistent advection of the color function.
This algebraic VOF method captures volume changes of the bulk phases with second-order accuracy [30] and has been used successfully for studies of bubble dynamics in compressible [15,30] and incompressible [46] interfacial flows. Nevertheless, the presented pressure-based algorithm is not limited to the employed algebraic VOF method; other methods to represent the bulk phases or advect the interface may equally be applied.
5.2. Fluid Properties
The treatment of density at fluid interfaces is based on the acoustically conservative interface discretization (ACID) method [30]. The primary assumption of the ACID method is that all cells in the finite-volume stencil of a given cell are assigned the same color function value, i.e., the color function is assumed to be constant in the entire finite-volume stencil. Density, which is discontinuous at the interface, is then evaluated based on this locally constant color function field, which recovers the contact discontinuity represented by the interface [33,47]. Denner et al. [30] reported robust and accurate results for acoustic and shock waves in interfacial flows, supporting the notion that the interface discretization indeed conserves the acoustic features of the flow.
Under the assumptions made by the ACID method, the density interpolated to face f of cell P is given as
The density at the upwind cell U of face f and the density at the downwind cell D of face f are defined based on the color function value of cell P, , as
where the partial densities and associated with fluids and are given by Equation (8). The densities at previous time-levels are evaluated similarly, based on , following as
and analogously for .
In order to treat the density implicitly, as given in Equation (20), the coefficient of the implicit pressure value is defined as
and the pressure constant as
with the polytropic constants and given by Equation (9) based on the reference pressure and reference density of the respective bulk phase.
The viscosity in cell P is defined by a linear interpolation based on the color function, given as
6. Results
The proposed algorithm is validated for the simulation of acoustic cavitation using test-cases representative of this kind of flow. The propagation of acoustic waves presented in Section 6.1 tests the accurate treatment of acoustic effects and the Rayleigh collapse in Section 6.2 tests the correct prediction of the entire pressure-driven bubble dynamics. Lastly, the wall-bounded cavitation of a bubble for a broad range of bubble stand-off distances in Section 6.3 scrutinizes the reliable prediction of complex cavitation events, also in comparison to experiments. For this validation, four different fluids are considered, with the fluid properties given in Table 1. While the Tait model of water is frequently used to simulate cavitation events in water, using the full NASG model of water provides an alternative description. The JA2 propellant gas is considered to be an alternative gas, to demonstrate the prediction of acoustic effects in a Noble–Abel gas.

Table 1.
Properties of the considered fluids.
6.1. Acoustic Waves
Reproducing the interaction between acoustic waves and fluid interfaces correctly is a basic requirement for the accurate prediction of acoustic cavitation. Given a small perturbation to the flow, with the amplitude of the velocity perturbation , the resulting acoustic wave propagates with the speed of sound , given for a general NASG fluid as
with a pressure wave of amplitude [47]. For all considered cases, the unperturbed flow velocity is and the ambient pressure is . The computational domain is represented with a mesh spacing of .
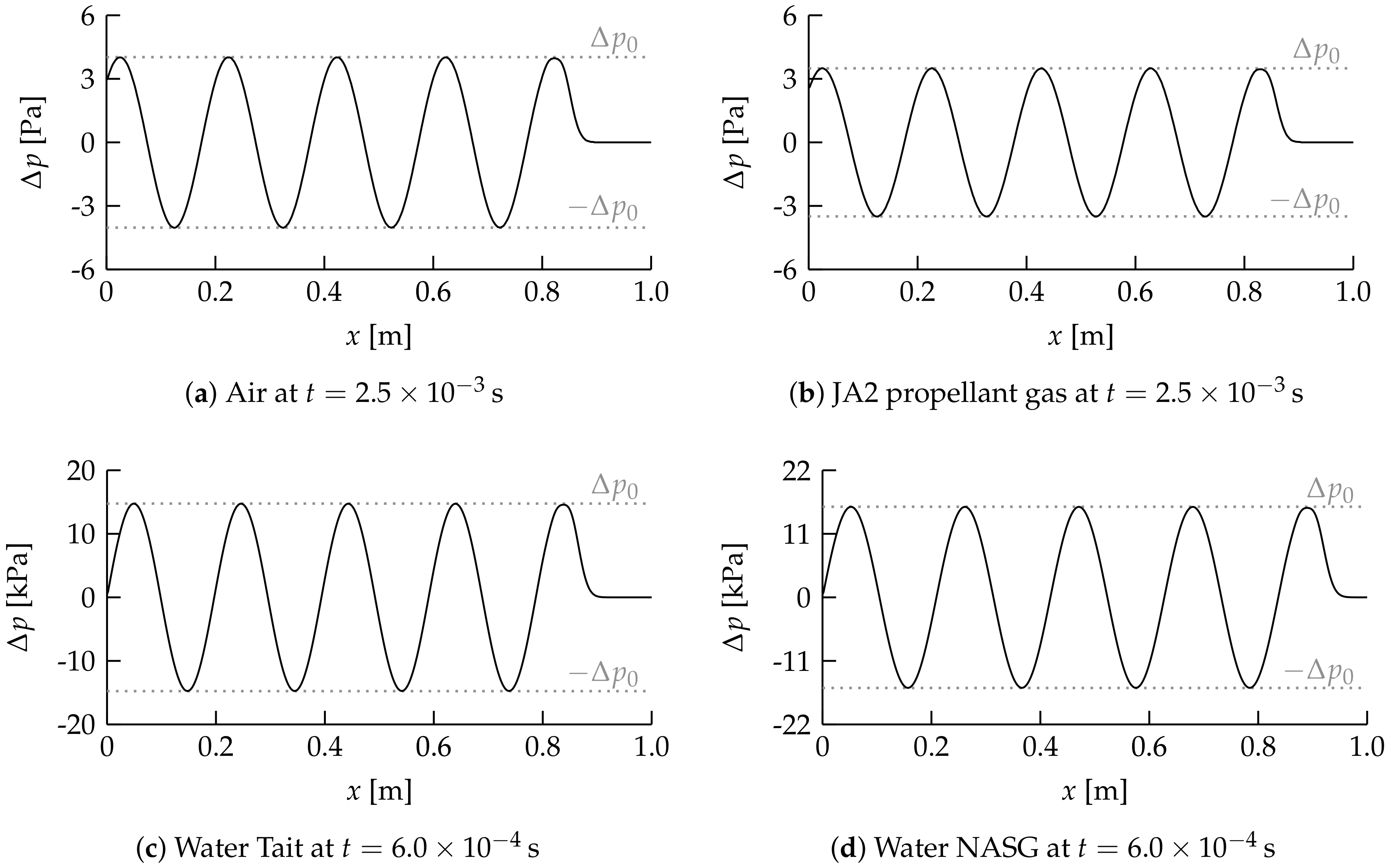
First, the propagation of acoustic waves in a single-phase flow is considered. The acoustic waves are generated by a periodically changing velocity at the domain inlet, which is defined as , where is the amplitude of the velocity perturbation and f is the excitation frequency given in Table 2. Figure 2 shows the pressure profiles of acoustic waves in each fluid shortly before the waves reach the domain outlet at . The wavelength and pressure amplitude predicted by the proposed algorithm for these acoustic waves are given in Table 2. For all cases and are in excellent agreement with the theoretical values and according to linear acoustic theory, also given in Table 2.

Table 2.
The excitation frequency f of the acoustic waves, the reference density and the associated speed of sound at the reference pressure of , the wavelength and pressure amplitude of the acoustic waves given by linear acoustic theory, and the wavelength and the pressure amplitude of the acoustic waves predicted by the proposed algorithm.
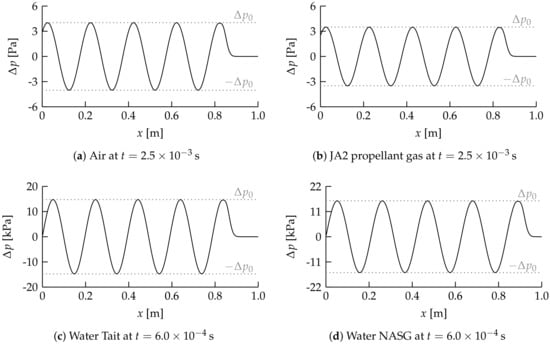
Figure 2.
Pressure profiles of acoustic waves in different fluids obtained using the proposed algorithm. The pressure amplitudes based on linear acoustic theory, , are shown as a reference.
The propagation of a single acoustic wave in gas-liquid flows is simulated to demonstrate the accurate prediction of the interaction of acoustic waves with fluid interfaces. The acoustic wave is initiated in the left phase by a Gaussian pressure pulse as
where and are the initial amplitude and the initial position of the pressure pulse, respectively. Based on linear acoustic theory [47], the pressure pulse reflected in the left phase at the fluid interface should have a pressure amplitude of
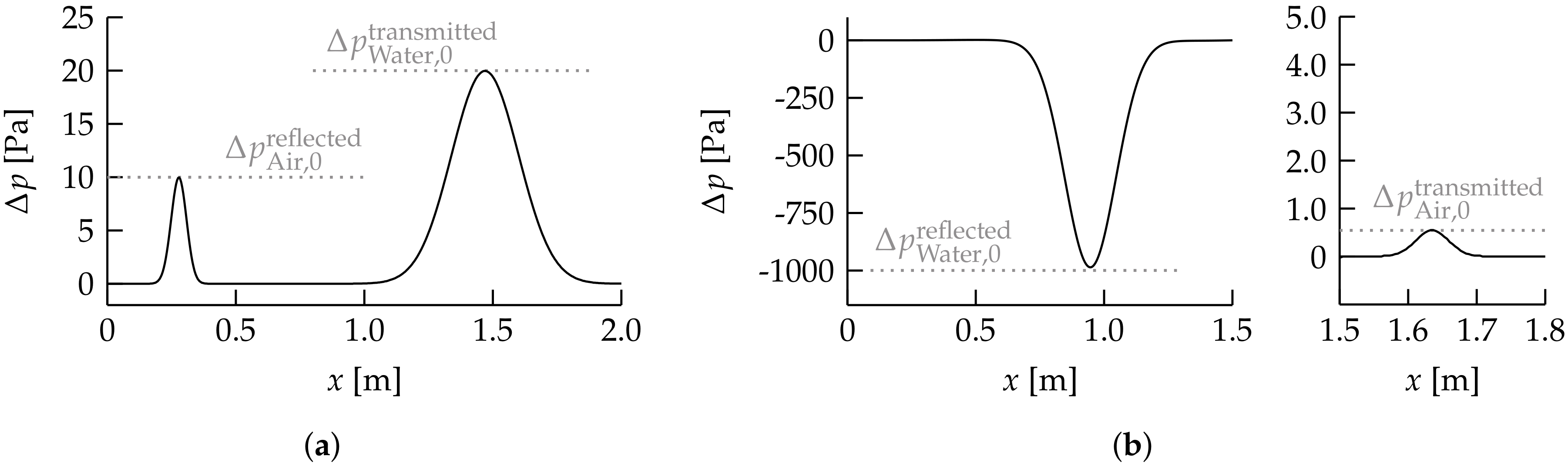
with the pressure amplitude of the incident pulse given as , and the pressure amplitude of the pulse transmitted to the right phase should be , where subscripts L and R denote the left and right phases, respectively, and is the characteristic acoustic impedance. The pressure profiles of the pulses are shown in Figure 3 for two air–water systems, after the pressure pulse interacted with the fluid interface. Figure 3a shows the pressure pulse, initialized in the gas phase with and at , in an air–water system, with water described using the properties of Water NASG given in Table 1. The pressure amplitude of the reflected and transmitted pulses are both in excellent agreement with linear acoustic theory. Similarly, the pressure amplitudes of the reflected and transmitted pulses are also in excellent agreement with linear acoustic theory for the case shown in Figure 3b, where the pressure pulse is initialized in the liquid phase with and at , and with water described using the properties of Water Tait given in Table 1.
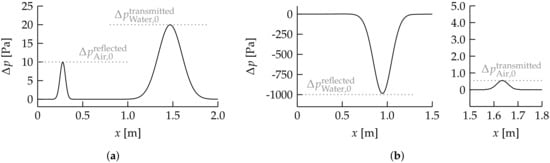
Figure 3.
Profiles of pressure pulses in different air–water systems obtained using the proposed algorithm. The amplitudes of the pressure pulses reflected and transmitted at the fluid interface based on linear acoustic theory are shown as a reference. (a) Air–water (Water NASG) system at . The pressure pulse is initialized with , and . The air-water interface is located at . (b) Water-air (Water Tait) system at . The reflected pressure pulse in water and the transmitted pressure pulse in air are shown in separate graphs, due to their very different amplitudes. The pressure pulse is initialized with , and . The air-water interface is located at .
6.2. Rayleigh Collapse
The behavior of a spherical bubble collapsing as a result of an initial overpressure in the liquid compared to the pressure in the gas bubble is considered, the so-called Rayleigh collapse [49], to scrutinize the prediction of pressure-driven bubble dynamics by the proposed algorithm. The Gilmore model [9], which is an extension of the classical RP model, for the dynamic behavior of a spherical gas bubble in a compressible liquid is used as a reference solution. The solution of the Gilmore model is, therefore, regarded as the exact solution of the dynamic bubble behavior under consideration. The dissipation due to both viscous stresses and acoustic radiation is included in these simulations, leading to a complex interplay of the hydrodynamics, e.g., viscous dissipation, and thermodynamics, e.g., energy dissipation due to the emission of the shock wave formed at the end of the collapse, which directly influences the evolution of the bubble radius. In particular, the accurate prediction of the bubble radius after multiple collapse-expansion cycles using finite-volume methods is known to be difficult to achieve [23,50].
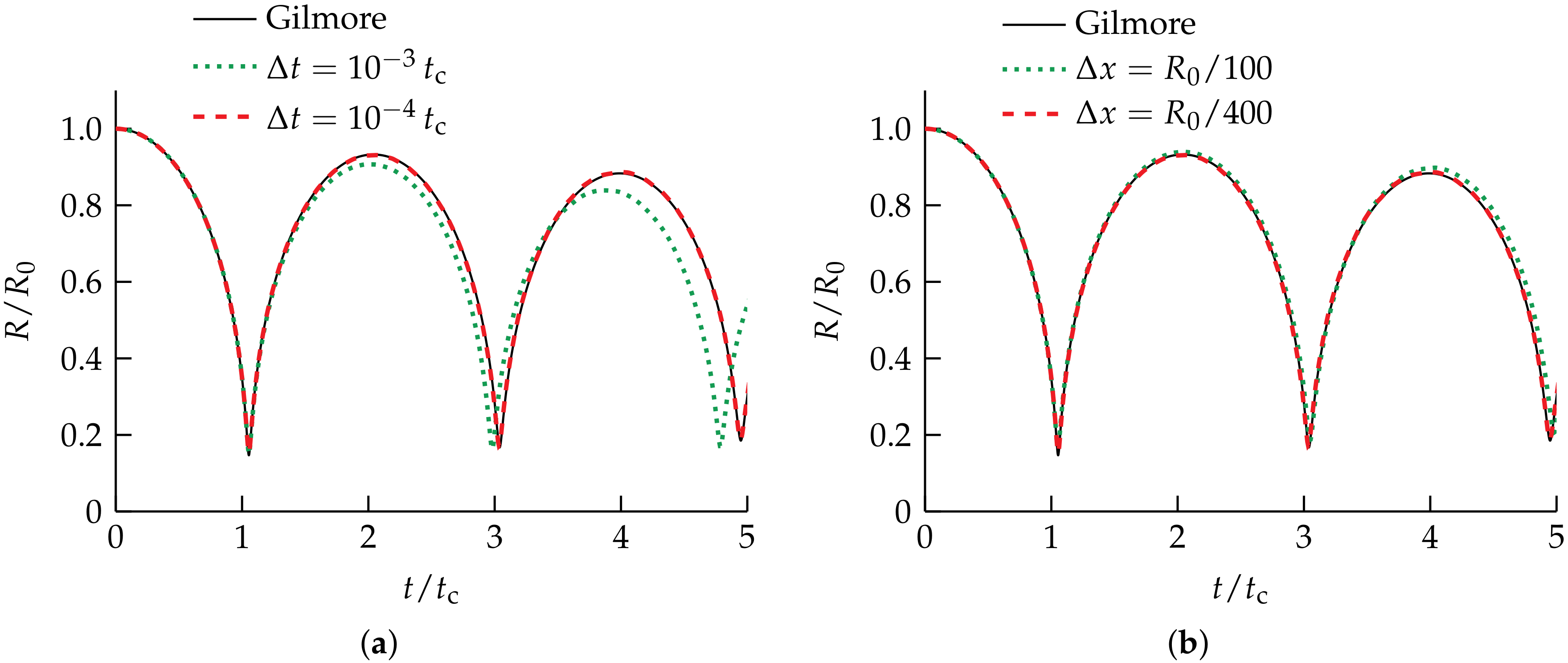
The initial pressure inside the bubble is and the initial pressure of the liquid is , with . The gas is modeled as air by the ideal-gas model with the properties given in Table 1 and a reference density of , and a viscosity of . The liquid is taken to be water described by the Tait model with the properties given for Water Tait in Table 1 and a reference density , and a viscosity of . The reference pressure is for both gas and liquid. Figure 4 shows the dimensionless bubble radius , normalized by the initial radius (which also corresponds to the maximum radius in this case), as a function of the dimensionless time , normalized by the Rayleigh collapse time , obtained with different spatial and temporal resolutions, compared against the solution obtained using the Gilmore model. Excellent agreement between the evolution of the bubble radius R predicted by the proposed algorithm and the Gilmore solution is observed in Figure 4, even after multiple collapse-expansion cycles, with the simulation results converging to the solution of the Gilmore model for sufficiently large spatial and temporal resolution.
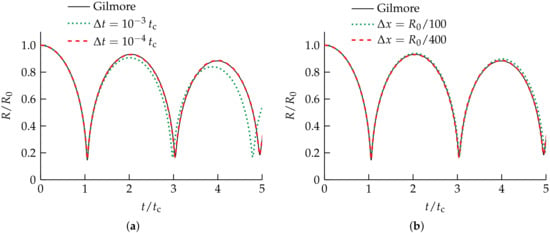
Figure 4.
Rayleigh collapse of a spherical bubble. Dimensionless radius as a function of dimensionless time , where is the initial radius and is the Rayleigh collapse time, computed using (a) different time-steps on a mesh with and (b) on meshes with different mesh spacings and a time-step of , compared against the solution of the Gilmore model [9].
6.3. Wall-Bounded Cavitation
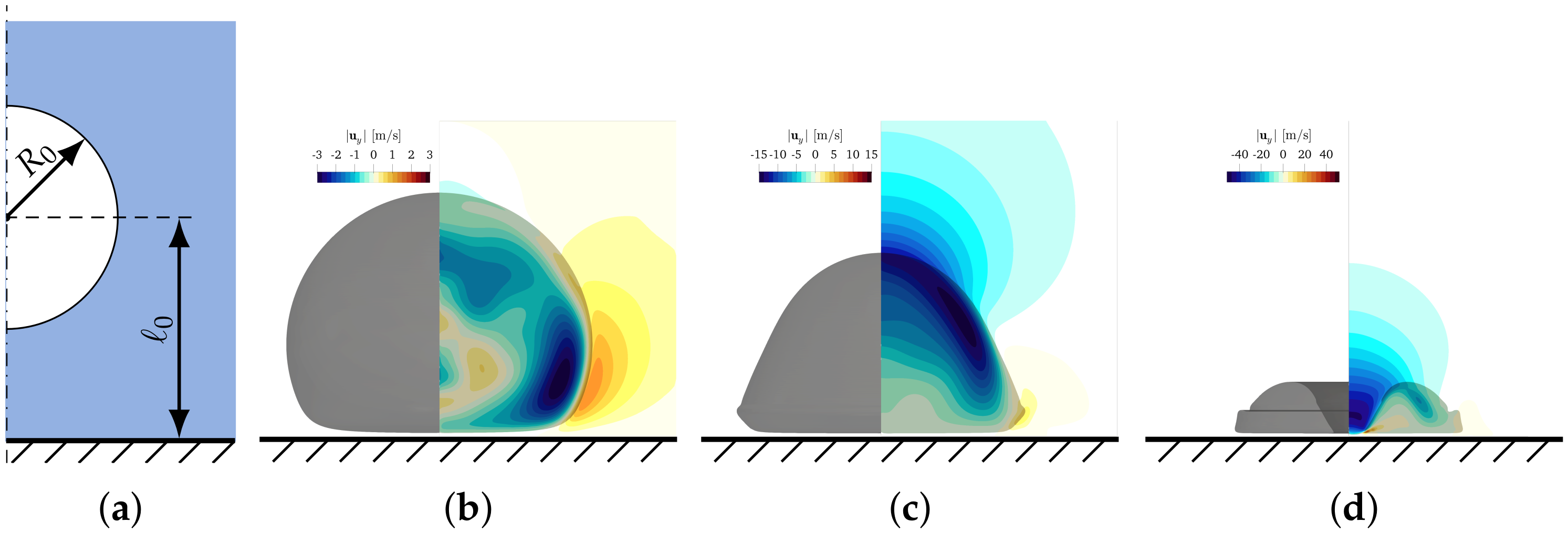
The wall-bounded collapse of a laser-induced cavitation bubble is simulated to test the fidelity of the proposed algorithm in predicting a complex pressure-driven cavitation process. The bubble is initialized with a radius of and a pressure to achieve a maximum radius of the upper hemisphere of the bubble of . The bubble is situated in water with an ambient pressure of at a distance from the wall, as illustrated in Figure 5a. The reference density at for air and water is and , respectively. Water is modeled using the properties of Water NASG given in Table 1 and has a viscosity of . Air is modeled as an ideal gas, using the properties given in Table 1, and has a viscosity of . Apart from the bottom wall illustrated explicitly in Figure 5, all boundaries of the computational domain are situated at a distance of from the bubble inception site, so that acoustic waves cannot reach the boundaries within the time span considered in the simulations. The computational domain is resolved with a mesh spacing of and a gradually refined mesh resolution near the wall, with a minimum mesh spacing of . The mesh is rapidly coarsened outside the region that the bubble occupies. The time-step is chosen to satisfy the Courant number .
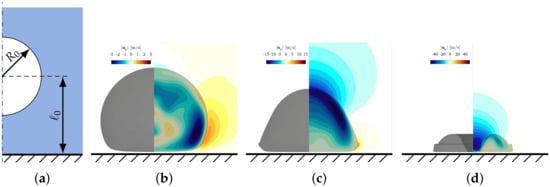
Figure 5.
Wall-bounded cavitation. (a) Simulation setup. (b–d) Instantaneous bubble shape and velocity contours of a bubble with and at times , and , respectively. The wall is explicitly illustrated in all figures.
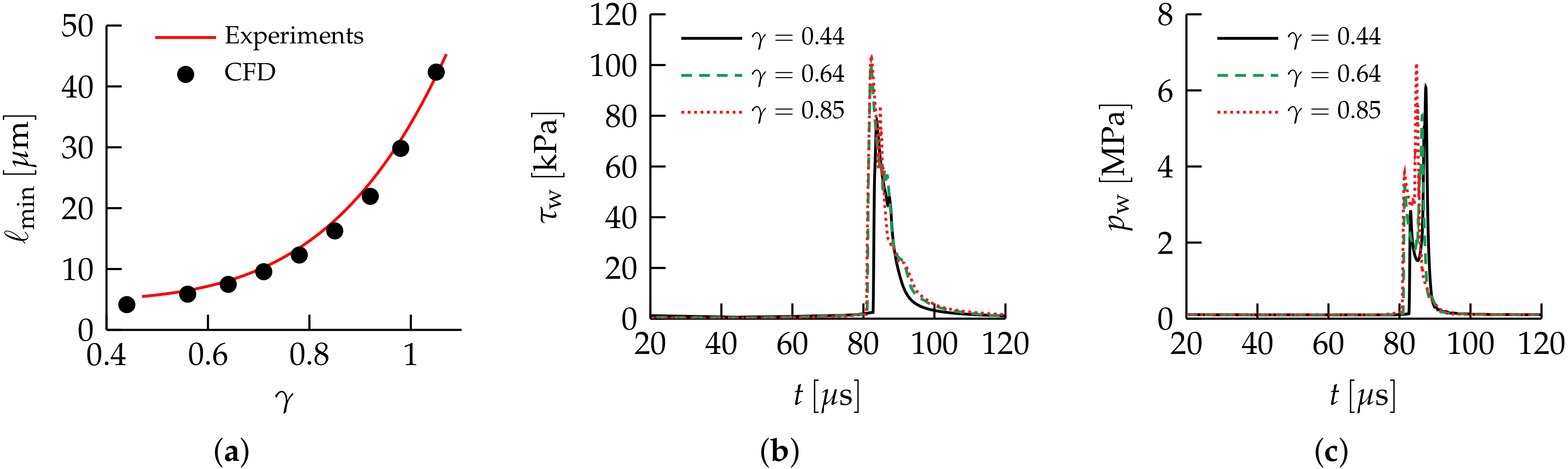
Figure 5b–d show the instantaneous bubble shape and contours of the velocity component perpendicular to the wall of a bubble with and at times , and , respectively. As the bubble initially grows and then collapses, a thin liquid film forms between the bubble and the wall, which can be clearly seen in Figure 5b–d and which has also previously been observed and measured in experiments [51]. Furthermore, the characteristic fast-moving liquid jet directed towards the wall that pierces the bubble during its collapse can be seen in Figure 5d. Figure 6a shows the minimum thickness, , of the liquid film separating the bubble and the wall at the time when the jet pierces through the bubble, i.e., the thickness of the small gap between the bubble and the wall seen in Figure 5d, predicted by the simulations for different dimensionless initial stand-off distances , in comparison with the experimental measurements of Reuter and Kaiser [51]. The fit of the correlation has a coefficient of determination of based on 91 experiments for bubbles with in the range [51]. Excellent agreement between the simulations and the experiments is observed, demonstrating the accuracy with which the proposed algorithm can predict such a complex cavitation process. The evolution of the peak shear stress and peak pressure at the wall are shown in Figure 6b,c, respectively, for selected initial stand-off distances. The pressure signal exhibits two peaks during the collapse of the bubble [52]; the first peak is caused by the pressure pulse emitted as the liquid jet impinges on the lower side of the bubble interface and the second peak is associated with the shock wave emitted at the end of the collapse, when the bubble (at this point having a toroidal shape) assumes its minimum volume. The results are in good agreement with previous studies regarding the order of magnitude of the generated wall shear stress [11,12] and the pressure amplitude of the shock wave formed as a result of the collapse [53,54] of a laser-induced bubble, with wall shear stresses exceeding for bubbles collapsing close to a wall.
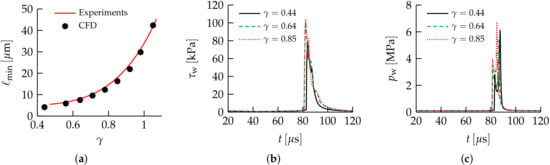
Figure 6.
Wall-bounded cavitation. (a) Results of the minimum liquid film thickness as a function of the dimensionless stand-off distance obtained with the proposed algorithm, compared against the correlation obtained by experimental measurements in the range [51]. (b,c) Evolution of the maximum wall shear stress and maximum wall pressure , respectively, for selected stand-off distances .
7. Conclusions
A fully coupled pressure-based algorithm for the simulation of the acoustic cavitation of bubbles in polytropic gas-liquid systems has been proposed. The algorithm is based on a conservative finite-volume discretization with a collocated variable arrangement [18], whereby the discretized governing conservation laws are solved simultaneously in a single linear system of equations for pressure and velocity, with density described by a polytropic assumption using the Noble-Abel stiffened-gas model [32]. The interface separating the interacting bulk phases is captured by a state-of-the-art algebraic VOF method [30].
The proposed numerical framework has been validated by representative test-cases, including the propagation and interface interaction of acoustic waves, as well as the Rayleigh collapse and the wall-bounded cavitation of a bubble. The propagation of acoustic waves demonstrates the accurate prediction of acoustic effects, whereas the excellent comparison of the bubble radius of the Rayleigh collapse against the Gilmore model demonstrates the correct prediction of the entire pressure-driven bubble dynamics. In particular, the demonstrated accurate prediction of the bubble radius after multiple collapse-expansion cycles compared to the theoretical solution, in this case given by the Gilmore model, is known to be difficult to achieve [23,50]. The considered wall-bounded cavitation of a bubble shows the reliable prediction of complex cavitation events. Especially the predicted thickness of the thin liquid film, which separates the bubble from the wall, is in very good agreement with recent experimental measurements [51] for a broad range of bubble stand-off distances, further establishing the reliable prediction of acoustic cavitation by the proposed algorithm.
Author Contributions
Conceptualization, F.D.; methodology, F.D., F.E. and B.v.W.; software, F.D., F.E. and B.v.W.; validation, F.D.; resources, F.D. and B.v.W.; writing—Original draft preparation, F.D.; writing—Review and editing, F.D., F.E. and B.v.W.; funding acquisition, F.D. and B.v.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 420239128.
Acknowledgments
We thank Jörg Schulenburg and Daniel Hasemann for their support with the computing systems at Otto-von-Guericke-Universität Magdeburg.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leighton, T.G. The Acoustic Bubble; Academy Press: London, UK, 1994. [Google Scholar]
- Reuter, F.; Mettin, R. Mechanisms of Single Bubble Cleaning. Ultrason. Sonochem. 2016, 29, 550–562. [Google Scholar] [CrossRef] [PubMed]
- Cavitation in Biomedicine; Wan, M., Feng, Y., ter Haar, G., Eds.; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Tovar, A.R.; Patel, M.V.; Lee, A.P. Lateral Air Cavities for Microfluidic Pumping with the Use of Acoustic Energy. Microfluid. Nanofluidics 2011, 10, 1269–1278. [Google Scholar] [CrossRef]
- Rabaud, D.; Thibault, P.; Mathieu, M.; Marmottant, P. Acoustically Bound Microfluidic Bubble Crystals. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L. On the Pressure Developed in a Liquid during the Collapse of a Spherical Cavity. Philos. Mag. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T. Physics of Bubble Oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Plesset, M.S. The Dynamics of Cavitation Bubbles. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; Technical Report No. 26-4; California Institute of Technology: Pasadena, CA, USA, 1952. [Google Scholar]
- Keller, J.B.; Miksis, M. Bubble Oscillations of Large Amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Lechner, C.; Koch, M.; Lauterborn, W.; Mettin, R. Pressure and Tension Waves from Bubble Collapse near a Solid Boundary: A Numerical Approach. J. Acoust. Soc. Am. 2017, 142, 3649–3659. [Google Scholar] [CrossRef]
- Zeng, Q.; Gonzalez-Avila, S.R.; Dijkink, R.; Koukouvinis, P.; Gavaises, M.; Ohl, C.D. Wall Shear Stress from Jetting Cavitation Bubbles. J. Fluid Mech. 2018, 846, 341–355. [Google Scholar] [CrossRef]
- Pan, S.; Adami, S.; Hu, X.; Adams, N.A. Phenomenology of Bubble-Collapse-Driven Penetration of Biomaterial-Surrogate Liquid-Liquid Interfaces. Phys. Rev. Fluids 2018, 3, 114005. [Google Scholar] [CrossRef]
- Goncalves, E.; Hoarau, Y.; Zeidan, D. Simulation of Shock-Induced Bubble Collapse Using a Four-Equation Model. Shock Waves 2019, 29, 221–234. [Google Scholar] [CrossRef]
- Denner, F.; van Wachem, B. Numerical Modelling of Shock-Bubble Interactions Using a Pressure-Based Algorithm without Riemann Solvers. Exp. Comput. Multiph. Flow 2019, 1, 271–285. [Google Scholar] [CrossRef]
- Wilson, C.T.; Hall, T.L.; Johnsen, E.; Mancia, L.; Rodriguez, M.; Lundt, J.E.; Colonius, T.; Henann, D.L.; Franck, C.; Xu, Z.; et al. Comparative Study of the Dynamics of Laser and Acoustically Generated Bubbles in Viscoelastic Media. Phys. Rev. E 2019, 99, 043103. [Google Scholar] [CrossRef] [PubMed]
- Plesset, M.S.; Prosperetti, A. Bubble Dynamics and Cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Denner, F.; Evrard, F.; van Wachem, B. Conservative Finite-Volume Framework and Pressure-Based Algorithm for Flows of Incompressible, Ideal-Gas and Real-Gas Fluids at All Speeds. J. Comput. Phys. 2020, 409, 109348. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical Solution of the Navier-Stokes Equations. Math. Comput. 1968, 22, 745. [Google Scholar] [CrossRef]
- Bell, J.B.; Colella, P.; Glaz, H.M. A Second-Order Projection Method for the Incompressible Navier-Stokes Equations. J. Comput. Phys. 1989, 85, 257–283. [Google Scholar] [CrossRef]
- Patankar, S.; Spalding, D. A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Miller, S.T.; Jasak, H.; Boger, D.A.; Paterson, E.G.; Nedungadi, A. A Pressure-Based, Compressible, Two-Phase Flow Finite Volume Method for Underwater Explosions. Comput. Fluids 2013, 87, 132–143. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical Modeling of Laser Generated Cavitation Bubbles with the Finite Volume and Volume of Fluid Method, Using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Darwish, M.; Sraj, I.; Moukalled, F. A Coupled Finite Volume Solver for the Solution of Incompressible Flows on Unstructured Grids. J. Comput. Phys. 2009, 228, 180–201. [Google Scholar] [CrossRef]
- Chen, Z.; Przekwas, A.J. A Coupled Pressure-Based Computational Method for Incompressible/Compressible Flows. J. Comput. Phys. 2010, 229, 9150–9165. [Google Scholar] [CrossRef]
- Denner, F.; van Wachem, B. Fully-Coupled Balanced-Force VOF Framework for Arbitrary Meshes with Least-Squares Curvature Evaluation from Volume Fractions. Numer. Heat Transf. Part B Fundam. 2014, 65, 218–255. [Google Scholar] [CrossRef]
- Darwish, M.; Moukalled, F. A Fully Coupled Navier-Stokes Solver for Fluid Flow at All Speeds. Numer. Heat Transf. Part B Fundam. 2014, 65, 410–444. [Google Scholar] [CrossRef]
- Xiao, C.N.; Denner, F.; van Wachem, B. Fully-Coupled Pressure-Based Finite-Volume Framework for the Simulation of Fluid Flows at All Speeds in Complex Geometries. J. Comput. Phys. 2017, 346, 91–130. [Google Scholar] [CrossRef]
- Denner, F. Fully-Coupled Pressure-Based Algorithm for Compressible Flows: Linearisation and Iterative Solution Strategies. Comput. Fluids 2018, 175, 53–65. [Google Scholar] [CrossRef]
- Denner, F.; Xiao, C.N.; van Wachem, B. Pressure-Based Algorithm for Compressible Interfacial Flows with Acoustically-Conservative Interface Discretisation. J. Comput. Phys. 2018, 367, 192–234. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Le Métayer, O.; Saurel, R. The Noble-Abel Stiffened-Gas Equation of State. Phys. Fluids 2016, 28, 046102. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Fluid Dynamics: A Practical Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Le Métayer, O.; Massoni, J.; Saurel, R. Élaboration des lois d’état d’un liquide et de sa vapeur pour les modèles d’écoulements diphasiques. Int. J. Therm. Sci. 2004, 43, 265–276. [Google Scholar] [CrossRef]
- Bartholomew, P.; Denner, F.; Abdol-Azis, M.; Marquis, A.; van Wachem, B. Unified Formulation of the Momentum-Weighted Interpolation for Collocated Variable Arrangements. J. Comput. Phys. 2018, 375, 177–208. [Google Scholar] [CrossRef]
- Denner, F.; van Wachem, B. TVD Differencing on Three-Dimensional Unstructured Meshes with Monotonicity-Preserving Correction of Mesh Skewness. J. Comput. Phys. 2015, 298, 466–479. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical Study of the Turbulent Flow Past an Airfoil with Trailing Edge Separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Denner, F.; van Wachem, B. Numerical Time-Step Restrictions as a Result of Capillary Waves. J. Comput. Phys. 2015, 285, 24–40. [Google Scholar] [CrossRef]
- Karimian, S.M.H.; Schneider, G.E. Pressure-Based Computational Method for Compressible and Incompressible Flows. J. Thermophys. Heat Transf. 1994, 8, 267–274. [Google Scholar] [CrossRef]
- Kunz, R.; Cope, W.; Venkateswaran, S. Development of an Implicit Method for Multi-Fluid Flow Simulations. J. Comput. Phys. 1999, 152, 78–101. [Google Scholar] [CrossRef][Green Version]
- Balay, S.; Gropp, W.; McInnes, L.C.; Smith, B.F. Efficient Management of Parallelism in Object Oriented Numerical Software Libraries. In Modern Software Tools in Scientific Computing; Arge, E., Bruasat, A., Langtangen, H., Eds.; Birkhäuser Press: Boston, MA, USA, 1997; pp. 163–202. [Google Scholar]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; et al. PETSc Web Page. 2020. Available online: http://www.mcs.anl.gov/petsc (accessed on 13 April 2020).
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Eijkhout, V.; Kaushik, D.; Knepley, M.G.; et al. PETSc Users Manual; Technical Report ANL-95/11 - Revision 3.8; Argonne National Laboratory: Lemont, IL, USA, 2017. [Google Scholar]
- Ubbink, O.; Issa, R. A Method for Capturing Sharp Fluid Interfaces on Arbitrary Meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- Gopala, V.; van Wachem, B. Volume of Fluid Methods for Immiscible-Fluid and Free-Surface Flows. Chem. Eng. J. 2008, 141, 204–221. [Google Scholar] [CrossRef]
- Denner, F. Wall Collision of Deformable Bubbles in the Creeping Flow Regime. Eur. J. Mech. B Fluids 2018, 70, 36–45. [Google Scholar] [CrossRef]
- Anderson, J.D. Modern Compressible Flow: With a Historical Perspective; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Johnston, I. The Noble-Abel Equation of State: Thermodynamic Derivations for Ballistics Modelling; Technical Report Technical Report DSTO-TN-0670; Defence Science and Technology Organisation: Edinburgh, Australia, 2005. [Google Scholar]
- Lauterborn, W.; Lechner, C.; Koch, M.; Mettin, R. Bubble Models and Real Bubbles: Rayleigh and Energy-Deposit Cases in a Tait-Compressible Liquid. IMA J. Appl. Math. 2018, 83, 556–589. [Google Scholar] [CrossRef]
- Schmidmayer, K.; Bryngelson, S.H.; Colonius, T. An Assessment of Multicomponent Flow Models and Interface Capturing Schemes for Spherical Bubble Dynamics. J. Comput. Phys. 2020, 402, 109080. [Google Scholar] [CrossRef]
- Reuter, F.; Kaiser, S.A. High-Speed Film-Thickness Measurements between a Collapsing Cavitation Bubble and a Solid Surface with Total Internal Reflection Shadowmetry. Phys. Fluids 2019, 31, 097108. [Google Scholar] [CrossRef]
- Ohl, C.; Kurz, T.; Geisler, R.; Lindau, O.; Lauterborn, W. Bubble Dynamics, Shock Waves and Sonoluminescence. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 357, 269–294. [Google Scholar] [CrossRef]
- Vogel, A.; Busch, S.; Parlitz, U. Shock Wave Emission and Cavitation Bubble Generation by Picosecond and Nanosecond Optical Breakdown in Water. J. Acoust. Soc. Am. 1996, 100, 148–165. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Kobel, P.; Tinguely, M.; Dorsaz, N.; Farhat, M. Shock Waves from Nonspherical Cavitation Bubbles. Phys. Rev. Fluids 2017, 2, 093601. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).