Chemical Signaling in the Turbulent Ocean—Hide and Seek at the Kolmogorov Scale
Abstract
1. Introduction
Theoretical Background
2. Materials and Methods
2.1. Calculations of Trail Lengths and Background Concentrations
2.2. Direct Numerical Simulations
3. Results and Discussion
3.1. Mate Finding is Easier in 2 Dimensions than in 3
3.2. Effect of Turbulence on Chemical Trails
3.3. Background Concentration
3.4. Effect of Near Surface Anisotropic Turbulence on Trail Formation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Calculation of Normalized Mean Signal Concentration
References
- Kiørboe, T. A Mechanistic Aproach to Plankton Ecology; Princeton University Press: Princeton, NJ, USA, 2008; p. 228. [Google Scholar]
- Berg, H.C. Random Walks in Biology; Princeton university press: Princeton, NJ, USA, 1993; p. 152. [Google Scholar]
- Bagoien, E.; Kiørboe, T. Blind dating-mate finding in planktonic copepods. I. Tracking the pheromone trail of Centropages typicus. Mar. Ecol. Prog. Ser. 2005, 300, 105–115. [Google Scholar] [CrossRef]
- Visser, A.W.; Jackson, G.A. Characteristics of the chemical plume behind a sinking particle in a turbulent water column. Mar. Ecol. Prog. Ser. 2004, 283, 55–71. [Google Scholar] [CrossRef][Green Version]
- Yen, J.; Lasley, R. Chemical Communication between Copepods: Finding the Mate in a Fluid Environment; Springer: New York, NY, USA, 2011; pp. 177–197. [Google Scholar]
- Heuschele, J.; Selander, E. The chemical ecology of copepods. J. Plankton Res. 2014, 36, 895–913. [Google Scholar] [CrossRef]
- Seuront, L.; Stanley, H.E. Anomalous diffusion and multifractality enhance mating encounters in the ocean. Proc. Natl. Acad. Sci. USA 2014, 111, 2206–2211. [Google Scholar] [CrossRef] [PubMed]
- Selander, E.; Kubanek, J.; Hamberg, M.; Andersson, M.X.; Cervin, G.; Pavia, H. Predator lipids induce paralytic shellfish toxins in bloom-forming algae. Proc. Natl. Acad. Sci. USA 2015, 112, 6395–6400. [Google Scholar] [CrossRef] [PubMed]
- Selander, E.; Berglund, E.; Engström, P.; Berggren, F.; Eklund, J.; Harðardóttir, S.; Lundholm, N.; Grebner, W.; Andersson, M. Copepods drive large-scale trait-mediated effects in marine plankton. Sci. Adv. 2019, 5, eaat5096. [Google Scholar] [CrossRef] [PubMed]
- Selander, E.; Jakobsen, H.H.; Lombard, F.; Kiørboe, T. Grazer cues induce stealth behavior in marine dinoflagellates. Proc. Natl. Acad. Sci. USA 2011, 108, 4030–4034. [Google Scholar] [CrossRef] [PubMed]
- Byron, E.; Whitman, P.; Goldman, C. Observations of copepod swarms in Lake Tahoe 1. Limnol. Oceanogr. 1983, 28, 378–382. [Google Scholar] [CrossRef]
- Fredriksson, S.; Arneborg, L.; Nilsson, H.; Handler, R. Surface shear stress dependence of gas transfer velocity parameterizations using DNS. J. Geophys. Res. Ocean. 2016, 121, 7369–7389. [Google Scholar] [CrossRef]
- Fredriksson, S.T.; Arneborg, L.; Nilsson, H.; Zhang, Q.; Handler, R.A. An evaluation of gas transfer velocity parameterizations during natural convection using DNS. J. Geophys. Res. Ocean. 2016, 121, 1400–1423. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Zhang, Q.; Handler, R.A.; Fredriksson, S.T. Direct numerical simulation of turbulent free convection in the presence of a surfactant. Int. J. Heat Mass Transf. 2013, 61, 82–93. [Google Scholar] [CrossRef]
- Csanady, G.T. Turbulent Diffusion in the Environment; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 3. [Google Scholar]
- Jackson, G.A.; Kiørboe, T. Zooplankton use of chemodetection to find and eat particles. Mar. Ecol. Prog. Ser. 2004, 269, 153–162. [Google Scholar] [CrossRef]
- Batchelor, G.K. Small-scale variation of convected quantities like temperature in turbulent fluid Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 1959, 5, 113–133. [Google Scholar] [CrossRef]
- Tiselius, P.; Jonsson, P.R. Foraging Behavior of 6 Calanoid Copepods-Observations and Hydrodynamic Analysis. Mar. Ecol. Prog. Ser. 1990, 66, 23–33. [Google Scholar] [CrossRef]
- Arias, A.; Selander, E.; Saiz, E.; Calbet, A. Predator chemical cues effects on the diel feeding behaviour of marine protists. Proc. R. Acad. Sci. Proc. B Biol. Sci. (in press).
- Evans, R.; Dal Poggetto, G.; Nilsson, M.; Morris, G.A. Improving the interpretation of small molecule diffusion coefficients. Anal. Chem. 2018, 90, 3987–3994. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, S.A. An Introduction to Ocean Turbulence; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Csanady, G.T. Air-Sea Interaction: Laws and Mechanisms; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Staalstrøm, A.; Arneborg, L.; Liljebladh, B.; Broström, G. Observations of turbulence caused by a combination of tides and mean baroclinic flow over a fjord sill. J. Phys. Oceanogr. 2015, 45, 355–368. [Google Scholar] [CrossRef]
- McKenna, S.; McGillis, W. The role of free-surface turbulence and surfactants in air–water gas transfer. Int. J. Heat Mass Transf. 2004, 47, 539–553. [Google Scholar] [CrossRef]

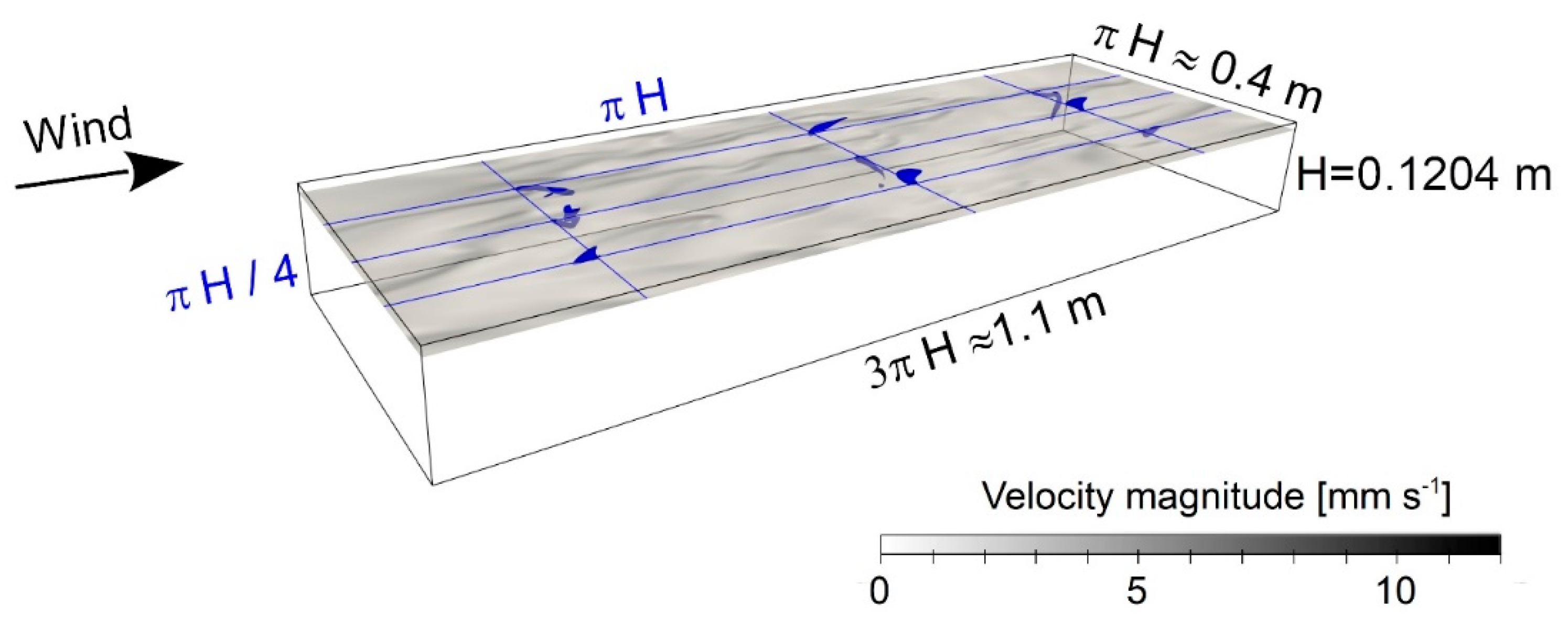
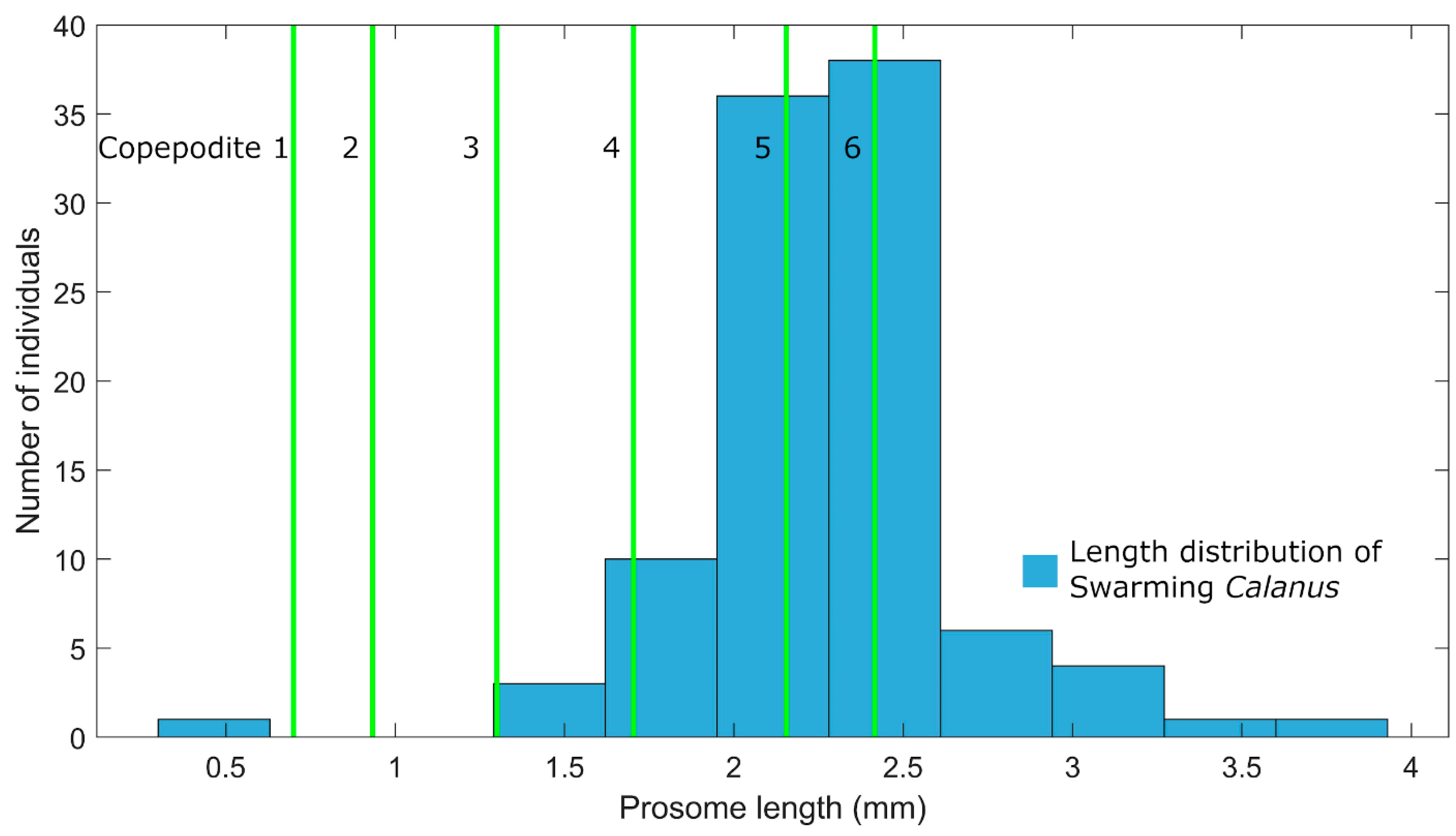
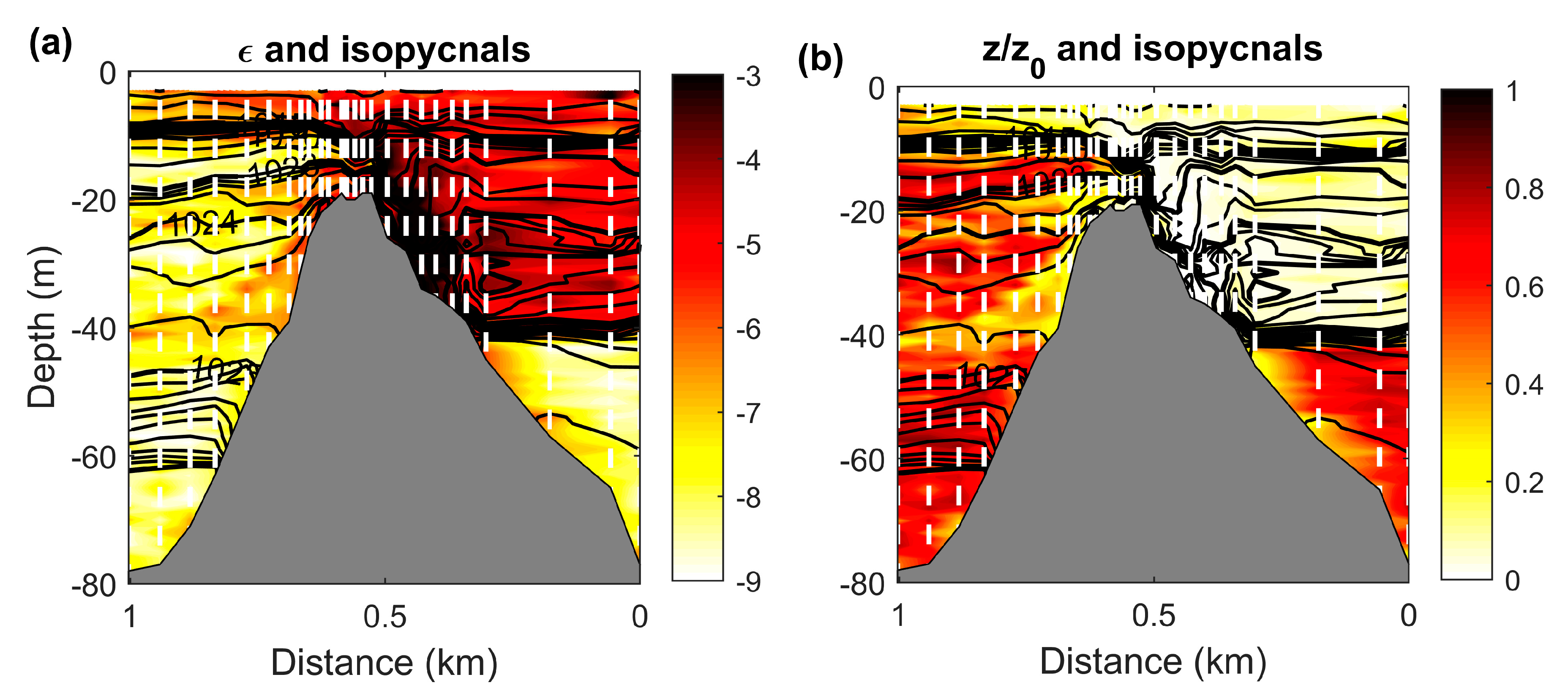
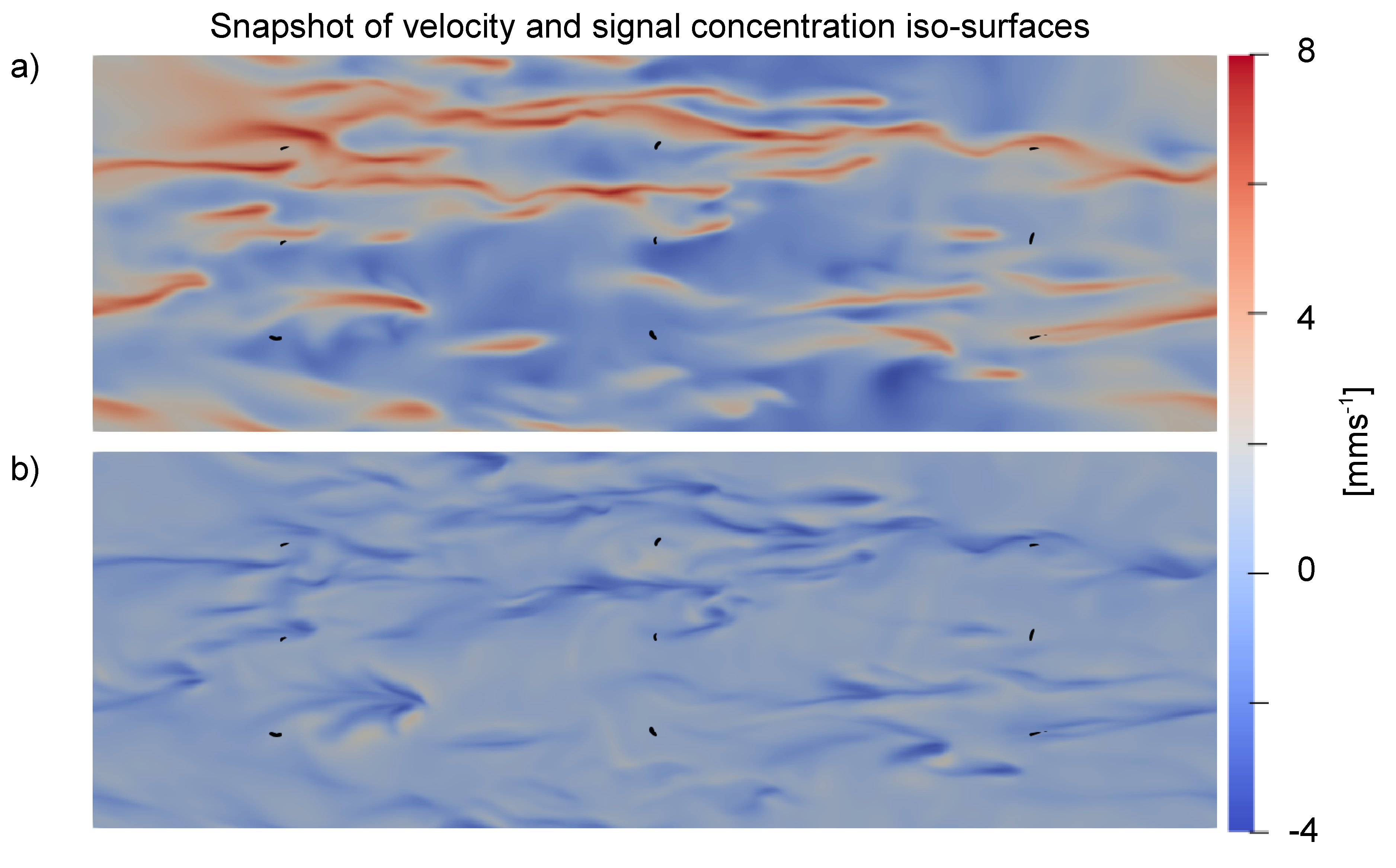

| Parameter | Symbol | Value | Reference |
|---|---|---|---|
| Copepod length | L | 0.1 cm | |
| Copepod swimming speed | U | 0.05–1 cm s−1 | [19] |
| Copepod concentration | n | 10–12 ind l−1 | sharkweb.smhi.se |
| Emission rate of copepodamides * | Q | 17 pmol ind−1 d−1 | [8] |
| Sensitivity threshold for copepods | C* | 1 nM | [6] and references there in |
| Sensitivity threshold for microplankton | Cp | 20-80 fM | [9] |
| Degradation rate | k | 0.21h−1(Ct = C0e−0.21t) | [20] |
| Molecular diffusivity | D | 3 × 10−6 cm2 s−1 | [21] |
| Kinematic viscosity | ν | 10−2 cm2 s−1 | |
| Dissipation rate of turbulent kinetic energy | ε | 10−6–103 cm2 s−3 | [22] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selander, E.; Fredriksson, S.T.; Arneborg, L. Chemical Signaling in the Turbulent Ocean—Hide and Seek at the Kolmogorov Scale. Fluids 2020, 5, 54. https://doi.org/10.3390/fluids5020054
Selander E, Fredriksson ST, Arneborg L. Chemical Signaling in the Turbulent Ocean—Hide and Seek at the Kolmogorov Scale. Fluids. 2020; 5(2):54. https://doi.org/10.3390/fluids5020054
Chicago/Turabian StyleSelander, Erik, Sam T. Fredriksson, and Lars Arneborg. 2020. "Chemical Signaling in the Turbulent Ocean—Hide and Seek at the Kolmogorov Scale" Fluids 5, no. 2: 54. https://doi.org/10.3390/fluids5020054
APA StyleSelander, E., Fredriksson, S. T., & Arneborg, L. (2020). Chemical Signaling in the Turbulent Ocean—Hide and Seek at the Kolmogorov Scale. Fluids, 5(2), 54. https://doi.org/10.3390/fluids5020054





