Volume and Frequency-Independent Spreading of Droplets Driven by Ultrasonic Surface Vibration
Abstract
1. Introduction
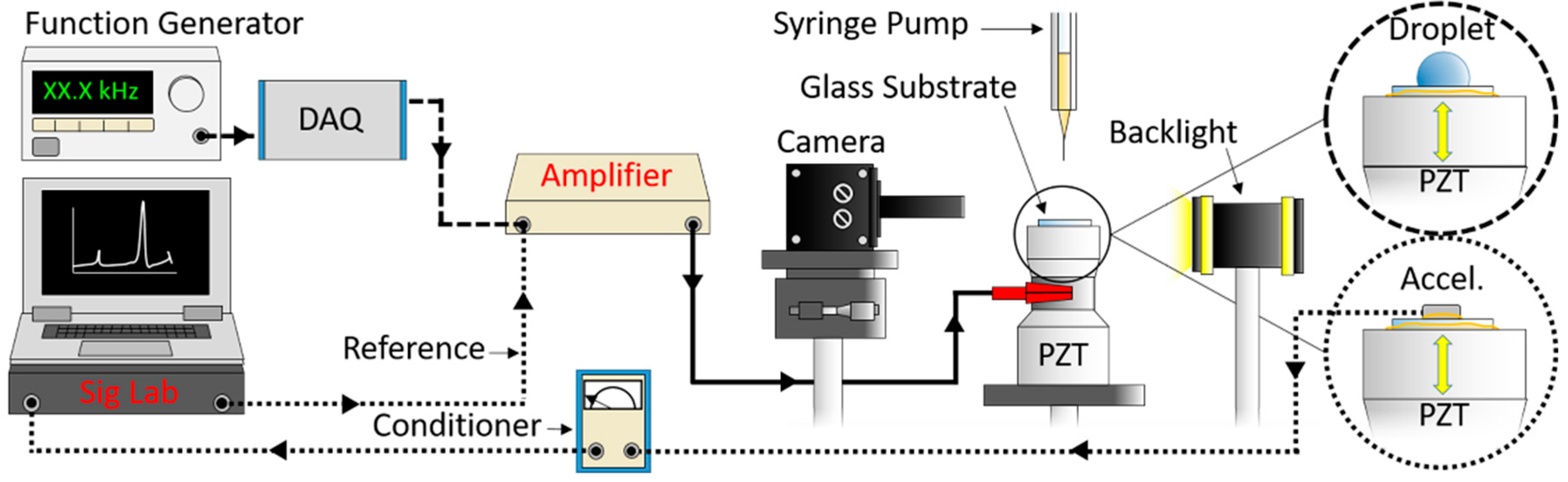
2. Materials and Methods
3. Results
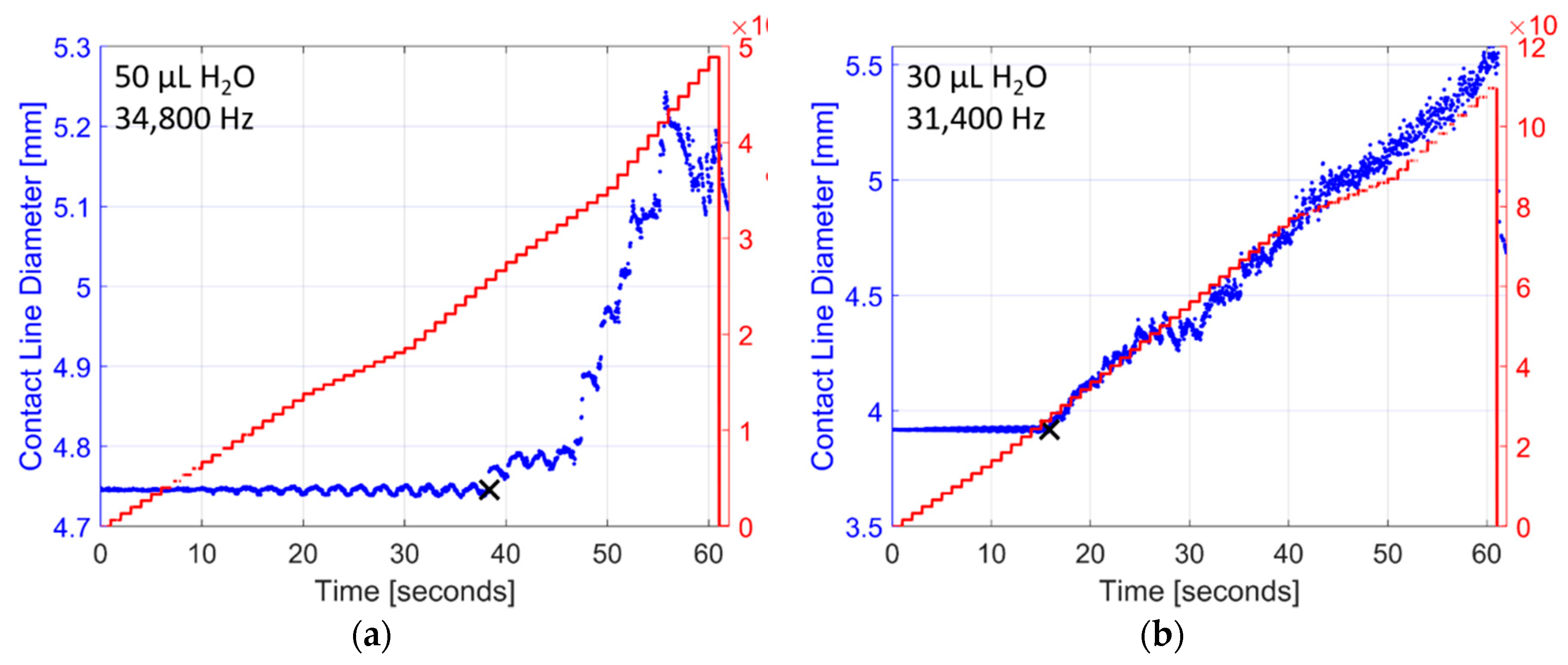
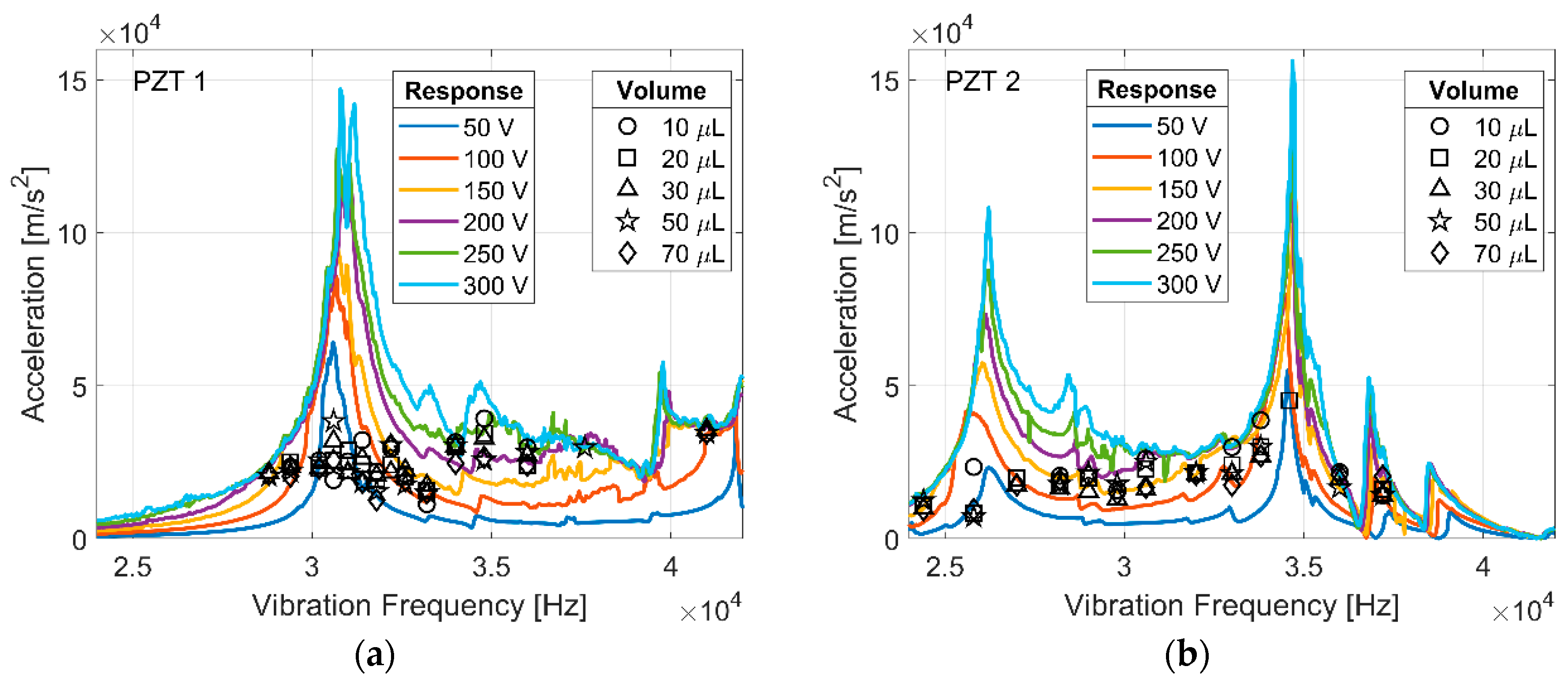
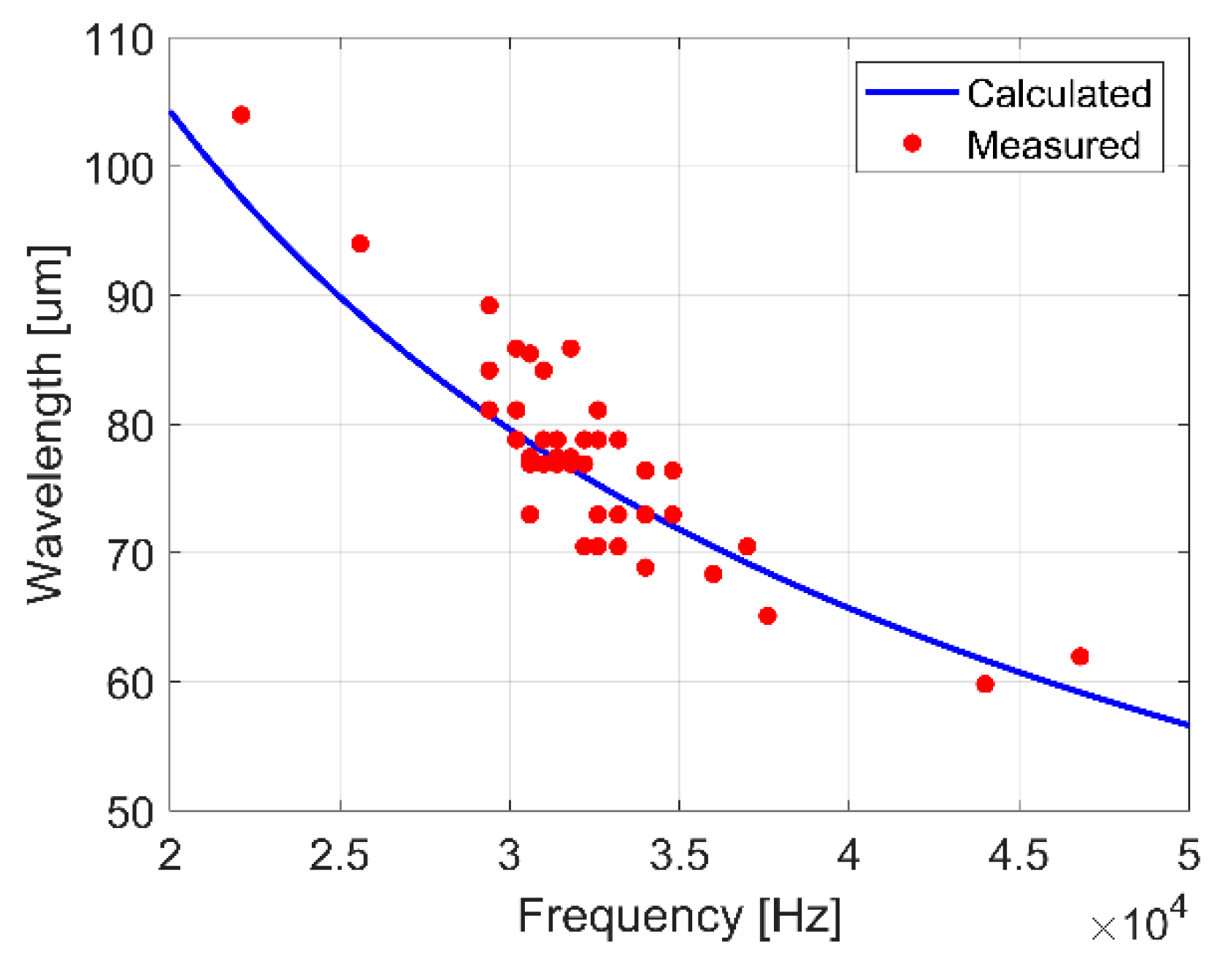
3.1. Droplet Volume, Vibration Frequency, and Transducer Frequency Response
3.2. Material Properties
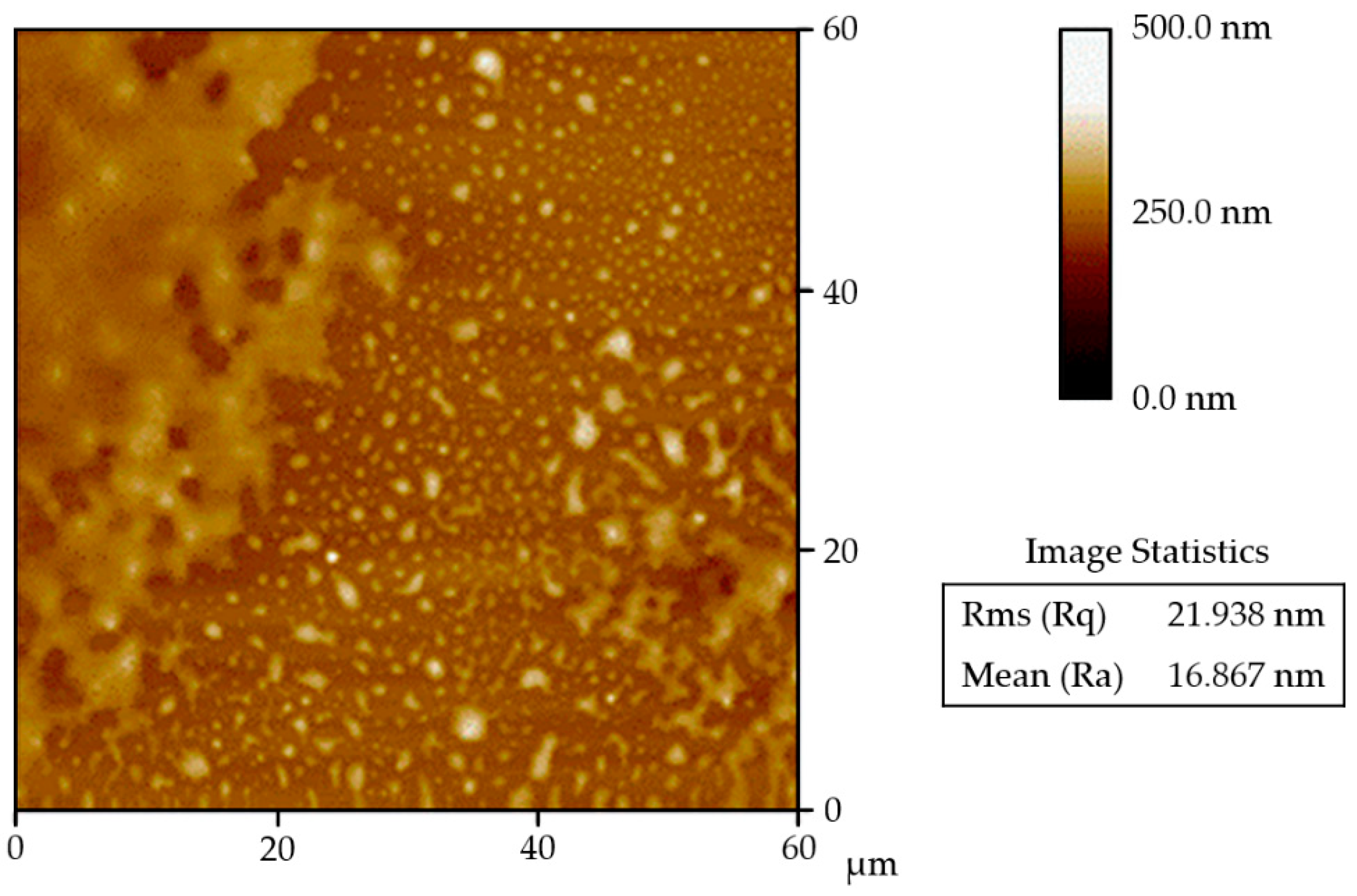
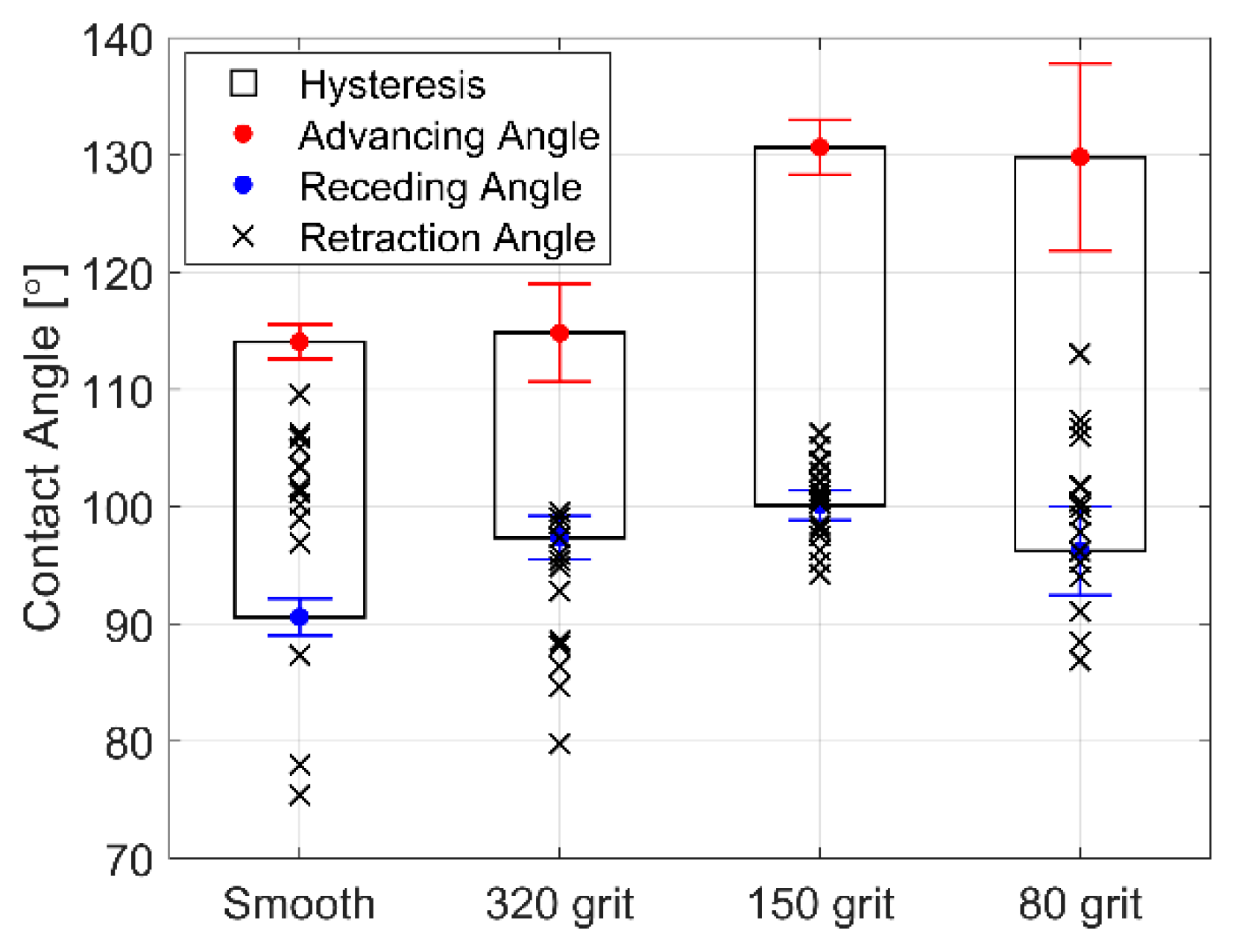
3.3. Surface Roughness
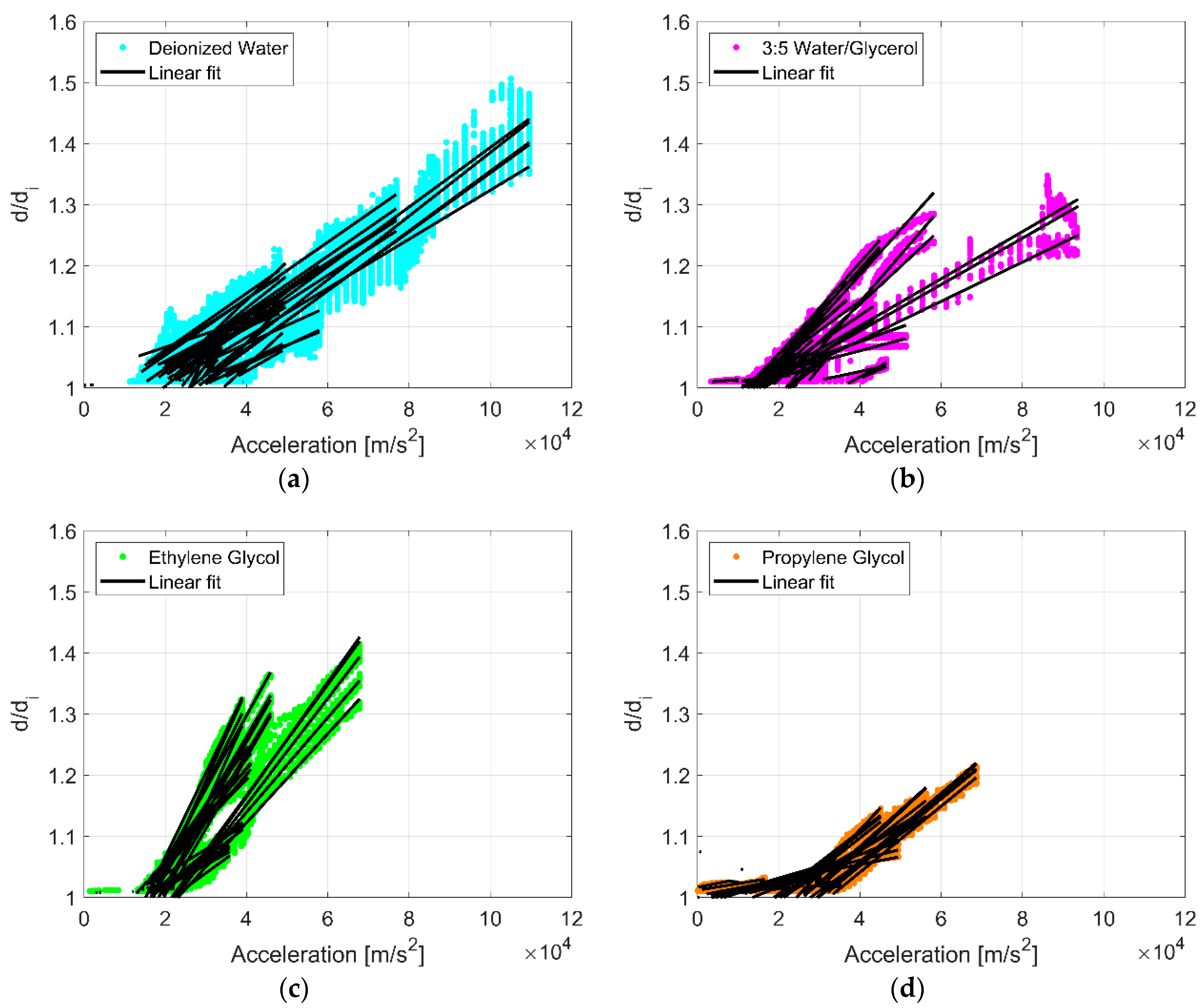
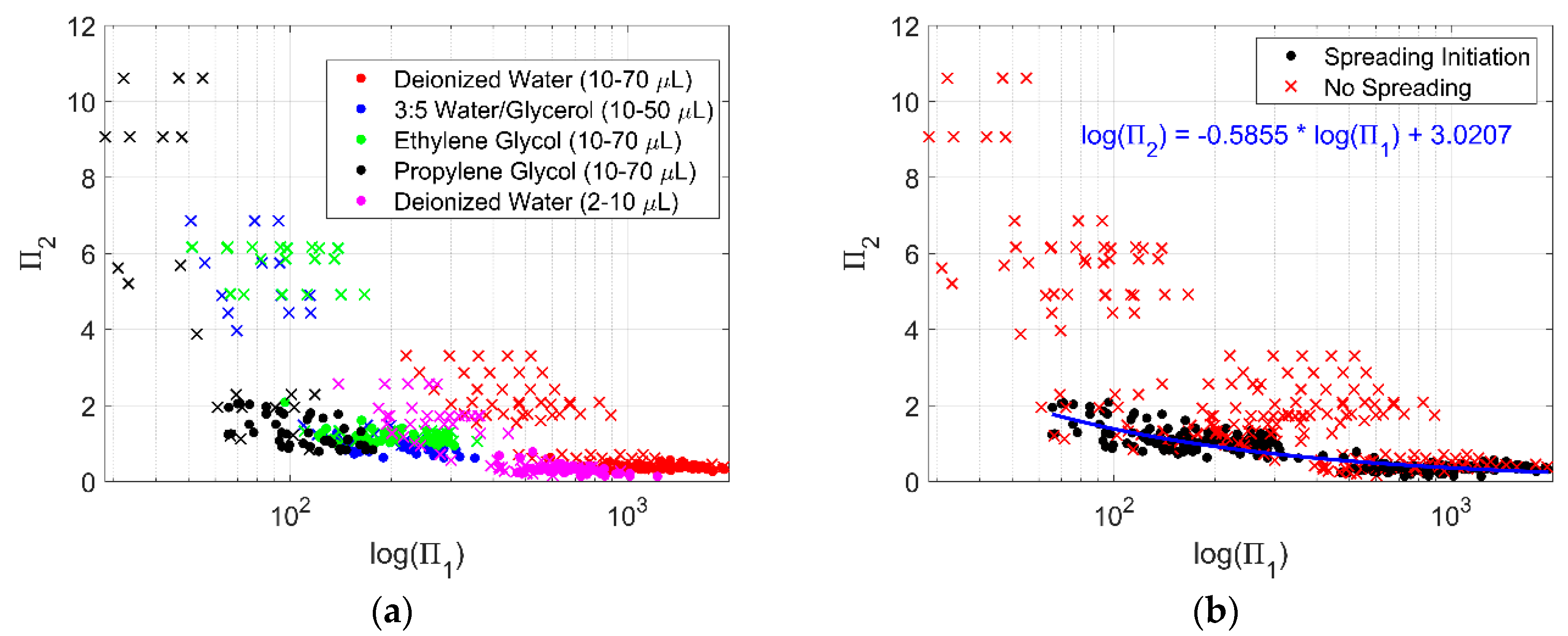
3.4. Non-Dimensional Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 10, 20, 30, 50, 70 | 24.0 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 25.2 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 26.0 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 27.4 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 28.2 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 28.8 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 29.4 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 31.4 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 31.8 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 32.2 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 32.6 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 33.2 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 34.0 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 34.8 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 36.0 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 37.6 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 38.8 | 1 |
| Deionized Water | 10, 20, 30, 50, 70 | 41.0 | 1 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| 3:5 Water/Glycerol | 10, 30, 50 | 24.0 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 24.8 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 25.6 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 26.0 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 26.6 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 27.0 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 27.4 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 28.0 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 28.8 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 29.4 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 29.8 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 30.4 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 30.8 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 31.2 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 32.0 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 32.6 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 33.2 | 1 |
| 3:5 Water/Glycerol | 10, 30, 50 | 34.0 | 1 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Ethylene Glycol | 10, 20, 30, 50, 70 | 24.6 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 26.8 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 29.0 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 29.4 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 29.6 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 29.8 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 30.0 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 30.4 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 31.2 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 33.2 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 35.6 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 38.8 | 1 |
| Ethylene Glycol | 10, 20, 30, 50, 70 | 41.0 | 1 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Propylene Glycol | 10, 20, 30, 50, 70 | 24.8 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 27.2 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 28.6 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 29.0 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 29.4 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 29.8 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 30.2 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 30.6 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 31.2 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 33.4 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 36.2 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 38.8 | 1 |
| Propylene Glycol | 10, 20, 30, 50, 70 | 42.0 | 1 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 2, 4, 6, 8, 10 | 24.2 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 26.8 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 27.4 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 28.0 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 28.6 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 29.0 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 29.4 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 29.8 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 30.2 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 30.6 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 31.0 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 31.6 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 32.2 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 35.4 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 38.6 | 1 |
| Deionized Water | 2, 4, 6, 8, 10 | 42.0 | 1 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 10, 20, 30, 50, 70 | 24.4 | 2 |
| Deionized Water | 10, 20, 50, 70 | 25.8 | 2 |
| Deionized Water | 20, 30, 70 | 27.0 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 28.2 | 2 |
| Deionized Water | 20, 30, 50, 70 | 29.0 | 2 |
| Deionized Water | 10, 30, 50, 70 | 29.8 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 30.6 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 32.0 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 33.0 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 33.8 | 2 |
| Deionized Water | 20, 30, 50, 70 | 34.6 | 2 |
| Deionized Water | 10, 30, 50, 70 | 36.0 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 37.2 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 38.4 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 39.6 | 2 |
| Deionized Water | 10, 20, 30, 50, 70 | 40.6 | 2 |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 10, 20, 30, 50, 70 | 24.8 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 26.2 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 27.4 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 28.2 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 28.6 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.2 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.8 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 30.4 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 31.0 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 31.6 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 32.2 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 32.8 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 34.4 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 36.8 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 39.0 | 1 (320 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 41.6 | 1 (320 grit) |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 10, 20, 30, 50, 70 | 25.2 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 26.6 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 27.2 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 27.8 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 28.4 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.0 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.6 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 30.2 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 30.8 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 31.4 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 32.0 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 32.8 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 35.2 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 37.6 | 1 (150 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 40.4 | 1 (150 grit) |
| Liquid | Droplet Volume [µL] | Frequency [kHz] | PZT |
|---|---|---|---|
| Deionized Water | 10, 20, 30, 50, 70 | 25.2 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 25.8 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 26.4 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 27.0 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 27.6 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 28.2 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 28.6 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.2 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 29.8 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 30.4 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 32.0 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 33.8 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 36.0 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 38.6 | 1 (80 grit) |
| Deionized Water | 10, 20, 30, 50, 70 | 41.0 | 1 (80 grit) |
References
- Destgeer, G.; Jung, J.H.; Park, J.; Ahmed, H.; Sung, H.J. Particle Separation inside a Sessile Droplet with Variable Contact Angle Using Surface Acoustic Waves. Anal. Chem. 2017, 89, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Daniel, S.; Chaudhury, M.K.; De Gennes, P.-G. Vibration-Actuated Drop Motion on Surfaces for Batch Microfluidic Processes. Langmuir 2005, 21, 4240–4248. [Google Scholar] [CrossRef] [PubMed]
- Chong, J.; Whitehill, J.D.; Neild, A. Low-volume filling of microplate wells using vibration. Anal. Biochem. 2012, 425, 10–12. [Google Scholar] [CrossRef] [PubMed]
- Ni, Q.; Capecci, D.E.; Schlafly, M.; Crane, N.B. Robust bidirectional continuous electrowetting based on metal–semiconductor (M–S) diodes. Microfluid. Nanofluidics 2016, 20, 122. [Google Scholar] [CrossRef]
- Nakajima, A.; Hashimoto, K.; Watanabe, T. Recent Studies on Super-Hydrophobic Films. Mon. Chem. Chem. Mon. 2001, 132, 31–41. [Google Scholar] [CrossRef]
- Rosen, M.J. Wetting and Its Modification by Surfactants. In Surfactants and Interfacial Phenomena; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 243–276. [Google Scholar]
- Frieder, M.; Jean-Christophe, B. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705. [Google Scholar]
- Whitehill, J.; Neild, A.; Ng, T.W.; Martyn, S.; Chong, J. Droplet spreading using low frequency vibration. Appl. Phys. Lett. 2011, 98, 133503. [Google Scholar] [CrossRef]
- Andrieu, C.; Sykes, C.; Brochard, F. Average Spreading Parameter on Heterogeneous Surfaces. Langmuir 1994, 10, 2077–2080. [Google Scholar] [CrossRef]
- Whitehill, J.D.; Neild, A.; Stokes, M.H. Forced spreading behavior of droplets undergoing low frequency vibration. Colloids Surf. A Physicochem. Eng. Asp. 2012, 393, 144–152. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Whyman, G.; Erlich, M. Resonance Cassie−Wenzel Wetting Transition for Horizontally Vibrated Drops Deposited on a Rough Surface. Langmuir 2007, 23, 12217–12221. [Google Scholar] [CrossRef]
- Manor, O.; Pismen, L.M. Effect of high-frequency in-plane substrate vibration on a three-phase contact angle. Phys. Fluids 2015, 27, 062101. [Google Scholar] [CrossRef]
- Mettu, S.; Chaudhury, M.K. Motion of Liquid Drops on Surfaces Induced by Asymmetric Vibration: Role of Contact Angle Hysteresis. Langmuir 2011, 27, 10327–10333. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Chaudhury, A.; Chaudhury, M.K. Lateral vibration of a water drop and its motion on a vibrating surface. Eur. Phys. J. E 2006, 21, 231–242. [Google Scholar] [CrossRef] [PubMed]
- Celestini, F.; Kofman, R. Vibration of submillimeter-size supported droplets. Phys. Rev. E 2006, 73, 041602. [Google Scholar] [CrossRef]
- Vukasinovic, B.; Smith, M.K.; Glezer, A. Dynamics of a sessile drop in forced vibration. J. Fluid Mech. 2007, 587, 395–423. [Google Scholar] [CrossRef]
- Eslamian, M.; Zabihi, F. Ultrasonic Substrate Vibration-Assisted Drop Casting (SVADC) for the Fabrication of Photovoltaic Solar Cell Arrays and Thin-Film Devices. Nanoscale Res. Lett. 2015, 10, 462. [Google Scholar] [CrossRef]
- Sharp, J.S.; Farmer, D.J.; Kelly, J. Contact Angle Dependence of the Resonant Frequency of Sessile Water Droplets. Langmuir 2011, 27, 9367–9371. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Khan, T.; Eslamian, M. Experiments and modeling of nonlinear frequency response of oscillations of a sessile droplet subjected to horizontal vibrations. Eur. Phys. J. E 2019, 42, 125. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Whyman, G.; Erlich, M. Cassie−Wenzel Wetting Transition in Vibrating Drops Deposited on Rough Surfaces: Is the Dynamic Cassie−Wenzel Wetting Transition a 2D or 1D Affair? Langmuir 2007, 23, 6501–6503. [Google Scholar] [CrossRef]
- Galleguillos-Silva, R.; Vargas-Hernández, Y.; Gaete-Garretón, L. Wettability of a surface subjected to high frequency mechanical vibrations. Ultrason. Sonochem. 2017, 35, 134–141. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Ahmadian-Yazdi, M.-R.; Eslamian, M. Experimental study on the characteristics of capillary surface waves on a liquid film on an ultrasonically vibrated substrate. Fluid Dyn. Res. 2018, 50, 065510. [Google Scholar] [CrossRef]
- Trapuzzano, M.A.; Crane, N.B.; Guldiken, R.; Tejada-Martínez, A. Forced Wetting of Liquids Using Ultrasonic Surface Vibration. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; Volume 1. [Google Scholar]
- Trapuzzano, M.; Crane, N.B.; Guldiken, R.; Tejada-Martínez, A. Wetting metamorphosis of hydrophobic fluoropolymer coatings submerged in water and ultrasonically vibrated. J. Coat. Technol. Res. 2019. [Google Scholar] [CrossRef]
- Trujillo-Pino, A.; Krissian, K.; Alemán-Flores, M.; Santana-Cedrés, D. Accurate subpixel edge location based on partial area effect. Image Vis. Comput. 2013, 31, 72–90. [Google Scholar] [CrossRef]
- Trujillo-Pino, A. Accurate Subpixel Edge Location. Detection of Subpixel Edges with Very High Precision in Grey Level Images. Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/48908-accurate-subpixel-edge-location?s_tid=FX_rc1_behav (accessed on 28 January 2020).
- Gal, O. Fit_Ellipse. Find the Best Fit for an Ellipse Using a Given Set of Points (a Closed Contour). Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/3215-fit_ellipse (accessed on 28 January 2020).
- Andersen, N.K. Drop Shape Analysis. Fit Contact Angle by Double Ellipses or Polynomials. Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/57919-drop-shape-analysis-fit-contact-angle-by-double-ellipses-or-polynomials?requestedDomain=en (accessed on 28 January 2020).
- PubChem Database. Propylene Glycol, CID = 1030. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/1030 (accessed on 28 January 2020).
- PubChem Database. Water, CID = 962. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/962 (accessed on 28 January 2020).
- PubChem Database. 1,2-Ethanediol, CID = 174. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/1_2-Ethanediol (accessed on 28 January 2020).
- Cheng, N.-S. Formula for the Viscosity of a Glycerol−Water Mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Volk, A.; Kähler, C.J. Density model for aqueous glycerol solutions. Exp. Fluids 2018, 59, 75. [Google Scholar] [CrossRef]
- Calculate Density and Viscosity of Glycerol/Water Mixtures. Available online: http://www.met.reading.ac.uk/~sws04cdw/viscosity_calc.html (accessed on 28 January 2020).
- Pagliaro, M.; Rossi, M. Glycerol: Properties and Production; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yue, H.; Zhao, Y.; Ma, X.; Gong, J. Ethylene glycol: Properties, synthesis, and applications. Chem. Soc. Rev. 2012, 41, 4218. [Google Scholar] [CrossRef]
- Lopez-Walle, B.; Gauthier, M.; Chaillet, N. Principle of a Submerged Freeze Gripper for Microassembly. IEEE Trans. Robot. 2008, 24, 897–902. [Google Scholar] [CrossRef]
- Trapuzzano, M.A. Controlled Wetting Using Ultrasonic Vibration. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2019. [Google Scholar]
- Munson, B.R.; Rothmayer, A.P.; Okiishi, T.H. Fundamentals of Fluid Mechanics, 7th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- De Gennes, P.G.F. Brochard-Wyart, and D. Quere, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2004. [Google Scholar]


| Liquid | Density (ρ) [kg/m3] | Surface Tension (σ) [N/m] | Dyn. Viscosity (μ) [Pa∗s] |
|---|---|---|---|
| Deionized Water | 996 | 0.072 | 0.0009 |
| 3:5 Water/Glycerol | 1172 | 0.067 | 0.0152 |
| Ethylene Glycol | 1115 | 0.048 | 0.0161 |
| Propylene Glycol | 1036 | 0.040 | 0.0581 |
| Liquid (volume) [µL] | Spreading Slope (std. dev.) [(m/s2)−1] × 10−6 | Spreading Acceleration (std. dev.) [m/s2] |
|---|---|---|
| Deionized Water (70) | 6.0 (3.3) | 18,445 (8425) |
| Deionized Water (50) | 4.9 (1.3) | 18,358 (6217) |
| Deionized Water (30) | 4.0 (0.7) | 17,262 (7635) |
| Deionized Water (20) | 5.0 (2.0) | 18,542 (8763) |
| Deionized Water (10) | 5.6 (1.7) | 20,487 (4609) |
| Deionized Water (8) | 5.8 (0.9) | 23,272 (840) |
| Deionized Water (6) | 4.5 (2.1) | 22,920 (5996) |
| Deionized Water (4) | 4.5 (1.5) | 29,382 (628) |
| Deionized Water (2) | – | – |
| Liquid (volume) [µL] | Spreading Slope (std. dev.) [(m/s2)−1] × 10−6 | Spreading Acceleration (std. dev.) [m/s2] |
|---|---|---|
| Deionized Water (6–70) | 4.9 (2.2) | 18,208 (7616) |
| 3:5 Water/Glycerol (10–50) | 5.7 (1.8) | 14,041 (3017) |
| Ethylene Glycol (10–70) | 8.4 (3.3) | 16,801 (3406) |
| Propylene Glycol (10–70) | 4.8 (1.4) | 22,677 (7605) |
| Surface | Ra (std. dev.), Rq (std. dev.) [µm] | Spreading Slope (std. dev.) [(m/s2)−1] × 10−6 | Spreading Acceleration (std. dev.) [m/s2] |
|---|---|---|---|
| Smooth | 0.02 (0.01), 0.03 (0.01) | 4.9 (2.2) | 18,208 (7616) |
| 320 grit | 0.58 (0.04), 0.75 (0.04) | 10.8 (6.2) | 18,994 (15,696) |
| 150 grit | 1.39 (0.15), 1.74 (0.30) | 12.7 (8.1) | 9819 (17,135) |
| 80 grit | 2.46 (0.37), 3.37 (0.01) | 24.1 (21.6) | 13,110 (9818) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trapuzzano, M.; Tejada-Martínez, A.; Guldiken, R.; Crane, N. Volume and Frequency-Independent Spreading of Droplets Driven by Ultrasonic Surface Vibration. Fluids 2020, 5, 18. https://doi.org/10.3390/fluids5010018
Trapuzzano M, Tejada-Martínez A, Guldiken R, Crane N. Volume and Frequency-Independent Spreading of Droplets Driven by Ultrasonic Surface Vibration. Fluids. 2020; 5(1):18. https://doi.org/10.3390/fluids5010018
Chicago/Turabian StyleTrapuzzano, Matthew, Andrés Tejada-Martínez, Rasim Guldiken, and Nathan Crane. 2020. "Volume and Frequency-Independent Spreading of Droplets Driven by Ultrasonic Surface Vibration" Fluids 5, no. 1: 18. https://doi.org/10.3390/fluids5010018
APA StyleTrapuzzano, M., Tejada-Martínez, A., Guldiken, R., & Crane, N. (2020). Volume and Frequency-Independent Spreading of Droplets Driven by Ultrasonic Surface Vibration. Fluids, 5(1), 18. https://doi.org/10.3390/fluids5010018






