Natural Convection in a Non-Newtonian Fluid: Effects of Particle Concentration
Abstract
:1. Introduction
2. Governing Equations
2.1. Conservation of Mass
2.2. Conservation of Linear Momentum
2.3. Conservation of Energy
2.4. Convection-Diffusion Equation for Particles
3. Constitutive Relations
3.1. Stress Tensor
3.2. Heat Flux Vector
3.3. Body (Buoyancy) Force
3.4. Particle Flux
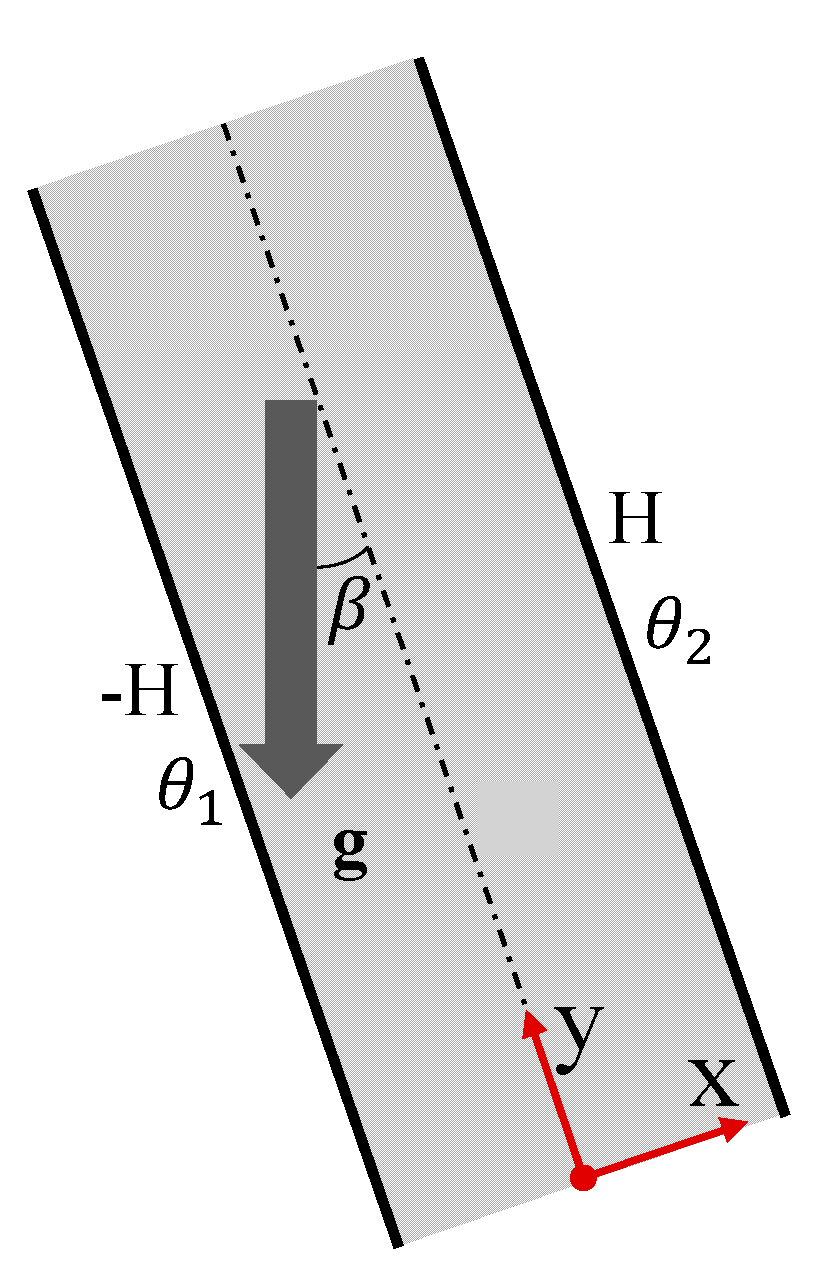
4. Flow Due to Natural Convection between Two Walls
5. Results and Discussions
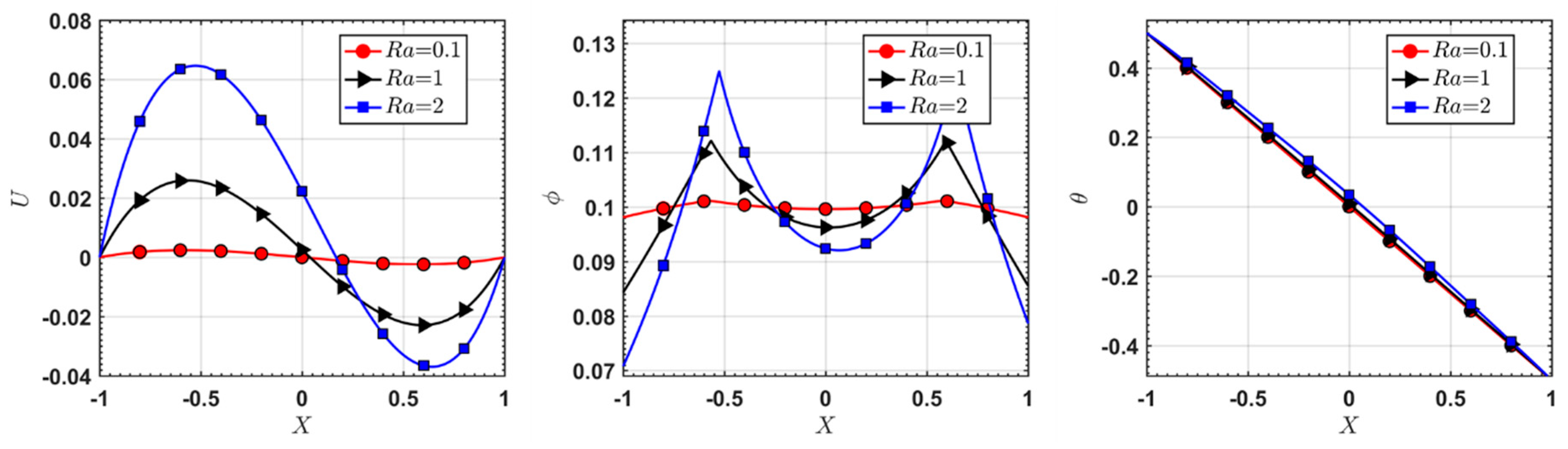
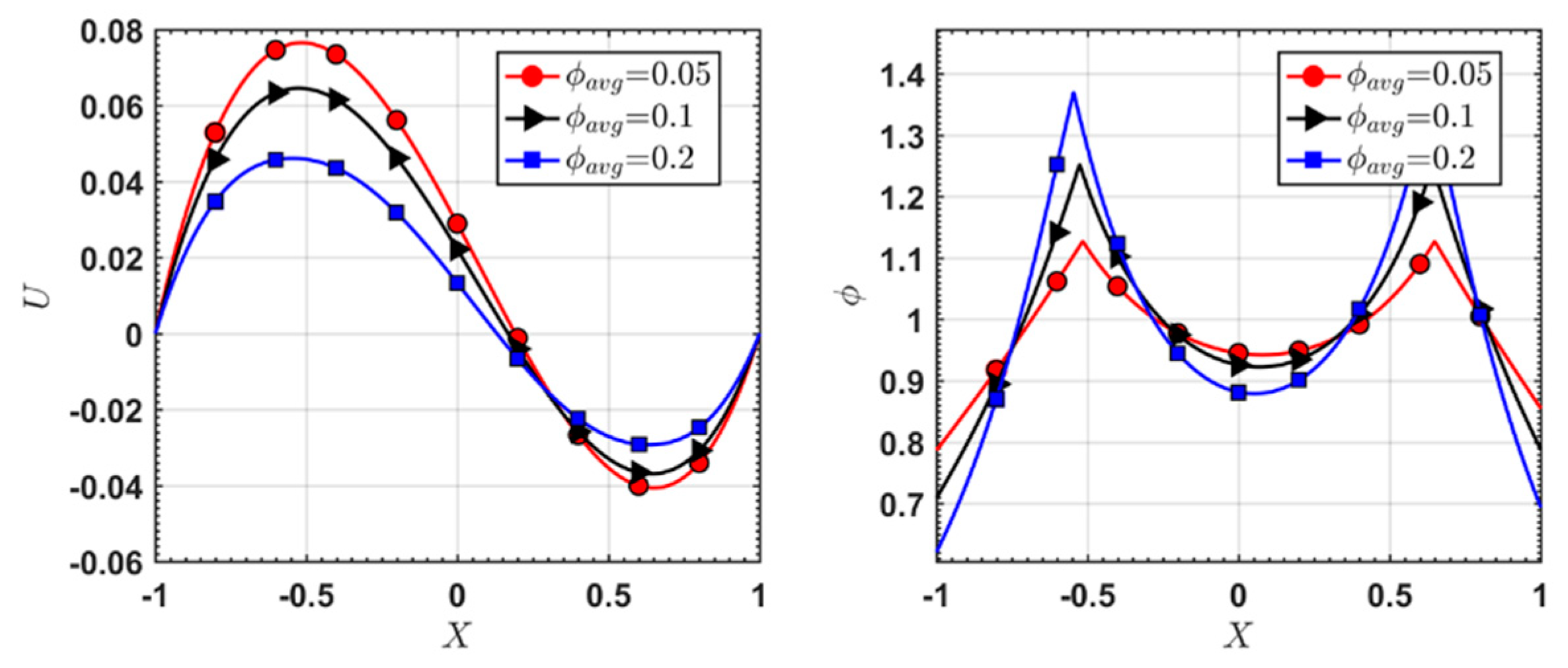
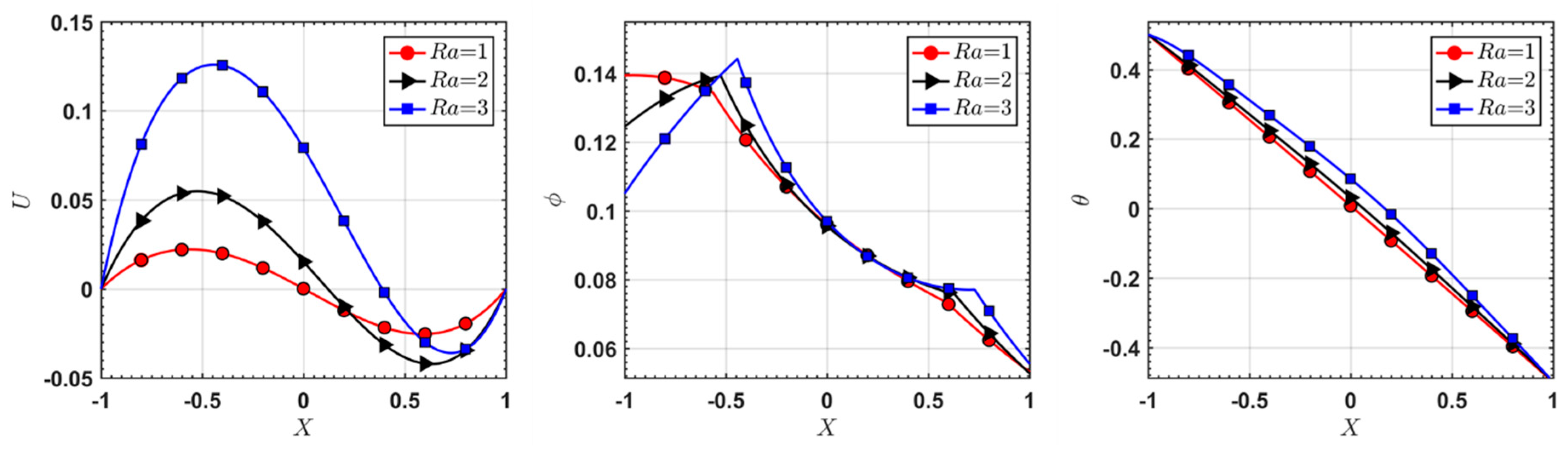
5.1. Natural Convection with Neutrally Buoyant Particles
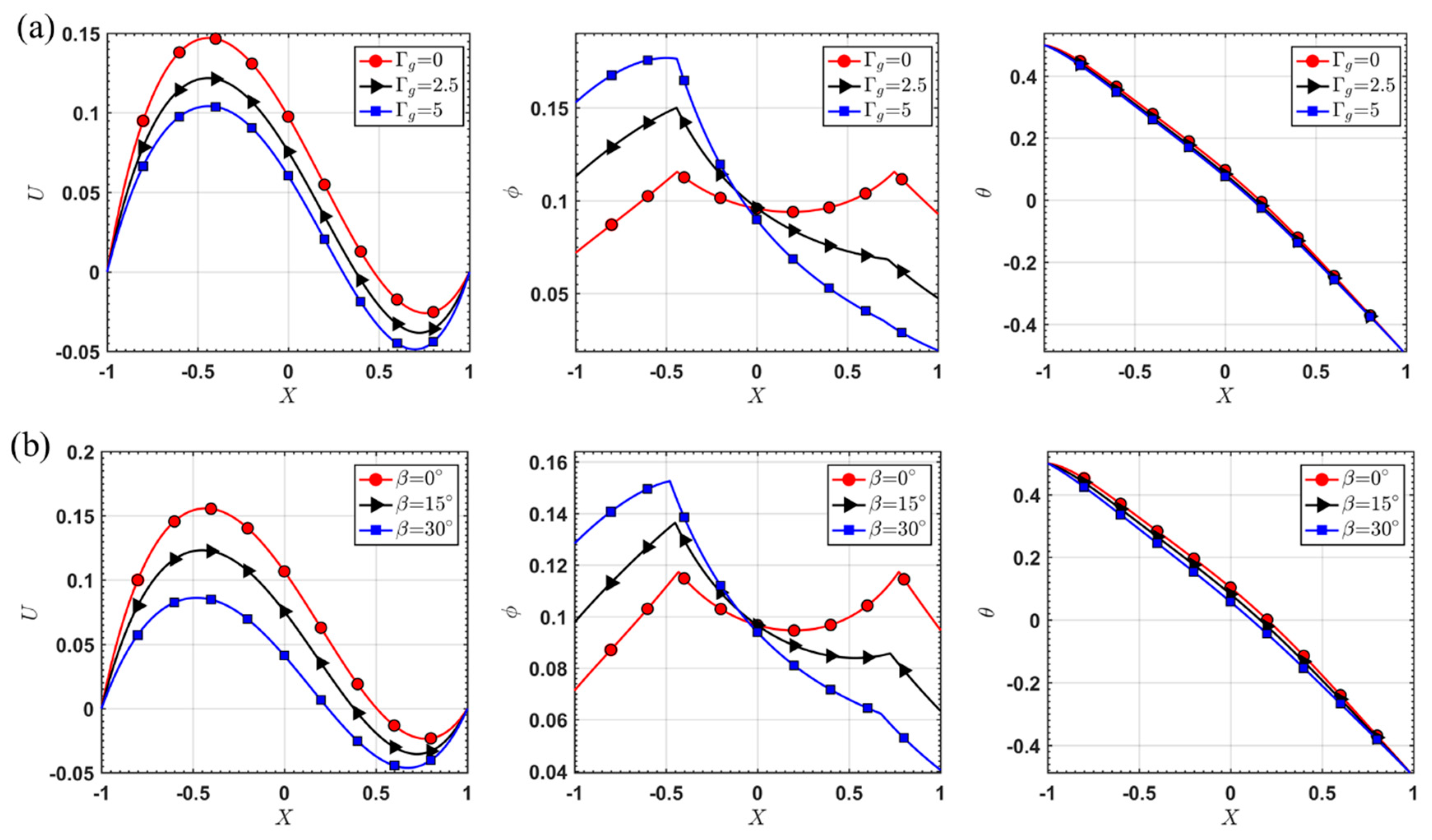
5.2. Natural Convection with Particle Sedimentation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Explanation |
| Density | |
| Specific internal energy | |
| Radiant heating | |
| Specific entropy density | |
| Gravity | |
| Characteristic length | |
| Thermal conductivity | |
| Coefficient of thermal expansion | |
| Shear rate | |
| Coefficients of particle flux | |
| Particle response time | |
| Power-law index | |
| Particle radius | |
| Diffusion coefficient | |
| Viscosity | |
| Temperature | |
| Volume fraction | |
| Pressure | |
| Inclination angle | |
| Spatial position | |
| Velocity | |
| Body force vector | |
| Heat flux vector | |
| Particle flux | |
| Cauchy stress tensor | |
| Gradient of the velocity vector | |
| Symmetric part of the velocity gradient | |
| Identity tensor | |
| Gradient symbol | |
| Divergence operator | |
| Trace operator |
References
- Turner, J.S. Buoyancy Effects in Fluids; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Chen, B.; Mikami, F.; Nishikawa, N. Experimental studies on transient features of natural convection in particles suspensions. Int. J. Heat Mass Transf. 2005, 48, 2933–2942. [Google Scholar] [CrossRef]
- Sun, X.; Massoudi, M.; Aubry, N.; Chen, Z.; Wu, W.-T. Natural convection and anisotropic heat transfer in a ferro-nanofluid under magnetic field. Int. J. Heat Mass Transf. 2019, 133, 581–595. [Google Scholar] [CrossRef]
- Kang, C.; Okada, M.; Hattori, A.; Oyama, K. Natural convection of water–fine particle suspension in a rectangular vessel heated and cooled from opposing vertical walls. Int. J. Heat Mass Transf. 2001, 44, 2973–2982. [Google Scholar] [CrossRef]
- Bustos, M.C.; Paiva, F.; Wendland, W. Control of continuous sedimentation of ideal suspensions as an initial and boundary value problem. Math. Methods Appl. Sci. 1990, 12, 533–548. [Google Scholar] [CrossRef]
- Metivier, C.; Li, C.; Magnin, A. Origin of the onset of Rayleigh-Bénard convection in a concentrated suspension of microgels with a yield stress behavior. Phys. Fluids 2017, 29, 104102. [Google Scholar] [CrossRef]
- Okada, M.; Suzuki, T. Natural convection of water-fine particle suspension in a rectangular cell. Int. J. Heat Mass Transf. 1997, 40, 3201–3208. [Google Scholar] [CrossRef]
- Batchelor, G.K. Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 1954, 80, 339–358. [Google Scholar] [CrossRef]
- Shenoy, A.V.; Mashelkar, R.A. Thermal convection in non-Newtonian fluids. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1982; Volume 15, pp. 143–225. [Google Scholar]
- Rajagopal, K.R.; Na, T.-Y. Natural convection flow of a non-Newtonian fluid between two vertical flat plates. Acta Mech. 1985, 54, 239–246. [Google Scholar] [CrossRef] [Green Version]
- Massoudi, M.; Christie, I. Natural convection flow of a non-Newtonian fluid between two concentric vertical cylinders. Acta Mech. 1990, 82, 11–19. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A.; Wulandana, R. Natural convection flow of a generalized second grade fluid between two vertical walls. Nonlinear Anal. Real World Appl. 2008, 9, 80–93. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Tao, L. Mechanics of Mixtures, Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 1995; Volume 35. [Google Scholar]
- Massoudi, M. Constitutive relations for the interaction force in multicomponent particulate flows. Int. J. Non. Linear. Mech. 2003, 38, 313–336. [Google Scholar] [CrossRef]
- Massoudi, M. A note on the meaning of mixture viscosity using the classical continuum theories of mixtures. Int. J. Eng. Sci. 2008, 46, 677–689. [Google Scholar] [CrossRef]
- Massoudi, M. A Mixture Theory formulation for hydraulic or pneumatic transport of solid particles. Int. J. Eng. Sci. 2010, 48, 1440–1461. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Liu, I.-S. Continuum Mechanics; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Dunn, J.E.; Fosdick, R.L. Thermodynamics, stability, and boundedness of fluids of complexity 2 and fluids of second grade. Arch. Ration. Mech. Anal. 1974, 56, 191–252. [Google Scholar] [CrossRef]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Macosko, C. Rheology: Principles, Measurements and Applications; Wiley-VCH Inc.: New York, NY, USA, 1994. [Google Scholar]
- Schowalter, W.R. Mechanics of Non-Newtonian Fluids; Pergamon Press: Oxford, UK, 1978. [Google Scholar]
- Bridges, C.; Rajagopal, K.R. Pulsatile Flow of a Chemically-Reacting Nonlinear Fluid. Comput. Math. Appl. 2006, 52, 1131–1144. [Google Scholar] [CrossRef] [Green Version]
- Krieger, I.M. Rheology of monodisperse latices. Adv. Colloid Interface Sci. 1972, 3, 111–136. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.-T.; Massoudi, M.; Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.-T.; Massoudi, M. Steady Flow of a Cement Slurry. Energies 2019, 12, 2604. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Effects of shear dependent viscosity and variable thermal conductivity on the flow and heat transfer in a slurry. Energies 2015, 8, 11546–11574. [Google Scholar] [CrossRef]
- Yang, H.; Aubry, N.; Massoudi, M. Heat transfer in granular materials: Effects of nonlinear heat conduction and viscous dissipation. Math. Methods Appl. Sci. 2013, 36, 1947–1964. [Google Scholar] [CrossRef]
- Yang, H.; Massoudi, M. Conduction and convection heat transfer in a dense granular suspension. Appl. Math. Comput. 2018, 332, 351–362. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—Part I: Effective thermal conductivity and background. Math. Methods Appl. Sci. 2006, 29, 1585–1598. [Google Scholar] [CrossRef]
- Massoudi, M. On the heat flux vector for flowing granular materials—part II: Derivation and special cases. Math. Methods Appl. Sci. 2006, 29, 1599–1613. [Google Scholar] [CrossRef]
- Massoudi, M.; Kirwan, A. On Thermomechanics of a Nonlinear Heat Conducting Suspension. Fluids 2016, 1, 19. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Ruzicka, M.; Srinivasa, A.R. On the Oberbeck-Boussinesq approximation. Math. Model. Methods Appl. Sci. 1996, 6, 1157–1167. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Saccomandi, G.; Vergori, L. On the Oberbeck–Boussinesq approximation for fluids with pressure dependent viscosities. Nonlinear Anal. Real World Appl. 2009, 10, 1139–1150. [Google Scholar] [CrossRef]
- Subia, S.R.; Ingber, M.S.; Mondy, L.A.; Altobelli, S.A.; Graham, A.L. Modelling of concentrated suspensions using a continuum constitutive equation. J. Fluid Mech. 1998, 373, 193–219. [Google Scholar] [CrossRef]
- Acrivos, A.; Mauri, R.; Fan, X. Shear-induced resuspension in a Couette device. Int. J. Multiph. flow 1993, 19, 797–802. [Google Scholar] [CrossRef]
- Wu, W.T.; Aubry, N.; Antaki, J.F.; Massoudi, M. A non-linear fluid suspension model for blood flow. Int. J. Non. Linear Mech. 2019, 109, 32–39. [Google Scholar] [CrossRef]
- Massoudi, M.; Uguz, A.K. Chemically-reacting fluids with variable transport properties. Appl. Math. Comput. 2012, 219, 1761–1775. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Dawson, P.R.; McTigue, D.F. A numerical model for natural convection in fluid-saturated creeping porous media. Numer. Heat Transf. 1985, 8, 45–63. [Google Scholar] [CrossRef]
- Pruša, V.; Rajagopal, K.R. On models for viscoelastic materials that are mechanically incompressible and thermally compressible or expansible and their Oberbeck–Boussinesq type approximations. Math. Model. Methods Appl. Sci. 2013, 23, 1761–1794. [Google Scholar] [CrossRef]
- Massoudi, M. Boundary conditions in mixture theory and in CFD applications of higher order models. Comput. Math. Appl. 2007, 53, 156–167. [Google Scholar] [CrossRef] [Green Version]
- MATLAB User’s Guide; The Mathworks Inc.: Natick, MA, USA, 1998.





| Section 5.1 | Section 5.2 | ||
|---|---|---|---|
| 0.1, 1.0, 2.0 | . | 1.0, 2.0, 3.0 | |
| 0.1, 1.0, 2.0 | 0.1, 1, 2.5 | ||
| 1, 10, 100 | 1, 10, 100 | ||
| 0.1, 2.5, 10 | 0.1, 10, 30 | ||
| 0.5, 0.0, 1 | NA | ||
| 0.1, 0.5, 0.8 | NA | ||
| 1, 3, 4 | NA | ||
| 0.05, 0.1, 0.2 | 0.05, 0.1, 0.15 | ||
| NA | , , | ||
| NA | 0, 2.5, 5 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, C.; Wu, W.-T.; Massoudi, M. Natural Convection in a Non-Newtonian Fluid: Effects of Particle Concentration. Fluids 2019, 4, 192. https://doi.org/10.3390/fluids4040192
Tao C, Wu W-T, Massoudi M. Natural Convection in a Non-Newtonian Fluid: Effects of Particle Concentration. Fluids. 2019; 4(4):192. https://doi.org/10.3390/fluids4040192
Chicago/Turabian StyleTao, Chengcheng, Wei-Tao Wu, and Mehrdad Massoudi. 2019. "Natural Convection in a Non-Newtonian Fluid: Effects of Particle Concentration" Fluids 4, no. 4: 192. https://doi.org/10.3390/fluids4040192





