Fluids in Music: The Mathematics of Pan’s Flutes

Abstract

We discuss the mathematics behind the Pan’s flute. We analyze how the sound is created, the relationship between the notes that the pipes produce, their frequencies and the length of the pipes. We find an equation which models the curve that appears at the bottom of any Pan’s flute due to the different pipe lengths.

1. Introduction

Fluids impact our everyday lives at any moment, from the air we breathe, to the blood circulating in our bodies, to the rivers and oceans that we swim in and drink from. Most of the examples concerning moving fluids are extremely complex with behavior governed by complicated equations involving many parameters. Applications of fluid mechanics are extremely varied and this translates in a plethora of methods and approaches to teach the subject. In this paper, we focus on the relation between fluids and musical instruments and present a somewhat atypical way to introduce fluids to undergraduate students.

Fluids, and in particular flowing air, are indispensable in the creation of sound in wind instruments and human voicing. The interaction between flowing air and different structures, e.g., inside of a tube, a reed or human vocal folds, produces air vibrations which are perceived as sounds by the human ear. The study of these interactions are useful to understanding and perfecting musical instruments or to identifying and curing vocal disorders. In this paper, we look at the geometry of Pan’s flutes and the relation between fluid dynamics and equal temperament scales brought together by this musical instrument.

Pan flutes are wind instruments consisting of multiple pipes which are gradually decreasing in length (see Figure 1). The pipes are typically made from bamboo, maple or other wood varieties. Other materials include plastic, metal or ivory. The tubes are stopped at one end, and are tuned to correct pitch by placing small pieces of rubber inside. Very often, the pipes are positioned to form a curved surface to allow quick and easy access to all pipes. The instrument featured in Figure 1 is a maple tenor Pan’s flute tuned in the key of G-major. The longest pipe measures about 29 cm and produces the lowest sound of the instrument, D4.

Table 1. The notes and their corresponding frequencies (rounded to the nearest integer) produced by the Pan’s flute.

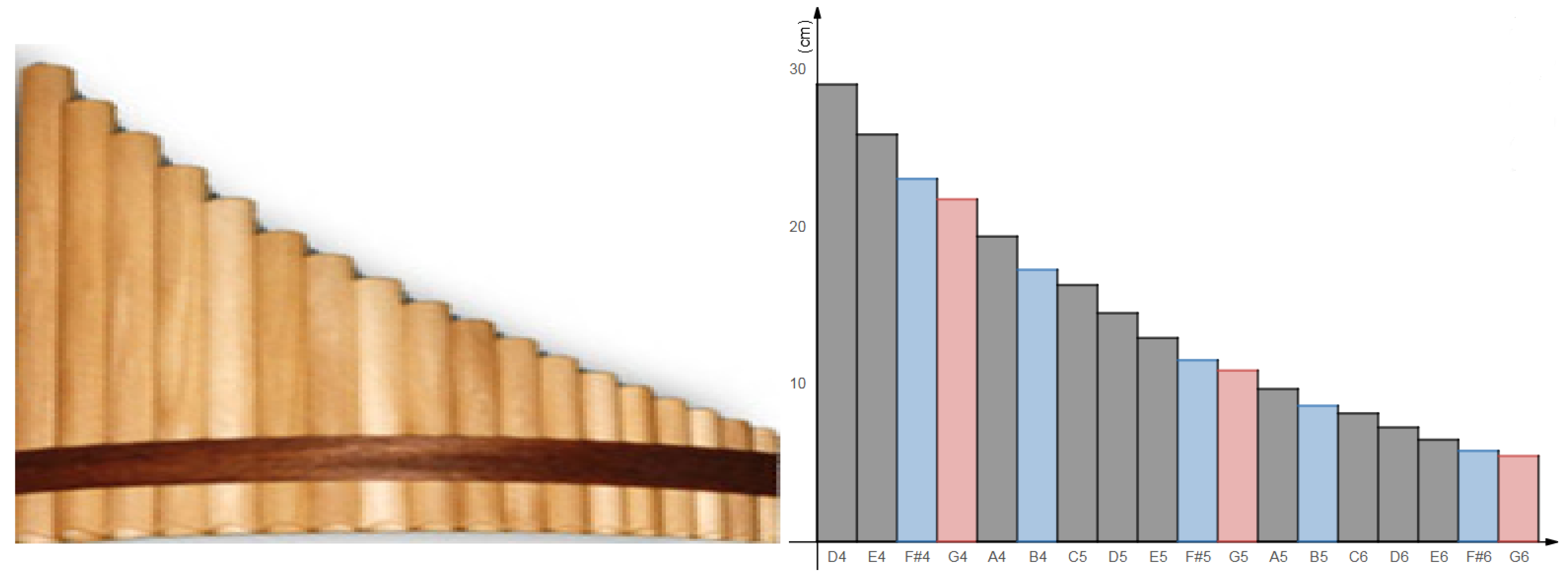
Notes	D4	E4	F#4	G4	A4	B4	C5	D5	E5	F#5	G5	A5	B5	C6	D6	E6	F#6	G6
Frequencies	294	330	370	392	440	494	523	587	659	740	784	880	988	1047	1175	1319	1480	1568

shows the notes produced by each pipe and corresponding frequencies measured by any physical tuner or a tuner app.

The goal of this research is to determine the relation between the length of the pipes and the notes played by each pipe, therefore providing a functional formula for the curve created at the top of the instrument in Figure 1. We will do this in two steps: first, determine a relation between the frequency and the length (function f in Figure 2) and then a relation between the notes and corresponding frequencies (function L in Figure 2). The composition between the two functions should provide the desired relationship.

The benefits of this apparent simple problem are twofold. First, one can learn about several math-physics areas and methods starting with fluid dynamics, wave equation, partial differential equations and continuing with elements of algebra in particular frequency ratios, and logarithmic and exponential functions. Second, the application of mathematics to a seemingly unrelated field like music (and art in general) is extremely exciting, novel and attractive to students who otherwise would not consider working on a mathematical research problem.

In this paper, we assume all pipes are ideal, i.e., the wavelength of the sound produced is proportional to the length of the tube. This is equivalent to assuming a zero diameter for the pipes of the Pan’s flute, which is an acceptable approximation for the current research. In reality, the diameter of the pipes plays a role in the pitch produced by the musical instrument: a pipe with a non-zero diameter appears to be acoustically longer than its physical length. When designing musical instruments consisting of large diameter pipes (organ, boom-whacker, etc.), an end-correction of the pipes needs to be applied. For an in-depth discussion of this effect, see [1].

2. The Relationship between the Frequency and the Length of a Pipe

Sound in pipes is produced by vibrating air pressure due to the air interaction with the walls of the pipe. The partial differential equation that models this physics is the wave equation for the acoustic pressure. The equation can be developed from the linearized one-dimensional continuity equation, the linearized one-dimensional force equation, and the equation of state (see for example [2]), and takes the form

$$\frac{{\partial }^{2}p}{\partial x^2}=\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2},$$

(1)

where $p(x,t)$ is the air pressure due to air moving inside of the pipe, x is the coordinate along the pipe, t is time, and $c\approx$ 340 m/s is the speed of sound in air. The boundary conditions associated with this differential equation are based on the physics of the problem: at the open end, the moving air has nothing to push against and therefore the pressure is zero; at the closed end, the air piles up and increases the pressure to a maximum value. Therefore, for a Pan’s flute pipe of length L, open at $x=L$ and closed at the $x=0$, the boundary conditions are

$$\begin{array}{cc}\hfill p(L,t)& =0,\hfill \\ \hfill p_x(0,t)& =0.\hfill \end{array}$$

(2)

It is worth mentioning that for other wind instruments, such as the flute, clarinet, etc., the partial differential equation given in Equation (1) is the same while the boundary conditions in Equation (2) change to reflect different constructions. The solutions of the boundary value problem described by Equations (1) and (2) are linear combinations of the normal modes [3]

$$p_n(x,t)=cos\left(\frac{2n-1}{2}\pi \frac{x}{L}\right)\left(b_{n}cos\left(\frac{2n-1}{2L}\pi ct\right)+c_{n}sin\left(\frac{2n-1}{2L}\pi ct\right)\right),$$

(3)

where $n=1,2,3\dots$ and $b_n$ and $c_n$ are constants. It is easy to see now that the frequency of the $nth$ mode is

$$f_n=\frac{(2n-1)c}{4L}.$$

(4)

These frequencies have a simple explanation related to musical instruments. Notes played on conventional instruments (wind, string, etc.) produce one main frequency, the fundamental, and a series of lower amplitude frequencies, partials, which are integer multiples of the fundamental frequency. For example, when blowing air into the largest pipe of the Pan’s flute in Figure 1, you will only hear the fundamental frequency of $f_1$ (the note D4) even though an infinite series of partials, having frequencies $3f_1$, $5f_1$, etc., are produced.

The 1st mode, the fundamental, is described by the frequency

$$f_1=\frac{340}{4L},$$

(5)

which is our first desired equation relating the frequency of the musical note produced by a pipe and the length of that pipe. For example, the longest pipe in our instrument produces a frequency of approximately 294 Hz, which means that its length is approximately

$$L=\frac{340}{4\times 294}=0.29m,$$

(6)

which agrees with the measurements in Figure 1.

3. The Relationship between the Musical Notes and the Frequencies

It was long postulated that different notes whose frequency ratios are expressible as ratios of small integers are consonant (for a more in depth discussion see [4]). For example, $f_1$ and $2f_1$ attain the ratio of the smallest possible integers, namely 2:1, the interval (the distance between them) being designated as an octave. Another example of a consonant interval is the perfect fifth, which is represented by two notes whose frequencies achieve a 3:2 ratio. Based on this condition of consonance, it was natural to build scales using the most consonant intervals possible, namely the octave and the perfect fifth. This produced the Pythagorean scale (see

Table 2. One octave of the Pythagorean scale of G major.

Note	G4	A4	B4	C5	D5	E5	F#5	G5
Ratio	1:1	9:8	81:64	4:3	3:2	27:16	243:128	2:1

).

The scale in Table 2 is obtained by choosing an octave (say G4–G5), then adding to the fist note (G4) a perfect fifth interval, thus obtaining the second note (D5). Adding another perfect fifth interval to D5, we obtain a frequency ratio of 9:4 (with respect to G4) that is outside of our octave. Reducing this interval by an octave (by dividing this frequency ratio by 2), we obtain a ratio of 9:8, which is our third note in the scale (A4). We continue the process until we discover all the notes in the scale (for more details, refer to [4]). In this system, adding/subtracting intervals amounts to multiplying/dividing frequency ratios, which is why it is commonly referred to as a logarithmic scale. One important observation is that the Pythagorean scale is based on the assumption that going up 12 fifths and coming down 7 octaves will return you exactly to the same starting note, or, in other words, that

$$2^{19}\approx 3^{12}.$$

(7)

While these numbers are close, they are not exactly equal, which gives rise to certain problems in the Pythagorean scale. Among the issues are other musical intervals, like the third, which are perceived as dissonant in this scale. Other scales were later developed to alleviate some of these problems—for example, just intonation, meantone and the equal temperament scale.

The equal temperament scale makes all the semitones equally distant (see

Table 3. One octave of the equal temperaments scale of G major.

Note	G4	A4	B4	C5	D5	E5	F#5	G5
Ratios	1:1	$2^{\frac{1}{6}}:1$	$2^{\frac{1}{3}}:1$	$2^{\frac{5}{12}}:1$	$2^{\frac{7}{12}}:1$	$2^{\frac{3}{4}}:1$	$2^{\frac{11}{12}}:1$	2:1

). It is designed to ‘fix’ all the problems associated with other scales by distributing the dissonance occurring in different intervals throughout the entire scale. This implies that, while classical intervals like the perfect fifth or the third are no longer going to have frequency ratios represented by small integer ratios, they are going to sound the same (relatively consonant) in any key and any pitch.

All the modern musical instruments, our Pan’s flute included, are tuned in the equal temperament scale. In this scale, the frequency f of any note can be obtained from the frequency $f_1$ of any reference note (we chose D4 as our reference note as it corresponds to the note produced by the first pipe of the Pan’s flute) from the formula

$$f=2^{\frac{x}{12}}{f}_1,$$

(8)

where x represents the number of semitones that separates the note with the frequency f from the first note: $x=0$ represents the first note, D4, $x=2$ represents the second note, E4, $x=4$ represents the third note, F#4, $x=5$ represents the fourth note, G4, and so on. Note that x does not cover all the positive integer values since the scale contains only the main notes in the G-major scale and does not include the sharps. This is consistent with the construction of the Pan’s flute that we use in this paper. Because of this, when plotting the lengths of the pipes as a function of x, we will need to adjust for these apparent irregular values taken by the variable x.

4. Putting It All Together

Combining Equations (5) and (8), we find

$$L=\frac{340}{4\times 2^{\frac{x}{12}}\times f_1},$$

(9)

which is the desired relation between the length of a pipe and the note played by that pipe. Plotting this curve on the same coordinate system with the model of the musical instrument, we obtain Figure 3, which shows a perfect match with our initial model of the Pan’s flute.

5. Conclusions

In this paper, we discuss a mathematical model of Pan’s flutes. The interaction of mathematics and music makes it an interesting application for undergraduate students as they find refuge from the mathematical rigor into the flexibility and creativity of arts. The study of wind instruments provides a rich environment for teaching fluid mechanics and other areas of applied mathematics in a fun and relaxed way.