A Relaxation Filtering Approach for Two-Dimensional Rayleigh–Taylor Instability-Induced Flows
Abstract
1. Introduction
2. Governing Equations
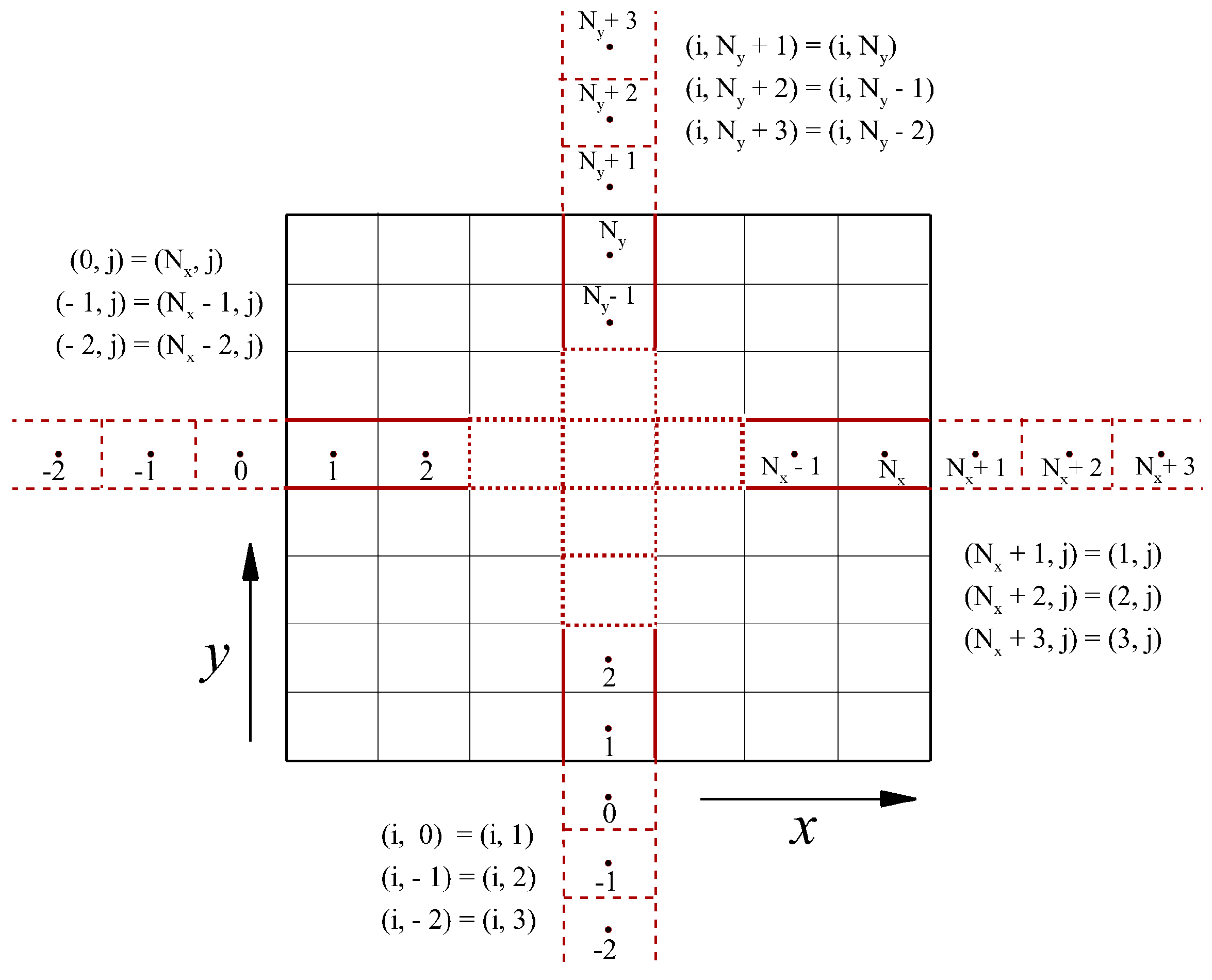
3. Numerical Methods
3.1. ILES Approach
3.1.1. Weno Reconstruction
3.1.2. Roe Riemann Solver
3.1.3. Rusanov Riemann Solver
3.2. Central Scheme with Relaxation Filtering (Cs+Rf) Approach
4. Results
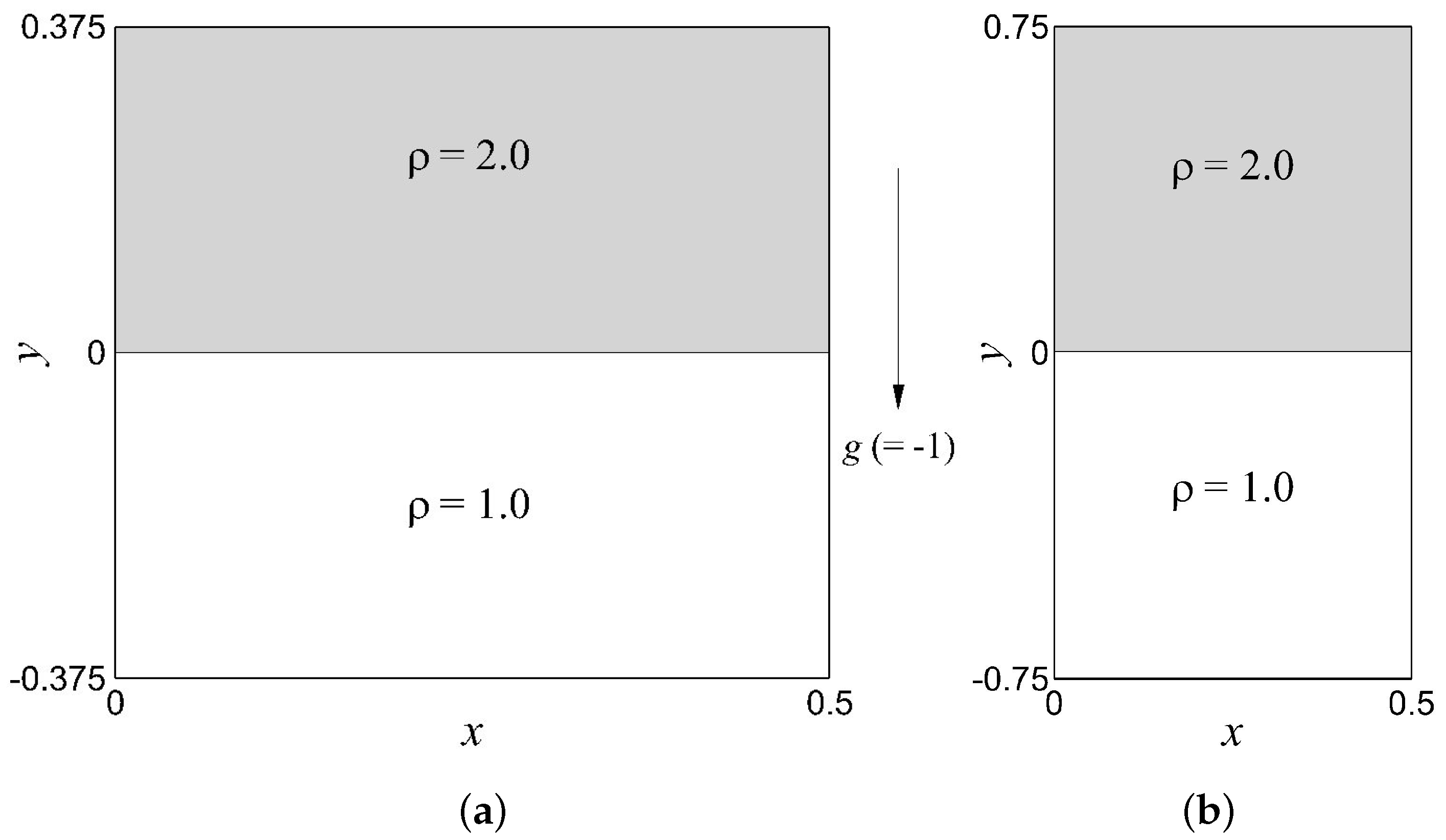
4.1. Two-Dimensional RTI Test Problem: Case Setup
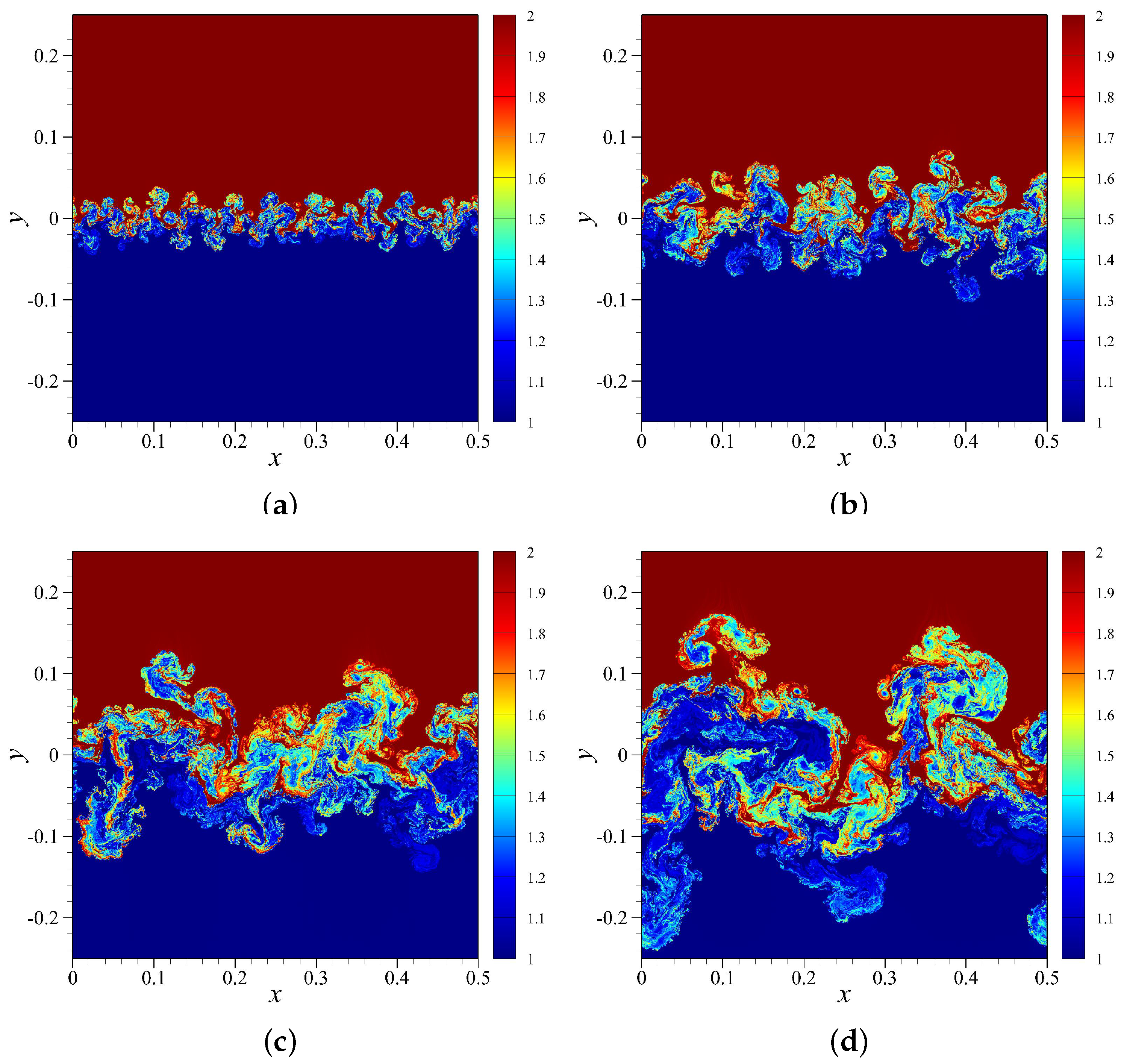
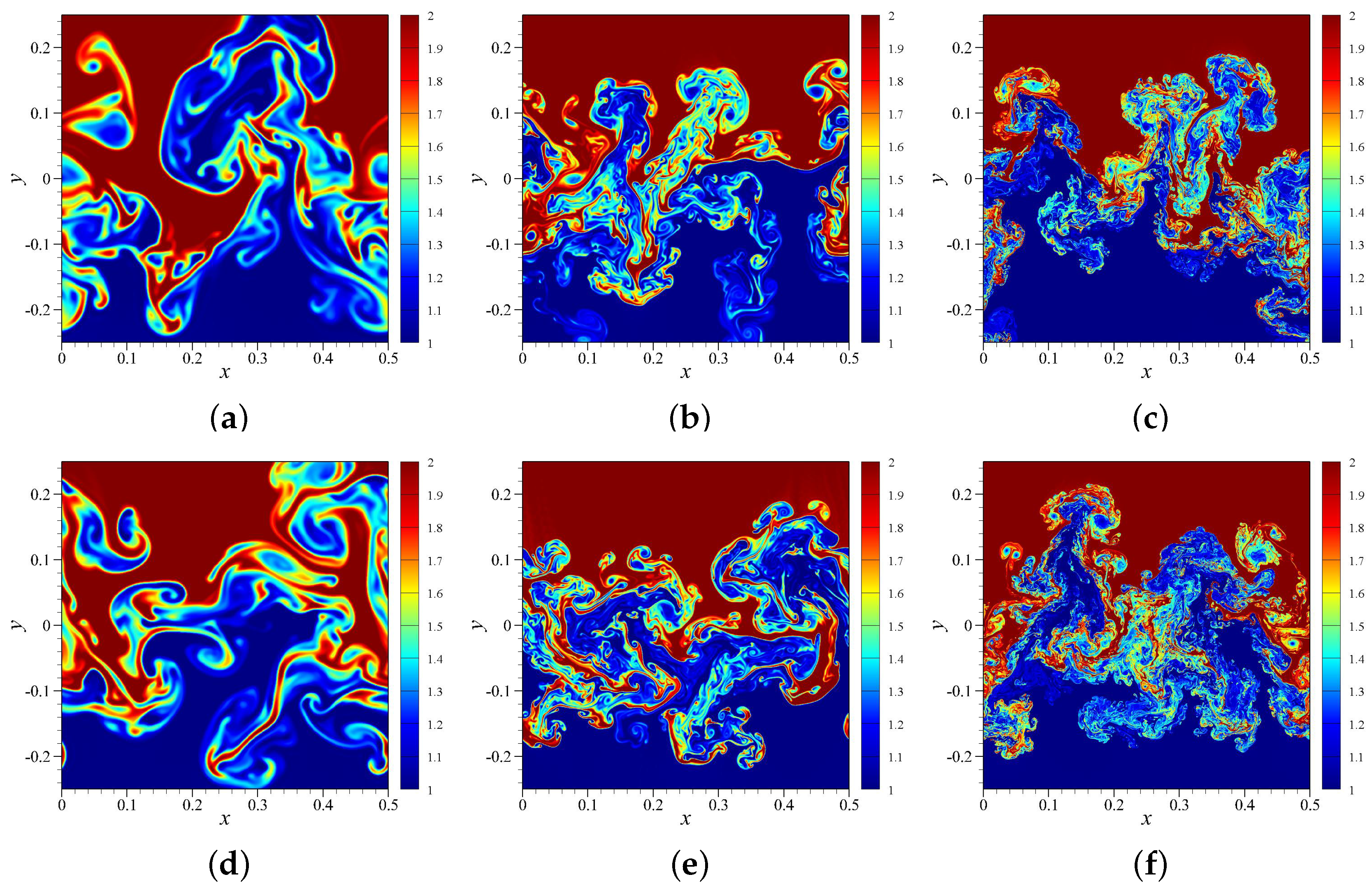
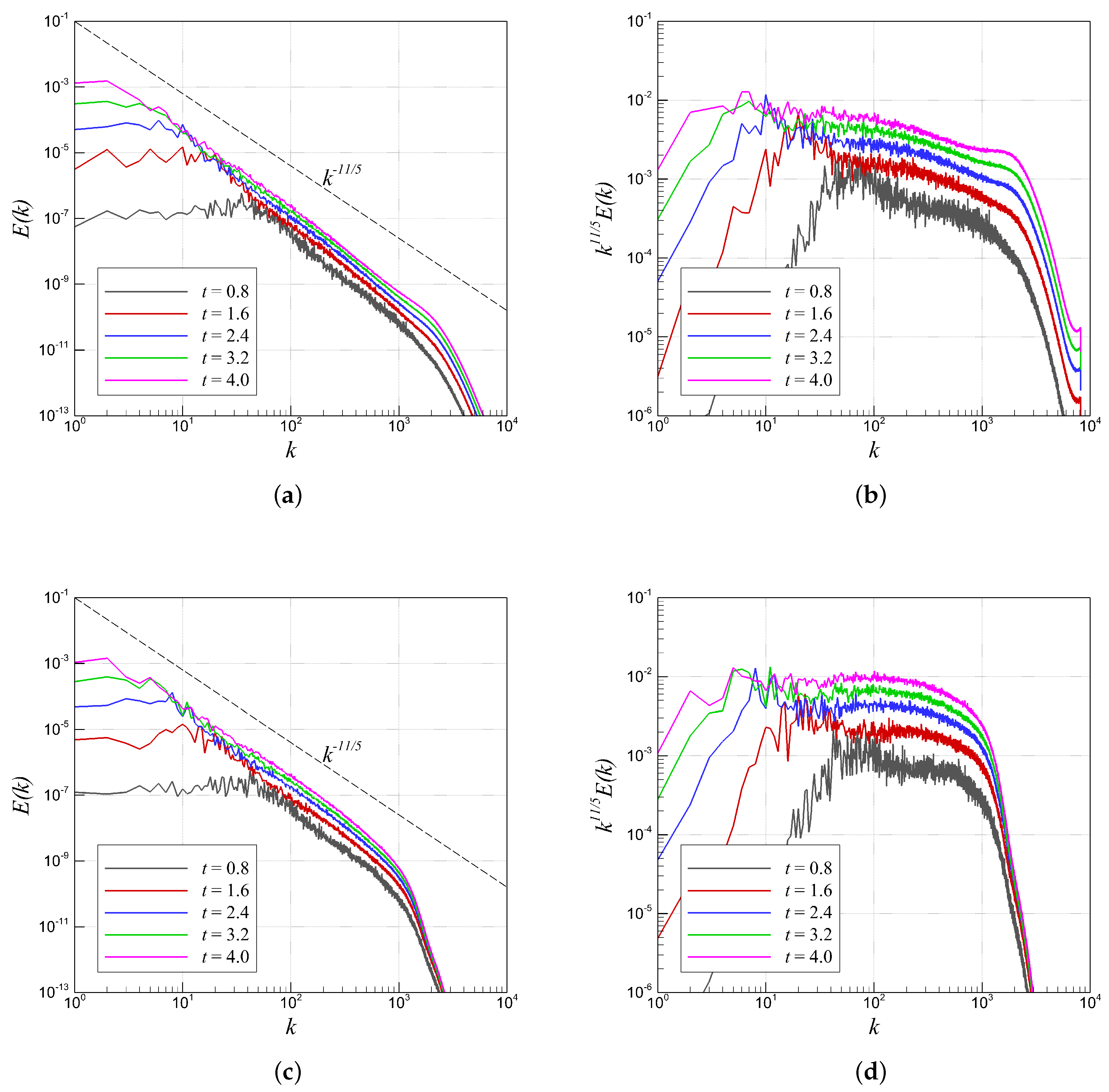
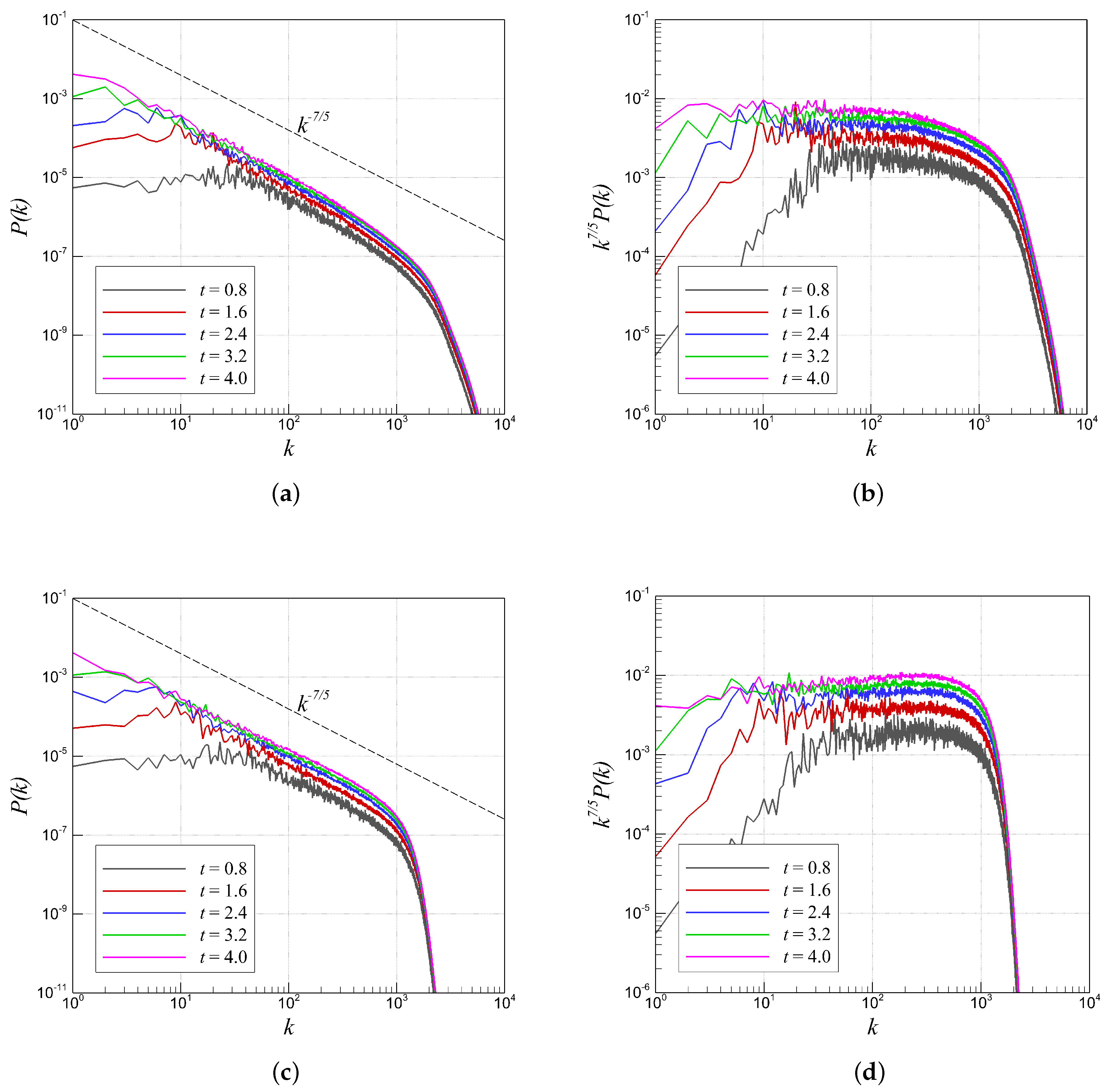
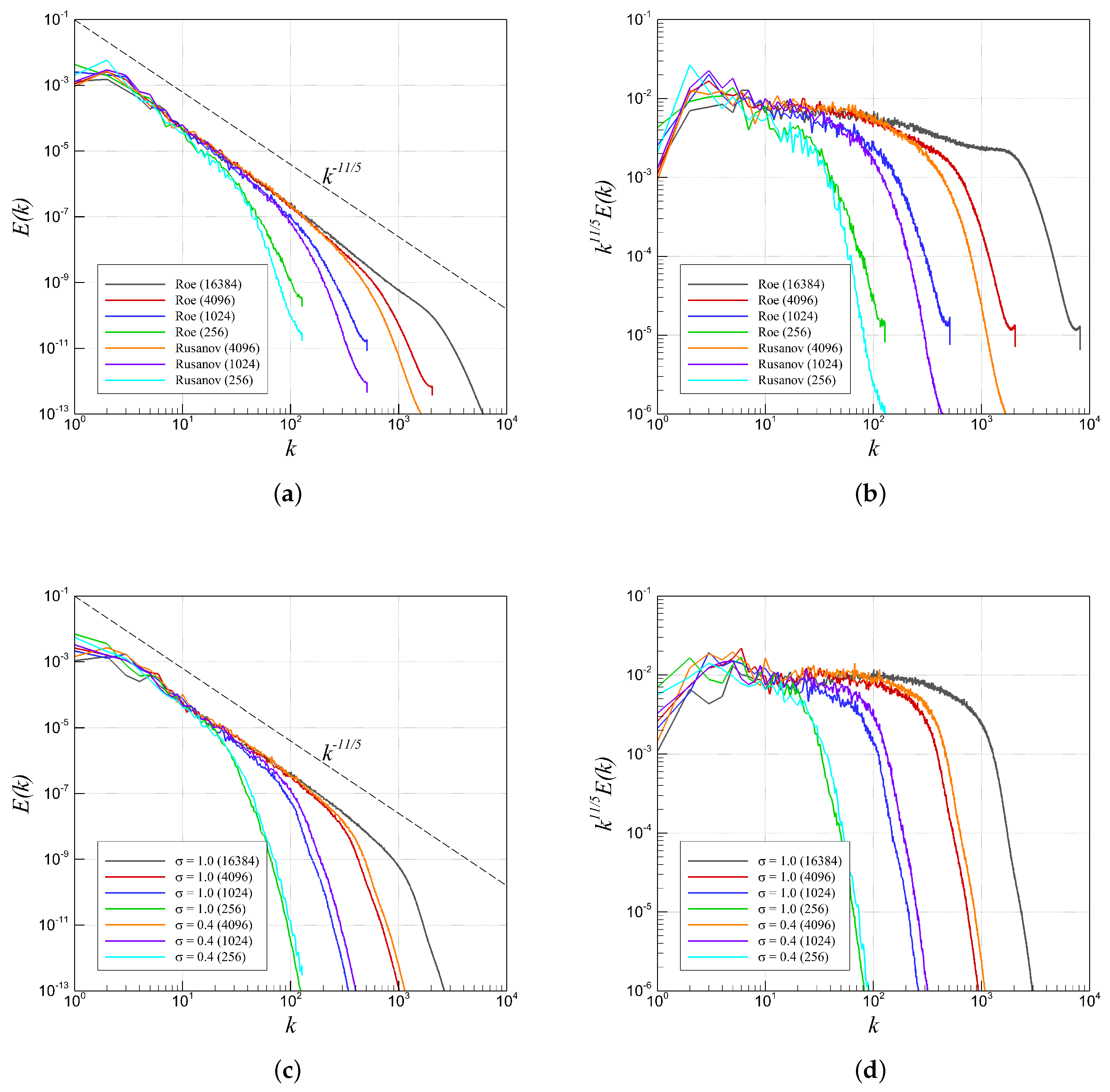
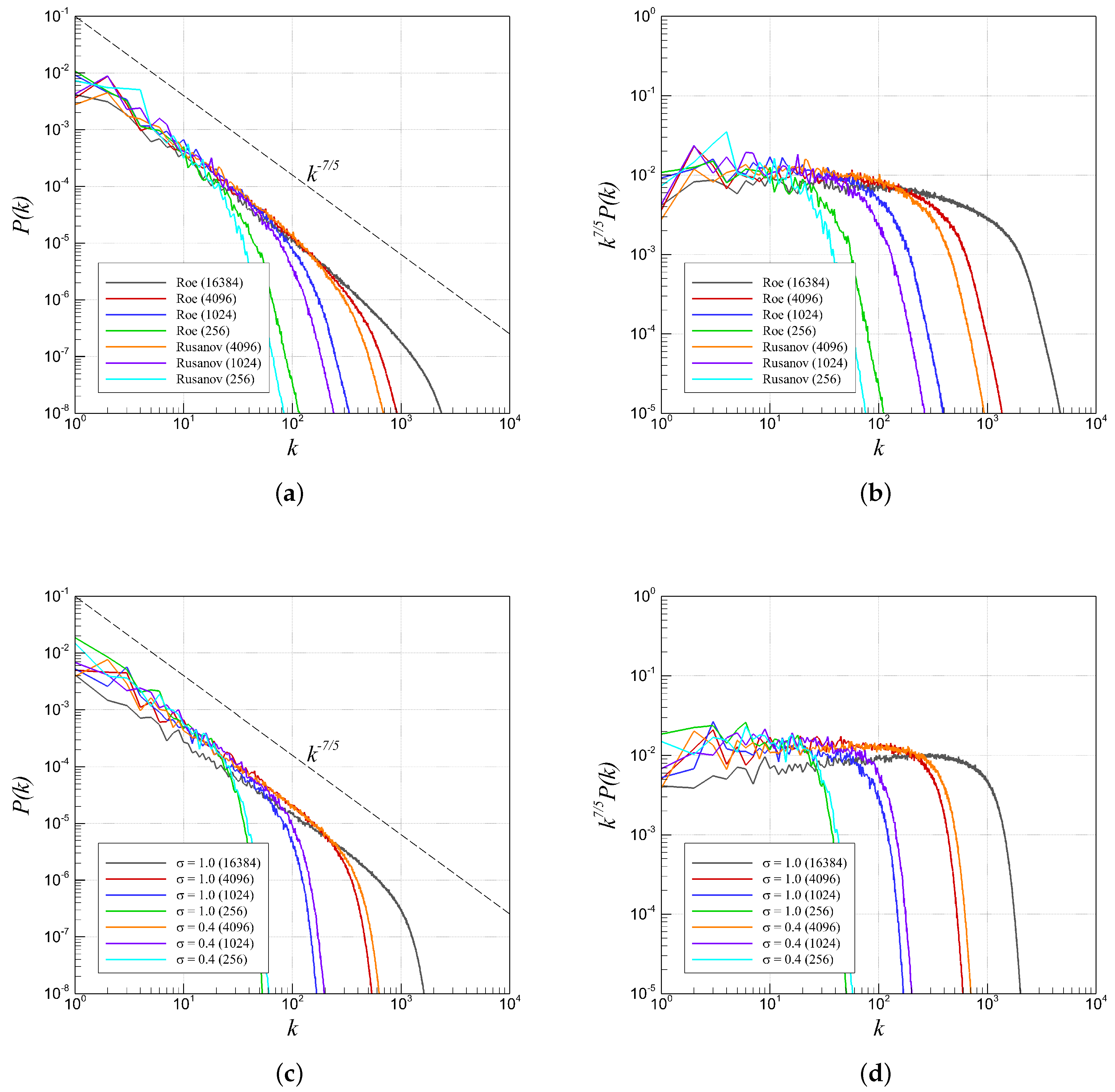
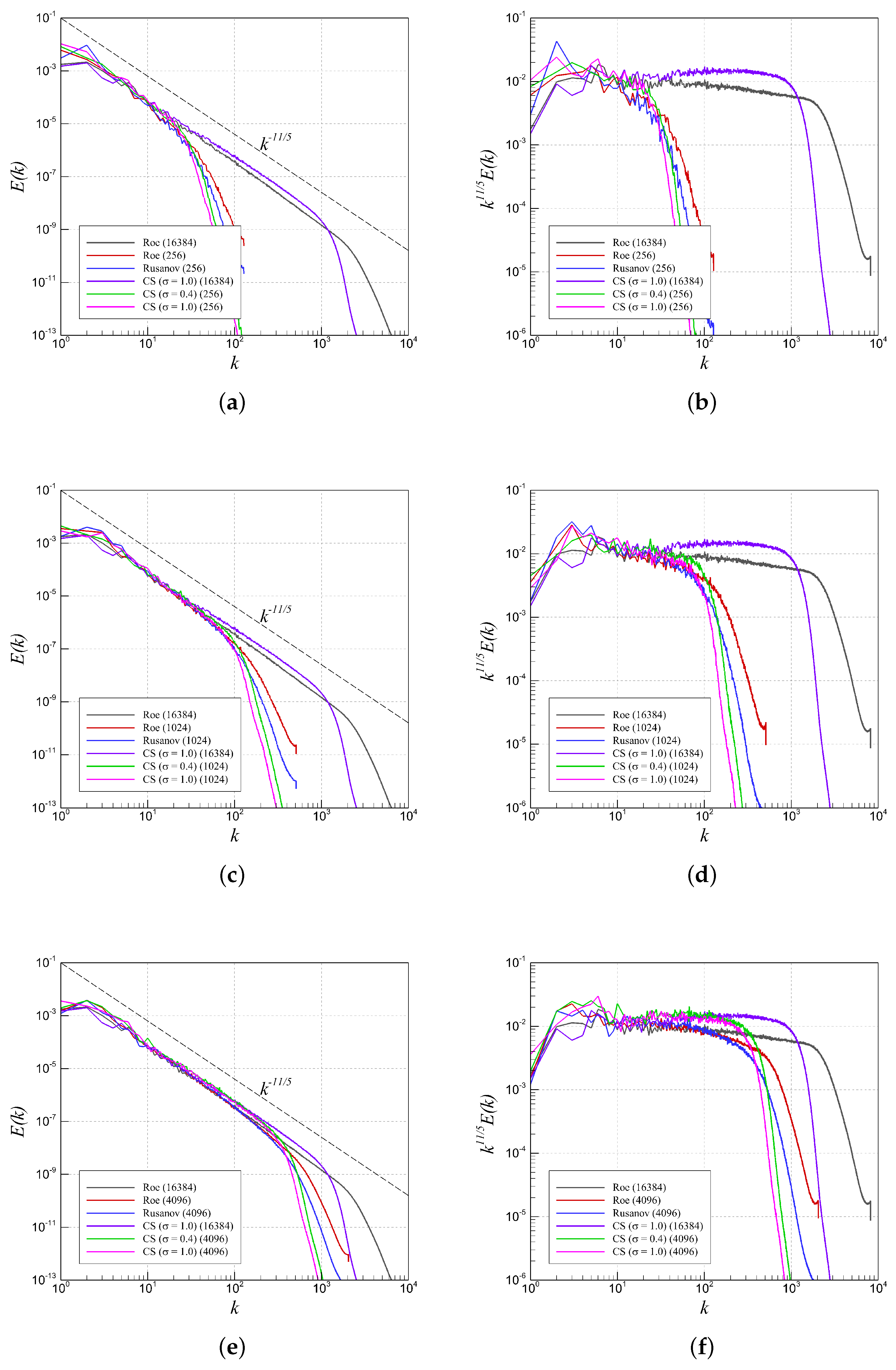
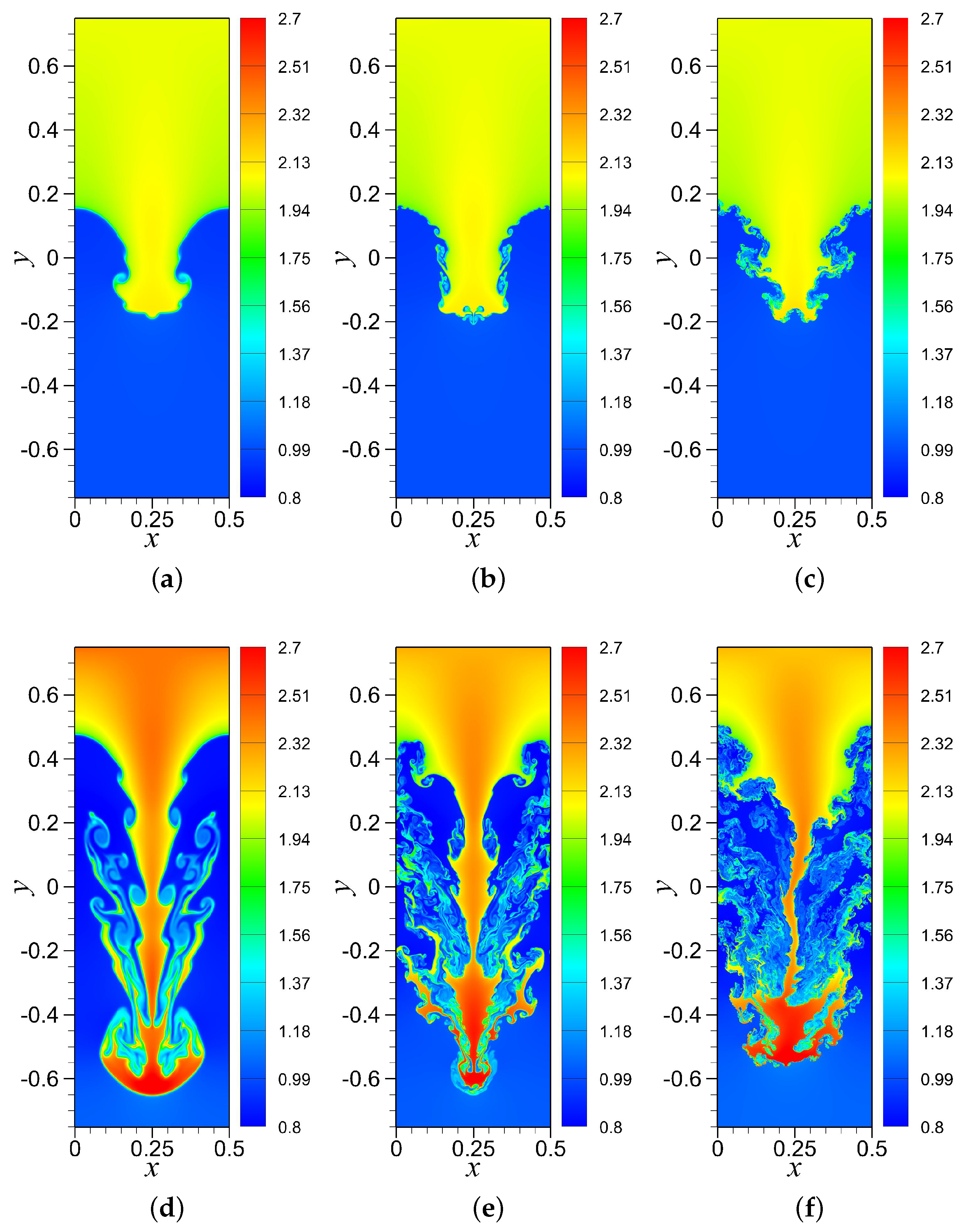
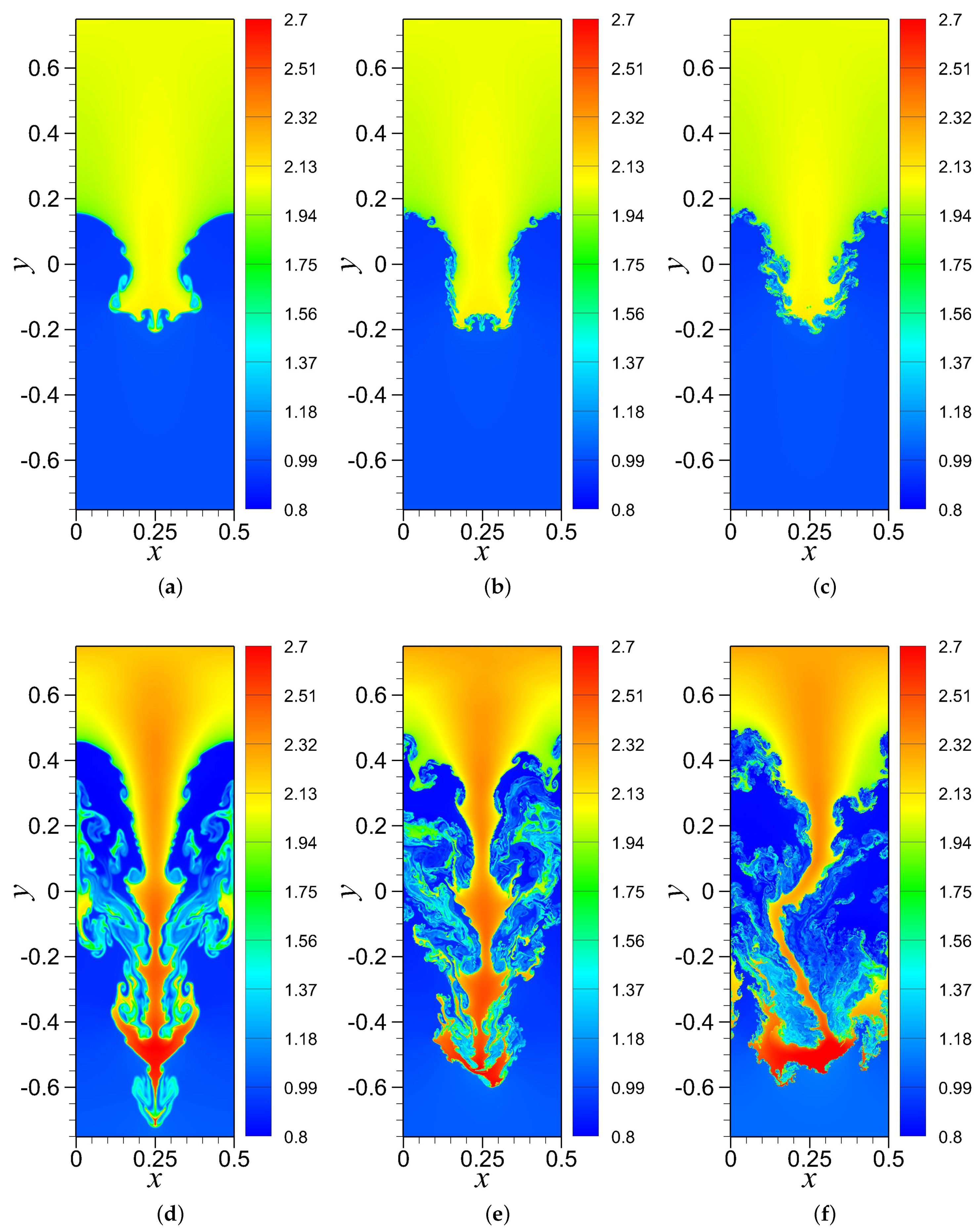
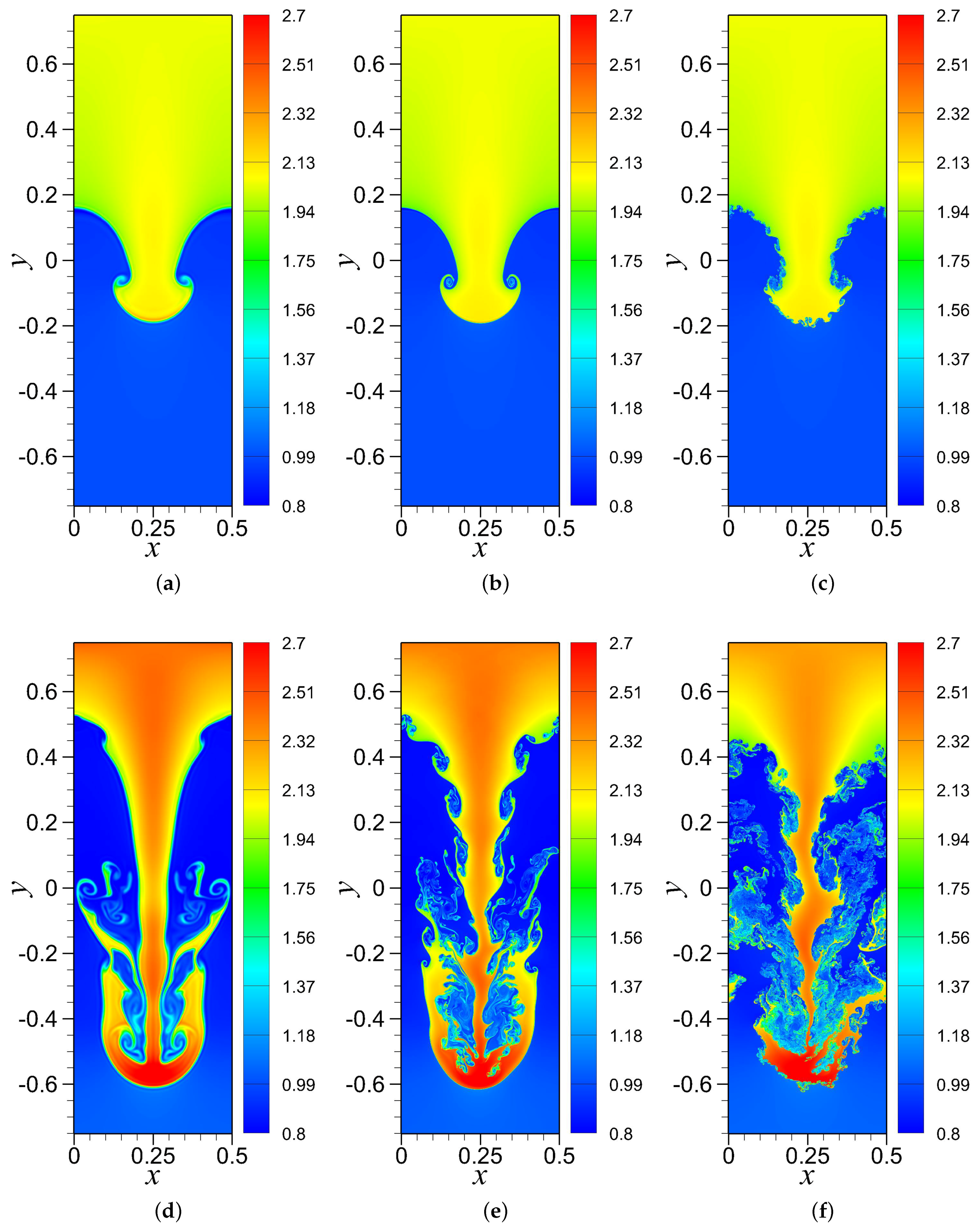
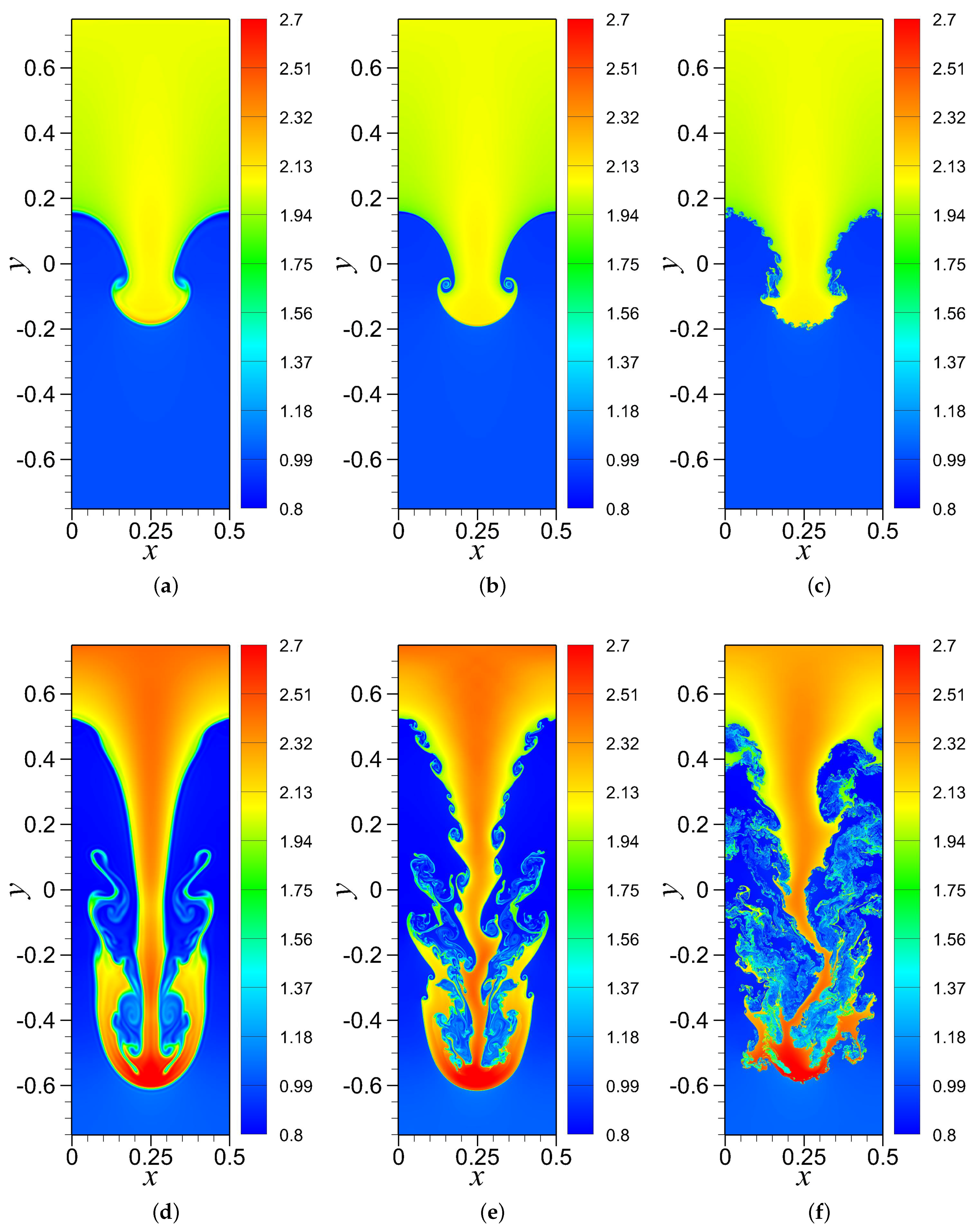
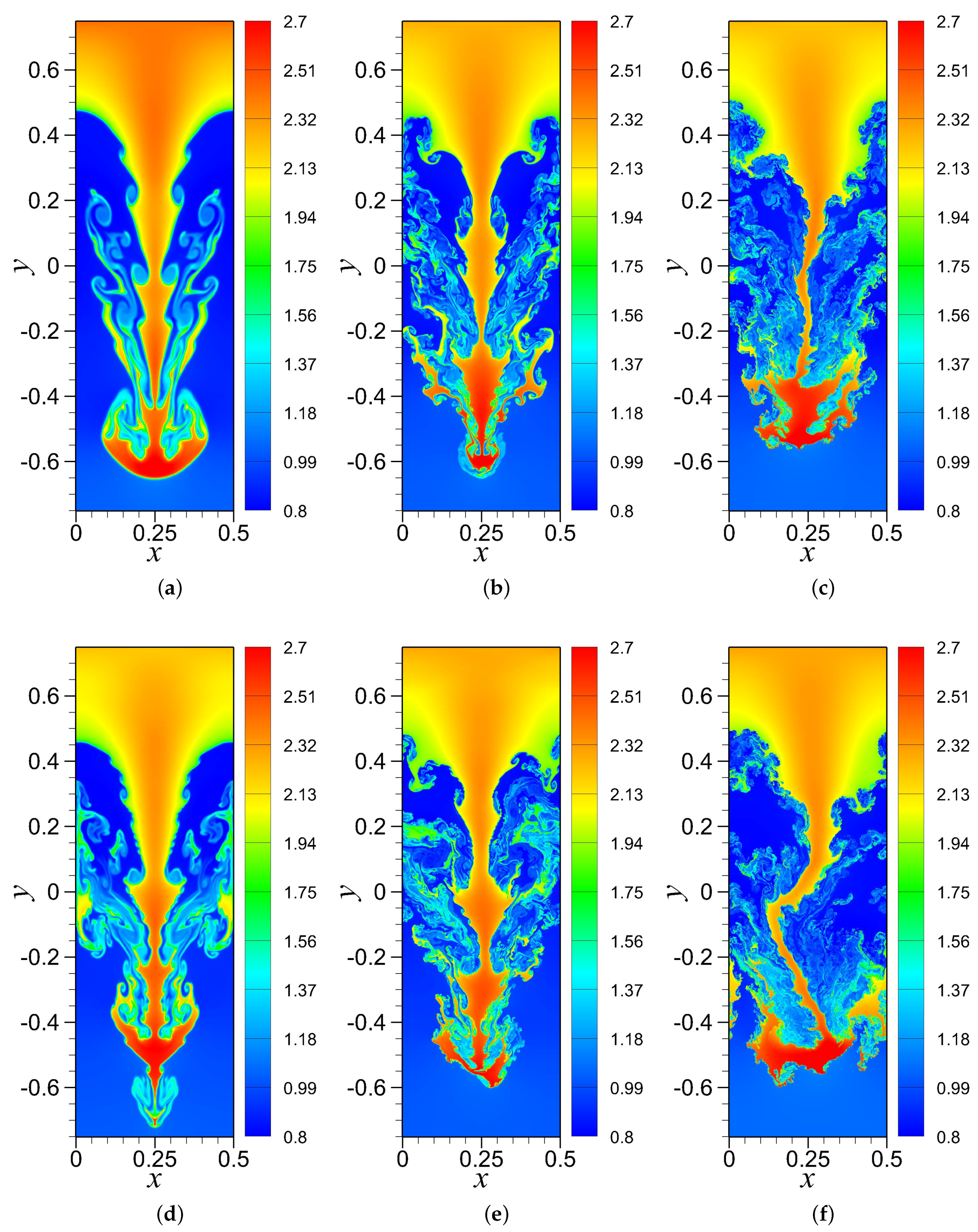
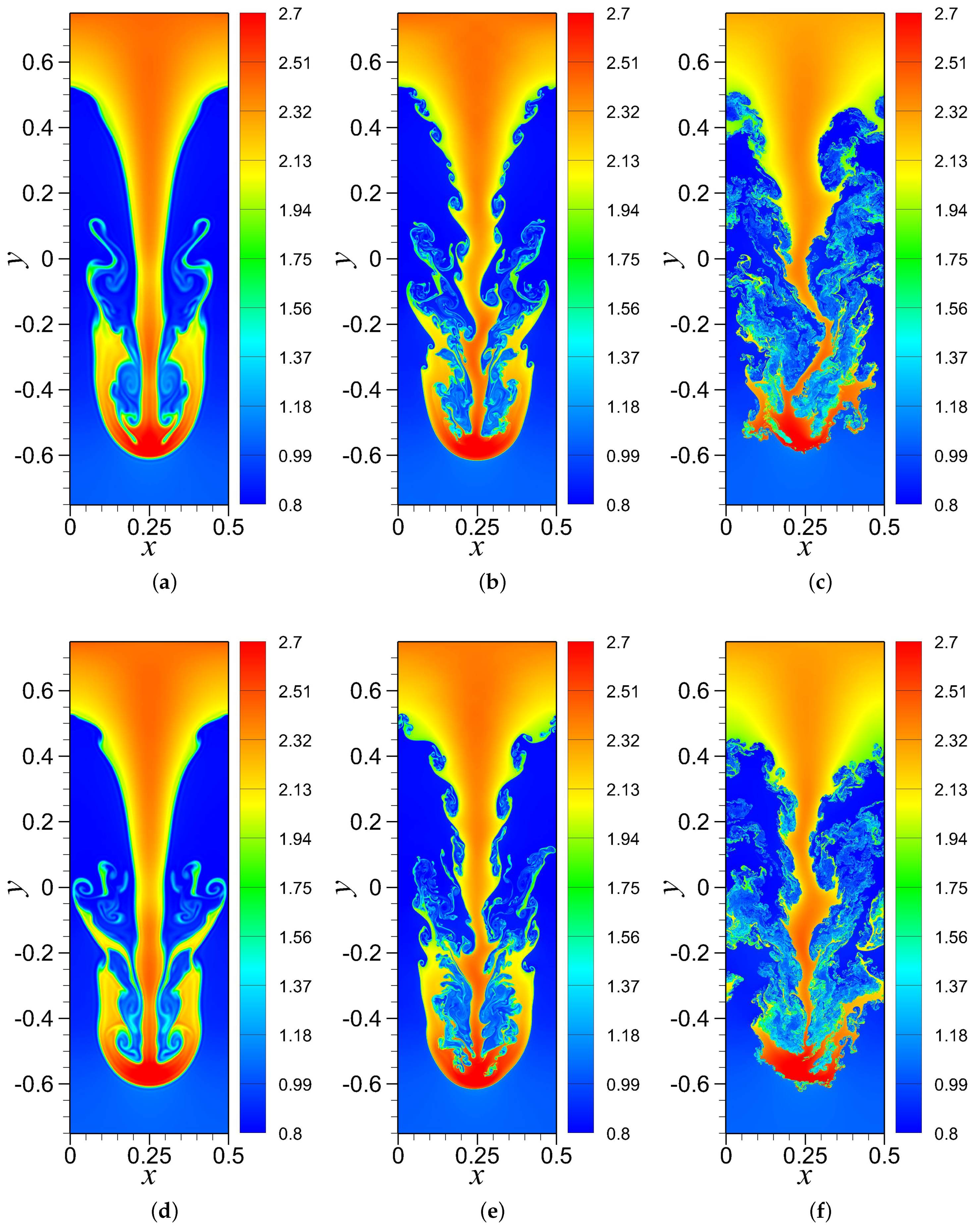
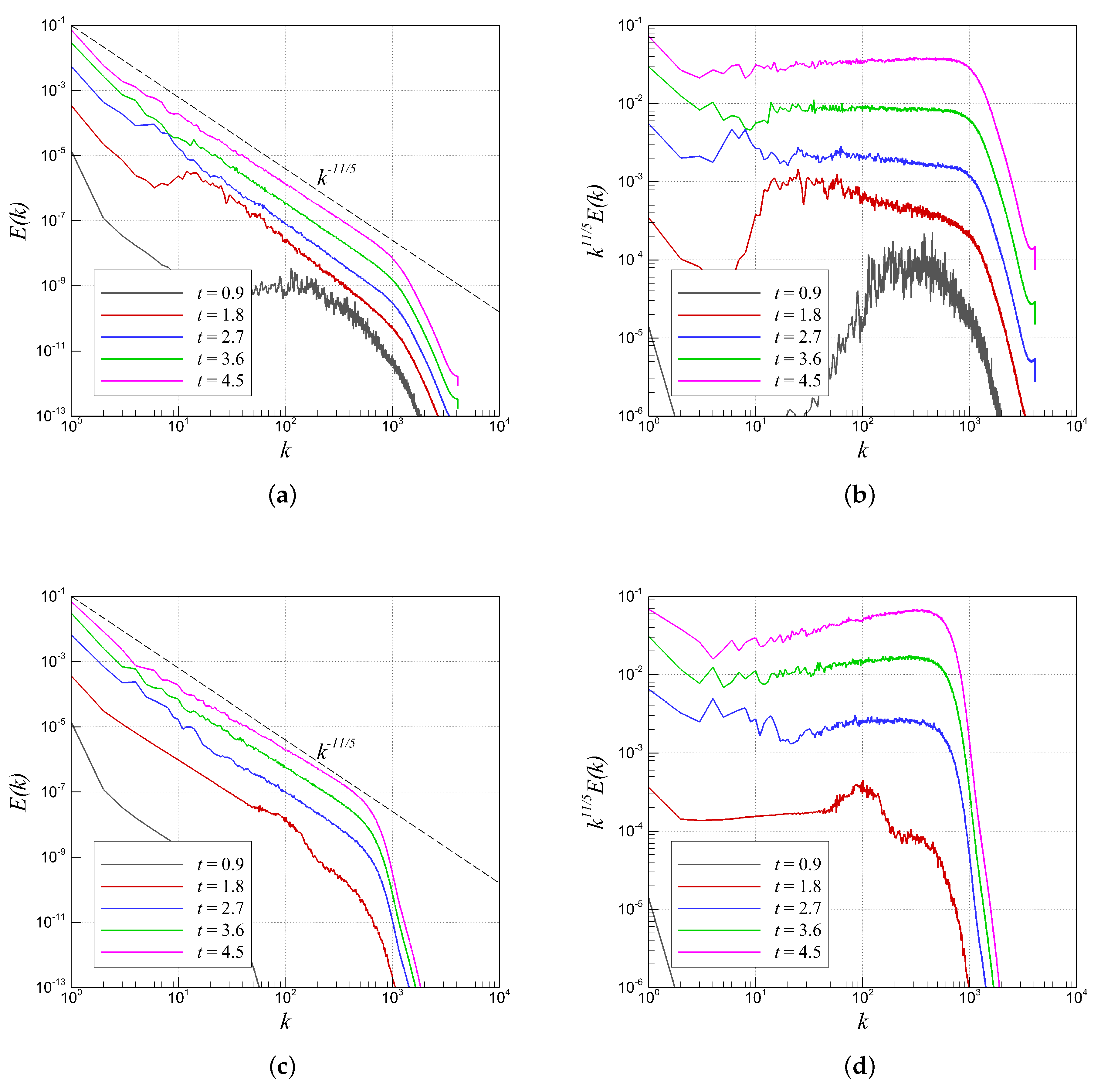
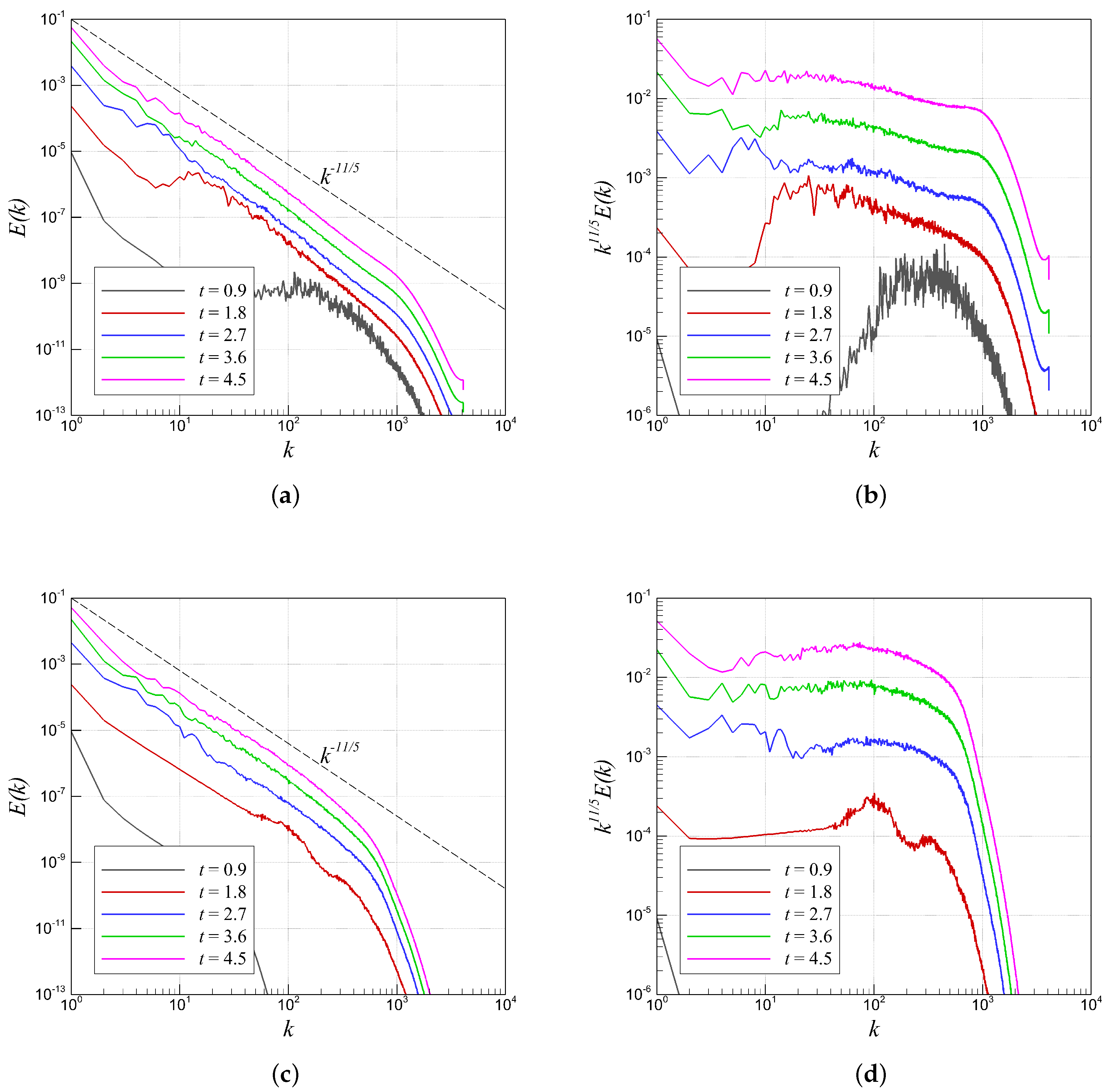
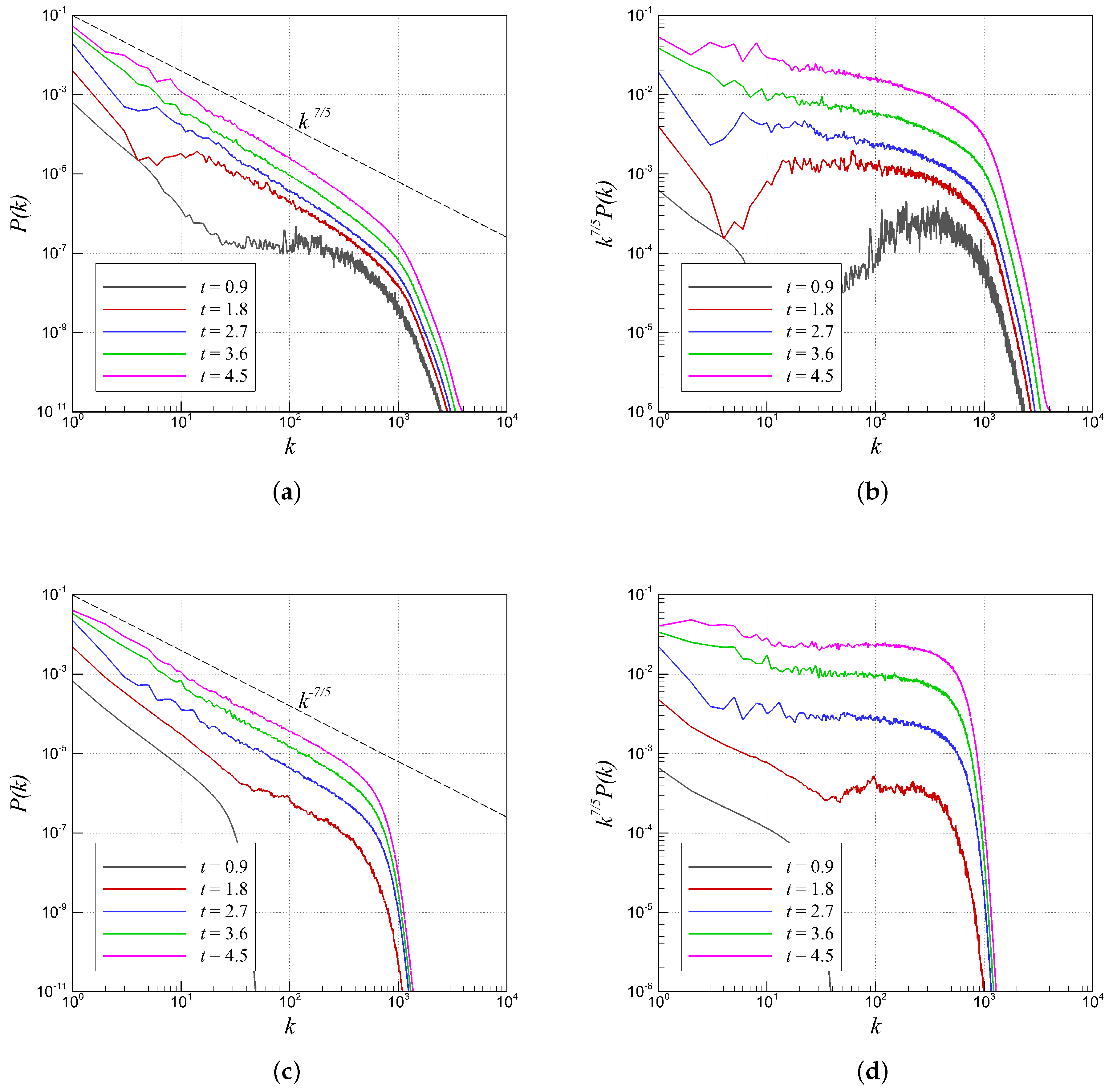
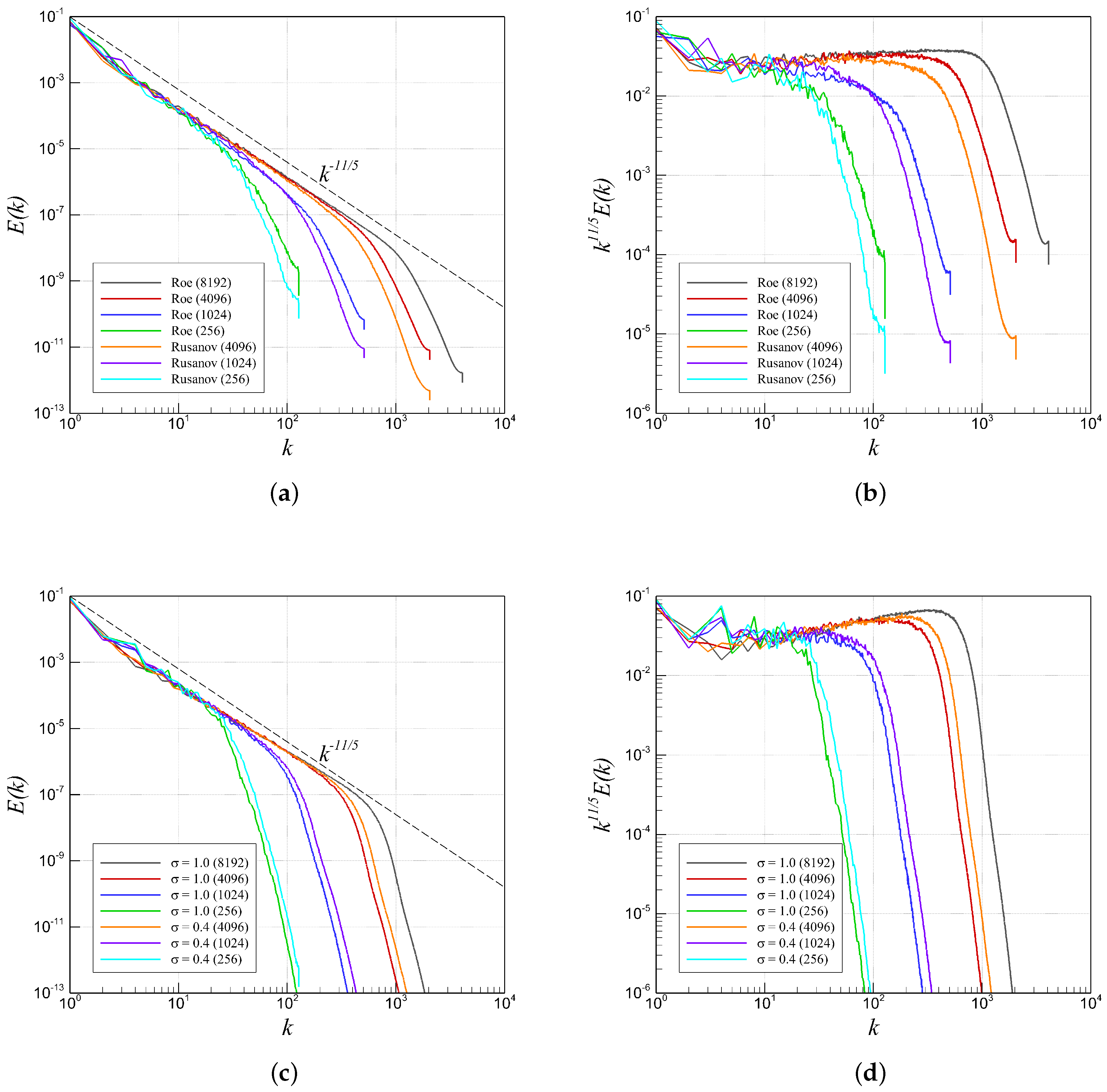
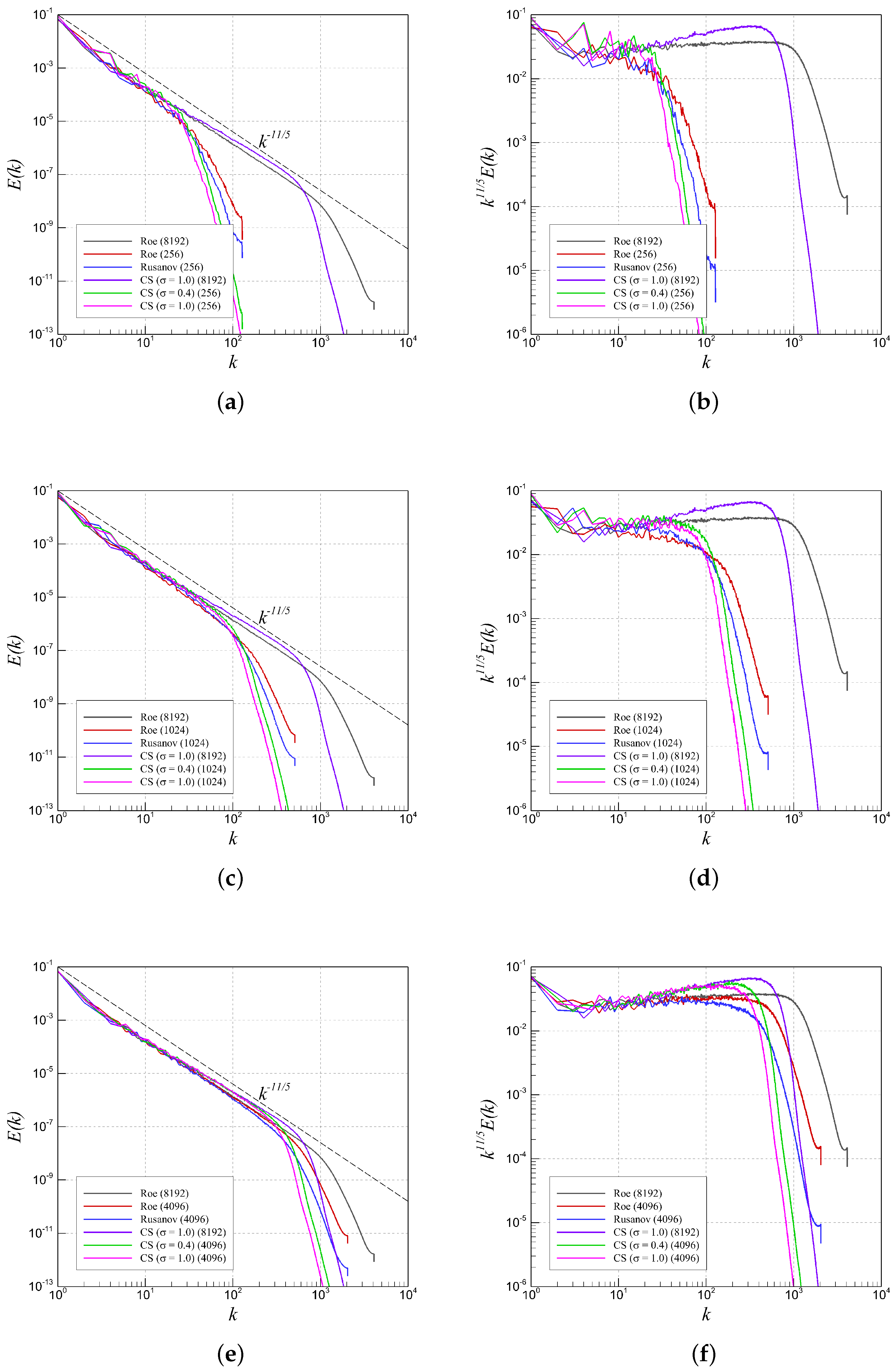
4.2. RTI with Random (Multi-Mode) Perturbation
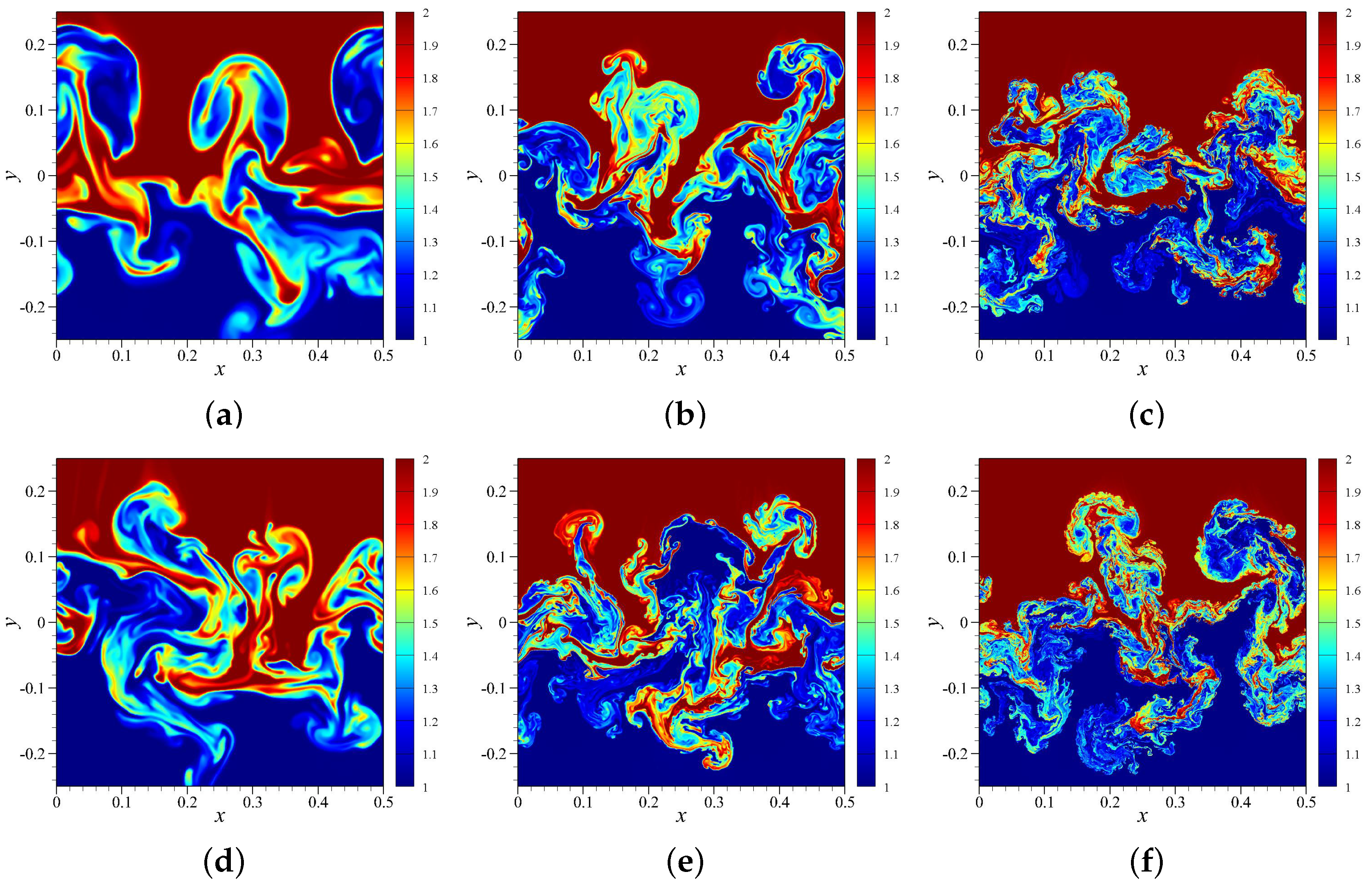
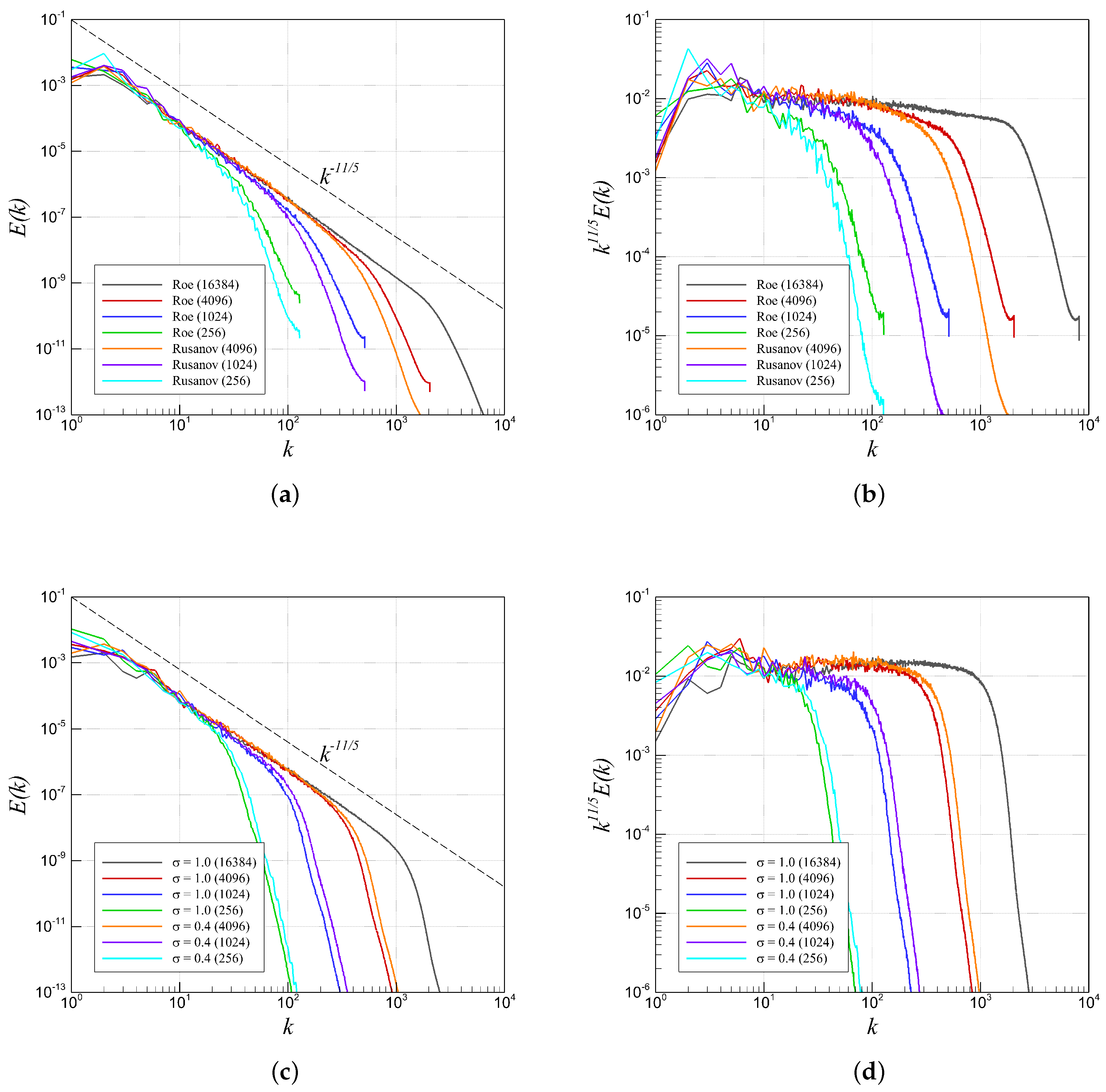
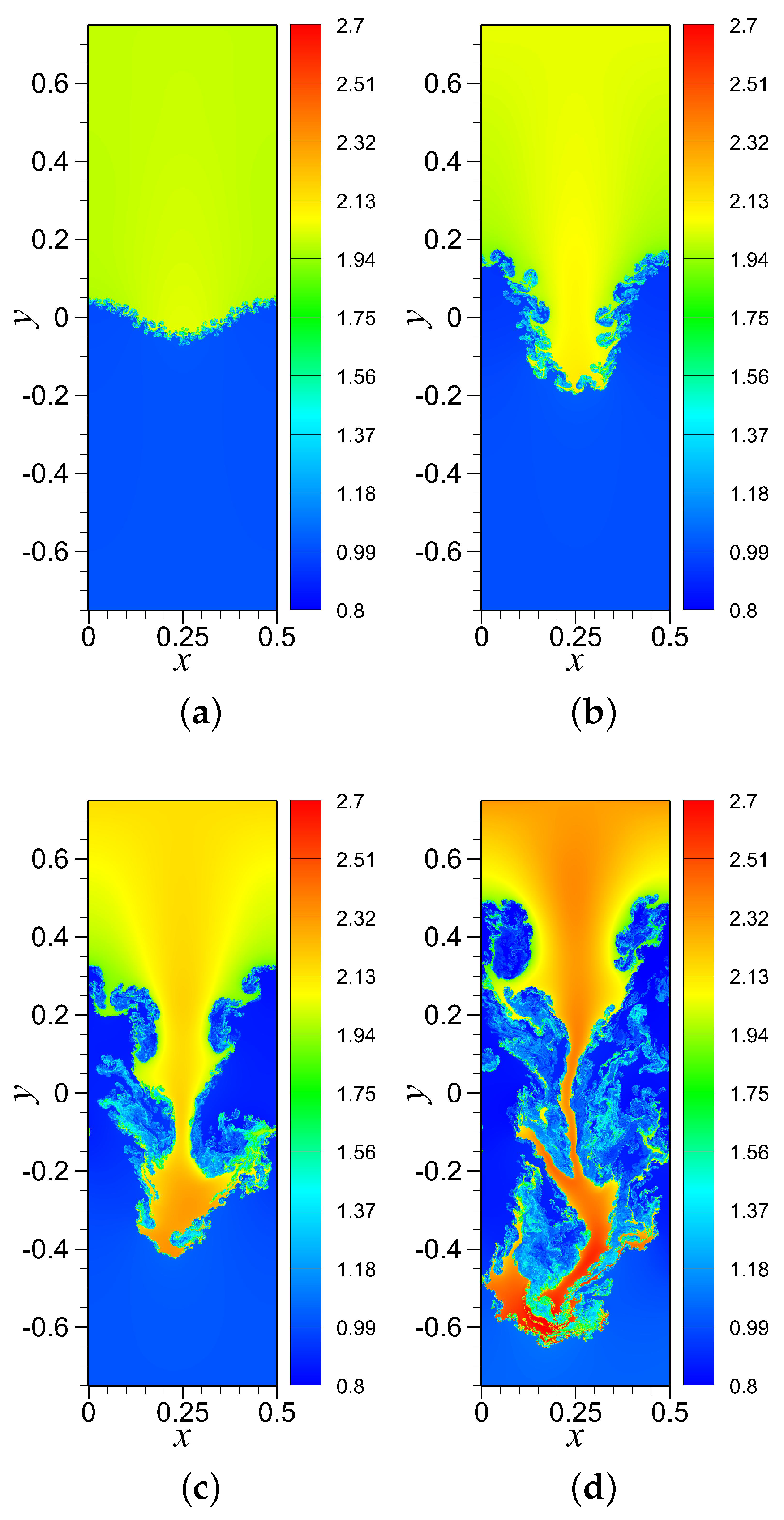
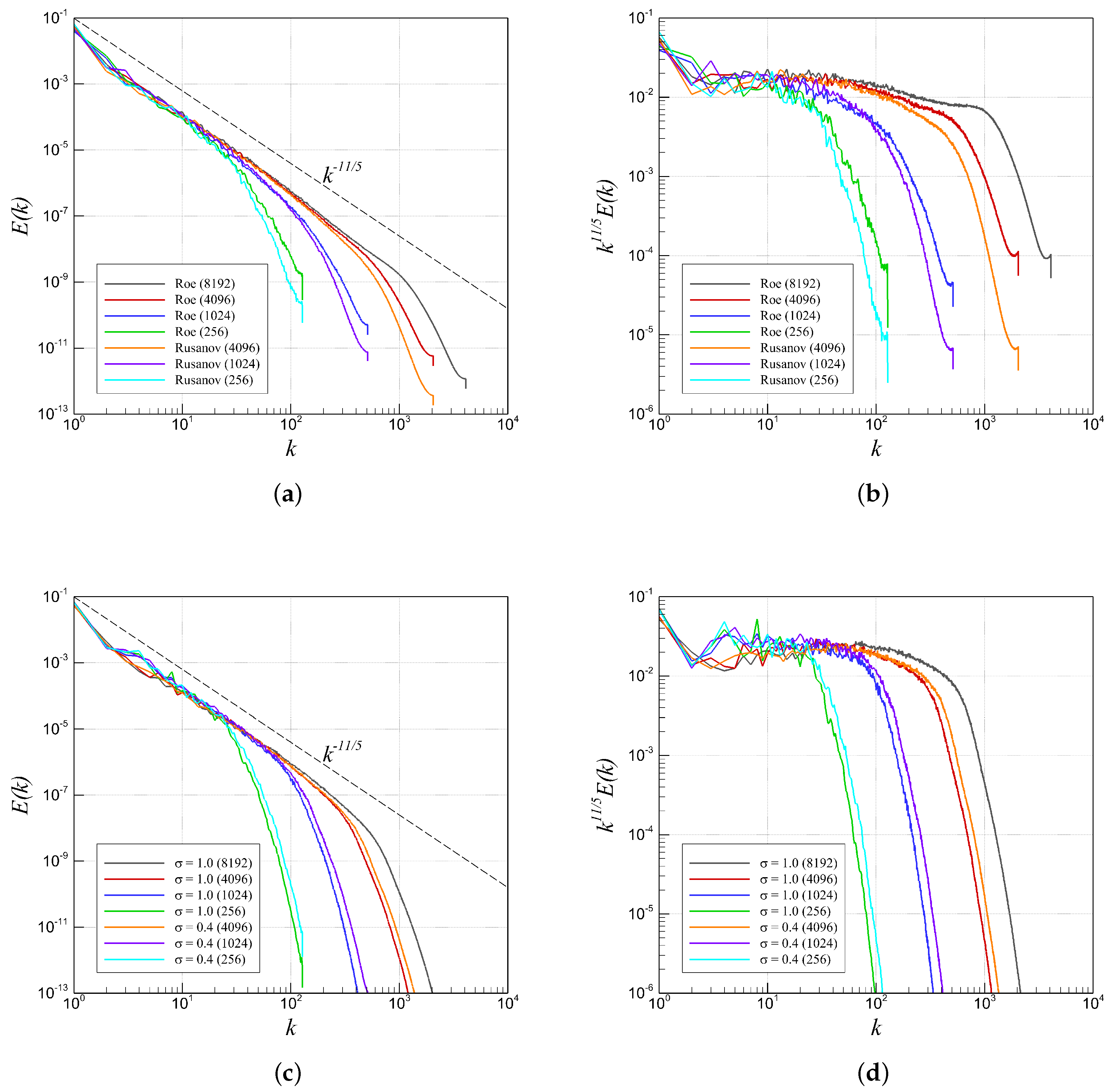
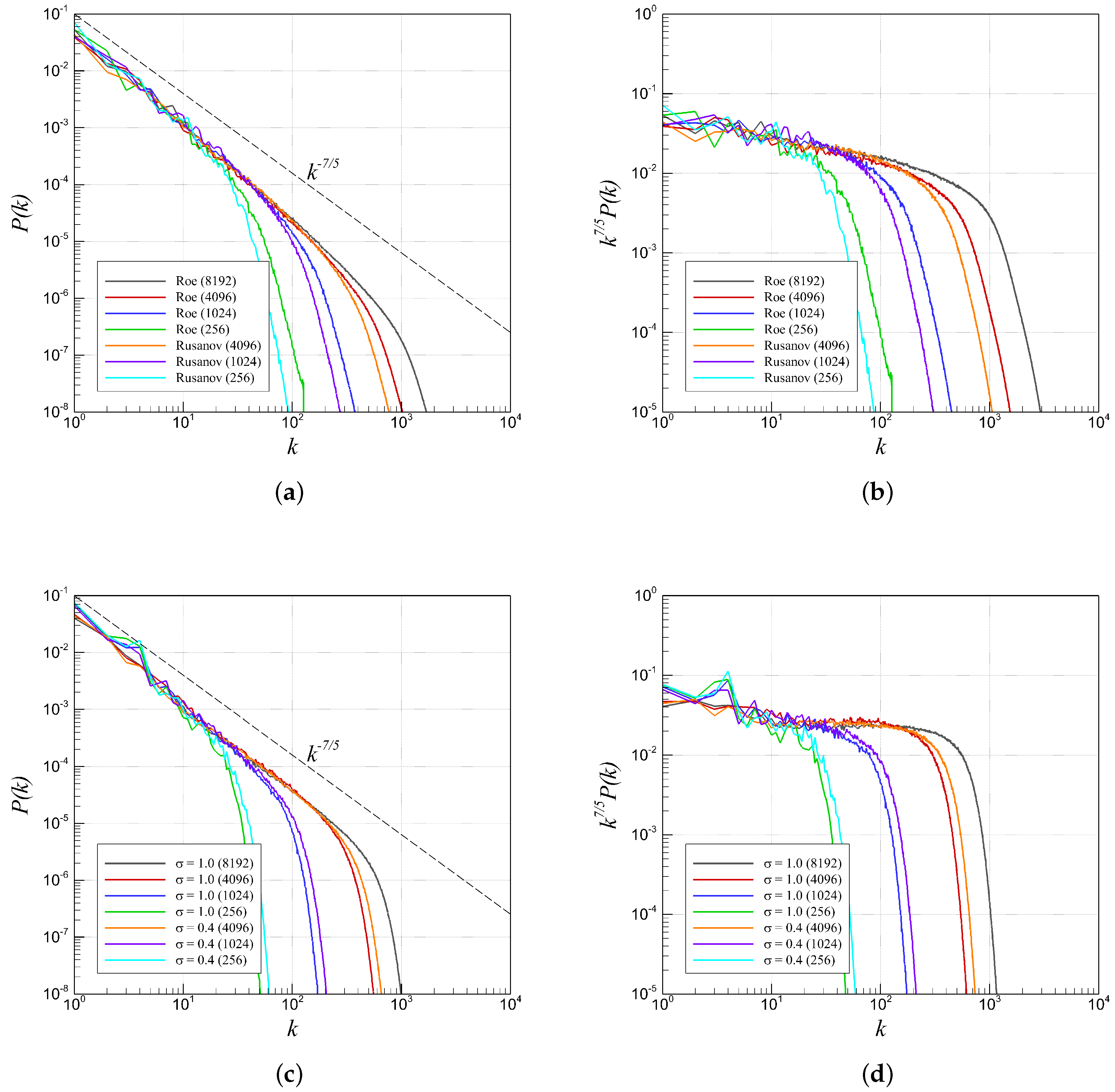
4.3. RTI with Single-Mode Perturbation
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, G.I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1950, 201, 192–196. [Google Scholar]
- Cui, A.; Street, R.L. Large-eddy simulation of coastal upwelling flow. Environ. Fluid Mech. 2004, 4, 197–223. [Google Scholar] [CrossRef]
- Jevons, W.S., II. On the cirrous form of cloud. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1857, 14, 22–35. [Google Scholar] [CrossRef]
- Bradley, P. The effect of mix on capsule yields as a function of shell thickness and gas fill. Phys. Plasmas 2014, 21, 062703. [Google Scholar] [CrossRef]
- Bell, J.; Day, M.; Rendleman, C.; Woosley, S.; Zingale, M. Direct numerical simulations of type Ia supernovae flames. II. The Rayleigh-Taylor instability. Astrophys. J. 2004, 608, 883. [Google Scholar] [CrossRef]
- Hillebrandt, W.; Niemeyer, J.C. Type Ia supernova explosion models. Annu. Rev. Astron. Astrophys. 2000, 38, 191–230. [Google Scholar] [CrossRef]
- Racca, R.A.; Annett, C.H. Simple demonstration of Rayleigh-Taylor instability. Am. J. Phys. 1985, 53, 484–486. [Google Scholar] [CrossRef]
- Chertkov, M.; Lebedev, V.; Vladimirova, N. Reactive Rayleigh–Taylor turbulence. J. Fluid Mech. 2009, 633, 1–16. [Google Scholar] [CrossRef]
- Veynante, D.; Trouvé, A.; Bray, K.; Mantel, T. Gradient and counter-gradient scalar transport in turbulent premixed flames. J. Fluid Mech. 1997, 332, 263–293. [Google Scholar] [CrossRef]
- Petrasso, R.D. Rayleigh’s challenge endures. Nature 1994, 367, 217. [Google Scholar] [CrossRef]
- Lewis, D.J. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1950, 202, 81–96. [Google Scholar]
- Lord, R. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Sci. Pap. 1900, 200–207. [Google Scholar]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 2017, 720–722, 1–136. [Google Scholar]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 2017, 723–725, 1–160. [Google Scholar] [CrossRef]
- Piriz, A.; Cortazar, O.; Lopez Cela, J.; Tahir, N. The Rayleigh-Taylor instability. Am. J. Phys. 2006, 74, 1095–1098. [Google Scholar] [CrossRef]
- Boffetta, G.; Mazzino, A. Incompressible Rayleigh–Taylor turbulence. Annu. Rev. Fluid Mech. 2017, 49, 119–143. [Google Scholar] [CrossRef]
- Sharp, D.H. Overview of Rayleigh-Taylor Instability; Technical Report; Los Alamos National Lab.: Los Alamos, NM, USA, 1983. [Google Scholar]
- Dimonte, G.; Youngs, D.; Dimits, A.; Weber, S.; Marinak, M.; Wunsch, S.; Garasi, C.; Robinson, A.; Andrews, M.; Ramaprabhu, P.; et al. A comparative study of the turbulent Rayleigh–Taylor instability using high-resolution three-dimensional numerical simulations: The Alpha-Group collaboration. Phys. Fluids 2004, 16, 1668–1693. [Google Scholar] [CrossRef]
- Mueschke, N.J.; Schilling, O. Investigation of Rayleigh–Taylor turbulence and mixing using direct numerical simulation with experimentally measured initial conditions. I. Comparison to experimental data. Phys. Fluids 2009, 21, 014106. [Google Scholar] [CrossRef]
- Wei, T.; Livescu, D. Late-time quadratic growth in single-mode Rayleigh-Taylor instability. Phys. Rev. E 2012, 86, 046405. [Google Scholar] [CrossRef]
- Dalziel, S.; Linden, P.; Youngs, D. Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 1999, 399, 1–48. [Google Scholar] [CrossRef]
- Ristorcelli, J.; Clark, T. Rayleigh–Taylor turbulence: Self-similar analysis and direct numerical simulations. J. Fluid Mech. 2004, 507, 213–253. [Google Scholar] [CrossRef]
- Xin, J.; Yan, R.; Wan, Z.H.; Sun, D.J.; Zheng, J.; Zhang, H.; Aluie, H.; Betti, R. Two mode coupling of the ablative Rayleigh-Taylor instabilities. Phys. Plasmas 2019, 26, 032703. [Google Scholar] [CrossRef]
- Jun, B.I.; Norman, M.L.; Stone, J.M. A numerical study of Rayleigh-Taylor instability in magnetic fluids. Astrophys. J. 1995, 453, 332. [Google Scholar] [CrossRef]
- Cabot, W. Comparison of two-and three-dimensional simulations of miscible Rayleigh-Taylor instability. Phys. Fluids 2006, 18, 045101. [Google Scholar] [CrossRef]
- Anuchina, N.; Volkov, V.; Gordeychuk, V.; Es’ kov, N.; Ilyutina, O.; Kozyrev, O. Numerical simulations of Rayleigh–Taylor and Richtmyer–Meshkov instability using MAH-3 code. J. Comput. Appl. Math. 2004, 168, 11–20. [Google Scholar] [CrossRef]
- Zhao, D.; Aluie, H. Inviscid criterion for decomposing scales. Phys. Rev. Fluids 2018, 3, 054603. [Google Scholar] [CrossRef]
- Livescu, D.; Ristorcelli, J. Buoyancy-driven variable-density turbulence. J. Fluid Mech. 2007, 591, 43–71. [Google Scholar] [CrossRef]
- Kokkinakis, I.; Drikakis, D.; Youngs, D.; Williams, R. Two-equation and multi-fluid turbulence models for Rayleigh–Taylor mixing. Int. J. Heat Fluid Flow 2015, 56, 233–250. [Google Scholar] [CrossRef]
- Youngs, D. Large eddy simulation and 1D/2D engineering models for Rayleigh-Taylor mixing. In Proceedings of the IWPCTM: 12th International Workshop on the Physics of Compressible Turbulent Mixing, Moscow, Russia, 12–17 July 2010; pp. 12–17. [Google Scholar]
- Ramaprabhu, P.; Dimonte, G.; Woodward, P.; Fryer, C.; Rockefeller, G.; Muthuraman, K.; Lin, P.H.; Jayaraj, J. The late-time dynamics of the single-mode Rayleigh-Taylor instability. Phys. Fluids 2012, 24, 074107. [Google Scholar] [CrossRef]
- Glimm, J.; Li, X.l.; Lin, A.D. Nonuniform approach to terminal velocity for single mode Rayleigh-Taylor instability. Acta Math. Appl. Sin. 2002, 18, 1–8. [Google Scholar] [CrossRef]
- Daly, B.J. Numerical study of two fluid Rayleigh-Taylor instability. Phys. Fluids 1967, 10, 297–307. [Google Scholar] [CrossRef]
- Kane, J.; Arnett, D.; Remington, B.; Glendinning, S.; Bazán, G.; Müller, E.; Fryxell, B.; Teyssier, R. Two-dimensional versus three-dimensional supernova hydrodynamic instability growth. Astrophys. J. 2000, 528, 989. [Google Scholar] [CrossRef]
- Goncharov, V. Analytical model of nonlinear, single-mode, classical Rayleigh-Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 2002, 88, 134502. [Google Scholar] [CrossRef]
- Young, Y.N.; Tufo, H.; Dubey, A.; Rosner, R. On the miscible Rayleigh–Taylor instability: Two and three dimensions. J. Fluid Mech. 2001, 447, 377–408. [Google Scholar] [CrossRef]
- Youngs, D.L. Three-dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids A Fluid Dyn. 1991, 3, 1312–1320. [Google Scholar] [CrossRef]
- Youngs, D.L. Numerical simulation of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 1994, 12, 725–750. [Google Scholar] [CrossRef]
- Shvarts, D.; Alon, U.; Ofer, D.; McCrory, R.; Verdon, C. Nonlinear evolution of multimode Rayleigh–Taylor instability in two and three dimensions. Phys. Plasmas 1995, 2, 2465–2472. [Google Scholar] [CrossRef]
- Oron, D.; Arazi, L.; Kartoon, D.; Rikanati, A.; Alon, U.; Shvarts, D. Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 2001, 8, 2883–2889. [Google Scholar] [CrossRef]
- Zhou, Y. A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 2001, 13, 538–543. [Google Scholar] [CrossRef]
- Shvarts, D.; Oron, D.; Kartoon, D.; Rikanati, A.; Sadot, O.; Srebro, Y.; Yedvab, Y.; Ofer, D.; Levin, A.; Sarid, E.; et al. Scaling laws of nonlinear Rayleigh-Taylor and Richtmyer-Meshkov instabilities in two and three dimensions (IFSA 1999). In Edward Teller Lectures: Lasers and Inertial Fusion Energy; World Scientific: Singapore, 2016; pp. 253–260. [Google Scholar]
- Chertkov, M. Phenomenology of Rayleigh-Taylor turbulence. Phys. Rev. Lett. 2003, 91, 115001. [Google Scholar] [CrossRef]
- Celani, A.; Mazzino, A.; Vozella, L. Rayleigh-Taylor turbulence in two dimensions. Phys. Rev. Lett. 2006, 96, 134504. [Google Scholar] [CrossRef]
- Margolin, L. The reality of artificial viscosity. Shock Waves 2019, 29, 27–35. [Google Scholar] [CrossRef]
- Brehm, C.; Barad, M.F.; Housman, J.A.; Kiris, C.C. A comparison of higher-order finite-difference shock capturing schemes. Comput. Fluids 2015, 122, 184–208. [Google Scholar] [CrossRef]
- Margolin, L.G.; Rider, W.J.; Grinstein, F.F. Modeling turbulent flow with implicit LES. J. Turbul. 2006, 7, N15. [Google Scholar] [CrossRef]
- Zhou, Y.; Thornber, B. A comparison of three approaches to compute the effective Reynolds number of the implicit large-eddy simulations. J. Fluids Eng. 2016, 138, 070905. [Google Scholar] [CrossRef]
- Maulik, R.; San, O. Resolution and energy dissipation characteristics of implicit LES and explicit filtering models for compressible turbulence. Fluids 2017, 2, 14. [Google Scholar] [CrossRef]
- San, O.; Kara, K. Numerical assessments of high-order accurate shock capturing schemes: Kelvin–Helmholtz type vortical structures in high-resolutions. Comput. Fluids 2014, 89, 254–276. [Google Scholar] [CrossRef]
- Titarev, V.A.; Toro, E.F. Finite-volume WENO schemes for three-dimensional conservation laws. J. Comput. Phys. 2004, 201, 238–260. [Google Scholar] [CrossRef]
- Pirozzoli, S. Numerical methods for high-speed flows. Annu. Rev. Fluid Mech. 2011, 43, 163–194. [Google Scholar] [CrossRef]
- Brehm, C. On consistent boundary closures for compact finite-difference WENO schemes. J. Comput. Phys. 2017, 334, 573–581. [Google Scholar] [CrossRef]
- Wong, M.L.; Lele, S.K. High-order localized dissipation weighted compact nonlinear scheme for shock-and interface-capturing in compressible flows. J. Comput. Phys. 2017, 339, 179–209. [Google Scholar] [CrossRef]
- Zhao, S.; Lardjane, N.; Fedioun, I. Comparison of improved finite-difference WENO schemes for the implicit large eddy simulation of turbulent non-reacting and reacting high-speed shear flows. Comput. Fluids 2014, 95, 74–87. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Q.; Adams, N.A. An adaptive central-upwind weighted essentially non-oscillatory scheme. J. Comput. Phys. 2010, 229, 8952–8965. [Google Scholar] [CrossRef]
- Mathew, J.; Foysi, H.; Friedrich, R. A new approach to LES based on explicit filtering. Int. J. Heat Fluid Flow 2006, 27, 594–602. [Google Scholar] [CrossRef]
- Lund, T. The use of explicit filters in large eddy simulation. Comput. Math. Appl. 2003, 46, 603–616. [Google Scholar] [CrossRef]
- Berland, J.; Lafon, P.; Daude, F.; Crouzet, F.; Bogey, C.; Bailly, C. Filter shape dependence and effective scale separation in large-eddy simulations based on relaxation filtering. Comput. Fluids 2011, 47, 65–74. [Google Scholar] [CrossRef]
- Bose, S.T.; Moin, P.; You, D. Grid-independent large-eddy simulation using explicit filtering. Phys. Fluids 2010, 22, 105103. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; Lund, T.S.; Moin, P. A general class of commutative filters for LES in complex geometries. J. Comput. Phys. 1998, 146, 82–104. [Google Scholar] [CrossRef]
- San, O. Analysis of low-pass filters for approximate deconvolution closure modelling in one-dimensional decaying Burgers turbulence. Int. J. Comput. Fluid Dyn. 2016, 30, 20–37. [Google Scholar] [CrossRef]
- Najafi-Yazdi, A.; Najafi-Yazdi, M.; Mongeau, L. A high resolution differential filter for large eddy simulation: Toward explicit filtering on unstructured grids. J. Comput. Phys. 2015, 292, 272–286. [Google Scholar] [CrossRef]
- Shivamoggi, B.K. Spectral laws for the compressible isotropic turbulence. In Instability, Transition, and Turbulence; Springer: New York, NY, USA, 1992; pp. 524–534. [Google Scholar]
- Shivamoggi, B.K. Multi-fractal aspects of the fine-scale structure of temperature fluctuations in isotropic turbulence. Phys. A Stat. Mech. Its Appl. 1995, 221, 460–477. [Google Scholar] [CrossRef]
- Shivamoggi, B.K. Intermittency in the enstrophy cascade of two-dimensional fully developed turbulence: Universal features. Ann. Phys. 2008, 323, 444–460. [Google Scholar] [CrossRef]
- Shivamoggi, B. Compressible turbulence: Multi-fractal scaling in the transition to the dissipative regime. Phys. A Stat. Mech. Its Appl. 2011, 390, 1534–1538. [Google Scholar] [CrossRef]
- Sun, B. The temporal scaling laws of compressible turbulence. Mod. Phys. Lett. B 2016, 30, 1650297. [Google Scholar] [CrossRef]
- Sun, B. Scaling laws of compressible turbulence. Appl. Math. Mech. 2017, 38, 765–778. [Google Scholar] [CrossRef][Green Version]
- Parent, B. Positivity-preserving high-resolution schemes for systems of conservation laws. J. Comput. Phys. 2012, 231, 173–189. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W. Total variation diminishing Runge-Kutta schemes. Math. Comput. Am. Math. Soc. 1998, 67, 73–85. [Google Scholar] [CrossRef]
- Godunov, S.K. A difference method for numerical calculation of discontinuous solutions of the equations of hydrodynamics. Mat. Sb. 1959, 89, 271–306. [Google Scholar]
- Grinstein, F.F.; Margolin, L.G.; Rider, W.J. Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Denaro, F.M. What does finite volume-based implicit filtering really resolve in large-eddy simulations? J. Comput. Phys. 2011, 230, 3849–3883. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high order accurate essentially non-oscillatory schemes, III. In Upwind and High-Resolution Schemes; Springer: New York, NY, USA, 1987; pp. 218–290. [Google Scholar]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Henrick, A.K.; Aslam, T.D.; Powers, J.M. Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points. J. Comput. Phys. 2005, 207, 542–567. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Rusanov, V.V. The calculation of the interaction of non-stationary shock waves with barriers. Zhurnal Vychislitel’Noi Mat. Mat. Fiz. 1961, 1, 267–279. [Google Scholar]
- Lax, P.D. Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 1954, 7, 159–193. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Hyman, J.M.; Knapp, R.J.; Scovel, J.C. High order finite volume approximations of differential operators on nonuniform grids. Phys. D Nonlinear Phenom. 1992, 60, 112–138. [Google Scholar] [CrossRef]
- Fauconnier, D.; Bogey, C.; Dick, E. On the performance of relaxation filtering for large-eddy simulation. J. Turbul. 2013, 14, 22–49. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Computation of a high Reynolds number jet and its radiated noise using large eddy simulation based on explicit filtering. Comput. Fluids 2006, 35, 1344–1358. [Google Scholar] [CrossRef]
- Bull, J.R.; Jameson, A. Explicit filtering and exact reconstruction of the sub-filter stresses in large eddy simulation. J. Comput. Phys. 2016, 306, 117–136. [Google Scholar] [CrossRef]
- San, O. A dynamic eddy-viscosity closure model for large eddy simulations of two-dimensional decaying turbulence. Int. J. Comput. Fluid Dyn. 2014, 28, 363–382. [Google Scholar] [CrossRef]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Gropp, W.D.; Gropp, W.; Lusk, E.; Skjellum, A.; Lusk, E. Using MPI: Portable Parallel Programming with the Message-Passing Interface; MIT Press: Cambridge, MA, USA, 1999; Volume 1. [Google Scholar]
- Banerjee, A.; Andrews, M.J. 3D simulations to investigate initial condition effects on the growth of Rayleigh–Taylor mixing. Int. J. Heat Mass Transf. 2009, 52, 3906–3917. [Google Scholar] [CrossRef]
- Vladimirova, N.; Chertkov, M. Self-similarity and universality in Rayleigh–Taylor, Boussinesq turbulence. Phys. Fluids 2009, 21, 015102. [Google Scholar] [CrossRef]
- Xu, Z.; Duo-Wang, T. Direct Numerical Simulation of the Rayleigh- Taylor Instability with the Spectral Element Method. Chin. Phys. Lett. 2009, 26, 084703. [Google Scholar] [CrossRef]
- Liska, R.; Wendroff, B. Comparison of several difference schemes on 1D and 2D test problems for the Euler equations. Siam J. Sci. Comput. 2003, 25, 995–1017. [Google Scholar] [CrossRef]
- Stone, J.M.; Gardiner, T.A.; Teuben, P.; Hawley, J.F.; Simon, J.B. Athena: A new code for astrophysical MHD. Astrophys. Suppl. Ser. 2008, 178, 137–177. [Google Scholar] [CrossRef]
- Poinsot, T.J.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Youngs, D.L. Rayleigh–Taylor mixing: Direct numerical simulation and implicit large eddy simulation. Phys. Scr. 2017, 92, 074006. [Google Scholar] [CrossRef]
- San, O.; Kara, K. Evaluation of Riemann flux solvers for WENO reconstruction schemes: Kelvin–Helmholtz instability. Comput. Fluids 2015, 117, 24–41. [Google Scholar] [CrossRef]
- Lele, S.K. Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 1994, 26, 211–254. [Google Scholar] [CrossRef]
- Kritsuk, A.G.; Norman, M.L.; Padoan, P.; Wagner, R. The statistics of supersonic isothermal turbulence. Astrophys. J. 2007, 665, 416. [Google Scholar] [CrossRef]
- Aluie, H. Scale decomposition in compressible turbulence. Phys. D Nonlinear Phenom. 2013, 247, 54–65. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Stratified Kelvin–Helmholtz turbulence of compressible shear flows. Nonlinear Process. Geophys. 2018, 25. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Kida, S.; Orszag, S.A. Energy and spectral dynamics in forced compressible turbulence. J. Sci. Comput. 1990, 5, 85–125. [Google Scholar] [CrossRef]
- Bolgiano, R., Jr. Turbulent spectra in a stably stratified atmosphere. J. Geophys. Res. 1959, 64, 2226–2229. [Google Scholar] [CrossRef]
- Livescu, D.; Wei, T.; Petersen, M. Direct Numerical Simulations of Rayleigh-Taylor Instability; Conference Series; IOP Publishing: Bristol, UK, 2011; Volume 318, p. 082007. [Google Scholar]
- Youngs, D.L. Numerical simulation of turbulent mixing by Rayleigh-Taylor instability. Phys. D Nonlinear Phenom. 1984, 12, 32–44. [Google Scholar] [CrossRef]
- Ramaprabhu, P.; Dimonte, G.; Andrews, M. A numerical study of the influence of initial perturbations on the turbulent Rayleigh–Taylor instability. J. Fluid Mech. 2005, 536, 285–319. [Google Scholar] [CrossRef]
- Shadloo, M.; Zainali, A.; Yildiz, M. Simulation of single mode Rayleigh–Taylor instability by SPH method. Comput. Mech. 2013, 51, 699–715. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, K.; Kim, J. On the long time simulation of the Rayleigh–Taylor instability. Int. J. Numer. Methods Eng. 2011, 85, 1633–1647. [Google Scholar] [CrossRef]
- Livescu, D.; Ristorcelli, J.; Petersen, M.; Gore, R. New phenomena in variable-density Rayleigh–Taylor turbulence. Phys. Scr. 2010, 2010, 014015. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, Y.T.; Shu, C.W. Resolution of high order WENO schemes for complicated flow structures. J. Comput. Phys. 2003, 186, 690–696. [Google Scholar] [CrossRef]
- Fu, L.; Hu, X.Y.; Adams, N.A. A family of high-order targeted ENO schemes for compressible-fluid simulations. J. Comput. Phys. 2016, 305, 333–359. [Google Scholar] [CrossRef]
- Latini, M.; Schilling, O.; Don, W.S. Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer–Meshkov instability. J. Comput. Phys. 2007, 221, 805–836. [Google Scholar] [CrossRef]
- Tritschler, V.; Hu, X.; Hickel, S.; Adams, N. Numerical simulation of a Richtmyer–Meshkov instability with an adaptive central-upwind sixth-order WENO scheme. Phys. Scr. 2013, 2013, 014016. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, S.M.; San, O. A Relaxation Filtering Approach for Two-Dimensional Rayleigh–Taylor Instability-Induced Flows. Fluids 2019, 4, 78. https://doi.org/10.3390/fluids4020078
Rahman SM, San O. A Relaxation Filtering Approach for Two-Dimensional Rayleigh–Taylor Instability-Induced Flows. Fluids. 2019; 4(2):78. https://doi.org/10.3390/fluids4020078
Chicago/Turabian StyleRahman, Sk. Mashfiqur, and Omer San. 2019. "A Relaxation Filtering Approach for Two-Dimensional Rayleigh–Taylor Instability-Induced Flows" Fluids 4, no. 2: 78. https://doi.org/10.3390/fluids4020078
APA StyleRahman, S. M., & San, O. (2019). A Relaxation Filtering Approach for Two-Dimensional Rayleigh–Taylor Instability-Induced Flows. Fluids, 4(2), 78. https://doi.org/10.3390/fluids4020078





