Discrete Element Simulation of Interaction between Hydraulic Fracturing and a Single Natural Fracture
Abstract
:1. Introduction
2. Analytical Methods
3. Numerical Modeling
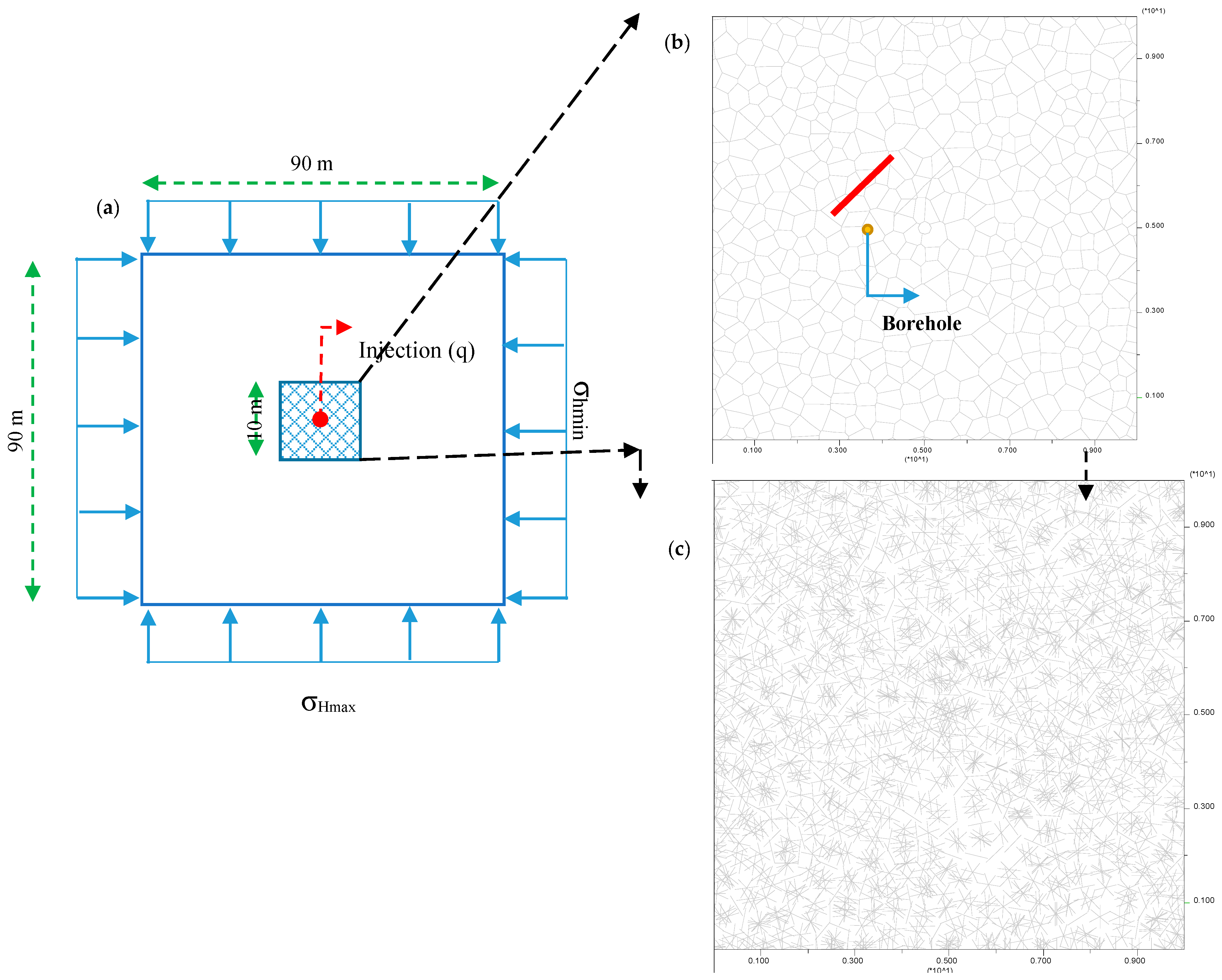
3.1. Discrete Element Method (DEM) for Simulating Hydraulic Fracturing (HF)
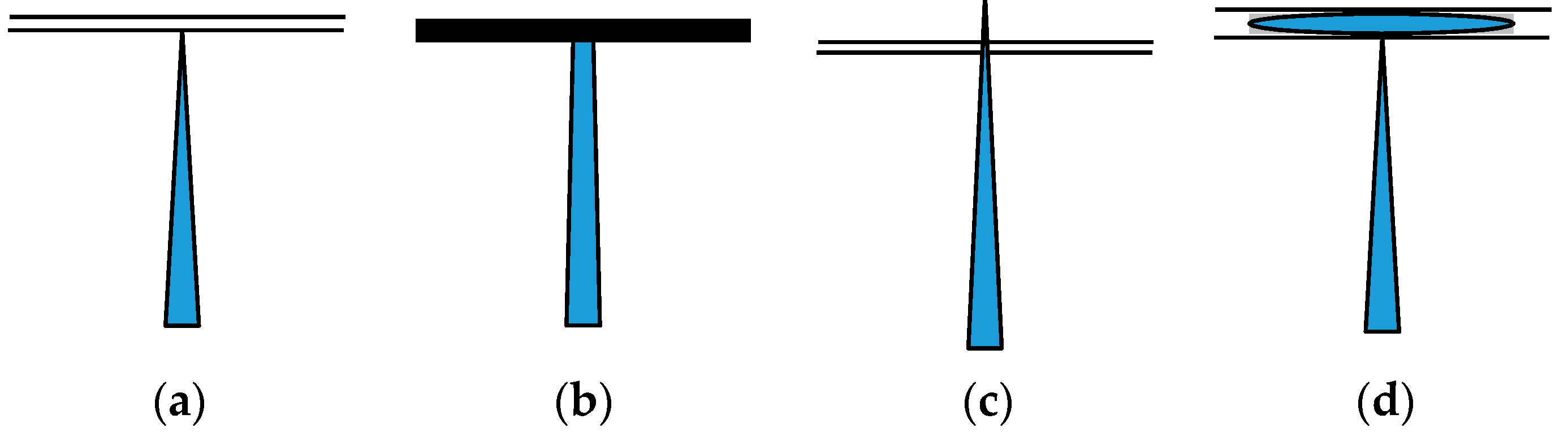
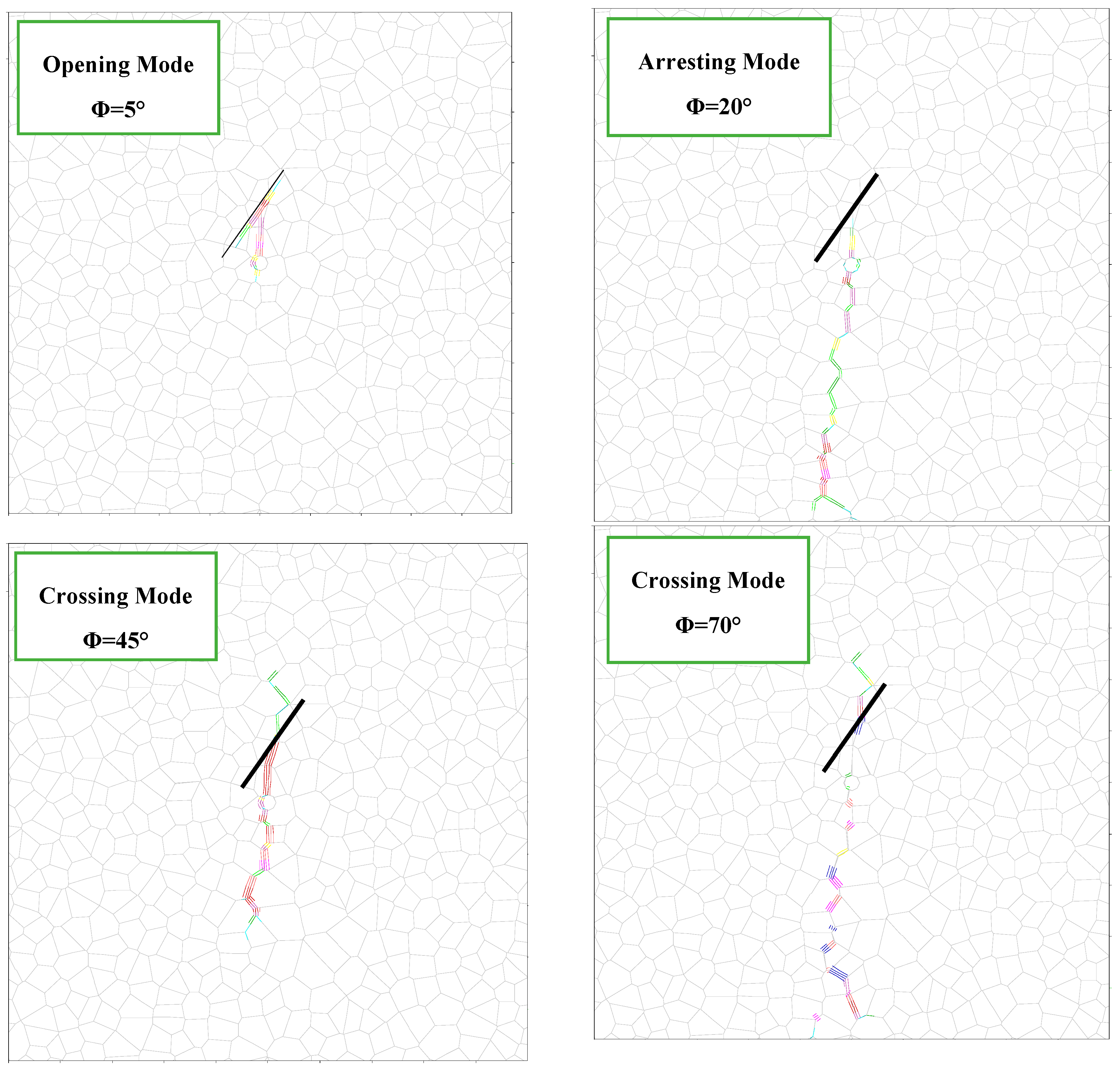
3.2. Interaction Modes in DEM Simulation
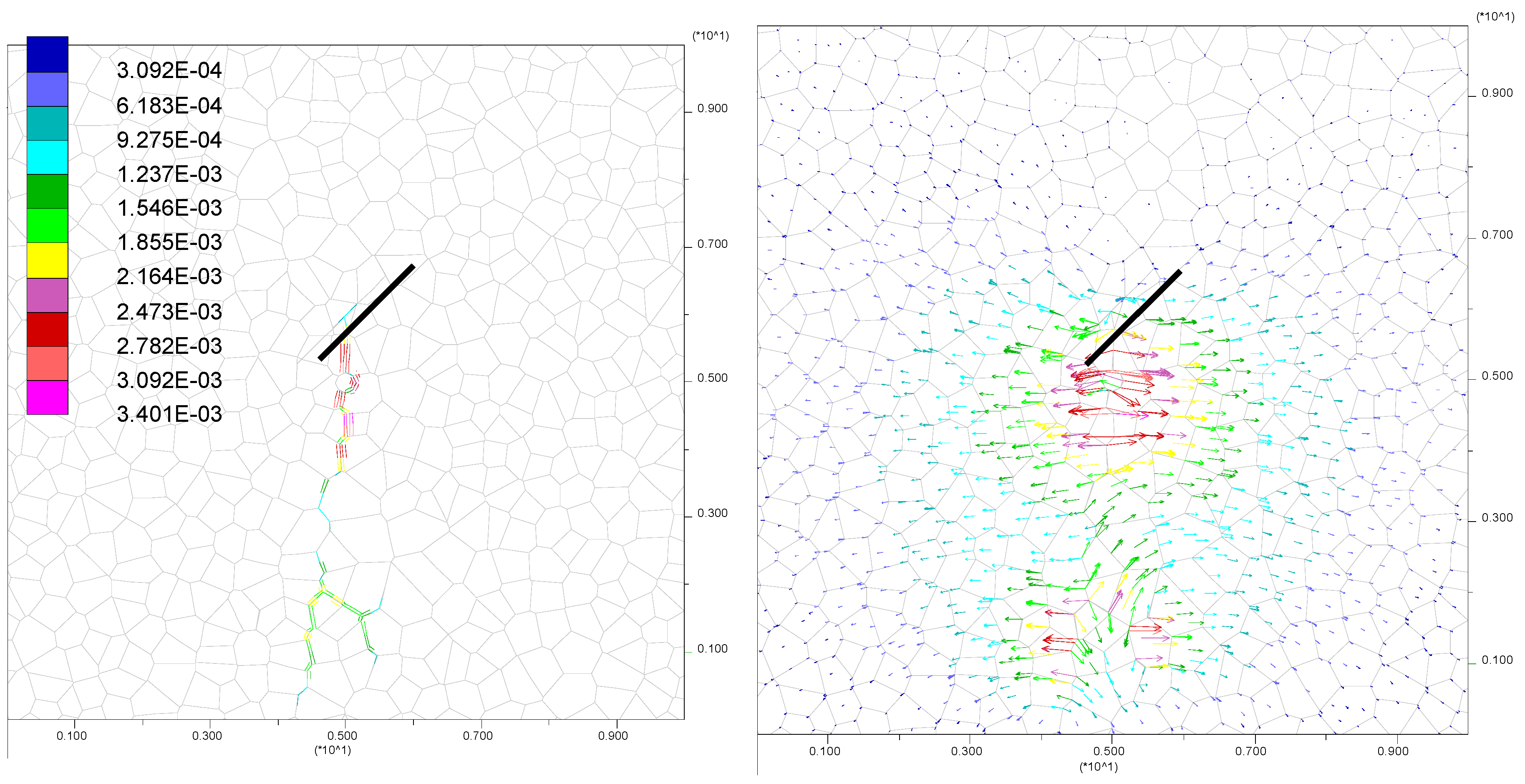
3.2.1. Opening Mode
3.2.2. Arresting Mode
3.2.3. Crossing Mode
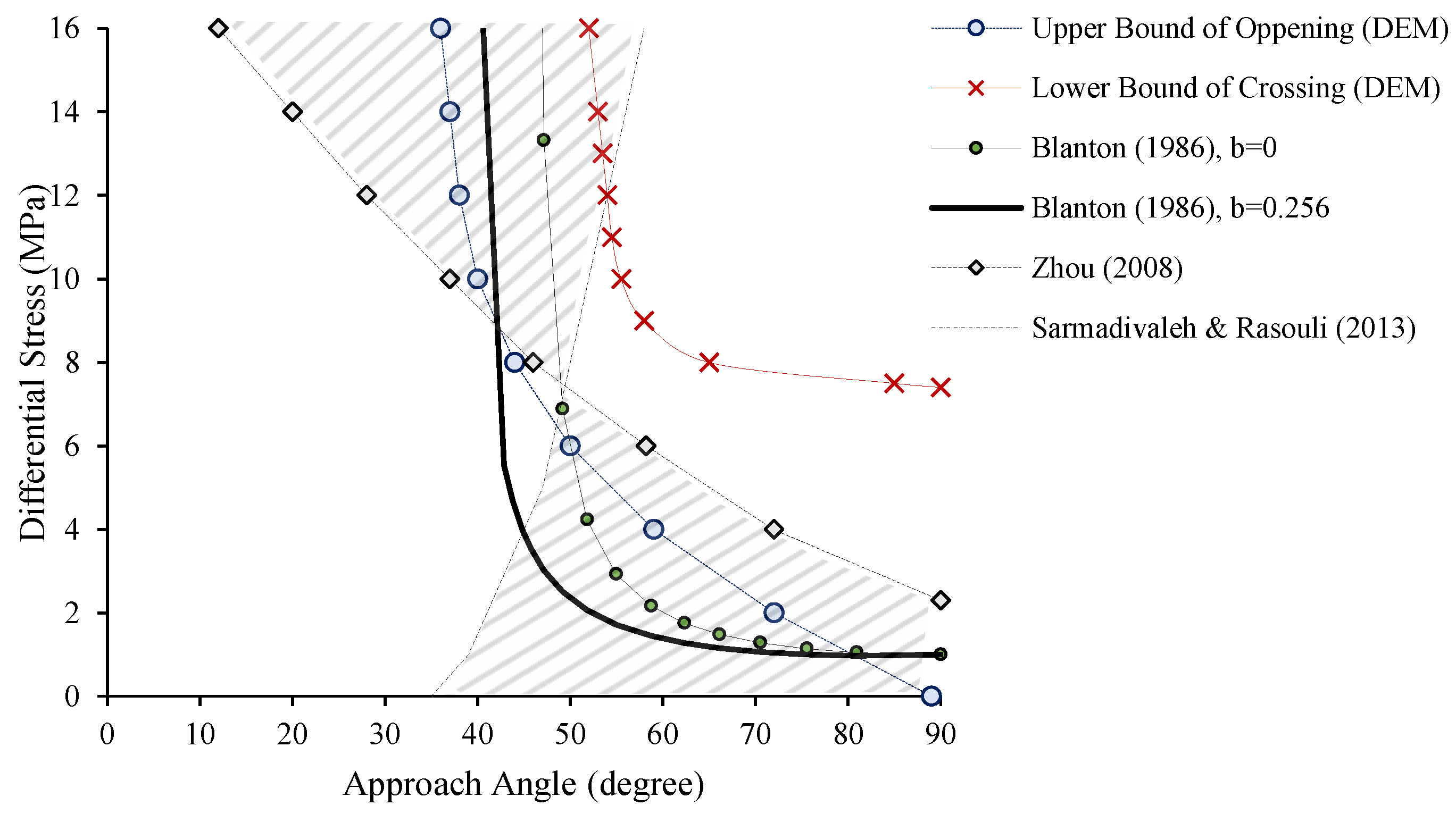
3.3. Comparison of Different Methods
4. Effect of Strength Parameters of Natural Fracture (NF) on HF Propagation
- -
- changing the interaction mode
- -
- increasing/decreasing the joint opening
5. Conclusions
- Overall, HF tends to cross the NF at an angle of more than 45° and a moderate differential stress (greater than 5 MPa); and the opening mode is dominated at an angle less than 45°.
- Interaction mode changes from opening to arresting mode and from arresting to crossing mode with an increase in ϕ from 5° to 70°.
- By increasing the amount of C, the resistance of the joint to the opening is increased by the injection pressure; therefore, NF is less opened under a constant value of injection pressure.
Author Contributions
Funding
Conflicts of Interest
References
- Zolfaghari, A.; Noel, M.; Dehghanpour, H.; Bearinger, D. Understanding the Origin of Flowback Salts: A Laboratory and Field Study. In Proceedings of the SPE/CSUR Unconventional Resources Conference-Canada, Calgary, AB, Canada, 30 September–2 October 2014. [Google Scholar] [CrossRef]
- Xu, Y.; Ezulike, O.D.; Zolfaghari, A.; Dehghanpour, H.; Virues, C. Complementary Surveillance Microseismic and Flowback Data Analysis: An Approach to Evaluate Complex Fracture Networks. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 26–28 September 2016. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Dehghanpour, H.; Ghanbari, E.; Bearinger, D. Fracture Characterization Using Flowback Salt-Concentration Transient. SPE J. 2016, 21, 233–244. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X.; Lund, J.; Mack, M.; Ganguly, U.; Suarez-Rivera, R. Hydraulic Fracture Crossing Natural Fracture at Non-orthogonal Angles, A Criterion, Its Validation and Applications. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2011. [Google Scholar]
- Warpinski, N.R.; Fnley, S.J.; Vollendorf, W.C.; O’Brien, M.; Eshom, E. The Interface Test Series: An In Situ Study of Factors Affecting the Containment of Hydraulic Fractures; Sandia National Laboratories Report SAND81-2408; Sandia National Laboratories: Albuquerque, NM, USA, 1982. [Google Scholar]
- Warpinski, N.R.; Teufel, L.W. Influence of Geologic Discontinuities on Hydraulic Fracture Propagation. J. Pet. Technol. 1987, 39, 209–220. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Zhang, G. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Sarmadivaleh, M.; Rasouli, V. Test Design and Sample Preparation Procedure for Experimental Investigation of Hydraulic Fracturing Interaction Modes. Rock Mech. Rock Eng. 2015, 48, 93–105. [Google Scholar] [CrossRef]
- Dehghan, A.; Goshtasbi, K.; Ahangari, K.; Jin, Y. Mechanism of fracture initiation and propagation using a tri-axial hydraulic fracturing test system in naturally fractured reservoirs. Eur. J. Environ. Civ. Eng. 2016, 20, 560–585. [Google Scholar] [CrossRef]
- Dehghan, A.; Goshtasbi, K.; Ahangari, K.; Jin, Y. The effect of natural fracture dip and strike on hydraulic fracture propagation. Int. J. Rock Mech. Min. Sci. 2015, 75, 210–215. [Google Scholar] [CrossRef]
- Guo, Y.; Deng, P.; Yang, C.; Chang, X.; Wang, L.; Zhou, J. Experimental Investigation on Hydraulic Fracture Propagation of Carbonate Rocks under Different Fracturing Fluids. Energies 2018, 11, 3502. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, Q.; Zhang, J. Effects of the Notch Angle, Notch Length and Injection Rate on Hydraulic Fracturing under True Triaxial Stress: An Experimental Study. Water 2018, 10, 801. [Google Scholar] [CrossRef]
- Blanton, T.L. Propagation of hydraulically and dynamically induced fractures in naturally fractured reservoirs. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, KY, USA, 18–21 May 1986. [Google Scholar]
- Renshaw, C.E.; Pollard, D.D. An experimentally verified criterion for propagation across unbonded frictional interfaces in brittle linear elastic materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 237–249. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at non-orthogonal angles. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Sarmadivaleh, M.; Rasouli, V. Modified Reinshaw and Pollard Criteria for a Non-Orthogonal Cohesive Natural Interface Intersected by an Induced Fracture. Rock Mech. Rock Eng. 2013, 47, 2107–2115. [Google Scholar] [CrossRef]
- Dahi-Taleghani, A.; Olson, J.E. Numerical modeling of multistrand hydraulic-fracture propagation: Accounting for the interaction between induced and natural fractures. SPE J. 2011, 16, 575–581. [Google Scholar] [CrossRef]
- Sesetty, V.; Ghassemi, A. Simulation of Hydraulic Fractures and Their Interactions with Natural Fractures. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- Behnia, M.; Goshtasbi, K.; Fatehi Marji, M.; Golshani, A. Numerical simulation of interaction between hydraulic and natural fractures in discontinuous media. Acta Geotech. 2015, 10, 533–546. [Google Scholar] [CrossRef]
- Behnia, M.; Goshtasbi, K.; Zhang, G.; Mirzeinaly Yazdi, S.H. Numerical modeling of hydraulic fracture propagation and reorientation. Eur. J. Environ. Civ. Eng. 2015, 19, 152–167. [Google Scholar] [CrossRef]
- Liu, L.; Li, L.; Elsworth, D.; Zhi, S.; Yu, Y. The Impact of Oriented Perforations on Fracture Propagation and Complexity in Hydraulic Fracturing. Processes 2018, 6, 213. [Google Scholar] [CrossRef]
- Liu, C.; Shen, Z.; Gan, L.; Jin, T.; Zhang, H.; Liu, D. A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials. Materials 2018, 11, 1921. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Zhou, J.; Zhang, L. Influence of Grain Size Heterogeneity and In-Situ Stress on the Hydraulic Fracturing Process by PFC2D Modeling. Energies 2018, 11, 1413. [Google Scholar] [CrossRef]
- Jaeger, J.; Cook, N.G.; Zimmerman, R. Fundamentals of Rock Mechanics; Blackwell: Oxford, UK, 2007. [Google Scholar]
- Cundall, P.A. Formulation of a three-dimensional distinct element model-Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. UDEC (Version 6.0) Manual; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2016. [Google Scholar]
- Rogers, S.; Elmo, D.; Dunphy, R.; Bearinger, D. Understanding Hydraulic Fracture Geometry and Interactions in the Horn River Basin through DFN and Numerical Modeling. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar] [CrossRef]
- Zangeneh, N.; Eberhardt, E.; Bustin, R.M. Investigation of the influence of natural fractures and in situ stress on hydraulic fracture propagation using a distinct-element approach. Can. Geotech. 2015, 52, 926–946. [Google Scholar] [CrossRef]






| Rock Mass Parameter | Unit | Value | |
| Elastic Modulus | GPa | 24 | |
| Poisson’s ratio | - | 0.25 | |
| Cohesion | MPa | 2 | |
| Friction Angle | Degree | 35 | |
| Tension Strength | MPa | 1 | |
| Fracture Parameters | DFN | Natural Fracture | |
| Normal Stiffness | GPa/m | 350 | 20 |
| Shear Stiffness | GPa/m | 140 | 10 |
| Cohesion | MPa | 2 | 0 |
| Friction Angle | Degree | 35 | 20 |
| Tension Strength | MPa | 1 | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basirat, R.; Goshtasbi, K.; Ahmadi, M. Discrete Element Simulation of Interaction between Hydraulic Fracturing and a Single Natural Fracture. Fluids 2019, 4, 76. https://doi.org/10.3390/fluids4020076
Basirat R, Goshtasbi K, Ahmadi M. Discrete Element Simulation of Interaction between Hydraulic Fracturing and a Single Natural Fracture. Fluids. 2019; 4(2):76. https://doi.org/10.3390/fluids4020076
Chicago/Turabian StyleBasirat, Rouhollah, Kamran Goshtasbi, and Morteza Ahmadi. 2019. "Discrete Element Simulation of Interaction between Hydraulic Fracturing and a Single Natural Fracture" Fluids 4, no. 2: 76. https://doi.org/10.3390/fluids4020076
APA StyleBasirat, R., Goshtasbi, K., & Ahmadi, M. (2019). Discrete Element Simulation of Interaction between Hydraulic Fracturing and a Single Natural Fracture. Fluids, 4(2), 76. https://doi.org/10.3390/fluids4020076





