1. Introduction
Groupiness is one of the most obvious properties of ocean waves. It is well known that the number of waves in the group is strictly related to the relative width of the spectrum: groups which include a large number of waves are characterised by narrow spectra. It is well known that groupiness can occur as a result of modulational instability ([
1,
2] [hereinafter BF instability]). Indeed, the linear stability analysis of a plane wave solution of the water wave problem (see [
1]) shows that the growth rate of the perturbation depends on the wavenumber of the perturbation and on the steepness of the wave. According to [
1,
2] a sinusoidal wave of amplitude
and wavenumber
is unstable if
, where
is the wavenumber of the perturbation. At each
, growth rate is different.
It is natural to think that in an idealised experiment, once the steepness of the wave has been fixed, the perturbation that will appear during the evolution corresponds to the most unstable mode, i.e., the one that grows faster. The wavelength of the perturbation determines the width of the spectrum. If leading-order terms in non-linearity and dispersion are considered, the maximum of the growth rate of instability occurs for perturbations characterized by the wavenumber
which satisfies the following relation:
The product is the steepness, , of the wave. This prediction corresponds to the standard Benjamin-Feir instability.
However, if waves are not weakly non-linear and spectra are not narrow-banded, such prediction may not be adequate and higher order theories should be considered [
3,
4,
5,
6]. Moreover, things may also change in the presence of short-crested waves [
7,
8,
9,
10,
11,
12,
13,
14], in wave trains with continuous spectrum [
15], directional wave fields [
16,
17,
18] or because of wind forcing [
10,
14,
19]. An extension of the Benjamin-Feir instability for a continuous wave spectrum characterized by random phases was considered in [
16] (see also [
20]). They found that the effect of randomness is to reduce the growth rate and the extent of the instability region. For field waves, the questions concerning the width of the spectrum remain particularly complicated; these waves are wind-forced, directional and shortcrested and therefore their modulational properties can be altered in a number of ways as mentioned above.
In the meantime, the width of the spectrum bears a significant practical importance for wave forecast applications. The forecast is conducted by means of spectral models, and one of the primary source functions in such models is that due to whitecapping dissipation of wave energy which describes distribution of the dissipation caused by wave breaking along the frequency. Ever since it was found that wave breaking correlates with wave groups [
21], attempts have been made to introduce a characteristic bandwidth for the wave spectrum. While a rationale can be put forward for dominant waves of the narrow-banded wind-wave spectrum e.g., [
22,
23], at shorter and longer scales, the choice of the breaking/dissipation bandwidth has been done in a rather arbitrary way or by analogy (see [
24] for review on the subject).
The natural modulational bandwidth of deep-water surface waves is the topic of this paper. The experimental data that we present support the idea that there exists a natural bandwidth of wave trains determined by their mean steepness, and this bandwidth is applicable to dominant wind-generated waves described by a typical narrow-banded spectrum too. The implications of this result for the wave spectrum and possible effects of the wind on such bandwidth are also discussed.
Over the last 30 years, theoretical, e.g., [
25], experimental, e.g., [
12] and numerical, e.g., [
26] approaches have been applied to investigate instability mechanisms active in non-linear wave trains with a primary wave and sidebands. A particular detailed study was undertaken by authors in [
14,
27] who also offered a review of relevant analytical theories. They showed that different growth rates of instabilities are possible, depending on the steepness of the carrier wave and the length of the perturbation; they also observed that for steeper waves there are significant deviations from predictions of the original BF theory even in the absence of the wind forcing.
While theories and numerical simulations usually rely on introduced sidebands to start the modulation which is then allowed to evolve, some experiments were conducted “unseeded" i.e., initially monochromatic wave trains, e.g., [
7,
12,
14]. The non-linear modulation developed in such uniform trains anyway, the sidebands grow from the background noise, and this fact points out that there possibly exists a natural bandwidth for non-linear waves, i.e., for waves whose steepness is not infinitesimal. Therefore, it is reasonable to try to define such natural bandwidth and it is not unreasonable to suppose that, once defined, this width may be also applicable to field waves where the modulations are definitely observed. This most certainly should be the case for dominant young seas which are narrow-banded, i.e., described by a sharp spectral peak, e.g., ([
28,
29] [hereinafter JONSWAP and DHH, respectively]).
For monochromatic wave trains, the issue of the natural bandwidth is not new. For example, [
10] observed that the cause of wave breaking was a naturally appearing modulation in the system of initially uniform steep waves, and the number of waves in the modulation depended on the initial steepness. That is, the bandwidth was defined by the steepness.
Here, we extend the result on BF instability of a monochromatic wave train, see Equation (
1), to a continuous spectrum of wind-generated waves. In particular, if this narrow-banded wave spectrum is characterised by a certain steepness, we conjecture that its spectral bandwidth depends only on the steepness as in the case of naturally appearing modulation in the uniform wave trains.
The analogy between BF instability and modulations of continuous-spectrum wave fields has been introduced before. In particular, [
30,
31] used the ratio
where
is bandwidth of a continuous spectrum,
is a measure of wave amplitude defined as
where
is the significant wave height,
is peak wavenumber. In [
30] this number was named the Benjamin-Feir Index,
, because of its similarity to the stability criterion previously expressed. Note that usually the theoretical analysis and most of numerics on the instability are performed considering plane waves in space and their evolution in time; however, in wave-tank experiments, the evolution in space and time is considered as periodic. Using the group velocity definition in deep-water, it is easy to show that the following relation holds
. The ratio
corresponds approximately also to the the number
N of waves in the modulation; Equation (
2) can then be rewritten as
Thus, , both for discrete and spectral waves, is assumed to signify the natural connection of a characteristic wave steepness and the length of wave modulation which appear as dependent quantities, i.e., steeper waves will correspond to fewer waves in a modulation. During the evolution of wave groups, the is not constant; in a natural continuous-spectrum conditions or in the presence of forcing the may vary. How variable is it? Can we still make some predictions on the spectral bandwidth for a given steepness?
2. Results
The experiment was conducted at the Air–Sea Interaction Salt water Tank (ASIST) at RSMAS, University of Miami. The tank is a stainless-steel construction with a working section of 15 m × 1 m × 1 m and is equipped with a fully programmable wave maker. The waves are attenuated at the opposite end of the facility by a minimum-reflection beach which has been the subject of a special research project. A gently sloping (10 degrees) grid of
cm diameter acrylic rods is used. A perforated acrylic plate is placed beneath the rods to split wave orbital velocities into multiple turbulent jets to increase the dissipation. The data used in the present analysis are described in detail in [
10].
In the experiment, monochromatic deep-water two-dimensional wave trains were generated by the wave paddle. The water depth was held at m thus providing deep-water conditions for the wave frequencies involved (wave trains with initial frequencies of Hz, 1.8 Hz and 2.0 Hz are analysed here). With a tank length of m, surface elevations were recorded at 4.55 m, 10.53 m, 11.59 m and m from the paddle. The experiment was dedicated to wave breaking, and some waves would break between the probes, which may or may not bring about implications for the present study of the natural modulation. Such cases will be noted in the figures below. ASIST has a programmable fan capable of generating centreline wind speeds in the range of 0 to 30 m/s. This fan was used to impose wind forcing over mechanically generated waves, and in the present study records of the forced waves will be used to investigate the wind effect on the modulation. Values of wind speed employed in this paper will be those extrapolated to 10 m height, and the wind-forcing conditions imposed ranged from no wind to extreme (). Here, c is wave phase speed.
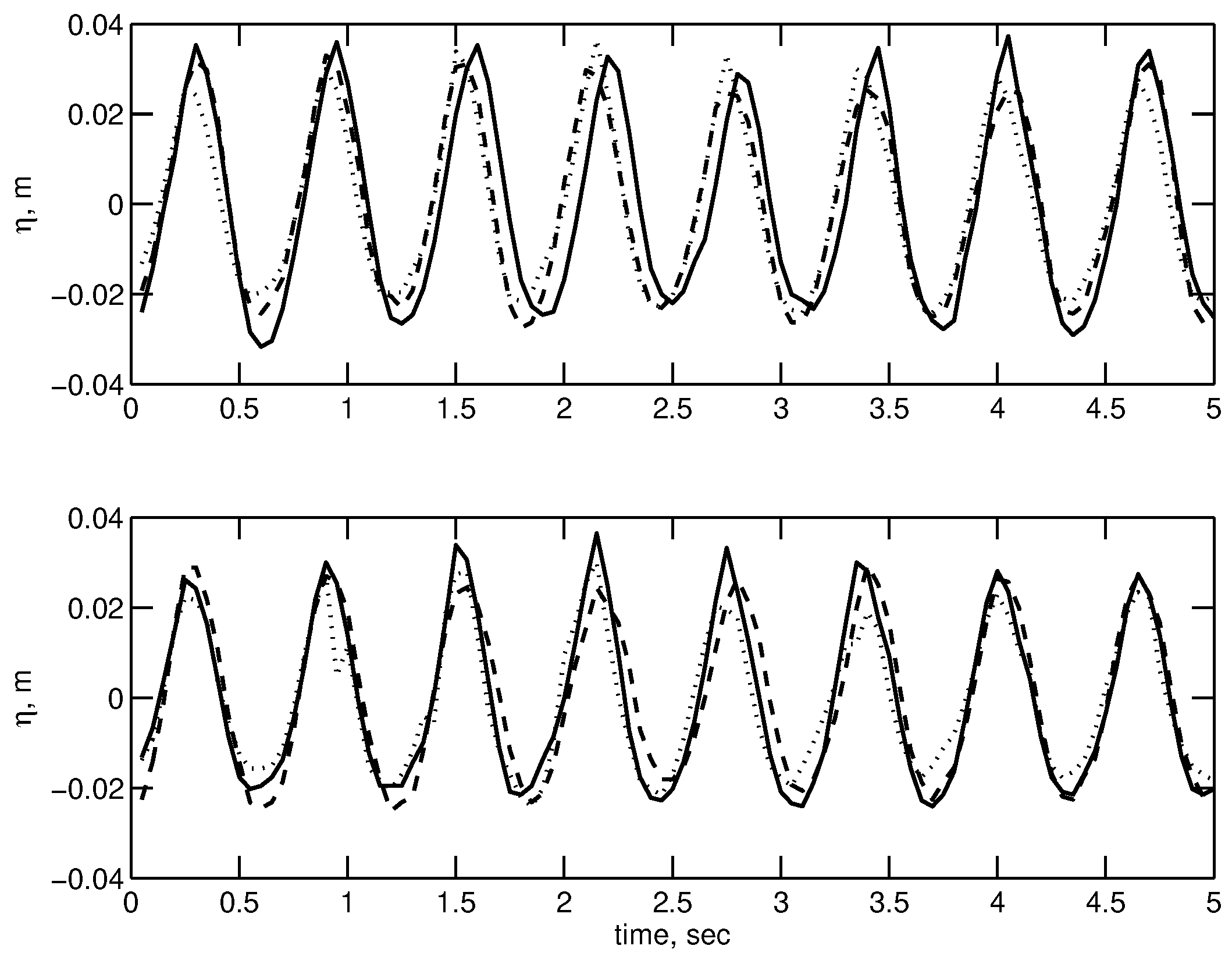
In
Figure 1 and
Figure 2, reproduced from [
10], time series of surface elevations
at the first and the second wave probes are shown. All the waves in these time series are generated with the same initial monochromatic frequency
Hz, but with different initial monochromatic steepness
and wind forcing
, as indicated.
At the first probe (
Figure 1),
m from the wavemaker, the waves are still near-monochromatic, with only marginal modulation due to BF influences and perhaps some parasitic modes present in the tank (e.g., non-potential part of the oscillations generated by the paddle, reflections, seiches etc.). The latter, if present, is part of the background noise from which the necessary modulational modes will grow in
Figure 2, see also [
14]. The top subplot has zero wind forcing. In the bottom subplot, waves of
are plotted with no wind forcing,
and a very strong wind of
. The effect of the wind on the profile of the mechanically generated wave is still not noticeable.
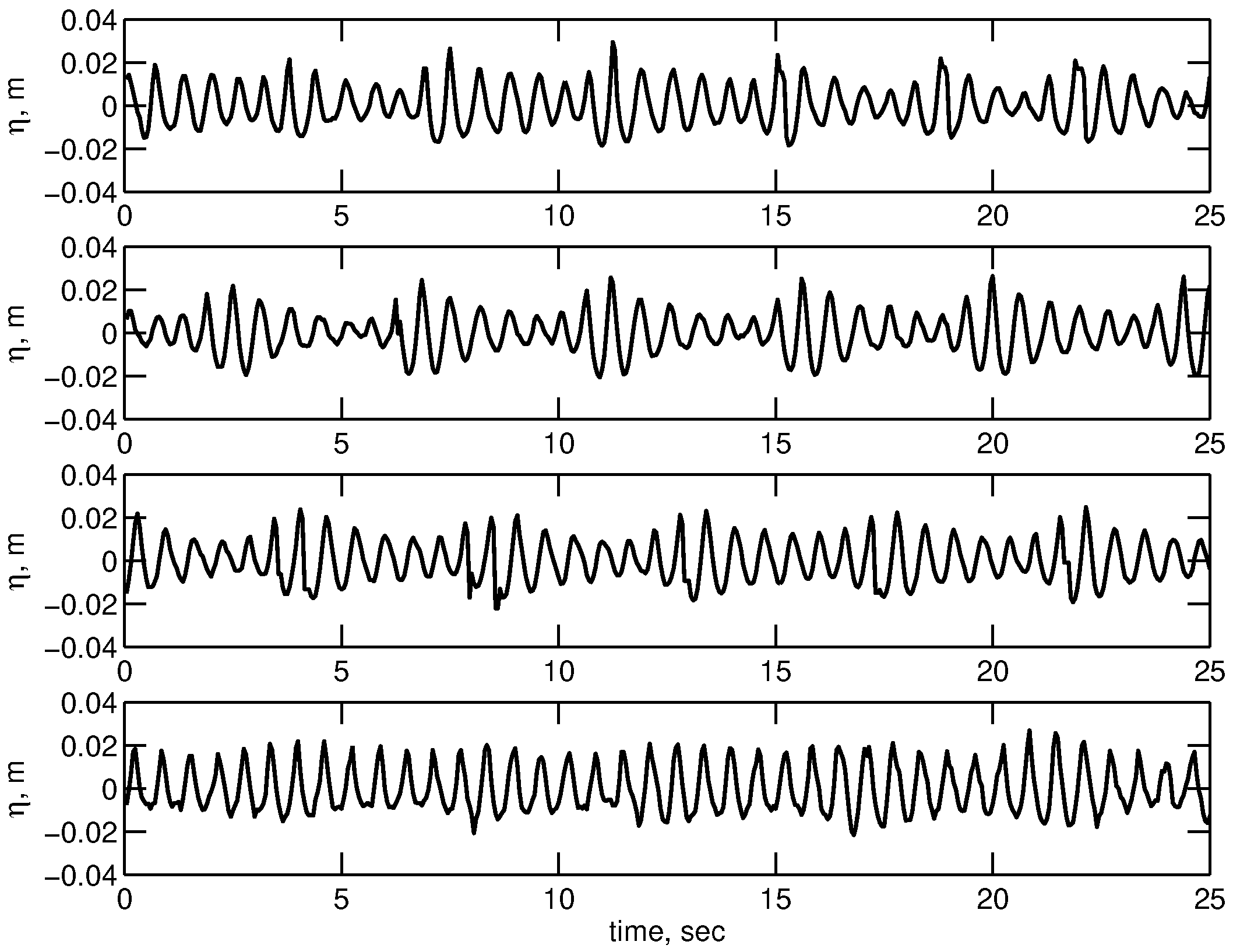
The wave profiles look very different at the second probe,
m from the paddle, some ten wave lengths downstream (
Figure 2). In all the cases, breaking still has not occurred. Waves in the top three panels evolve without wind forcing, and in the bottom subplot waves are shown strongly forced (
). The top subplot shows initially very steep waves of
. By the time they reach probe 2, they have developed into very strongly modulated groups of some 6 waves. Less initially steep waves (
, second subplot, and
, third subplot) evolve into more elongated modulated groups of some 7/7.5 waves, respectively. Note again that no initial modulation was introduced (see
Figure 1). Thus, as if
for the wave system was constant, a larger initial steepness leads to fewer waves in the modulation which results from the BF-like instability.
The effect that the wind forcing has on BF-like modulation is shown in the bottom subplot of
Figure 2. Here, very strongly wind-forced mechanically generated waves of
are plotted. Whilst the number of waves in the modulation did not seem to change, i.e.,
apparently remained approximately constant, the depth of the modulation
R changed dramatically:
where
R is height ratio of the highest
to the lowest
waves in the group. The difference in modulation depth is 1.6 times—from
to
. This fact indicates that the wind affected the growth rates of the instability.
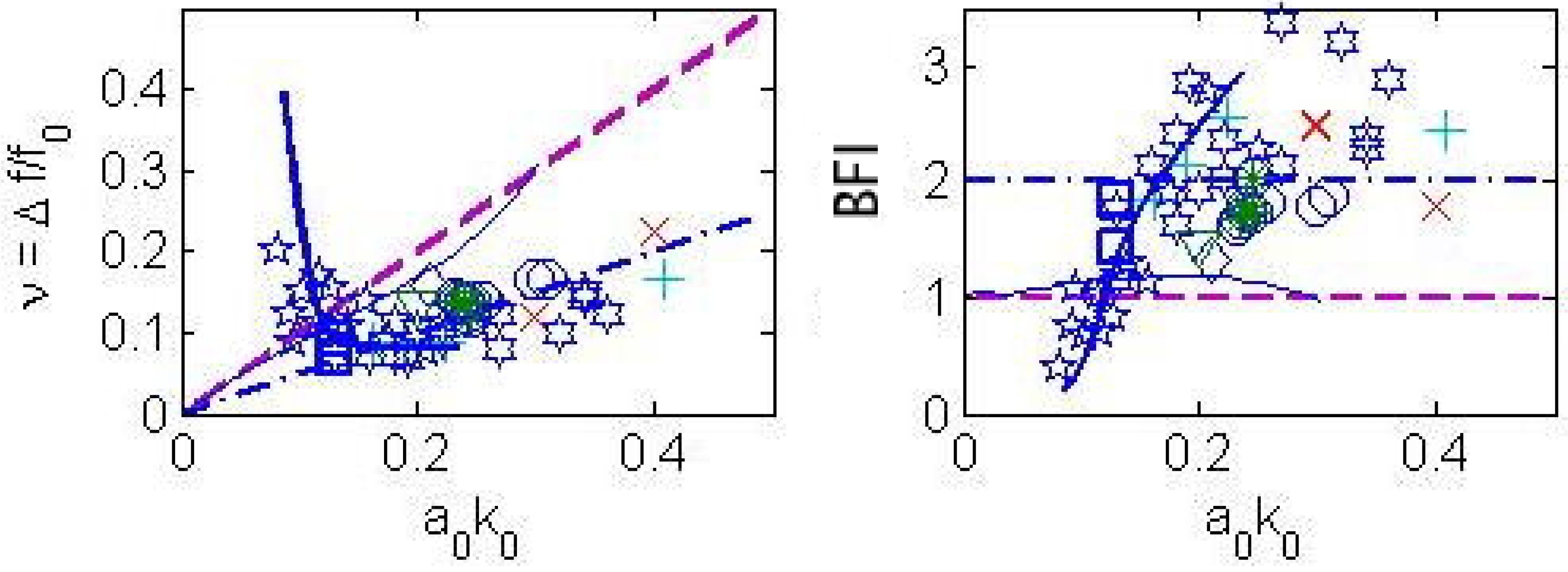
In
Figure 3, bandwidth
(left panel) and
(right panel) are plotted versus
measured at the first wave probe. The ASIST laboratory data points for
Hz,
Hz and
Hz are indicated with circles, crosses and pluses respectively. Measurements are taken at the second and third probes. Two points by other authors, [
12] (diamond) and [
14] (triangle), both inferred from Figure 15 of [
14], are also shown. In order to verify robustness of trends and their independence of the tank geometry, available non-seeded data points from experiments taken at wave tanks of the University of Tokyo, Japan (pentagrams, [
17]) and the National Cheng Kung University, Taiwan (hexagrams, [
32]) were added.
Squares and thick solid lines (blue) correspond to parameterisations of the field spectra of wind-generated waves? The dash-dotted line (blue) is? the fastest-growing instability is shown with dashed lines (magenta), and the high-order-non-linearity theory of [22] with thin solid lines (blue).
For reference, the dash-doted lines indicates the trend
, the outcome of the small-amplitude theory of [
1] for the fastest-growing instability is shown with dashed lines, and the high-order-non-linearity theory of [
4] with thin solid lines (following [
14]). While the scatter is considerable, there is some systematic behaviour of the steep data points around these lines. We should note that the set of conditions in which the modulation naturally developed is very diverse. First of all, the wave steepness ranges from gentle to extremely steep (
is the Stokes limit at which the waves break [
7]). Secondly, it covers the range where three-dimensional instabilities become essential (i.e.,
[
14],
[
12]). Third and very interesting, the wind-forced points (filled circles), and the forcing varies very broadly as
= 0–11 (see
Figure 4 below), grouped together with other points. And finally, the two most distant points (
) correspond to waves which have broken between the first probe where their
was recorded and the probe where the bandwidth readings were taken. In the course of the breaking, their height was considerably reduced, downshifting of the carrier frequency has occurred, i.e., [
10,
14], but the modulational properties still maintain to conform well with the general trend. Interesting also is behaviour of
at low wave steepnesses, when the waves do not break, e.g., [
7].
To verify whether the same trends are feasible in the field conditions, for real directional wind-generated waves with continuous spectrum
, two most generally accepted experimental parameterisations were chosen, JONSWAP [
29]:
and DHH [
28]:
Here,
is the level of equilibrium interval (tail) of the spectrum,
g is gravitational constant,
is the peak enhancement factor, and
is the width of spectral peak. The parameterisations differ in the way they describe the high-frequency tail of the wave spectrum, but both have the same feature of enhanced sharp spectral peak. In JONSWAP, dimensionless width of the enhancement
, within the scatter obtained in the experiment, is assumed constant, but has different values to the right (
) and to the left (
) from the peak. Therefore, there are two points (squares) which correspond to this spectrum in the figure. In the DHH spectrum, the peak is symmetrical, but its width was parameterised gradually changing as the spectrum develops (thick solid line)
(
is phase speed at the spectral peak
).
In both cases, as shown in the figure, it is possible to link this width with a characteristic steepness where is significant wave height and is the zeroth moment of the spectrum. The JONSWAP points support the general trend in the left panel quite well. The DHH-spectrum parameterisation agrees with the discrete data points of the corresponding steepness range very well. It crosses the BF small-amplitude line for which correspond to the wave development stages of .
A number of reasons can be held responsible for this low-steepness deviation. Whatever we can say about this deviation at present would be speculation, but in any case it seems to be well supported by the laboratory waves with discrete spectrum. Thus, we can state a surprisingly good agreement of the laboratory observations of the natural modulational bandwidth with behaviour of field waves. Perhaps, JONSWAP and particularly DHH spectra bear more physical meaning than just parameterisation fits to measurements. Further investigation and explanations of this observation is left to the future.
Corresponding
of the laboratory and field observations is plotted in the right panel of
Figure 3. The DHH dependence envelopes the laboratory observations quite well. There is a transition between
of steep waves to the smaller amplitude value of
, and it is likely that the experimentally observed DHH spectrum describes such transition for field waves. The steep-wave index
appears not a rigid number, but rather, above the transition zone, saturates in the range of
= 1.8-43. Particularly broad is the range of natural instability index at steepnesses around
. Internal variability within these ranges needs further investigation.
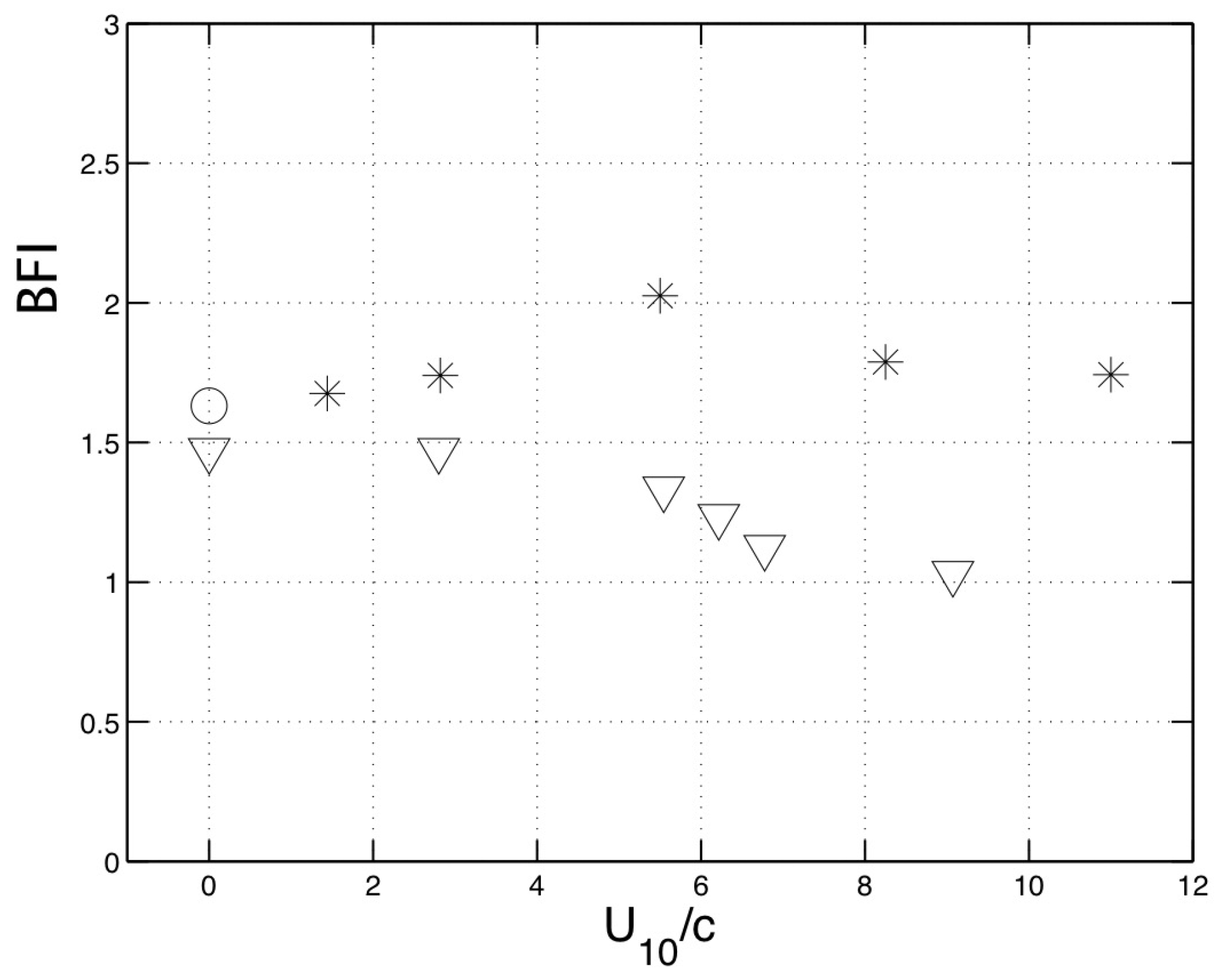
Behaviour of the modulation in the presence of wind requires special attention. On one hand, even under extreme wind forcing, the data points in
Figure 3 are not distinguishable from their unforced counterparts. Dependence of
as a function of wind forcing
is plotted in
Figure 4 where both data of this study and those taken from Figure 15 of [
14] are shown. There is neither a noticeable trend nor consistent deviations from the no wind scenario.
On the other hand, as seen in
Figure 2, depth (
4) of such modulation is much smaller, even though the waves still break. Does it mean that, while the natural modulational bandwidth is not affected by the wind forcing, the wind slows down development of the modulation, but is still pumping up the energy of waves? As shown in [
10], the wave breaking in presence of the wind is more frequent, and at the breaking onset the waves acquire the same ultimate steepness as within the BF modulation without the wind, but the breaking is less severe. Thus, the wind forcing does not appear to influence the natural modulational bandwidth, but plays other important roles in the modulational process which still remain to be understood.
3. Discussion and Conclusions
Before formulating the final conclusion, we would like to discuss implications of the results for the spectral modelling of wave energy dissipation. As mentioned above, most of this dissipation is usually attributed to the wave breaking which takes place across the entire spectral band. Since occurrence of breaking dominant waves appears to correlate with wave groups, e.g., ([
21,
33], among many others), it is often assumed that shorter waves also form groups which bring about breaking at the respective scales. If such groups do exist, within the continuous spectrum of wind-generated waves information about them is lost. This spectrum only has one peak, and it is not clear whether the short-scale waves do form groups indeed, and if they do, what is a relevant bandwidth. Such bandwidth is usually introduced by analogy, that is assumed similar to that of the spectral peak, e.g., [
34,
35]. If we were to maintain this analogy, following the results on connection of the natural modulational bandwidth with the wave steepness, we should propose that it is
which should stay constant across the spectrum, rather than bandwidth, where
is dimensionless enhancement of the spectral density with respect to the saturated spectral tail in (
5), i.e.,
would indicate the relative change of steepness across the spectrum. That is, as the spectral density drops away from the peak, the bandwidth
should decrease (see also, [
10,
17]).
Indeed, the idea of the bandwidth broadening has been tested and is finding indirect support [
36]. If (
8) applied directly, however, such bandwidth drops very rapidly away from the peak and asymptotes at the level of
0.044 which would correspond to
waves in the modulation. Therefore, even if such modulation exists, it is very weak.
In conclusion, we would like to summarise that indications of the existence of a natural modulational bandwidth due to BF-like instability mechanism, which is consistently observed in initially monocromatic two-dimensional unforced waves, in wind-forced waves, in the presence of three-dimensional instabilities, and even in wind-generated fields characterised by continuous frequency-directional spectrum. Parameterisation of this spectrum by [
28] describes transition from low values to high values of the natural-instability index
remarkably well. The modulational index
(
3) saturates in the range of
and does not appear to be directly affected by wave-breaking in the wave system.