The relationship between pressure
and potential in a liquid is determined by the Bernoulli integral
where
is the equilibrium pressure in the liquid far from the bubble,
is the pressure in the acoustic wave. The potential in the Bernoulli equation is defined within an arbitrary function of time. For this reason, the potential at large distances from the bubble
is commonly taken to be zero. The amplitude of the bubble oscillation is assumed to be small. This allows one to neglect the nonlinear terms
in the Bernoulli equation.
The dynamic boundary condition expresses the balance of forces: the pressure on two sides of the bubble wall differ only because of surface tension:
where
and
denote the pressure in the liquid and in the bubble respectively,
is the unit vector normal to the bubble surface
,
is the coefficient of surface tension of the gas/liquid interface. We adopt a widely used equation of state for gas in a bubble corresponding to a polytropic law,
V,
are the instantaneous and equilibrium bubble volume,
is the polytropic exponent,
is the equilibrium pressure in the bubble.
The pressure in the acoustic wave can be considered spatially uniform at a distance less than characteristic wavelength. For this reason, the assumption that the bubble possesses axial symmetry and has no angular momentum will be justified. The choice of a particular coordinate system will help us to find an analytical solution to the problem. This coordinate system should have axial symmetry and lead to the separation of variables in the Laplace equation.
2.2. Dynamics of a Tethered Bubble
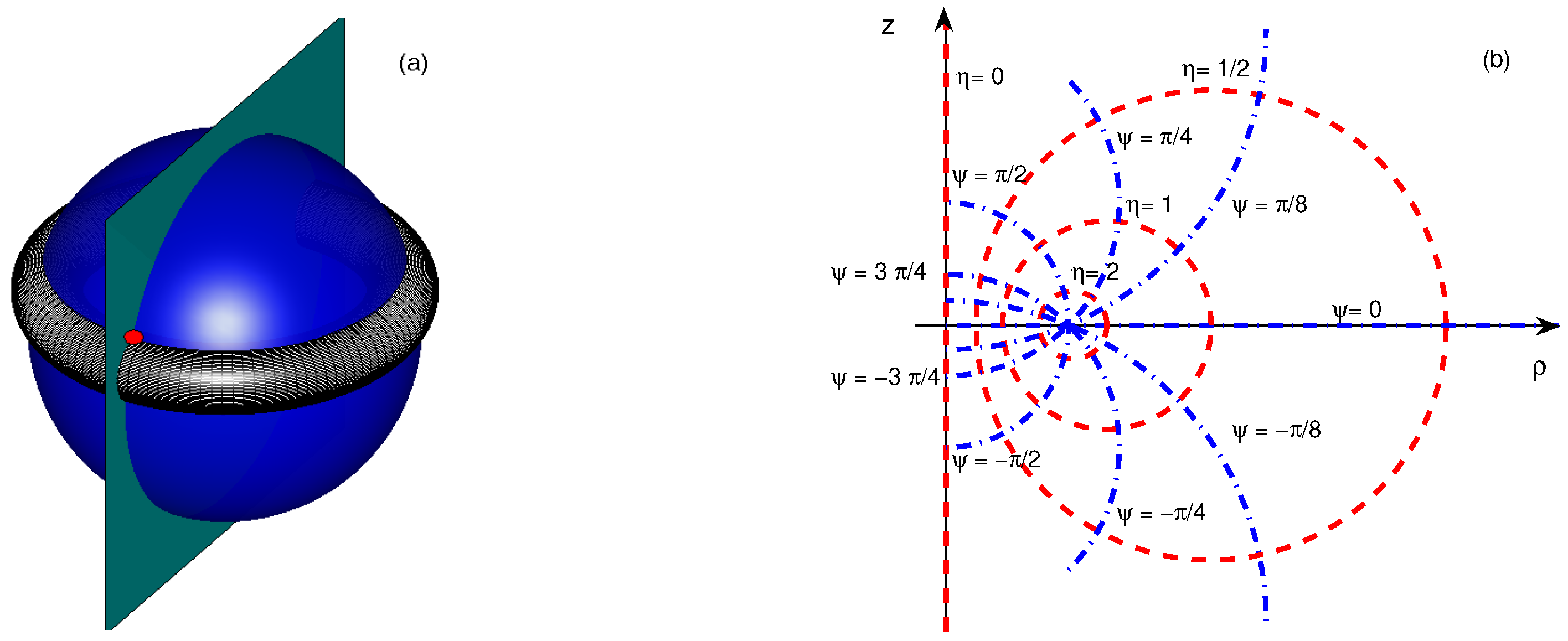
Toroidal coordinates is a natural coordinate system for analysis of oscillations of tethered bubbles since the equilibrium surface of a such bubble is a spherical bowl. The Laplace equation has the following form in toroidal coordinates
where
,
are the Lamè coefficients.
The boundary conditions to this equation should be specified on the bubble wall
(where
is the contact angle) and on the boundary
which corresponds to the interface (see
Figure 1). The relation between the diameter of the ring of contact
L and the equilibrium radius of the bubble
is given by
.
To separate the variables in the Laplace equation, we replace
by
[
35]. In view of the axial symmetry of the system, Equation (
7) acquires the form
here
is the Legendre operator. An important class of integral expansions involving spherical harmonics is commonly known as Mehler-Fock integral transforms. This suggests that the solution of Equation (
8) can be found in the form [
36]:
Equations (
9) and (
10) represent the forward and inverse transformations. Here,
is the Legendre functions of the first kind. The degree of the associated Legendre function appears as the integration variable in the inversion formula.
The kernel of the integral transform,
, obeys the equation
The substitution of the solution of Equation (
11) into Equation (
9) yields the general form of the required solution
where
and
should be determined from the boundary conditions on the bubble wall.
We shall assume that the characteristic length of the acoustic wave exceeds the dimensions of the bubble not only in the liquid, but also in the gas. Under these conditions, the pressure inside the bubble will change periodically in time, but remain spatially homogeneous. It follows from the Bernoulli equation that the surface of such a homobaric bubble will be equipotential, if neglecting surface tension and nonlinear term. We shall analyze only linear volume oscillations of the relatively large bubbles and therefore can use this approximation .
For the relatively simple case when the lower medium is absolutely rigid
we have
. After using the Heine identity [
36]
one obtains
which provides finding in the close form the solution of the problem:
The Legendre function of complex index could be expressed by means of the following integral
Substitution of this expression into Equation (
15) allows one to convert it to the form
In this form, the behavior of the potential in the vicinity of the tethered bubble was derived earlier [
37]. However, the method by which these results were obtained was complicated and of an intuitive, rather than a regular nature. By using the transformation of inversion relative to the ring of contact, the original problem has been reduced to the form corresponding to the field of point charge in the wedge. The inverse transformation of the known solution of electrostatics led to Equation (
17). A small difference between the earlier [
37] and the present approaches consists in using the different boundary conditions for the potential at the bubble wall
and far from the bubble
: it was assumed in the Ref. [
37] that
,
but we set
,
in the present approach. This difference is not important, since the potential is determined to within an arbitrary function of time.
Substitution of solutions in the form of (
15) and (
17) into the kinematic boundary condition Equation (
4) establishes the relationship between the time variation in the bubble volume
and the value of the potential at the bubble wall
Introducing the notation
C (capacity), we use the existing analogy of dynamics of homobaric bubble and electrostatics [
38]. The form of Equation (
18) substantially simplifies the expression given in Ref. [
37] where
C was described by a double integral. Different forms of representation for
C correspond to the two forms of the solution found Equations (
15) and (
17). When performing numerical calculations, the third line of Equation (
18) is useful. In turn, the form presented on the second line of Equation (
18) is more convenient for the discovery of the fact that the integral for
C can be reduced to analytical formulas for definite values of wetting angles:
[
37].
Substituting
expressed through the change of volume in the dynamic boundary condition (
3), we obtain an analogue of the Rayleigh equation [
37]
It follows directly from this equation that the fundamental frequency of the tethered bubble has the form
where
is the fundamental frequency of a free bubble of the same radius of curvature
. The ratio of these frequencies
depends only on
. The plot of the dependence
on
presented in the Ref. [
37] is the only predicted physical effect that can be verified experimentally. This is an obvious defect in the developed approach. However, the unified approach based on the use of toroidal coordinates makes it possible to significantly expand this list. Thus, some of the effects described in the next section, related to the analysis of the behavior of the bubbles located at a close distance from the boundary surface in bi-spherical coordinates, have a close analogues for a tethered bubbles, which can be studied in toroidal coordinates.
2.3. Bubble Dynamics Close to Interface
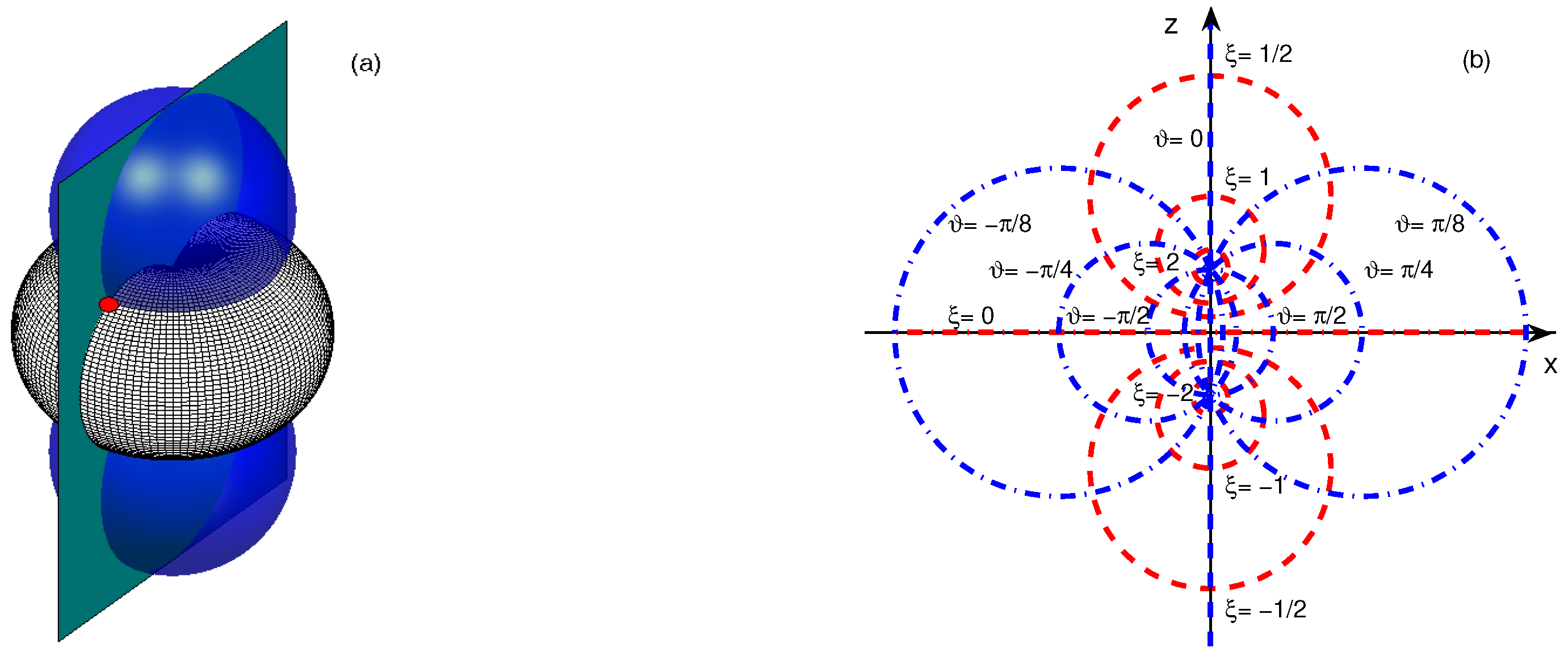
In this section, we use a bi-spherical coordinate system for separating variables in the Laplace equation. In contrast to toroidal coordinates, this system is conformally equivalent to a system of spherical coordinates. However, these two coordinate systems are not equivalent with respect to the Euclidean group [
30].
The bi-spherical coordinates (
) are related to Cartesian coordinates (
) by the relations:
where
goes from
to ∞,
and
go from 0 to
and from 0 to
, correspondingly. The surface
is the bubble, while the interface corresponds to
. For
,
corresponds to
. Illustration of the bi-spherical coordinate system is shown in
Figure 2a,b.
By its structure, the Laplace equation in bi-spherical coordinates is close to Equation (
7) and has the following form
where
,
,
are the Lamè coefficients.
A solution procedure for the Laplace equation in bi-spherical coordinates requires the introduction of the following substitution: . In view of the assumed axial symmetry, the function does not depend on the azimuthal angle. For the function , the variables are separated.
We begin with the simplest solution [
39] obeying rigid boundary conditions. Applying the equipotentiality condition
on the bubble wall and the impermeability condition on the rigid boundary
, we find the analytic solution of the boundary value problem
here
are the Legendre functions. The structure of Equation (
23) is similar to that obtained in Ref. [
40] for the free surface and corresponds to another limiting case, that of a rigid boundary.
The time derivation of the bubble volume,
, can be expressed through the potential at the bubble wall
Substitution of this relation into the dynamic boundary condition (
3) leads to the Rayleigh equation for the volume variation
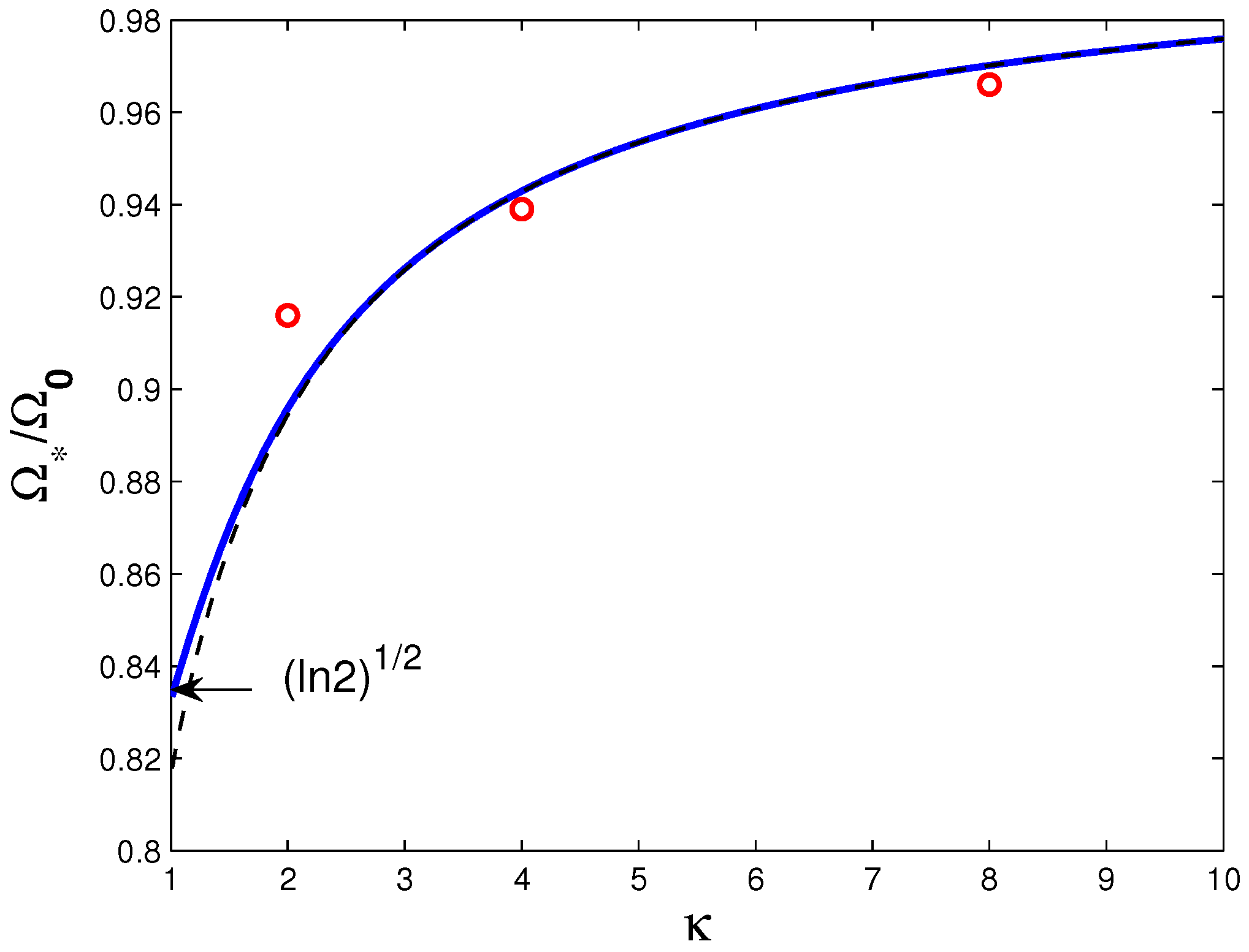
Here,
is the natural frequencies of the bubble located at the distance
h above the rigid bottom. A graph of the ratio
as function of
is shown in
Figure 3 of the Ref. [
39].
The presence of a rigid boundary decreases the natural frequency. The figure also includes a comparison of these calculated values with measured values. There is a continuous transition from the state of the tethered bubble to the state of the bubble located at some distance from the surface. This is the state of the bubble which touches the surface at one point. The shift of the natural frequency obtained for this case [
37] and the results of the Ref. [
39], which uses bi-spherical coordinates, give the same value.
The problem of describing the dynamics of a bubble located at some distance from the boundary is much simpler than the description of a tethered bubble, since it does not require analysis of the behavior in the vicinity of the contact line. For this reason, a much more detailed study of the features of the behavior of such an inclusion can be obtained.
First, we consider the acoustic correction to the incompressible Rayleigh-Plesset Equation (
25). The implementation of this procedure follows the approach suggested by [
41,
42] and account for the presence of the rigid boundary. The radiation damping results from the emission of energy away from the bubble as sound. Use is made of the method of matched asymptotic expansion in which the small parameter is
. In this way we find [
39]
The damping constant differs from that for a free bubble by a co-factor . Since the presence of a rigid wall doubles the amplitude of potential in the far field, then the power (which is proportional to the square of the amplitude) leads to the factor 4. However, the radiation from the bubble near the rigid wall occurs only in a half of the solid angle. For this reason, only the factor 2 enters into the final expression for the radiation damping. This result is valid only for the case when the wavelength is much greater than the distance to the rigid wall and one can ignore the phase difference between the direct wave and the one reflected from the wall. The factor reflects the variation in the bubble inertial mass near the wall. This term quickly approaches unity with increasing distance from the bubble to the wall.
So far, we have assumed the flow near the bubble and the rigid wall to be inviscid and irrotational. In reality, the presence of viscosity implies that the tangential and normal components of the stress must be continuous at the surface of the bubble. The velocity should be vanished at the rigid wall. To accommodate these boundary conditions other types of solution of the viscous equations of motion are required. For the millimeter sized bubbles and kHz frequency range, the viscous length , ( is small compared with the equilibrium radius . Thus vorticity is restricted to the thin boundary layers near the bubble interface and the rigid wall.
A straightforward method for taking into account the vorticity would be to proceed by successive approximations. On the other hand, if we restrict our analysis to finding the value of viscous damping, and not the details of flow in the near interface region, we can use the approach based on the total energy conservation in incompressible liquid. In this approach, time derivative of energy is balanced by dissipative function. Longuet-Higgins [
43] used this approach in finding viscous damping of surface modes on the bubble wall. As was shown in Ref. [
39], the damping factor of bubble oscillations due to dissipation near the boundary has the form
One can identify three factors in this expression. The first one
characterizes the viscous losses at the free surface—the bubble wall. The second factor shows how the viscous losses near the rigid wall exceed the losses at the free surface
. The third factor
describes the law of diminishing losses with increasing the distance from the bubble to the rigid wall
. The explicit form of
is given in Ref. [
39]. For large values of the argument
is given by the formula
.
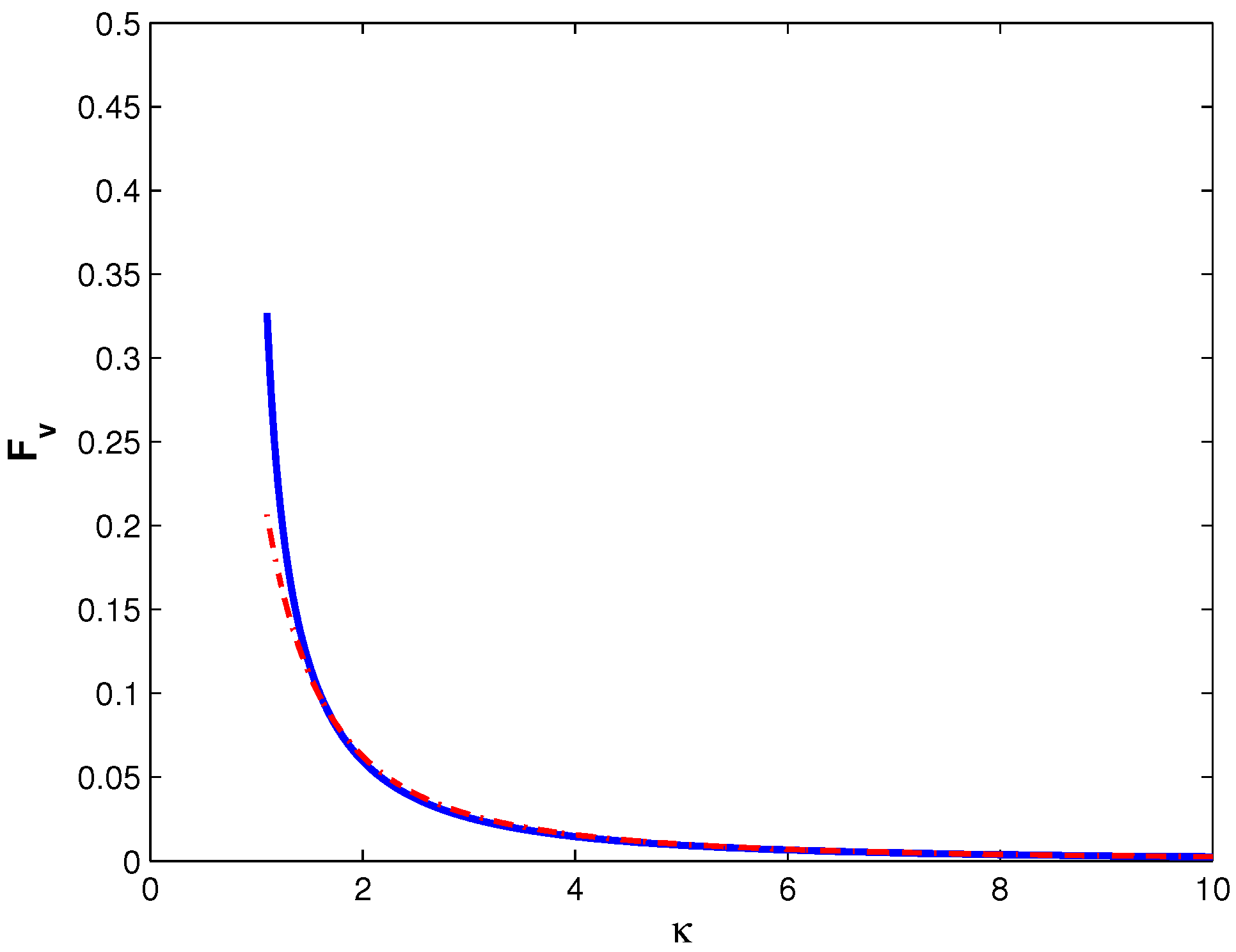
Figure 4 illustrates the behavior of
on
for the most interesting range of distances. The starting point is the state when the bubble near touches the boundary, and then this interval extends up to a relatively large distances (
,
).
Please note that although the surface value of the potential over the bubble wall is constant, the value of the normal derivative, which determines the displacement and deformation of the bubble shape
, varies with the angle
. To illustrate the variation in the bubble shape during its oscillations near the rigid wall, the angular dependence of the displacement
on
has been evaluated [
39].
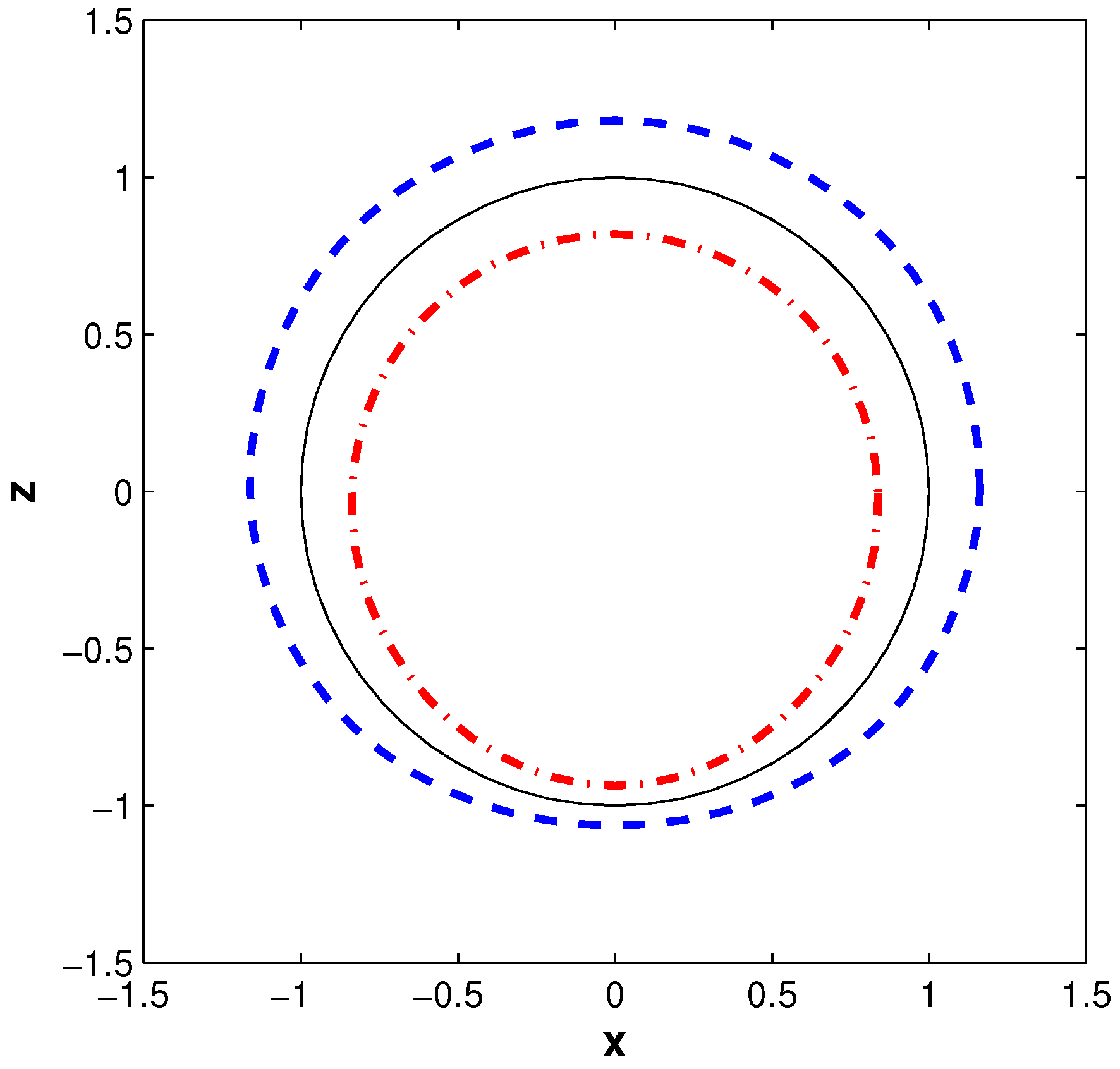
Figure 5 shows the distortions reached during the expansion (dashed line) and contraction (dot-dashed line) phases of oscillations, for the dimensionless amplitude
. The bubble equilibrium shape is shown by the the solid line. The dependencies shown in the figure demonstrate a rather non-obvious fact that the bubble shape can be qualitatively well described by the first terms of the multipole expansion even at a relatively short distance from the boundary. This approach provides an efficient way to evaluate the accuracy of the approximate methods [
17,
18]. In applying these methods it was assumed that the bubble undergoes only radial and translational oscillations near an interface.
The interaction of a bubble with a boundary is traditionally taken into account by introducing a mirror monopole source. The applicability of this method is restricted by the condition of smallness of the bubble size compared to the distance to the bounding surface. An approach using specific coordinate systems for separating variables was successfully used in describing the behavior of tethered inclusions and bubbles located near rigid boundaries. The boundary of most media is not absolutely rigid, so the next step in applying the method is to examine the bubble behavior near an interface between two liquids.
2.4. Bubble Oscillations Near an Interface between Two Liquids
In this case, the parameters of the second medium—its density and the speed of sound—influence the behavior of the bubble. At the interfaces, the boundary conditions should be satisfied, which include continuity of displacements and equality of forces. In each medium, the potential satisfies the Helmholtz equation. However, if we use the integral representation of this equation, this will make it possible to express the potential in the medium (1), where the bubble is located, through the boundary values on the interfaces:
where
is the Green’s function,
is the position of the observation point,
corresponds to points at the bubble surface and interface and
is the derivative with respect to the normal (the normal is directed inside the bubble and inside medium (2)).
In the first stage [
44], we will analyze natural bubble oscillations, and, therefore, the right-hand side of Equation (
28) does not contain the term describing the source. The choice of the Green’s function in Equation (
28) makes it possible to simplify considerably the procedure for finding the solution. Following [
45], we choose it in the form satisfying the boundary conditions at the interface between two liquids. For a planar interface, this leads to the fact that the integral over
vanishes, so that only the integral over the bubble surface remains in Equation (
28).
When solving Equation (
28), we use the asymptotic expansion method, with the small parameter being the ratio
of the bubble size and the bubble-to-boundary distance to the wavelength. In the vicinity of the bubble,
, the media can be considered incompressible. Far from the bubble,
, the finite speed of propagation is essential.
We will take into account only two first terms of the series expansion, which, as shown by Prosperettit [
41], is sufficient to determine the natural frequency and the radiation damping of bubble oscillations.
The zero-order and first-order equations have the form
This system of equations becomes completely defined if we supplement it with the boundary conditions at the bubble wall Equations (
3) and (
4).
The first two terms of the expansion of the Green’s function that appear in Equations (
30) have the form [
44]:
where
is the unit vector along the
z axis,
,
. The zero-order Green’s function can be interpreted as follows: it consists of two monopole sources in an incompressible liquid, namely, a direct source and a mirror one with respect to the interface, the mirror source intensity being such that the boundary conditions are satisfied. The first-order Green’s function
is constant and independent of spatial coordinates. It should be noted that the above formulas are valid within the wave zone.
To find the zero-approximation solution
, we use the fact that the liquid within the wave zone near the bubble can be considered incompressible. This means that the potential is a solution of the Laplace equation along with the integral equation (the first lune of Equation (
30)). The convenience of the integral equation is that we do not need to worry about satisfying the boundary conditions at the interface
. It suffices to substitute a general solution to the Laplace equation and explicit form of the Green’s function into the integral equation. Thus, the zero-approximation solution takes on the form [
44]:
The solution to the first-approximation is independent of spatial coordinates and has the form [
44]
This leads [
44] to the modified Rayleigh Equation (
26) in which the frequency
is replaced by
and
is replaced by
Spatial variations of
and
are governed by the behavior of factor
which involves an explicit dependence on bubble-to-boundary distance
h and bubble size
:
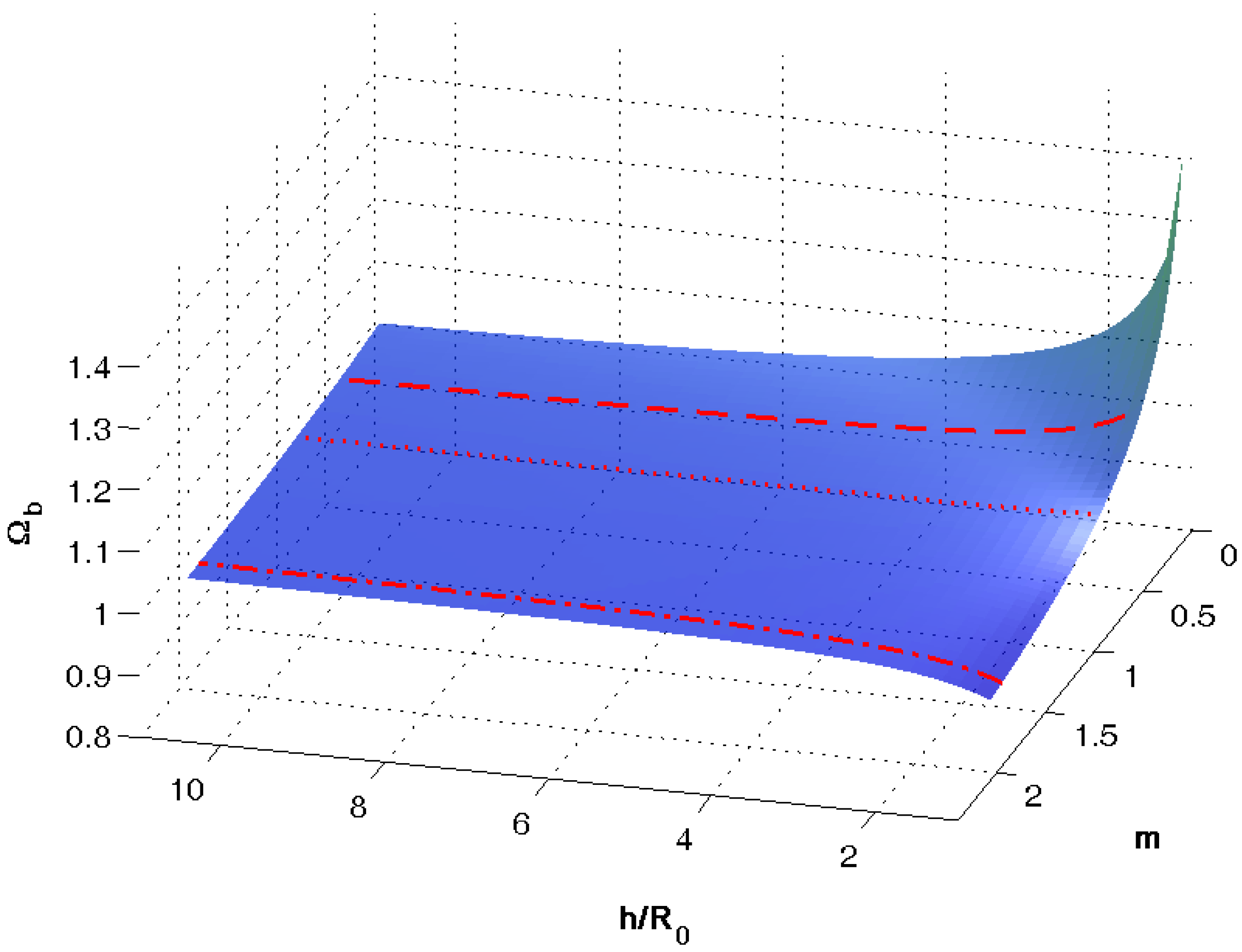
Figure 6 illustrates the behavior of dimensionless natural frequency
as function of the normalized distance to the boundary
and the ratio of densities
. The typical ratio of sediment density to water density is
, for blood and artery wall this ratio is close to unity
. The behavior of the natural frequency of the bubble displayed above the sediment layer is depicted by dash-doted line. The dependence of this frequency for a bubble located in the sediment layer is shown by a dashed curve. The bubble natural frequency in blood near the artery wall is represented by a dotted line.
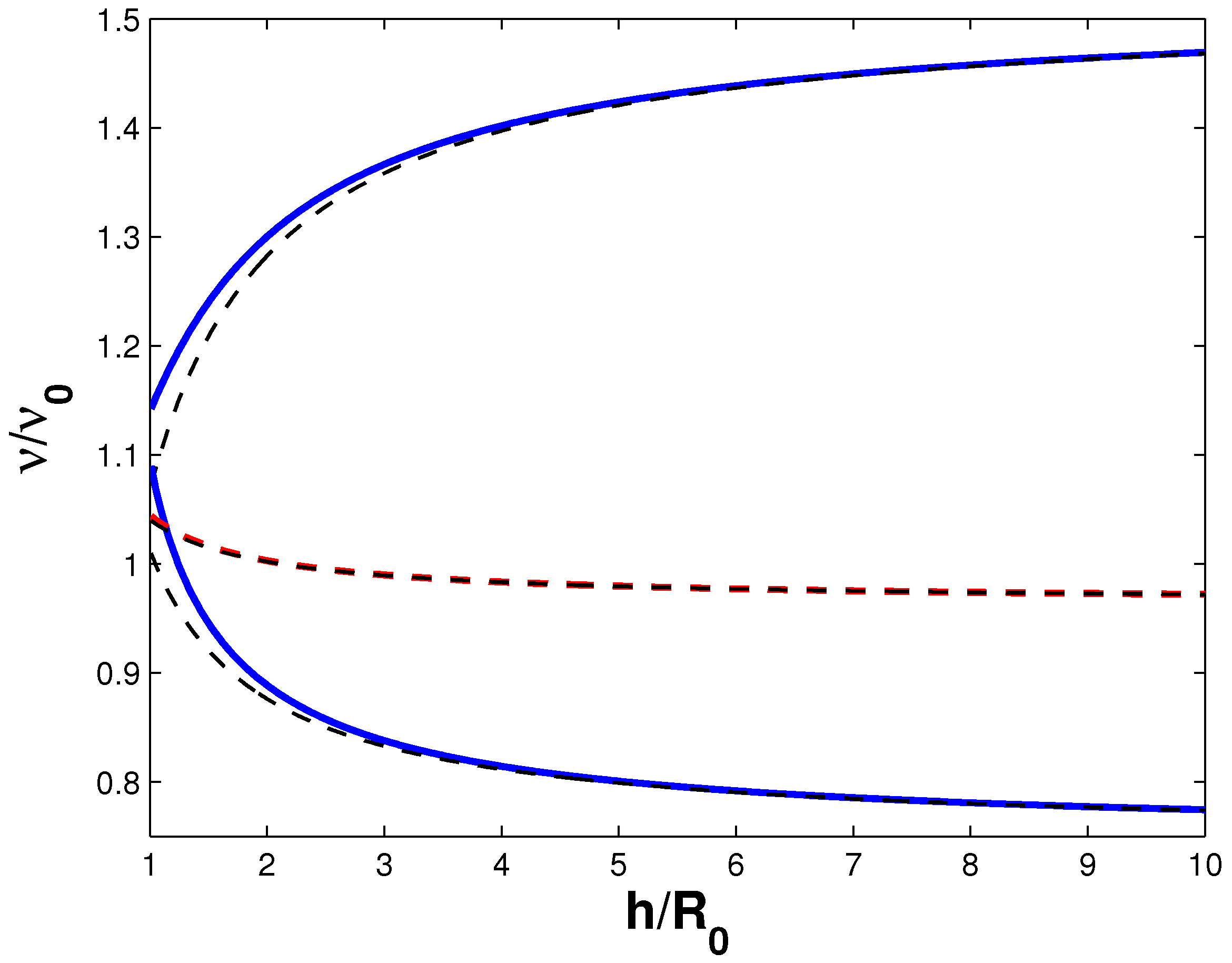
The dimensionless damping factor
(normalized to the damping factor of a free bubble
) is shown in
Figure 7. The damping factor is calculated for resonance frequency, and its spatial variability is determined only by the factor
. Since the radiation damping in addition to the dimensionless distance,
, depends also on two parameters characterizing the media (the ratio of densities,
m, and the ratio of sound speeds,
n), it is not possible to describe its behavior by one (even a three-dimensional plot). For this reason, two-dimensional graphs describing the dependence of the damping on the distance to the boundary,
, are given. However, each of the graphs corresponds to the typical physical parameters of the media,
m,
n.
So, for a bubble near the sediment layer (the upper curve in
Figure 7), the damping factor decreases on approaching to the boundary because of the decrease in frequency
. For a bubble in the sediment layer, the damping factor increases on approaching to the boundary (the lower solid curve in
Figure 7) because of the increase in frequency
. As the distance to the boundary increases, however, within the range which is smaller than the wavelength, the damping factor of a bubble above the sediment layer is higher than that of a free bubble, because sediments represent a heavier and less-compressible medium. The presence of this medium can be roughly estimated by the presence of a mirror bubble oscillating in phase. Conversely, for a bubble in the sediment layer, the mirror bubble oscillates in anti-phase and, hence, reduces damping. For damping of a bubble in blood, which is shown by the thick dashed line in
Figure 6, the difference in the parameters of media is so small that the variation in the bubble oscillation parameters is almost undetectable. It should be noted that the above results relate only to the contribution of radiation damping. Blood is a non-Newtonian fluid and the viscous component of the complex viscosity can lead to a marked influence on the bubble dynamics at physiological hematocrit values (~45%) [
46].
Oscillations of a bubble near an interface, in addition to the distortion of the bubble shape, lead to deformation of the boundary. This new, in comparison with a rigid boundary, effect is used in experimental studies related to biomedical applications [
15,
16]. The vertical displacement of the interface between the media
is determined directly from the found solution and has the form
It should be noted that small (micron) size bubbles were used in the mentioned experiments. The presented approach is valid for relatively large bubbles for which the contribution of surface tension can be ignored. For this reason, comparison is possible only after the inclusion into consideration of the effects associated with deviation from equipotentiality of the bubble wall.
The presented results describe a relatively simple case of a boundary separating two liquids. However, the possibilities of the approach used are much broader and allow us to consider a much more complicated case of the interface between liquid and elastic media. The technical difficulties in solving this problem consist in the cumbersomeness of calculating the asymptotic of the Green’s function Equation (
28). In the integral representation of this function, the coefficient of reflection from the liquid half-space should be replaced by the reflection coefficient from the elastic half-space. The existence of surface waves at the boundary of these media is manifested as a pole of the reflection coefficient, which makes it difficult to calculate the asymptotic behavior and leads to the necessity of introducing etalon integrals.