Quasi-Steady versus Navier–Stokes Solutions of Flapping Wing Aerodynamics
Abstract
1. Introduction
2. Materials and Methods
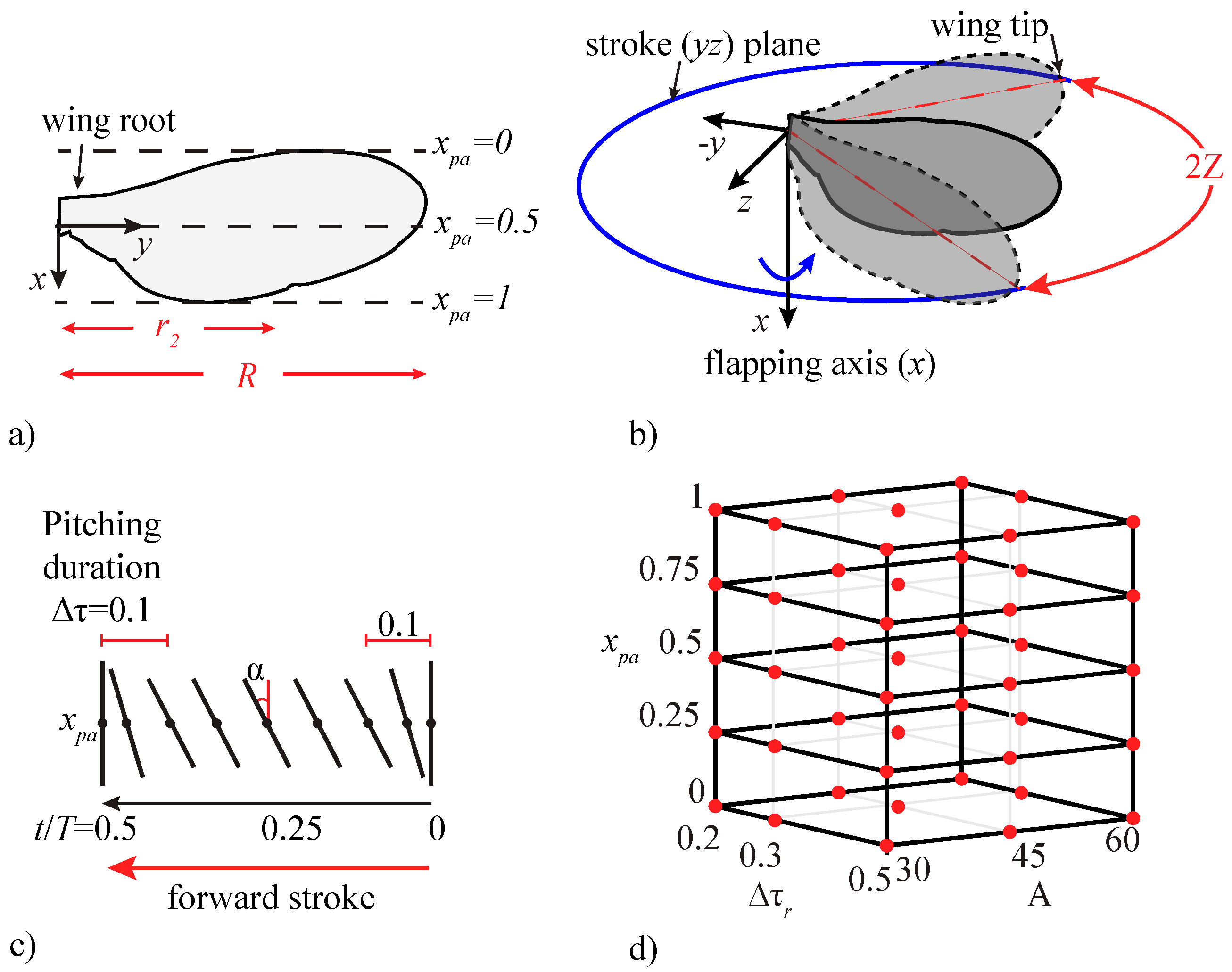
2.1. Case Setup and Wing Kinematics
2.2. Aerodynamic Models
- A 3D Navier–Stokes equations solution of the rigid wing motion.
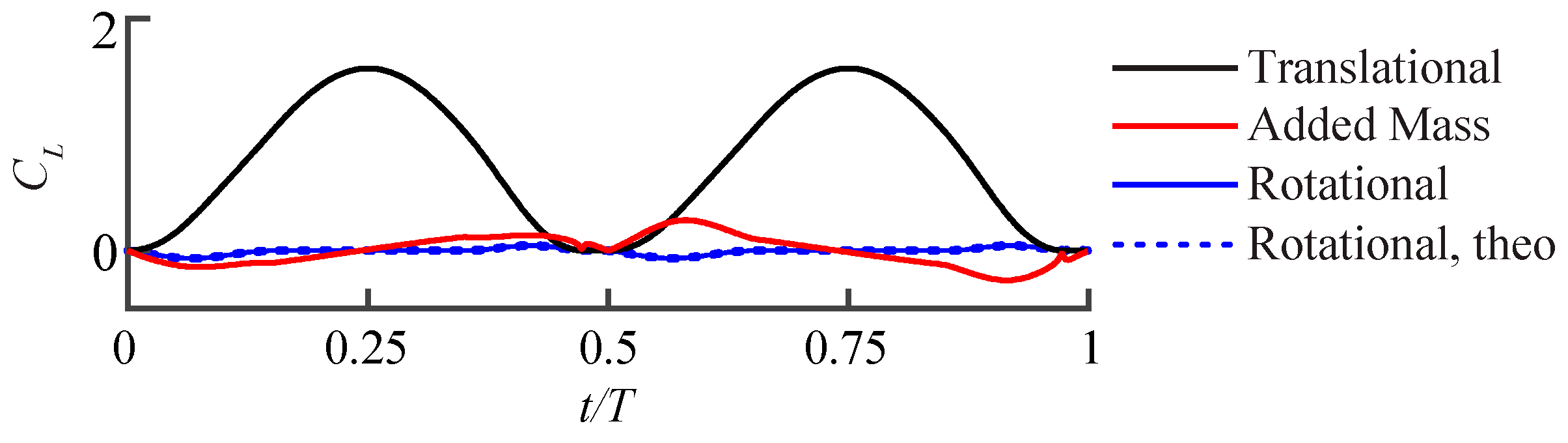
2.2.1. Quasi-Steady Aerodynamic Model
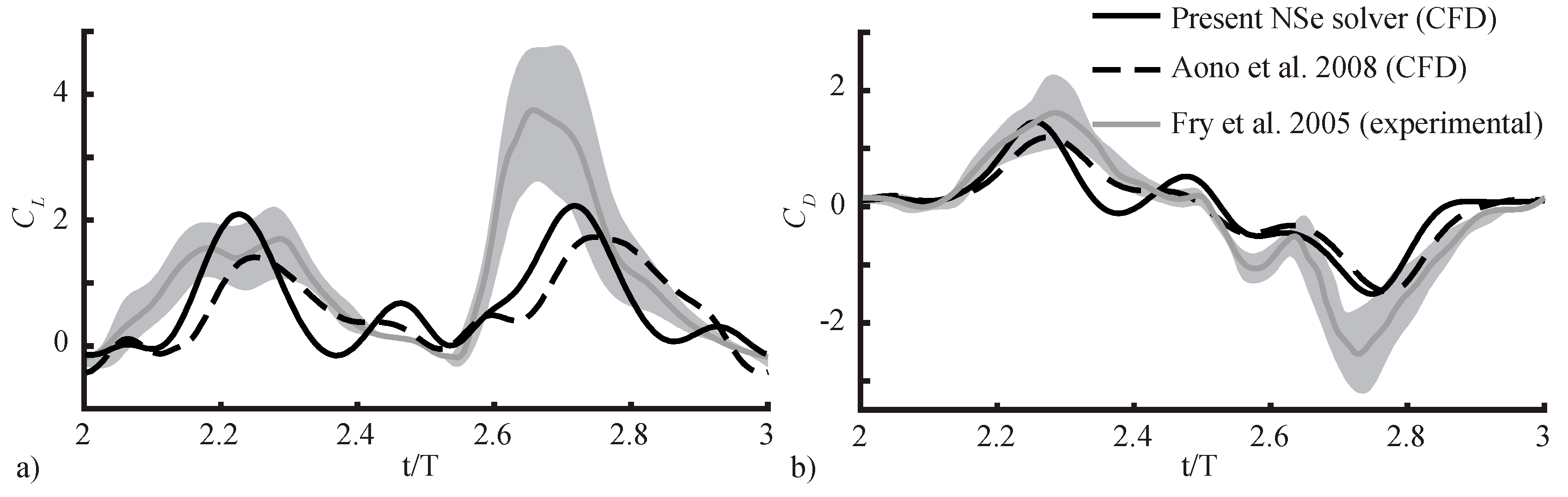
2.2.2. Navier–Stokes Equation Model
2.2.3. Spatial and Temporal Sensitivity Study
3. Results and Discussion
3.1. Aerodynamic Response under the Three-Dimensional Pitch-Flap Motion
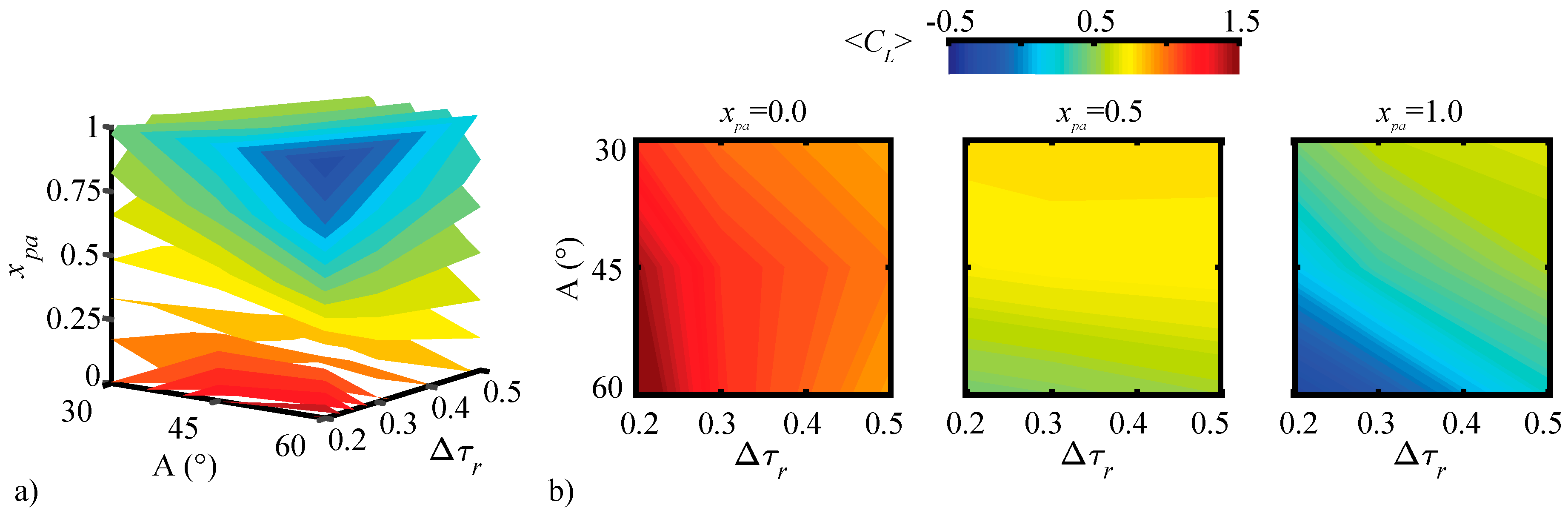
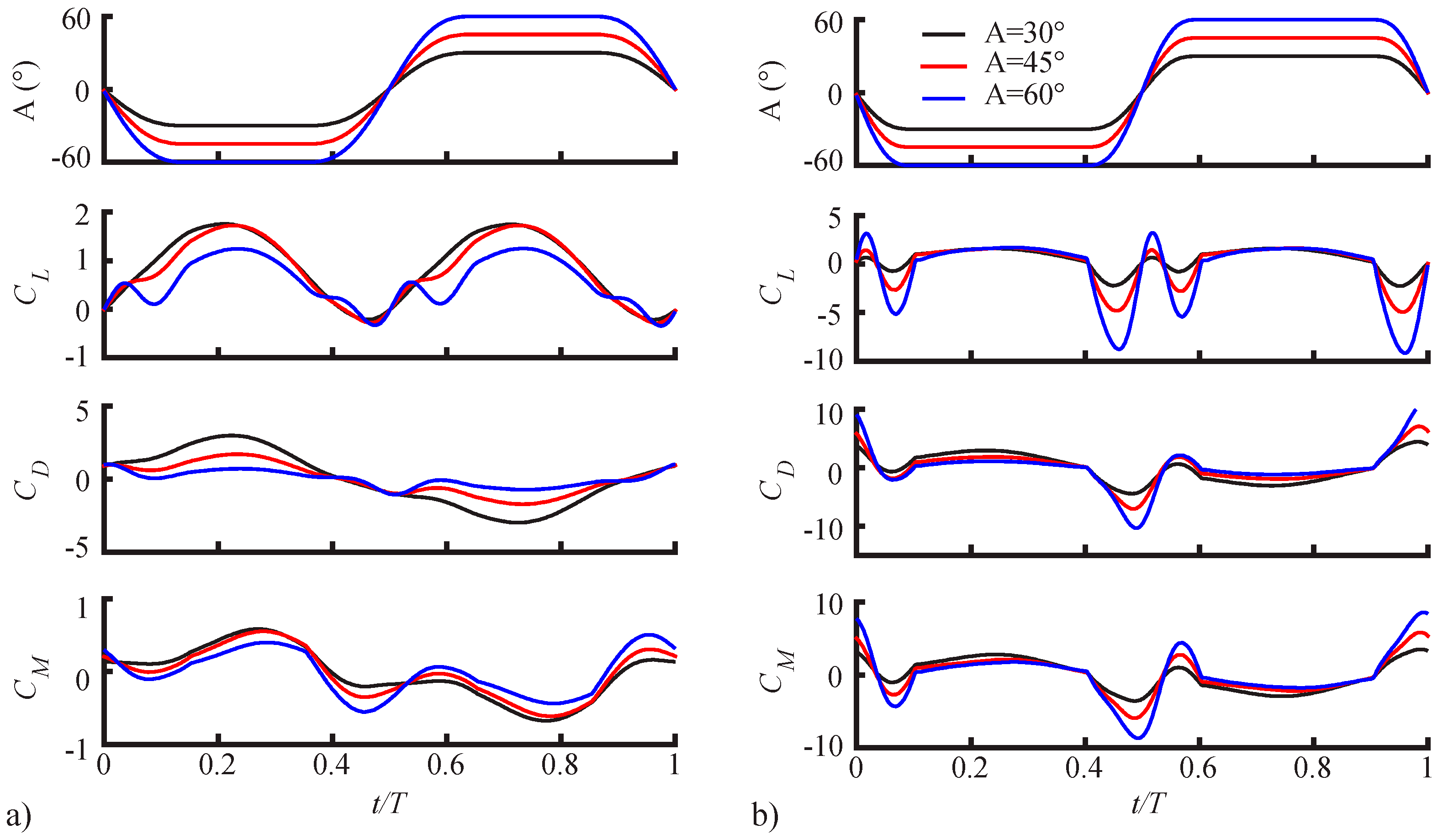
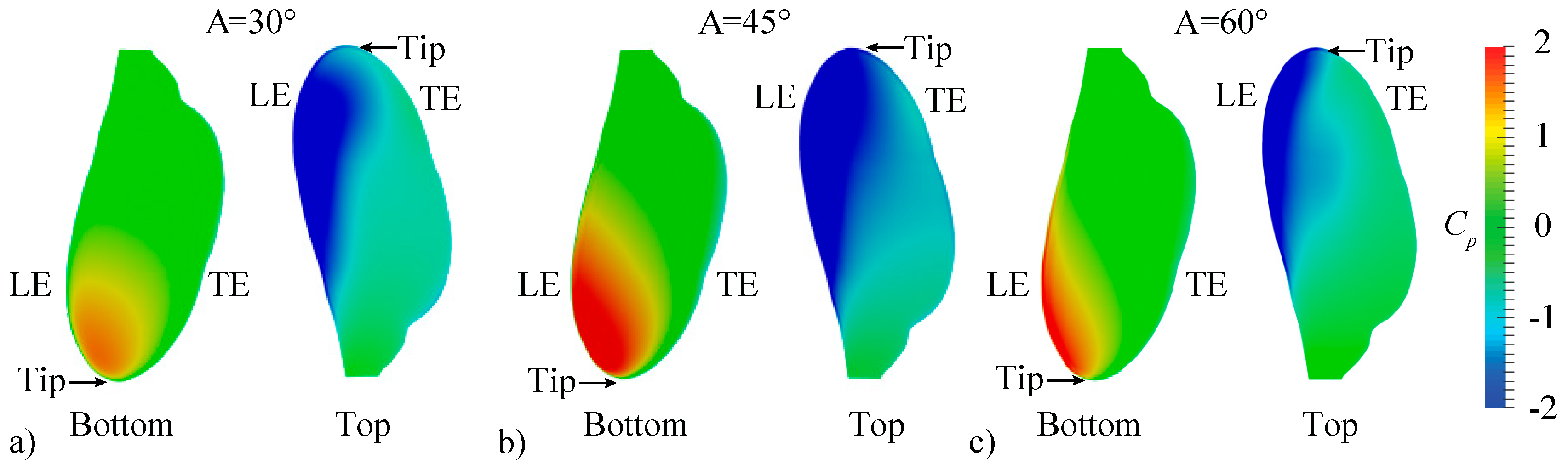
3.1.1. Pitching Amplitude Trends
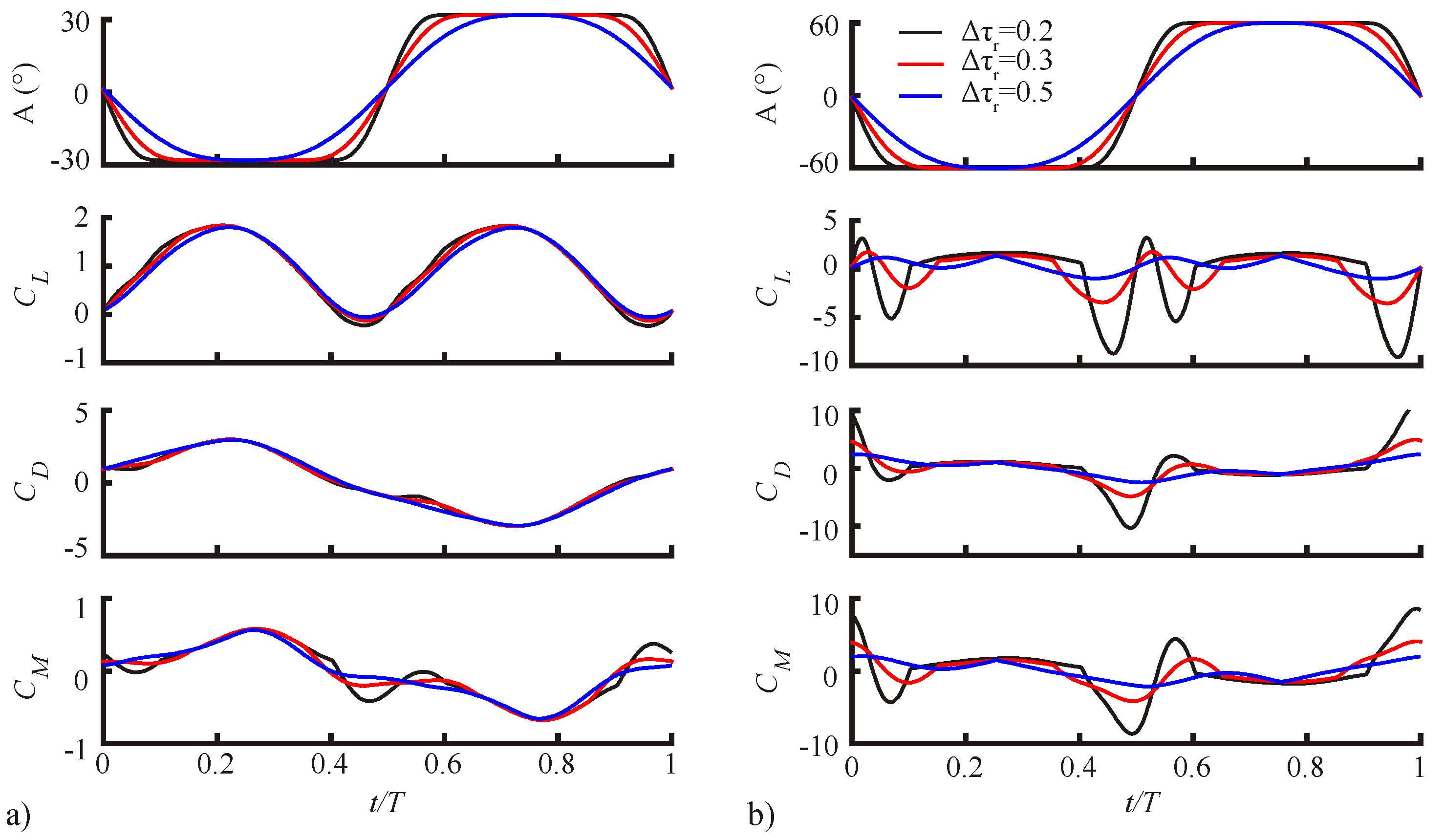
3.1.2. Pitching Duration Trends
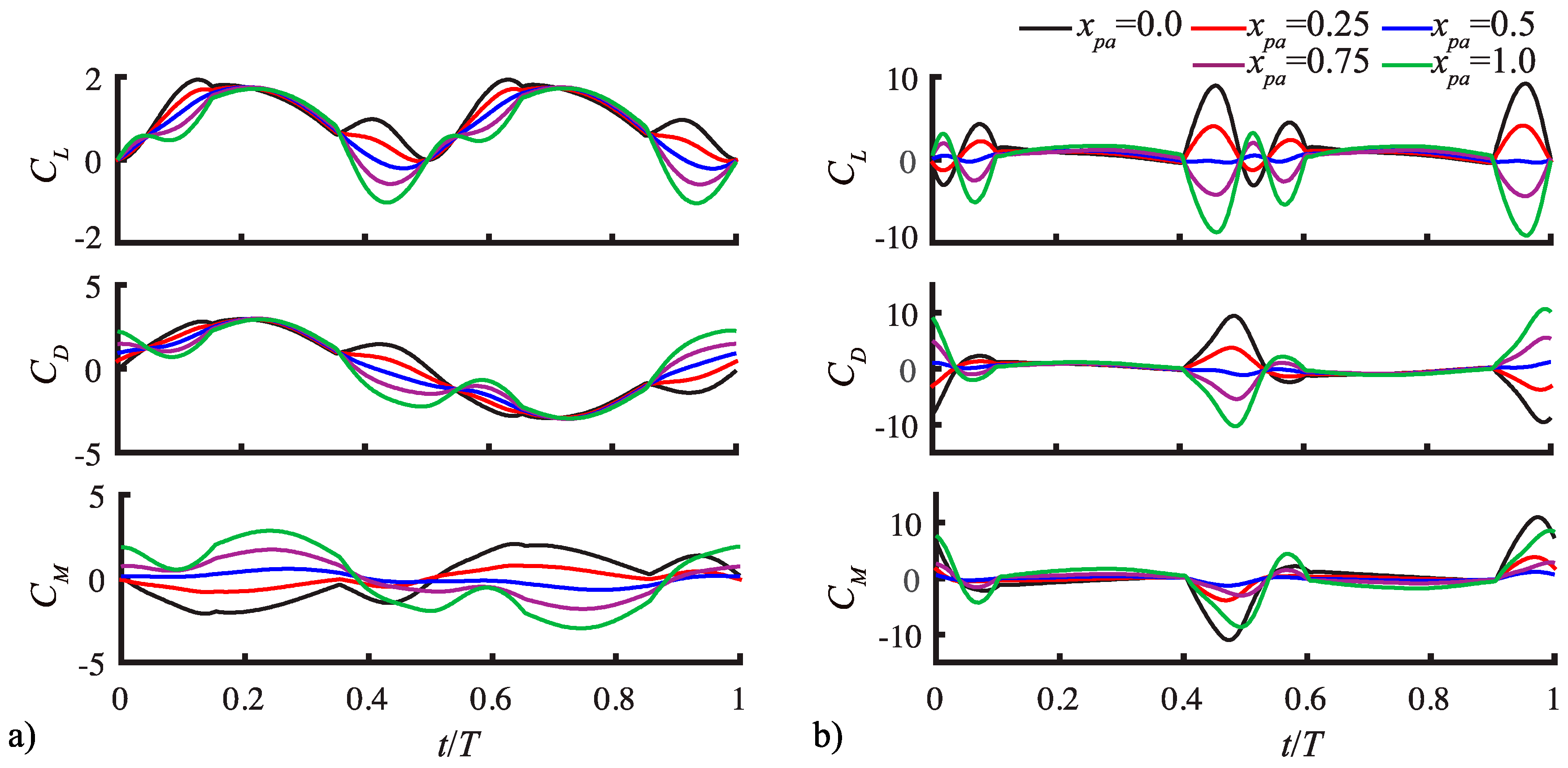
3.1.3. Pitching Axis Trends
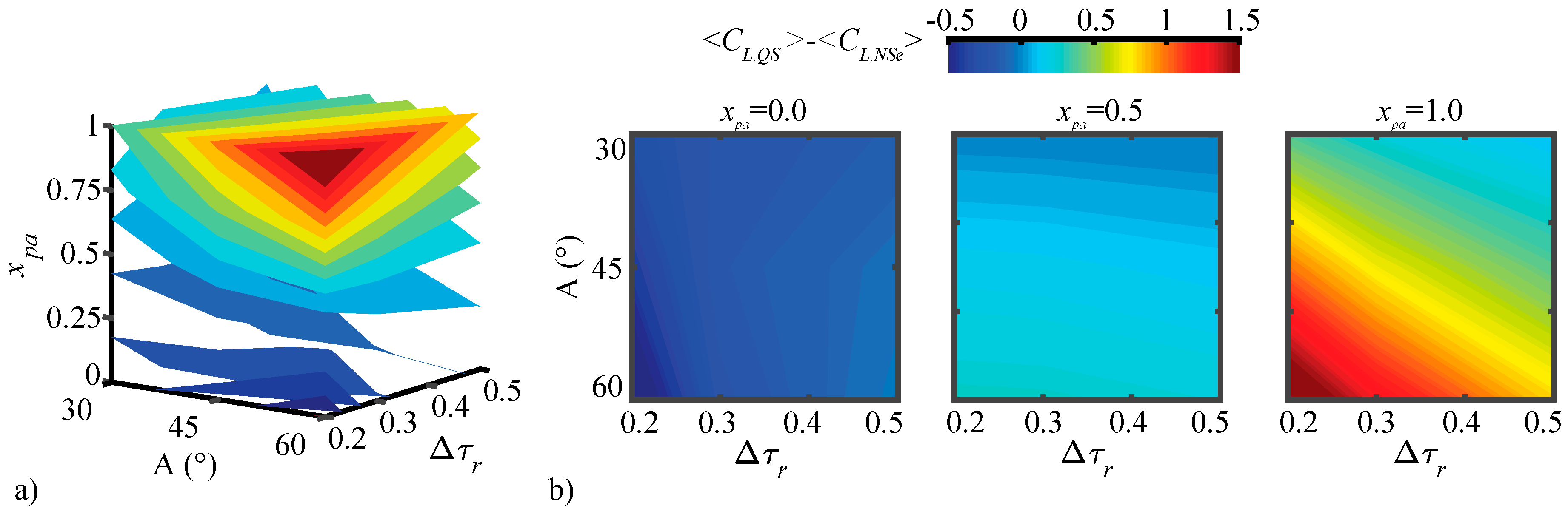
3.2. Assessment of the QS Model
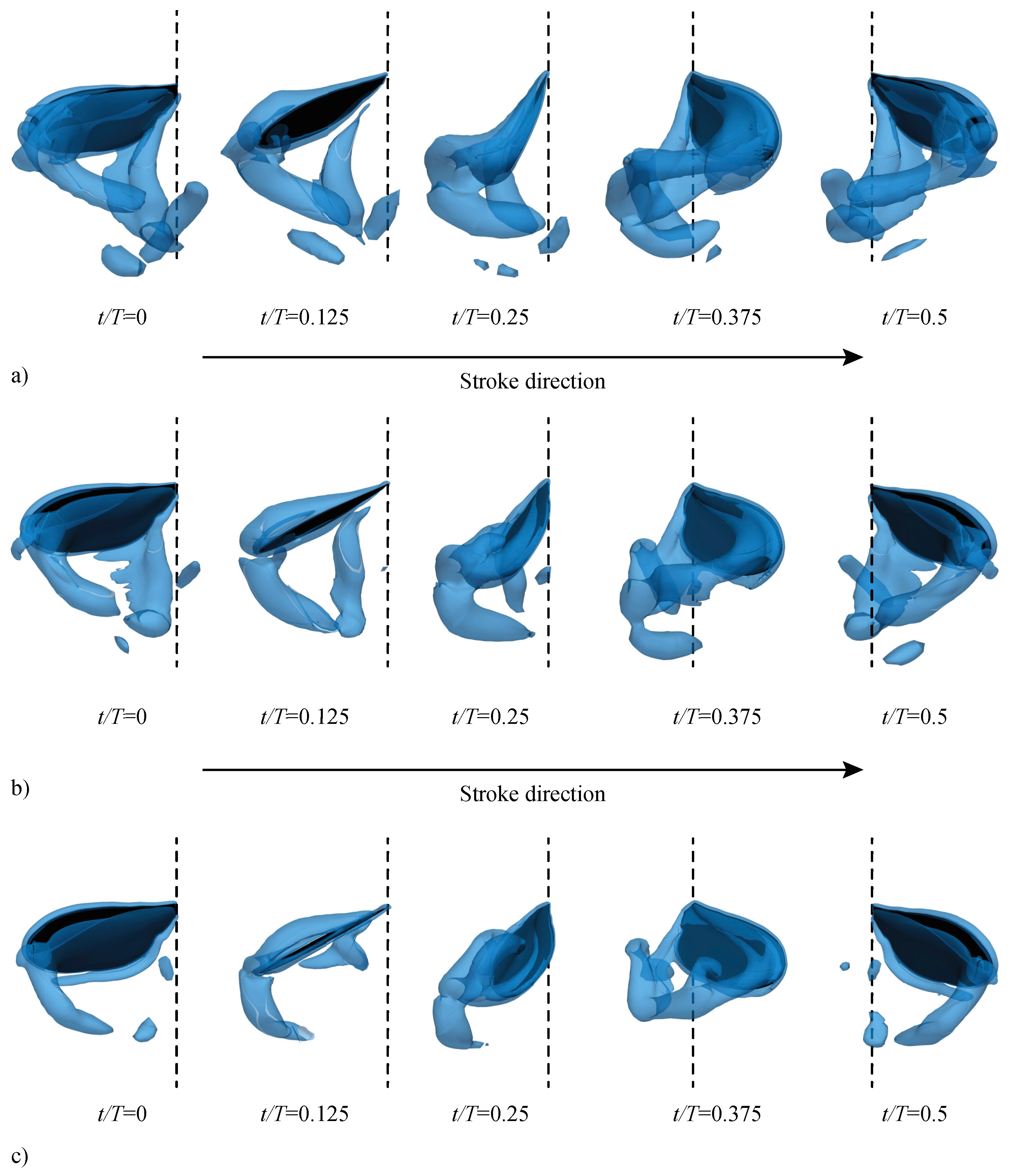
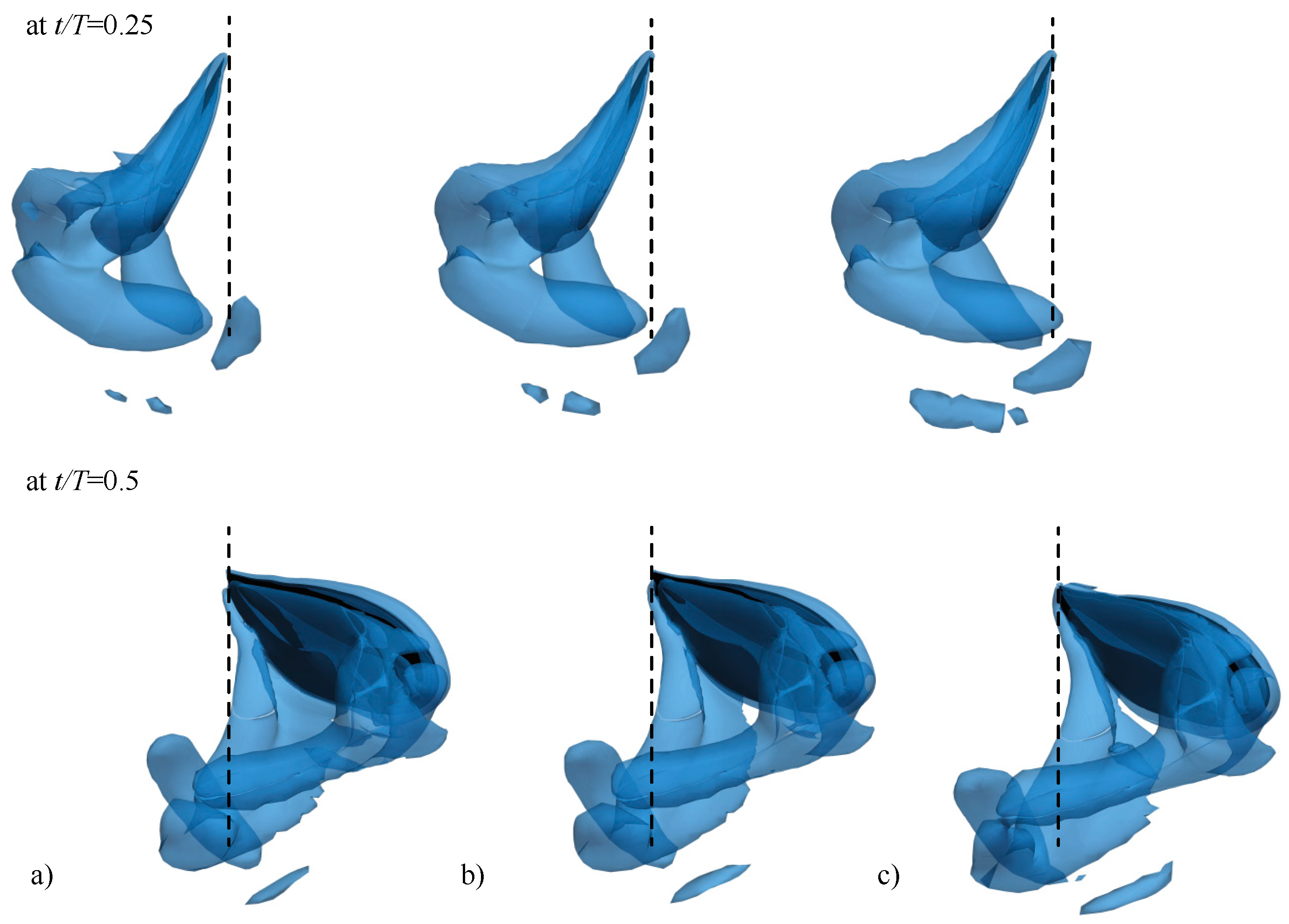
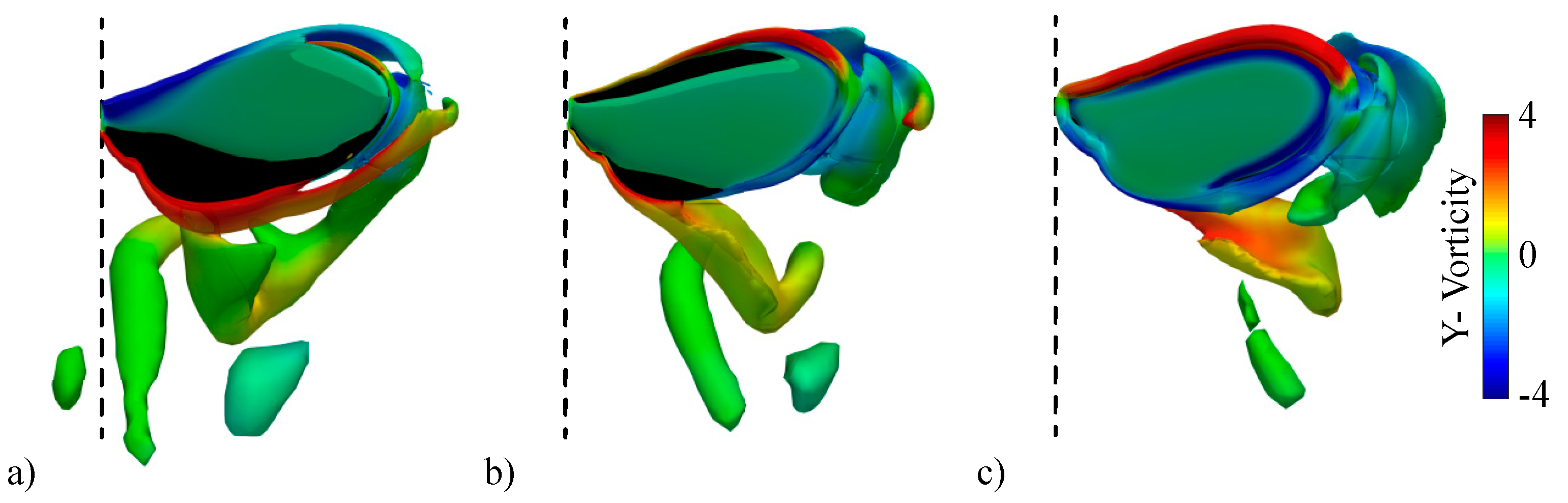
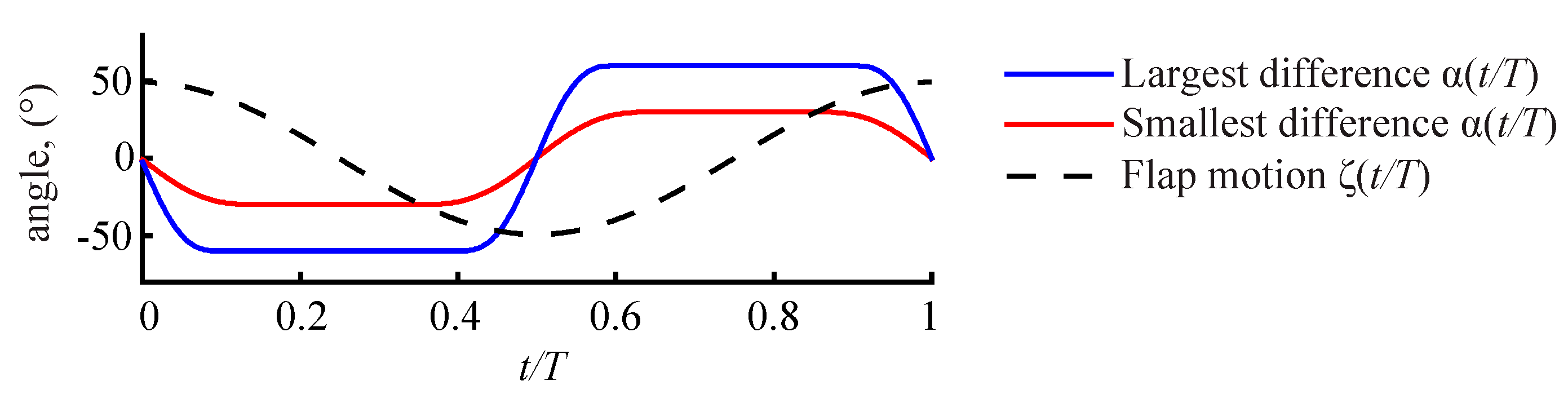
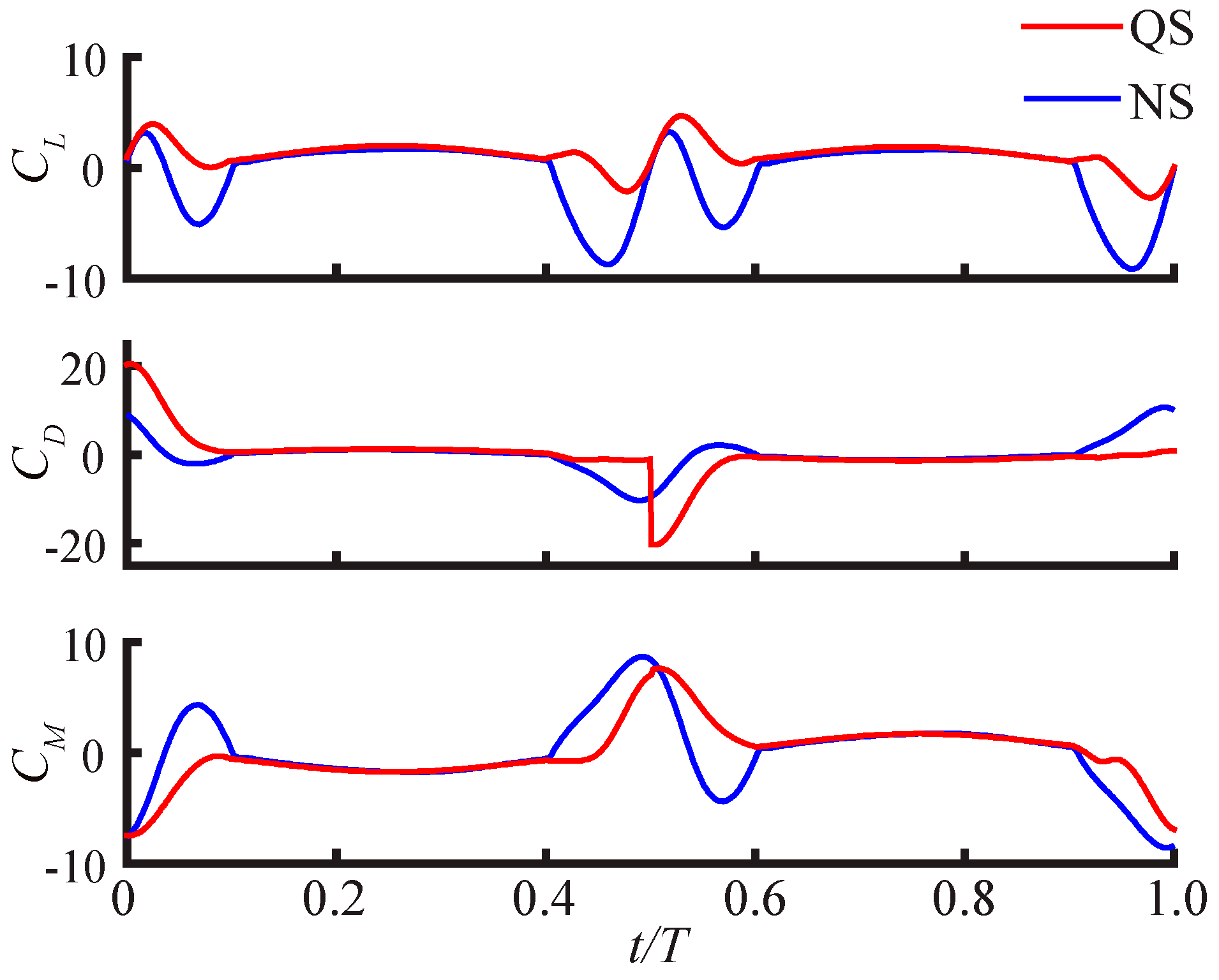
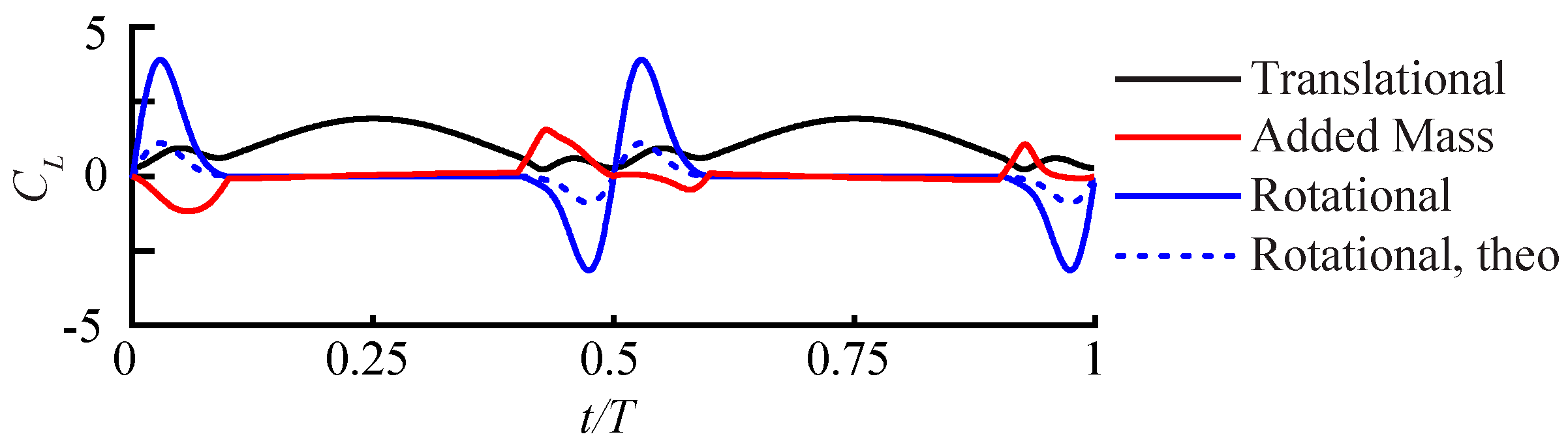
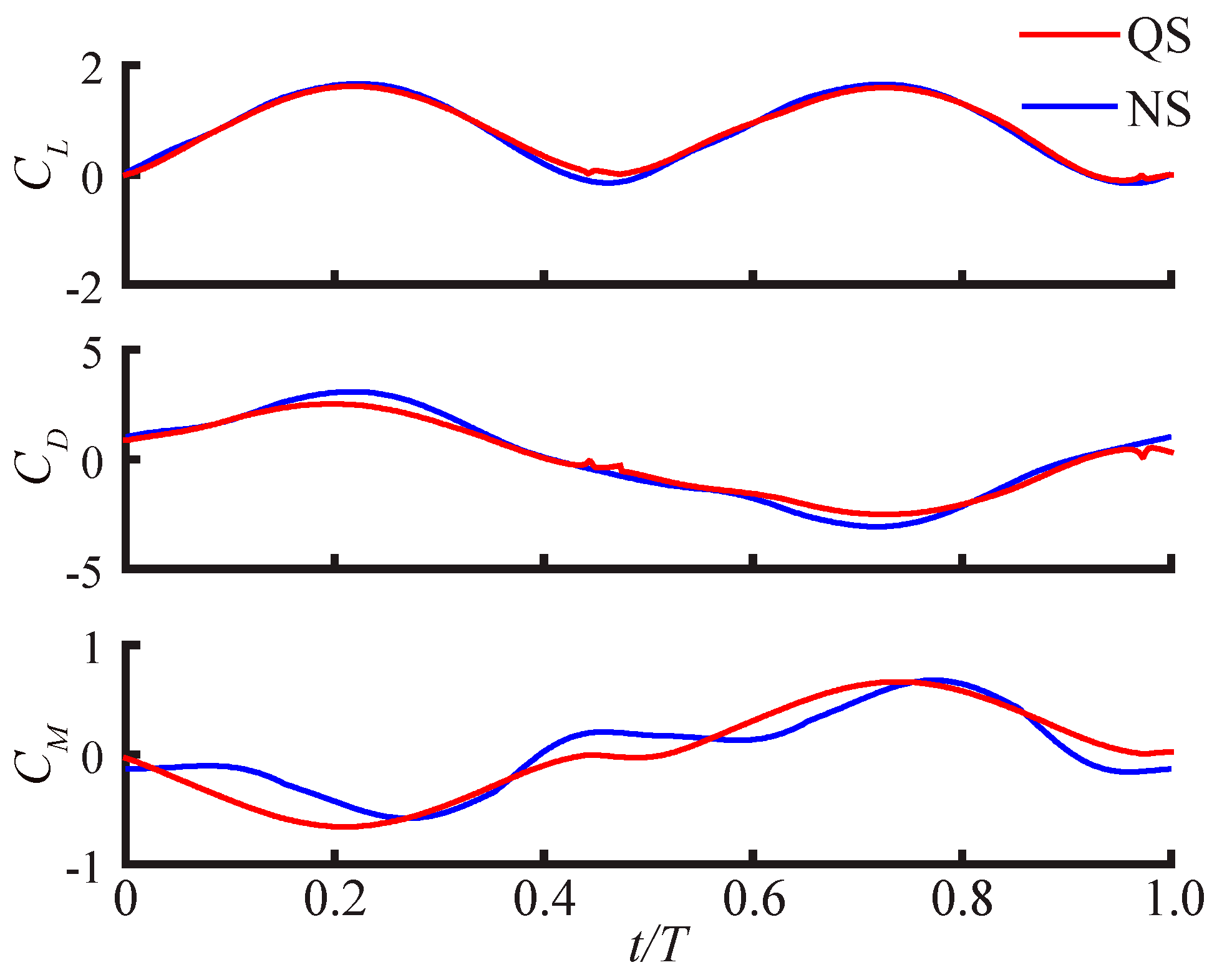
3.2.1. Largest Difference Motion: Case 39
3.2.2. Smallest Difference Motion: Case 22
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Case | α (°) | Δτr | xpa | Case | α (°) | Δτr | xpa | Case | α (°) | Δτr | xpa |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 30 | 0.2 | 0 | 16 | 30 | 0.5 | 0.25 | 31 | 30 | 0.3 | 0.75 |
| 2 | 45 | 0.2 | 0 | 17 | 45 | 0.5 | 0.25 | 32 | 45 | 0.3 | 0.75 |
| 3 | 60 | 0.2 | 0 | 18 | 60 | 0.5 | 0.25 | 33 | 60 | 0.3 | 0.75 |
| 4 | 30 | 0.3 | 0 | 19 | 30 | 0.2 | 0.5 | 34 | 30 | 0.5 | 0.75 |
| 5 | 45 | 0.3 | 0 | 20 | 45 | 0.2 | 0.5 | 35 | 45 | 0.5 | 0.75 |
| 6 | 60 | 0.3 | 0 | 21 | 60 | 0.2 | 0.5 | 36 | 60 | 0.5 | 0.75 |
| 7 | 30 | 0.5 | 0 | 22 | 30 | 0.3 | 0.5 | 37 | 30 | 0.2 | 1 |
| 8 | 45 | 0.5 | 0 | 23 | 45 | 0.3 | 0.5 | 38 | 45 | 0.2 | 1 |
| 9 | 60 | 0.5 | 0 | 24 | 60 | 0.3 | 0.5 | 39 | 60 | 0.2 | 1 |
| 10 | 30 | 0.2 | 0.25 | 25 | 30 | 0.5 | 0.5 | 40 | 30 | 0.3 | 1 |
| 11 | 45 | 0.2 | 0.25 | 26 | 45 | 0.5 | 0.5 | 41 | 45 | 0.3 | 1 |
| 12 | 60 | 0.2 | 0.25 | 27 | 60 | 0.5 | 0.5 | 42 | 60 | 0.3 | 1 |
| 13 | 30 | 0.3 | 0.25 | 28 | 30 | 0.2 | 0.75 | 43 | 30 | 0.5 | 1 |
| 14 | 45 | 0.3 | 0.25 | 29 | 45 | 0.2 | 0.75 | 44 | 45 | 0.5 | 1 |
| 15 | 60 | 0.3 | 0.25 | 30 | 60 | 0.2 | 0.75 | 45 | 60 | 0.5 | 1 |
Appendix B
References
- Salmon, J.L.; Bluman, J.E.; Kang, C.-K. Quasi-steady versus Navier-Stokes Solutions of Flapping Wing Aerodynamics. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; pp. 1–21. [Google Scholar] [CrossRef]
- Ma, K.Y.; Chirarattananon, P.; Fuller, S.B.; Wood, R.J. Controlled Flight of a Biologically Inspired, Insect-Scale Robot. Science 2013, 340, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Aono, H.; Chimakurthi, S.K.; Trizila, P.; Kang, C.; Cesnik, C.E.S.; Liu, H. Recent Progress in Flapping Wing Aerodynamics and Aeroelasticity. Prog. Aerosp. Sci. 2010, 46, 284–327. [Google Scholar] [CrossRef]
- Shyy, W.; Aono, H.; Kang, C.-K.; Liu, H. An Introduction to Flapping Wing Aerodynamics; Cambridge University Press: New York, NY, USA, 2013; ISBN 9781107037267. [Google Scholar]
- Shyy, W.; Kang, C.K.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150712. [Google Scholar] [CrossRef] [PubMed]
- Weis-fogh, T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Exp. Biol. 1973, 59, 169–230. [Google Scholar]
- Bergou, A.J.; Xu, S.; Wang, Z.J. Passive wing pitch reversal in insect flight. J. Fluid Mech. 2007, 591, 321–337. [Google Scholar] [CrossRef]
- Dickinson, M.H. Wing rotation and the aerodynamic basis of insect flight. Science. 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Weis-Fogh, T. Energetics of Flight in Hummingbirds and in Drosophila. J. Exp. Biol. 1972, 56, 79–104. [Google Scholar]
- Wang, Z.J. Dissecting Insect Flight. Annu. Rev. Fluid Mech. 2005, 37, 183–210. [Google Scholar] [CrossRef]
- Sun, M.; Xiong, Y. Dynamic flight stability of a hovering bumblebee. J. Exp. Biol. 2005, 208, 447–459. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Tang, J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J. Exp. Biol. 2002, 205, 55–70. [Google Scholar] [PubMed]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. I. The Quasi-Steady Analysis. Philos. Trans. R. Soc. B Biol. Sci. 1984, 305, 1–15. [Google Scholar] [CrossRef]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. II. Morphological Parameters. Philos. Trans. R. Soc. Lond. Ser. B-Biol. Sci. 1984, 305, 17–40. [Google Scholar] [CrossRef]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. III. Kinematics. Philos. Trans. R. Soc. B Biol. Sci. 1984, 305, 41–78. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 2005, 541, 65–90. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [PubMed]
- Berman, G.J.; Wang, Z.J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Bolender, M.A. Open-Loop Stability of Flapping Flight in Hover. In Proceedings of the AIAA Guidance Navigation Control Conference Exhibition, Toronto, ON, Canada, 2–5 August 2010; pp. 1–18. [Google Scholar] [CrossRef]
- Dickson, W.B.; Straw, A.D.; Dickinson, M.H. Integrative Model of Drosophila Flight. AIAA J. 2008, 46, 2150–2164. [Google Scholar] [CrossRef]
- Wang, Z.J.; Birch, J.M.; Dickinson, M.H. Unsteady forces and flows in low Reynolds number hovering flight: Two-dimensional computations vs robotic wing experiments. J. Exp. Biol. 2004, 207, 449–460. [Google Scholar] [CrossRef] [PubMed]
- Han, J.-S.; Chang, J.W.; Cho, H.-K. Vortices behavior depending on the aspect ratio of an insect-like flapping wing in hover. Exp. Fluids 2015, 56, 181. [Google Scholar] [CrossRef]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth Manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.A.; Agrawal, S.K. Optimal Hovering Kinematics of Flapping Wings for Micro Air Vehicles. AIAA J. 2011, 49, 257–268. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The control of flight force by a flapping wing: Lift and drag production. J. Exp. Biol. 2001, 204, 2607–2626. [Google Scholar] [PubMed]
- Lee, Y.J.; Lua, K.B.; Lim, T.T.; Yeo, K.S. A quasi-steady aerodynamic model for flapping flight with improved adaptability. Bioinspir. Biomim. 2016, 11, 036005. [Google Scholar] [CrossRef] [PubMed]
- Nakata, T.; Liu, H.; Bomphrey, R.J. A CFD-informed quasi-steady model of flapping-wing aerodynamics. J. Fluid Mech. 2015, 783, 323–343. [Google Scholar] [CrossRef] [PubMed]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Flight dynamics and control of flapping-wing MAVs: A review. Nonlinear Dyn. 2012, 70, 907–939. [Google Scholar] [CrossRef]
- Bluman, J.E.; Kang, C.-K. Wing-wake interaction destabilizes hover equilibrium of a flapping insect-scale wing. Bioinspir. Biomim. 2017, 12, 046004. [Google Scholar] [CrossRef] [PubMed]
- Lua, K.B.; Lim, T.T.; Yeo, K.S. Scaling of aerodynamic forces of three-dimensional flapping wings. AIAA J. 2014, 52, 1–7. [Google Scholar] [CrossRef]
- Bluman, J.E.; Sridhar, M.K.; Kang, C. The Influence of Wing Flexibility on the Stability of a Biomimetic Flapping Wing Micro Air Vehicle in Hover. In Proceedings of the AIAA SciTech Forum: 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Han, J.S.; Kim, J.K.; Chang, J.W.; Han, J.H. An improved quasi-steady aerodynamic model for insect wings that considers movement of the center of pressure. Bioinspir. Biomim. 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Leishman, J. Principles of Helicopter Aerodynamics, 2nd ed.; Shyy, W., Rycroft, M.J., Eds.; Cambridge University Press: Cambridge, NY, USA, 2006; ISBN 0-521-85860-7. [Google Scholar]
- Fung, Y.C. An Introduction to the Theory of Aeroelasticity; Dover Publications Inc.: Mineola, NY, USA, 2008. [Google Scholar]
- Tang, J.; Viieru, D.; Shyy, W. Effects of Reynolds number and flapping kinematics on hovering aerodynamics. AIAA J. 2008, 46, 967–976. [Google Scholar] [CrossRef]
- Shyy, W.; Lian, L.; Tang, J.; Liu, H.; Trizila, P.; Stanford, B.; Bernal, L.P.; Cesnik, C.E.S.; Friedmann, P.; Ifju, P. Computational aerodynamics of low Reynolds number plunging, pitching and flexible wings for MAV applications. Acta Mech. Sin. 2008, 24, 351–373. [Google Scholar] [CrossRef]
- Lian, Y.; Shyy, W.; Viieru, D.; Zhang, B. Membrane wing aerodynamics for micro air vehicles. Prog. Aerosp. Sci. 2003, 39, 425–465. [Google Scholar] [CrossRef]
- Kamakoti, R.; Shyy, W. Evaluation of geometric conservation law using pressure-based fluid solver and moving grid technique. Int. J. Heat Fluid Flow 2004, 14, 851–865. [Google Scholar] [CrossRef]
- Trizila, P.; Kang, C.-K.; Aono, H.; Shyy, W.; Visbal, M. Low-Reynolds-number aerodynamics of a flapping rigid flat plate. AIAA J. 2011, 49, 806–823. [Google Scholar] [CrossRef]
- Trizila, P.C. Aerodynamics of Low Reynolds Number Rigid Flapping Wing under Hover and Freestream Conditions; University of Michigan: Ann Arbor, MI, USA, 2011. [Google Scholar]
- Lentink, D.; Dickinson, M.H. Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Exp. Biol. 2009, 212, 2705–2719. [Google Scholar] [CrossRef] [PubMed]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 2005, 208, 2303–2318. [Google Scholar] [CrossRef] [PubMed]
- Aono, H.; Liang, F.; Liu, H. Near- and far-field aerodynamics in insect hovering flight: An integrated computational study. J. Exp. Biol. 2008, 211, 239–257. [Google Scholar] [CrossRef] [PubMed]
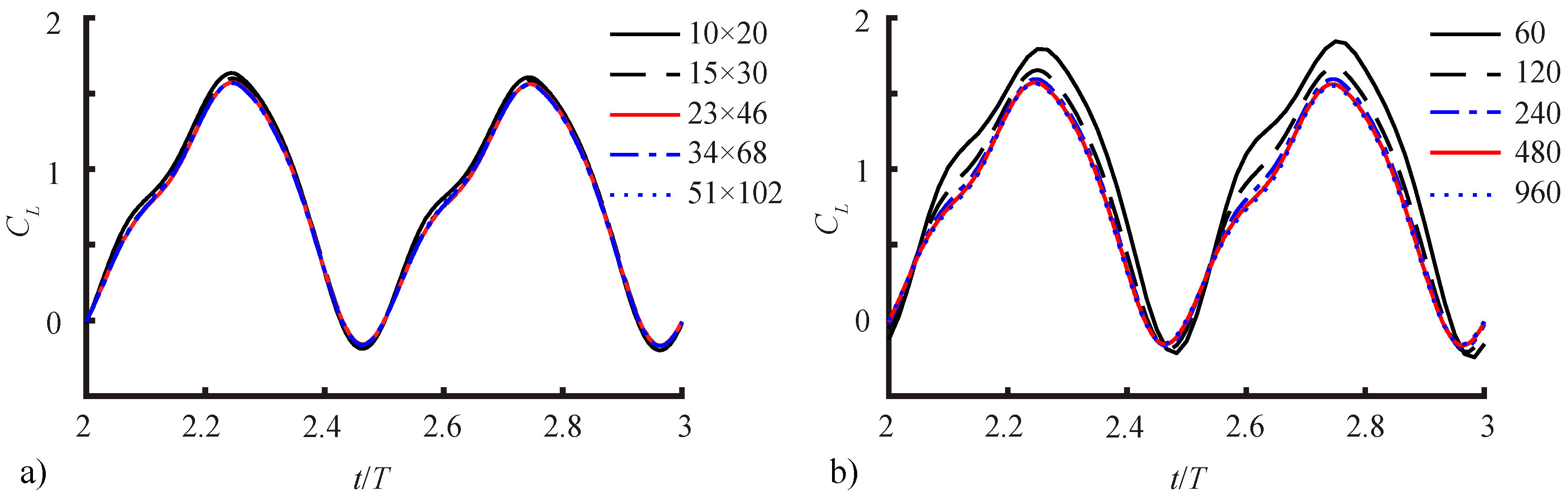
| Cells | Timesteps/Period | Total Cells | <CL> | L1-Norm | L2-Norm | |
|---|---|---|---|---|---|---|
| spatial | 10 × 20 × 40 | 480 | 46,930 | 0.7820 | 0.0518 | 0.0571 |
| 15 × 30 × 60 | 480 | 168,200 | 0.7667 | 0.0220 | 0.0257 | |
| 23 × 46 × 92 | 480 | 631,800 | 0.7543 | 0.0113 | 0.0152 | |
| 34 × 68 × 136 | 480 | 2,091,874 | 0.7543 | 0.0075 | 0.0094 | |
| 51 × 102 × 204 | 480 | 7,181,504 | 0.7574 | --- | --- | |
| temporal | 23 × 46 × 92 | 60 | 631,800 | 1.0504 | 0.1243 | 0.2990 |
| 23 × 46 × 92 | 120 | 631,800 | 0.8705 | 0.1071 | 0.1830 | |
| 23 × 46 × 92 | 240 | 631,800 | 0.7874 | 0.0848 | 0.1032 | |
| 23 × 46 × 92 | 480 | 631,800 | 0.7543 | 0.0519 | 0.0448 | |
| 23 × 46 × 92 | 960 | 631,800 | 0.7336 | --- | --- |
| A | Δτr | xpa | Pitching Motion |
|---|---|---|---|
| 30°, 45°, 60° | 0.3 | 0.5 | Mild |
| 30°, 45°, 60° | 0.2 | 1.0 | Extreme |
| 30° | 0.2, 0.3, 0.5 | 0.5 | Mild |
| 60° | 0.2, 0.3, 0.5 | 1.0 | Extreme |
| 30° | 0.3 | 0.0, 0.25, 0.5, 0.75, 1.0 | Mild |
| 60° | 0.2 | 0.0, 0.25, 0.5, 0.75, 1.0 | Extreme |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pohly, J.A.; Salmon, J.L.; Bluman, J.E.; Nedunchezian, K.; Kang, C.-k. Quasi-Steady versus Navier–Stokes Solutions of Flapping Wing Aerodynamics. Fluids 2018, 3, 81. https://doi.org/10.3390/fluids3040081
Pohly JA, Salmon JL, Bluman JE, Nedunchezian K, Kang C-k. Quasi-Steady versus Navier–Stokes Solutions of Flapping Wing Aerodynamics. Fluids. 2018; 3(4):81. https://doi.org/10.3390/fluids3040081
Chicago/Turabian StylePohly, Jeremy A., James L. Salmon, James E. Bluman, Kabilan Nedunchezian, and Chang-kwon Kang. 2018. "Quasi-Steady versus Navier–Stokes Solutions of Flapping Wing Aerodynamics" Fluids 3, no. 4: 81. https://doi.org/10.3390/fluids3040081
APA StylePohly, J. A., Salmon, J. L., Bluman, J. E., Nedunchezian, K., & Kang, C.-k. (2018). Quasi-Steady versus Navier–Stokes Solutions of Flapping Wing Aerodynamics. Fluids, 3(4), 81. https://doi.org/10.3390/fluids3040081





