Abstract
The spreading of viscous and viscoelastic fluids on flat and curved surfaces is an important problem in many industrial and biomedical processes. In this work the spreading of a linear viscoelastic fluid with changing rheological properties over flat surfaces is investigated via a macroscopic model. The computational model is based on a macroscopic mathematical description of the gravitational, capillary, viscous, and elastic forces. The dynamics of droplet spreading are determined in sessile and pendant configurations for different droplet extrusion or formation times for a hyaluronic acid solution undergoing gelation. The computational model is employed to describe the spreading of hydrogel droplets for different extrusion times, droplet volumes, and surface/droplet configurations. The effect of extrusion time is shown to be significant in the rate and extent of spreading.
Keywords:
spreading; gelation; hydrogel; hyaluronic; viscoelastic; viscous; gravitational; capillary 1. Introduction
The spreading of viscous and viscoelastic droplets over surfaces is an immensely important subject that has been studied extensively [1,2,3,4]. The detailed computational description is inherently an extremely challenging problem as it involves complex flow fields, movement and deformation of the droplet interface as well as creation of a new interface and these processes alter the boundary to the computational domain. Fluid viscoelasticity further complicates the problem and can manifest in many ways, e.g., memory, elastic forces, yield-stress effects.
To date computational techniques to solve these types of problems have been developed following a case-by-case problem-oriented approach, e.g., Reference [5]. On the other hand, commercial Computation Fluid Dynamics, CFD, products until recently have lacked efficient boundary updating for many of the large deformation problems. Currently, commercial products based on Finite Element Method, FEM, techniques with well-structured grids appear to be the most accurate in terms of surface updating during large deformations [6]. Continuing efforts to develop computational techniques for such challenging programs include many hybrid approaches, e.g., boundary element methods for the interface and FEM for the internal nonlinear viscoelastic or inertial terms [7]. These and other approaches require significant expertise and further testing before they can be adopted by the general scientific community.
At the same time there is significant amount of experimental investigations involving free-surface flows of viscous or viscoelastic fluids. Spreading of droplets over flat surfaces is a very common laboratory test to determine “spreadability” of fluids, (e.g., with lubricant oils [8] and food products [9]) as well as an industrial test (e.g., with foamed cement [10]). The droplet spreading tests can become even more difficult to interpret when considering viscoelastic fluids, curved surfaces, or time-variable fluid properties. Because of these difficulties there is a need to provide a simple means to describe spreading tests of complex fluids in order to extract more meaningful data as well as to obtain a better understanding of more complex coating processes.
In this work we develop a simple droplet spreading model for a linear viscoelastic fluid and connect it to nonlinear processes that affect the rheological properties of the fluid. The literature is currently lacking in such simple models. These models can be employed to facilitate the interpretation of simple spreading tests and potentially as a design tool for many processes involving spreading and time varying fluid properties. In the section that follows the computational model is described building on the work of Härth and Schubert [11]. Next the specific hyaluronic acid system which forms droplets examined in this work is described. In the third section the model is tested with the spreading of viscoelastic droplets with time-varying properties.
2. Droplet Spreading Model
To develop a simple macroscopic film spreading model the macroscopic model of Härth and Schubert [11] is employed which considers viscous, gravitational, and surface forces for partially or fully wetting droplets. The model is extended to include elastic forces, consider pendant drop configurations in addition to sessile drop, and is applied to a gelling system with time-varying rheological properties. It should be noted that the spherical cap approximation is realistic if the initial droplet radius is less than the capillary length, , or the Bond number, Bo, is less than one [12]:
where is the fluid density, g, is the gravitational acceleration constant, γL is the fluid surface energy, and R0 is the initial curvature at the apex which is equal to the initial spherical cap radius.
The basic geometry of a spherical-cap droplet spreading on a flat surface is shown in Figure 1.
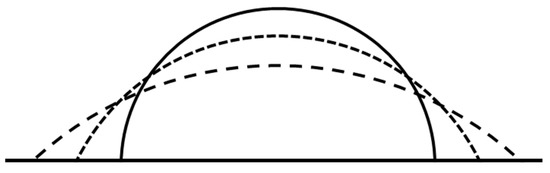
Figure 1.
Drop shapes during spreading. Initial spherical cap (solid line), transition shape (short-dashed line), steady state “pancake” shape (long-dotted line).
For a spherical cap droplet of base radius, r, and height, h, the volume, V, is given by:
and it is constant with time as long as there are no physical or chemical changes in the fluid and as long as there are no mass losses, e.g., due to evaporation.
Consequently the differential in height is given by [13]:
2.1. Forces Acting on Droplet during Spreading
The total force, F, acting in the radial direction is the sum of capillary, viscous, gravitational, and elastic terms. To determine these forces a macroscopic approach is followed assuming flat droplets, i.e., h << r, and small Bond numbers, i.e., Bo < 1. The forces are determined by considering the various contributions to the droplet energy, E, during an infinitesimal spreading step of dr and dh (Figure 2) during which the total radial force, F, is given as:
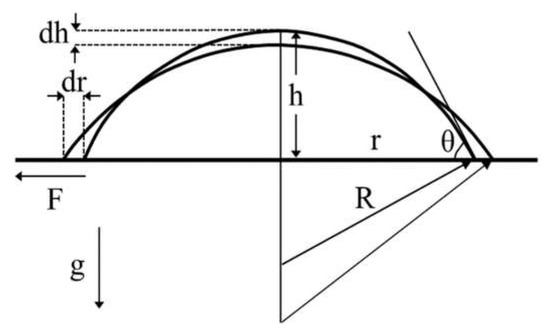
Figure 2.
Spreading of droplet over a flat surface over a time period of dt.
With these assumptions it was shown in [11] that the capillary force, FC, is given by:
where S is the spreading coefficient given by:
where γS is the surface energy of the solid and γSL is the surface/fluid interface energy.
Following Härth and Schubert, and by considering the potential energy of a spherical cap as an integral over horizontal slabs of thickness dz:
the gravitational force, FG, is determined to be [11]:
where R is the radius of the spherical cap (Figure 2) which is equal to:
The viscous force, FV, can only be approximated in a macroscopic approach because of the unknown velocity profile, e.g., adjacent to the contact line. The movement of the contact line can be very complicated and dynamic. The contact line does not always move smoothly (e.g., stick-slip motion, see [1]) and is not always well defined (e.g., the fluid over the contact line can move over a thin layer of air). When considering microscopic effects van der Waals forces [14] and line tension effects [15] can become important and nanoscale effects require different considerations [16].
The viscous force for a Newtonian fluid undergoing simple shear flow is proportional to a shear stress, τ, multiplied by a surface area, A, parallel to the direction of flow according to:
where η is the viscosity and is the shear rate. Here it is assumed that the dominating nature of flow is simple shear as a stick boundary condition can be assumed for most of the contact area of the droplet. This assumption over-estimates the shear rate only in a small region near the moving contact line which during the slip transition does not flow via simple shear. Consequently, we have:
where w is the average height of the droplet. It should be noted that in Härth and Schubert the viscous force (without the 2π term) was adapted to:
where ξ = 37.1 m−1 is considered a universal constant.
In this work the elastic contribution of a linear viscoelastic fluid of the Maxwell type:
where η is the Maxwell viscosity and the relaxation time λ is given by
where E is the elasticity of the Maxwell fluid.
In order to determine the elastic contribution from linear viscoelastic Equation (14) it is clear that there should be a first-order relaxation term and that the average elastic stress should be proportional to the average relative deformation, ε(t), and the elasticity Ε, according to:
The average relative deformation is approximated by the deviation from the initial spherical shape so that:
Following the same procedure as with the viscous force we obtain the elastic force term for a Maxwell fluid:
The net driving force, Ftot, in the radial direction for deformation and spreading of a viscoelastic droplet on a flat surface is a sum of capillary, gravitational, viscous, and elastic terms.
2.2. Spreading Model
For highly viscous or viscoelastic fluids a quasi-steady state assumption is valid in which the net acceleration is much smaller than the other processes. The rate of change in the radius, dr/dt, can then be obtained from:
Consequently, Equation (19) can be solved for to obtain:
The above equation is solved together with:
which is obtained from Equation (3) together with Equation (9) for R in order to provide the time variation of the radius of contact, r, height, h, and aspect ratio, Z = r/h. If the initial contact radius = r(0) is known for a given droplet volume V then, from Equation (2), the following cubic equation is solved for the initial height of the spherical cap, h0 = h(0):
Setting x = r/R0 and y = h/R0 and dividing by R0 we have:
where the terms in square brackets have units of 1/s.
Equation (23) is solved together with Equation (21) in the following form:
Selecting a characteristic time of we can obtain the following dimensionless forms:
and
where , , Ca is the Capillary number, , and De is the Deborah number, .
The effect of inverted droplets (i.e., pendant droplets) hanging from a flat surface can be studied by changing the sign in the gravitational term of Equations (23) and (24) or the dimensionless Equations (25) and (26).
2.3. Varying Rheological Properties
Rheological properties can change with time due to physical (e.g., compositional changes due to evaporation) and chemical (e.g., reaction) processes. These changes are reflected in rheological measurements, e.g., oscillatory rheometry, leading to time varying storage (i.e., G’) and loss (i.e., G”) moduli of the fluid.
In order to describe the deformation of a viscoelastic hydrogel droplet undergoing gelation a simple linear viscoelastic model with time varying material properties was considered. Note that the Maxwell fluid element converges to Newtonian when E → ∞ as the viscosity pot and the spring are in series. The loss and storage moduli data, at a specific frequency, ω, can be related to the Maxwell fluid coefficients according to [11]:
and
It should be noted that more complicated rheological models require additional rheological data to be properly characterized and cannot be easily decomposed into viscous and elastic component as in this simple analysis.
2.4. System Studied
The system studied consists of an enzymatically crosslinking hyaluronic acid (HA) system [17]. Specifically, Lee et al. [17] provide results for oscillatory rheometry experiments which were performed while HA-tyramine hydrogel was formed via crosslinking of tyramine moieties catalyzed by hydrogen peroxide (H2O2) and horseradish peroxidase (HRP). The oscillatory rheometry results for the loss and storage moduli (obtained with a constant deformation of 1% at 1 Hz and at a temperature of 37 °C) are summarized in Table 1. Note that for this specific system (i.e., with 728 mM of H2O2 and 0.025 units per ml of HRP) the gel point [18] where the hydrogel transitions from a viscoelastic liquid to a viscoelastic solid occurs at 48 s.

Table 1.
Loss and storage moduli (extracted from [11]).
2.5. Physical Model and Simulation Algorithms
As a test system an extrusion syringe was considered where a droplet is directed to a flat surface either facing upwards (i.e., sessile configuration) or downwards (i.e., pendant configuration). The gelling fluid is extruded onto the surface where it forms an initial half droplet. The syringe is retracted to allow the droplet to spread freely. It is assumed that the HA solution is mixed instantaneously and completely at the beginning of the syringe and gelation continues throughout the extrusion and spreading processes. Figure 3 displays a typical setup in pendant configuration.
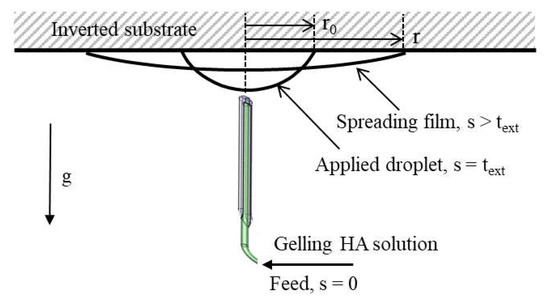
Figure 3.
Film application and spreading onto an inverted substrate. s = time from inflow to syringe = t + text. Flow rate Q ~ 1–10 cm3/min.
Early experimental studies (not reported here) indicate that a critical property for spreading and film formation is the extrusion time, text, or the time required to form the initial droplet especially for rapidly gelling systems. If the extrusion times are too large no spreading is observed of the droplet and there is no film formation. Large droplets were found to detach easily especially with low viscosity droplets, i.e., short extrusion times.
In this work a computational including the residence time of the gelling HA solution in the syringe is taken into account. The known geometric properties of the system are the droplet volume and the initial contact radius. The known physical properties are the density, surface tension, viscosity, spreading coefficient, and the rheological properties of the gelling HA solution, i.e., loss and storage moduli.
The simulation procedure is shown in Figure 4. The simulation begins with solution of the cubic Equation (22) for the droplet height. Next, the spreading equations, i.e., (25) and (26) are solved with time. At each time step the total time of gelation, s, and of spreading, t, are determined. Based on the rheology data of Lee et al. [17] the rheological parameters λ and η are calculated at the corresponding gelation time, s. Simulations proceed until the net change per time step becomes less than a limit value.
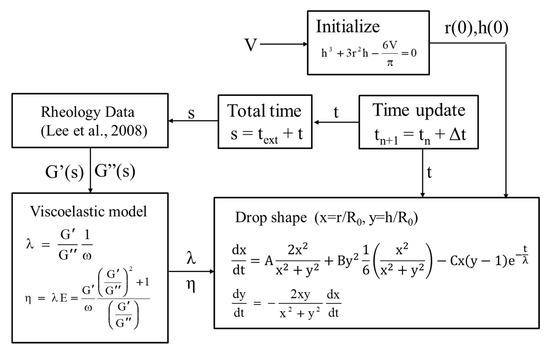
Figure 4.
Film spreading algorithm for linear viscoelastic fluids with variable properties.
In this work the Maxwell model is used as a simple representation of a linear viscoelastic fluid. This approach can be implemented with more complex linear viscolelastic models. The drop shape algorithm assumes spherical cap shapes which has been shown to agree with experimental data for broad “pancake” shaped droplets. The total time “s” is employed in the rheology model and includes the extrusion time. In this way the extrusion model is connected to the spreading model. For example, if the extrusion rate is very slow (or the extrusion time is very large) then the extruded droplets will be too viscous and elastic to adequately spread and will detach instead. It should be noted that for Newtonian fluids the computational model reduces to a model similar to that of Härth and Schubert which was validated for the spreading of sessile Newtonian fluid droplets [11].
3. Results
For the gelling hyaluronic system studied in this work a density difference of Δρ = 103 Kg/m3 and surface tensions of γ = 15 and 45 mN/m were assumed. Also, the initial contact radii and the droplet volumes ranged between 0.2–1 cm and 2–4 cm3, respectively. The fluid, i.e., gelling hyaluronic acid solution, was assumed to fully wet the surface (i.e., S = 0) and to form a droplet after an extrusion time of text, Various extrusion times from 10 to 120 s were examined. Both flat upward-facing and inverted geometries corresponding to sessile (g > 0) and pendant (g < 0) configurations for the initial droplet were considered.
The results are shown in Table 2 in terms of the final contact radius, r, height, h, droplet radius, Rc, and the spreading aspect ratio Z = r/h. For sessile and pendant droplets, the spreading process results in an exponentially decreasing contact line velocity. As expected the surface tension plays an important role. The spreading aspect ratio for case 1 (γL = 15 mN/m) was Z = 7.7 and for case 3 (i.e., γL = 4 mN/m) it was nearly four times larger at Z = 27.7.

Table 2.
Simulation Results.
The effect of droplet formation or extrusion time was also examined. From the results in Table 2 it is clear that delaying the film spreading (by increasing the application or extrusion time) changes the rheological properties of the gel to such a point that the elastic forces inhibit spreading. As the extrusion time increased from text = 10 to 60 s the spreading aspect ratio decreased from Z = 27.7 to 2.9. If the extrusion time is increased further, then the gel does not spread at all despite it wetting the surface.
Because the Bond number is small, the effect of inverted or pendant droplets can be studied by changing the sign in the gravitational term in Equation (26) which in Table 2 is denoted with negative gravity. It is clear that stable pendant droplets can be obtained below a specific mass and these display spreading but to a smaller degree than the corresponding sessile droplets of the same mass.
From Equation (25) it can be shown that the spreading pendant films are stable, i.e., spreading and not retracting, when or, in terms of the Bond number defined using the initial height of the film h0:
Note that when pendant drops are retracting they either form a stable pendant droplet or detach. Both of these outcomes are beyond the scope of the current macroscopic model which examines only stable, i.e., Bo < 1, and flat, i.e., h/r < 1, droplets.
In Figure 5 the spreading of hydrogel droplets on an inverted surface is shown. It is clear that the final aspect ratio, Z = r/h, depends strongly the initial contact radius of the droplet as well as the extrusion time due to the gelling reaction and changing rheological properties. The dashed line separates the spreading and retracting regimes in terms of the initial contact radius according to Equations (2) and (29). Note that with the current model metastable configurations are possible in the retracting regime, i.e., for r0 < 1.237 cm, where the droplet is unstable but kinetically frozen.
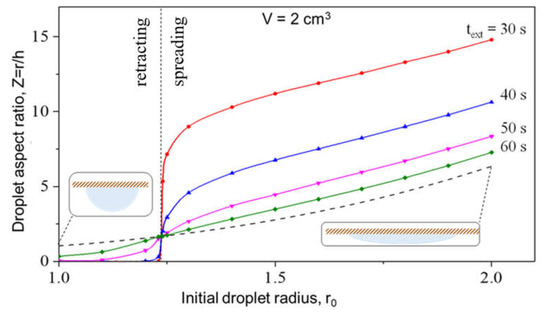
Figure 5.
Initial (dashed line) and final (full line) droplet aspect ratios, i.e., Z = r/h, for different extrusion times and initial droplet contact radii, r0. (V = 2 cm3, γ = 45 mN/m).
In Figure 6 it can be seen that for a given droplet volume (i.e., V = 2 cm3) increasing the extrusion time results in decreased droplet spreading due to increased elasticity and viscosity. This reflects the coupling of the applicator syringe and droplet spreading problem. Clearly very slow application speeds will result in inadequate spreading.
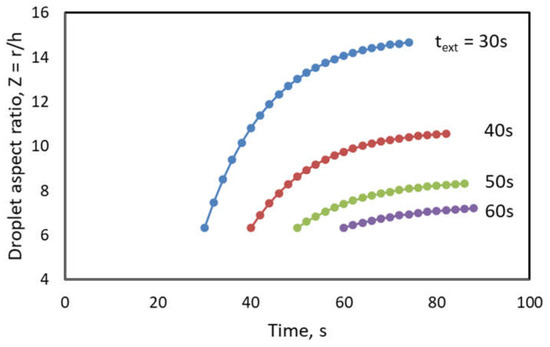
Figure 6.
Droplet shape as a function of total time, s, for different extrusion times. (V = 2 cm3, γ = 45 mN/m).
In Figure 7 the effect of elasticity on droplet spreading is shown. The elasticity was increased by ×3 and ×8 times compared to the normal case with an extrusion time of 30 s. The effect of elasticity alone is to significantly decrease the response time and the extent of spreading. This is expected to be a general effect even with other—reasonable—rheological models.
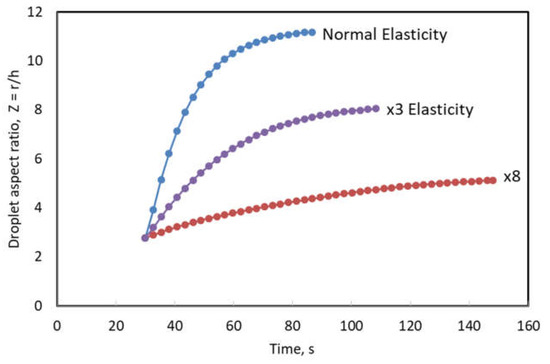
Figure 7.
Effect of elasticity on droplet spreading. text = 30 s (V = 2 cm3, γ = 45 mN/m).
4. Discussion and Conclusions
In this work the model of Härth and Schubert [11] is extended to account for linear viscoelastic effects. The model is employed to describe both sessile and pendant drop configurations in a case study with spreading of gelling hyaluronic acid solution. The effect of gelling time and elasticity are shown to be significant in terms of the extent of spreading of the gelling hyaluronic acid solution.
The computational approach described in this work can be implemented with other simple linear viscoelastic models. The approach could be extended beyond spherical caps, e.g., to ellipsoidal caps, as a more general approximation of sessile and pendant droplets. Furthermore, limitations could be placed on the moving contact angles which are determined by . More realistic descriptions of changes on the contact angle at the moving contact line necessitate some type of model of the underlying surface which can be a challenging task. For example, soft deformable surfaces can display significant deformation at the contact line [19].
Application of hydrogel or other viscoelastic fluids by spreading over biological membranes and mucous layers and other surfaces remains a very complex subject. A complicating factor is when the spreading fluid is undergoing chemical or physical changes resulting in variable rheological properties with time. This type of a dynamic system may be a desirable solution when spreading occurs while the fluid is still of relative low viscosity but, after spreading has finished, rheological changes such as increased viscosity and mucoadhesiveness help to keep the film in place.
This work demonstrates a simple model providing a connection between dynamic rheological data and droplet spreading behavior. Although many assumptions are made, the model can describe the spreading behavior over flat surfaces, including the effect of viscoelasticity. Approximate models can also help in designing and interpreting spreading experiments of complex viscoelastic fluids. Approximate models can help reduce the design space of a system involving several elements such as mixing, delivery, spreading. The potential exists to employ these types of simple models to more complex hydrogel delivery systems, e.g., via droplet sprays, other gelling mechanism, e.g., thermos-reversible, and other geometries, e.g., slightly curved surfaces. Of the many possible improvements to the model, including the interaction of the film with the substrate, beyond the simple surface energy of Equation (4), seems the most interesting and can be achieved by considering mucoadhesion models or including mechanisms for contact line motion dynamics.
Author Contributions
Conceptualization, A.A. and C.K.; Methodology, A.A.; Software, A.A.; Validation, A.A.; Formal Analysis, A.A.; Investigation, A.A. and C.K.; Resources, C.K.; Data Curation, A.A.; Writing-Original Draft Preparation, A.A.; Writing-Review & Editing, A.A.; Visualization, A.A.; Supervision, A.A. and C.K.; Project Administration, C.K.; Funding Acquisition, C.K.
Funding
The present research has been financially supported by EU under the European Framework Programme for Research and Innovation Horizon 2020 (Grant No. 721098).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Dussan, E.B. On the spreading of liquids on solid surfaces: Static and dynamic contact lines. Ann. Rev. Fluid Mech. 1979, 11, 371–400. [Google Scholar] [CrossRef]
- Uppal, A.S.; Craster, R.V.; Matar, O.K. Dynamics of spreading thixotropic droplets. J. Non-Newton. Fluid Mech. 2017, 240, 1–14. [Google Scholar] [CrossRef]
- Xu, H.; Clarke, A.; Rothstein, J.P.; Poole, R.J. Viscoelastic drops moving on hydrophilic and superhydrophobic surfaces. J. Colloid Interface Sci. 2018, 513, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Volume 1. Fluid Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Bonito, A.; Picasso, M.; Laso, M. Numerical simulation of 3D viscoelastic flows with free surfaces. J. Comput. Phys. 2006, 215, 691–716. [Google Scholar] [CrossRef]
- Hirt, C.W. Surface Tension Validation—Simple Test Problems; Flow Science Report; Flow Science: Santa Fe, NM, USA, 2016; pp. 10–16. [Google Scholar]
- Nguyen-Thien, T.; Tran-Cong, T.; Phan-Thien, N. An improved boundary element method for analysis of profile polymer extrusion. Eng. Anal. Bound. Elem. 1997, 20, 81–89. [Google Scholar] [CrossRef]
- Spengler, G.; Wunsch, F. Schmierung und Lagerung in der Feinwerktechnik; VDI: Dusseldorf, Germany, 1970. [Google Scholar]
- Lund, A.M.; Garcia, J.M.; Chambers, E. Line spread as a visual clinical tool for thickened liquids. Am. J. Speech Lang Pathol. 2013, 22, 566–571. [Google Scholar] [CrossRef]
- Hilal, A.A.; Thom, N.H.; Dawson, A.R. The Use of Additives to Enhance Properties of Pre-Formed Foamed Concrete. IACSIT Int. J. Eng. Technol. 2015, 7, 286–293. [Google Scholar] [CrossRef]
- Härth, M.; Schubert, D.W. Simple Approach for Spreading Dynamics of Polymeric Fluids. Macromol. Chem. Phys. 2012, 213, 654–665. [Google Scholar] [CrossRef]
- de Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena. Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2004. [Google Scholar]
- Butt, H.-J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; Wiley: Weinheim, Germany, 2003. [Google Scholar]
- Pérez, E.; Schäffer, E.; Steiner, U. Spreading Dynamics of Polydimethylsiloxane Drops: Crossover from Laplace to Van der Waals Spreading. J. Colloid Interface Sci. 2001, 234, 178–193. [Google Scholar] [CrossRef] [PubMed]
- Fan, H. Liquid droplet spreading with line tension effect. J. Phys. Condens. Matter 2006, 18, 4481–4488. [Google Scholar] [CrossRef]
- An, H.; Liu, G.; Craig, V.S. Wetting of nanophases: Nanobubbles, nanodroplets and micropancakes on hydrophobic surfaces. Adv. Colloid Interface Sci. 2015, 222, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Lee, F.; Chung, J.-E.; Kurisawa, M. An injectable enzymatically crosslinked hyaluronic acid-tyramine hydrogel system with independent tuning of mechanical strength and gelation rate. Soft Matter 2008, 4, 880–887. [Google Scholar] [CrossRef]
- Winter, H.H.; Chambon, F. Analysis of Linear Viscoelasticity of a Crosslinking Polymer at the Gel Point. J. Rheol. 1986, 30, 367–382. [Google Scholar] [CrossRef]
- Carre, A.; Gastel, J.-C.; Shanahan, M.E.R. Viscoelastic effects in the spreading of liquids. Nature 1996, 379, 432–434. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).