1. Introduction
To describe non-Newtonian phenomena such as stress relaxation, nonlinear creep and normal stress differences exhibited by geomaterials like asphalt or biomaterials like the vitreous in the eye, rate-type viscoelastic fluid models are commonly used. These materials exhibit more than one relaxation mechanism (see Narayan et al. [
1], Sharif-Kashani et al. [
2]) that can be identified by the different relaxation times observed in experimental studies. The presence of more than one relaxation time excludes the classical Maxwell model (originally proposed by Maxwell [
3] in one spatial dimension) or the Oldroyd-B model (see Oldroyd [
4] who developed the first general systematic three-dimensional theory to develop proper frame indifferent rate-type viscoelastic models) from one’s consideration. On the other hand, the presence of multiple relaxation times in the response of materials in creep or stress relaxation tests can be well described by rate-type fluid models of higher order. An example of a higher order model capable of describing two different relaxation times is the model due to Burgers. In the case of asphalt, Monismith and Secor [
5], Narayan et al. [
1] and Málek et al. [
6] used the model due to Burgers to corroborate experimental data, while in the case of the vitreous of the bovine eye, Sharif-Kashani et al. [
2] correlated experimental data also using a Burgers model.
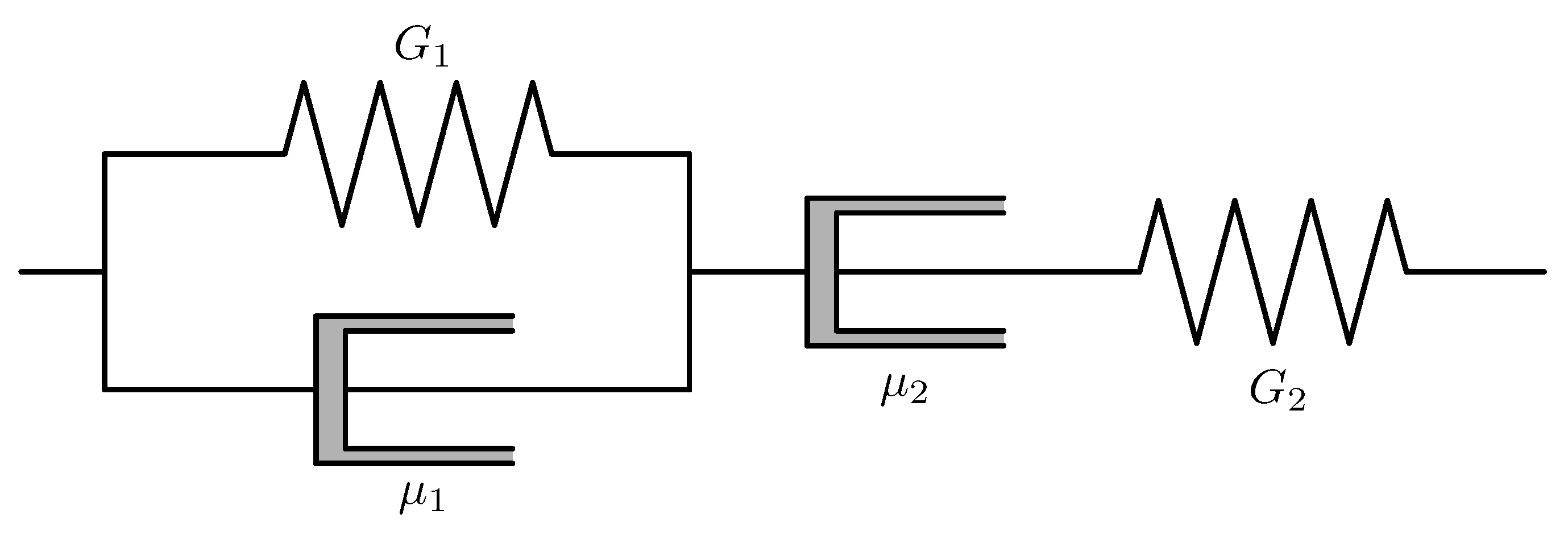
The model proposed by Burgers [
7] in one spatial dimension can be associated with as many as four different mechanical systems consisting of springs and dashpots. The Maxwell fluid model and the Kelvin–Voigt solid model are special cases of the Burgers model (see
Figure 1).
The relation between the stress
and the strain
for this one-dimensional model satisfies the second order differential equation
where the constant parameters
can be expressed in the terms of the shear moduli
,
and the viscosities
,
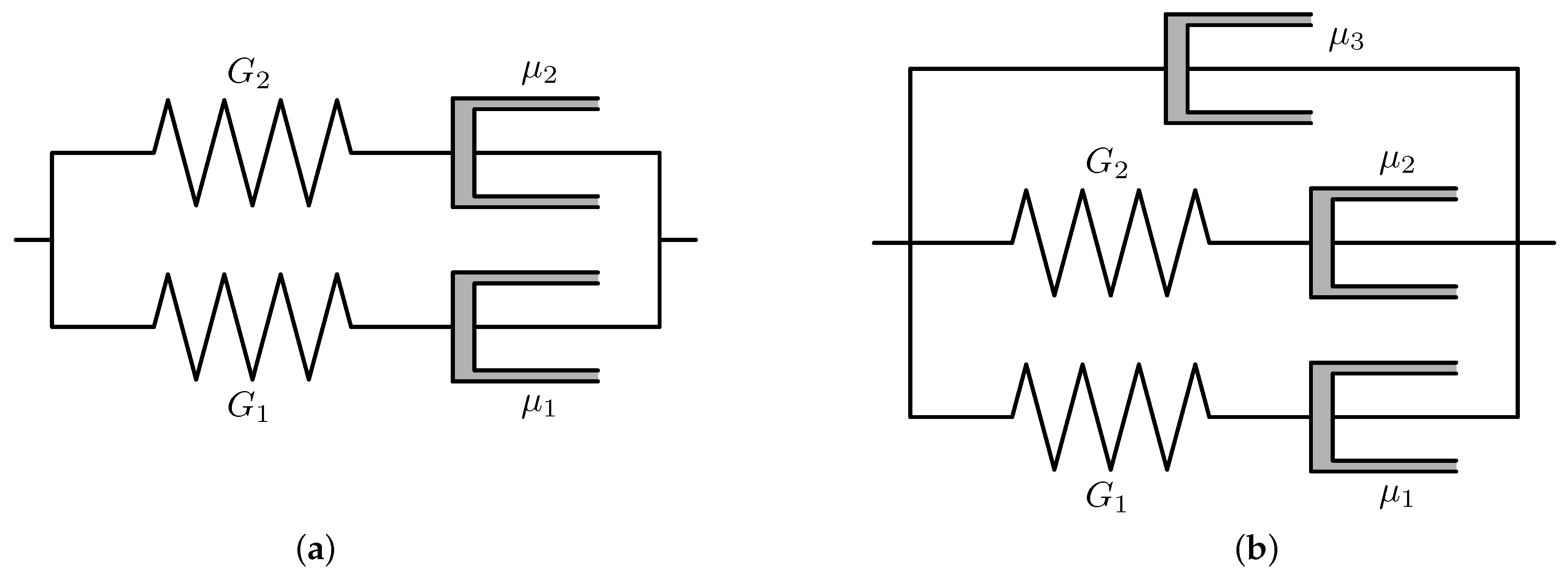
. We can also consider a system of two Maxwell elements in parallel, see
Figure 2a, that gives the same constitutive relation as in (
1).
Since many materials possess some additional viscous dissipation (connected, for example, with the properties of an aqueous plasma), it is desirable to add an additional dashpot in parallel (see
Figure 2b). A possible generalization of the setting sketched in
Figure 2b to three dimensions reads as
where
is the Cauchy stress,
is the identity tensor, and
is a scalar associated with the fact that the fluid is incompressible (Note that
p is merely the indeterminate part of the stress and the symbol gives the impression that it is the pressure, a term that is ill-understood, see [
8]. We continue to use the symbol
p as it is a conventional notation.). The symbol
denotes the upper convected Oldroyd derivative,
is the velocity and
is the symmetric part of velocity gradient (see the definitions of the kinematical quantities introduced in the next section). There are however subtle issues connected with these constitutive equations. First, a generalization from one-dimensional mechanical analog to three-dimensional model is not unique and, in principle, other objective derivatives such as the Jaumann–Zaremba or Gordon–Schowalter can be used instead of the upper convected Oldroyd derivative. Second, it is not at all obvious that generalizations of the form (
2) satisfy the second law of thermodynamics.
In order to overcome these issues, Rajagopal and Srinivasa [
9] proposed a methodology to derive thermodynamically consistent viscoelastic rate-type fluid models. Their derivation is based on the notion that as the body produces entropy the natural configuration associated with the body evolves. The existence of a natural configuration that evolves as a body deforms allows one to split the total deformation into that associated with the purely elastic response and the dissipative response. Then by prescribing two constitutive relations for two scalar quantities: the Helmholtz free energy
(or the Gibbs potential) describing the elastic response of the body and the rate of entropy production
that characterizes how the body dissipates energy, they obtained the form of the Cauchy stress tensor
including its evolution equation. Later, this approach was used to obtain a generalization of Burgers’ model (Rajagopal and Srinivasa [
10], Krishnan and Rajagopal [
11], Krishnan and Rajagopal [
12], Karra and Rajagopal [
13], Málek et al. [
14]). A new idea that is used in these studies is to connect two different relaxation times with two different underlying natural configurations. Even though the complex models that are obtained do not exactly coincide with the model (
2), it was shown that when the elastic response between the natural configuration and the current configuration is linearized, then all these models reduce to the model (
2). This may, at first glance, indicate that the classical Burgers model is an approximation rather than a proper model in its own right.
The first purpose of this study is to show that model (
2) can be obtained directly without any additional linearization or through a reduction of more complex models. In this regard, we follow a recent study Málek et al. [
15] where we show how to derive the classical Maxwell and Oldroyd-B model using the thermodynamic approach based on the notion of natural configuration. The basic step that makes the analysis possible is the following. The standard models due to Maxwell, Oldroyd and Burgers usually concern incompressible materials. It means that all admissible deformations have to be isochoric. Since the introduction of the notion of natural configuration allows one to split any process into an elastic response from an evolving natural configuration and a dissipative process describing (irreversible) changes in the natural configuration, it seems reasonable to require that, if the total process is isochoric, then its instantaneous elastic part is isochoric as well. However, Málek et al. [
6] found that, if they gave up the requirement that both the elastic and dissipative responses be isochoric and only required that the compound response be isochoric, then they were able to develop the Maxwell and Oldroyd-B model without resorting to any approximation. We refer the reader to [
15] for a detailed discussion of this issue. Following [
15], we will require, in this study, that the total deformation process is isochoric while its instantaneous elastic part and its purely dissipative part are not necessarily isochoric.
The constitutive assumptions for the Helmholtz energy
and the rate of entropy production
provide, in a straightforward way, a priori energy estimates (see for example [
16,
17]), lead to the correct and complete form of the evolution equation for temperature ([
18]) and automatically guarantee the stability of the rest state. Furthermore, the knowledge of the Lyapunov functional connected with such complex systems helps one to construct a distance measure that can be used in studying the stability of the steady states, error between two solutions (regular and weak one, discrete and continuous), etc. (see [
19,
20,
21,
22]).
The generalized Burgers models are obtained using two natural configurations, which yields a set of two first order differential equations for the parts of the Cauchy stress tensor. This immediately provides two pieces of information. First, owing to its clear physical interpretation, it is easier to provide proper initial conditions. Otherwise, for the classical second order differential Equation (
2), we would need to provide initial conditions both for the unknown and its derivative, which is a difficult task (see Průša and Rajagopal [
23]). Second, the split into two symmetric first order equations renders the numerical implementation of the Burgers model easier because, without such a split, it would be quite difficult to numerically implement the standard second order equation (see Hron et al. [
24], Málek et al. [
14], Tůma et al. [
25]).
The second purpose of this paper is to develop a new hierarchy of viscoelastic rate-type fluid models of Maxwell, Oldroyd-B and Burgers type. This is achieved by modifying the rate of entropy production corresponding to the classical Burgers model. Moreover, by restricting to only one natural configuration, we also obtain new variants of Maxwell and Oldroyd-B type models, depending on one additional scalar parameter.
The structure of the paper is as follows. In
Section 2, we introduce basic kinematical quantities distinguishing whether the kinematical setting consists of two (reference, current), three (reference, current, natural) or four (reference, current and two natural) configurations. We also describe the thermodynamic framework used in this study and document its efficacy by illustrating selected examples; these examples also motivate the form for the constitutive equations postulated in
Section 3 and
Section 4. In
Section 3, we first recall how one can derive the three-dimensional viscoelastic rate-type fluid models of the first order (Maxwell, Oldroyd-B, Giesekus) and simultaneously guarantee that these models are compatible with the second law of thermodynamics. Then, we extend this approach to a more general class of viscoelastic rate-type fluid models. The final section is devoted to a similar discussion, but within the context of viscoelastic rate-type fluid models of the second order, and the development of several variants of Burgers’ models.
3. Derivation of the Variants of Maxwell and Oldroyd-B Models
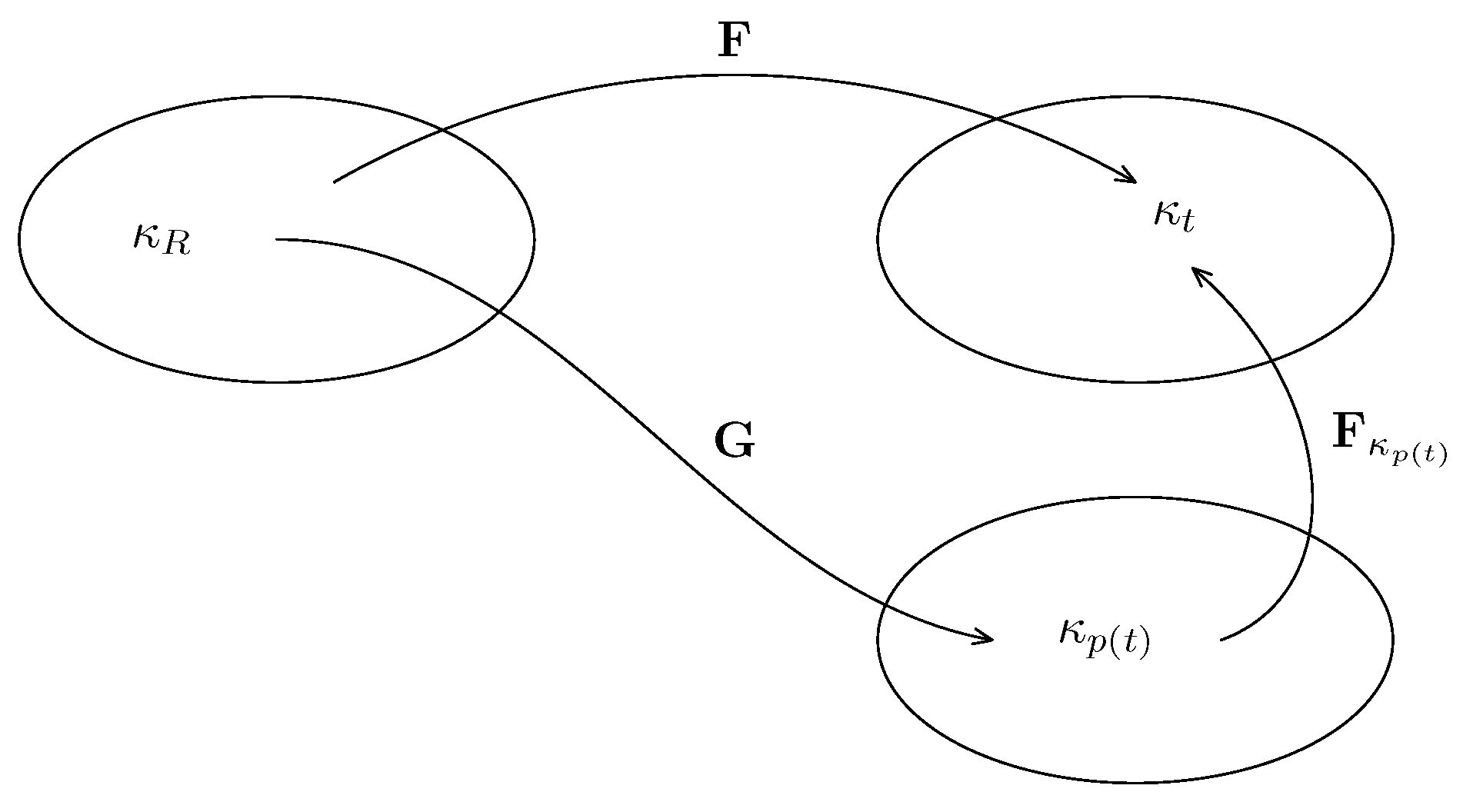
In this section, we consider a setting described by three configurations: reference, current and a natural one (see
Figure 4). We first recall the derivation developed in [
6,
9,
27] and then provide its extension. Throughout the rest of this paper, we suppose that
but
and
G do not fulfill
.
We assume that (compare with (36))
Inserting (50) into (21c), using also (
14) and (43), we obtain
This identity is the starting point for developing a plethora of models of the Maxwell type or the Oldroyd-B type. We say that the model is of Maxwell type if
and is of Oldroyd-B type if
One could decompose the dissipative term
into the product of deviatoric parts and the product of traces (which would distinguish the dissipative contributions due to volume changing processes from the isochoric processes). The reason that we do not do so here is threefold. First, getting into these details would tend to hinder the clarity of the central ideas of the development. Second, it is unnecessary for the development of the rate-type models that are carried out in this work. Finally, the interested reader can find the consequences of splitting the dissipation in such a manner in [
27] where it has been carried out systematically within the context of general compressible bodies.
In [
9], Rajagopal and Srinivasa treat the case
(which is relaxed here and consequently (51) differs from the equation for
obtained in [
9]), considering two types of dissipation connected with
. First, the choice
leads to
Second, the choice
leads to
The relation (54) and similarly the relation (56) are the identities that lead to rate-type equation for the stress as shown next.
Multiplying (56) from the left by
and from the right by
, and recalling
, we obtain
Recalling (52), (53) and setting
, we conclude that
where we have also used the fact that
.
The model (60) with
is the Oldroyd-B model [
4], while (60) with
is the Maxwell model.
On the other hand, multiplying (54) from the left by
and from the right by
and using (
14), we arrive at
Setting again
we end up with
which is the fluid model due to Giesekus [
30].
Both of the above models can be shown to be special cases of a more general model. In order to show this, we set (instead of (54) and (56))
This leads to
where
comes from the polar decomposition of
, i.e.,
.
Clearly, if , then we get the case leading to the Giesekus model, while, if , then we get the Maxwell/Oldroyd-B model depending on whether is zero/positive.
Now, multiplying (63) from the left by
and from the right by
, we finally get
which as discussed above generalizes the three-dimensional models developed by Maxwell, Oldroyd-B, Giesekus and includes them as special cases.
4. Burgers Model
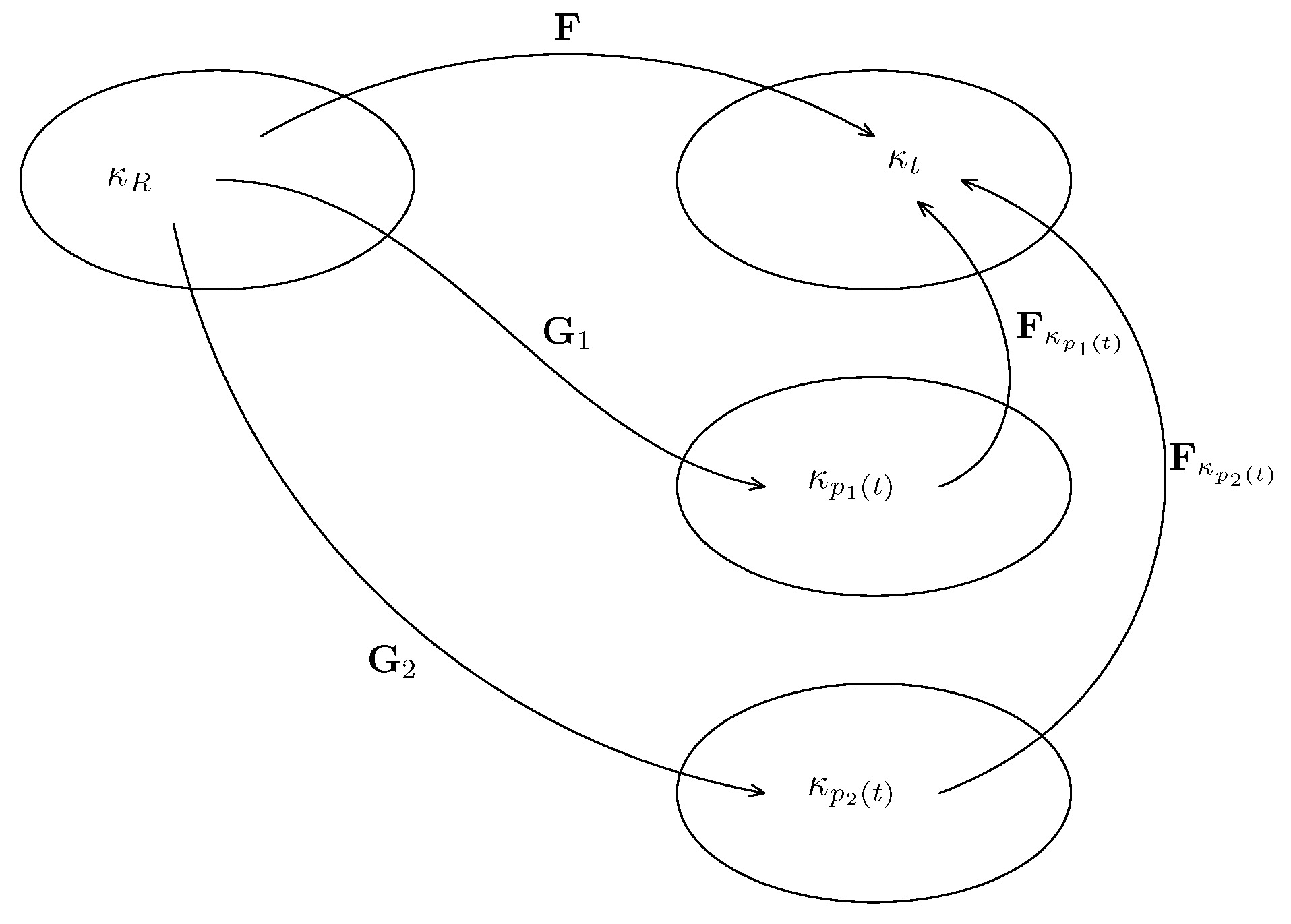
Finally, we consider a setting wherein there are two evolving natural configurations associated with the body (see
Figure 4 and kinematics summarized in (
15)–(
19)). Again, we assume that (49) holds and, motivated by the discussion in the preceding section, we assume that
Inserting (66) into (21c), using (
18), (
19) and (49), we obtain
Next, as in
Section 3, we postulate that
which upon inserting these relations into (67), yields
Using the fact that
, where
is the right stretch tensor obtained from the polar decomposition of
, i.e.,
, we conclude from (49) and (71) that
thus,
.
The constitutive equations for a class of Burgers models are obtained from (68)–(70) in the following way. We multiply (69) from the left by
and from the right by
and we also multiply (70) from the left by
and from the right by
. Referring to (
18), we observe that Equations (68)–(70) lead to
By choosing
, one gets
Next, following [
6], we show that the model (74) is equivalent to the Burgers model (
2). Indeed, first, we define
and
and
. Using (74b) and (74c), we have
Applying the upper convected Oldroyd derivative to (75) and using (74b) and (74c) again, we obtain
Multiplying the Equation (75) by
, and adding the result to (76), we obtain
which coincides with (
2).
It is also worth mentioning how the Equation (73) looks for
:
When
and
, we obtain a model where one response corresponds to the Giesekus model and the other to the Maxwell model (note that the natural configurations are interchangable):
Finally, we show that the Equations (68)–(70), which represent the initial forms for the final structure of constitutive equations, can be obtained using the knowledge of how the material dissipates the energy and referring to the assumption that the material response is such that it maximizes the rate of entropy production.
Following the methodology outlined in
Section 2.2, we first specify how the material dissipates the energy. Referring to (71), we set
to be the function appearing on right-hand side of (71). Note that
is in virtue of (72) non-negative, and is quadratic in
,
,
, and includes
and
as parameters. In the rest of this section, we simplify the notation by omitting the subscripts, i.e.,
In accordance with the scheme described in
Section 2.2, we determine the constitutive equation by the maximization
over the set of
fulfilling
where
is given in (67). This constrained maximization is performed by employing the Lagrange multiplier method. We set
where
ℓ is the Lagrange multiplier corresponding to the constraint (81). The necessary conditions for the extrema are
which results in
Upon taking the scalar product of (84a) with
and (84a) with
and (84c) with
and adding these results together, we obtain
Then, it follows from (84a) (compare with (68)) that
Now, similar to the arguments advanced in [
9], we show that
and
commute. Let
have an eigenvector
corresponding to an eigenvalue
. Then,
has the same eigenvector
corresponding to the eigenvalue
. After substituting for
ℓ, we apply both sides of 84b on
and obtain
Since
is positive definite,
is positive and
is invertible with the same eigenvector
. Thus,
which means that
is also an eigenvector of
. Thus, the tensors
and
commute and we obtain relations given in (69) and (70), which we wished to show.
5. Conclusions
The models developed by Maxwell, Oldroyd and Burgers to describe the viscoelastic response of fluids are comprised of elastic and viscous responses. Recently, Rajagopal and Srinivasa [
9] developed a thermodynamic framework wherein they assumed two scalar functions, the stored energy and the rate of entropy production, and assuming further that the rate of entropy production has to be maximized as the body undergoes deformation, they developed nonlinear models for viscoelastic fluids that are generalizations of the models due to Maxwell, Oldroyd and Burgers. When attention is restricted to incompressible viscoelastic fluids, the models developed by Rajagopal and Srinivasa [
9], when the elastic response was linearized, in the sense that the displacement gradients are small so that the square of the norm of the displacement gradients can be ignored in comparison to the norm of the displacement gradient, leads exactly to the models developed by Maxwell, Oldroyd and Burgers. This might suggest that the models due to Maxwell, Oldroyd and Burgers allow only small elastic responses. In this paper, we show that this is not the case, provided we allow both the elastic and viscous responses to be non-isochoric while the combined response meets the condition of isochoricity. Such an assumption implies that an instantaneous elastic isochoric response as well as an instantaneous viscous response are not possible as we assume that the elastic response as well as the viscous response are not isochoric to begin with. The notion that a process can be instantaneous is an oxymoron as the word process implies something that takes time (the Oxford English Dictionary [
31] defines process as “to go on” implying clearly something that takes time). Thus, one cannot expect any process to be instantaneous; however, we resort to the use of such processes in view of certain mathematical considerations (e.g., within the context of linear theories, this allows us to study the response to Heaviside functions using Laplace transforms). In this paper, we have shown that, in all other processes, the assumptions that are used lead to the models developed by Maxwell, Oldroyd and Burgers without having to resort to any approximation of the elastic response, that is, they are exactly the models developed by Maxwell, Oldroyd and Burgers.
We also introduced new generalizations (one-parameter families) of models of the Maxwell, Oldroyd and Burgers type that are compatible with the second law of thermodynamics.