Numerical Study of Noise Barriers’ Side Edge Effects on Pollutant Dispersion near Roadside under Various Thermal Stability Conditions
Abstract
1. Introduction
2. Materials and Methods
3. Results
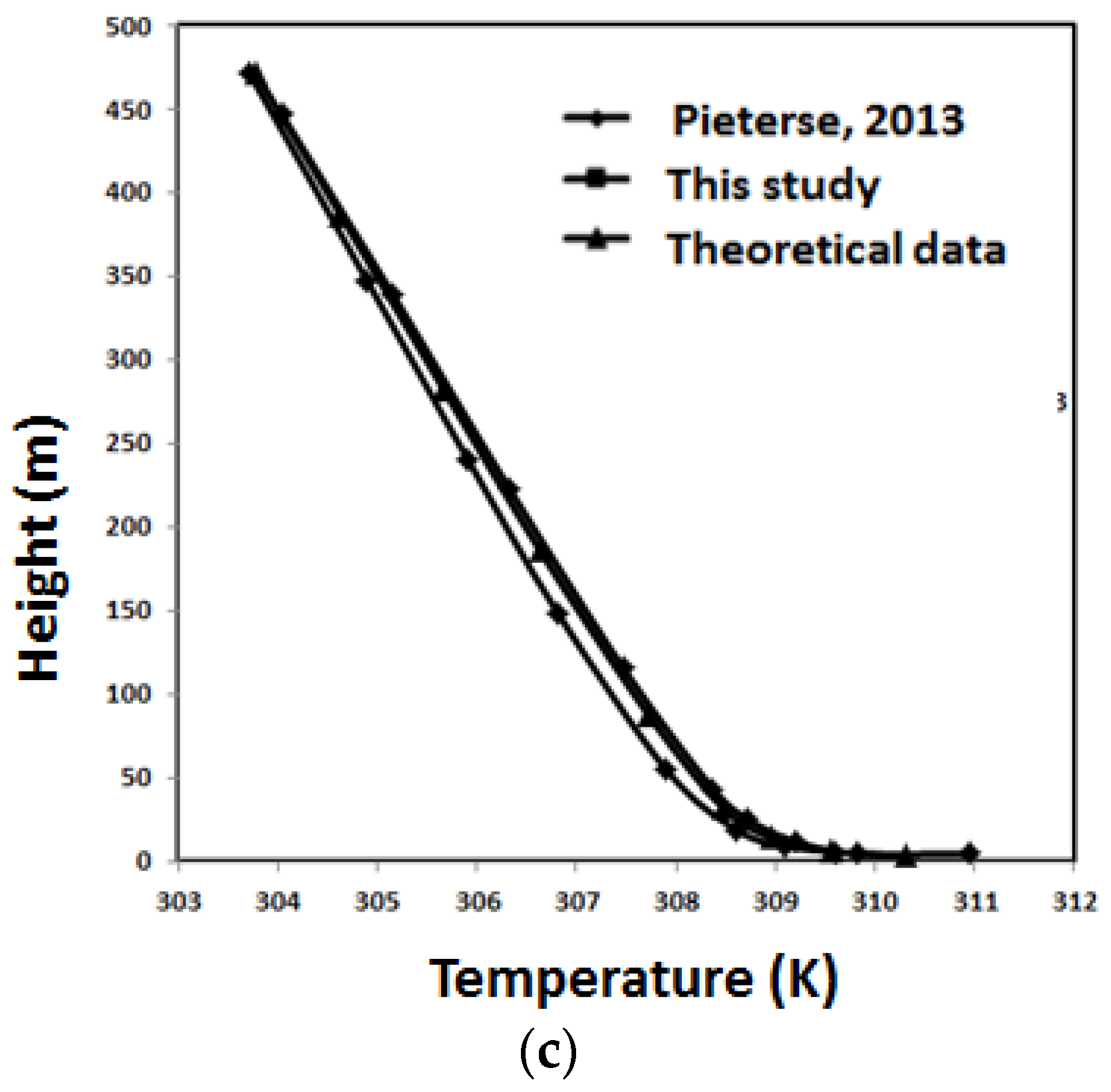
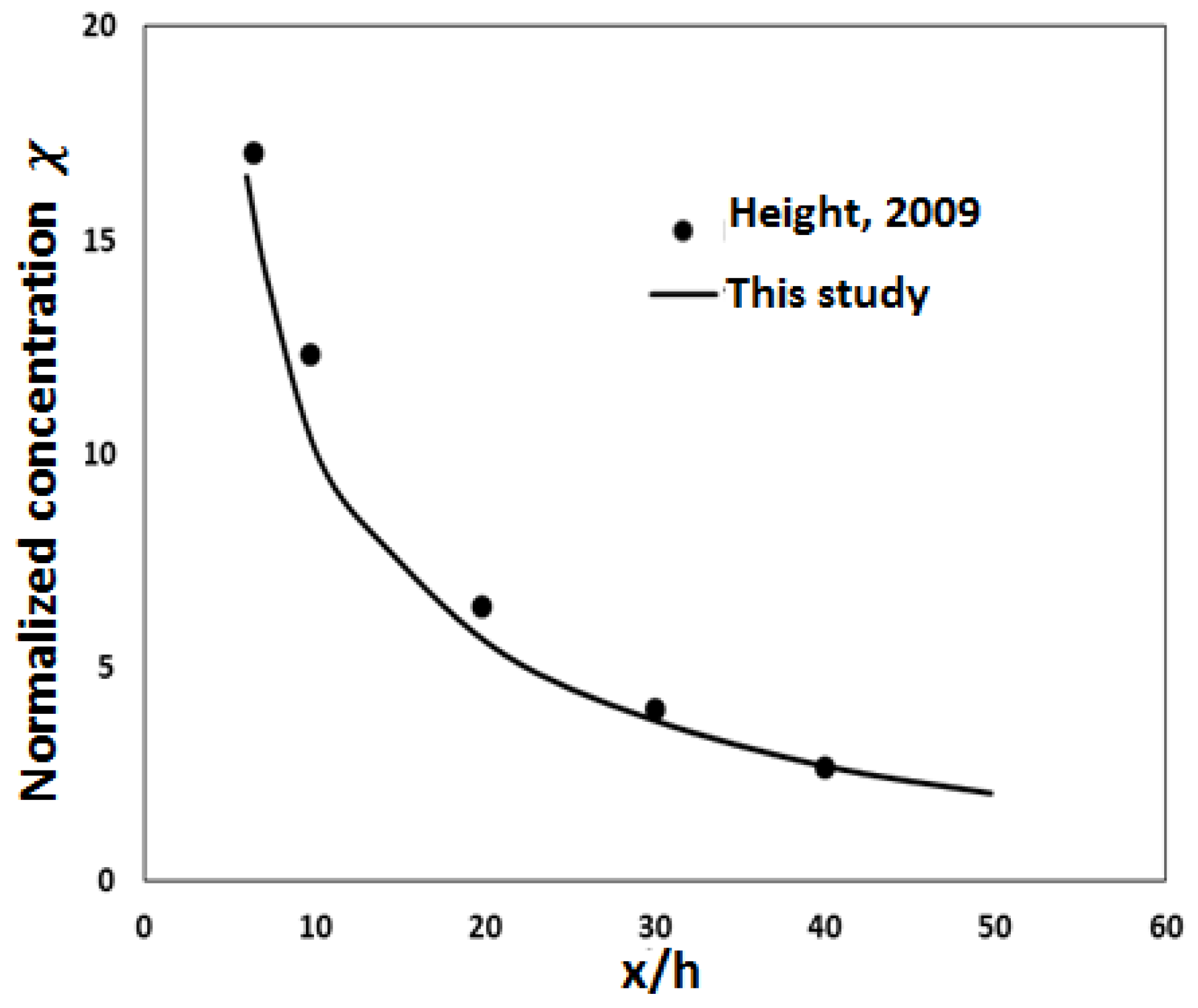
3.1. Model Validation
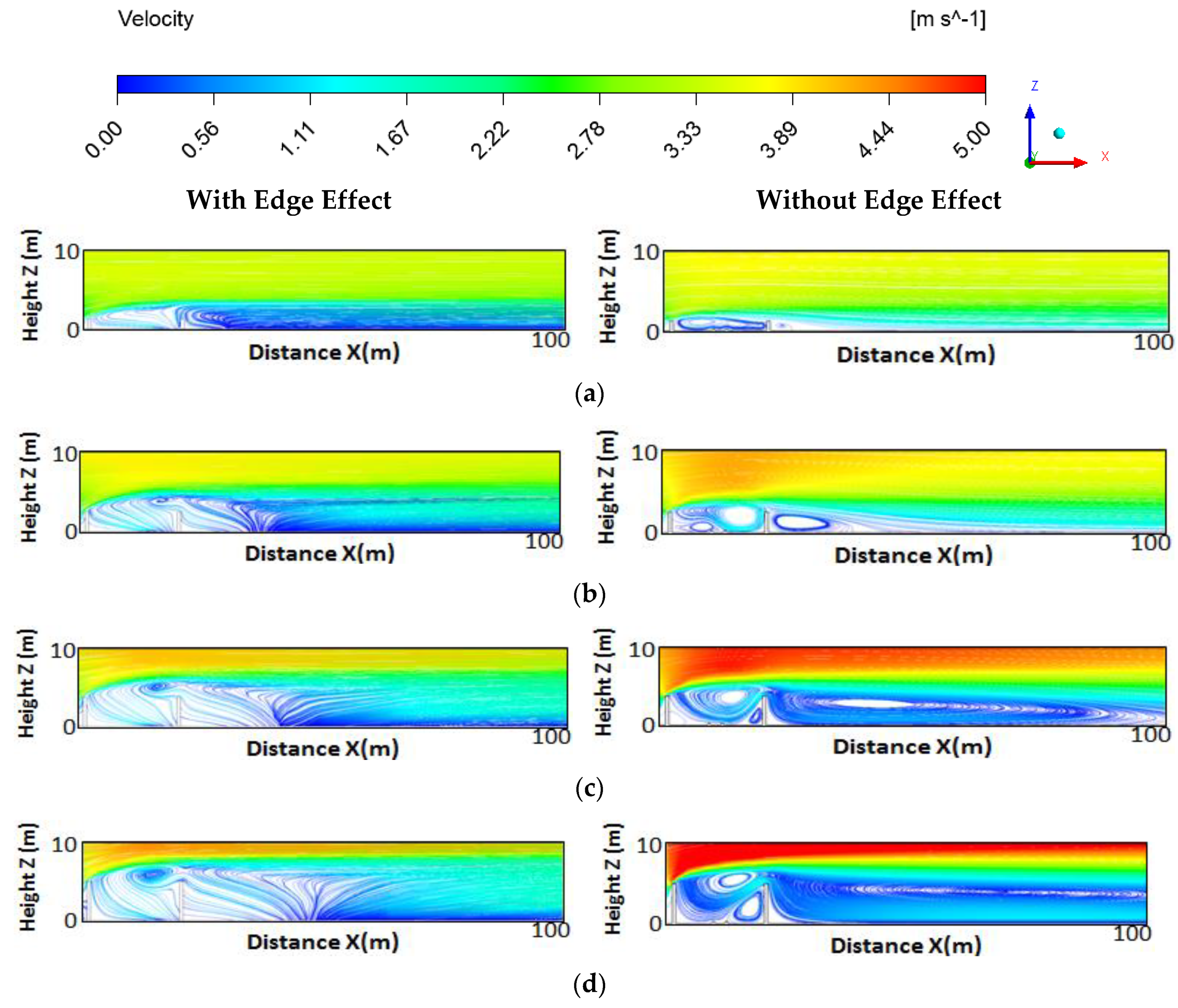
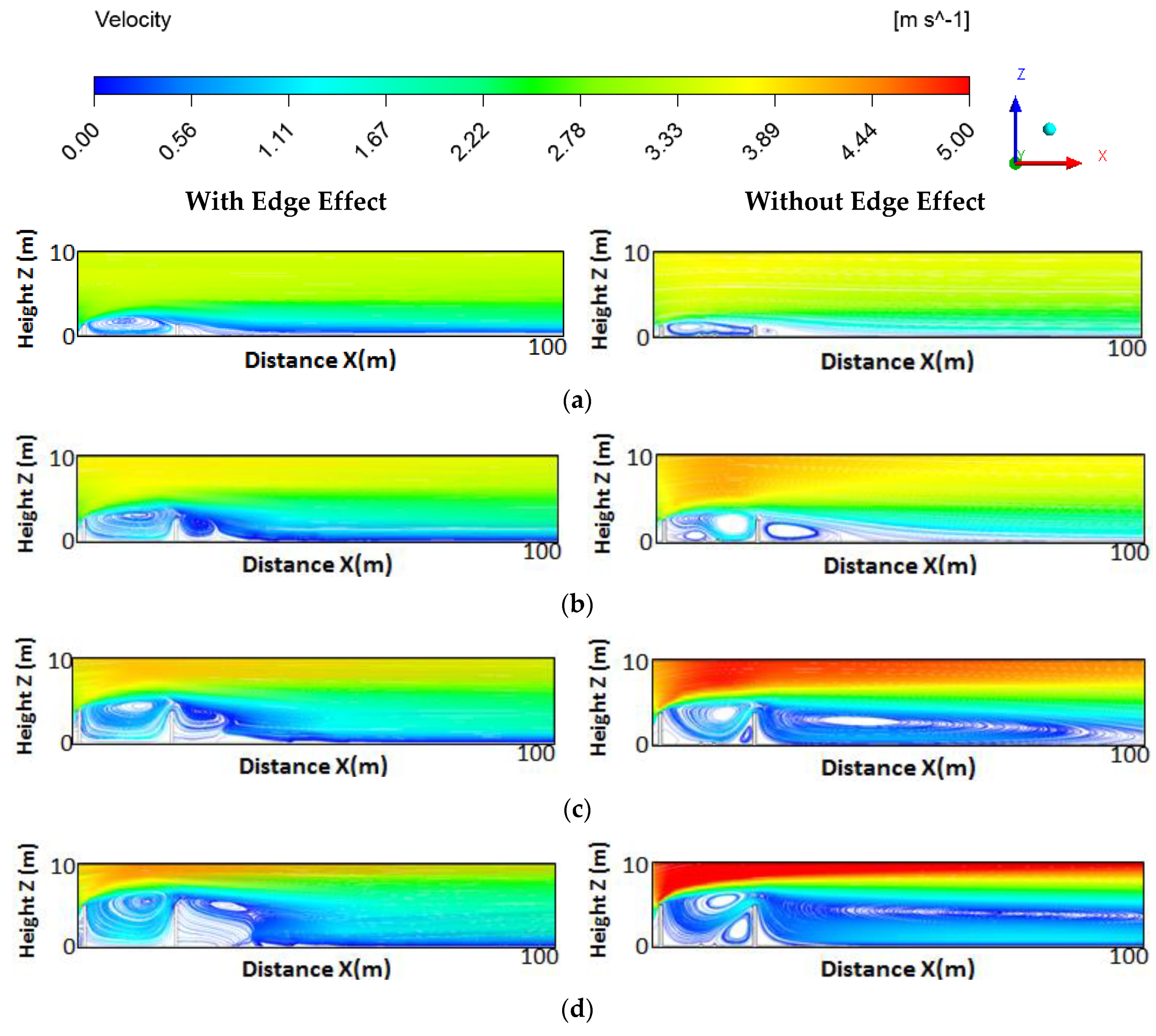
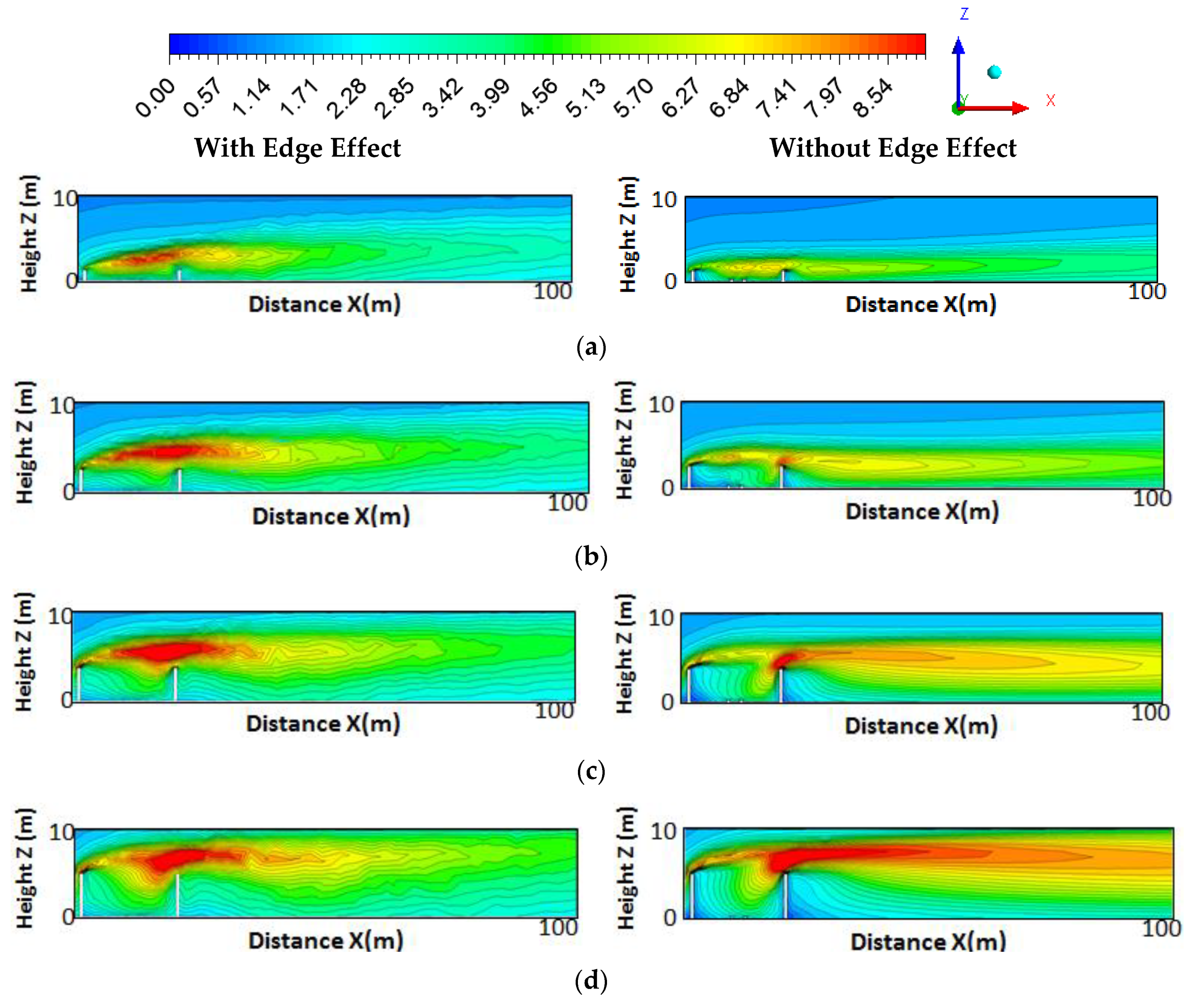
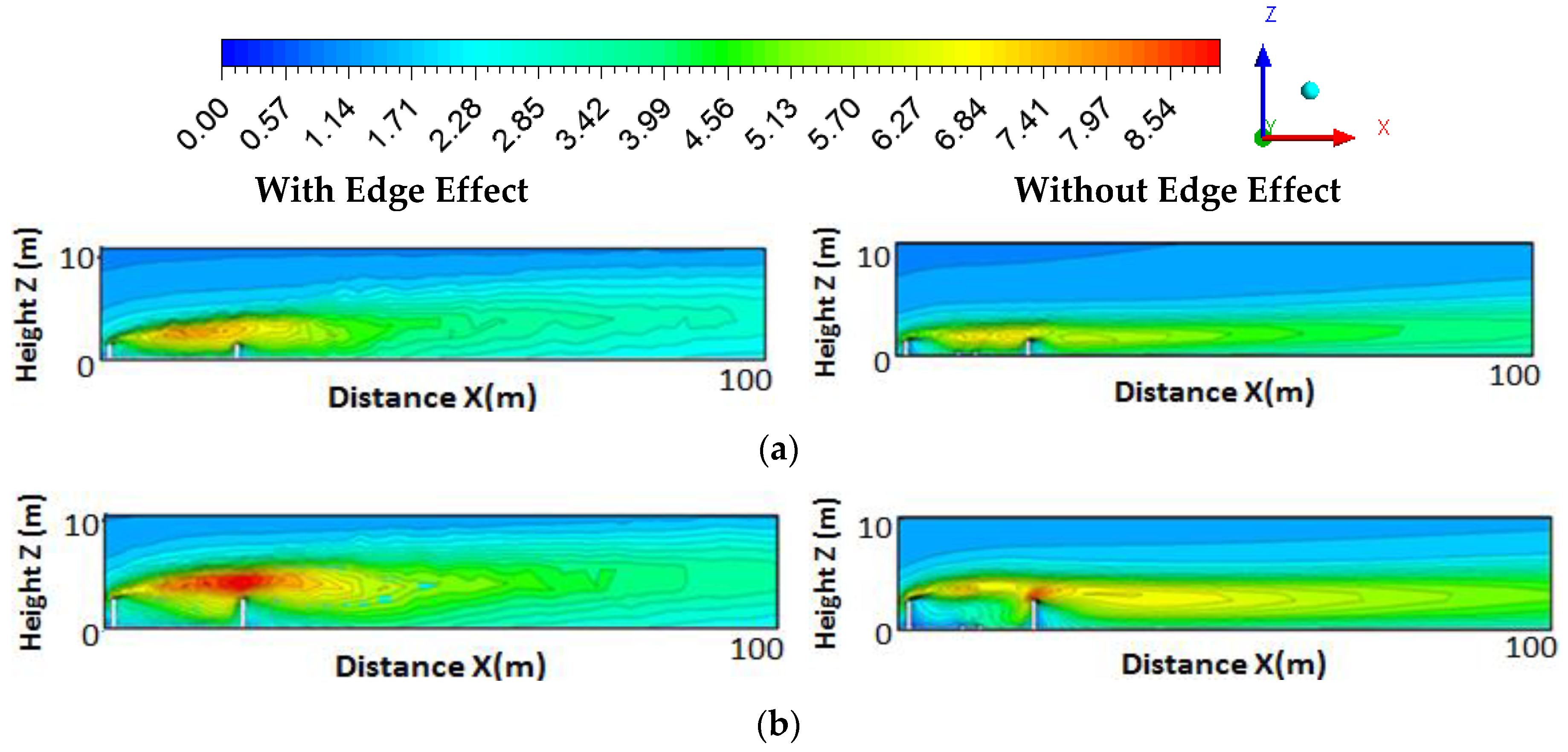
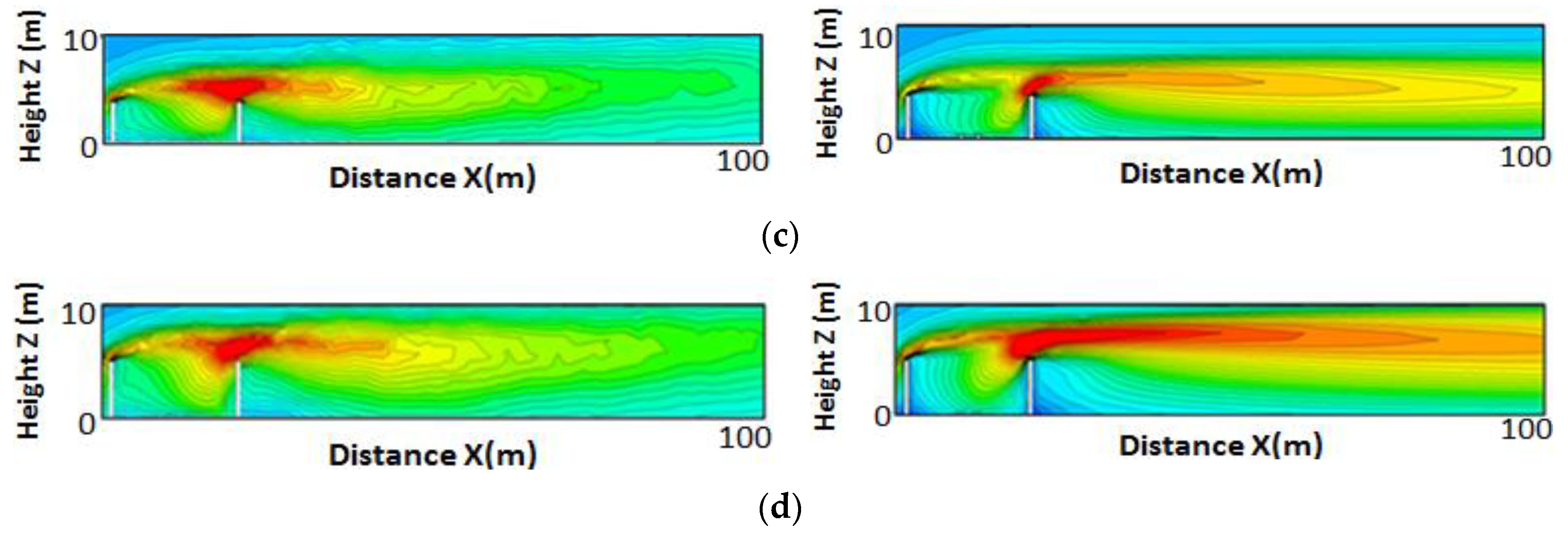
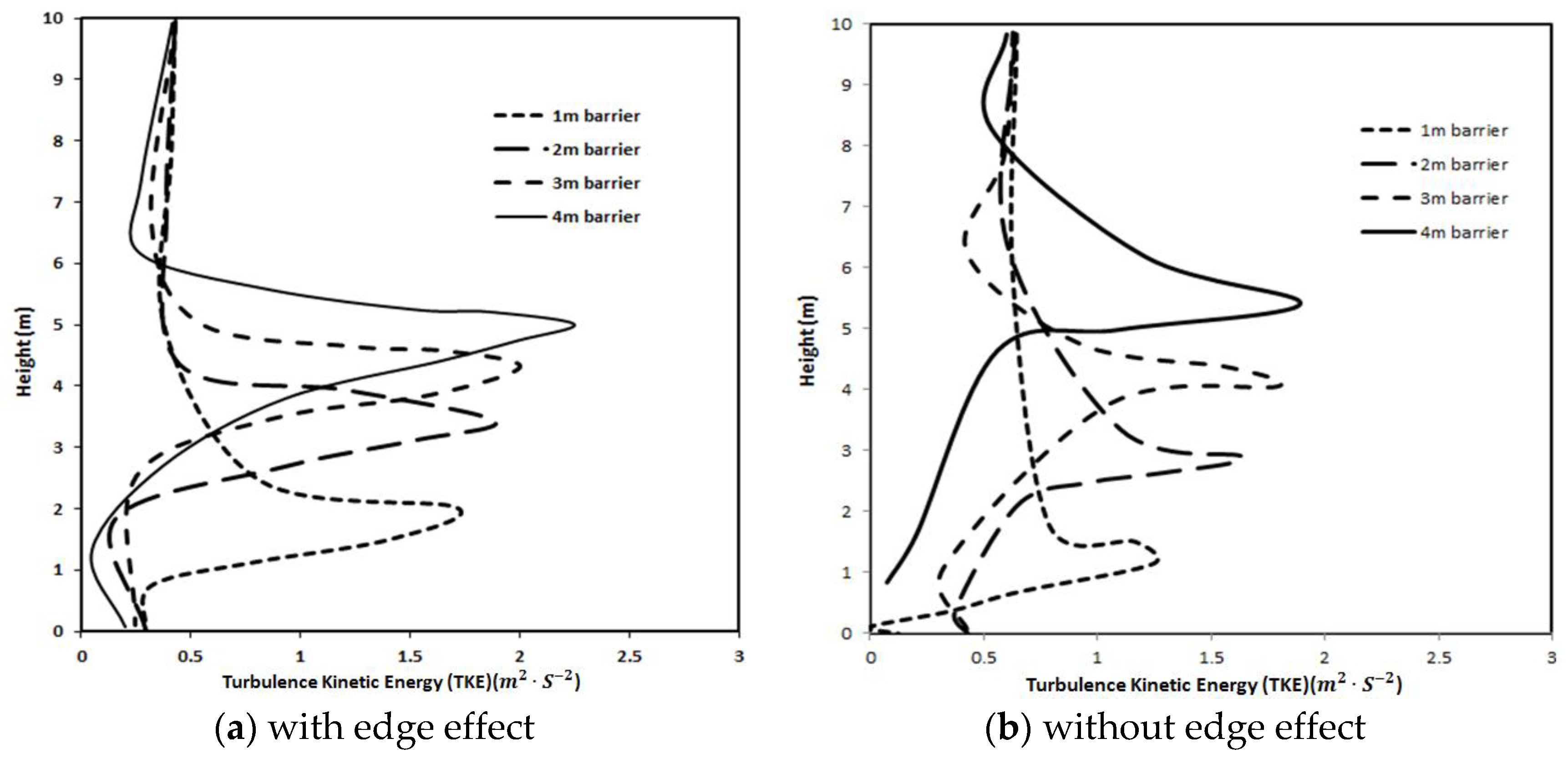
3.2. Numerical Analysis of Barrier Edge Effect under Neutral Condition
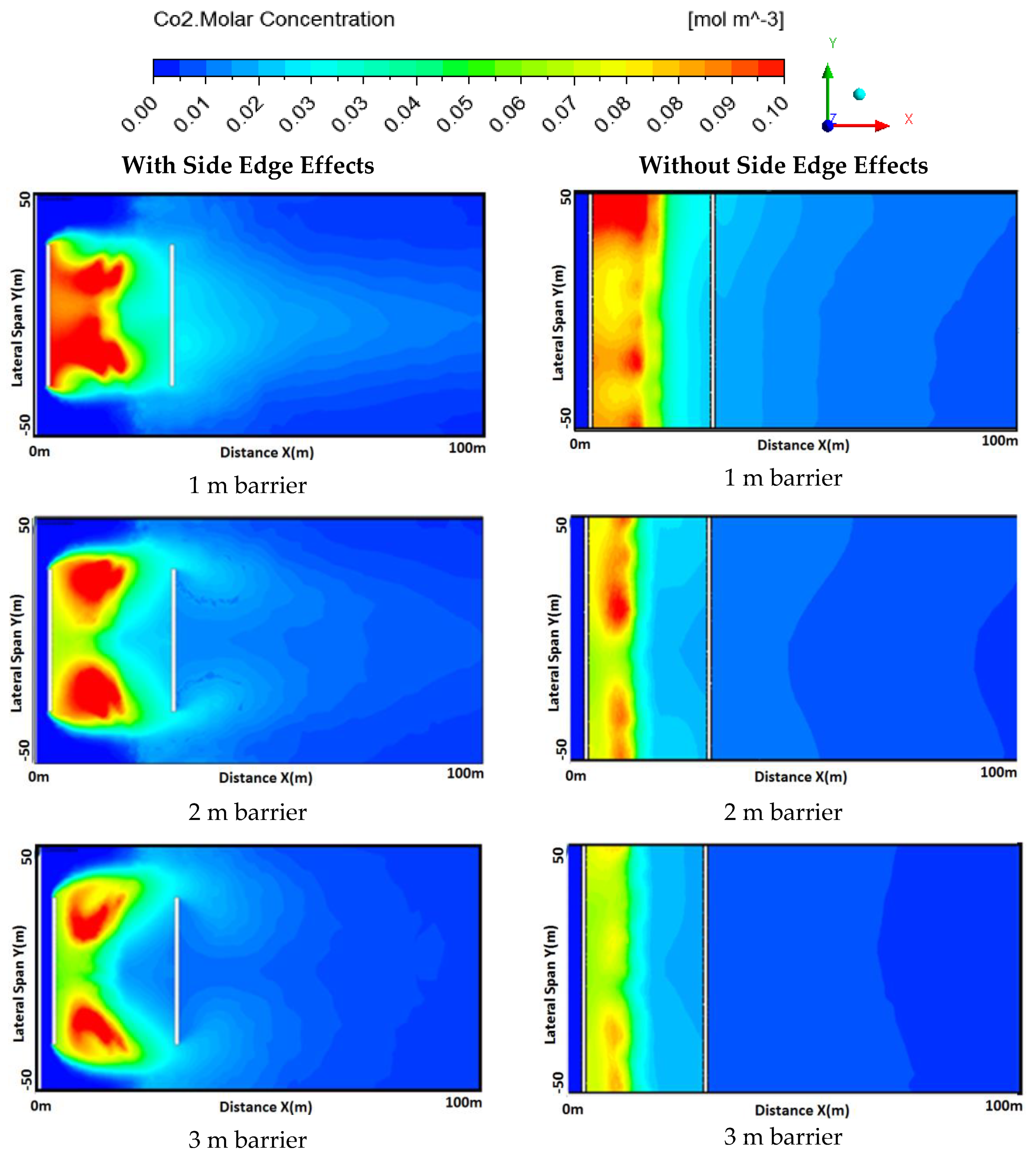
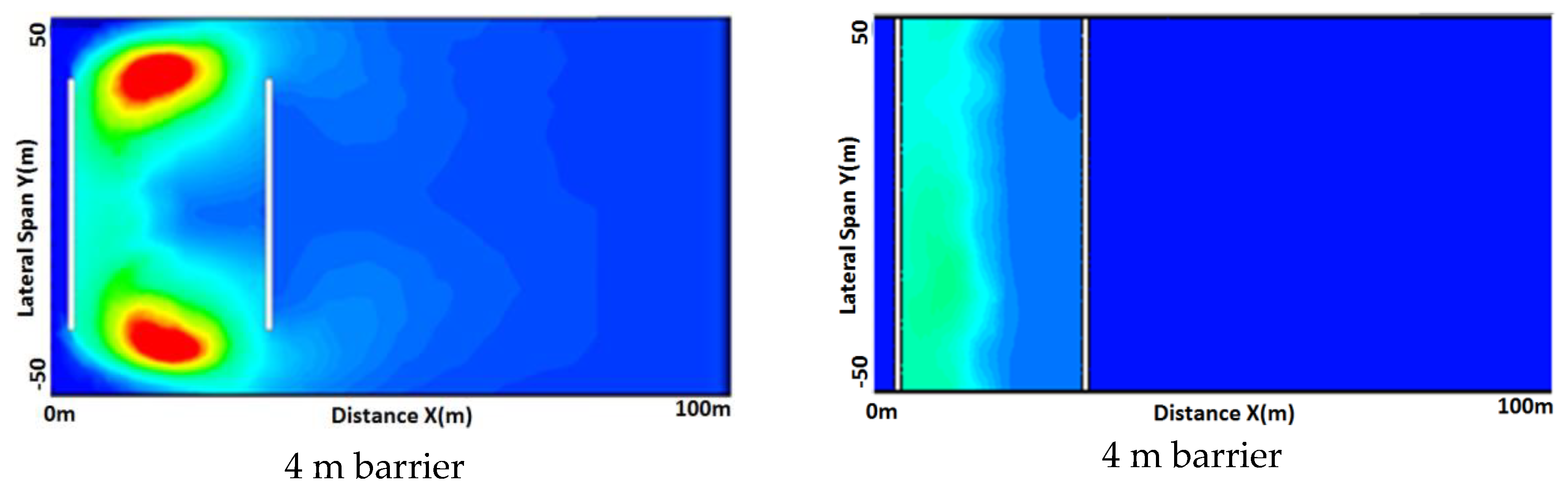
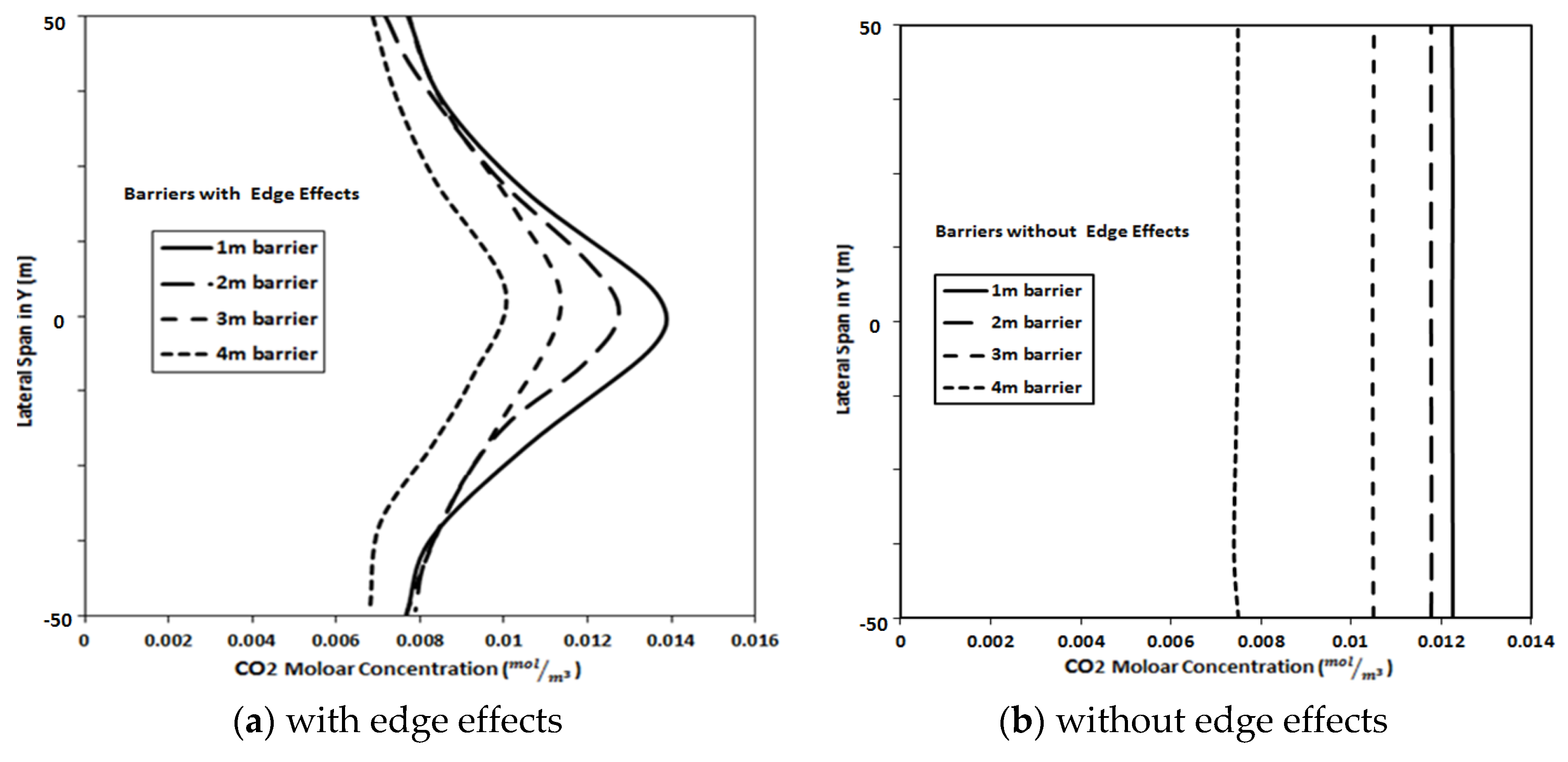
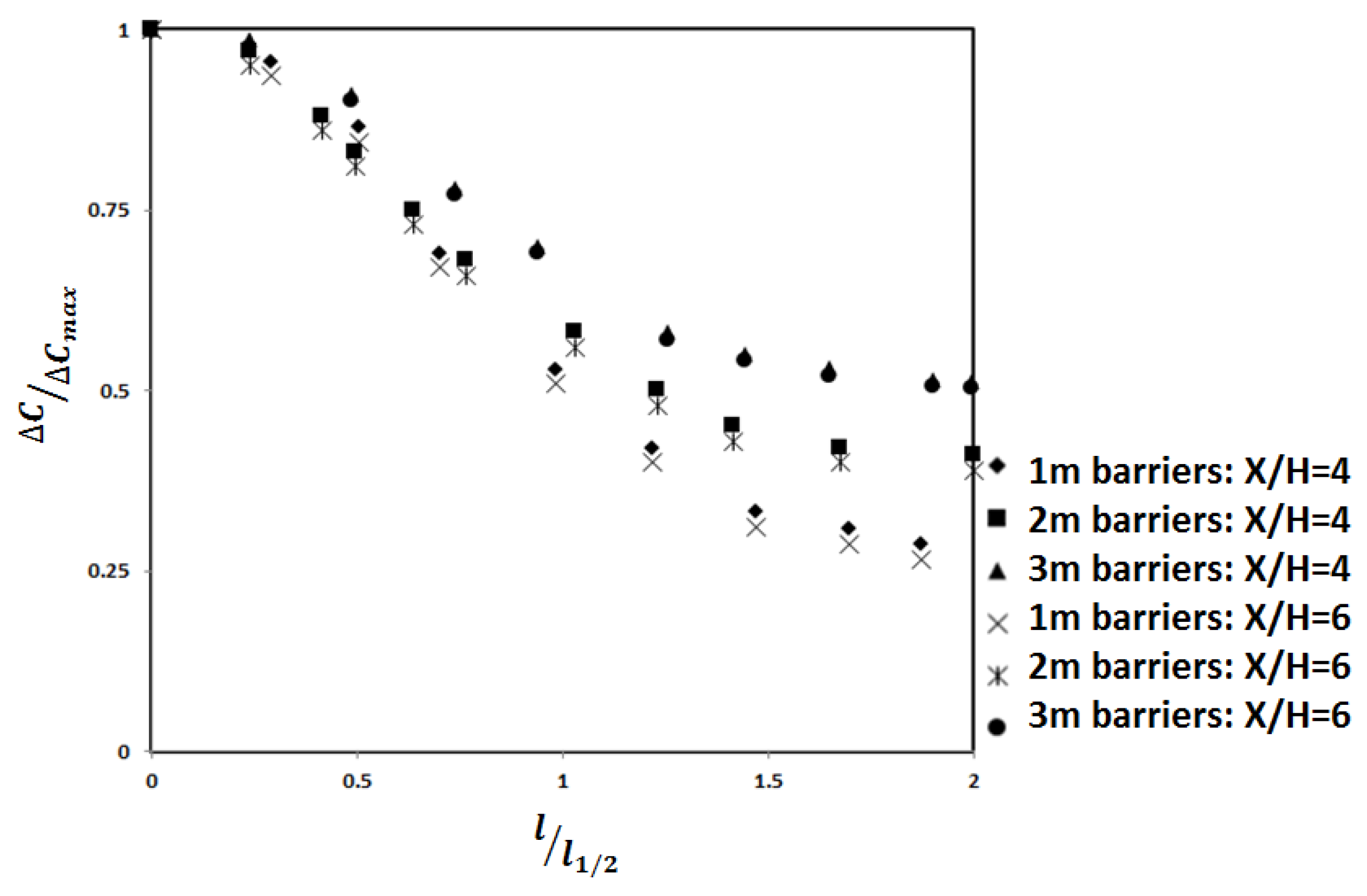
Flow Characteristics Comparison between Edge Effects and Non-Edge Effects
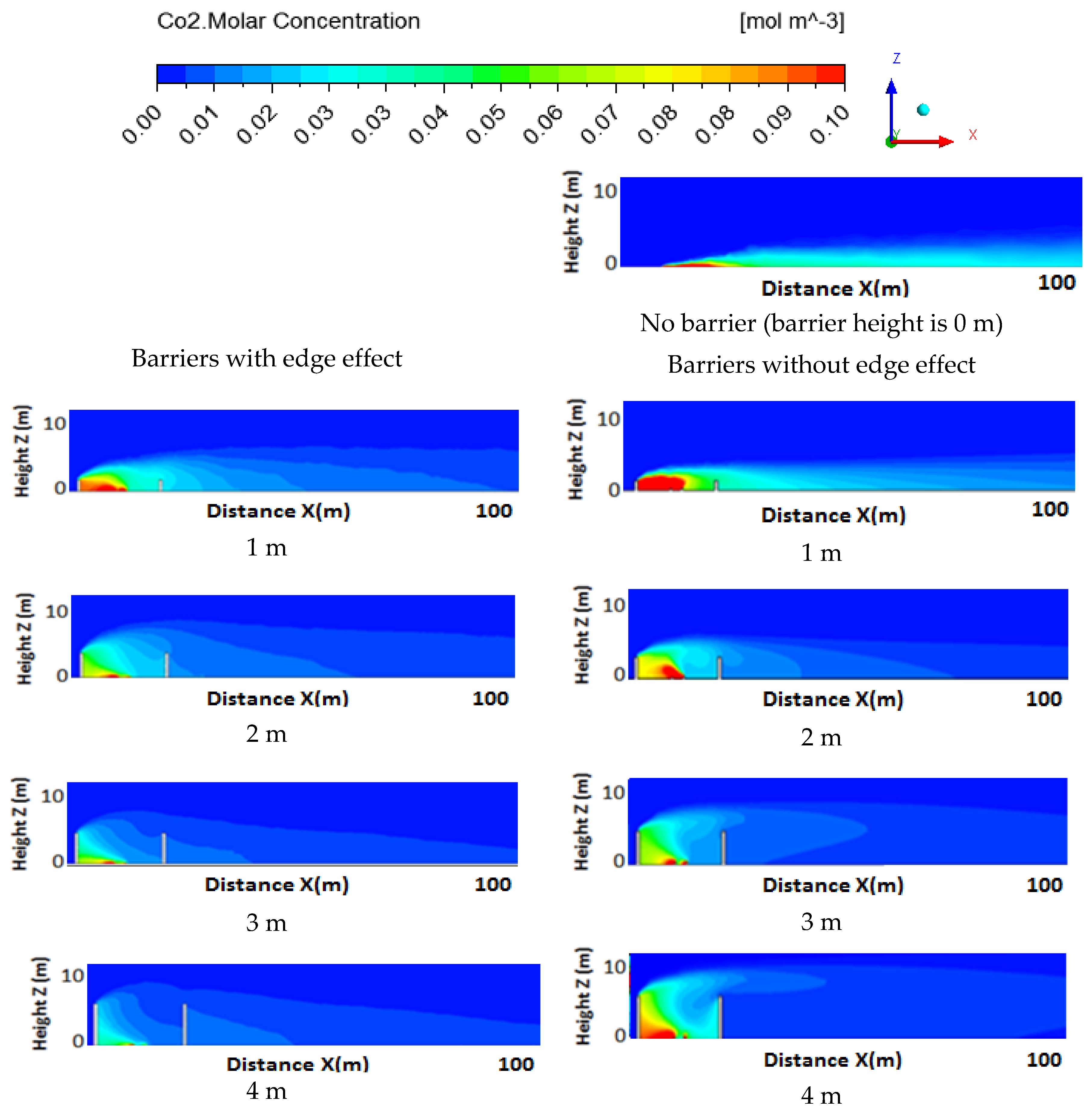
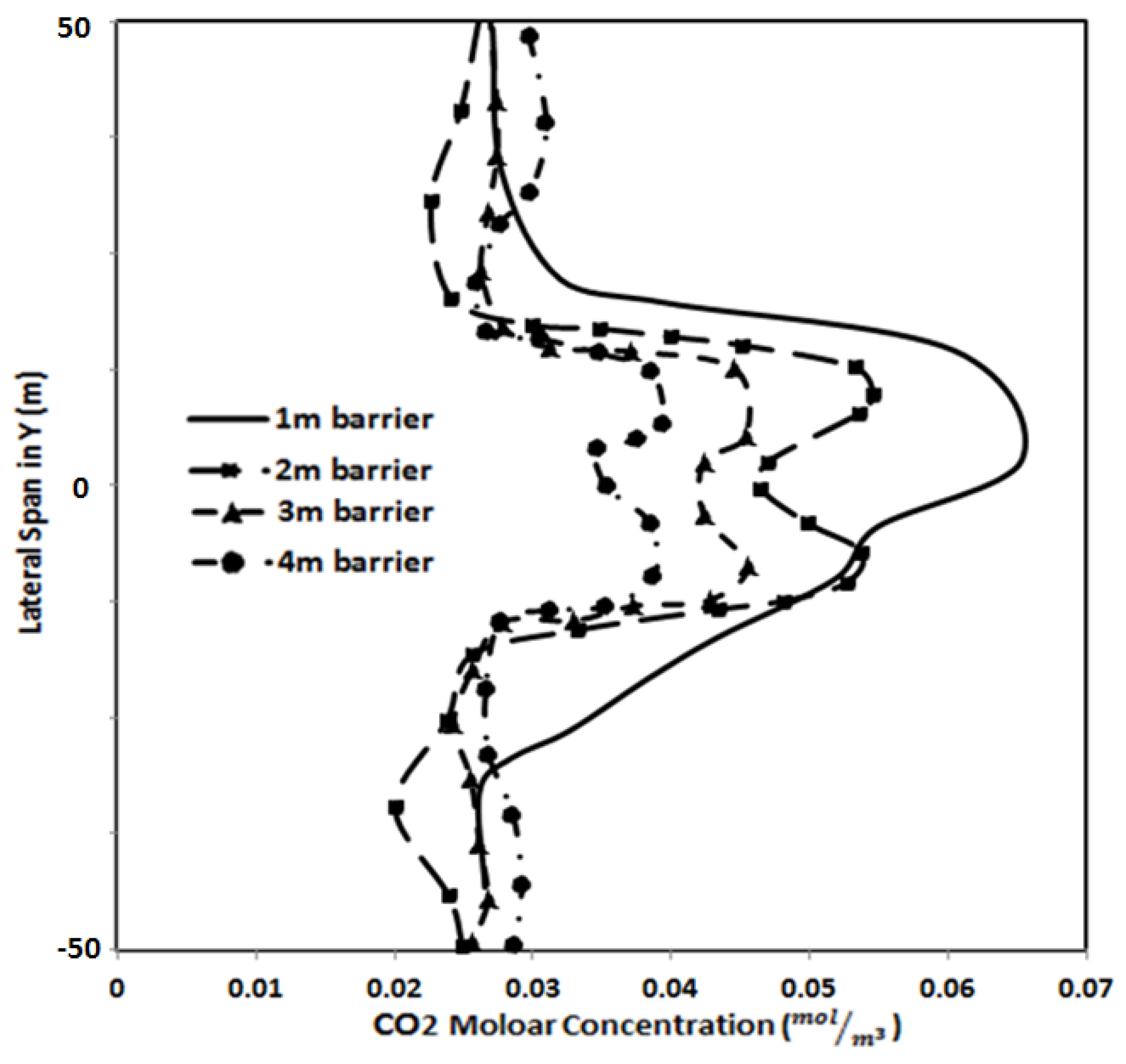
3.3. Pollutant Dispersion Characteristics under Neutral Condition
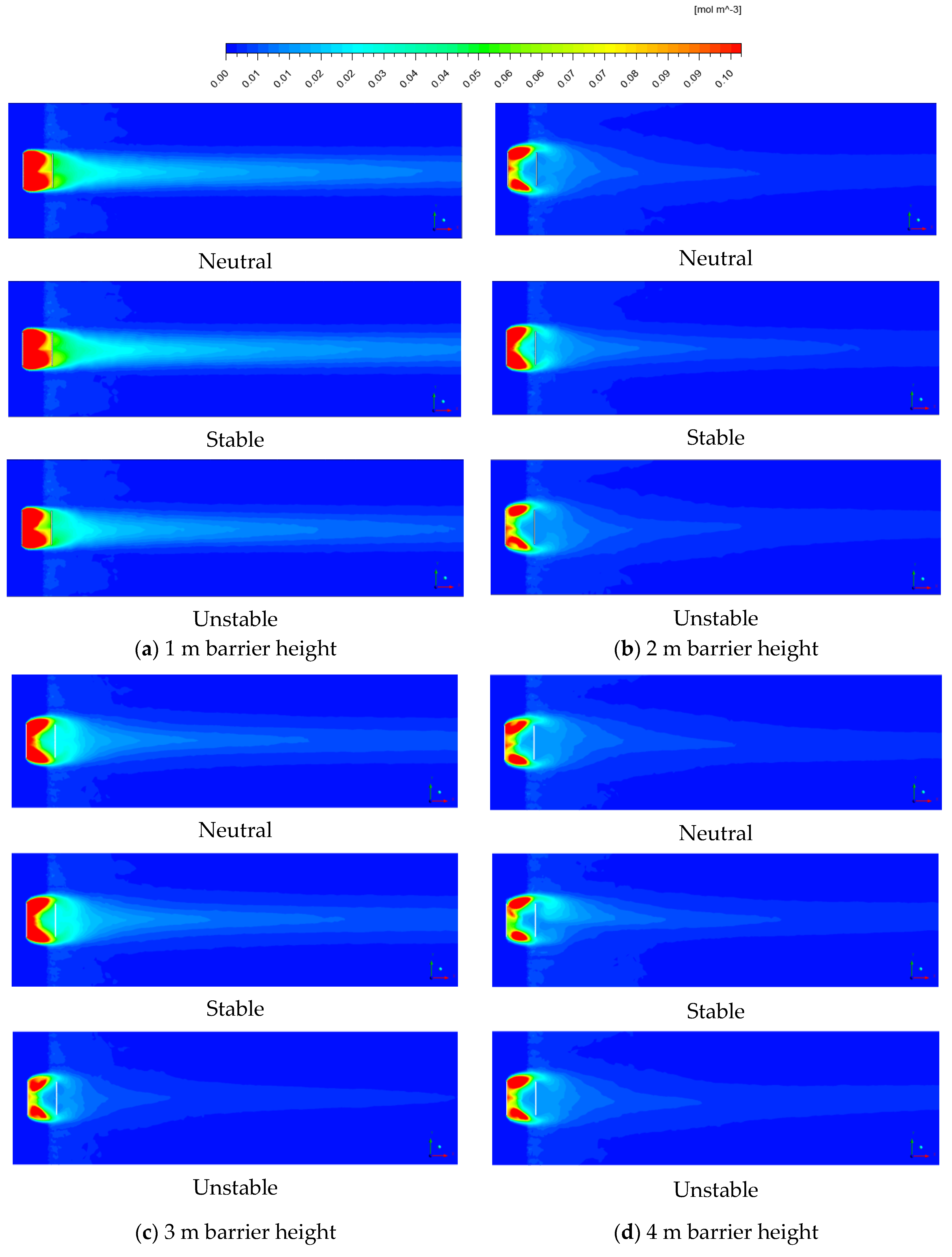
3.4. Barrier Edge Effect under Various Thermal Conditions
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Pressbooks. Available online: https://ohiostate.pressbooks.pub/sciencebites/chapter/causes-and-consequences-of-air-pollution-in-beijing-china/ (accessed on 1 May 2018).
- EPA. Available online: https://www.epa.gov/newsreleases/us-epa-partners-study-roadside-vegetation-and-air-quality-local-school (accessed on 1 May 2018).
- EPA. Available online: https://www.epa.gov/sites/production/files/2015-10/documents/ochp_2015_near_road_pollution_booklet_v16_508.pdf (accessed on 1 May 2018).
- Heist, D.K.; Perry, S.G.; Brixey, L.A. A wind tunnel study of roadway configurations on the dispersion of traffic-related pollution. Atmos. Environ. 2009, 43, 5101–5111. [Google Scholar] [CrossRef]
- Baldauf, R.; Thoma, E.; Khlystov, A.; Isakov, V.; Bowker, G.; Long, T.; Snow, R. Impacts of noise barriers on near-road air quality. Atmos. Environ. 2008, 42, 7502–7507. [Google Scholar] [CrossRef]
- Ning, Z.; Huddaa, N.; Dahera, N.; Kam, W.; Herner, J.; Kozawa, K.; Mara, S.; Sioutas, C. Impact of roadside noise barriers on particle size distributions and pollutants concentrations near freeways. Atmos. Environ. 2010, 44, 3118–3127. [Google Scholar] [CrossRef]
- Hagler, G.S.W.; Lin, M.Y.; Khlystov, A.; Baldauf, R.W.; Iskov, V.; Faircloth, J.; Jackson, L.E. Field investigation of roadside vegetative and structural barrier impact on near-road ultrafine particle concentrations under a variety of wind conditions. Sci. Total Environ. 2012, 419, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Finn, D.; Clawson, K.L.; Roger, R.G.; Rich, J.D.; Eckman, R.M. Tracer studies to characterize the effects of roadside noise barriers on near-road pollutant dispersion under varying atmospheric stability conditions. Atmos. Environ. 2010, 44, 204–214. [Google Scholar] [CrossRef]
- RBaldauf, W.; Iskov, V.; Deshmarkh, P.; Venkatram, A.; Yang, B.; Zhang, K.M. Influence of solid noise barriers on near-road and on-road air quality. Atmos. Environ. 2016, 129, 265–276. [Google Scholar] [CrossRef]
- Hagler, G.S.W.; Tang, W.; Freeman, M.J.; Heist, D.K.; Perry, S.J.; Vette, A.F. Model evaluation of roadside barrier impact on near-road air pollution. Atmos. Environ. 2011, 45, 2522–2530. [Google Scholar] [CrossRef]
- Schulte, N.; Snyder, M.; Isacov, V.; Heist, D.; Venkatram, A. Effects of solid barriers on dispersion of roadway emissions. Atmos. Environ. 2014, 97, 286–295. [Google Scholar] [CrossRef]
- Lee, E.S.; Ranasinghe, D.R.; Ahangar, F.E.; Amini, S.; Mara, S.; Choi, W.; Paulson, S.; Zhu, Y. Field evaluation of vegetation and noise barriers for mitigation of near-freeway air pollution under variable wind conditions. Atmos. Environ. 2018, 175, 92–99. [Google Scholar] [CrossRef]
- Amini, S.; Ahangar, F.; Heist, D.; Perry, S.; Venkatram, A. Modeling Dispersion of Emissions from Depressed Roadways. Atmos. Environ. 2018, 186, 189–197. [Google Scholar] [CrossRef]
- Steffens, J.T.; Heist, D.K.; Perry, S.G.; Zhang, K.M. Modeling the effects of a solid barrier on pollutant dispersion under various atmospheric stability conditions. Atmos. Environ. 2013, 69, 76–85. [Google Scholar] [CrossRef]
- ANSYS. 14.1.1 Species Transport Equation. In ANSYS FLUENT 18.1 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Pieterse, J.E.; Harms, T.M. CFD investigation of atmospheric boundary layer under different thermal stabilities conditions. J. Wind Energy Ind. Aerodyn. 2013, 121, 82–97. [Google Scholar] [CrossRef]
- Alinot, C.; Masson, C. Aerodynamic Simulations of Wind Turbine Operating in Atmospheric Boundary layer with Various Thermal Stratifications. In Proceedings of the 2002 ASME Wind Energy Symposium, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Executive Summary. Light-Duty Automotive Technology, Carbon Dioxide Emissions, and Fuel Economy Trends: 1975 Through 2017; EPA, EPA-420-S-18-001; EPA: Washington, DC, USA, January 2018. [Google Scholar]
- ANSYS. 17.5 Eulerian Model. In ANSYS FLUENT 18.1 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Hussian, M.; Lee, B.E. An Investigation of Wind Forces on Three-Dimensional Roughness Elements in a Simulated Atmospheric Boundary Layer Flow. Part II: Flow over Large Arrays of Identical Roughness Elements and the Effect of Frontal and Side Aspect Ratio Variants; University of Sheffield Department of Building Science Rep. BS-56; University of Sheffield: Sheffield, UK, 1980; 81p. [Google Scholar]
- Abkar, M.; Porte-Agel, F. Influence of Atmospheric Stability on Wind-Turbine Wakes: A Large-Eddy Simulation Study. AIP Phys. Fluids 2015, 27, 035104. [Google Scholar] [CrossRef]
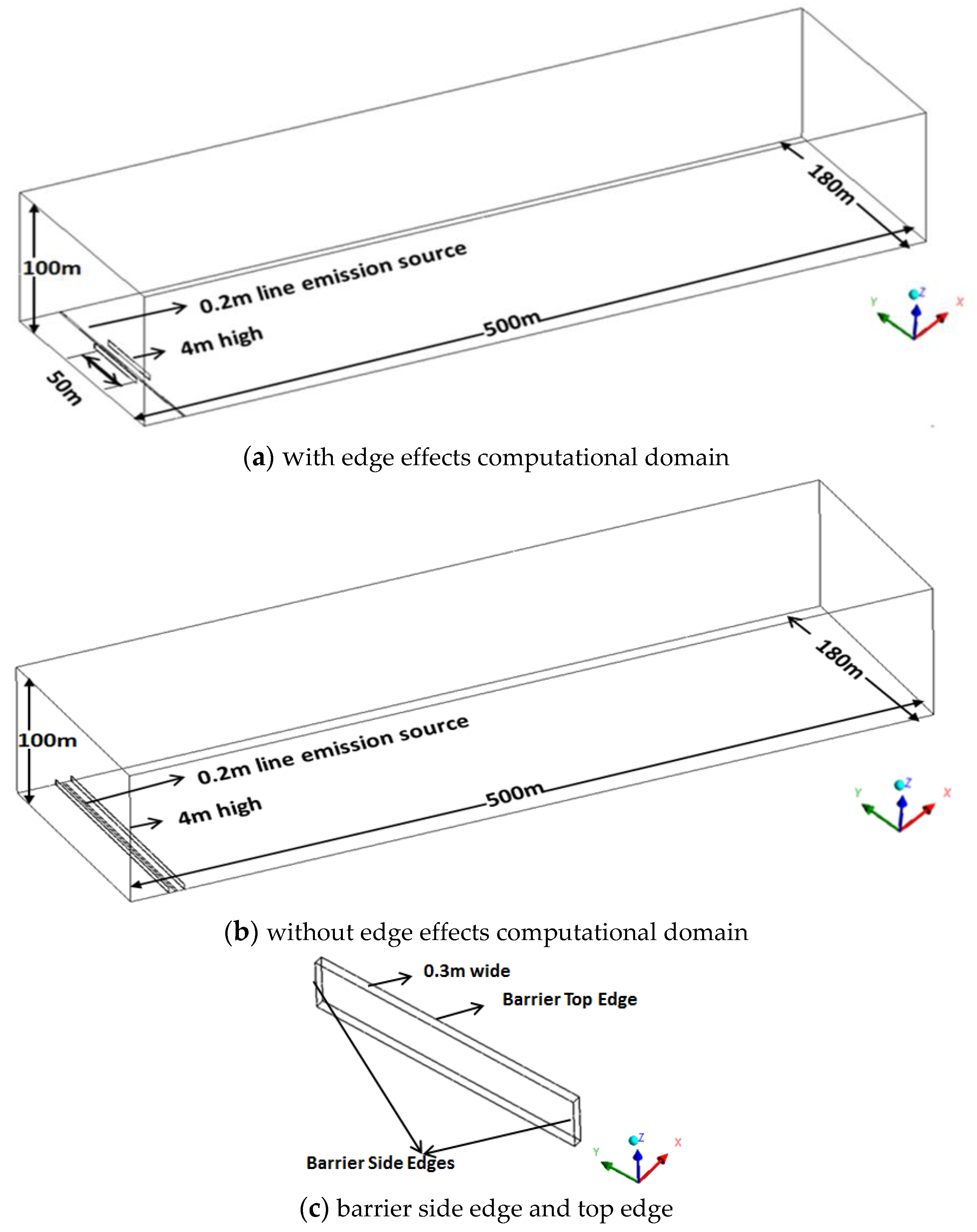
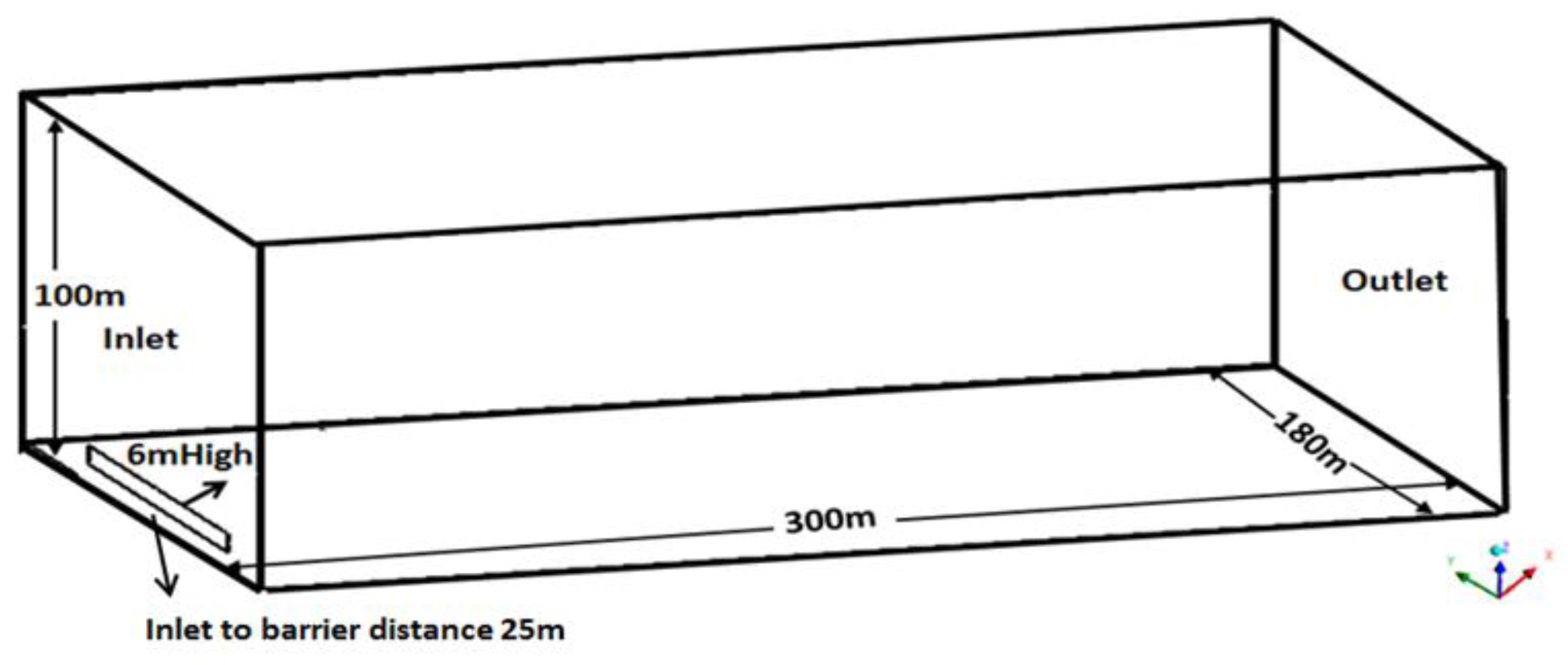
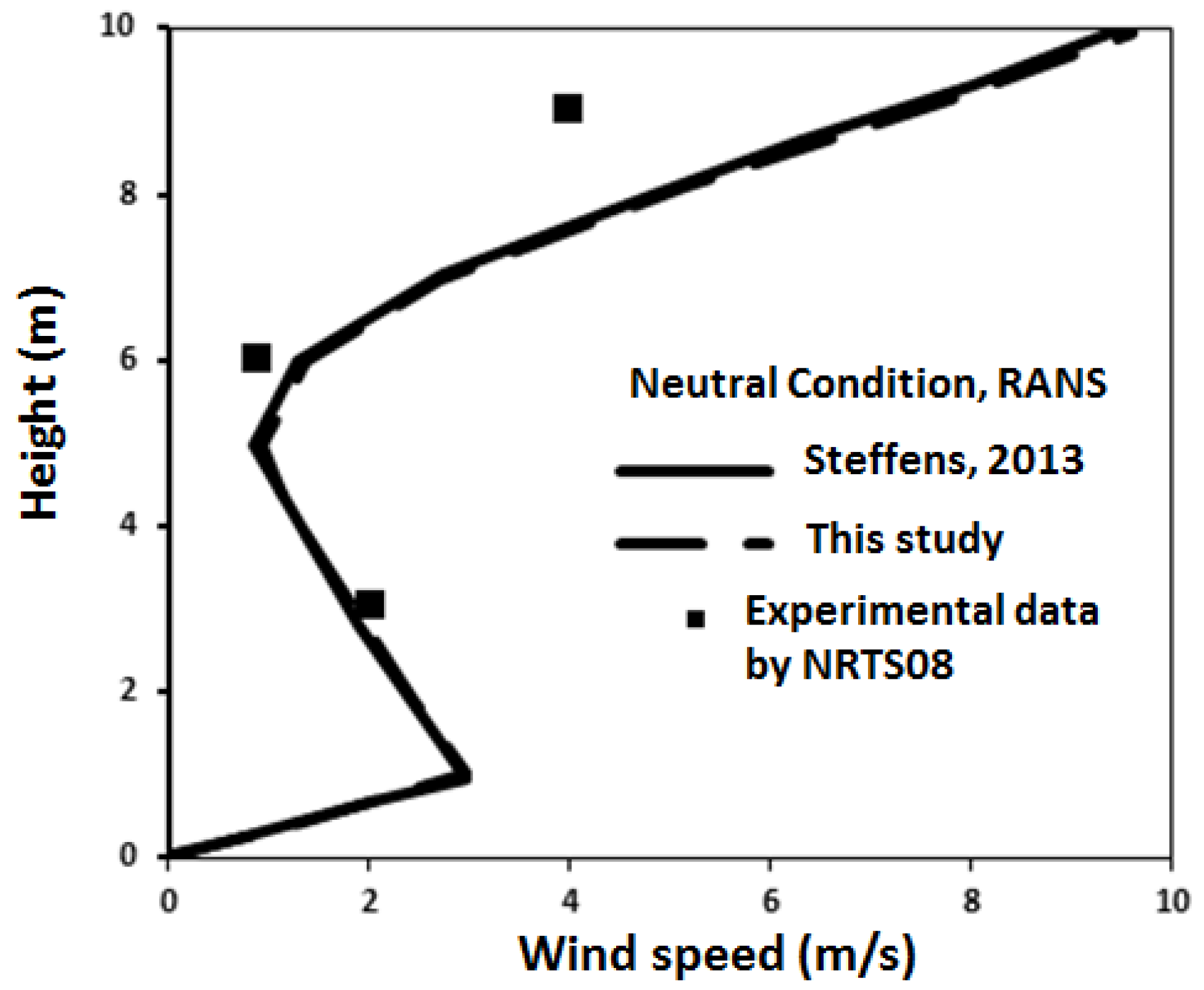
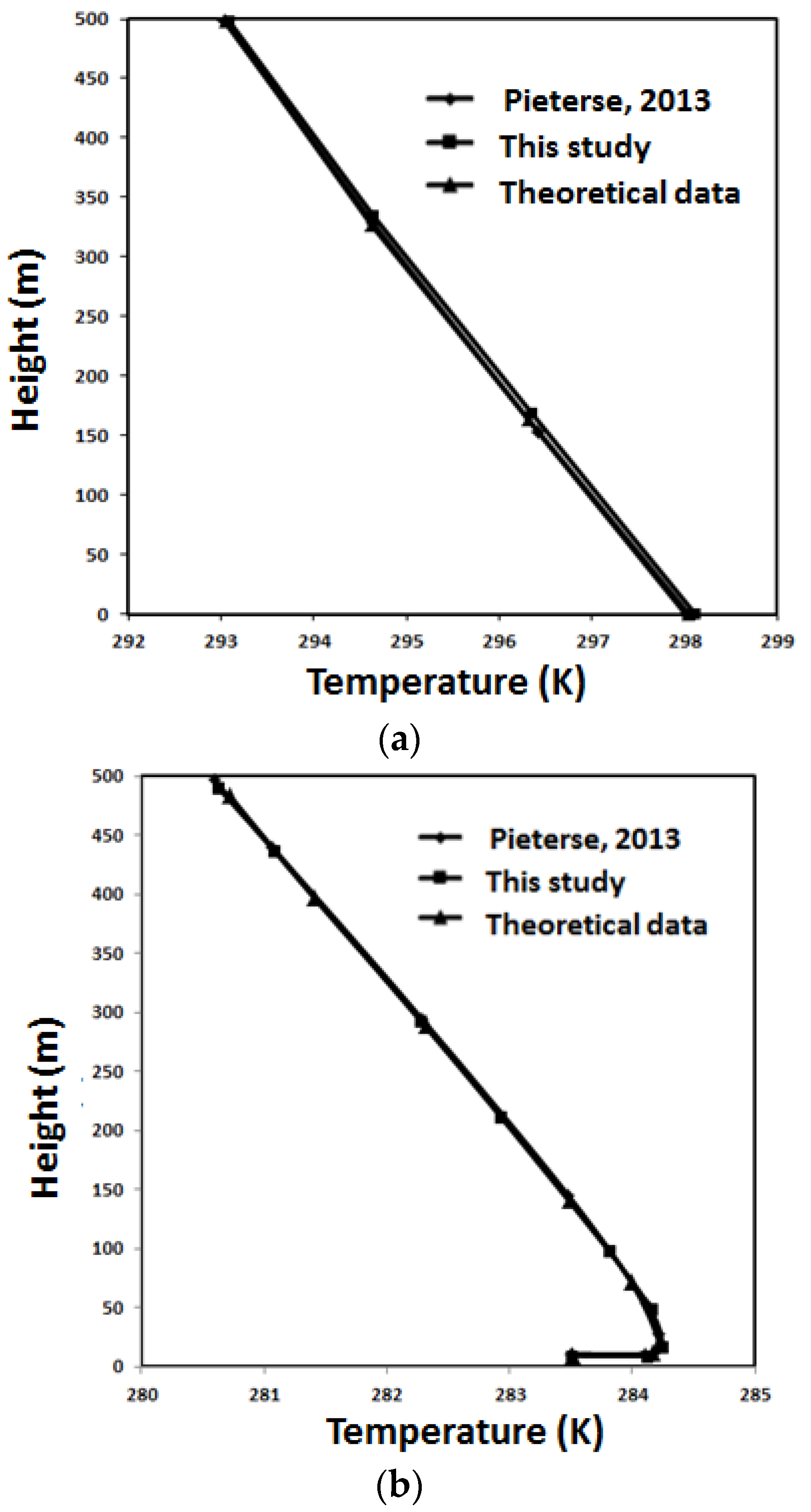
| Boundary | Boundary Type | Profiles |
|---|---|---|
| Inlet | Velocity Inlet | Numerical Inlet UDF |
| Temperature Inlet: Neutral UDF | ||
| Outlet | Outflow | Outflow with backflow rate = 1 |
| Top | Slip Moving Wall | Non-Shear Stress |
| Bottom | No Slip Wall | Roughness Height: 0.25 |
| Roughness Constant: 0.25 | ||
| Source | Mass Flow Inlet | Mass Flow Rate = 0.006 kg/s, |
| Direction Normal to Boundary | ||
| Barriers | No Slip Wall | Roughness Height: 0 |
| Roughness Constant: 0.25 |
| Barrier with Edge Effects | Barrier without Edge Effects | ||
|---|---|---|---|
| Barrier Height (m) | |||
| 1 | 1.70 | 1.25 | |
| 2 | 1.96 | 1.56 | |
| 3 | 2.00 | 1.86 | |
| 4 | 2.30 | 1.98 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Wang, X. Numerical Study of Noise Barriers’ Side Edge Effects on Pollutant Dispersion near Roadside under Various Thermal Stability Conditions. Fluids 2018, 3, 105. https://doi.org/10.3390/fluids3040105
Gong L, Wang X. Numerical Study of Noise Barriers’ Side Edge Effects on Pollutant Dispersion near Roadside under Various Thermal Stability Conditions. Fluids. 2018; 3(4):105. https://doi.org/10.3390/fluids3040105
Chicago/Turabian StyleGong, Liyuan, and Xiuling Wang. 2018. "Numerical Study of Noise Barriers’ Side Edge Effects on Pollutant Dispersion near Roadside under Various Thermal Stability Conditions" Fluids 3, no. 4: 105. https://doi.org/10.3390/fluids3040105
APA StyleGong, L., & Wang, X. (2018). Numerical Study of Noise Barriers’ Side Edge Effects on Pollutant Dispersion near Roadside under Various Thermal Stability Conditions. Fluids, 3(4), 105. https://doi.org/10.3390/fluids3040105




