Thermal Fluid Analysis of Cold Plasma Methane Reformer
Abstract
:1. Introduction
2. Experimental Modeling
2.1. Partial Oxidation
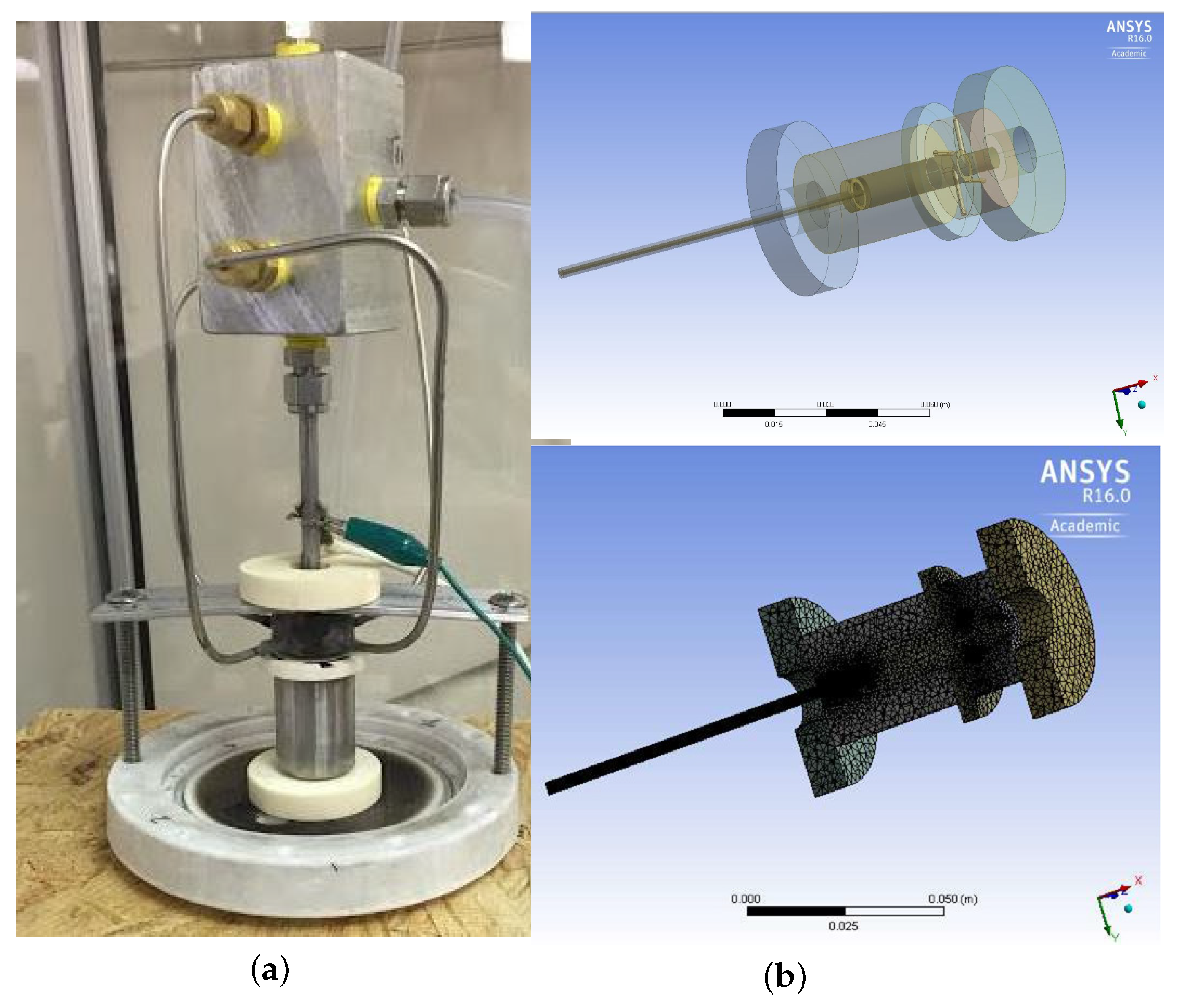
2.2. 3D Gliding Arc Vortex Reformer
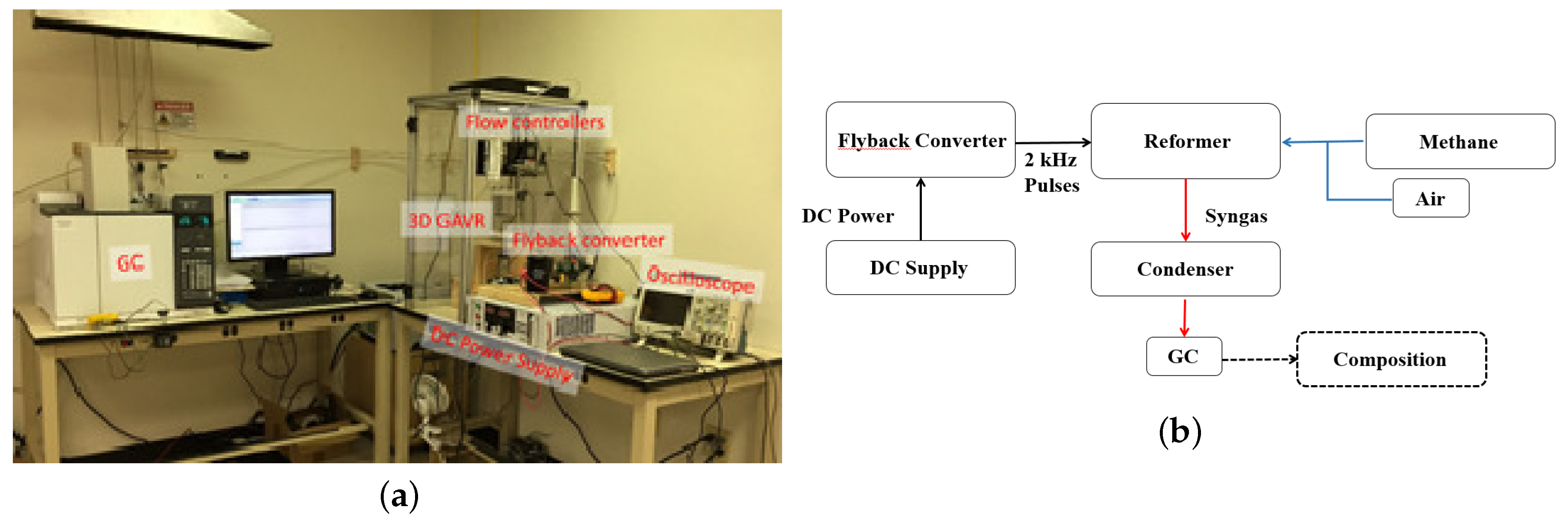
2.3. Experimental Setup
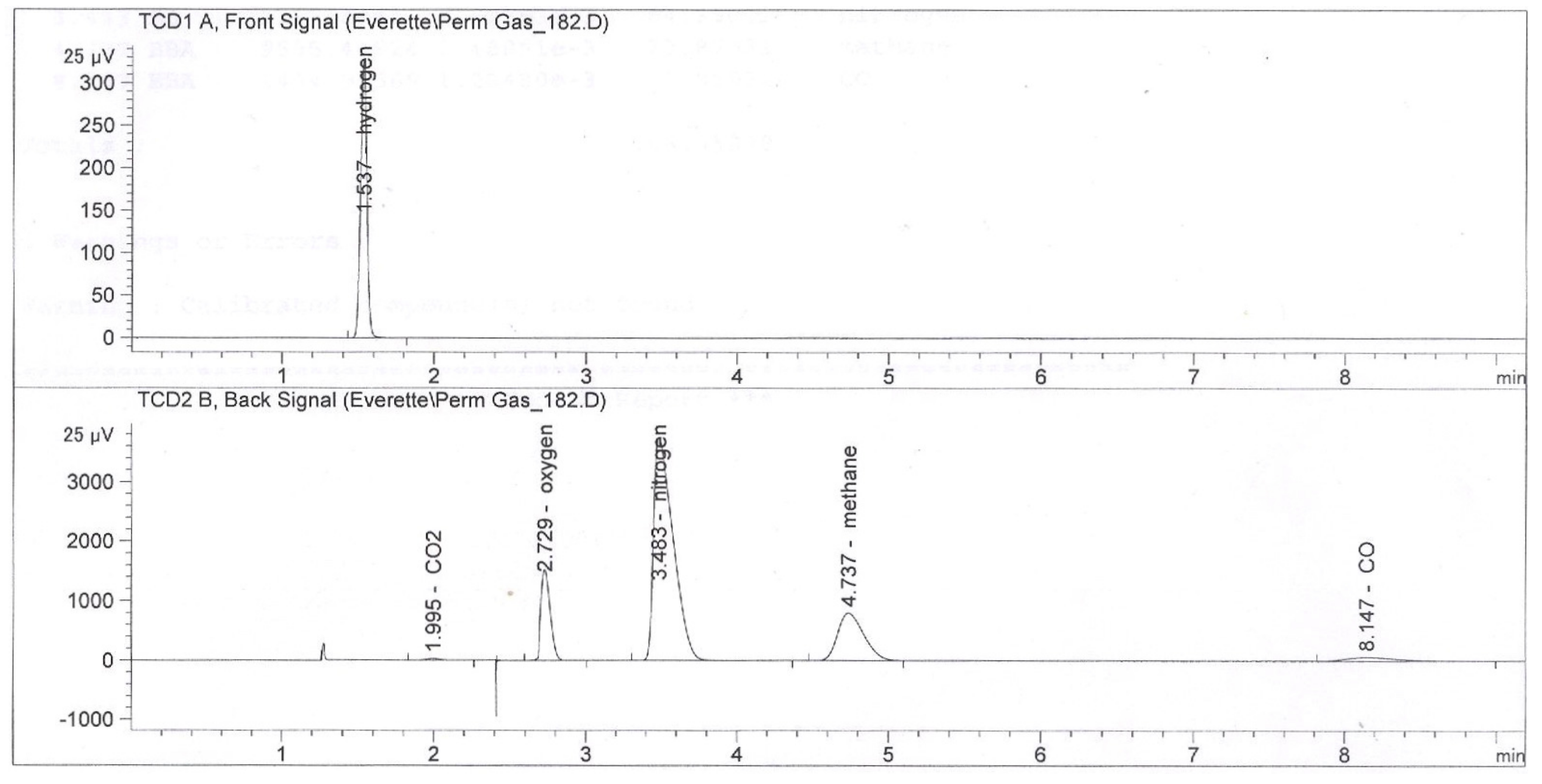
2.4. Calculation Method
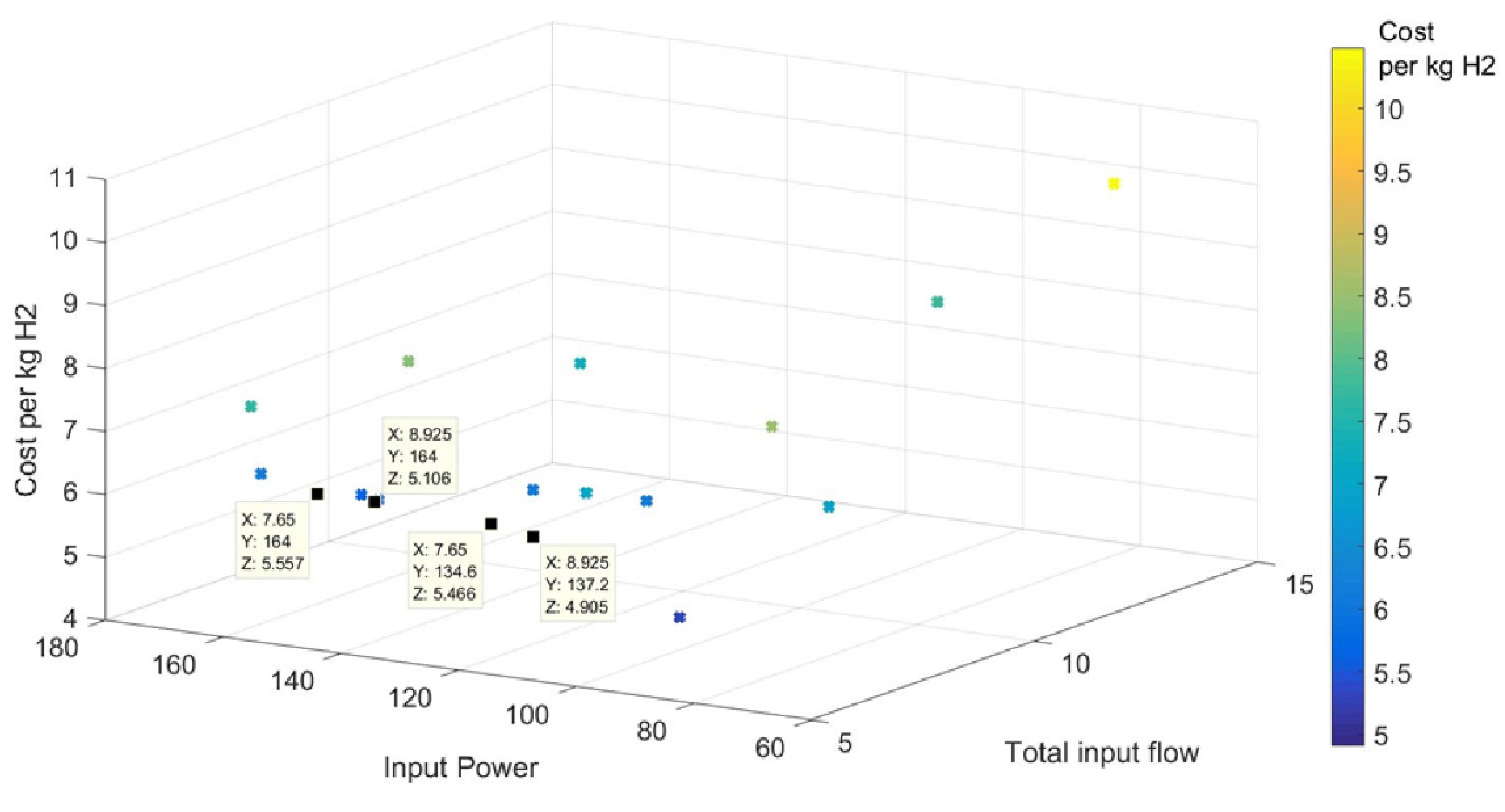
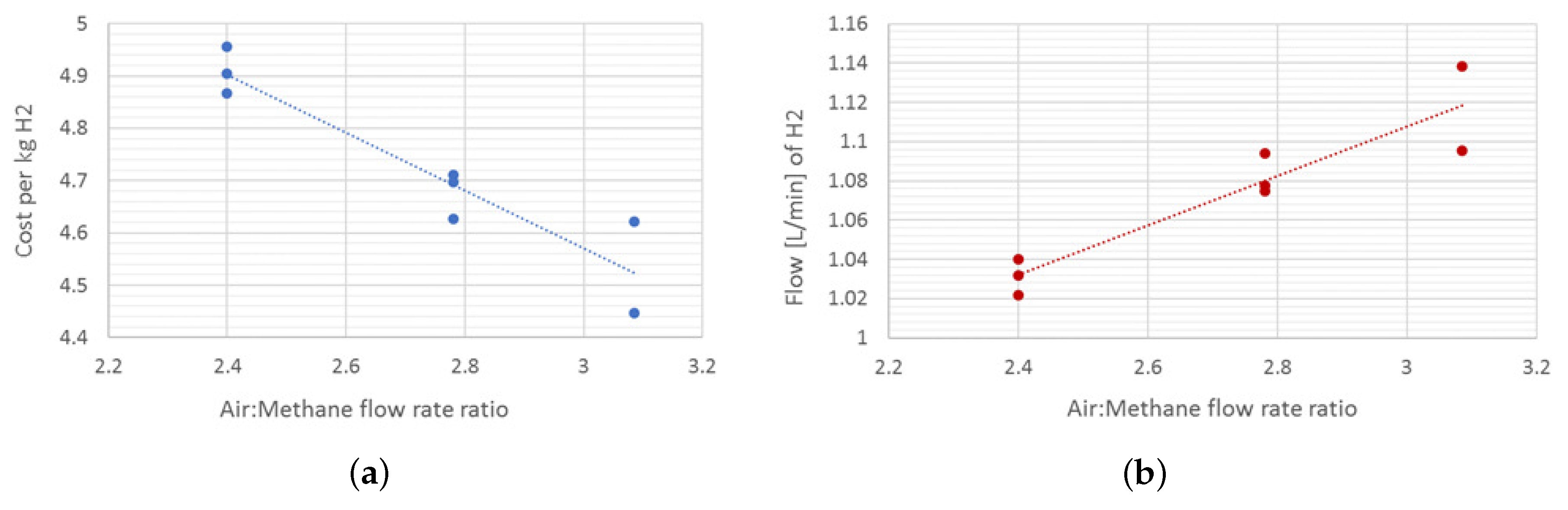
2.5. Results
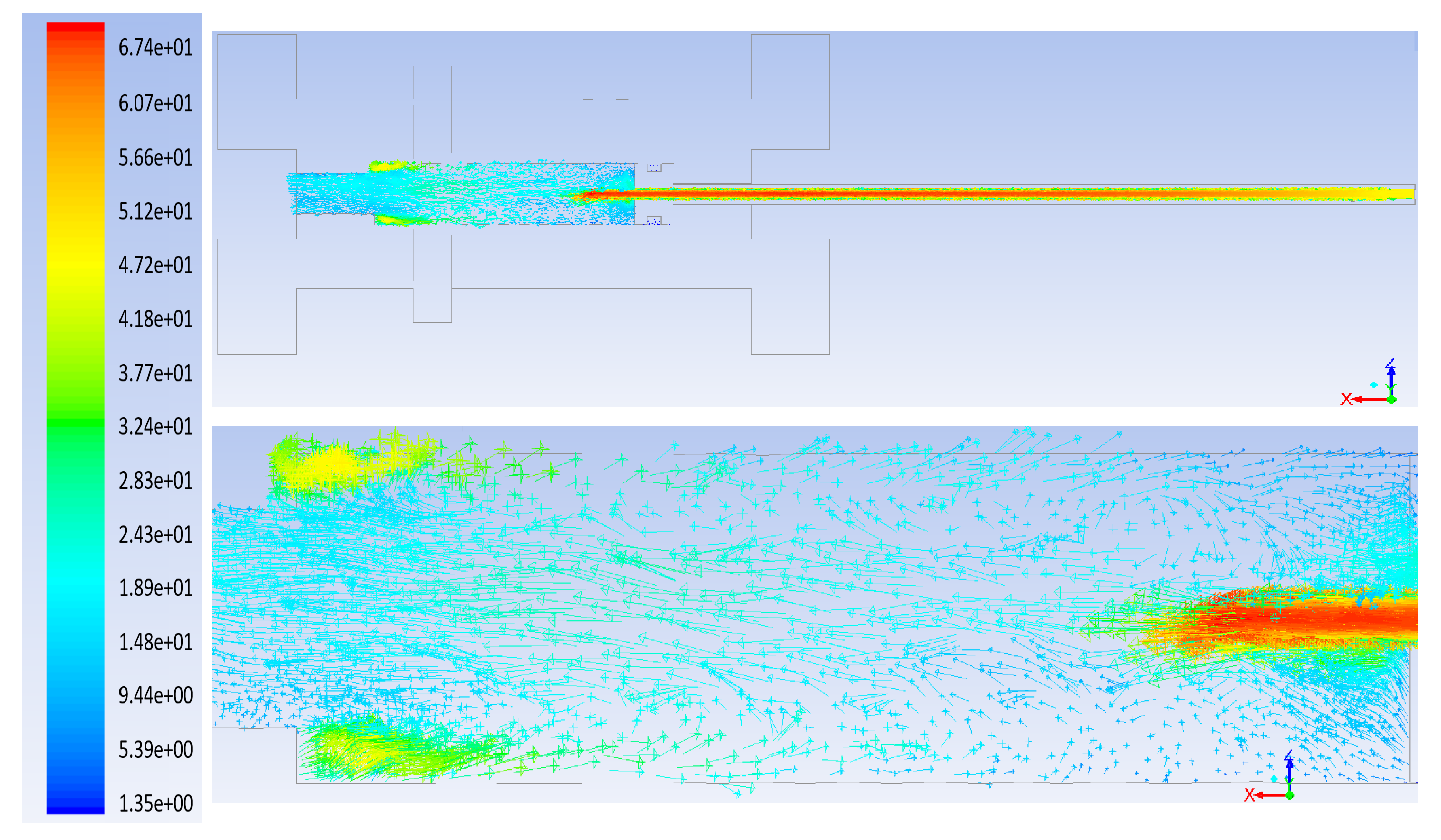
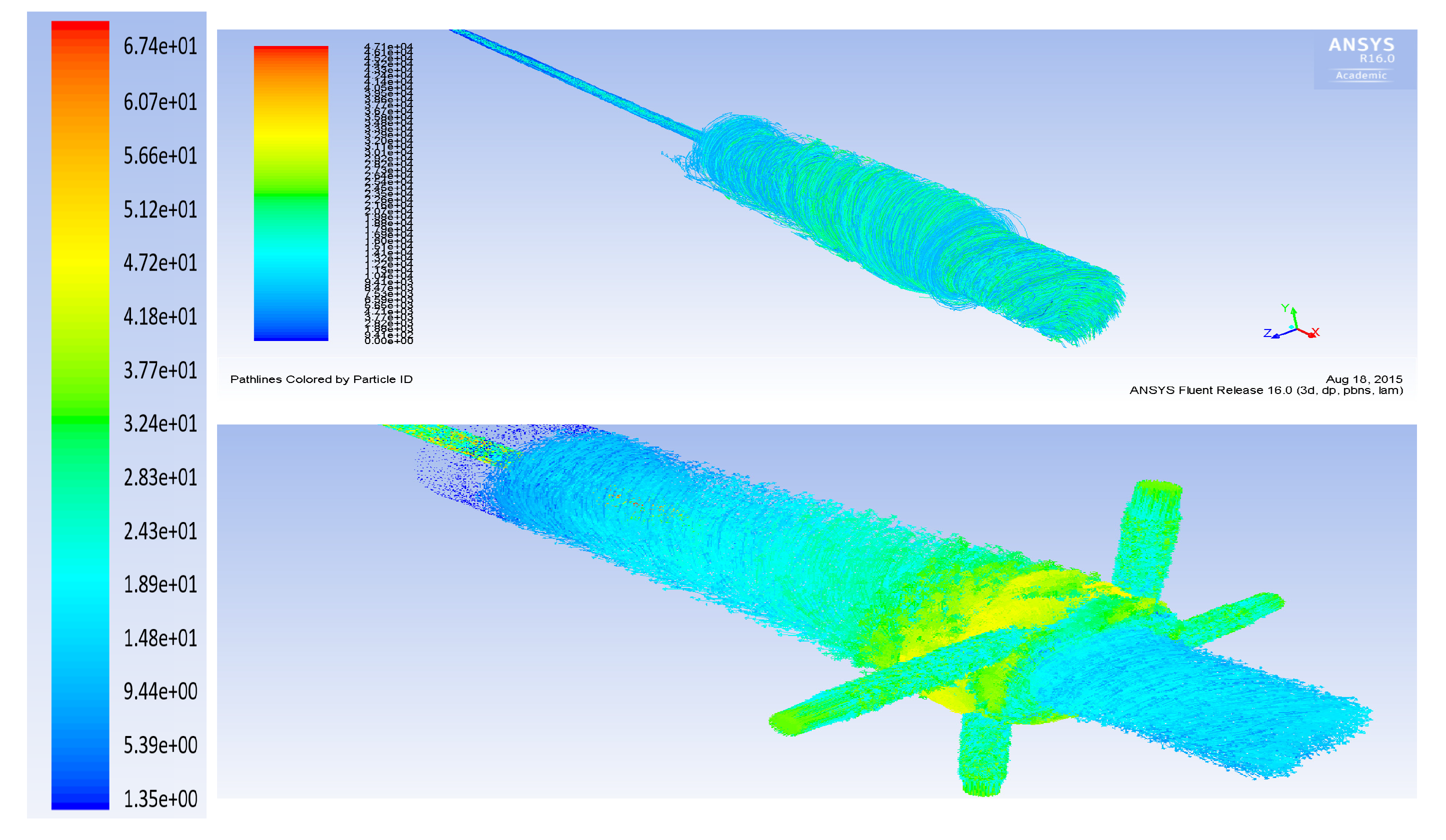
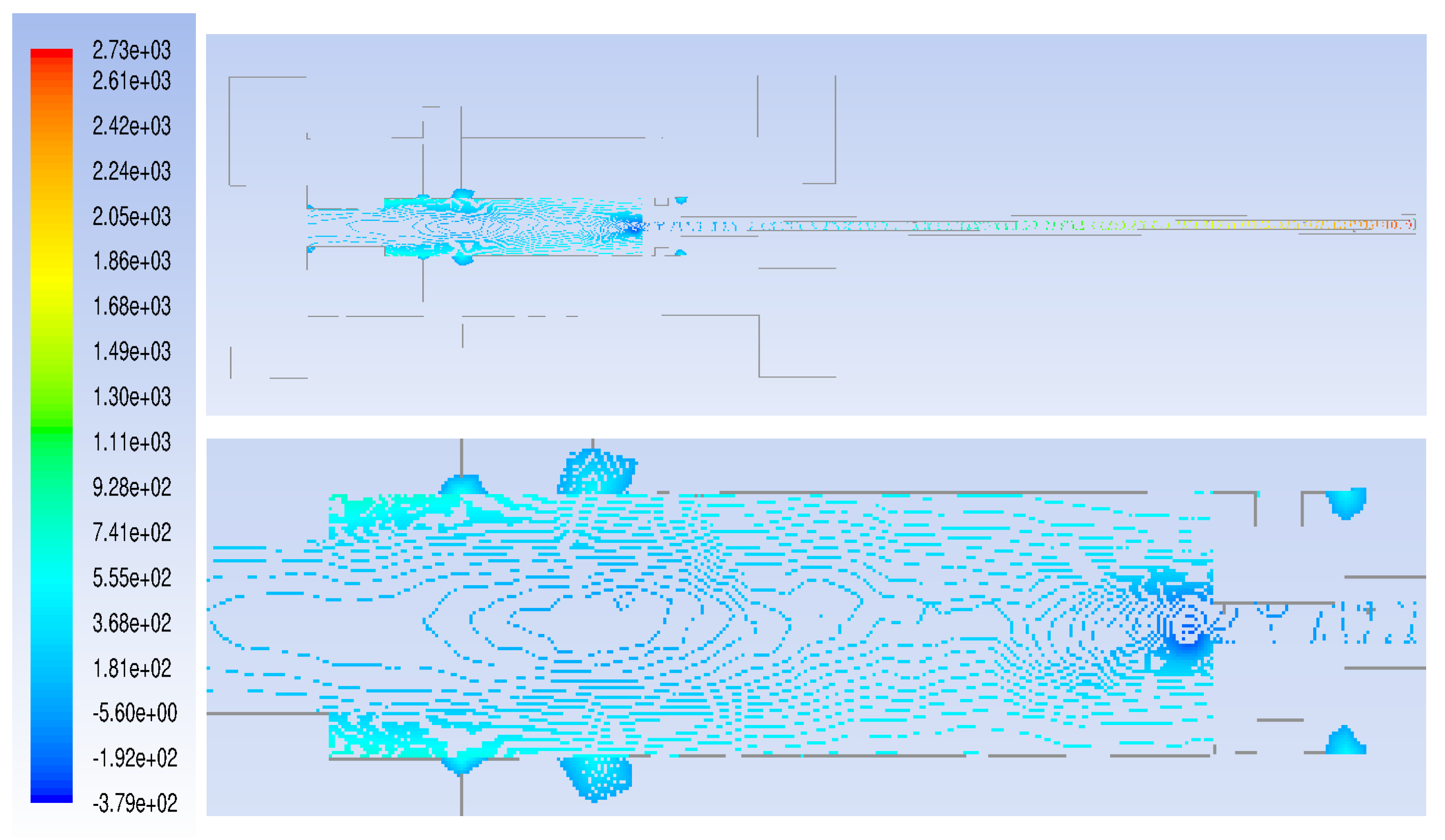
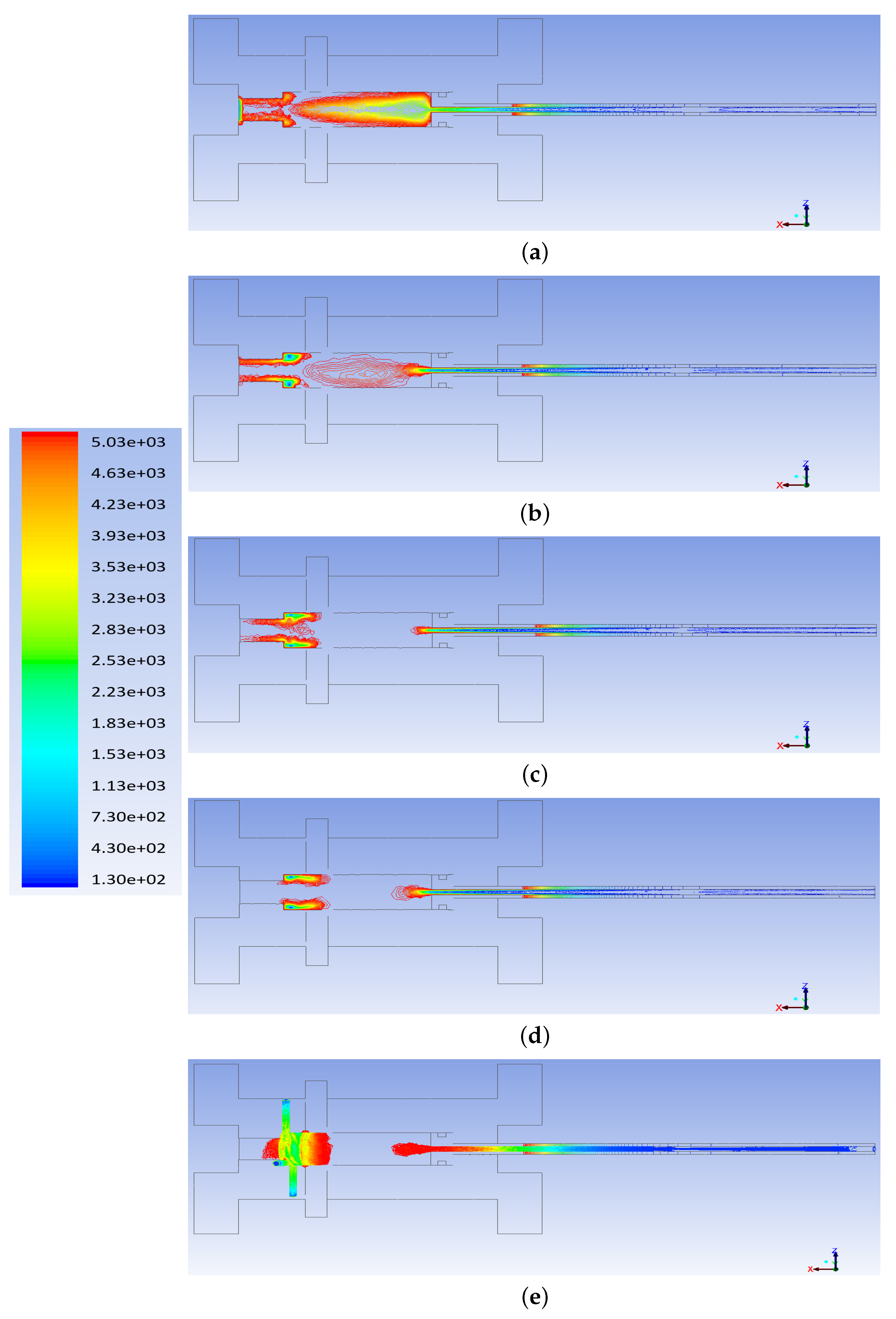
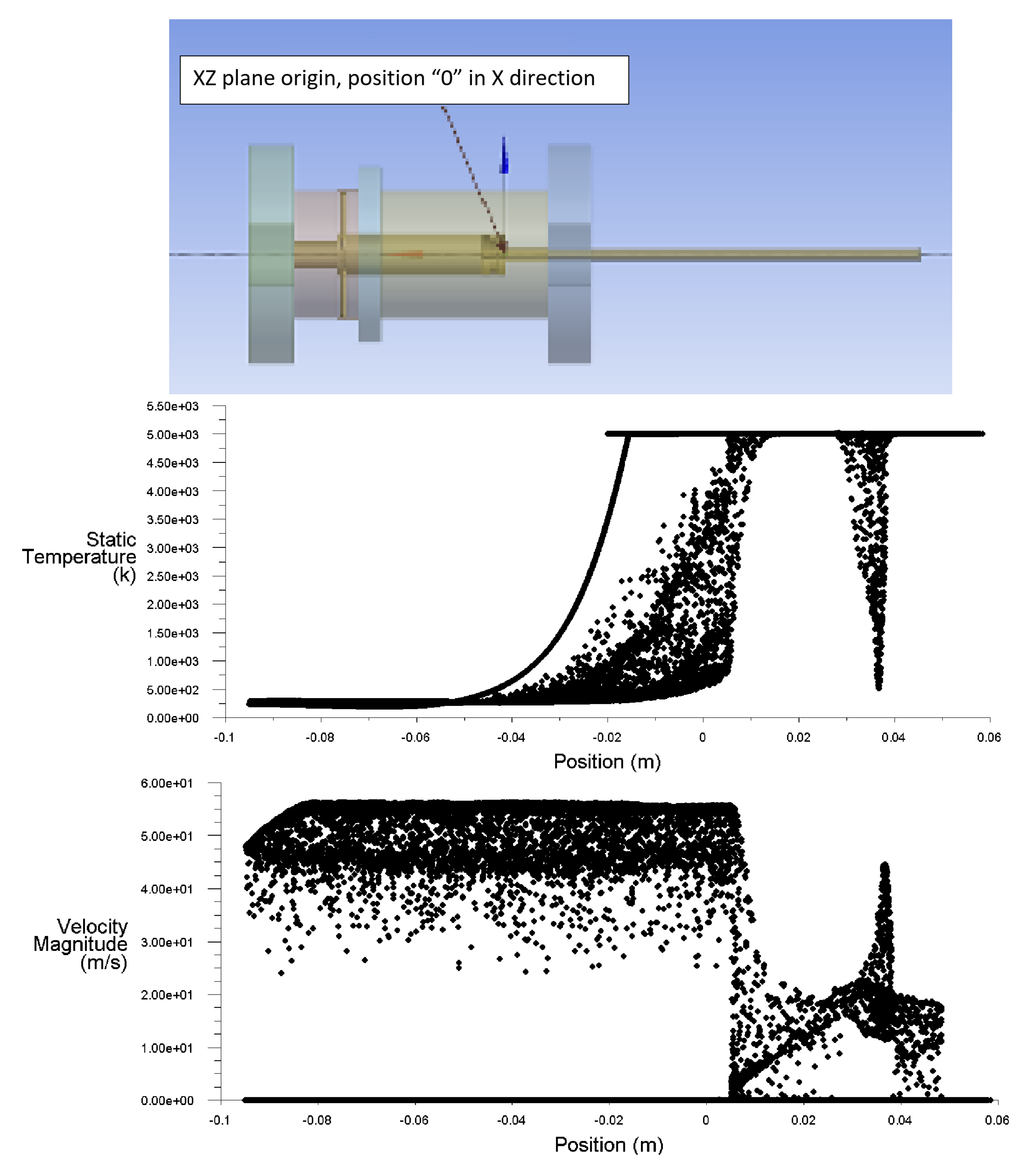
3. Computational Fluid Dynamics Modeling
- The flow rate of the axial top inlet port of the air is set around 12.65 SLPM which is applied as an input air.
- The mixture flow rates are assigned around 12.35 SLPM in total (5 SLPM air, and 7.35 SLPM methane for future modeling), which is divided into the four tangential swirl jets equally. For this modeling, this value is assigned just as the air entering the chamber through the swirl jets.
- The input power is 550 W and it is set as the input heat flux of the arc which is around 894 kW/m. This heat flux is applied at the two surfaces where the arc is created during the process.
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Aleknaviciute, I. Plasma Assisted Decomposition of Methane and Propane and Cracking of Liquid Hexadecane. Ph.D. Thesis, Brunel University, Uxbridge, UK, 2014. [Google Scholar]
- Tao, X.; Bai, M.; Li, X.; Long, H.; Shang, S.; Yin, Y.; Dai, X. CH4-CO2 reforming by plasma—Challenges and opportunities. Prog. Energy Combust. Sci. 2011, 37, 113–124. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Ye, T.; Zhao, P.; Xia, W. Hydrogen production by reforming methane in a corona inducing dielectric barrier discharge and catalyst hybrid reactor. Chin. Sci. Bull. 2011, 56, 2162–2166. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Traversa, E. Solid oxide fuel cells (SOFCs): A review of an environmentally clean and efficient source of energy. Renew. Sustain. Energy Rev. 2002, 6, 433–455. [Google Scholar] [CrossRef]
- Jiang, W.; Fahimi, B. Multiport power electronic interface-concept, modeling, and design. IEEE Trans. Power Electron. 2011, 26, 1890–1900. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. An energetic–exergetic comparison between PEMFC and SOFC-based micro-CHP systems. Int. J. Hydrog. Energy 2011, 36, 3206–3214. [Google Scholar] [CrossRef]
- Gandiglio, M.; Lanzini, A.; Santarelli, M.; Leone, P. Design and optimization of a proton exchange membrane fuel cell CHP system for residential use. Energy Build. 2014, 69, 381–393. [Google Scholar] [CrossRef]
- Oh, S.D.; Kim, K.Y.; Oh, S.B.; Kwak, H.Y. Optimal operation of a 1-kW PEMFC-based CHP system for residential applications. Appl. Energy 2012, 95, 93–101. [Google Scholar] [CrossRef]
- Arsalis, A.; Nielsen, M.P.; Kær, S.K. Modeling and parametric study of a 1 kW e HT-PEMFC-based residential micro-CHP system. Int. J. Hydrog. Energy 2011, 36, 5010–5020. [Google Scholar] [CrossRef]
- Barelli, L.; Ottaviano, A. Solid oxide fuel cell technology coupled with methane dry reforming: A viable option for high efficiency plant with reduced CO2 emissions. Energy 2014, 71, 118–129. [Google Scholar] [CrossRef]
- Sreethawong, T.; Thakonpatthanakun, P.; Chavadej, S. Partial oxidation of methane with air for synthesis gas production in a multistage gliding arc discharge system. Int. J. Hydrog. Energy 2007, 32, 1067–1079. [Google Scholar] [CrossRef]
- O’Connor, A.M.; Ross, J.R. The effect of O2 addition on the carbon dioxide reforming of methane over Pt/ZrO2 catalysts. Catal. Today 1998, 46, 203–210. [Google Scholar] [CrossRef]
- Wang, S.; Lu, G.; Millar, G.J. Carbon dioxide reforming of methane to produce synthesis gas over metal-supported catalysts: State of the art. Energy Fuels 1996, 10, 896–904. [Google Scholar] [CrossRef]
- Jing, Q.; Lou, H.; Fei, J.; Hou, Z.; Zheng, X. Syngas production from reforming of methane with CO2 and O2 over Ni/SrO–SiO2 catalysts in a fluidized bed reactor. Int. J. Hydrog. Energy 2004, 29, 1245–1251. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Schmidt, L. Catalytic partial oxidation of natural gas to syngas. Fuel Process. Technol. 1995, 42, 109–127. [Google Scholar] [CrossRef]
- Odeyemi, O.O. Generation of Hydrogen-Rich Gas Using Non Equilibrium Plasma Discharges. PhD Thesis, Drexel University, Philadelphia, PA, USA, 2013. [Google Scholar]
- Petitpas, G.; Rollier, J.D.; Darmon, A.; Gonzalez-Aguilar, J.; Metkemeijer, R.; Fulcheri, L. A comparative study of non-thermal plasma assisted reforming technologies. Int. J. Hydrog. Energy 2007, 32, 2848–2867. [Google Scholar] [CrossRef]
- Gallagher, M.J.; Geiger, R.; Polevich, A.; Rabinovich, A.; Gutsol, A.; Fridman, A. On-board plasma-assisted conversion of heavy hydrocarbons into synthesis gas. Fuel 2010, 89, 1187–1192. [Google Scholar] [CrossRef]
- Deminsky, M.; Jivotov, V.; Potapkin, B.; Rusanov, V. Plasma-assisted production of hydrogen from hydrocarbons. Pure Appl. Chem. 2002, 74, 413–418. [Google Scholar] [CrossRef]
- Aleknaviciute, I.; Karayiannis, T.; Collins, M.; Xanthos, C. Towards clean and sustainable distributed energy system: The potential of integrated PEMFC-CHP. Int. J. Low-Carbon Technol. 2016, 11, 296–304. [Google Scholar] [CrossRef]
- Giddey, S.; Badwal, S.; Kulkarni, A.; Munnings, C. A comprehensive review of direct carbon fuel cell technology. Prog. Energy Combust. Sci. 2012, 38, 360–399. [Google Scholar] [CrossRef]
- Czernichowski, A. GlidArc assisted preparation of the synthesis gas from natural and waste hydrocarbons gases. Oil Gas Sci. Technol. 2001, 56, 181–198. [Google Scholar] [CrossRef]
- Diatczyk, J.; Komarzyniec, G.; Stryczewska, H. Power consumption of gliding arc discharge plasma reactor. Int. J. Plasma Environ. Sci. Technol. 2011, 5, 12–16. [Google Scholar]
- Bonner, B. Current Hydrogen Cost. Available online: https://www.hydrogen.energy.gov/pdfs/htac_oct13_10_bonner.pdf (accessed on 26 April 2018).
- Gutsol, A.; Bakken, J. A new vortex method of plasma insulation and explanation of the Ranque effect. J. Phys. D Appl. Phys. 1998, 31, 704. [Google Scholar] [CrossRef]
- Gutsol, A.; Larjo, J.; Hernberg, R. Comparative calorimetric study of ICP generator with forward-vortex and reverse-vortex stabilization. Plasma Chem. Plasma Process. 2002, 22, 351–369. [Google Scholar] [CrossRef]


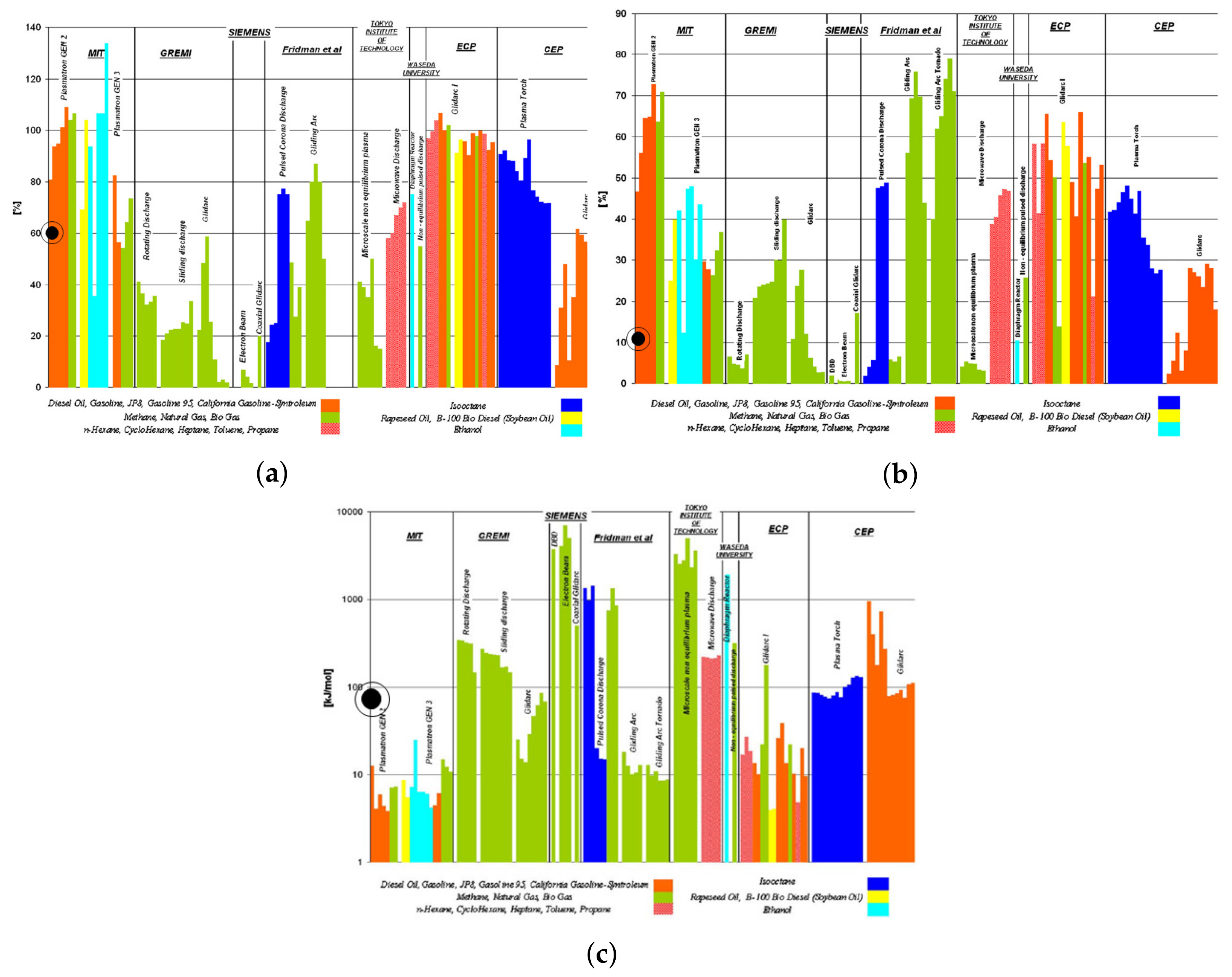
| CH Flow (L/min) | Air Flow (L/min) | V | I | %CH | %CO | %CO | %H |
|---|---|---|---|---|---|---|---|
| 4.167 | 10 | 120.1 | 0.9 | 23.88 | 1.87 | 0.35 | 4.99 |
| CH (L/min) | Air (L/min) | Total Flow | Power | %CH | %CO | %CO | %H | H() | Ratio | CH %conv. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.5 | 3.6 | 5.1 | 67.45 | 24.96 | 2.16 | 0.27 | 6.27 | 8.54 | 0.32 | 282.45 | 0.25&8.86 | |
| 1.5 | 3.6 | 5.1 | 83.029 | 20.19 | 3.78 | 0.53 | 9.88 | 5.31 | 0.56 | 404.17 | 0.49 | 17.62 |
| 1.5 | 3.6 | 5.1 | 98.9 | 21.65 | 3.10 | 0.41 | 8.30 | 7.07 | 0.46 | 277.64 | 0.38 | 13.96 |
| 1.5 | 3.6 | 5.1 | 155.93 | 19.20 | 3.75 | 0.63 | 9.25 | 7.68 | 0.54 | 209.64 | 0.48 | 18.55 |
| 1.875 | 4.5 | 6.375 | 67.45 | 22.91 | 2.56 | 0.41 | 6.67 | 6.95 | 0.45 | 397.62 | 0.29 | 11.46 |
| 1.875 | 4.5 | 6.375 | 164 | 18.51 | 4.11 | 0.74 | 10.27 | 6.19 | 0.76 | 278.89 | 0.55 | 20.75 |
| 1.875 | 4.5 | 6.375 | 138.8 | 16.33 | 5.87 | 1.50 | 7.07 | 8.30 | 0.52 | 223.68 | 0.43 | 31.09 |
| 2.25 | 5.4 | 7.65 | 108.09 | 21.26 | 3.08 | 0.51 | 8.08 | 6.18 | 0.68 | 375.48 | 0.38 | 14.45 |
| 2.25 | 5.4 | 7.65 | 127.4 | 20.45 | 3.35 | 0.59 | 8.66 | 6.10 | 0.74 | 347.84 | 0.42 | 16.17 |
| 2.25 | 5.4 | 7.65 | 148.51 | 20.14 | 3.59 | 0.65 | 9.17 | 6.20 | 0.78 | 316.52 | 0.46 | 17.38 |
| 2.25 | 5.4 | 7.65 | 153.6 | 19.33 | 3.94 | 0.73 | 10.18 | 5.60 | 0.88 | 344.84 | 0.53 | 19.46 |
| 2.25 | 5.4 | 7.65 | 156.6 | 19.14 | 3.96 | 0.74 | 10.15 | 5.64 | 0.89 | 339.31 | 0.53 | 19.72 |
| 2.25 | 5.4 | 7.65 | 164 | 18.90 | 4.08 | 0.77 | 10.50 | 5.56 | 0.92 | 336.68 | 0.56 | 20.43 |
| 2.25 | 5.4 | 7.65 | 134.55 | 15.48 | 4.07 | 1.10 | 8.39 | 5.47 | 0.85 | 377.14 | 0.54 | 25.04 |
| 2.625 | 6.3 | 8.925 | 164 | 18.86 | 4.23 | 0.84 | 10.63 | 5.11 | 1.08 | 394.84 | 0.56 | 21.18 |
| 2.625 | 6.3 | 8.925 | 137.16 | 15.49 | 4.39 | 1.20 | 8.96 | 4.91 | 1.03 | 451.49 | 0.58 | 26.52 |
| 3 | 7.2 | 10.2 | 138.8 | 13.57 | 4.36 | 1.35 | 5.20 | 7.33 | 0.75 | 323.69 | 0.38 | 29.61 |
| 3.75 | 9 | 12.75 | 67.45 | 25.49 | 1.42 | 0.29 | 3.81 | 10.48 | 0.49 | 431.76 | 0.15 | 6.29 |
| 4.167 | 10 | 14.167 | 108.09 | 22.72 | 2.22 | 0.49 | 5.32 | 7.70 | 0.81 | 447.17 | 0.23 | 10.64 |
| CH (L/min) | Air (L/min) | V | I | %CH | %CO | %CO | %H | H() | CH %conv. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.625 | 8.1 | 67.9 | 2.02 | 6.06 | 5.78 | 3.57 | 6.95 | 4.62 | 1.10 | 1.15 | 6.68 |
| 2.625 | 8.1 | 67.9 | 2.02 | 5.71 | 6.00 | 3.64 | 7.20 | 4.45 | 1.14 | 1.26 | 62.83 |
| 2.625 | 7.3 | 67.9 | 2.02 | 11.71 | 4.68 | 1.77 | 8.03 | 4.71 | 1.07 | 0.69 | 35.52 |
| 2.625 | 7.3 | 67.9 | 2.02 | 11.51 | 4.78 | 1.85 | 8.05 | 4.70 | 1.08 | 0.70 | 36.56 |
| 2.625 | 7.3 | 67.9 | 2.02 | 11.39 | 4.88 | 1.89 | 8.18 | 4.63 | 1.09 | 0.72 | 37.27 |
| 2.625 | 6.3 | 67.9 | 2.02 | 15.27 | 4.45 | 1.25 | 8.98 | 4.87 | 1.04 | 0.59 | 27.19 |
| 2.625 | 6.3 | 67.9 | 2.02 | 15.49 | 4.39 | 1.20 | 8.96 | 4.91 | 1.03 | 0.58 | 26.52 |
| 2.625 | 6.3 | 67.9 | 2.02 | 15.58 | 4.34 | 1.18 | 8.88 | 4.96 | 1.02 | 0.57 | 26.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobhansarbandi, S.; Maharjan, L.; Fahimi, B.; Hassanipour, F. Thermal Fluid Analysis of Cold Plasma Methane Reformer. Fluids 2018, 3, 31. https://doi.org/10.3390/fluids3020031
Sobhansarbandi S, Maharjan L, Fahimi B, Hassanipour F. Thermal Fluid Analysis of Cold Plasma Methane Reformer. Fluids. 2018; 3(2):31. https://doi.org/10.3390/fluids3020031
Chicago/Turabian StyleSobhansarbandi, Sarvenaz, Lizon Maharjan, Babak Fahimi, and Fatemeh Hassanipour. 2018. "Thermal Fluid Analysis of Cold Plasma Methane Reformer" Fluids 3, no. 2: 31. https://doi.org/10.3390/fluids3020031
APA StyleSobhansarbandi, S., Maharjan, L., Fahimi, B., & Hassanipour, F. (2018). Thermal Fluid Analysis of Cold Plasma Methane Reformer. Fluids, 3(2), 31. https://doi.org/10.3390/fluids3020031






