Time-Dependent Shear Stress Distributions during Extended Flow Perfusion Culture of Bone Tissue Engineered Constructs
Abstract
1. Introduction
2. Results
2.1. Construct Cellularity
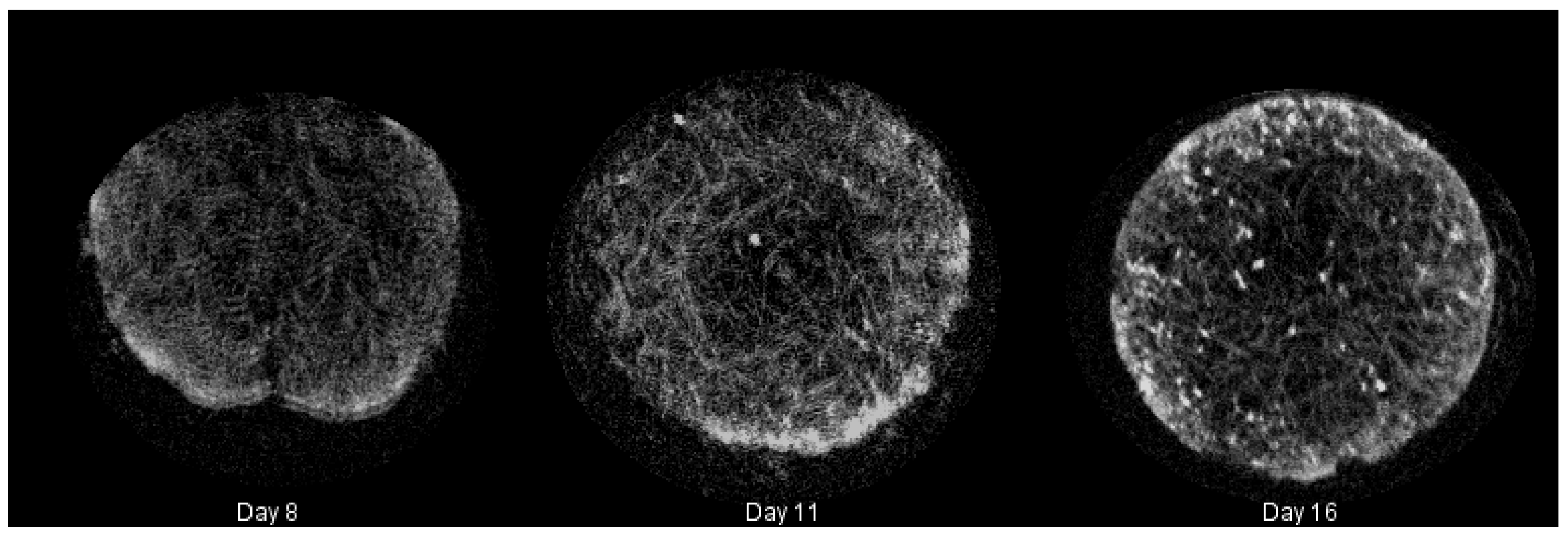
2.2. Calcium Deposition
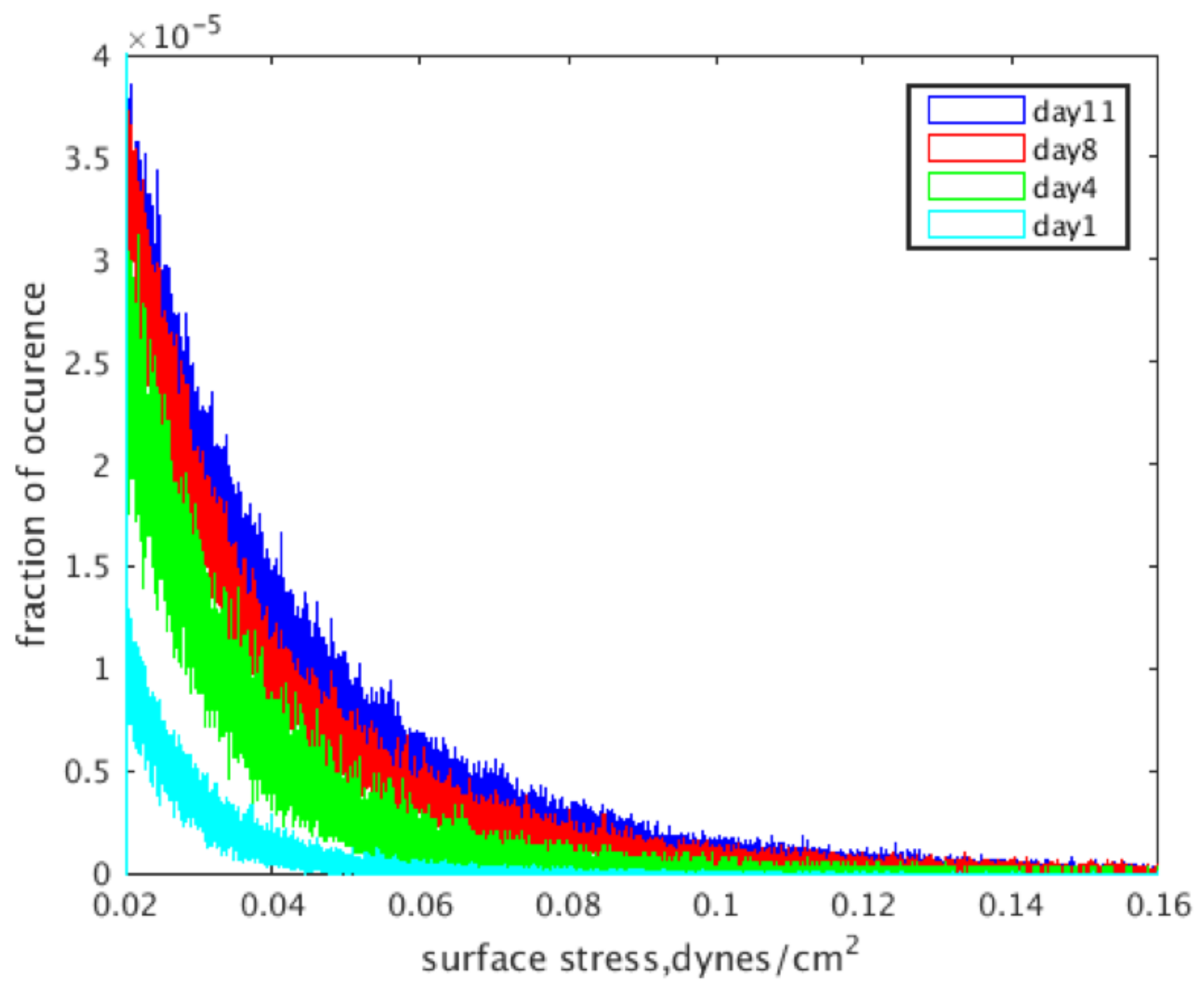
2.3. Shear Stress Distributions over Time
2.4. Effects of Calcium Deposition on Localized Shear Fields
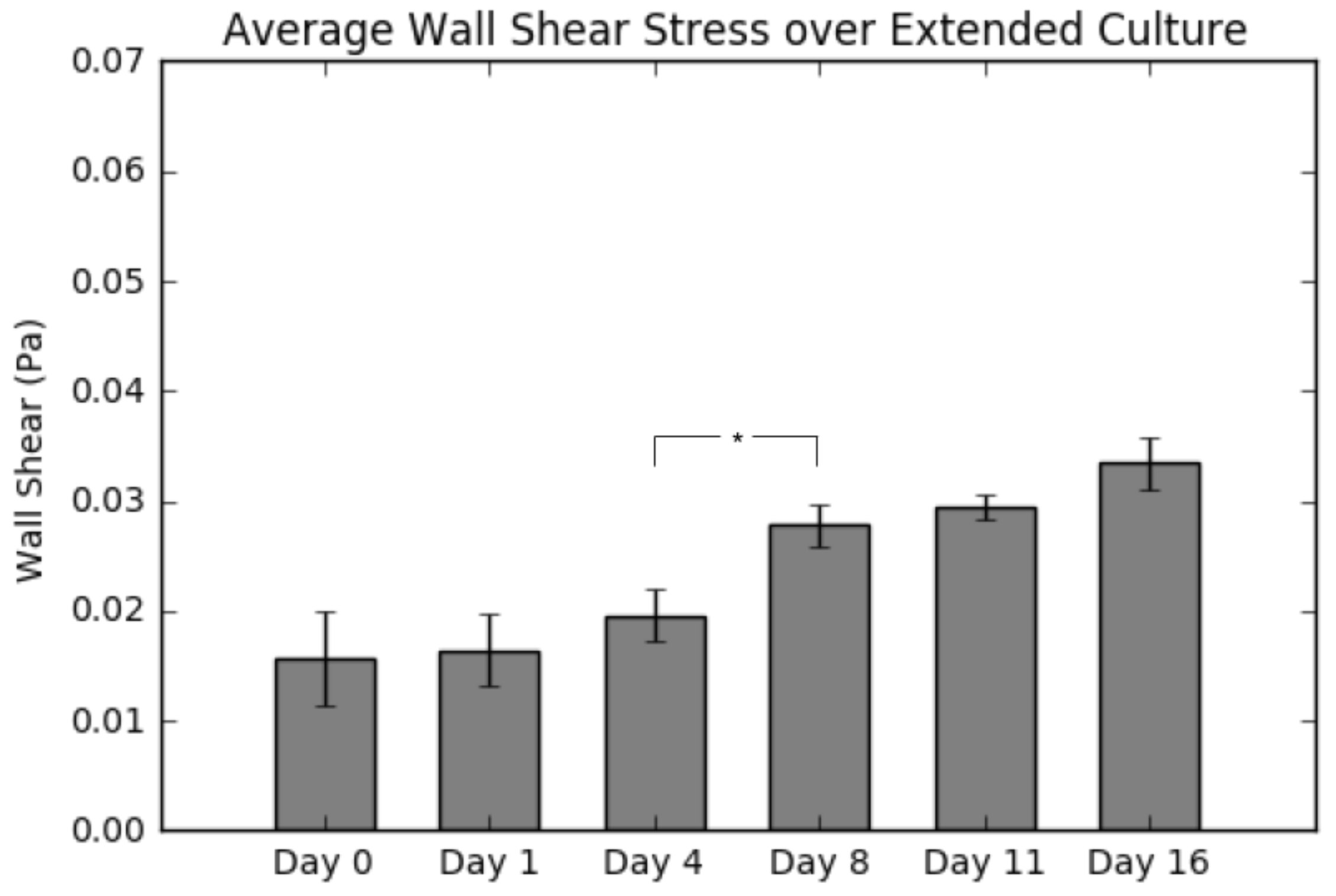
2.5. Average Wall Shear Stress
3. Discussion
4. Materials and Methods
4.1. Scaffold Manufacturing
4.2. Cell Expansion, Seeding and Culture
4.3. Construct Cellularity
4.4. Construct Calcium Deposition
4.5. Imaging and Reconstruction
4.6. CFD Simulations
Lattice Boltzmann Simulations
4.7. Statistical Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- VanGordon, S.B. Three-Dimensional Bone Tissue Engineering Strategies Using Polymeric Scaffolds. Ph.D. Thesis, The University of Oklahoma, Norman, OK, USA, 2012. [Google Scholar]
- Voronov, R.; VanGordon, S.; Sikavitsas, V.I.; Papavassiliou, D.V. Computational modeling of flow-induced shear stresses within 3D salt-leached porous scaffolds imaged via micro-CT. J. Biomech. 2010, 43, 1279–1286. [Google Scholar] [CrossRef] [PubMed]
- Melchels, F.P.; Tonnarelli, B.; Olivares, A.L.; Martin, I.; Lacroix, D.; Feijen, J.; Wendt, D.J.; Grijpma, D.W. The influence of the scaffold design on the distribution of adhering cells after perfusion cell seeding. Biomaterials 2011, 32, 2878–2884. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Barreto, J.F.; Linehan, S.M.; Shambaugh, R.L.; Sikavitsas, V.I. Flow perfusion improves seeding of tissue engineering scaffolds with different architectures. Ann. Biomed. Eng. 2007, 35, 429–442. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Barreto, J.F.; Sikavitsas, V.I. Improved mesenchymal stem cell seeding on RGD-modified poly(l-lactic acid) scaffolds using flow perfusion. Macromol. Biosci. 2007, 7, 579–588. [Google Scholar] [CrossRef] [PubMed]
- Du, D.J.; Furukawa KS, U.T. 3D culture of osteoblast-like cells by unidirectional or oscillatory flow for bone tissue engineering. Biotechnol. Bioeng. 2009, 102, 1670–1678. [Google Scholar] [CrossRef] [PubMed]
- Papantoniou, I.; Guyot, Y.; Sonnaert, M.; Kerckhofs, G.; Luyten, F.P.; Geris, L.; Schrooten, J. Spatial optimization in perfusion bioreactors improves bone tissue-engineered construct quality attributes. Biotechnol. Bioeng. 2014, 111, 2560–2570. [Google Scholar] [CrossRef] [PubMed]
- Campolo, M.; Curcio, F.; Soldati, A. Minimal perfusion flow for osteogenic growth of mesenchymal stem cells on lattice scaffolds. AIChE J. 2013, 59, 3131–3144. [Google Scholar] [CrossRef]
- Maes, F.; Van Ransbeeck, P.; Van Oosterwyck, H.; Verdonck, P. Modeling fluid flow through irregular scaffolds for perfusion bioreactors. Biotechnol. Bioeng. 2009, 103, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Cioffi, M.; Boschetti, F.; Raimondi, M.T.; Dubini, G. Modeling evaluation of the fluid-dynamic microenvironment in tissue-engineered constructs: A micro-CT based model. Biotechnol. Bioeng. 2006, 93, 500–510. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; Checa, S.; Prendergast, P.J.; Lacroix, D. Simulation of angiogenesis and cell differentiation in a CaP scaffold subjected to compressive strains using a lattice modeling approach. Biomaterials 2010, 31, 2446–2452. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Bergstrom, D.J.; Chen, X.B. A mathematical model and computational framework for three-dimensional chondrocyte cell growth in a porous tissue scaffold placed inside a bi-directional flow perfusion bioreactor. Biotechnol. Bioeng. 2015, 112, 2601–2610. [Google Scholar] [CrossRef] [PubMed]
- Guyot, Y.; Luyten, F.P.; Schrooten, J.; Geris, L. A three—Dimensional computational fluid dynamics model of shear stress distribution during neotissue growth in a perfusion bioreactor. Biotechnol. Bioeng. 2015, 112, 2591–2600. [Google Scholar] [CrossRef] [PubMed]
- Guyot, Y.; Papantoniou, I.; Luyten, F.P.; Geris, L. Coupling curvature-dependent and shear stress-stimulated neotissue growth in dynamic bioreactor cultures: A 3D computational model of a complete scaffold. Biomech. Model. Mechanobiol. 2015, 15, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Nava, M.M.; Raimondi, M.T.; Pietrabissa, R. A multiphysics 3D model of tissue growth under interstitial perfusion in a tissue-engineering bioreactor. Biomech. Model. Mechanobiol. 2013, 12, 1169–1179. [Google Scholar] [CrossRef] [PubMed]
- Checa, S.; Prendergast, P.J. A Mechanobiological Model for Tissue Differentiation that Includes Angiogenesis: A Lattice-Based Modeling Approach. Ann. Biomed. Eng. 2009, 37, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Voronov, R.S.; VanGordon, S.B.; Sikavitsas, V.I.; Papavassiliou, D.V. Distribution of flow-induced stresses in highly porous media. Appl. Phys. Lett. 2010, 97, 024101. [Google Scholar] [CrossRef]
- Porter, B.; Zauel, R.; Stockman, H.; Guldberg, R.; Fyhrie, D. 3-D computational modeling of media flow through scaffolds in a perfusion bioreactor. J. Biomech. 2005, 38, 543–549. [Google Scholar] [CrossRef] [PubMed]
- Childers, E.P.; Wang, M.O.; Becker, M.L.; Fisher, J.P.; Dean, D. 3D printing of resorbable poly(propylene fumarate) tissue engineering scaffolds. MRS Bull. 2015, 40, 119–126. [Google Scholar] [CrossRef]
- McCoy, R.J.; Jungreuthmayer, C.; O’Brien, F.J. Influence of flow rate and scaffold pore size on cell behavior during mechanical stimulation in a flow perfusion bioreactor. Biotechnol. Bioeng. 2012, 109, 1583–1594. [Google Scholar] [CrossRef] [PubMed]
- Wendt, D.; Marsano, A.; Jakob, M.; Heberer, M.; Martin, I. Oscillating perfusion of cell suspensions through three-dimensional scaffolds enhances cell seeding efficiency and uniformity. Biotechnol. Bioeng. 2003, 84, 205–214. [Google Scholar] [CrossRef] [PubMed]
- VanGordon, S.B.; Voronov, R.S.; Blue, T.B.; Shambaugh, R.L.; Papavassiliou, D.V.; Sikavitsas, V.I. Effects of scaffold architecture on preosteoblastic cultures under continuous fluid shear. Ind. Eng. Chem. Res. 2011, 50, 620–629. [Google Scholar] [CrossRef]
- Kasper, F.K.; Liao, J.; Kretlow, J.D.; Sikavitsas, V.I.; Mikos, A.G. Flow Perfusion Culture of Mesenchymal Stem Cells for Bone Tissue Engineering; StemBook, Harvard Stem Cell Institute: Cambridge, MA, USA, 2008. [Google Scholar]
- Bancroft, G.N.; Sikavitsas, V.I.; Van Den Dolder, J.; Sheffield, T.L.; Ambrose, C.G.; Jansen, J.A.; Mikos, A.G. Fluid flow increases mineralized matrix deposition in 3D perfusion culture of marrow stromal osteoblasts in a dose-dependent manner. Proc. Natl. Acad. Sci. USA 2002, 99, 12600–12605. [Google Scholar] [CrossRef] [PubMed]
- Porter, J.R.; Ruckh, T.T.; Popat, K.C. Bone tissue engineering: A review in bone biomimetics and drug delivery strategies. Biotechnol. Prog. 2009, 25, 1539–1560. [Google Scholar] [CrossRef] [PubMed]
- Voronov, R.S.; VanGordon, S.B.; Shambaugh, R.L.; Papavassiliou, D.V.; Sikavitsas, V.I. 3D tissue-engineered construct analysis via conventional high-resolution microcomputed tomography without X-ray contrast. Tissue Eng. Part C Methods 2013, 19, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Pham, N.H.; Voronov, R.S.; VanGordon, S.B.; Sikavitsas, V.I.; Papavassiliou, D.V. Predicting the stress distribution within scaffolds with ordered architecture. Biorheology 2012, 49, 235–247. [Google Scholar] [PubMed]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T., Jr. Lattice Boltzmann Modeling an Introduction for Geoscientists and Engineers; Springer: Berlin, Germany; New York, NY, USA, 2006; 172p. [Google Scholar]
- Kandhai, D.; Koponen, A.; Hoekstra, A.G.; Kataja, M.; Timonen, J.; Sloot, P.M.A. Lattice-Boltzmann hydrodynamics on parallel systems. Comput. Phys. Commun. 1998, 111, 14–26. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhang, X.X.; Bengough, A.G.; Crawford, J.W. Domain-decomposition method for parallel lattice Boltzmann simulation of incompressible flow in porous media. Phys. Rev. E 2005, 72, 016706. [Google Scholar] [CrossRef] [PubMed]
- Cosgrove, J.A.; Buick, J.M.; Tonge, S.J.; Munro, C.G.; Greated, C.A.; Campbell, D.M. Application of the lattice Boltzmann method to transition in oscillatory channel flow. J. Phys. Math. Gen. 2003, 36, 2609–2620. [Google Scholar] [CrossRef]
- Gabbanelli, S.; Drazer, G.; Koplik, J. Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar] [CrossRef] [PubMed]
- Boyd, J.; Buick, J.; Green, S. A second-order accurate lattice Boltzmann non-Newtonian flow model. J. Phys. Math. Gen. 2006, 39, 14241–14247. [Google Scholar] [CrossRef]
- Yoshino, A.; Hotta, Y.; Hirozane, T.; Endo, M. A numerical method for incompressible non-Newtonian fluid flows based on the lattice Boltzmann method. J. Non-Newton. Fluid Mech. 2007, 147, 69–78. [Google Scholar] [CrossRef]
- Swift, M.R.; Orlandini, E.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 1996, 54, 5041–5052. [Google Scholar] [CrossRef]
- McNamara, G.; Zanetti, G. Use of the Boltzmann equation to simulate Lattice-gas automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef] [PubMed]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Voronov, R.S.; VanGordon, S.B.; Sikavitsas, V.I.; Papavassiliou, D.V. Efficient Lagrangian scalar tracking method for reactive local mass transport simulation through porous media. Int. J. Numer. Methods Fluids 2011, 67, 501–517. [Google Scholar] [CrossRef]
- Qian, Y.H.; Dhumieres, D.; Lallemand, P. Lattice Bgk models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Lakhotia, S.; Papoutsakis, E.T. Agitation induced cell injury in microcarrier cultures—Protective effect of viscosity is agitation intensity dependent—Experiments and modeling. Biotechnol. Bioeng. 1992, 39, 95–107. [Google Scholar] [CrossRef] [PubMed]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, C.; Kadri, O.E.; Voronov, R.S.; Sikavitsas, V.I. Time-Dependent Shear Stress Distributions during Extended Flow Perfusion Culture of Bone Tissue Engineered Constructs. Fluids 2018, 3, 25. https://doi.org/10.3390/fluids3020025
Williams C, Kadri OE, Voronov RS, Sikavitsas VI. Time-Dependent Shear Stress Distributions during Extended Flow Perfusion Culture of Bone Tissue Engineered Constructs. Fluids. 2018; 3(2):25. https://doi.org/10.3390/fluids3020025
Chicago/Turabian StyleWilliams, Cortes, Olufemi E. Kadri, Roman S. Voronov, and Vassilios I. Sikavitsas. 2018. "Time-Dependent Shear Stress Distributions during Extended Flow Perfusion Culture of Bone Tissue Engineered Constructs" Fluids 3, no. 2: 25. https://doi.org/10.3390/fluids3020025
APA StyleWilliams, C., Kadri, O. E., Voronov, R. S., & Sikavitsas, V. I. (2018). Time-Dependent Shear Stress Distributions during Extended Flow Perfusion Culture of Bone Tissue Engineered Constructs. Fluids, 3(2), 25. https://doi.org/10.3390/fluids3020025





