1. Introduction
In the past few years, there have been at least two studies of tropical cyclone dynamics using a model called “Three-Dimensional Vortex Perturbation Analysis and Simulation” (3DVPAS), a linearized numerical model designed to analyze some aspects of symmetric and asymmetric vortex dynamics, including the dynamics of tropical cyclone and tornado vortices [
1,
2]. The 3DVPAS model neglects all nonlinear terms involving the axisymmetric flow, but generalizes classic balance models in that it retains linear unbalanced processes including radially and vertically propagating inertia-gravity waves. The studies reported in [
1,
2] apply the 3DVPAS model to the evolution of an axisymmetric tropical cyclone vortex by forcing the model with azimuthally-averaged outputs from three-dimensional, non-hydrostatic numerical simulations of an intensifying tropical cyclone, or a tropical cyclone undergoing secondary eyewall formation. The averaged outputs represent heating and forces arising from eddy processes in the numerical simulations. Therefore, these studies can be seen as a revival of the axisymmetric “convective ring model” of tropical cyclone intensification originally proposed in [
3,
4], but can be seen also as a generalization thereof because the original ring model assumed axisymmetric balance dynamics.
Ref. [
1] used the 3DVPAS model to diagnose the relative roles of the heat and tangential momentum forcing in the formation of a simulated secondary eyewall as predicted by the three-dimensional Weather Research and Forecasting (WRF) model. The solutions for the transverse circulation using the 3DVPAS model were found to be qualitatively similar to the transverse circulation diagnosed from the WRF model. However, the theoretical justification for the neglect of the nonlinear terms was not provided. At a minimum, one needs to verify that all the nonlinear terms, when evaluated using the linear solutions, are small in comparison to the retained linear terms.
In a more recent study, Ref. [
2] used the same methodology as employed in [
1] to diagnose the relative roles of the heat and tangential momentum forcing distributions in the intensification of a tropical cyclone using again the WRF model, but for another intensifying storm.
Because of the linearization built into the 3DVPAS model, this use of it cannot address the situation within the frictional boundary layer in the inner-core region of the storm where the flow is intrinsically nonlinear [
5,
6,
7]. As discussed in earlier publications (e.g., [
7,
8,
9,
10]), there is an intrinsically nonlinear boundary layer spinup process, which, as discussed in [
7], involves strong, non-Ekman-like nonlinearities in an essential way, with dramatic consequences such as the generation of strong supergradient winds within the boundary layer. These supergradient winds include the strongest and most destructive winds found anywhere within a mature tropical cyclone.
The inherently linear nature of the 3DVPAS model means that its use in Refs. [
1,
2] produces results that are misleading in two ways. The first is simply that important nonlinear terms are neglected, and the second is that, in using the results to examine the relative importance of heat and tangential momentum forcing, the linear superposition principle is tacitly assumed. That is, it is assumed that the heat and momentum forcing processes can be considered separately, with effects that are additive. The superposition principle fails as soon as nonlinearity is significant, and fails drastically when nonlinearity is strong. In particular, its use in Ref. [
2] to cast doubt on the nonlinear boundary layer spinup mechanism is, in our view, unjustified.
The objectives of this paper are twofold. The first is to examine the validity of the 3DVPAS model, summarized in
Section 2, for a class of axisymmetric vortex flows forced by azimuthally-averaged diabatic and frictional terms diagnosed from a state-of-the art three-dimensional mesoscale numerical model (
Section 3). The specific goal in this context is to quantify the errors introduced by the neglect of the nonlinear terms in the governing equations in the inner-core region of the storm (
Section 4). We show that the inner-core nonlinear terms are already significant even at an early stage of tropical cyclone intensification, much earlier than expected from the recent results of [
7] who examined a later stage of tropical cyclone intensification and secondary eyewall formation. Our findings, together with those of [
7], suggest that the emergence of strong nonlinearities outside the scope of 3DVPAS invalidates the use of 3DVPAS for diagnosing and interpreting complex numerical model solutions for maturing and mature tropical cyclones that possess such strong nonlinearities.
A second, and subsidiary, objective (
Section 5) is to examine the use of the traditional Sawyer–Eliassen (hereafter SE) model of transverse circulations, in this same context of maturing and mature tropical cyclones. The SE model was used in [
2] to cast further doubt on the existence of nonlinear spinup. However, the SE model is linear, by assumption, in the same sense as the 3DVPAS model, and is subject to additional limitations through its assumption of strictly balanced motion. Neither assumption is compatible with the nonlinear boundary-layer dynamics. For instance, when the boundary-layer inflow separates and turns upward into the eyewall, not only are the non-Ekman-like nonlinearities strong, but departures from balance can become significant in the form of axisymmetric inertia-gravity waves launched into the eyewall upflow [
11].
Section 5 discusses the extent to which these limitations might be overcome in future work.
Section 6 offers concluding remarks.
2. A Forced Axisymmetric Convective Ring Model Revisited
The time-dependent linear vortex model 3DVPAS was developed originally to examine linear, non-hydrostatic, asymmetric wave-like disturbances and their wave, mean-flow interactions in tropical cyclones and tornado vortices [
12]. The model solves for linear disturbances to a basic-state circular vortex in gradient and hydrostatic balance and has produced many insightful results for a wide class of asymmetric vortex wave and instability problems in tornado and tropical-cyclone-like vortices (e.g., [
12,
13,
14,
15,
16,
17]).
Follow-up work by [
17,
18] adapted this model to solve for the azimuthal-wavenumber-zero disturbance and corresponding velocity and temperature tendencies subject to the imposed forcing of diabatic heating, and momentum sources/sinks for physically-motivated forcing distributions in either tornadoes or tropical cyclones. This is the version of the model used in [
1,
2], where the model configurations assume an initially zero radial and vertical flow and a zero vertical gradient of basic-state tangential velocity below a nominal height that spans a large part of the boundary layer; see assumption (1) below Equation (
11).
The 3DVPAS model used here is the version described in [
19]. It uses a non-standard form of the anelastic equations known as the “vortex-anelastic equations”, in which the basic-state density
and potential temperature
are allowed to depend on radial distance
r as well as on altitude
z, as appropriate for a strong vortex. For the full set of equations, the reader is referred to [
19].
The subset of equations from Ref. [
19] needed here, and the notation to be used, are as follows. The azimuthal-wavenumber-zero disturbance flow predicted by the 3DVPAS model is denoted by a zero subscript. The asymmetric (eddy) disturbance flow is denoted by a prime. By definition, primed quantites have zero azimuthal average. They are diagnosed from the WRF model output at hour 27 (see below). The corresponding eddy forcing terms, in Equations (
6) and (
10) below, are switched on at the initial time
of the 3DVPAS model. For times
, we write
, where
is the frozen-in-time circular vortex tangential velocity field in gradient wind and hydrostatic balance at
(i.e., at WRF hour 27), and
, the tangential velocity disturbance that develops in response to the imposed eddy forcing and satisfies
. Similarly, we write
, where
is the forced radial velocity disturbance satisfying
. Similar definitions apply for the vertical velocity, pressure, and potential temperature fields. Respectively, these are
,
, and
, where
,
, and
. The anelastic density field
is a fixed basic-state-only quantity,
.
With these definitions, the horizontal momentum equations become
where
denotes twice the local absolute rotation rate of the basic-state vortex, and
denotes its local absolute vorticity. The remaining terms are defined in Equations (
5)–(
8) below. The basic-state pressure field
is assumed to be in gradient wind balance with
:
and in hydrostatic balance with
,
where
g is the gravitational acceleration. This basic-state vortex is constructed by azimuthally averaging the WRF model output, as described in the next section; see also assumption (1) below Equation (
11).
The terms
and
in Equations (
1) and (
2) represent the imposed forcing and are defined by
Here an overbar denotes the azimuthal average, and, as before, the primed (eddy) quantities the deviations therefrom, with zero average; denotes the eddy vertical vorticity ), is the azimuthal angle and and denote the subgrid-scale velocity tendencies associated with surface friction and unresolved turbulent mixing processes (modeled by diffusion) in the planetary boundary layer and vortex interior.
The terms
and
in Equations (
1) and (
2) are the nonlinear terms arising from the self-advection and curvilinear acceleration of the wavenumber-zero disturbance flow, and are defined as follows:
and there is a similar term
in the (non-hydrostatic) vertical momentum equation equal to minus the self-advection of
by the wavenumber-zero disturbance flow. The vertical momentum equation also contains a term
term analogous to
in Equation (
5), but with
replaced by
in the radial and vertical derivatives. However, we do not display these terms because the corresponding disturbances to hydrostatic balance were found to be relatively unimportant.
In a similar manner, the tendency equation for the wavenumber-zero disturbance potential temperature is given by
The thermal forcing function
Q in Equation (
9) is defined similarly to Equations (
5) and (
6) as follows:
where
is the diabatic (radiative plus latent-heat) contribution to the material derivative of the potential temperature in the WRF model, and
denotes the heating rate due to subgrid-scale diffusion of potential temperature. In Equation (
9),
is the nonlinear term arising from the advection of the wavenumber-zero disturbance potential temperature by the wavenumber-zero disturbance flow and is defined as follows:
When the quadratic terms
,
,
, and
associated with the wavenumber-zero disturbance flow are small compared with the corresponding linear terms (defined by the first-order disturbance terms on the right-hand sides of Equations (
1), (
2) and (
9)), it is justifiable to drop these quadratic terms in the foregoing equations. The 3DVPAS model for the wavenumber-zero disturbance flow is defined by the resulting linearized equations.
In their application of the 3DVPAS equations, Refs. [
1,
2] make three additional assumptions. We will make the same assumptions here so as not to introduce additional complexity when comparing with their published solutions: (1) in evaluating
from the azimuthally-averaged tangential wind in the WRF model, we take its value at 490 m altitude and extend that value downward so as to be independent of
z below 490 m; (2) we assume a stress-free boundary condition on the disturbance horizontal velocity at
; (3) we neglect the
forcing term, and its vertical counterpart
, keeping only
and
Q, i.e., using only Equations (
6) and (
10).
Although we thus follow [
1,
2] in adopting their assumptions (1)–(3), we should point out before going further that we consider all three to be questionable. Assumption (1) is questionable because the condition
at the lower boundary is inconsistent with the frictional, subgrid scale forcing diagnosed there from the WRF model, which is used to force the linear 3DVPAS model. Assumption (2) is questionable because the stress-free boundary condition implies that the disturbance flow at the lower boundary is subject to an artificial momentum source at the boundary. Finally, regarding assumption (3), although the neglect of
is certainly acceptable for the system-scale vortex dynamics, recent work by [
7] has shown that
is, by contrast,
not negligible—in fact comparable to
in the boundary layer, as is usual in rotating frictional boundary layers. Ref. [
7] used a modestly high resolution cloud-permitting numerical simulation of an idealized tropical cyclone. We find the same to be true for the WRF model output used here (not shown).
is comparable to
in the boundary layer because of the subgrid (frictional) contributions
and
that tend to dominate there. Together with assumptions (1) and (2), the neglect of
seriously distorts the boundary-layer dynamics by suppressing the frictionally-induced imbalance of the radial force field, which is an important component in producing strong low-level inflow.
We point out here further that Refs. [
1,
2] tacitly make an additional assumption by discarding the prime–prime eddy terms in Equations (
6) and (
10). Both Refs. [
1,
2] use the linear model with only the
terms retained in Equations (
6) and (
10) along with the
term in Equation (
10). (From Ref. [
1] (p. 2632): “
The latent heating and the azimuthal component of friction from WRF are used to force 3DVPAS”. From Ref. [
2] (p. 1294): “
The 12-h time-averaged WRF diabatic heating and PBL tangential wind tendency are shown in Figure 13c and 13d, respectively. The diabatic heating comes from direct model output from the WSM6 microphysics scheme, and the PBL term is the parameterized frictional tendency on tangential winds from the Yonsei University (YSU) scheme. We use these time-averaged tendencies as constant forcing terms for 3DVPAS”.) However, since the WRF model is a fully three-dimensional model, and since three-dimensional eddy processes have been shown to be a non-negligible and important components of the intensification process of an idealized tropical cyclone [
11], we prefer to retain the prime–prime eddy terms here.
For the calculations presented here, the forcing terms for the disturbance tangential velocity and diabatic heating (including the azimuthal average of the corresponding prime-prime eddy terms) are calculated from the WRF model output using the residual method:
and
Here, (
U,
V,
W,
) denote the azimuthally-averaged radial, tangential and vertical velocity components, and the potential temperature, diagnosed from the WRF model output. By contrast with assumption (1) above, the symbol
V now temporarily includes the model’s boundary–layer structure below 490 m. These quantities and the differential operations in Equations (
12) and (
13) are evaluated at hour 27 in the WRF simulation, corresponding to
in the 3DVPAS model. The time derivatives are computed as centered differences using data at hours 28 and 26. No formal accuracy is lost here by using the residual method because it has the same accuracy as a direct evaluation of
and
Q from Equations (
5), (
6) and (
10). (To address a possible question about the potential inaccuracy of the residual method, for obtaining the partial time derivative terms using relatively coarse (1 h) model output, we have found that in Equations (
12) and (
13), the forcing terms
and
Q are dominated by the vertical and horizontal advection terms, and are relatively insensitive to the time derivatives and therefore still less sensitive to the precise time interval used to evaluate the finite differences. To assess the robustness of the residual method,
and
Q were calculated in two ways: the first calculation retained the advection terms, but discarded the time derivative terms altogether; the second calculation retained both the time derivative and the advection terms using the 1 h model output. The two results were found to be virtually identical.)
3. Forcing the 3DVPAS Model
The data used to force the 3DVPAS model are derived from a realistic WRF simulation of Hurricane Igor (2010). The storm reached tropical cyclone Category 4 in the Saffir–Simpson scale [
20]. At the chosen time, hour 27, the storm was far less intense and in Category 1, but we will see that, even then, the nonlinearities were already becoming significant. Quadratic nonlinearities scale with the square of the wind speed, and so increase very steeply as Category 1 goes into Category 4.
The full-physics simulation was integrated with the Advanced Research core of the WRF model (ARW, [
21]) version 3.2. The simulation was integrated by the Hurricane Group in the Mesoscale and Microscale Meteorology Division of the National Center for Atmospheric Research (NCAR). It is one of a set of model integrations that have been carried out since 2004 [
22,
23]. The simulation has three nested domains, with horizontal grid spacings of 12, 4 and 1.33 km (with
,
, and
grid points, respectively), each of them with 35 vertical levels and each of them in a two-way nesting configuration. The outer domain is fixed and the two inner nests are centered at the location of the minimum 500 hPa geopotential height, with repositioning performed every 15 min. The Kain–Fritsch cumulus parameterization is used on the outer domain, but the inner domains have no cumulus parameterization since they run in cloud-permitting mode. The simulation uses the Yonsei University (YSU) scheme for the planetary boundary layer [
24], a first-order closure scheme similar to the scheme of [
25], but thought to be less biased towards excessive vertical mixing [
26]. The surface drag algorithm follows [
27]. The surface exchange coefficient for heat flux uses a similarity relationship [
21] and that for water vapor follows [
28]. The simulation was initialized at 12:00 a.m. UTC 11 September and integrated for 120 h. At hour 27, having reached Category 1, the storm was only just becoming a tropical cyclone, and a coherent eyewall was imminent rather than fully formed.
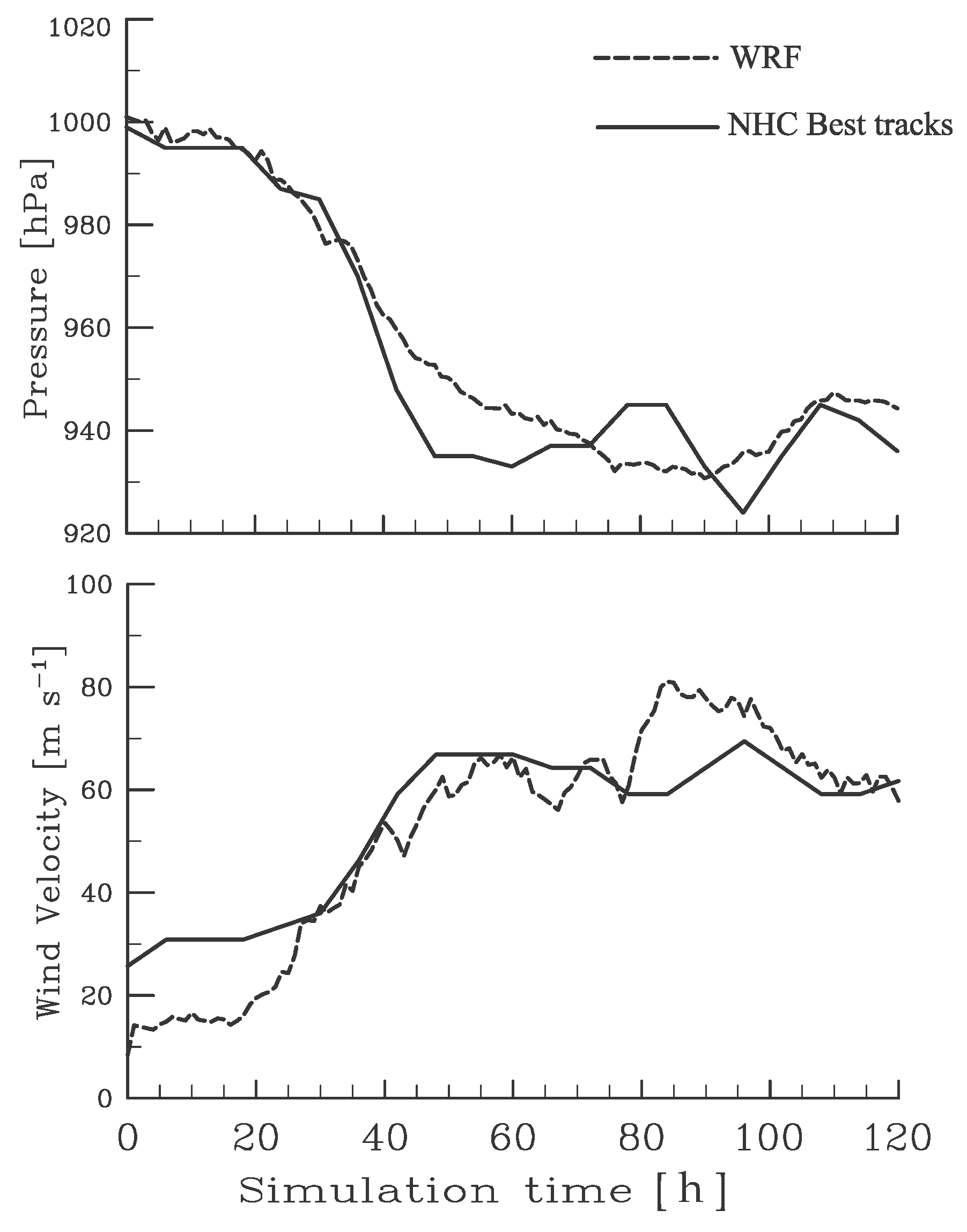
Figure 1 shows the hourly evolution of maximum azimuthally averaged tangential wind velocity and minimum sea level pressure in the inner core of the WRF integration along with the corresponding 6-hourly National Hurricane Center best track information. The figure shows a relatively good performance of the simulation, particularly near hour 27, the focus time of our analysis. The model integration captures the evolution of minimum sea level pressure particularly well in the first 40 h of integration. Within this period, the evolution of maximum wind velocity is relatively well captured also, after a gestation period during which the boundary layer becomes established and moistened by the surface moisture flux (not shown). The storm intensity evolution after hour 70 is largely influenced by the eyewall replacement cycle that Igor (2010) underwent. This notable structure, as well as the intensity change of Hurricane Igor, were well captured by the model integration (not shown) despite some discrepancies between the model integration and the Best Tracks dataset in terms of the variables shown in
Figure 1.
To obtain the basic-state vortex fields, the azimuthal average pressure and density fields at hour 27 are used to derive
V as the corresponding gradient wind field from Equation (
3), as in [
29]. The resulting
V field is then smoothed with three-point running averages in the horizontal and in the vertical, applied twice each. (If the un-smoothed gradient wind is used to integrate the 3DVPAS model as explained in this manuscript, the model kinematic fields evolve unrealistically and absurdly large values are soon generated. In particular, the radial velocity exhibits values that surpass 50 m
in the upper troposphere, within the first two hours of integration.) The
V field below 490 m is then altered to comply with assumption (1) below Equation (
11). From the
V field thus altered, the balanced pressure, density and temperature fields, including a correspondingly altered
field, are obtained using Equations (
3) and (
4) and the methodology of [
30].
4. Results
The time period around hour 27 is sufficient for illustrating the main point of this paper, i.e. the failure of the linear approximation even at this early stage of intensification. Similar analyses have been carried out for later times, including the time of the secondary eyewall formation period of Igor. As expected, they all show nonlinearities much stronger than those found below.
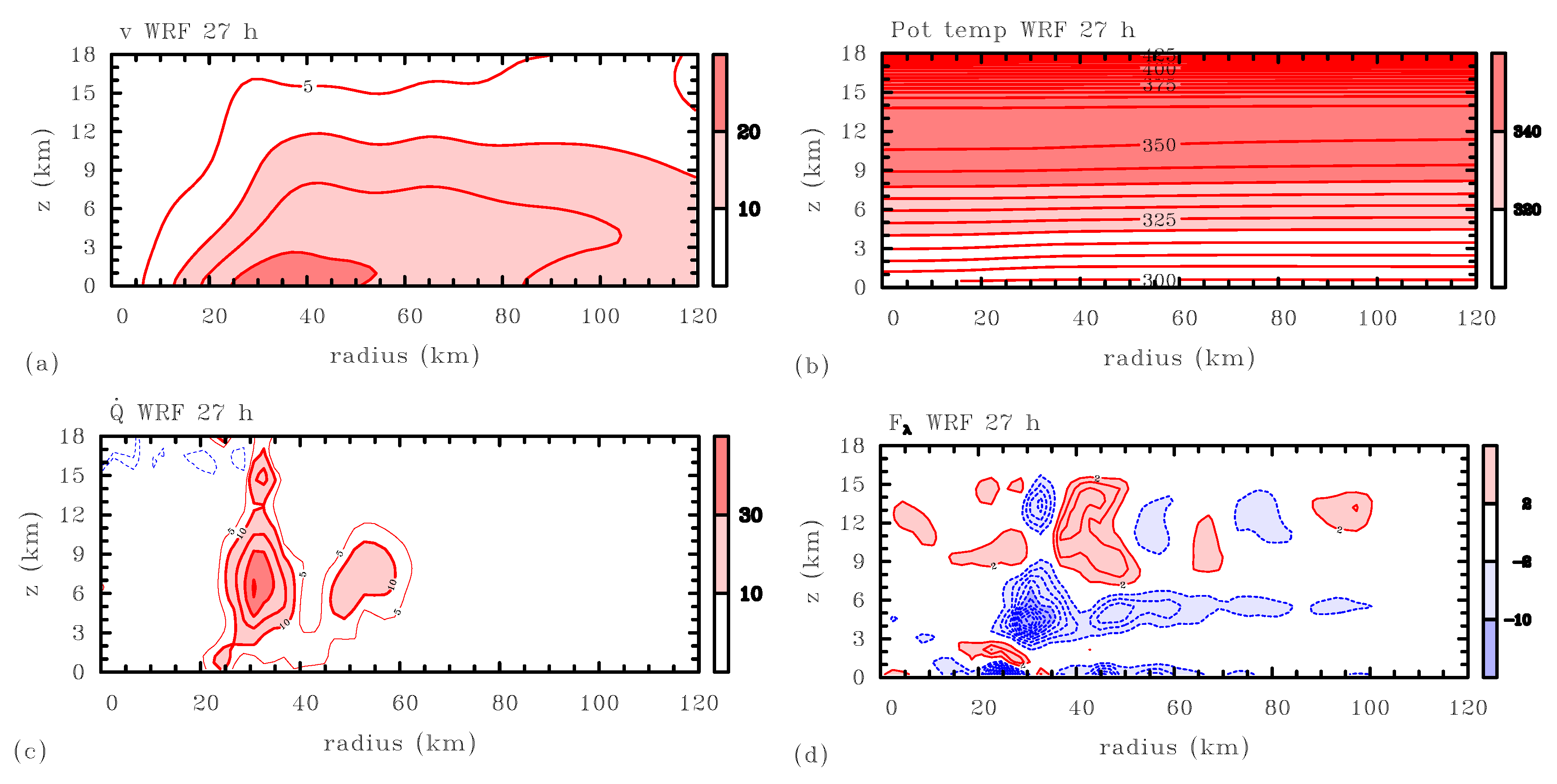
Figure 2 shows the basic-state
V and
fields and the corresponding forcing terms
Q and
, as inferred from the WRF simulation at hour 27, but made consistent with assumption (1) as just explained. The
V and
fields are characteristic of a warm-cored cyclonic vortex in hydrostatic and gradient-wind balance.
V has a maximum of approximately 25 m
near the lower surface and decreases monotonically with height, while the
isopleths curve downwards with decreasing radius. By itself, the
Q pattern (
Figure 2c) suggests an annular eyewall with a localized heating pattern extending through the troposphere and sloping outwards. However, at this early stage of development, the convection exhibits a high degree of asymmetry and the
Q pattern comes from vertically coherent vortical plumes [
11,
31]. The
field (
Figure 2d) exhibits a more complex pattern. First, as expected near the surface, there is a broad region out to a radius of about 60–70 km where
is largely negative. This reflects the near-surface friction felt by the tangential wind. Other prominent features are regions of strong positive and negative
within and near the incipient eyewall. Since
is computed as a residual, from Equation (
12), it contains implicitly the rectified effect of eddy processes as noted above Equation (
12).
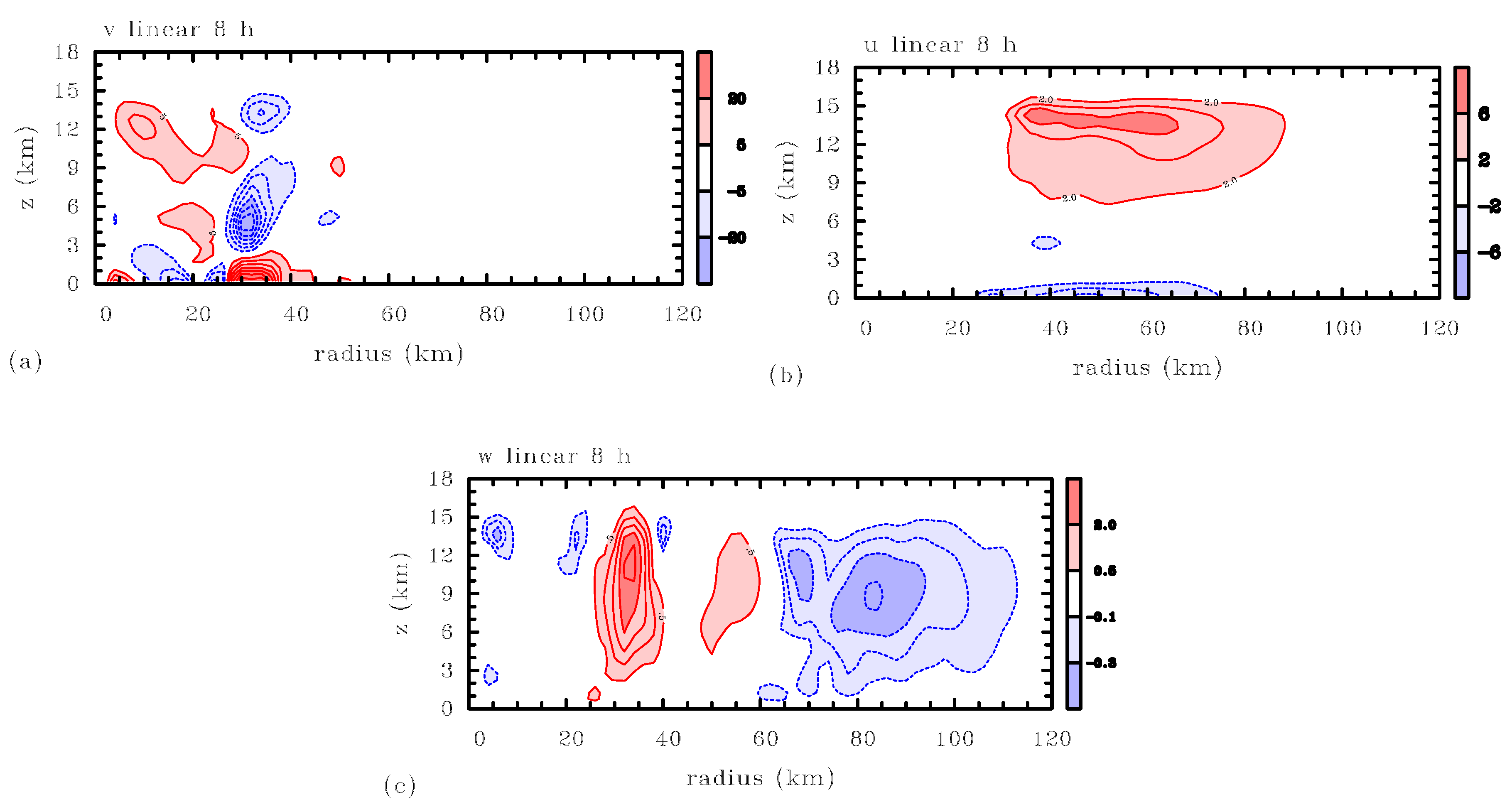
Figure 3 shows the
,
, and
fields from the linear 3DVPAS model output at
h, similar to integration times used in [
1,
2]. The
pattern has positive values in the lower troposphere, just below the base of the
Q maximum in
Figure 2c, and negative values within that maximum. The positive
values at low levels are due primarily to the radial influx of basic-state vertical absolute vorticity, the linear term
in Equation (
2). It dominates the other linear term
as well as the forcing term
, whose negative values are evident in
Figure 2d. Earlier, at
h, we have already seen positive values of
at low levels, as hinted in
Figure 4a below. Returning to
Figure 3a and
h, we see that
is negative somewhat higher in the troposphere. This is probably due primarily to the negative
values seen there in
Figure 2d. In
Figure 3b, the
field shows a shallow layer of relatively strong inflow below 1 km, and an upper-level outflow in the layer between about 11 and 15 km. In
Figure 3c, the
structure near the incipient eyewall largely mimics the
Q structure seen in
Figure 2d, with a primary maximum of 2.5 m
at
km and
km. The
structure has a secondary maximum between 0.5 m
and 1.0 m
at
km and
km and a strong, broad minimum at
km and
km.
Returning to the main point of this paper, we show now that, in this Hurricane Igor example, the 3DVPAS model becomes invalid, that is to say self-inconsistent, well before h. We show this by taking the 3DVPAS model output and using that output to evaluate some of the nonlinear terms that are neglected in the model. We then observe that these terms are not all uniformly small in magnitude by comparison with the terms that are retained, in defining the model and its response to the imposed forcing.
We focus attention on Equations (
1) and (
2), in which the tendencies or rates of change as the model responds to the imposed forcing are determined entirely by the forcing terms together with the linear terms. The linear terms are the first pair of terms on each right-hand side of Equations (1) and (2), whose sums will be referred to as the “
u linear tendency” and the “
v linear tendency”, respectively.
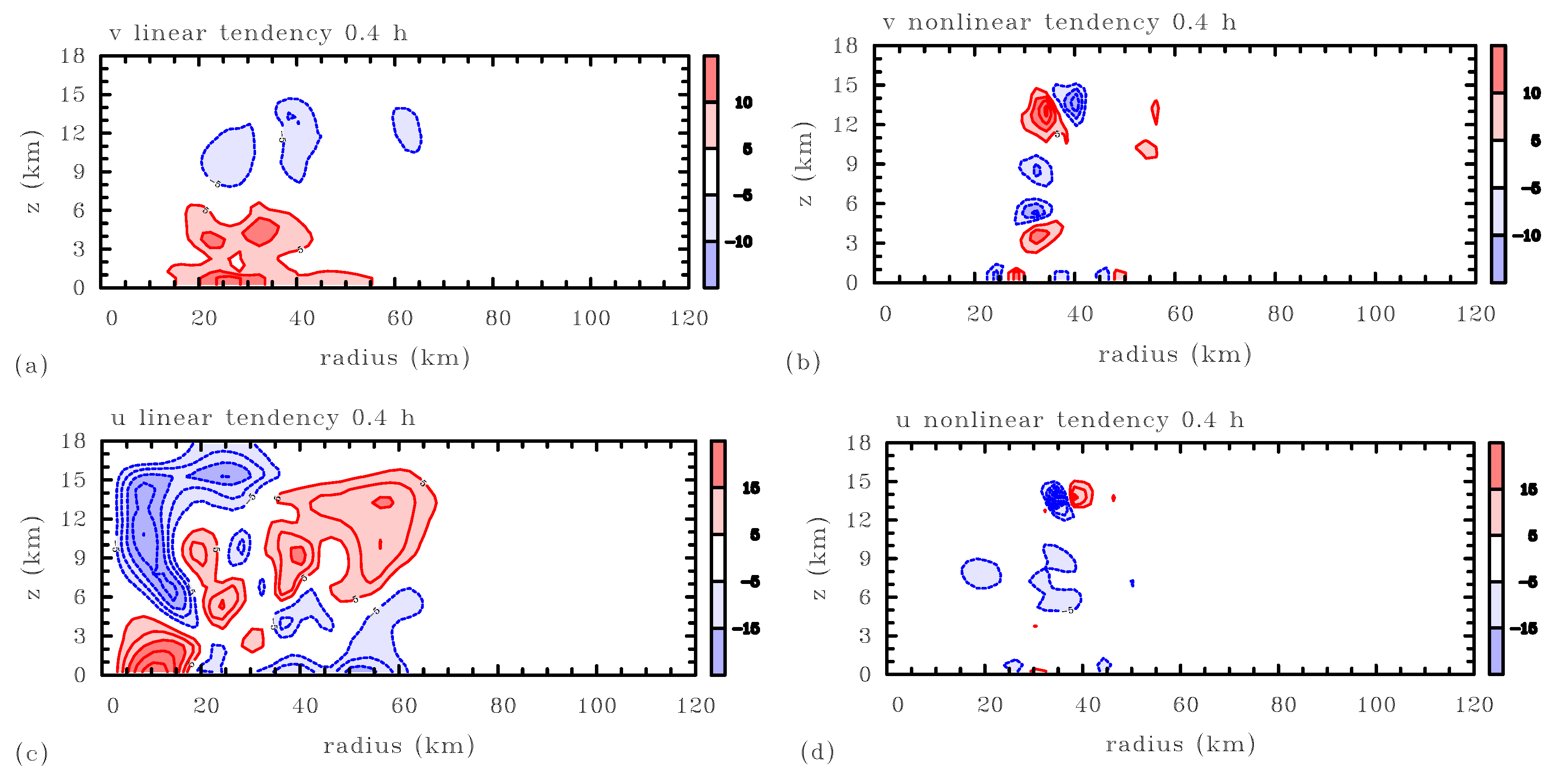
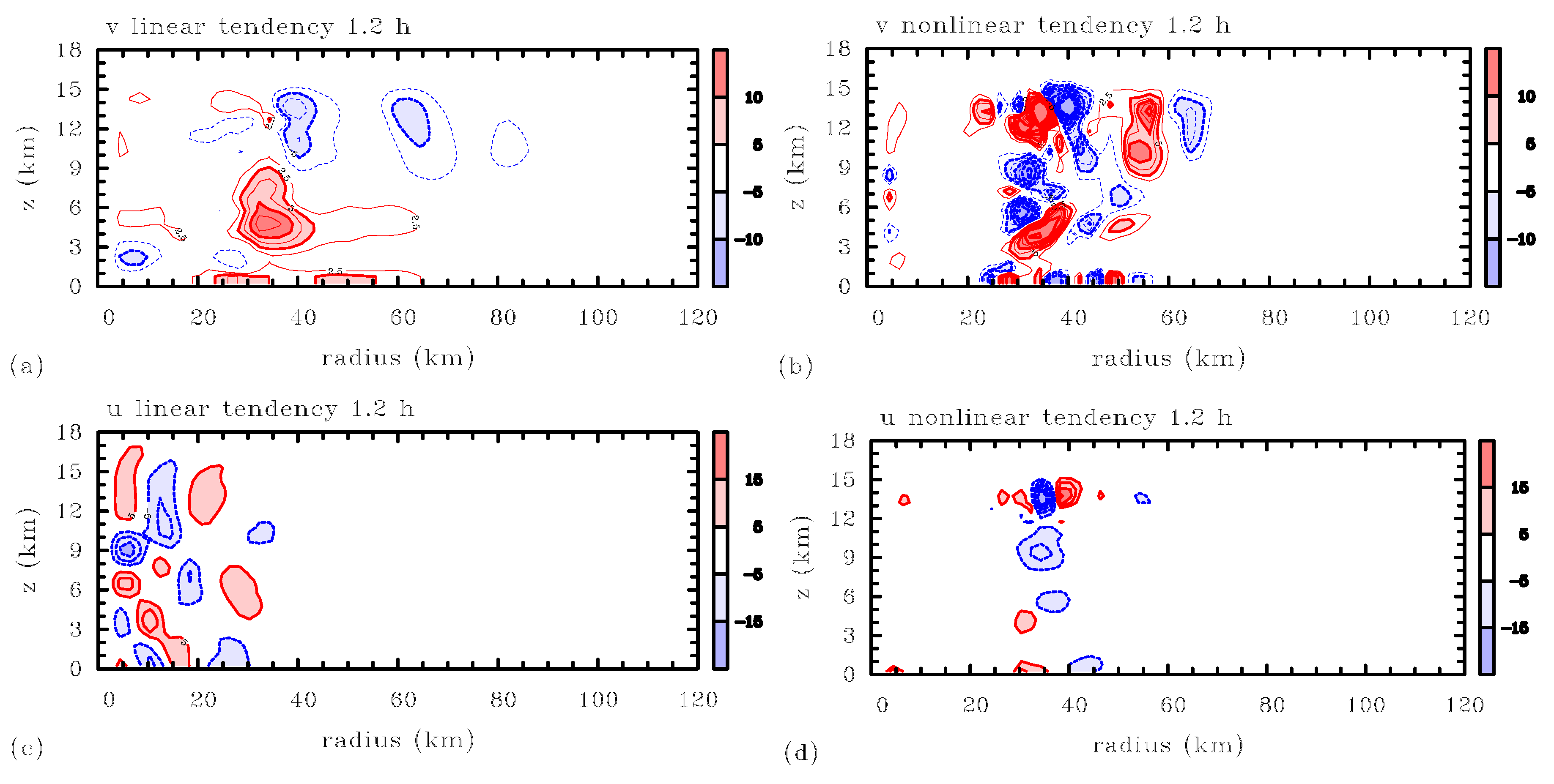
Figure 4 and
Figure 5 compare those linear tendencies (panels on the left) with the the nonlinear terms
and
neglected in the model (panels on the right). The neglected terms, evaluated from the linear solution, will be referred to as the “
u nonlinear tendency” and the “
v nonlinear tendency”, respectively.
Even at the very early time
h (
Figure 4), there are parts of the domain in which the nonlinear tendencies are, conspicuously, not much smaller than the linear tendencies, indeed comparable or greater in magnitude, most notably in the region of the incipient eyewall. A little later, at
h (
Figure 5), the nonlinear tendencies are very much bigger in some places. This is more than enough to support our conclusion that, in this example, the 3DVPAS model has predicted its own breakdown and has become self-inconsistent, and therefore invalid. Still less is the model valid at
h. If the analysis is repeated, but with forcing terms derived from the WRF model at times closer to full intensity, then we find, not surprisingly, that the magnitudes of the nonlinear terms have increased very steeply indeed.
At
h, there are already hints in
Figure 5d of what can be seen much more clearly in Ref. [
7], namely the emergence of strong, non-Ekman-like nonlinearities near the base of the eyewall at the later stages of intensification, giving rise to strong supergradient winds, much stronger than those obtained from Ekman-like dynamics. This is the signature of the nonlinear spinup mechanism, which significantly increases the destructive power of a tropical cyclone. The signature becomes very clear as Igor approaches full intensity.
5. 3DVPAS Dynamics, Sawyer–Eliassen Balance Dynamics, and Their Possible Extensions
Refs. [
1,
2,
17,
18] bring up the issue of 3DVPAS dynamics versus the dynamics of the traditional Sawyer–Eliassen (SE) model of transverse circulations. Since both are linearized models in the sense already discussed, the only differences are those arising from the unbalanced dynamics allowed by 3DVPAS versus the strictly balanced dynamics built in to SE. The SE model, as is well known, incorporates hydrostatic and gradient-wind balance from the start.
If, for instance, 3DVPAS is run with steady forcing terms, as above, and we wait for long enough after the forcing terms are switched on (
h, typically between 6 and 12 h, in examples like the foregoing), then the 3DVPAS behavior approaches that of the SE model. Somewhat confusingly, Ref. [
17] calls this long-time behaviour “quasi-steady”, even though the tangential wind and potential temperature are still changing like
t, in the well known way. It is not, of course, essential to use steady forcing terms. More generally, as discussed below, we may expect 3DVPAS behavior to resemble SE behavior whenever the forcing terms vary slowly enough in time.
Being a statement about the comparative behaviors of two linearized models, the foregoing is entirely separate from our main point, that the linearization itself becomes invalid at comparatively short times h in the context of maturing and mature tropical cyclones, especially as regards the inner-core boundary layer. It is of interest, nevertheless, to ask whether in that context either model could be rendered useful by restoring the neglected nonlinear N terms. The rest of this section will tentatively conclude that both models could indeed become useful in this way, although the numerical experiments needed to examine the question more closely are beyond the scope of this paper and will be left for future work.
We proceed as follows. Starting within the framework of the unbalanced 3DVPAS equations, we derive an extended SE equation that retains
all forcing terms in the disturbance equations of
Section 2, as well as the nonlinear
N terms in the momentum equations and in the corresponding thermodynamic equation. Retention of the radial as well as the tangential horizontal forcing terms is consistent with the findings of the previous section. We retain also the time derivatives that are usually neglected, but then discuss which of these should be included in order to make the equation as useful as possible in the current context.
For simplicity, we adopt the Boussineq approximation wherein density disturbances are retained only when multiplied by the gravitational acceleration, but neglected elsewhere (e.g., [
29], Ch.7). The generalization to the vortex-anelastic equations is straightforward. The reference density with disturbances neglected will be denoted by
, a constant. The disturbance continuity equation is that of incompressible flow,
and the disturbance vertical momentum equation is
where
is shorthand for the sum
referred to below in Equation (
8), and where
satisfies the Boussinesq counterpart of Equation (
9),
Here,
and
are the background and disturbance Boussinesq buoyancy accelerations, and
is shorthand for the sum of the last two terms in Equation (
9), i.e., the thermal forcing term
Q and the nonlinear term
, or rather their Boussinesq counterparts.
B and
are defined in the standard way as gravitational acceleration times fractional density anomaly. To complete the system, we use the Boussinesq forms of Equations (
1) and (
2), which are unaltered apart from replacing
by
in Equation (
1) and introducing the shorthand notations
and
.
Now we can derive a single equation for the transverse circulation
by subtracting
from Equation (
15) from
from Equation (
1), and then eliminating
and
using Equations (
2) and (
16), respectively. The result is
As defined in
Section 2, upper-case
V denotes the azimuthally-averaged tangential velocity of the circular vortex and (
,
) denotes the local absolute vertical vorticity and twice the absolute rotation rate of the circular vortex flow, respectively.
When a streamfunction
is introduced for the transverse circulation such that Equation (
14) is satisfied, i.e.,
and
, then a single partial differential equation results for
. The resulting equation (not written) is analogous to the single streamfunction equation derived by Hoskins [
32] in his pioneering study of the symmetric stability and instability of middle-latitude fronts. Notice that if
,
,
and
and the response described by (
17) are all assumed to
vary sufficiently slowly, then we may neglect all the time derivatives in Equation (
17), giving us the standard SE equation, in which balance allows us to replace
by
.
More subtly, however, we may consistently keep the first time derivatives on the right-hand side of Equation (
17), while neglecting the second time derivatives on the left-hand side, if rates of variation are “fairly slow” in the following sense. To neglect the second derivatives, we need
to be small in comparison with
and
, the squares of the local inertial frequency and buoyancy frequency. There is a range of conditions for which the first derivatives can nevertheless remain significant, especially in the first term on the third line of Equation (
17), whose magnitude in comparison with the last term on the middle line can be significant. On the reasonable assumption that
, we need to compare
with
, which is more like the
square root of the local inertial frequency. In our judgment, such “fairly slow” evolution is often relevant to tropical cyclone evolution ([
33]). We then have
This has diagnostic form, like the standard SE equation, if the right-hand side can be regarded as known. It will therefore be called an extended SE equation. However, it should be remembered that the nonlinear
N terms on the right then need to be treated iteratively. It needs also to be checked whether the partial differential operator on the left is elliptic. Ellipticity can fail in the inner-core boundary layer under nonlinear spinup conditions, which may be one of the reasons why Refs. [
1,
2] made their assumptions (1)–(3).
Equation (
18) is elliptic if the vortex is symmetrically stable (i.e., if the inertial stability on isentropic surfaces is greater than zero); and symmetric stability is assured [
33] when
, assuming that we can use the balance relation
for this purpose.
The extended SE Equation (
18) can be used to describe at least some of the effects of nonlinear boundary-layer spinup, via iterative correction. That is, the
N terms included on the right can be evaluated from a linear solution, then the equation solved again, the
N terms evaluated more accurately, and so on. This iterative procedure corresponds to that used in the classic idealized studies by Kuo [
34,
35], in which an Ekman-like boundary layer model was iteratively corrected for the non-Ekman-like nonlinearities, verifying that these produced significant strengthening of the supergradient winds near the top of the boundary layer. However, such an iterative procedure cannot describe the sort of drastic breakdown of balance that can occur as the boundary layer undergoes separation and turns upward into an eyewall.
It is here that Equation (
17), the fully-unbalanced counterpart of (
18), could become useful. At this level of description, with all the time derivatives included, we would have something equivalent to 3DVPAS dynamics rather than to a somewhat-extended SE dynamics. Although this remains to be verified—a topic for future work—it is possible that we could then begin to describe the emission of freely-propagating inertia-gravity waves from the separating boundary layer into the eyewall.
6. Conclusions
We have re-examined the utility of an unbalanced axisymmetric convective ring model using the dry, non-hydrostatic, time dependent linear vortex model 3DVPAS. This model was developed originally to examine linear asymmetric disturbances and their wave-mean-flow interactions in tropical cyclones and tornado vortices, and has produced many insightful results for that class of problems. Recent work [
1,
2] has used the 3DVPAS model in a different way, to study intensifying tropical cyclones by solving for the azimuthal-wavenumber-zero disturbance flow and corresponding tangential wind tendency subject to the imposed forcing of heat and tangential momentum sources. Using diabatic heating, tangential friction, and eddy forcing terms derived from a three-dimensional numerical simulation of an intensifying tropical cyclone vortex, Hurricane Igor, we have again investigated this different way of using of the 3DVPAS model, but this time with attention to whether, in this context, it is valid to neglect the nonlinear effects omitted from the model, the
N terms in the equations described in
Section 2.
We found that the linear 3DVPAS solutions quickly break down in the sense that the neglected N terms, calculated from the output of the linear model, become comparable to or larger than the linear terms in the governing momentum equations. This breakdown occurs on a time scale given approximately by the time required to develop the vortex boundary layer and incipient eyewall in the 3DVPAS model. The breakdown of the linear solution is found to be particularly severe in the inner-core boundary layer and in the eyewall of the simulated vortex.
The demonstrated breakdown of linearity supports the scientific arguments made in [
6] that (a) non-Ekman-like nonlinearities and nonlinear spinup are important in the inner-core boundary layer of an intensifying tropical cyclone and are responsible for the realistic growth of peak supergradient winds, and that (b) it is not valid to use a linearized model to isolate the separate effects of diabatic heating from those of friction. This is simply because the linear superposition principle breaks down whenever the dynamics are not linear.
Further to our second objective regarding the traditional Sawyer–Eliassen (SE) model, we have shown how an extended SE Equation (
18) may be derived from the 3DVPAS model formulation, the latter corresponding to Equation (
17) above, with the addition of the nonlinear
N terms and also the radial and vertical momentum source terms associated with vertical subgrid scale mixing associated with boundary layer processes that have been neglected in prior applications.
The traditional SE model requires that the forcing terms vary sufficiently slowly with time, a requirement that is typically quite severe in a tropical cyclone undergoing rapid intensification. For this reason, our extended SE Equation (
18) also includes the first time derivatives shown on its right-hand side, which allows somewhat faster variation with time, discussed in
Section 5 as “fairly slow” variation. For still faster variation and fully unbalanced motion, it is necessary to retain also a pair of second time derivatives, those on the left of Equation (
17), which restores the level of modeling to that of 3DVPAS.
It would be interesting in future work to make use of Equations (
17) and (
18), and their vortex-anelastic counterparts, in an approach to modeling and better understanding the nonlinear effects in intensifying tropical cyclones. The first stage would be to evaluate the nonlinear
N terms from the linear solutions, as in
Section 4, then solve Equations (
17) or (
18) again, then repeat the process to make iterative corrections that represent the effects of the
N terms with increasing accuracy. Such an iterative process would correspond to that explored in the classic work of Kuo [
34,
35] on non-Ekman-like boundary-layer nonlinearities, and promises to yield a sharpened understanding of the growth of supergradient winds.