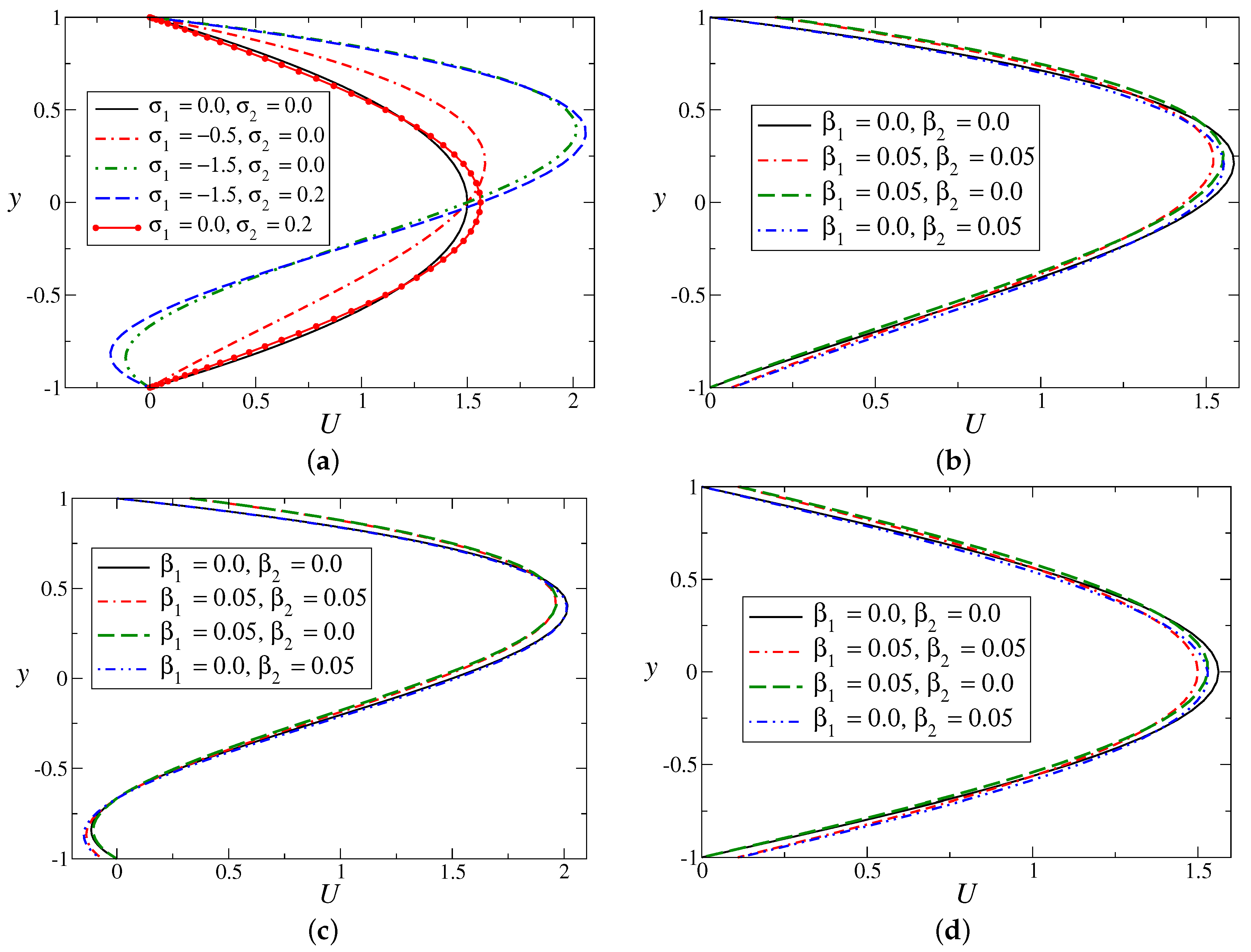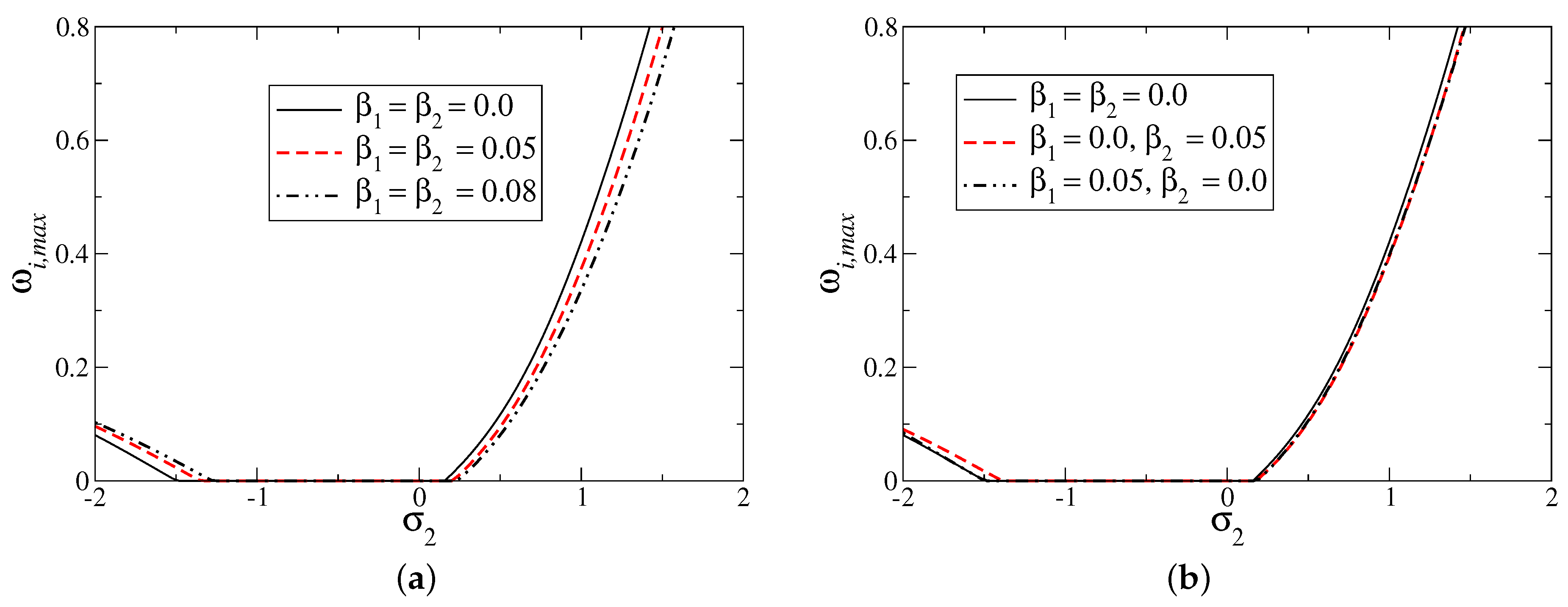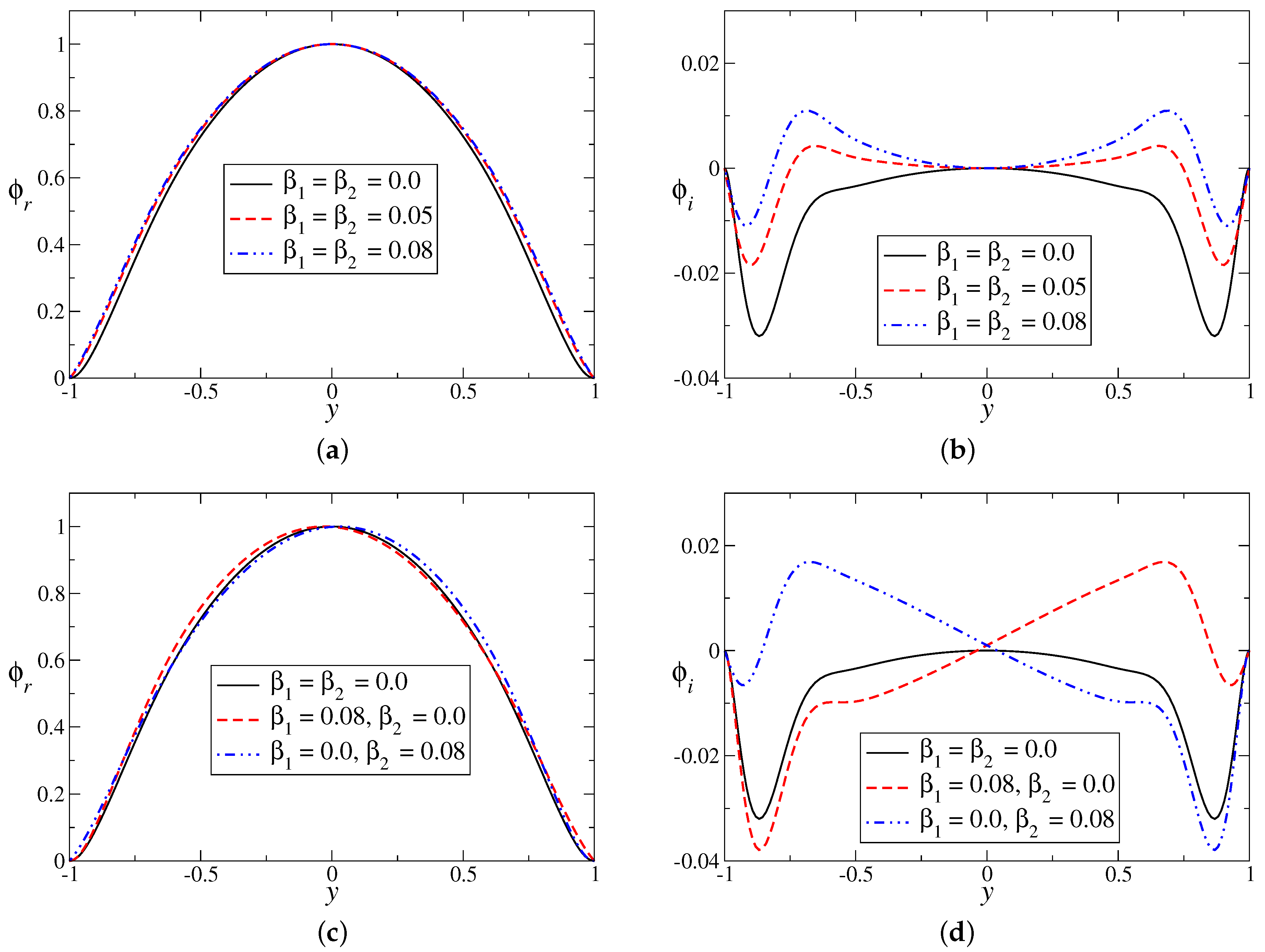1. Introduction
The paper deals with the linear stability of a nearly parallel asymmetric slippery channel flow by considering the Orr–Sommerfeld system derived from the Navier–Stokes equations linearized with respect to small disturbances [
1,
2]. The asymmetric channel flow with hydrophobic/rough/slippery walls can have many biological and industrial applications. Flows in renal tubules and movement of blood inside the blood-vessels may be the possible applications of such flow [
3,
4]. Linear stability theory has played an important role to develop many branches of fluid mechanics during much of the 20th century. It has been applied to understand the effects of flow parameters on the number of parallel flows, such as Couette- and Poiseuille-type flows, which are physically realisable and naturally important [
1,
2]. A similar analysis has also been used to approximate and solve nearly parallel flows [
5,
6,
7,
8]. A shear layer flow and a channel flow with cross velocity are the examples of nearly parallel flow for which a smooth transition between uniform velocity lines or path lines can be seen [
8,
9].
The stability analysis of pressure-driven flow has a long-term history, starting with the experiments of Reynolds (1883) on the transition to turbulence for a liquid flow through a circular pipe [
10]. Such a flow consists of an incompressible fluid under isothermal conditions, usually contained in a very long channel, along which there is a constant pressure gradient. The fluid moves in a laminar way along the pressure gradient and produces a time-independent parabolic velocity profile for the case of symmetric flow. The linear instabilities of such laminar flow are governed by the Orr–Sommerfeld equation [
1,
10], an eigenvalue problem with phase speed of the waves as the eigenvalue and the Reynolds number (
) as a parameter. The solution of the eigenvalue problem estimates the range of wave numbers and the value of the smallest Reynolds number for which the flow is unstable [
1,
2].
The current study focuses on the Orr–Sommerfeld analysis of complex asymmetric slippery channel flows, which are in the class of nearly parallel flow [
8,
9,
11,
12]. It is known that the eigenvalues and eigenfunctions of a Orr–Sommerfeld system are very sensitive with respect to the mean/background flow profile and/or the boundary conditions [
13,
14,
15]. Moreover, the behaviour of background/mean flow differs depending on the boundaries for the flow system. In this study, a family of asymmetric mean velocity profiles has been considered to understand the stability behaviour of the complicated wall-bounded Poiseuille-type flows.
The no-slip condition at the solid boundary/wall is a well-accepted and commonly used boundary condition in fluid mechanics to check the stability of a flow system through a channel or over an inclination [
1,
2,
16]. The entity of this condition is that the relative velocity of the fluid particles on the solid boundary/wall is zero. The assumption is valid and the results obtained by considering the no-slip boundary condition are comparable with those of corresponding experiments for wall-bounded flows; however, many recent experiments on micro-/nano-scale flows in the presence of pressure gradient, shear or electric field suggest that the no-slip condition does not always hold well in reality [
16,
17,
18]. For example, in the case of flow over super hydrophobic substrates or rough/textured surfaces at the micro-scale, to examine the flow dynamics properly, one can model such substrates by smooth surfaces with an effective slip on that surface [
19,
20,
21,
22]. Therefore, the velocity slip at the solid boundary/wall is a very essential aspect of fluid flows and so should not be considered as a casual irregularity [
23,
24,
25,
26,
27]. One must give particular attention to the factors such as surface roughness, wettability and the presence of gaseous layers that might have an effect on the measured interfacial slip [
4,
28,
29]. The very recent work by Pralits et al. [
30] has also pointed out that super hydrophobic walls of a plane microchannel flow could be modeled using the Navier slip condition through a slip-tensor, and the results depend parametrically on the slip-length and orientation.
The study by Lauga and Cossu [
31], applying the wall-slip effects on the symmetric-plane Poiseuille flow of a single fluid with both symmetric (same slip at both walls) and non-symmetric slip (slip at the lower wall, different from that at the upper wall) conditions showed that the critical Reynolds number for the onset of instability increased very significantly with wall slip as compared to that in a rigid channel. Numerical computations for microchannel flows in the slip-flow region performed by Gan and Wu [
32] displayed short-wave instability due to wall slip and showed that the slip-flow model is stable for long waves. Ling et al. [
33] extended the study of Lauga and Cossu [
31] by considering asymmetric-slip boundary conditions at the walls, and their results indicated that depending on the slip length, slip has the dual role of either stabilizing or destabilizing the flow system. Sahu et al. [
34] explored the role of slip on the linear stability of a diverging channel flow. The effects of boundary slip on the linear stability of interface-dominated, viscosity-stratified, microchannel flow have been analyzed by You and Zheng [
24]. In all of these studies, the authors found significant effects of wall velocity slip on the stability of the considered flows. There are also investigations on many other physically reliable and complicated flow systems that are strongly influenced by wall velocity slip [
30,
35,
36,
37]. Moreover, the recent work by Torrilhon [
38] discusses the development of continuum models for microscopic flows or flow systems in which the Knudsen number becomes significant. We note that a higher Knudsen number suggests stronger wall slip.
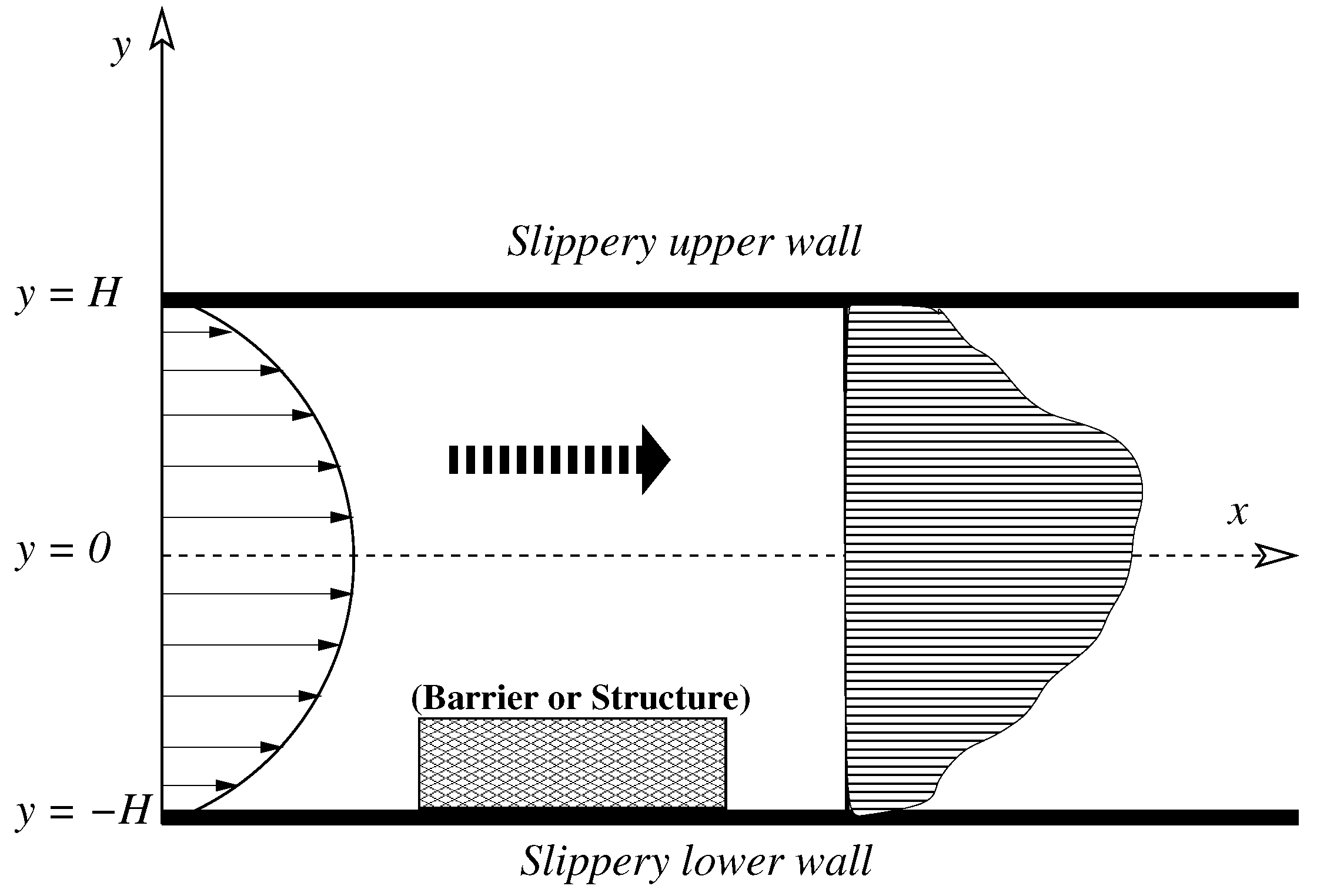
The asymmetric Poiseuille flow [
8,
9,
11] is one kind of complex-type flow that can be found in many industrial and natural applications [
3,
4] as a result of the presence of steps, barriers, structures or grooves [
39,
40,
41] inside the flow field. The barrier/structure may be present near the wall boundary or away from boundary [
42]. Such an asymmetric flow can also be possible in curved spaces [
43,
44], in a pipe/channel with a sudden enlargement of the cross-section or for a rotating channel flow. Fransson and Alfredsson [
8] investigated the hydrodynamic stability of channel flow with cross-flow, for which the base flow is asymmetric as a result of homogeneous cross-flow. The report by Kachuma and Sobey [
9] showed that in a channel flow past a step, there is a region near a wall vortex, particularly the second vortex, in which the flow is asymmetric but almost parallel over a length. The length is sufficiently large compared to the channel width, and thus a parallel flow model can be applied. The present study has also used a similar idea to check the effects of wall velocity slip on the asymmetric flow of Newtonian liquid in a confined geometry. The solution of the flow system has been obtained by employing the Navier slip boundary condition at the walls instead of using the no-slip condition. The Navier slip boundary condition is the outcome of the phenomenon [
18] that a liquid can slip on a solid surface and thus inflict a non-zero velocity of the fluid relative to the solid. In the case of micro-flows, the amount of slip at the wall is linearly proportional to the gradient of the tangential velocity at the wall and the proportionality constant defined as the slip length [
18,
45]. If the slip boundary conditions are used, the Navier–Stokes equations of a flow system are valid for slip lengths of up to 0.1 [
18,
45]. The range of the dimensionless slip parameter (
) from
to
could be realized for a flow in a hydrophobic channel of height ranging from 0.8
m (40
m) to 4
m (200
m) and corresponds to a slip length of 20 nm (40 nm) [
35].
In consideration of the above, we are motivated to check wall-slip effects on the hydrodynamic stability of asymmetric channel flow. The paper is organized as follows: after an overview of the problem statement and methodology in
Section 2, validation and details of the pertinent stability results are presented in
Section 3. Concluding remarks are given in
Section 4.
3. Results and Discussion
The stability results are first obtained for the plane Poiseuille flow in a rigid/slippery channel to check the correctness of our numerical code by validating the available results in literature. We found that the critical Reynolds number (
) for the rigid channel case is
, and it is
of the critical Reynolds number (
) obtained by Drazin and Reid [
1] in their study. We remark that, in the present study, the Reynolds number is based on the average velocity; however, for Drazin and Reid, the Reynolds number was defined as based on the maximum velocity. In view of the choice of characteristic velocity scale as the maximum velocity by Lauga and Cossu [
31],
in this study is
times that obtained by Lauga and Cossu [
31], for all
. The results obtained from our code agree with the available results for both
and
after considering the proper scaling.
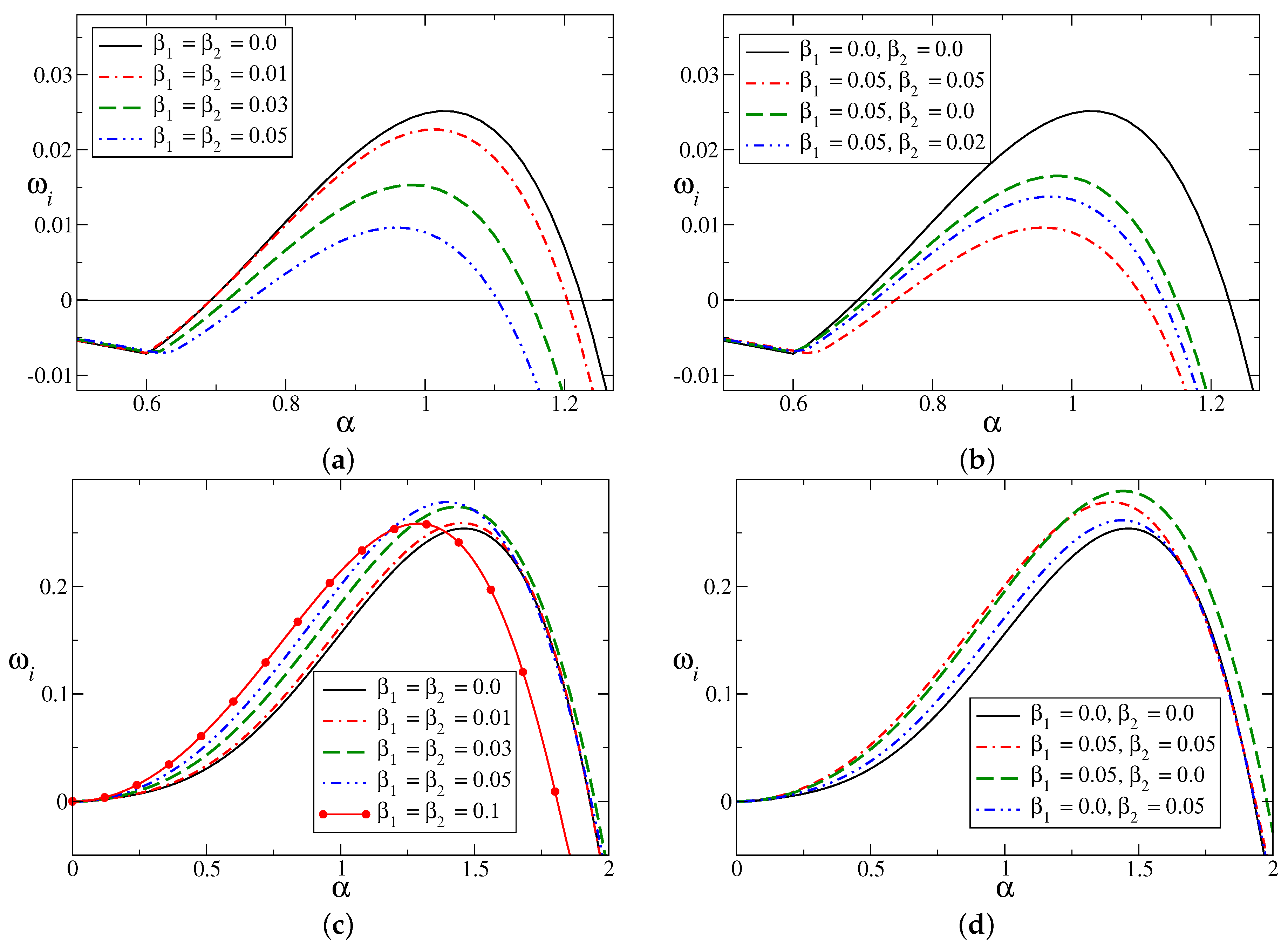
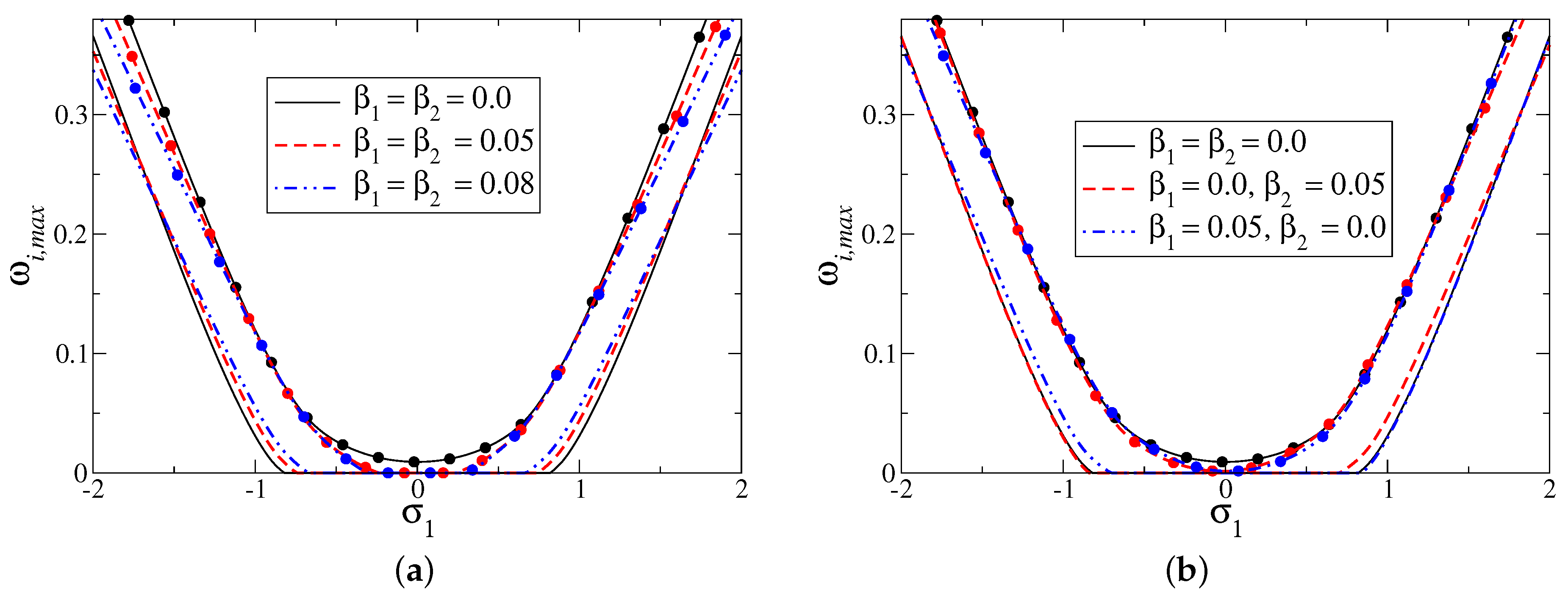
Figure 4 presents the growth rate for the most unstable mode of the perturbed flow for different values of
and
when the Reynolds number
. The solid lines (for
) render the results for the plane Poiseuille flow with [
31] and without [
1] wall slip.
Figure 4a discovers the results of rigid channel flow (
) considered by Kachuma and Sobey [
9]. It is evident from
Figure 4b that symmetric-type wall slip has the motivation to suppress the unstable mode by decreasing the growth and the range of unstable wave numbers, except in the case
. In the presence of model parameters (non-zero
and/or
), the growth rate is higher for the set of unstable wave numbers. The growth rate is dominant for
because of the occurrence of sharp skewness in the velocity profile (see
Figure 2).
The effects of symmetric and non-symmetric slip on the growth rate of the asymmetric flow are investigated more neatly in
Figure 5. The mean velocity profile contains only one non-zero model parameter (
) in
Figure 5a–d, the values of the model parameters are
and
. In the absence of the skewness parameter (
), both types of slip stabilize the flow by reducing the growth rate of the disturbances with respect to time for all wave numbers. However, in the presence of back-flow (for
; see
Figure 2) near the wall, velocity slip promotes the growth of disturbance as compared to the no-slip case for the considered value of the Reynolds number (
;
Figure 5c,d).
Figure 5d shows that the growth rate is maximum when the system has velocity slip only on the upper wall (
).
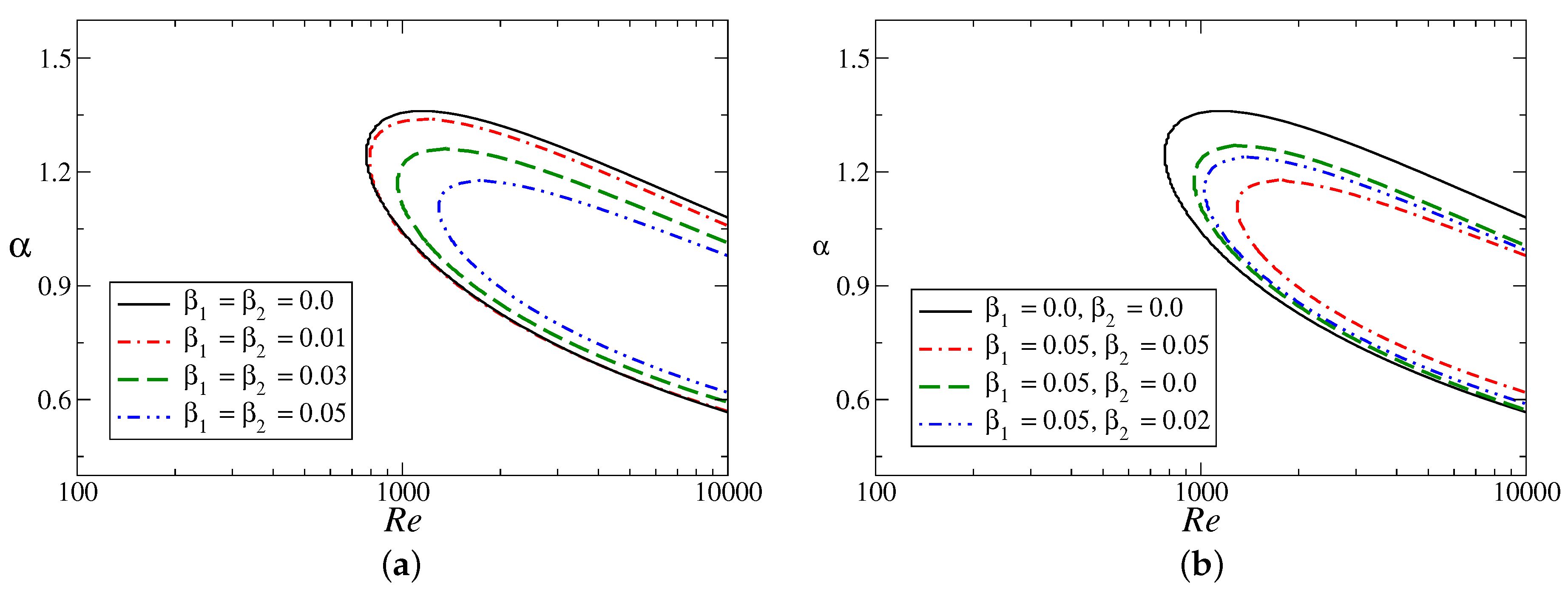
Neutral stability boundaries for different wall slips are presented in
Figure 6. The values of the modeled parameters used in this figure are
and
, which suggests a change in maximum velocity alone. Curves with
correspond to the rigid-channel case results.
Figure 6 clearly points out that the asymmetric flow with
is very much unstable as compared to the classical symmetric slippery channel flow studied by Lauga and Cossu [
31]. The asymmetric flow is unstable at Reynolds numbers (
) smaller than 1000, and thus the critical Reynolds number (
) for this flow is much less than that for the case of the plane Poiseuille flow (
). This may create a serious issue for the applications in which one requires a more stable asymmetric flow. The results for a slippery channel confirm that such a difficulty could be overcome by designing the wall as a slippery or hydrophobic surface. The flow is more stable because of the presence of velocity slip at the walls for the considered flow parameter in
Figure 6. Wall slip significantly delays the occurrence of the instability by means of increasing the critical Reynolds number and lowering the bandwidth of unstable wave numbers. We note that the flow with velocity slip only at the upper wall (
) is more unstable (
Figure 6b) as compared to the flow with velocity slip only at the lower wall (
).
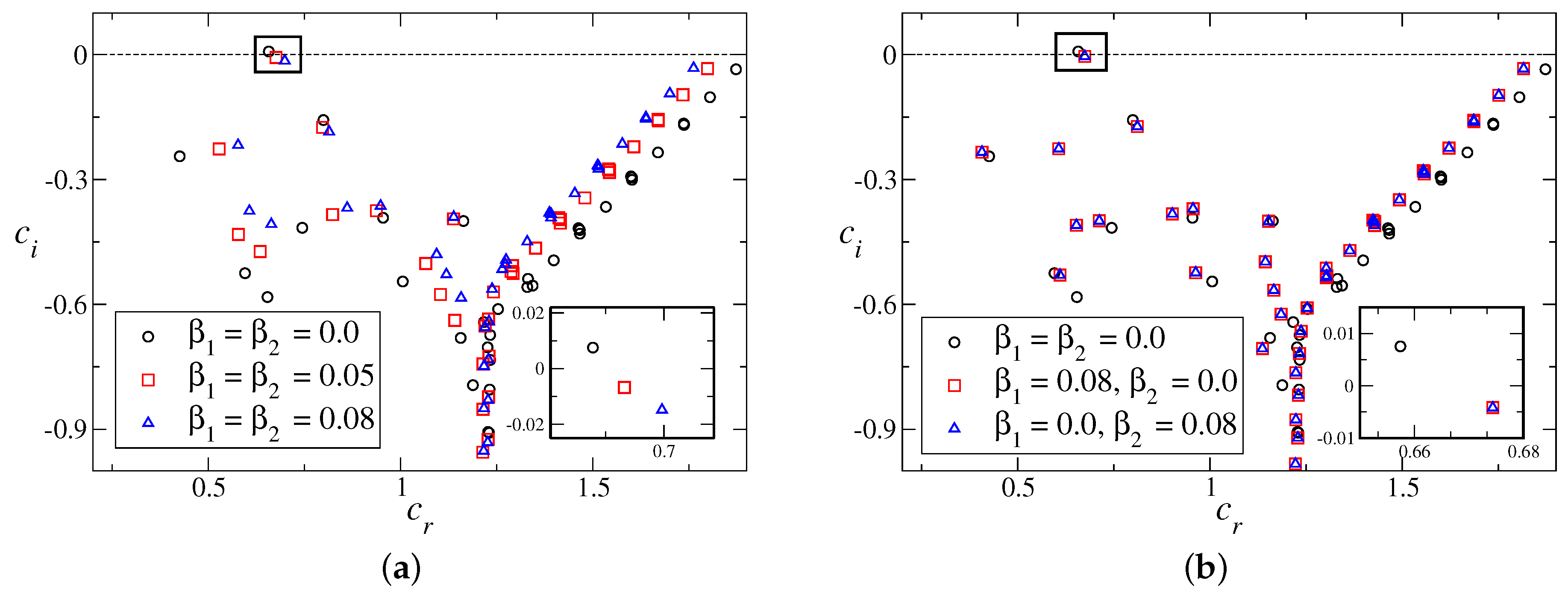
The spectrum of the Orr–Sommerfeld operator for the above flow configuration is framed in
Figure 7, when the Reynolds number
. The well-known Y shape for the channel flow is formed by the eigenvalues in the complex plane. The classical A, P and S branches [
2] are present with the unstable mode on the branch A. The behaviour of the most unstable eigenmodes for different slip parameters are shown by the inset plot. Both symmetric- and asymmetric-type slips suppress the growth rate of the most unstable mode, but the effect of symmetric slip (
Figure 7a) is stronger. Moreover, all the eigenmodes are stable for slippery channel flow. In the case of asymmetric slip, the nature of the most excited mode is shown in
Figure 7b for two different configurations of wall slip.
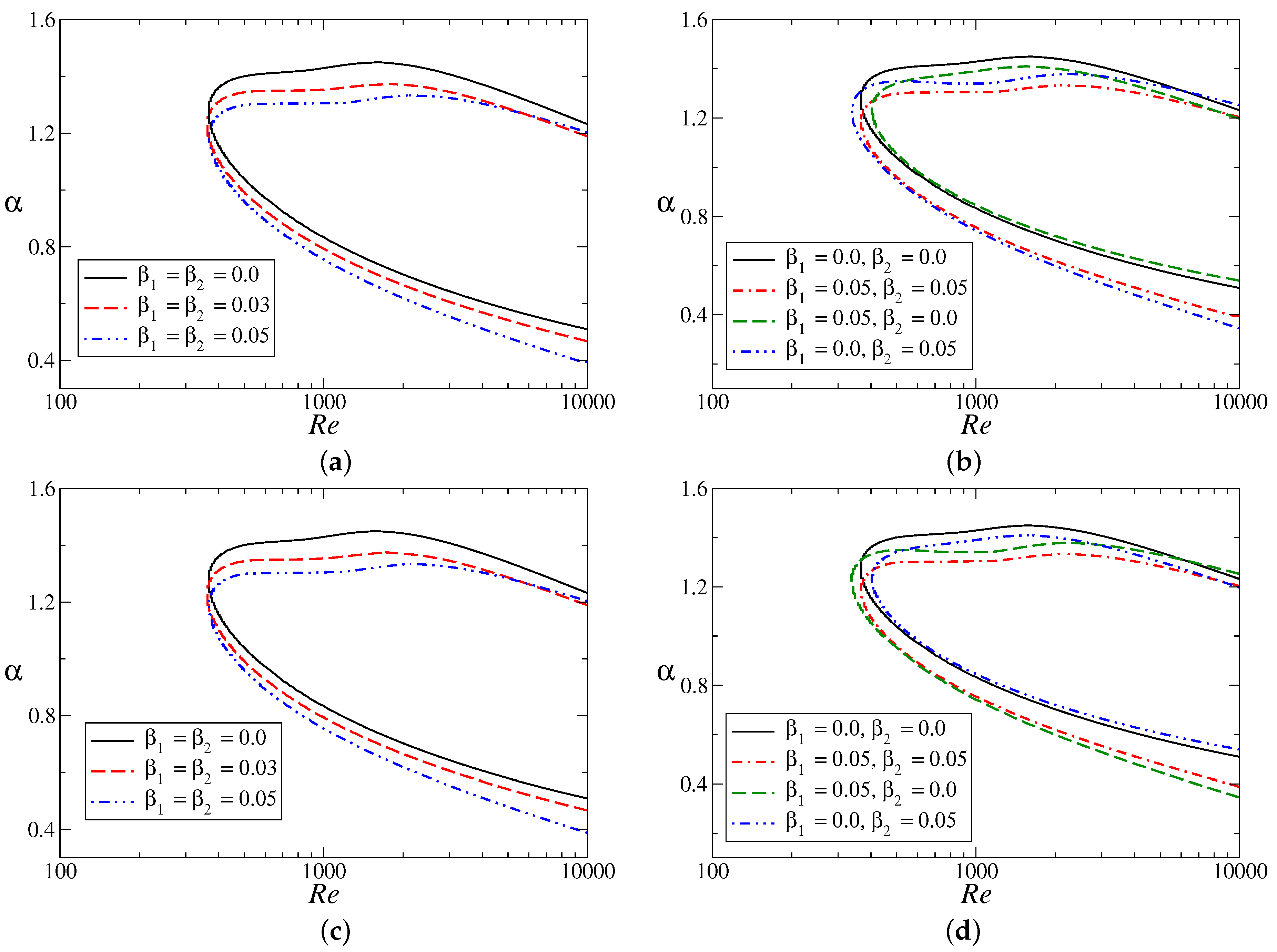
Next, we move to the flow configuration for which both the model parameters are non-zero.
Figure 8 displays stability boundaries in the
floor. The asymmetric channel flow is unstable at very low Reynolds numbers (critical Reynolds number is of
) for the parameter values
and
(
Figure 8a,b), and
(
Figure 8c,d). There is no qualitative change in the stability curves as a result of the sign change of
(skewness changing parameter). Additionally, symmetric slip has a minor effect in this parameter range. However, asymmetric-type slip plays a very interesting role depending on the value of
(
Figure 8b,d). Asymmetric-type wall velocity slip can destabilize the flow by decreasing the critical Reynolds number (see
Figure 8b with
and
Figure 8d with
). Most importantly, the presence of slip only on the upper wall stabilizes the flow system when
(>0;
Figure 8b) and it destabilizes the flow when
(<0;
Figure 8d). The reverse statement is true for the flow configuration with velocity slip only on the lower wall. We note that the symmetry and skewness of the velocity profile are completely dependent on the absolute value as well as on the sign of the parameter
.
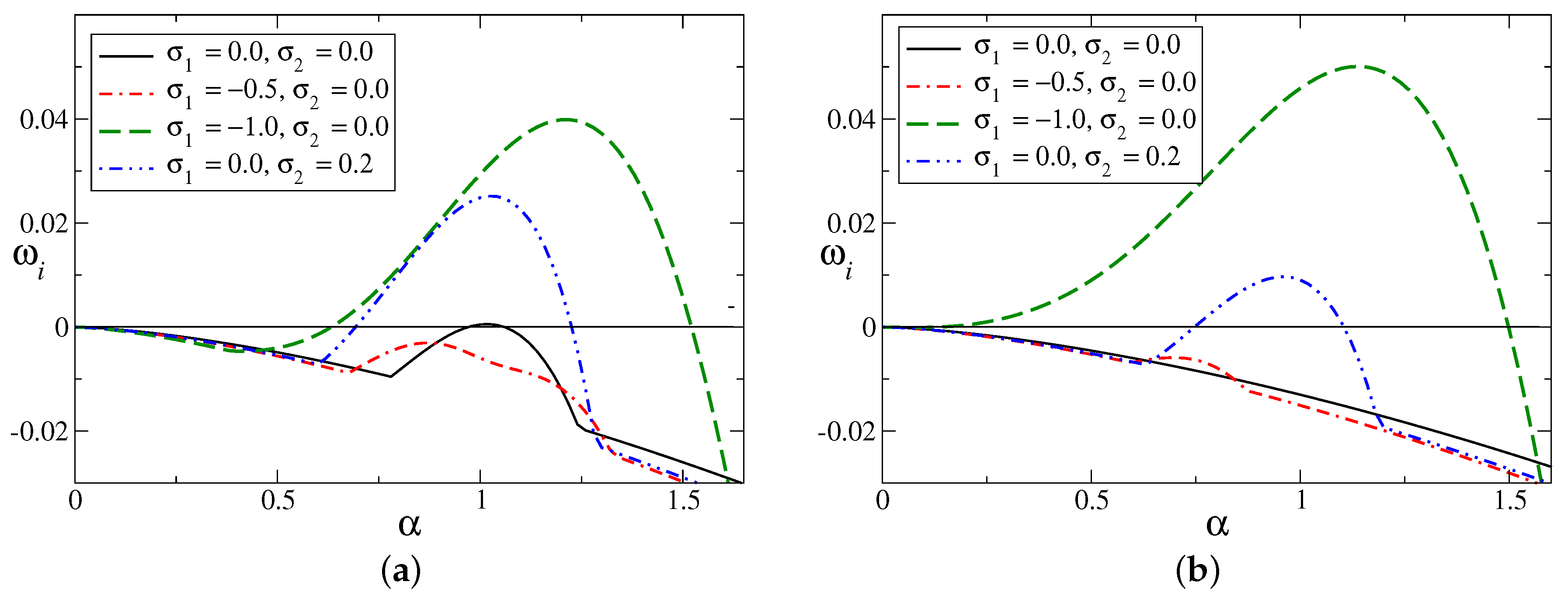
Figure 9 and
Figure 10 are drawn to check the effects of
(when
is fixed) and
(when
is fixed) on the maximum growth (
) over all the unstable wave numbers for a fixed Raynolds number (
). The flow system is unstable (
) for
if
and for
if
(see
Figure 9). Wall slip has dual influences on the maximum growth rate depending on the value of
. It can stabilize the flow by reducing the time growth of the dominant disturbance for a moderate to high magnitude of
, but a destabilizing role of wall slip is found for a smaller magnitude of
(
Figure 9a). The twofold behaviour of the asymmetric slip is shown in
Figure 9b.
Figure 10 shows that the instability of the flow depends monotonically on the positive
in the case of fixed
. For positive values of
, wall velocity slip suppresses the most unstable mode because of a reduction in the maximum growth rate, which is in contrast with
.
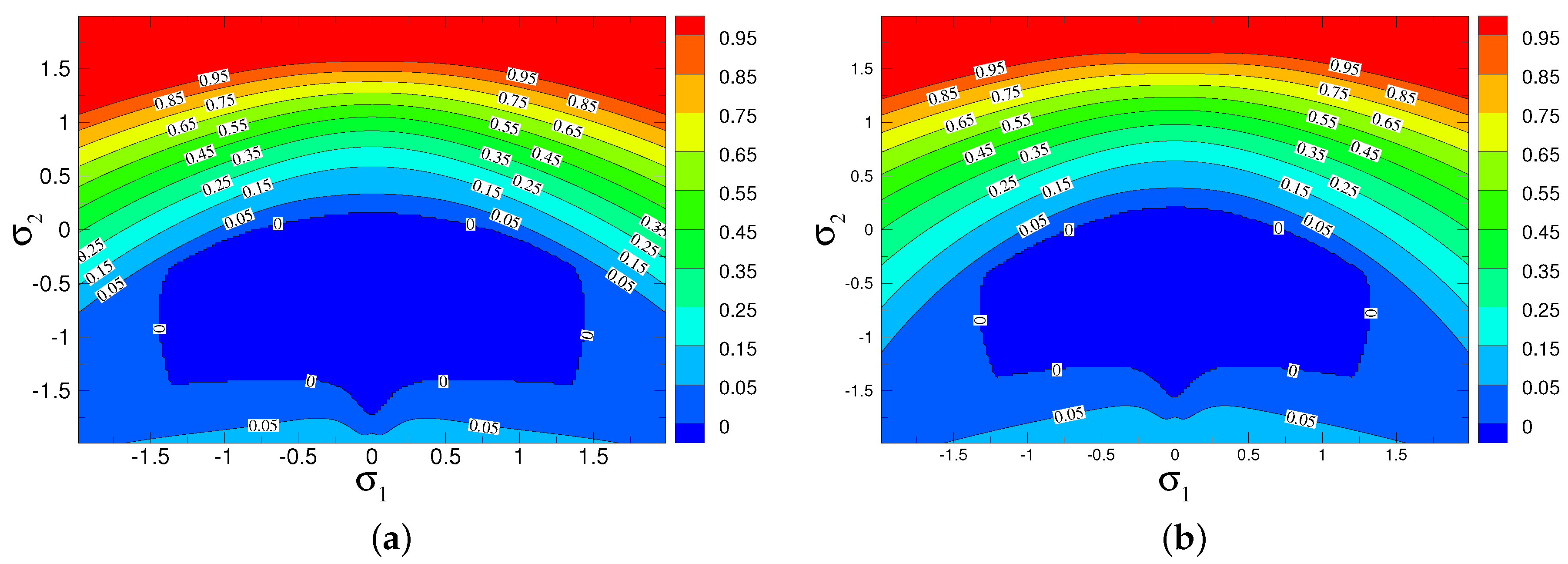
We have summarized instability fashion at a fixed Reynolds number (
) by drawing contours of maximum growth rate (
), considering all modes and across a range of
,
for no-slip (
Figure 11a) and symmetric slip (
Figure 11b) conditions. This regime diagram in
plane gives the overall instability ceremonial. Note that in the unstable region,
.
Figure 11 exposes that both the flow parameters
and
play a major role to determine the stability at a given
and
. A region defined by
and
is most stable, and flow is destabilized outside this region. Overall, the configuration with higher magnitude of
,
is more unstable. By a close inspection, we see that the flow instability is regulated by the symmetric slip but that stabilization or destabilization completely depends on the typical combination of
and
values.
The sample set of eigenfunctions for the most unstable eigenmode are shown in
Figure 12. It is notable that the presence of wall velocity slip has disturbed the look of the typical eigenfunctions. The real (
) and imaginary (
) part of stream functions are presented in
Figure 12a,c and in
Figure 12b,d, respectively, for symmetric and asymmetric slip conditions. Although
is weakly dependent on slip parameters, the wall velocity slips destroy the symmetry of
for the case of asymmetric slip (
Figure 12d). This may provide some mechanism in terms of energy disturbance between the mean and perturbed flow, for the dynamics of the flow instabilities.