The Impact of Horizontal Resolution on Energy Transfers in Global Ocean Models
Abstract
1. Introduction
2. Theory
2.1. Kinetic Energy in Physical Space
2.2. Two-Layer Turbulence
2.3. Kinetic Energy in Spectral Space
3. Model Data
4. Results
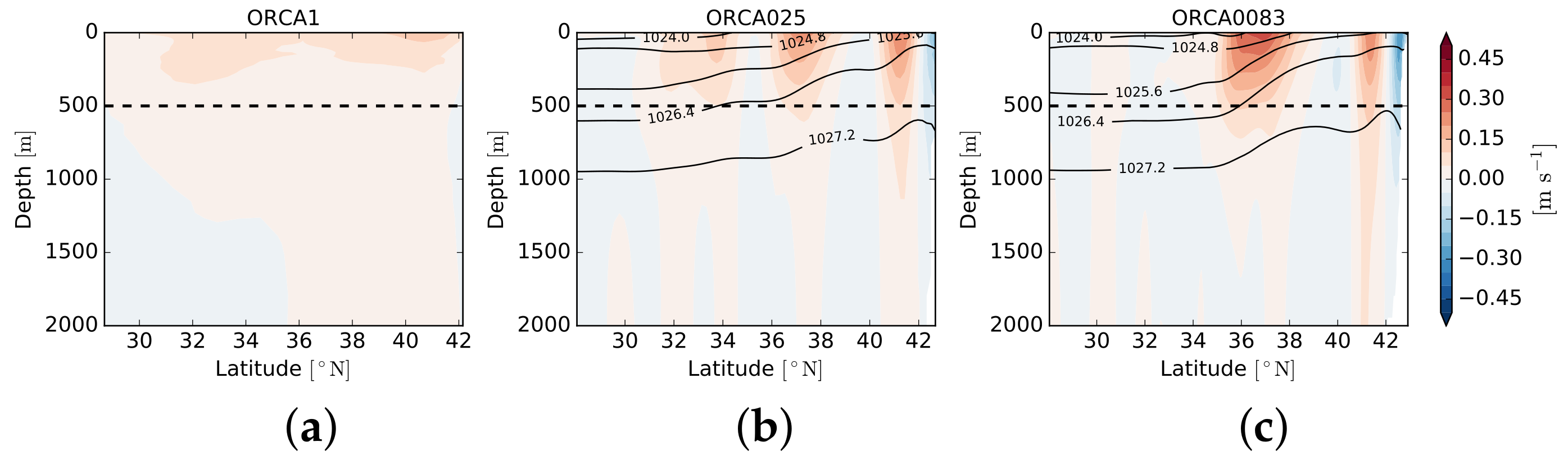
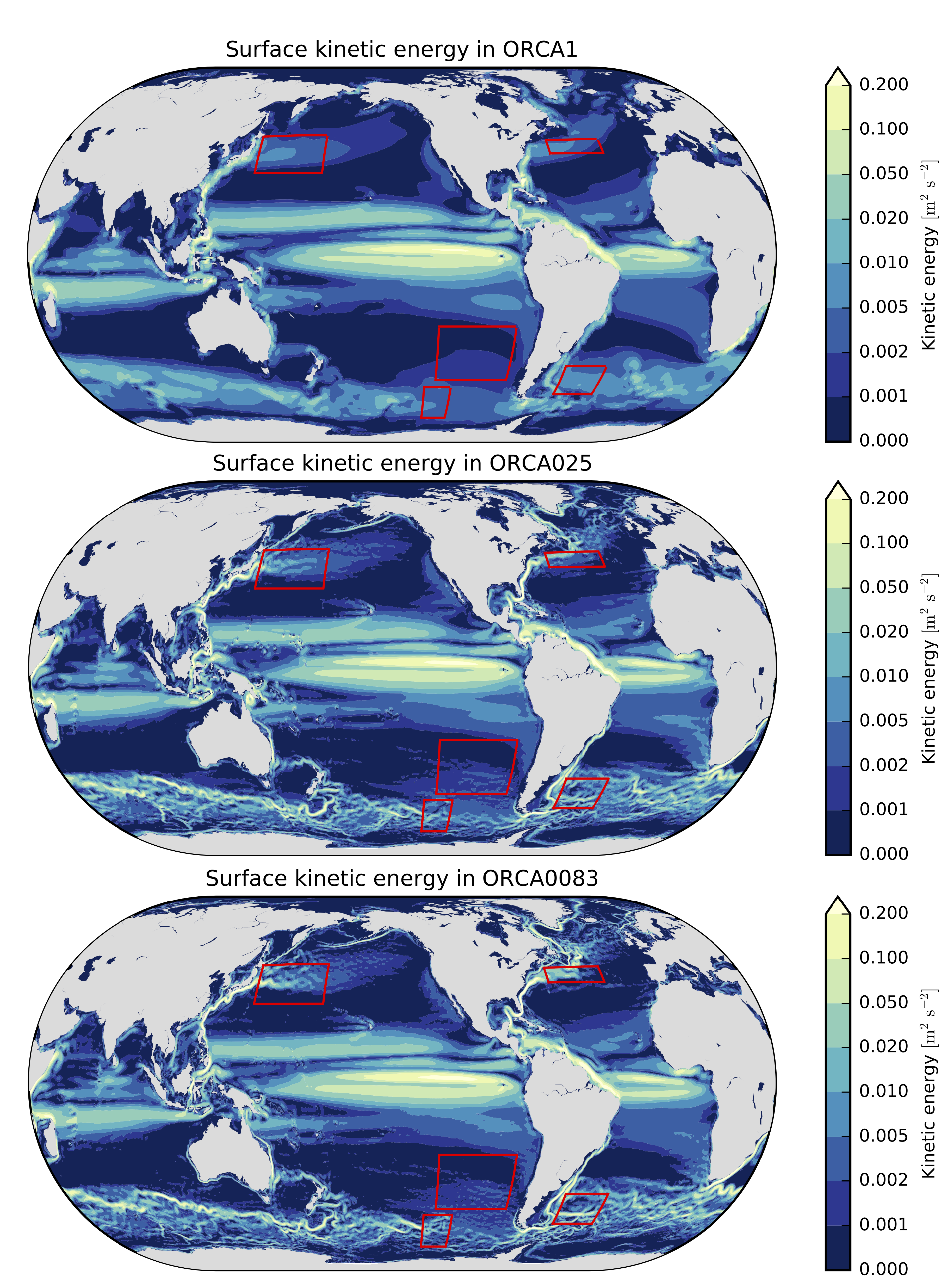
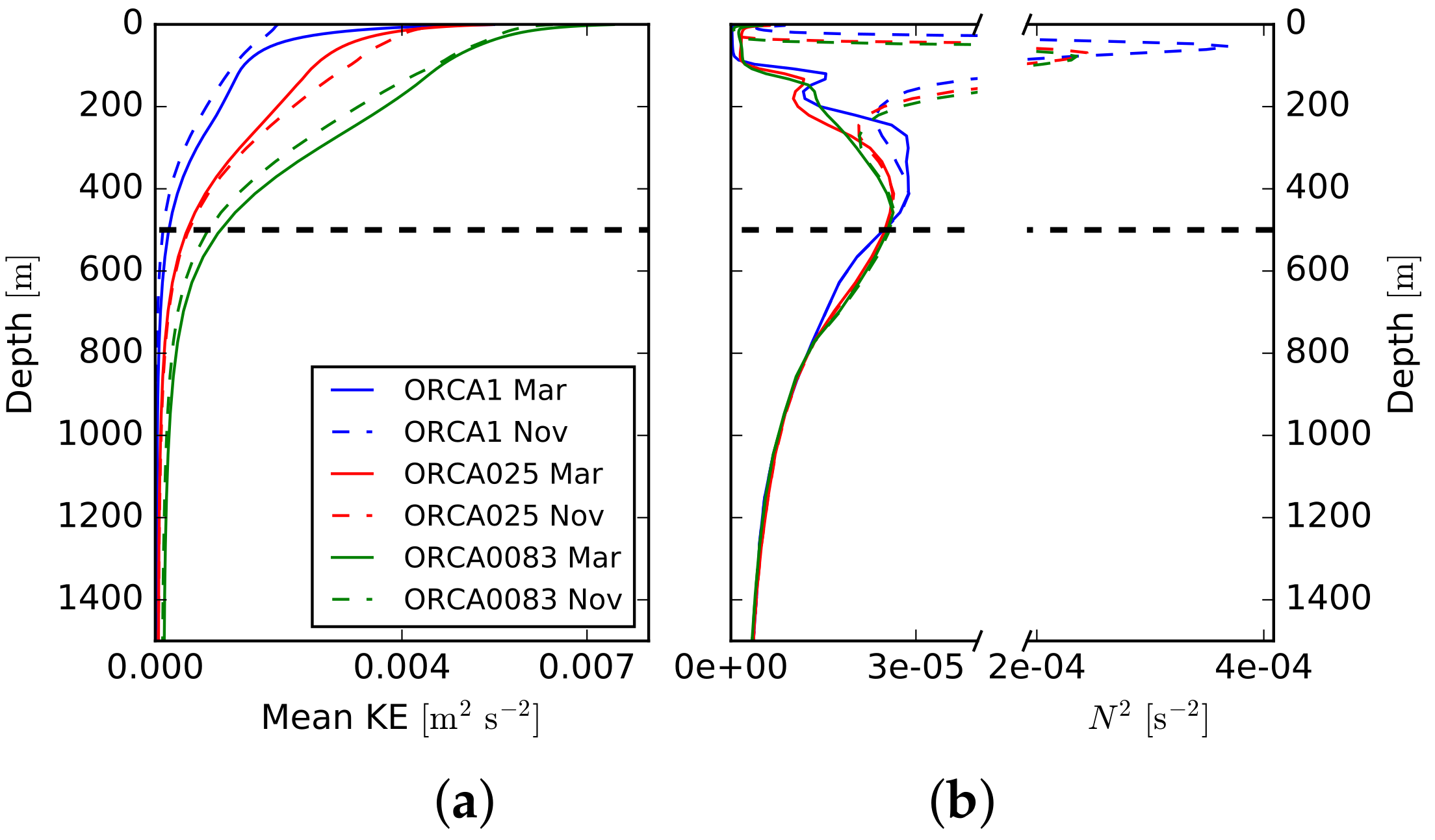
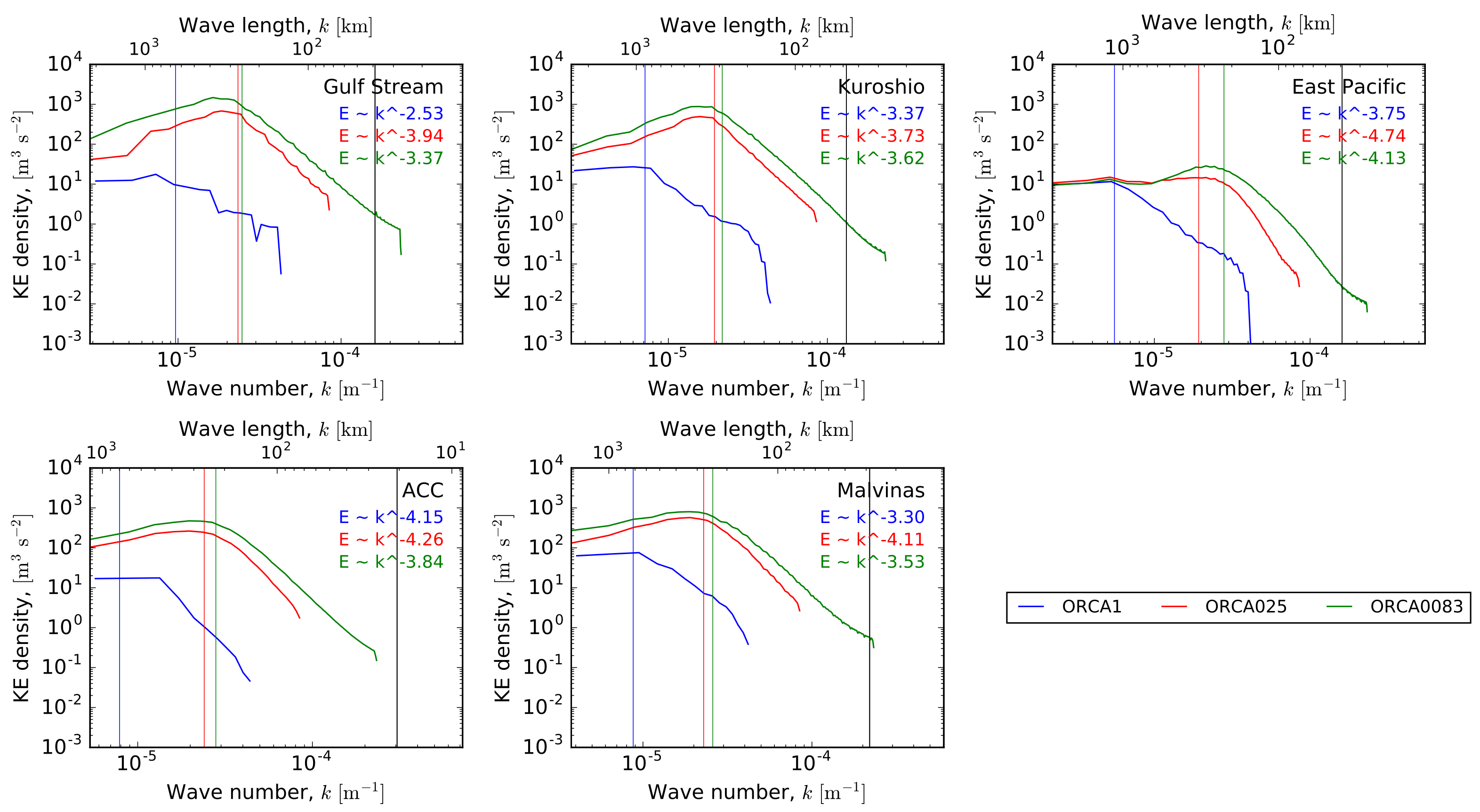
4.1. Kinetic Energy (KE) in Physical Space
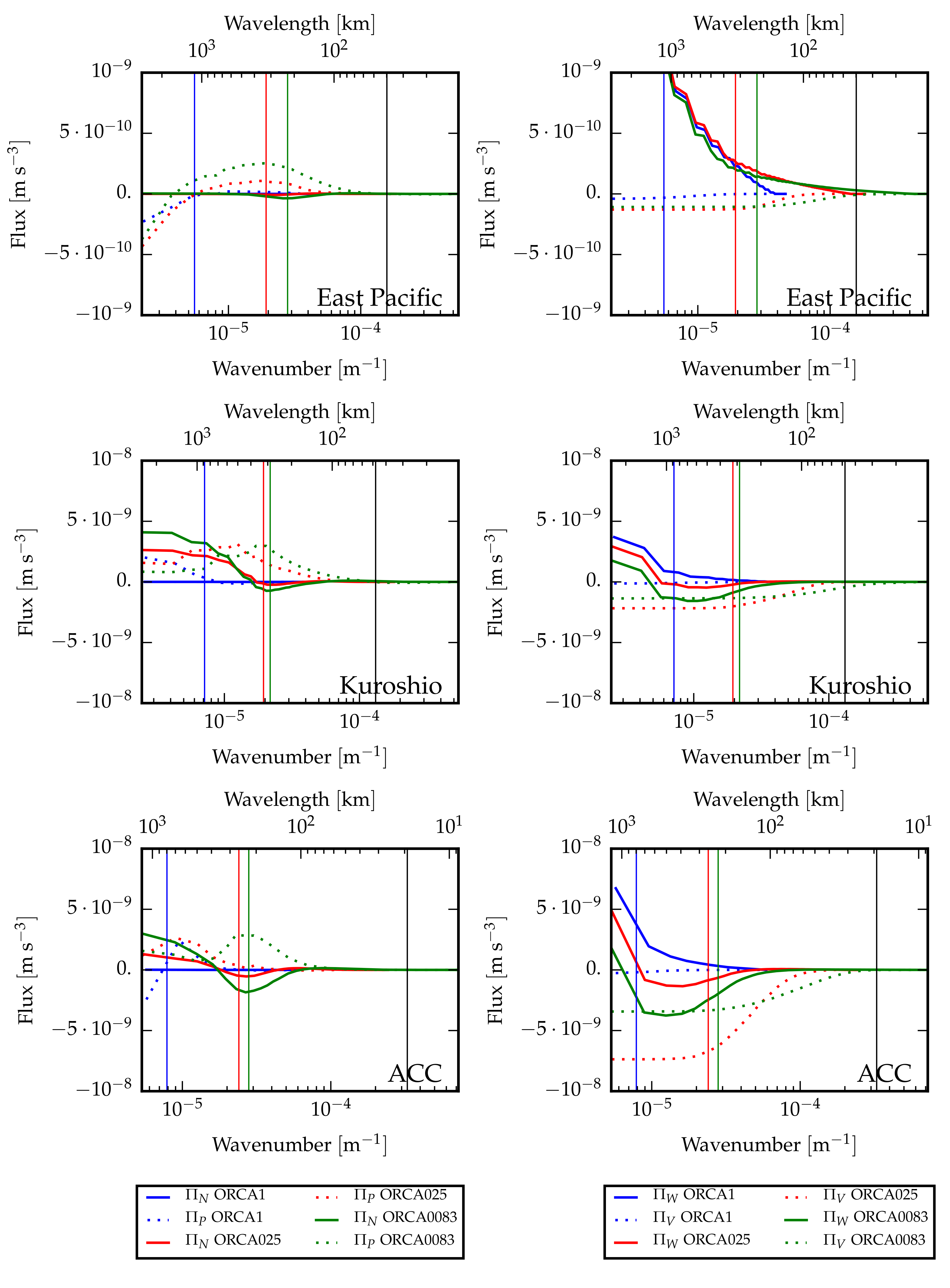
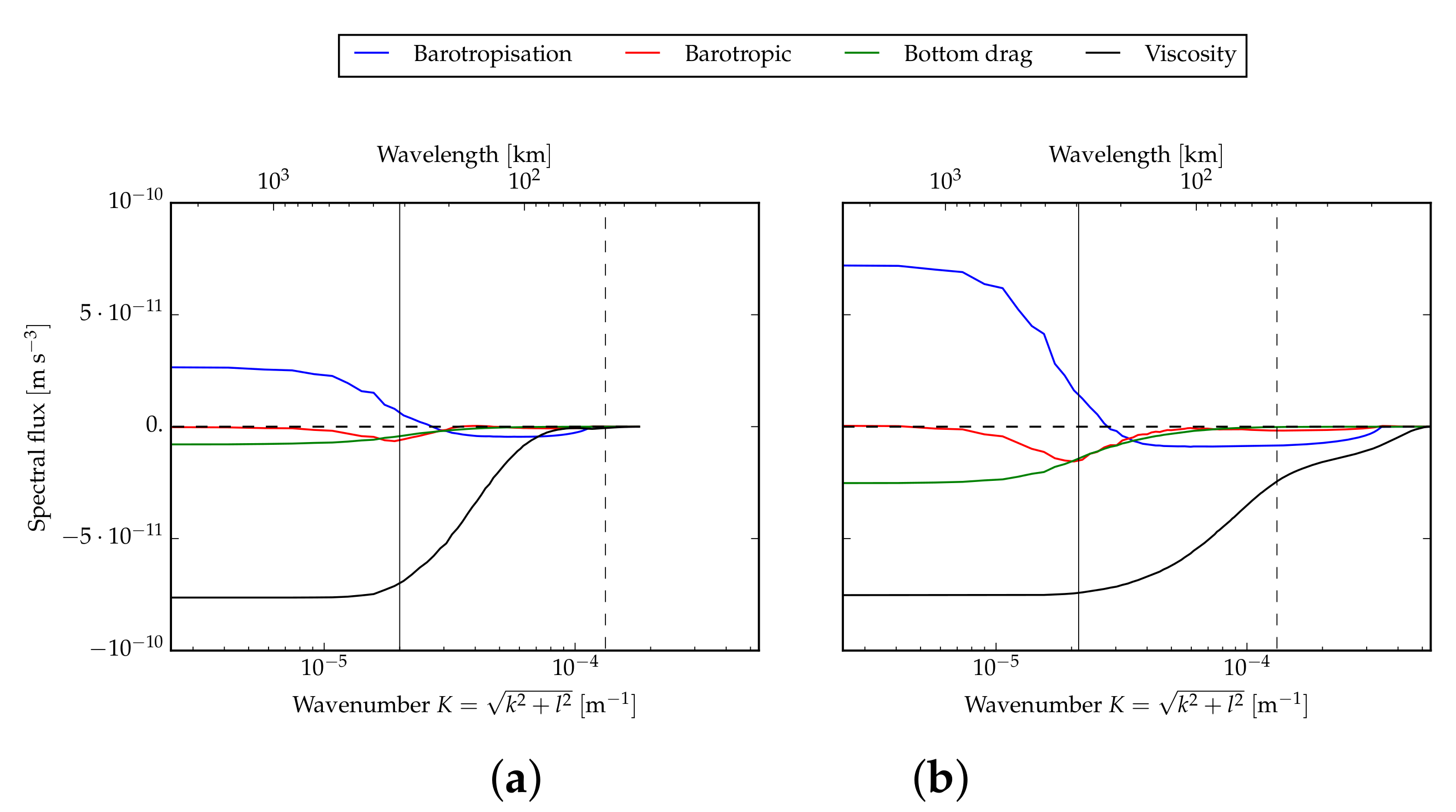
4.2. Spectral Fluxes in the Upper Ocean
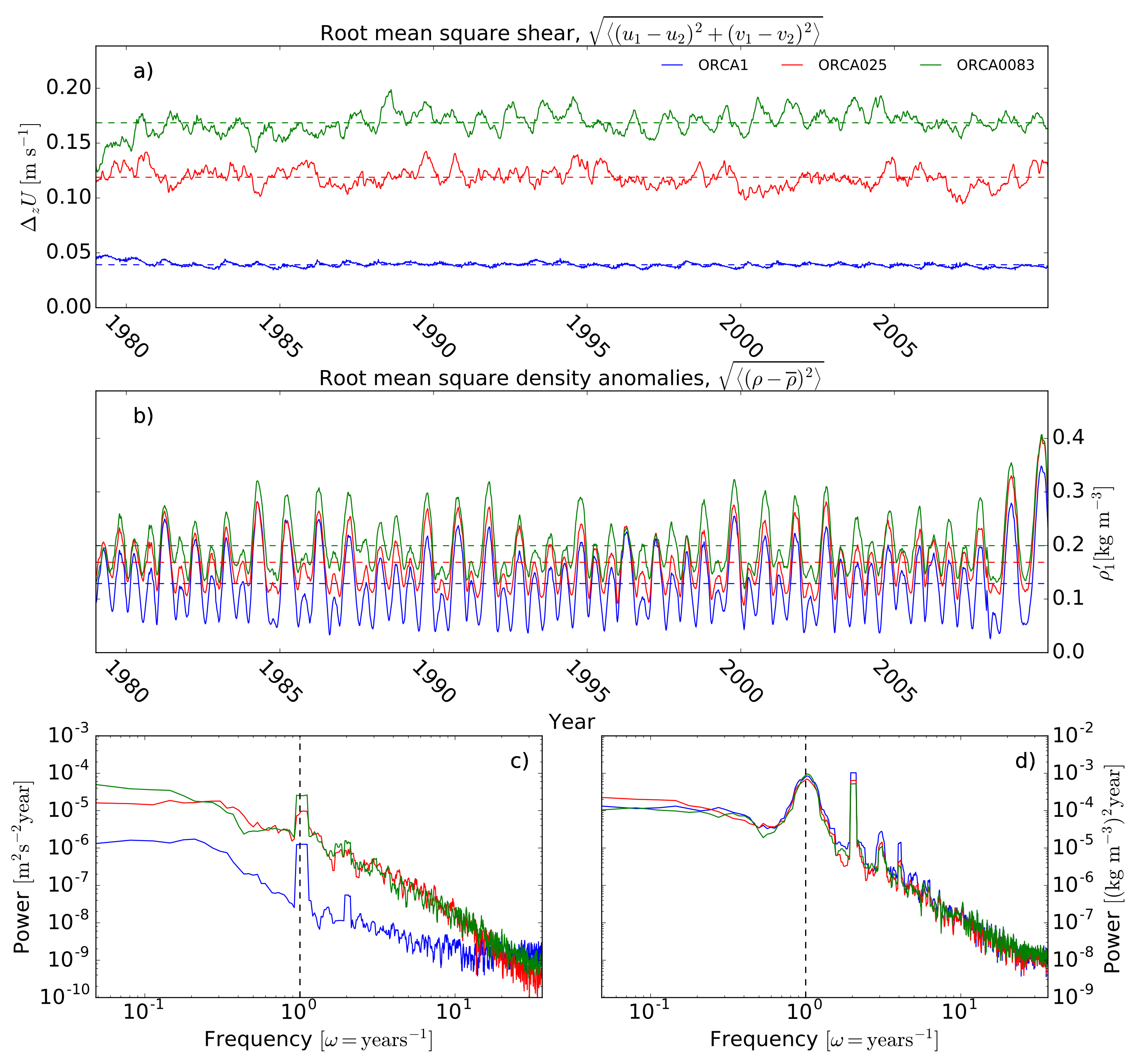
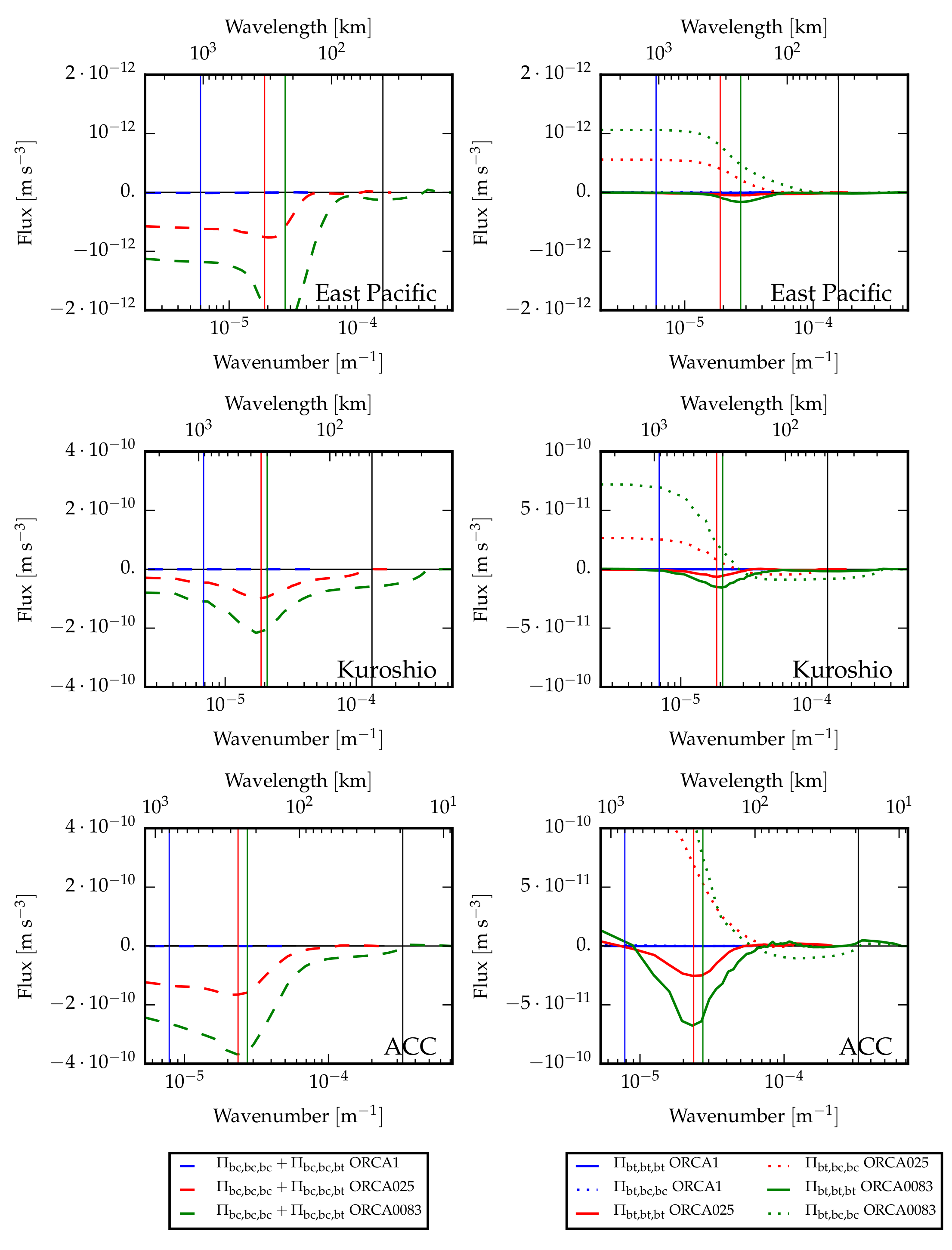
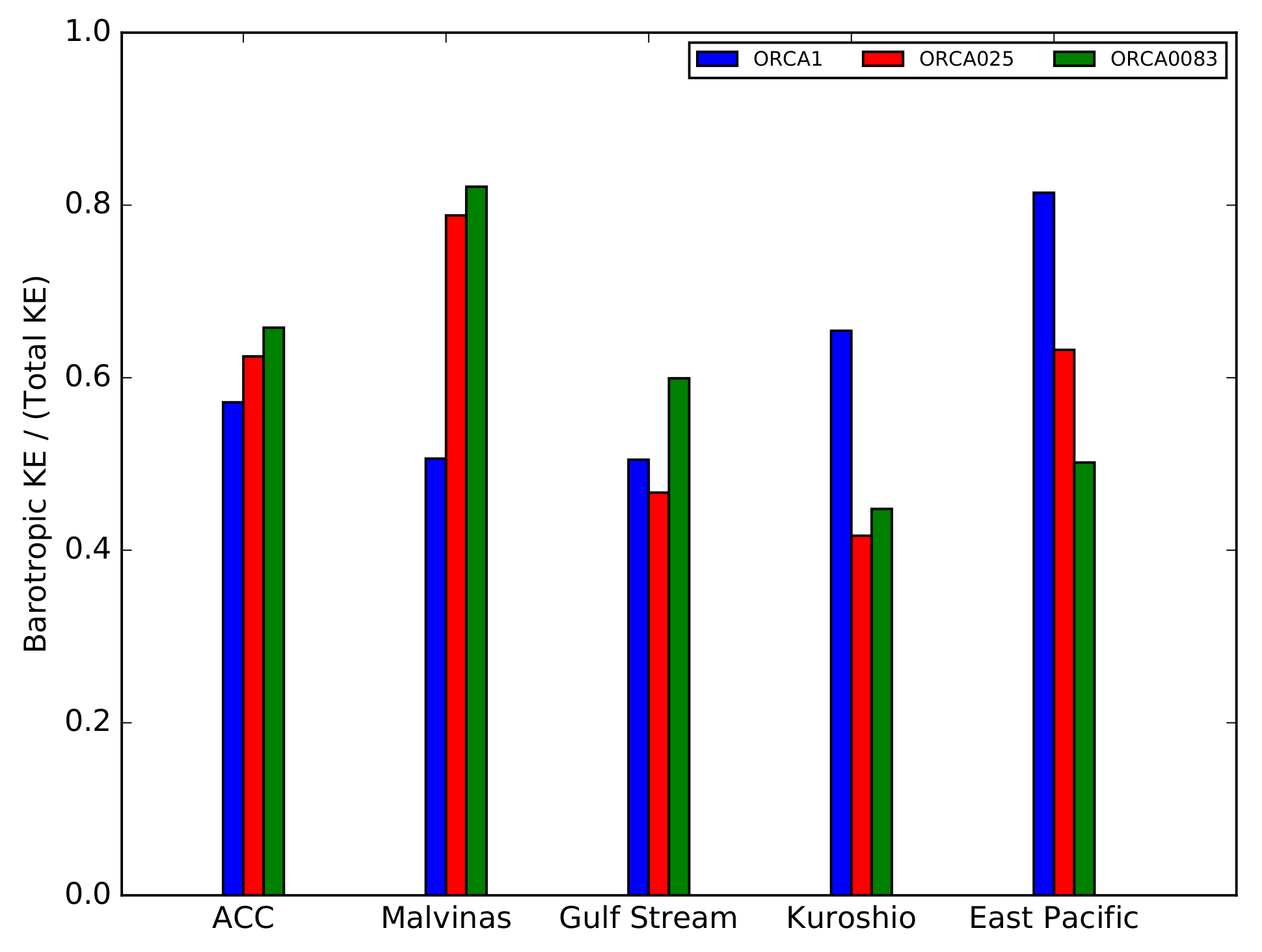
4.3. Baroclinic and Barotropic Kinetic Energy (KE)
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Arbic, B.K.; Polzin, K.L.; Scott, R.B.; Richman, J.G.; Shriver, J.F. On eddy viscosity, energy cascades, and the horizontal resolution of gridded satellite altimeter products. J. Phys. Oceanogr. 2012. [Google Scholar] [CrossRef]
- Hallberg, R.W. Using a resolution function to regulate parameterizations of oceanic mesoscale eddy effects. Ocean Model. 2013, 72, 92–103. [Google Scholar] [CrossRef]
- Hewitt, H.T.; Roberts, M.J.; Hyder, P.; Graham, T.; Rae, J.; Belcher, S.E.; Bourdallé-Badie, R.; Copsey, D.; Coward, A.; Guiavarch, C.; et al. The impact of resolving the Rossby radius at mid-latitudes in the ocean: Results from a high-resolution version of the Met Office GC2 coupled model. Geosci. Model Dev. 2016, 9, 3655–3670. [Google Scholar] [CrossRef]
- Zhang, Y.; Vallis, G.K. Ocean Heat Uptake in Eddying and Non-Eddying Ocean Circulation Models in a Warming Climate. J. Phys. Oceanogr. 2013, 43, 2211–2229. [Google Scholar] [CrossRef]
- Oschlies, A. Improved Representation of Upper-Ocean Dynamics and Mixed Layer Depths in a Model of the North Atlantic on Switching from Eddy-Permitting to Eddy-Resolving Grid Resolution. J. Phys. Oceanogr. 2002, 32, 2277–2298. [Google Scholar] [CrossRef]
- Griffies, S.M.; Winton, M.; Anderson, W.G.; Benson, R.; Delworth, T.L.; Dufour, C.O.; Dunne, J.P.; Goddard, P.; Morrison, A.K.; Rosati, A.; et al. Impacts on Ocean Heat from Transient Mesoscale Eddies in a Hierarchy of Climate Models. J. Clim. 2015, 28, 952–977. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Inertial Ranges in Two-Dimensional Turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Dissipation of Energy in the Locally Isotropic Turbulence. Proc. Math. Phys. Sci. 1991, 434, 15–17. [Google Scholar] [CrossRef]
- Salmon, R. Baroclinic instability and geostrophic turbulence. Geophys. Astrophys. Fluid Dyn. 1980, 15, 167–211. [Google Scholar] [CrossRef]
- Scott, R.B.; Wang, F. Direct Evidence of an Oceanic Inverse Kinetic Energy Cascade from Satellite Altimetry. J. Phys. Oceanogr. 2005, 35, 1650–1666. [Google Scholar] [CrossRef]
- Fu, L.L.; Flierl, G.R. Nonlinear energy and enstrophy transfers in a realistically stratified ocean. Dyn. Atmos. Oceans 1980, 4, 219–246. [Google Scholar] [CrossRef]
- Held, I.M.; Larichev, V.D. A Scaling Theory for Horizontally Homogeneous, Baroclinically Unstable Flow on a Beta Plane. J. Atmos. Sci. 1996, 53, 946–952. [Google Scholar] [CrossRef]
- Smith, K.S.; Vallis, G.K. The Scales and Equilibration of Midocean Eddies: Freely Evolving Flow. J. Phys. Oceanogr. 2001, 31, 554–571. [Google Scholar] [CrossRef]
- Treguier, A.M.; Hua, B.L. Influence of bottom topography on stratified quasi-geostrophic turbulence in the ocean. Geophys. Astrophys. Fluid Dyn. 1988, 43, 265–305. [Google Scholar] [CrossRef]
- Chemke, R.; Kaspi, Y. The latitudinal dependence of the oceanic barotropic eddy kinetic energy and macroturbulence energy transport. Geophys. Res. Lett. 2016, 43, 2723–2731. [Google Scholar] [CrossRef]
- Scott, R.B.; Arbic, B.K. Spectral Energy Fluxes in Geostrophic Turbulence: Implications for Ocean Energetics. J. Phys. Oceanogr. 2007, 37, 673–688. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to Submesoscale Transition in the California Current System. Part III: Energy Balance and Flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- Gent, P.R.; McWilliams, J.C. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 1990, 20, 150–155. [Google Scholar] [CrossRef]
- Jansen, M.F.; Held, I.M. Parameterizing subgrid-scale eddy effects using energetically consistent backscatter. Ocean Model. 2014, 80, 36–48. [Google Scholar] [CrossRef]
- Zanna, L.; Porta Mana, P.; Anstey, J.; David, T.; Bolton, T. Scale-aware deterministic and stochastic parametrizations of eddy-mean flow interaction. Ocean Model. 2017, 111, 66–80. [Google Scholar] [CrossRef]
- Griffies, S.M.; Hallberg, R.W. Biharmonic Friction with a Smagorinsky-Like Viscosity for Use in Large-Scale Eddy-Permitting Ocean Models. Mon. Weather Rev. 2000, 128, 2935–2946. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Menemenlis, D. Can Large Eddy Simulation Techniques Improve Mesoscale Rich Ocean Models? In Ocean Modeling in an Eddying Regime; American Geophysical Union: Washington, DC, USA, 2008; pp. 319–337. [Google Scholar]
- Bachman, S.D.; Fox-Kemper, B.; Pearson, B. A scale-aware subgrid model for quasi-geostrophic turbulence. J. Geophys. Res. Oceans 2017, 122, 1529–1554. [Google Scholar] [CrossRef]
- Shevchenko, I.; Berloff, P. Multi-layer quasi-geostrophic ocean dynamics in Eddy-resolving regimes. Ocean Model. 2015, 94, 1–14. [Google Scholar] [CrossRef]
- Anstey, J.A.; Zanna, L. A deformation-based parametrization of ocean mesoscale eddy reynolds stresses. Ocean Model. 2017, 112, 99–111. [Google Scholar] [CrossRef]
- Brankart, J.M. Impact of uncertainties in the horizontal density gradient upon low resolution global ocean modelling. Ocean Model. 2013, 66, 64–76. [Google Scholar] [CrossRef]
- Schloesser, F.; Eden, C. Diagnosing the energy cascade in a model of the North Atlantic. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Madec, G. NEMO Ocean Engine; Technical Report; Institut Pierre-Simon Laplace (IPSL): Paris, France, 2008. [Google Scholar]
- Holland, W.R. The Role of Mesoscale Eddies in the General Circulation of the Ocean—Numerical Experiments Using a Wind-Driven Quasi-Geostrophic Model. J. Phys. Oceanogr. 1978, 8, 363–392. [Google Scholar] [CrossRef]
- Böning, C.W.; Budich, R.G. Eddy Dynamics in a Primitive Equation Model: Sensitivity to Horizontal Resolution and Friction. J. Phys. Oceanogr. 1992, 22, 361–381. [Google Scholar] [CrossRef]
- Nilsson, J.A.U.; Döös, K.; Ruti, P.M.; Artale, V.; Coward, A.C.; Brodeau, L. Observed and Modeled Global Ocean Turbulence Regimes as Deduced from Surface Trajectory Data. J. Phys. Oceanogr. 2013, 43, 2249–2269. [Google Scholar] [CrossRef]
- Aluie, H.; Hecht, M.; Vallis, G.K. Mapping the Energy Cascade in the North Atlantic Ocean: The Coarse-graining Approach. J. Phys. Oceanogr. 2017. submitted for publication. [Google Scholar]
- Tulloch, R.; Marshall, J.; Hill, C.; Smith, K.S. Scales, Growth Rates, and Spectral Fluxes of Baroclinic Instability in the Ocean. J. Phys. Oceanogr. 2011, 41, 1057–1076. [Google Scholar] [CrossRef]
- Chelton, D.B.; deSzoeke, R.A.; Schlax, M.G.; El Naggar, K.; Siwertz, N. Geographical Variability of the First Baroclinic Rossby Radius of Deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Marzocchi, A.; Hirschi, J.J.M.; Holliday, N.P.; Cunningham, S.A.; Blaker, A.T.; Coward, A.C. The North Atlantic subpolar circulation in an eddy-resolving global ocean model. J. Mar. Syst. 2015, 142, 126–143. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Holland, P.R.; Bruneau, N.; Enright, C.; Losch, M.; Kurtz, N.T.; Kwok, R. Modeled trends in Antarctic sea ice thickness. J. Clim. 2014, 27. [Google Scholar] [CrossRef]
- Wunsch, C. The Vertical Partition of Oceanic Horizontal Kinetic Energy. J. Phys. Oceanogr. 1997, 27, 1770–1794. [Google Scholar] [CrossRef]
- Itoh, S.; Yasuda, I.; Ueno, H.; Suga, T.; Kakehi, S. Regeneration of a warm anticyclonic ring by cold water masses within the western subarctic gyre of the North Pacific. J. Oceanogr. 2014, 70, 211–223. [Google Scholar] [CrossRef]
- Molemaker, M.J.; McWilliams, J.C. Local balance and cross-scale flux of available potential energy. J. Fluid Mech. 2010, 645, 295. [Google Scholar] [CrossRef]
- Qiu, B. Kuroshio Extension Variability and Forcing of the Pacific Decadal Oscillations: Responses and Potential Feedback. J. Phys. Oceanogr. 2003, 33, 2465–2482. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Pierini, S.; Dijkstra, H. A. Intrinsic low-frequency variability of the Gulf Stream. Nonlin. Processes Geophys. 2012, 19, 155–164. [Google Scholar] [CrossRef]
- Langlais, C.E.; Rintoul, S.R.; Zika, J.D. Sensitivity of Antarctic Circumpolar Current Transport and Eddy Activity to Wind Patterns in the Southern Ocean. J. Phys. Oceanogr. 2015, 45, 1051–1067. [Google Scholar] [CrossRef]
- Arbic, B.K.; Scott, R.B.; Flierl, G.R.; Morten, A.J.; Richman, J.G.; Shriver, J.F. Nonlinear Cascades of Surface Oceanic Geostrophic Kinetic Energy in the Frequency Domain. J. Phys. Oceanogr. 2012, 42, 1577–1600. [Google Scholar] [CrossRef]
- Sérazin, G.; Penduff, T.; Grégorio, S.; Barnier, B.; Molines, J.M.; Terray, L. Intrinsic Variability of Sea Level from Global Ocean Simulations: Spatiotemporal Scales. J. Clim. 2015, 28, 4279–4292. [Google Scholar] [CrossRef]
- Chemke, R.; Dror, T.; Kaspi, Y. Barotropic kinetic energy and enstrophy transfers in the atmosphere. Geophys. Res. Lett. 2016, 43, 7725–7734. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Sasai, Y.; Qiu, B. Regionality and seasonality of submesoscale and mesoscale turbulence in the North Pacific Ocean. Ocean Dyn. 2017, 67, 1195–1216. [Google Scholar] [CrossRef]
- Zhai, X.; Johnson, H.L.; Marshall, D.P.; Wunsch, C. On the Wind Power Input to the Ocean General Circulation. J. Phys. Oceanogr. 2012. [Google Scholar] [CrossRef]
- Rhines, P.B. Waves and turbulence on a beta-plane. J. Fluid Mech. 1975, 69, 417–443. [Google Scholar] [CrossRef]
- Chemke, R.; Kaspi, Y. The latitudinal dependence of atmospheric jet scales and macroturbulent energy cascades. J. Atmos. Sci. 2015. [Google Scholar] [CrossRef]
- Nikurashin, M.; Vallis, G.K.; Adcroft, A. Routes to energy dissipation for geostrophic flows in the Southern Ocean. Nat. Geosci. 2012, 6, 48–51. [Google Scholar] [CrossRef]
- Shevchenko, I.; Berloff, P. On the roles of baroclinic modes in eddy-resolving midlatitude ocean dynamics. Ocean Model. 2017, 111, 55–65. [Google Scholar] [CrossRef]
- Bower, A.S.; Rossby, H.T.; Lillibridge, J.L.; Bower, A.S.; Rossby, H.T.; Lillibridge, J.L. The Gulf Stream—Barrier or Blender? J. Phys. Oceanogr. 1985, 15, 24–32. [Google Scholar] [CrossRef]
- Abernathey, R.; Marshall, J.; Mazloff, M.; Shuckburgh, E.; Abernathey, R.; Marshall, J.; Mazloff, M.; Shuckburgh, E. Enhancement of Mesoscale Eddy Stirring at Steering Levels in the Southern Ocean. J. Phys. Oceanogr. 2010, 40, 170–184. [Google Scholar] [CrossRef]
- Klocker, A.; Ferrari, R.; LaCasce, J.H.; Merrifield, S.T. Reconciling float-based and tracer-based estimates of lateral diffusivities. J. Mar. Res. 2012, 70, 569–602. [Google Scholar] [CrossRef]
- Stewart, K.D.; Spence, P.; Waterman, S.; Sommer, J.L.; Molines, J.M.; Lilly, J.M.; England, M.H. Anisotropy of eddy variability in the global ocean. Ocean Model. 2015, 95, 53–65. [Google Scholar] [CrossRef]
- Chen, R.; Thompson, A.F.; Flierl, G.R.; Chen, R.; Thompson, A.F.; Flierl, G.R. Time-Dependent Eddy-Mean Energy Diagrams and Their Application to the Ocean. J. Phys. Oceanogr. 2016, 46, 2827–2850. [Google Scholar] [CrossRef]
- Storch, J.S.V.; Eden, C.; Fast, I.; Haak, H.; Hernández-Deckers, D.; Maier-Reimer, E.; Marotzke, J.; Stammer, D. An Estimate of the Lorenz Energy Cycle for the World Ocean Based on the STORM/NCEP Simulation. J. Phys. Oceanogr. 2012, 42, 2185–2205. [Google Scholar] [CrossRef]
- Zhai, X.; Johnson, H.L.; Marshall, D.P. Significant sink of ocean-eddy energy near western boundaries. Nat. Geosci. 2010, 3, 608–612. [Google Scholar] [CrossRef]
- Jochum, M.; Danabasoglu, G.; Holland, M.; Kwon, Y.O.; Large, W.G. Ocean viscosity and climate. J. Geophys. Res. Oceans 2008, 113, C06017. [Google Scholar] [CrossRef]
- Pearson, B.; Fox-Kemper, B.; Bachman, S.; Bryan, F. Evaluation of scale-aware subgrid mesoscale eddy models in a global eddy-rich model. Ocean Model. 2017, 115, 42–58. [Google Scholar] [CrossRef]
- Williams, P.D.; Howe, N.J.; Gregory, J.M.; Smith, R.S.; Joshi, M.M. Improved climate simulations through a stochastic parameterization of ocean eddies. J. Clim. 2016. [Google Scholar] [CrossRef]
- Foias, C.; Holm, D.D.; Titi, E.S. The Navier-Stokes-alpha model of fluid turbulence. Phys. D Nonlinear Phenom. 2001, 152-153, 505–519. [Google Scholar] [CrossRef]
- Hecht, M.W.; Holm, D.D.; Petersen, M.R.; Wingate, B.A. Implementation of the LANS-α turbulence model in a primitive equation ocean model. J. Comput. Phys. 2008, 227, 5691–5716. [Google Scholar] [CrossRef]
- Jansen, M.F.; Held, I.M.; Adcroft, A.; Hallberg, R. Energy budget-based backscatter in an eddy permitting primitive equation model. Ocean Model. 2015, 94, 15–26. [Google Scholar] [CrossRef]
- Rocha, C.B.; Chereskin, T.K.; Gille, S.T.; Menemenlis, D.; Rocha, C.B.; Chereskin, T.K.; Gille, S.T.; Menemenlis, D. Mesoscale to Submesoscale Wavenumber Spectra in Drake Passage. J. Phys. Oceanogr. 2016, 46, 601–620. [Google Scholar] [CrossRef]
| Parameter | ORCA1-N406 | ORCA025-N401 | ORCA0083-N001 |
|---|---|---|---|
| Hor. res. | |||
| z levels | |||
| Time step, | |||
| Hor. visc. order, | |||
| Hor. visc., | |||
| Vert. visc., | |||
| Drag coeff., | |||
| Backgr. turb. KE, | |||
| Tracer diff., | |||
| Tracer diff. form | Iso-neutral | Iso-neutral | Iso-neutral |
| Eddy param. | Yes, [18] | No | No |
| Ref. density, |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kjellsson, J.; Zanna, L. The Impact of Horizontal Resolution on Energy Transfers in Global Ocean Models. Fluids 2017, 2, 45. https://doi.org/10.3390/fluids2030045
Kjellsson J, Zanna L. The Impact of Horizontal Resolution on Energy Transfers in Global Ocean Models. Fluids. 2017; 2(3):45. https://doi.org/10.3390/fluids2030045
Chicago/Turabian StyleKjellsson, Joakim, and Laure Zanna. 2017. "The Impact of Horizontal Resolution on Energy Transfers in Global Ocean Models" Fluids 2, no. 3: 45. https://doi.org/10.3390/fluids2030045
APA StyleKjellsson, J., & Zanna, L. (2017). The Impact of Horizontal Resolution on Energy Transfers in Global Ocean Models. Fluids, 2(3), 45. https://doi.org/10.3390/fluids2030045





