An Oceanic Ultra-Violet Catastrophe, Wave-Particle Duality and a Strongly Nonlinear Concept for Geophysical Turbulence
Abstract
:1. Introduction
2. Materials and Methods
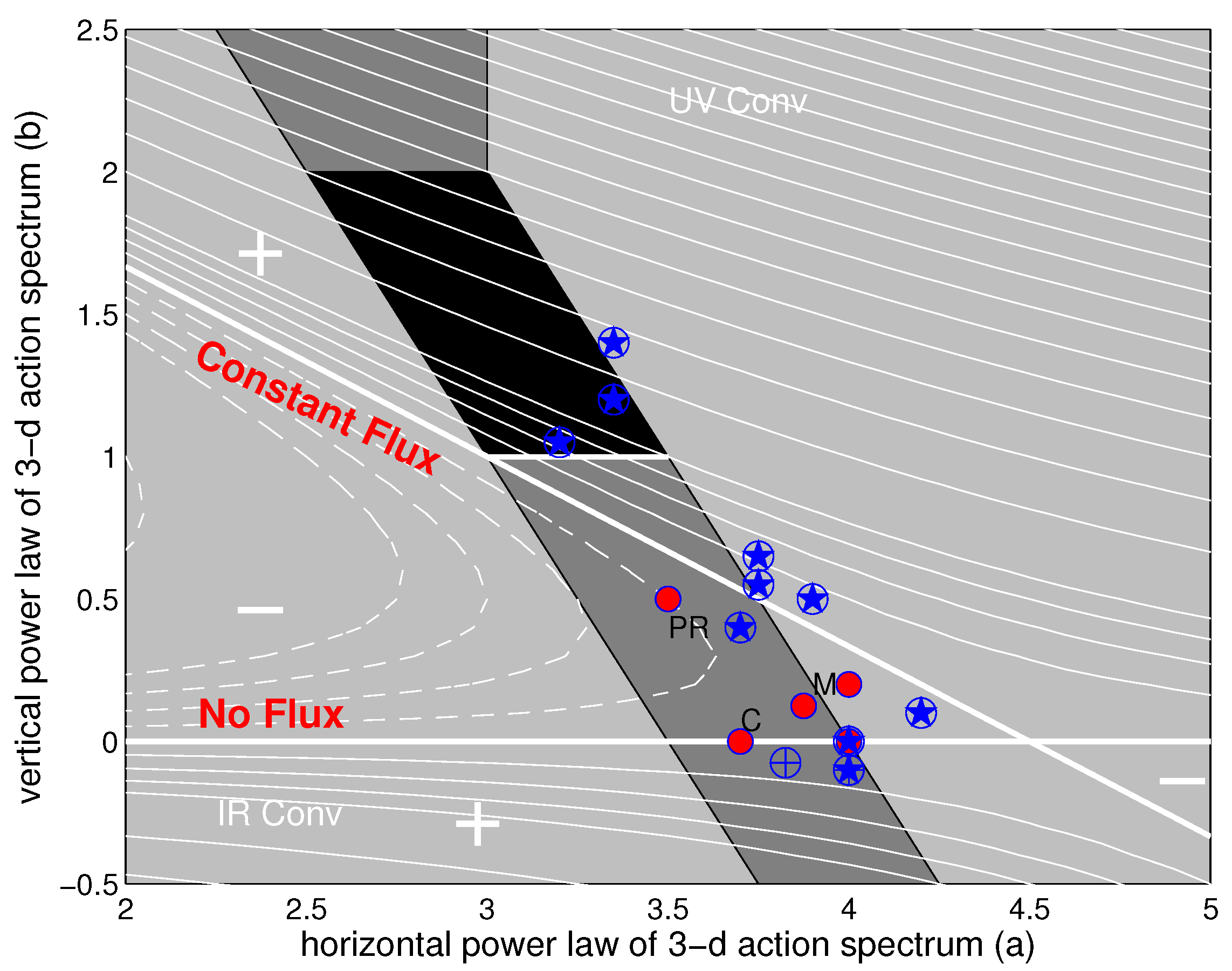
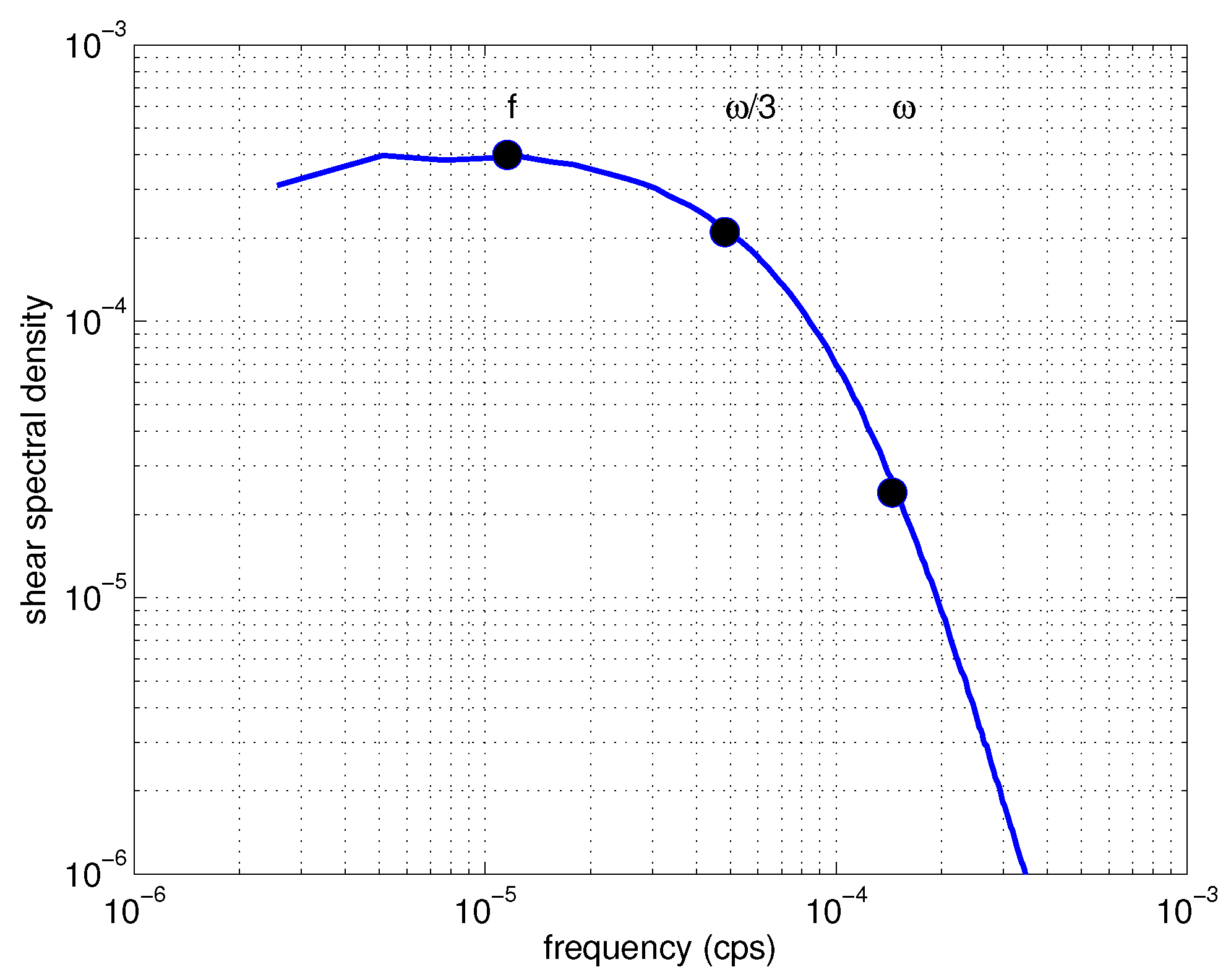
2.1. The Empirical Spectrum
2.2. Ray Tracing
2.3. Metrics of Diffusion
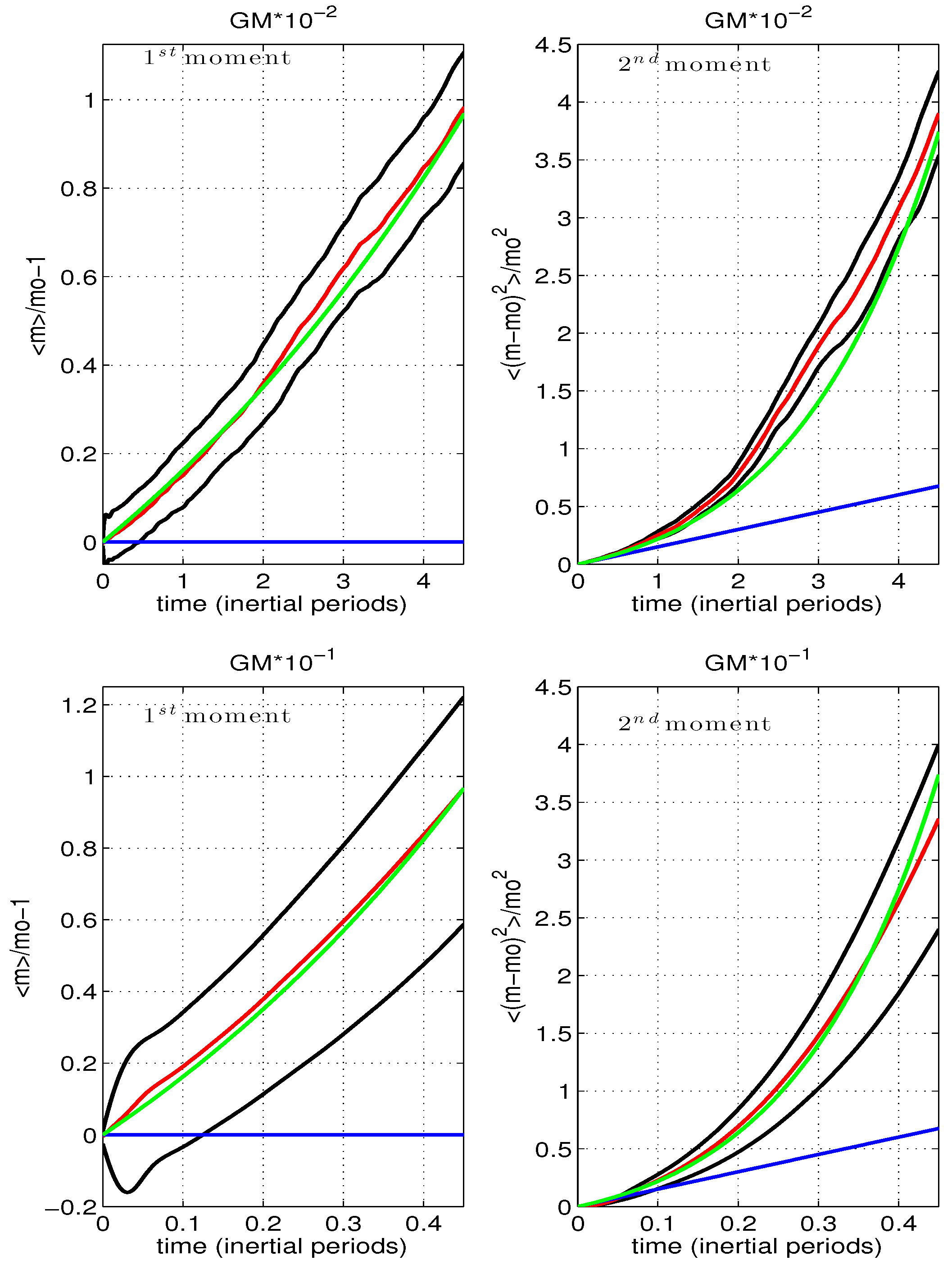
2.3.1. The Moment Method
2.3.2. Diffusion in the Spectral Domain
3. Results: Ray Tracing
3.1. Low Dimensional Systems
3.2. High Dimensional Systems
3.2.1. Analysis via the Moment Method
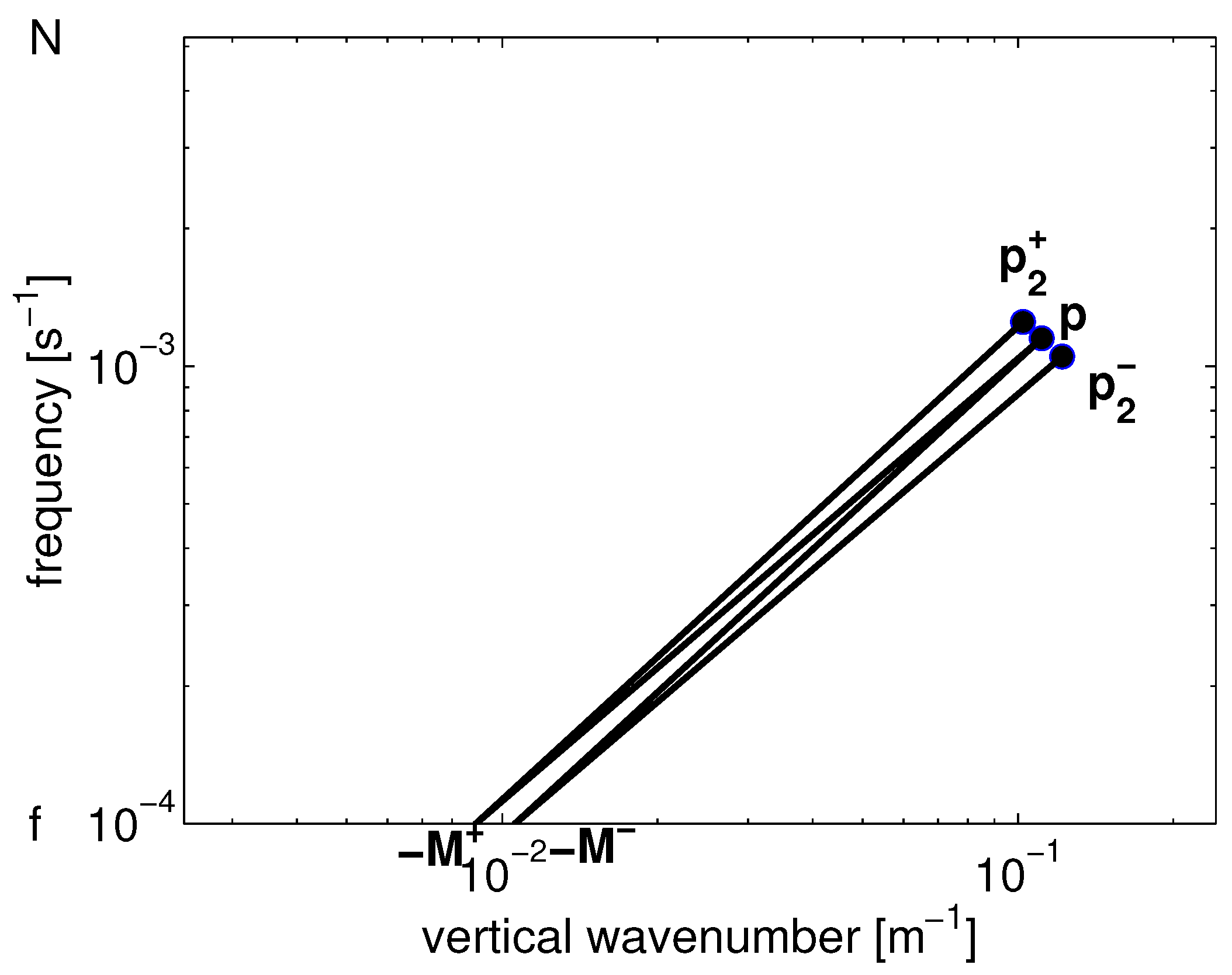
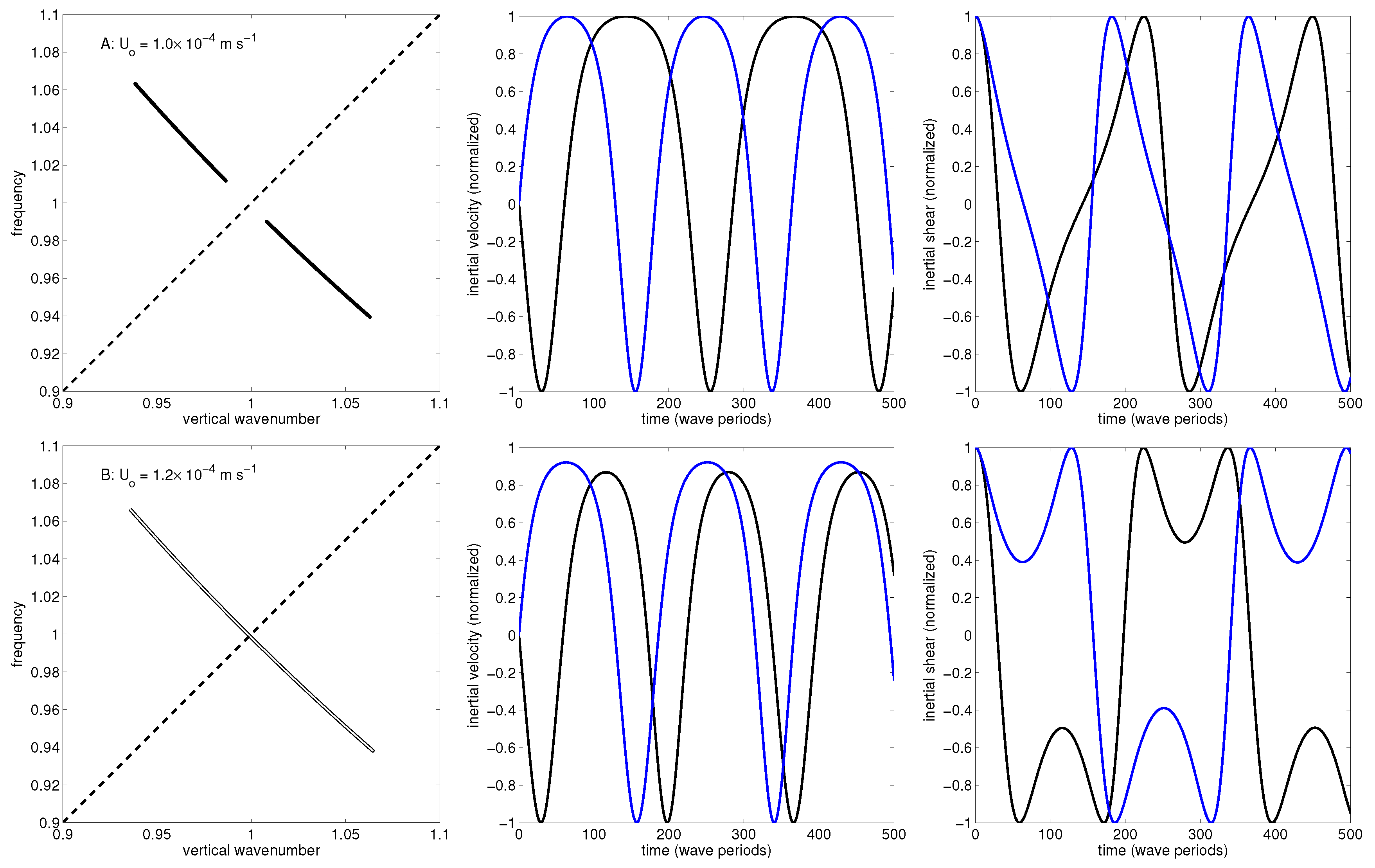
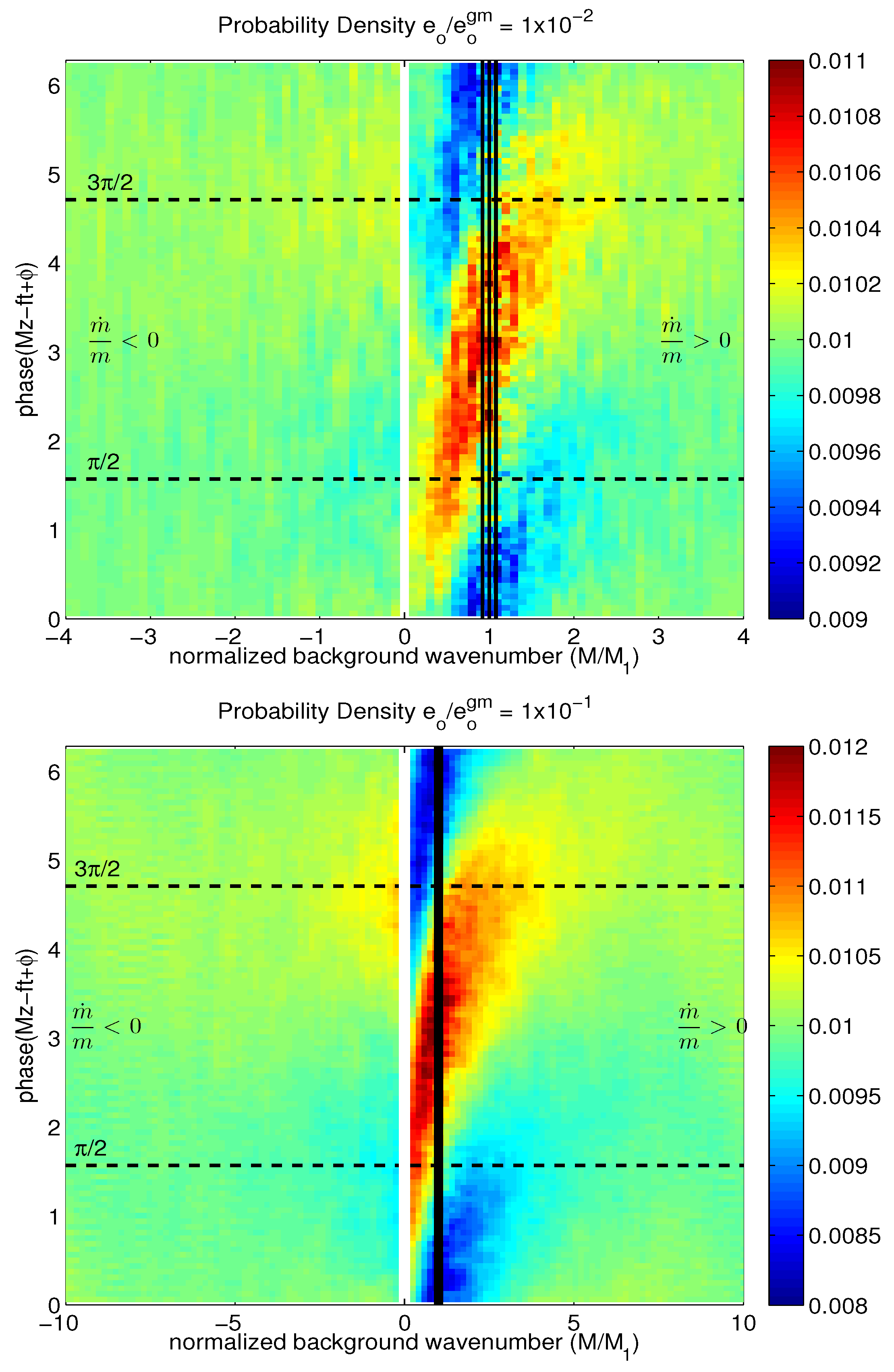
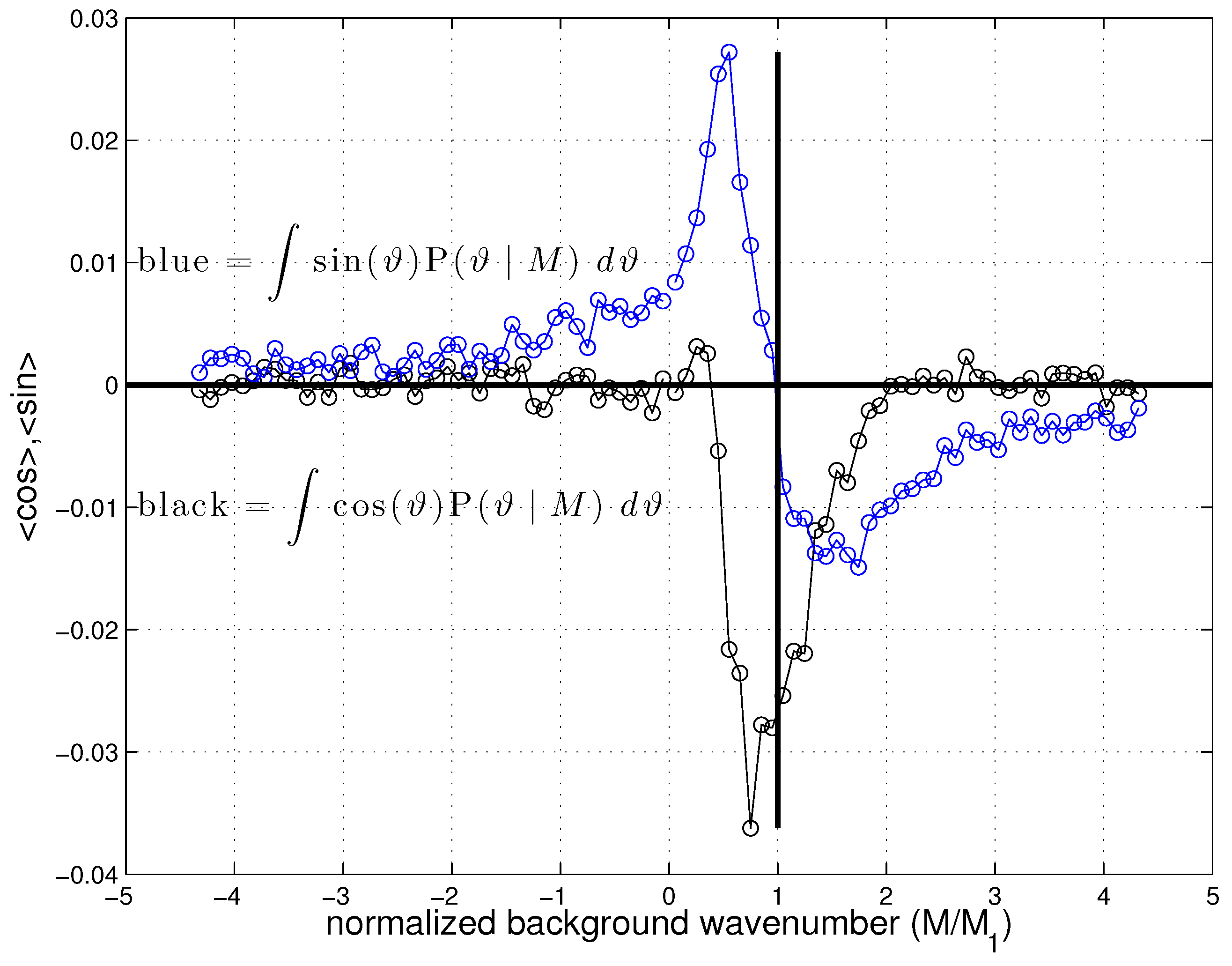
3.2.2. Phase Correlations
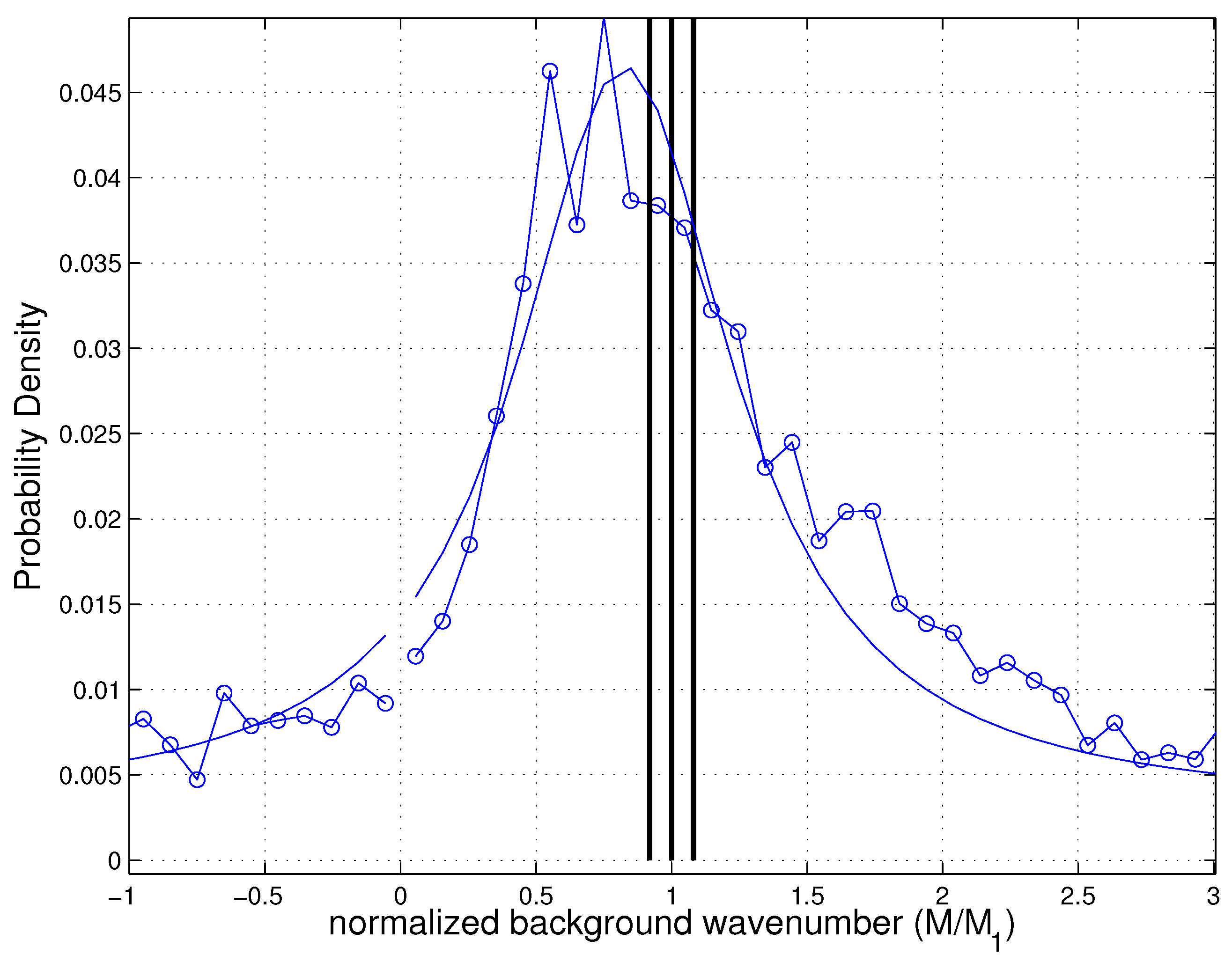
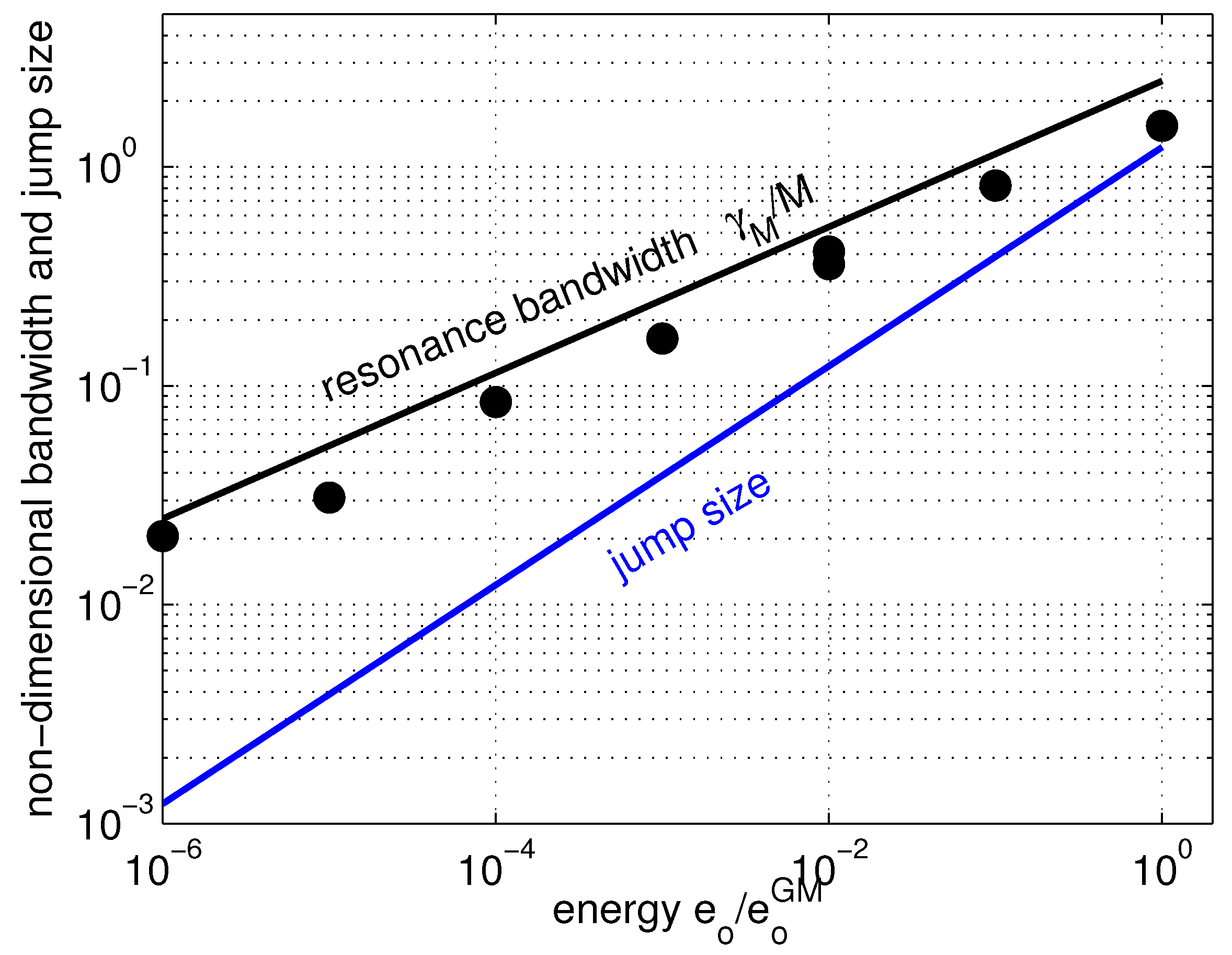
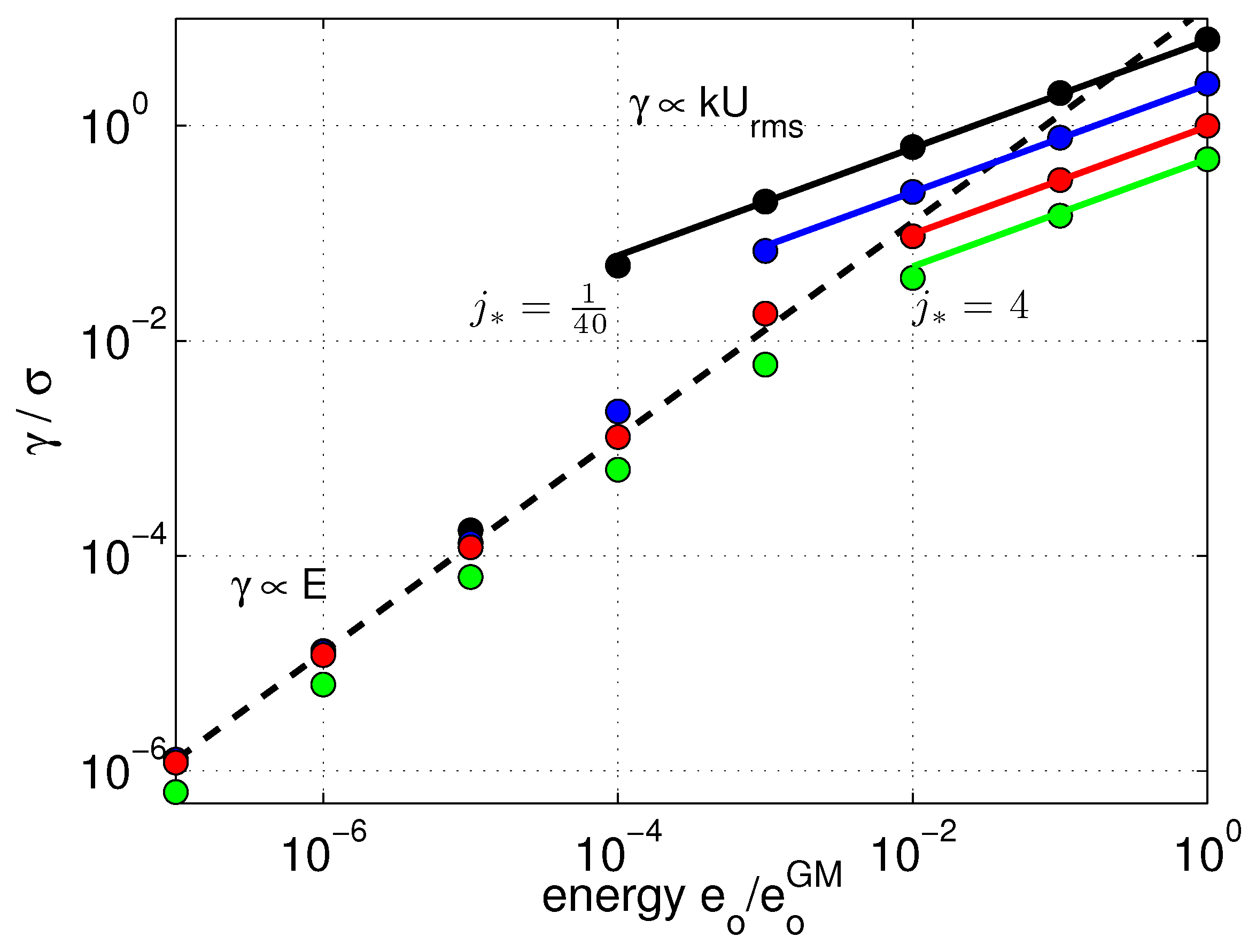
3.2.3. The Resonant Response and a Resonant Well
3.2.4. The Non-Resonant Response and Jump Size
3.3. Summary
4. Results: Kinetic Equations
4.1. Background
4.2. The DIA Equations
4.3. The Small Amplitude Limit
4.4. Broadening at Finite Amplitude
4.5. The Frequency Shift
4.6. A Fokker-Planck Equation
4.7. Summary
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Ray-Tracing Set-Up Parameters
| Name | |||||||
|---|---|---|---|---|---|---|---|
| 12.19.0c | 2500 | 30,000 | 2401 | 0.025 | 160 | ||
| 11.7.1a | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 11.7.1b | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 10.23.2a | 10,000 | 3000 | 24,001 | 0.5 | 1600 | ||
| 10.23.2b | 3000 | 24,001 | 0.5 | 1600 | |||
| 11.13.20 | 1200 | 40,000 | 2001 | 0.25 | 32 | ||
| 11.13.30 | 5000 | 10,000 | 2001 | 0.25 | 32 | ||
| 11.13.40 | 5000 | 10,000 | 5001 | 0.5 | 16 | ||
| 11.13.50 | 10,000 | 10,000 | 6001 | 3.2 | 4.8 | ||
| 7.3.6abcdefghij | 50,000 | 1200 | 24,001 | 3.2 | 4.8 |
| Name | |||||||
|---|---|---|---|---|---|---|---|
| 12.19.0c | 30,000 | 2401 | 0.025 | 160 | |||
| 11.7.1a | 1000 | 30,000 | 2401 | 0.025 | 1600 | ||
| 10.23.2a | 5000 | 3000 | 24,001 | 0.025 | 1600 | ||
| 12.6.2 | 5000 | 3000 | 24,001 | 0.025 | 1600 | ||
| 12.7.3 | 20,000 | 1500 | 24,001 | 0.5 | 16 | ||
| 7.3.6abcdefghij | 50,000 | 1200 | 24,001 | 3.2 | 4.8 | ||
| 12.19.0g | 30,000 | 4801 | 0.025 | 640 | |||
| 11.7.1c.v7.3 | 30,000 | 4801 | 0.025 | 640 |
References
- Kolmogorv, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. 1941, 30, 299–303. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity wave spectrum. Part I. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity wave spectrum. Part II. Conservation theorems, wave-particle analogy, irreversibility. J. Fluid Mech. 1963, 15, 385–398. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Lvov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence; Springer: Berlin, Germany, 1992. [Google Scholar]
- McComas, C.H.; Müller, P. The dynamic balance of internal waves. J. Phys. Oceanogr. 1981, 11, 970–986. [Google Scholar] [CrossRef]
- Polzin, K.L.; Lvov, Y.S. Toward regional characterizations of the oceanic internal wave spectrum. Rev. Geophys. 2011, 49. [Google Scholar] [CrossRef]
- Munk, W. Internal waves and small-scale processes. In Evolution of Physical Oceanography; Warren, B.A., Wunsch, C., Eds.; The MIT Press: Cambridge, MA, USA, 1981; pp. 264–291. [Google Scholar]
- Pelinovskii, E.N.; Raevsky, M.A. Weak turbulence of internal ocean waves. In Izvestiya Akademii Nauk SSSR, Fizika Atmosfery i Okeana, translated in Izvestiya Academy of Sciences USSR, Atmospheric and Oceanic Physics; American Geophysical Union: Washington, DC, USA, 1977; Volume 13, pp. 187–193. [Google Scholar]
- Lvov, Y.V.; Polzin, K.L.; Tabak, E.G.; Yokoyama, N. Oceanic internal wavefield: Theory of scale-invariant spectra. J. Phys. Oceanogr. 2010, 40, 2605–2623. [Google Scholar] [CrossRef]
- Gregg, M.C. Scaling turbulent dissipation in the thermocline. J. Geophys. Res. 1989, 94, 9686–9698. [Google Scholar] [CrossRef]
- Polzin, K.L. A heuristic description of internal wave dynamics. J. Phys. Oceanogr. 2004, 34, 214–230. [Google Scholar] [CrossRef]
- Polzin, K.L.; Toole, J.M.; Schmitt, R.W. Finescale parameterizations of turbulent dissipation. J. Phys. Oceanogr. 1995, 25, 306–328. [Google Scholar] [CrossRef]
- Polzin, K.L.; Naveira Garabato, A.C.; Sloyan, B.M.; Huussen, T.; Waterman, S.N. Finescale Parameterizations of Turbulent Dissipation. J. Geophys. Res. 2014, 119, 1383–1419. [Google Scholar] [CrossRef]
- McComas, C.H.; Müller, P. Timescales of resonant interactions among oceanic internal waves. J. Phys. Oceanogr. 1981, 11, 139–147. [Google Scholar] [CrossRef]
- Pomphrey, N.; Meiss, J.D.; Watson, K.M. Description of nonlinear internal wave interactions using Langevin methods. J. Geophys. Res. 1980, 85, 1085–1094. [Google Scholar] [CrossRef]
- Henyey, F.S.; Pomphrey, N. Eikonal description of internal wave interactions: A non-diffusive picture of “induced diffusion”. Dyn. Atmos. Oceans 1983, 7, 189–208. [Google Scholar] [CrossRef]
- Nazarenko, S. Wave Turbulence; Springer: Berlin, Germany, 2011; ISBN 978-3642159411. [Google Scholar]
- Connaughton, C.; Nazarenko, S.; Quinn, B. Rossby and drift wave turbulence and zonal flows: The Charney? Hasegawa? Mima model and its extensions. Phys. Rep. 2015, 604, 1–71. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley-Interscience: New York, NY, USA, 1974; p. 636. [Google Scholar]
- McComas, C.H.; Bretherton, F.P. Resonant interaction of oceanic internal waves. J. Geophys. Res. 1977, 83, 1397–1412. [Google Scholar] [CrossRef]
- Müller, P.; Holloway, G.; Henyey, F.; Pomphrey, N. Nonlinear interactions among internal gravity waves. Rev. Geophys. 1986, 24, 493–536. [Google Scholar] [CrossRef]
- Nazarenko, S.V.; Newell, A.C.; Galtier, S. Non-local MHD turbulence. Physica D 2001, 152, 646–652. [Google Scholar] [CrossRef]
- Lvov, V.S.; Lvov, Y.V.; Newell, A.C.; Zakharov, V.E. Statistical description of acoustic turbulence. Phys. Rev. E 1977, 56, 390–405. [Google Scholar] [CrossRef]
- Gershgorin, B.; Lvov, Y.V.; Nazarenko, S. Canonical Hamiltonians for waves in inhomogeneous media. J. Math. Phys. 2009, 50, 013527. [Google Scholar] [CrossRef]
- Holloway, G. Oceanic internal waves are not weak waves. J. Phys. Oceanogr. 1980, 10, 906–914. [Google Scholar] [CrossRef]
- Holloway, G. On interaction timescales of oceanic internal waves. J. Phys. Oceanogr. 1982, 12, 293–296. [Google Scholar] [CrossRef]
- Cohen, L.; Lee, C. Instantaneous bandwidth for signals and spectrogram. In Proceedings of the IEEE International Conference Acoustics Speech Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 2451–2454. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: New York, NY, USA, 2004; p. 415. [Google Scholar]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1921, 2, 196–211. [Google Scholar] [CrossRef]
- Broutman, D.; Rottman, J.W.; Eckermann, S.D. Ray methods for internal waves in the atmosphere and ocean. Annu. Rev. Fluid Mech. 2004, 36, 233–253. [Google Scholar] [CrossRef]
- Sun, H.; Kunze, E. Internal wave–wave interactions. Part II: Spectral energy transfer and turbulent production. J. Phys. Oceanogr. 1999, 29, 2905–2919. [Google Scholar] [CrossRef]
- Lvov, Y.V.; Polzin, K.L.; Yokoyama, N. Wave-wave interactions in stratified fluids: A comparison of approaches. J. Phys. Oceanogr. 2012, 42, 669–691. [Google Scholar] [CrossRef]
- Müller, P.; Olbers, D.J. On the dynamics of internal waves in the deep ocean. J. Geophys. Res. 1975, 80, 3848–3860. [Google Scholar] [CrossRef]
- Lvov, V.S.; Procaccia, I. Exact Resummation in the Theory of Hydrodynamic Turbulence. 0. Line-Resummed Diagrammatic Perturbation Approach. In Lecture Notes of the Les Houches 1994 Summer School “Fluctuating Geometries in Statistical Mechanics and Field Theory”; David, F., Ginsparg, P., Eds.; North-Holland: Amsterdam, The Netherlands, 1995; pp. 1027–1075. [Google Scholar]
- Lvov, Y.V.; Tabak, E.G. A Hamiltonian Formulation for Long Internal Waves. Physica D 2004, 195, 106–122. [Google Scholar] [CrossRef]
- Majda, A.J.; McLaughlin, D.W.; Tabak, E.G. A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 1997, 6, 9–44. [Google Scholar] [CrossRef]
- Rumpf, B.; Newell, A.C.; Zakharov, V.E. Turbulent transfer of energy by radiating pulses. Phys. Rev. Lett. 2009, 103, 074502. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Lahini, Y.; Avidan, A.; Pozzi, F.; Sorel, M.; Morandotti, R.; Christodoulides, D.N.; Silberberg, Y. Anderson localization and nonlinearity in one dimensional disordered photonic lattices. Phys. Rev. Lett. 2008, 100, 013906. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polzin, K.L.; Lvov, Y.V. An Oceanic Ultra-Violet Catastrophe, Wave-Particle Duality and a Strongly Nonlinear Concept for Geophysical Turbulence. Fluids 2017, 2, 36. https://doi.org/10.3390/fluids2030036
Polzin KL, Lvov YV. An Oceanic Ultra-Violet Catastrophe, Wave-Particle Duality and a Strongly Nonlinear Concept for Geophysical Turbulence. Fluids. 2017; 2(3):36. https://doi.org/10.3390/fluids2030036
Chicago/Turabian StylePolzin, Kurt L., and Yuri V. Lvov. 2017. "An Oceanic Ultra-Violet Catastrophe, Wave-Particle Duality and a Strongly Nonlinear Concept for Geophysical Turbulence" Fluids 2, no. 3: 36. https://doi.org/10.3390/fluids2030036
APA StylePolzin, K. L., & Lvov, Y. V. (2017). An Oceanic Ultra-Violet Catastrophe, Wave-Particle Duality and a Strongly Nonlinear Concept for Geophysical Turbulence. Fluids, 2(3), 36. https://doi.org/10.3390/fluids2030036






