A Computational Simulation Study of Fluid Mechanics of Low-Speed Wind Tunnel Contractions
Abstract
:1. Introduction
2. Problem Formulation
2.1. Contraction Dimensions
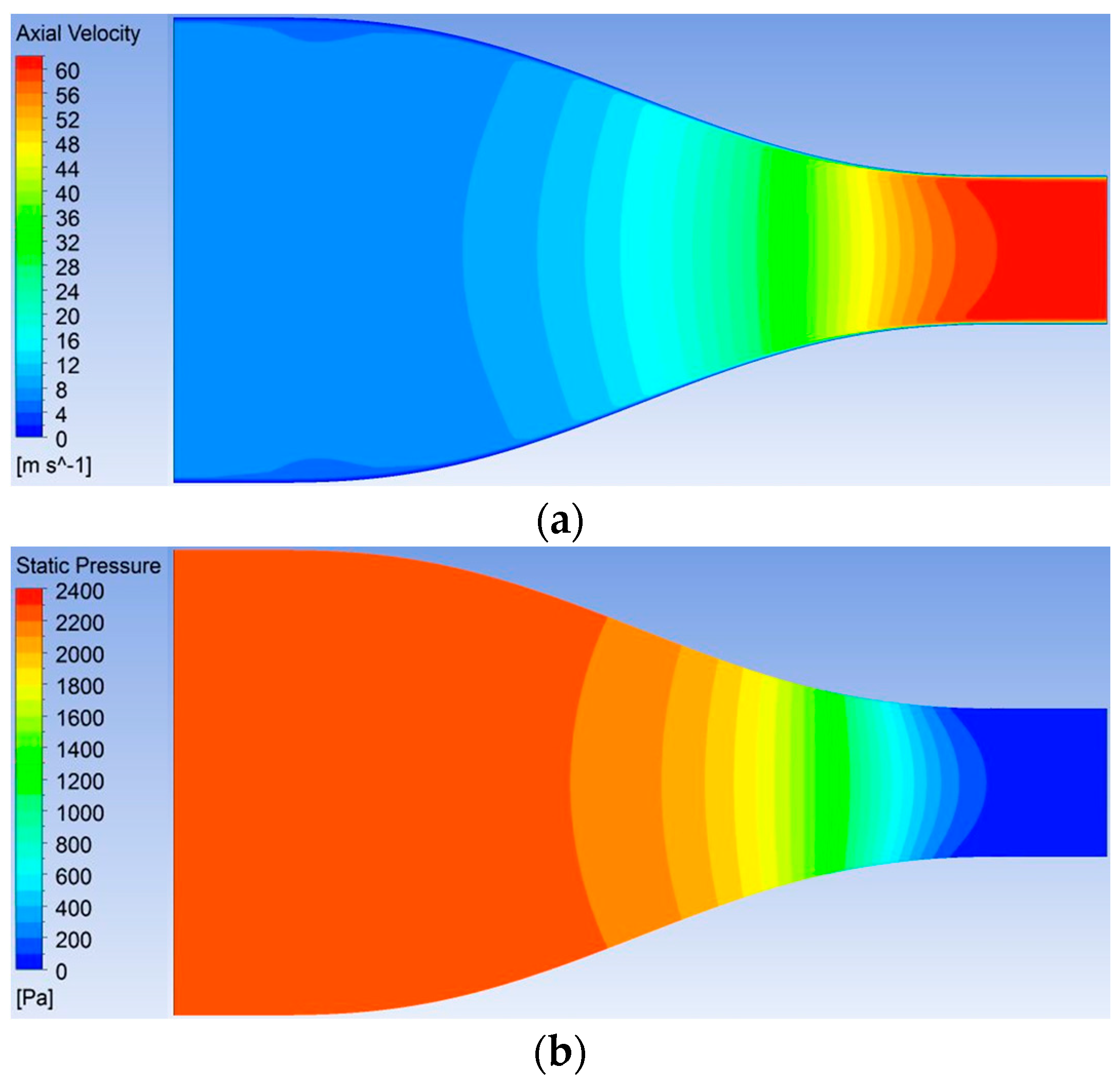
2.2. Computational Fluid Dynamics Model
2.3. Boundary Conditions
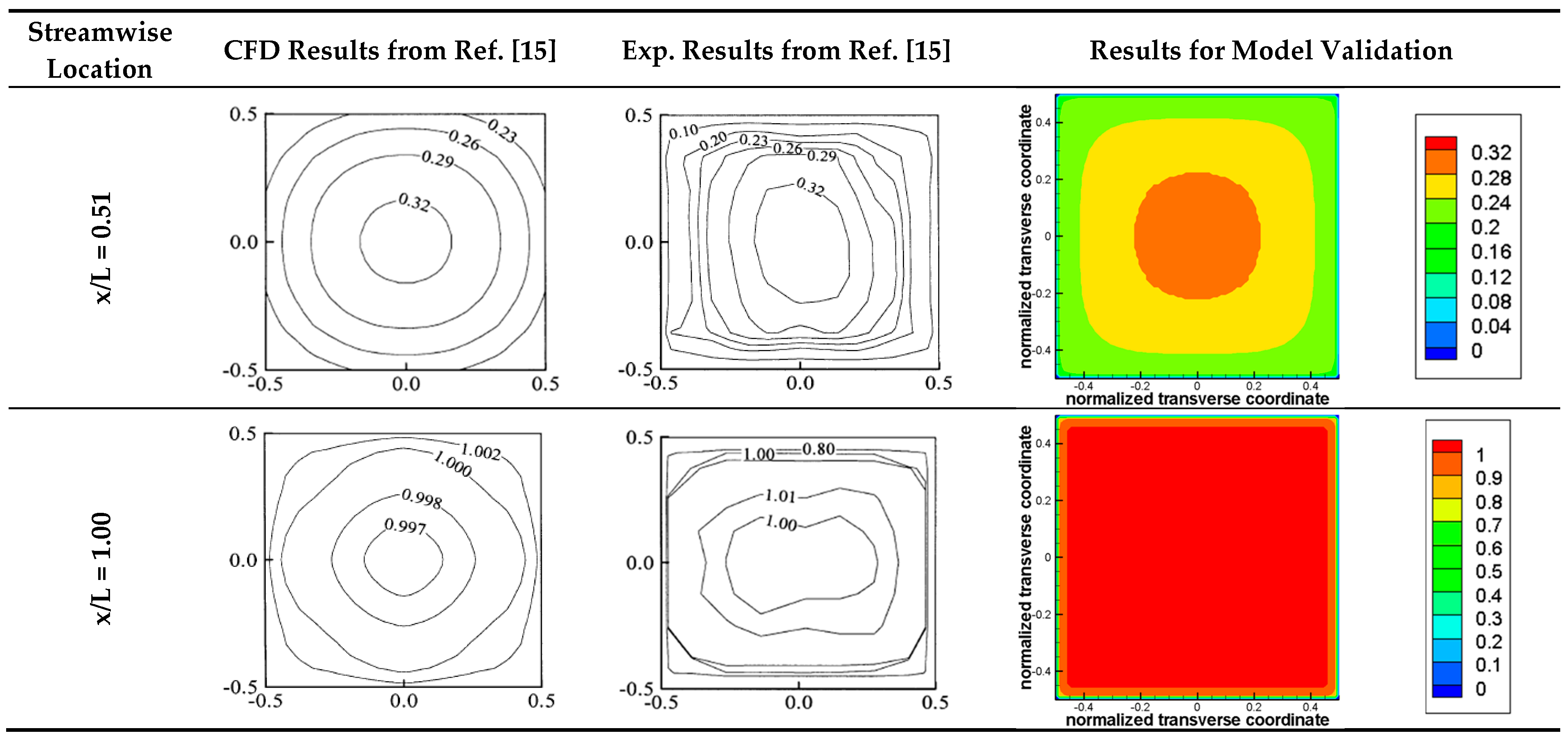
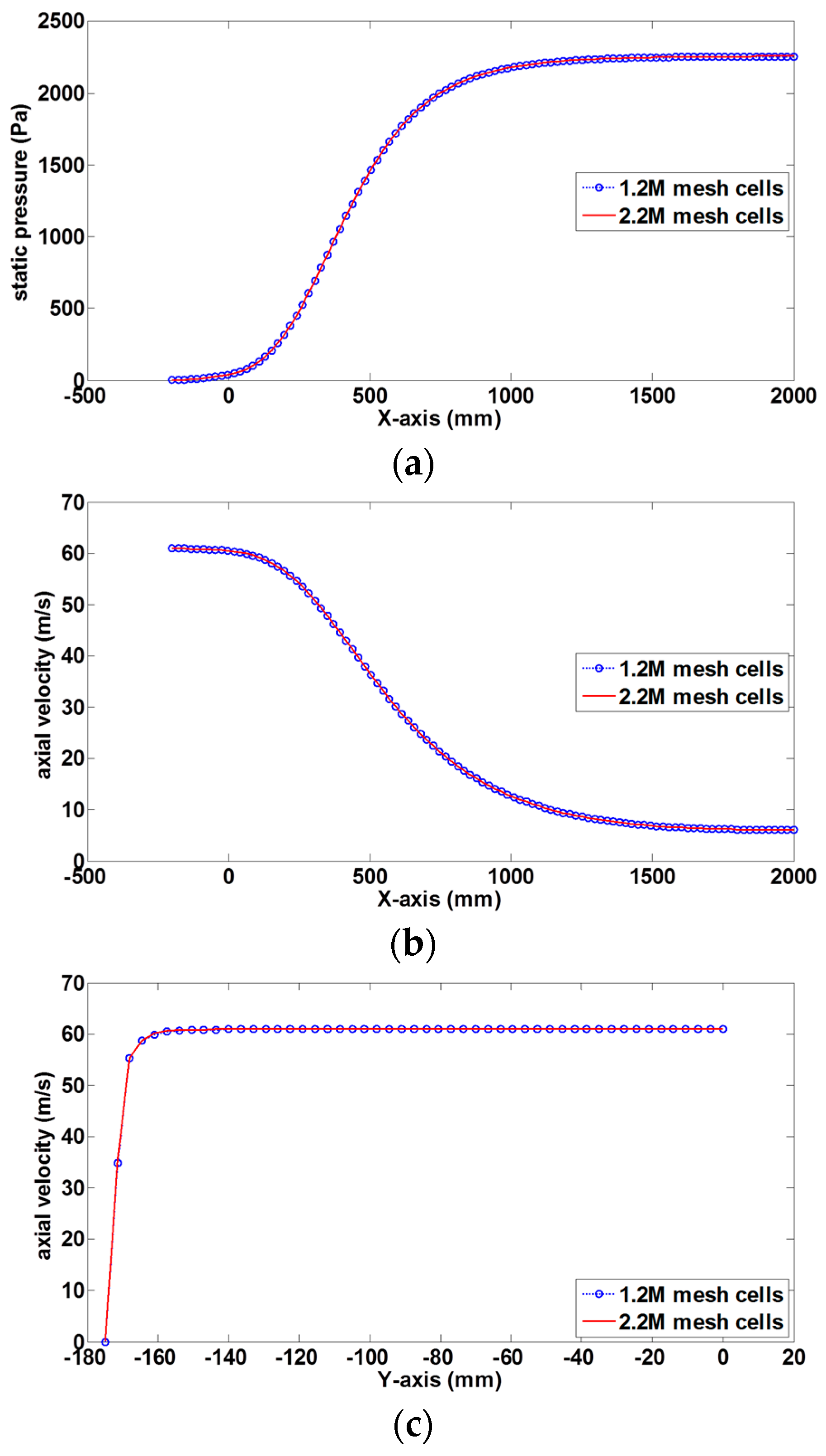
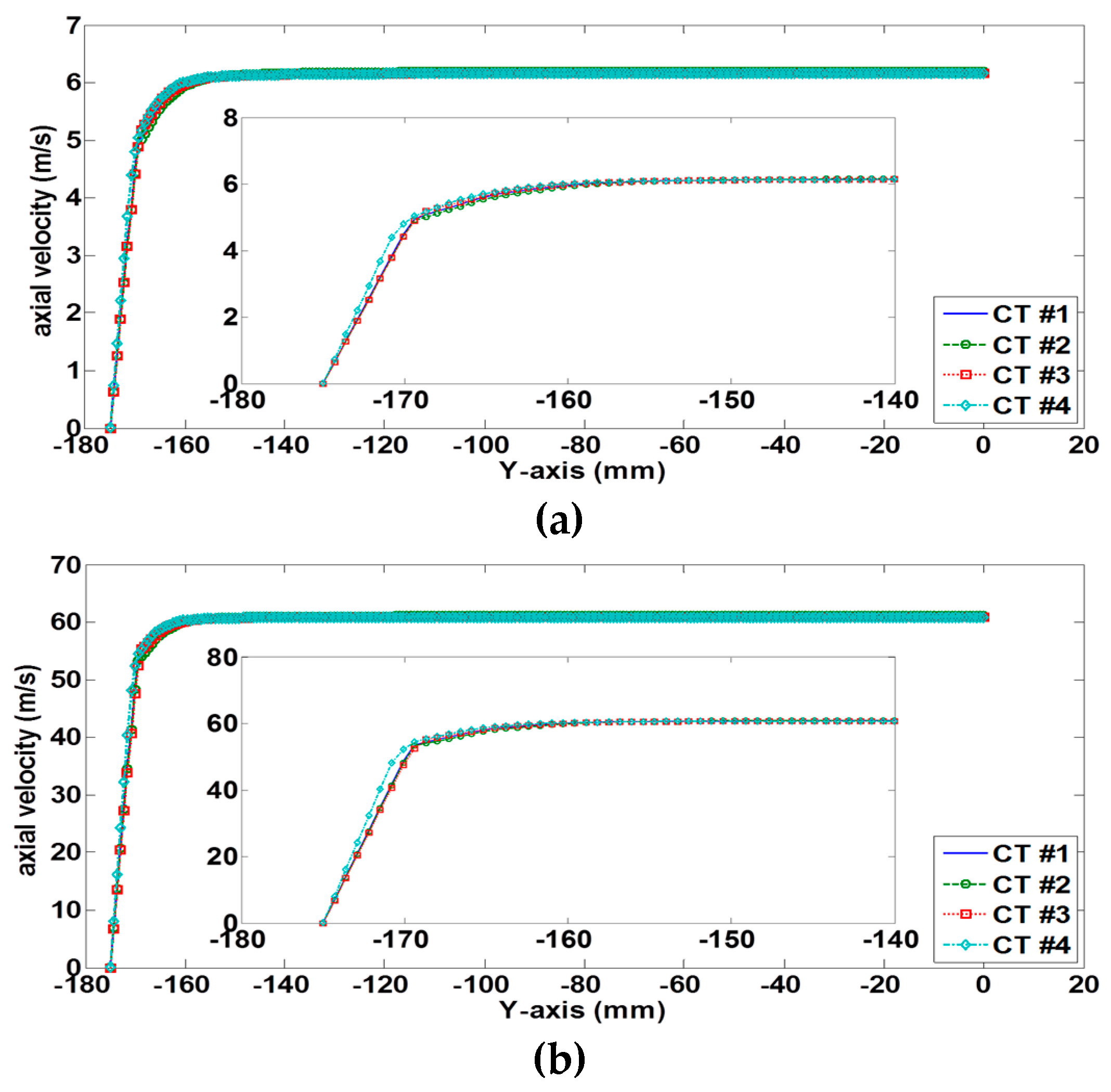
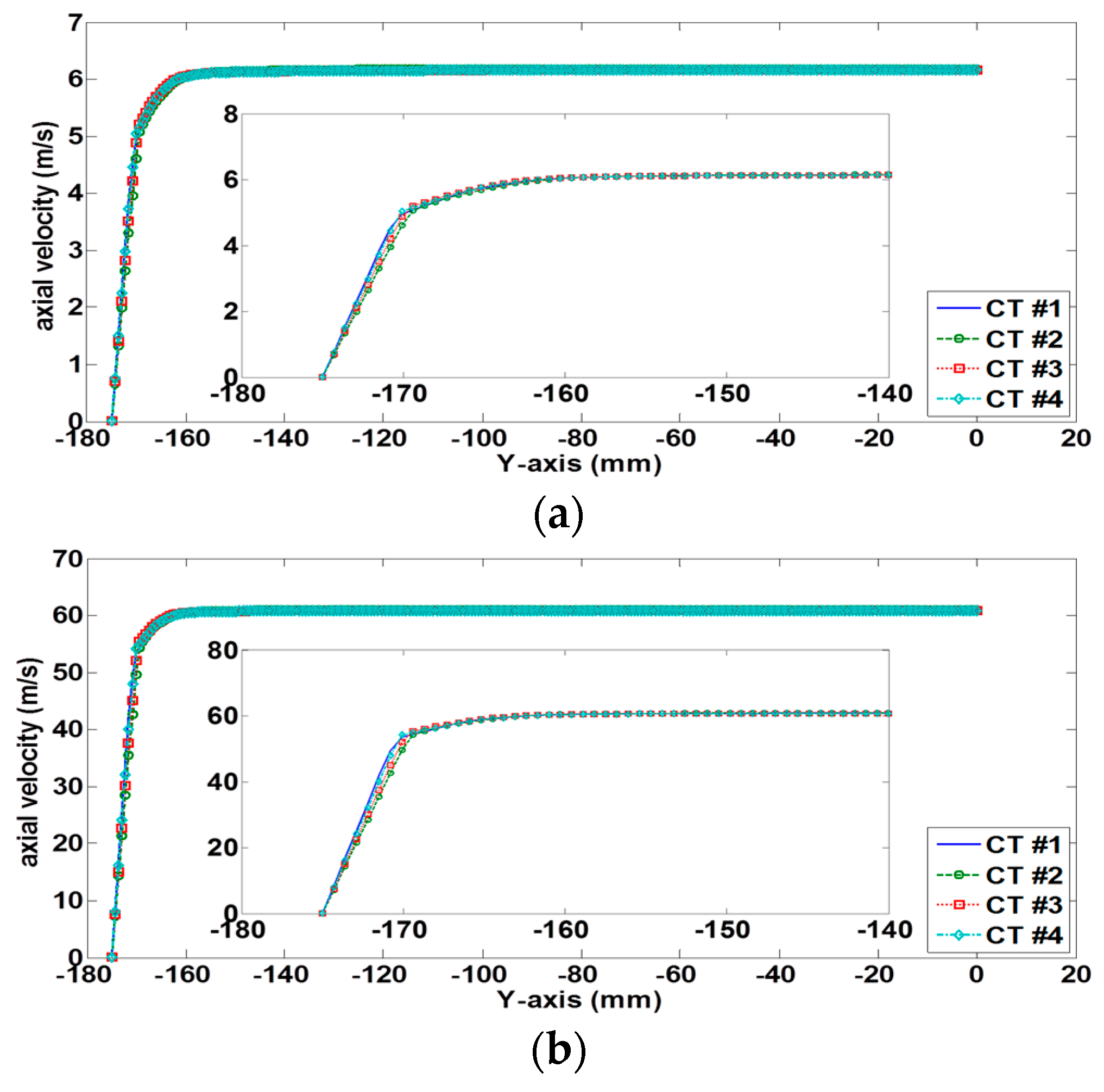
2.4. Model Validation, Mesh Setting, and Mesh Independent Test
3. Results and Discussion
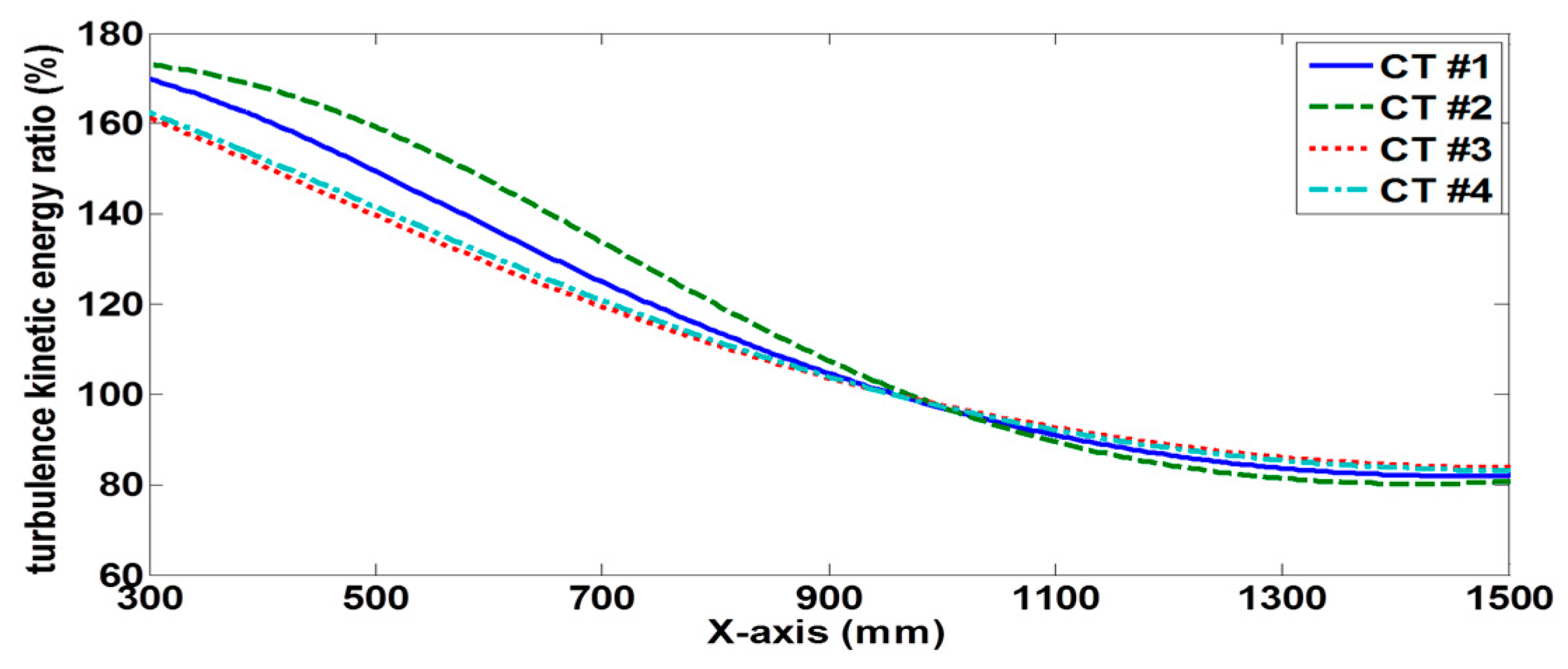
3.1. Effect of Contraction Wall Shape
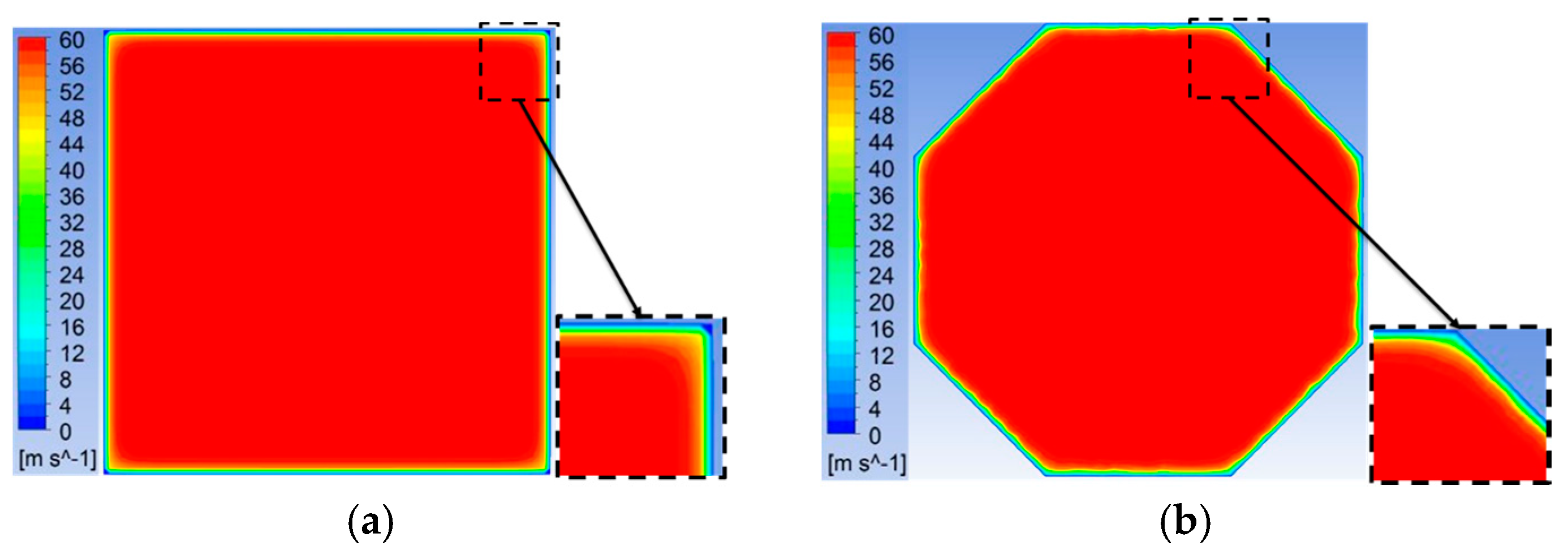
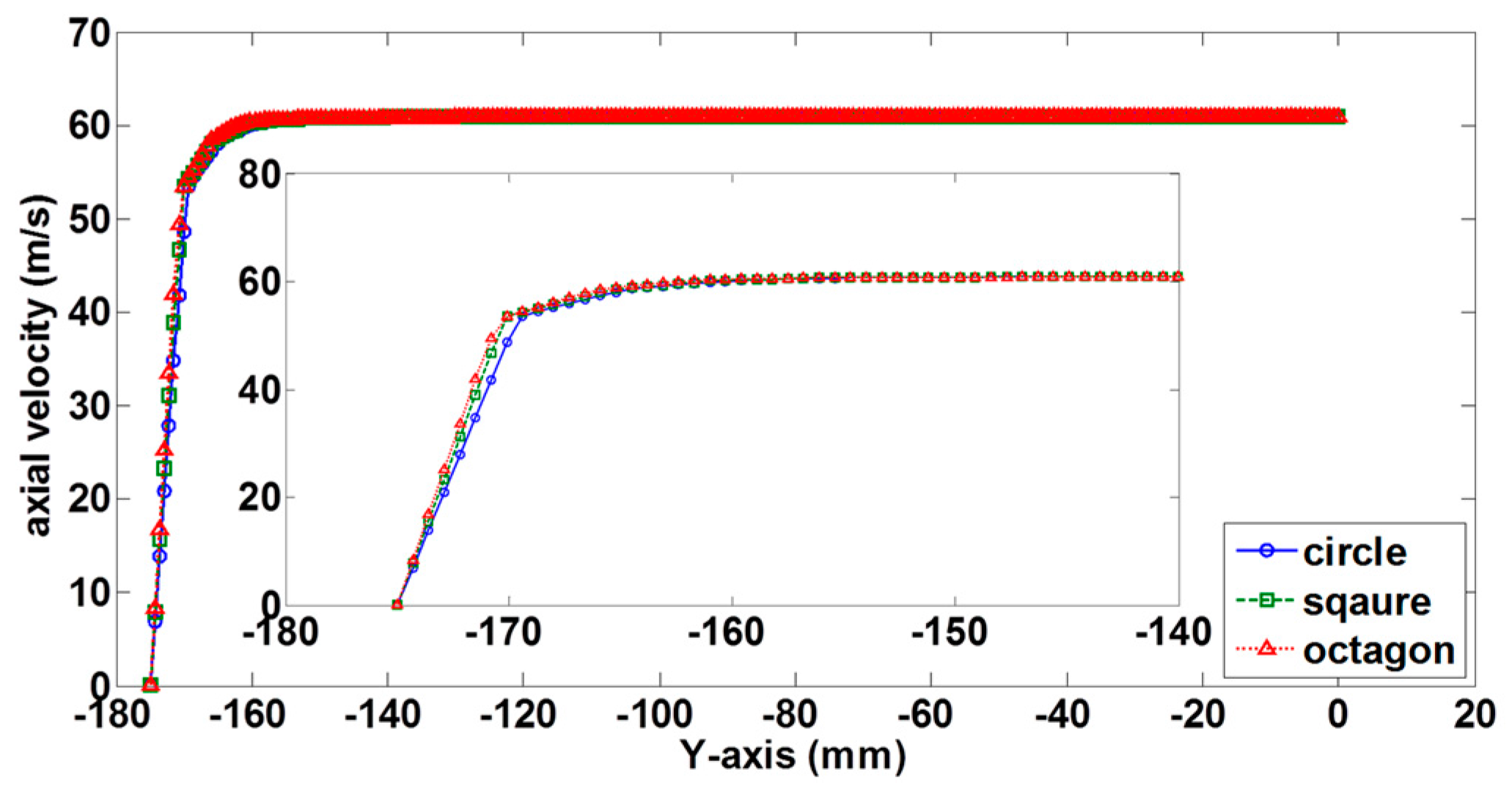
3.2. Effect of Contraction Cross-Sectional Shape
4. Conclusions
- Different contraction wall shapes investigated in this study result in pressure loss difference up to 17 Pa, contributing about 4% in the pressure loss of the entire wind tunnel system. The effect of cross-sectional shape would only lead to pressure loss differences less than 10 Pa. Thus, the wall shape is more critical than the cross-sectional shape of a wind tunnel.
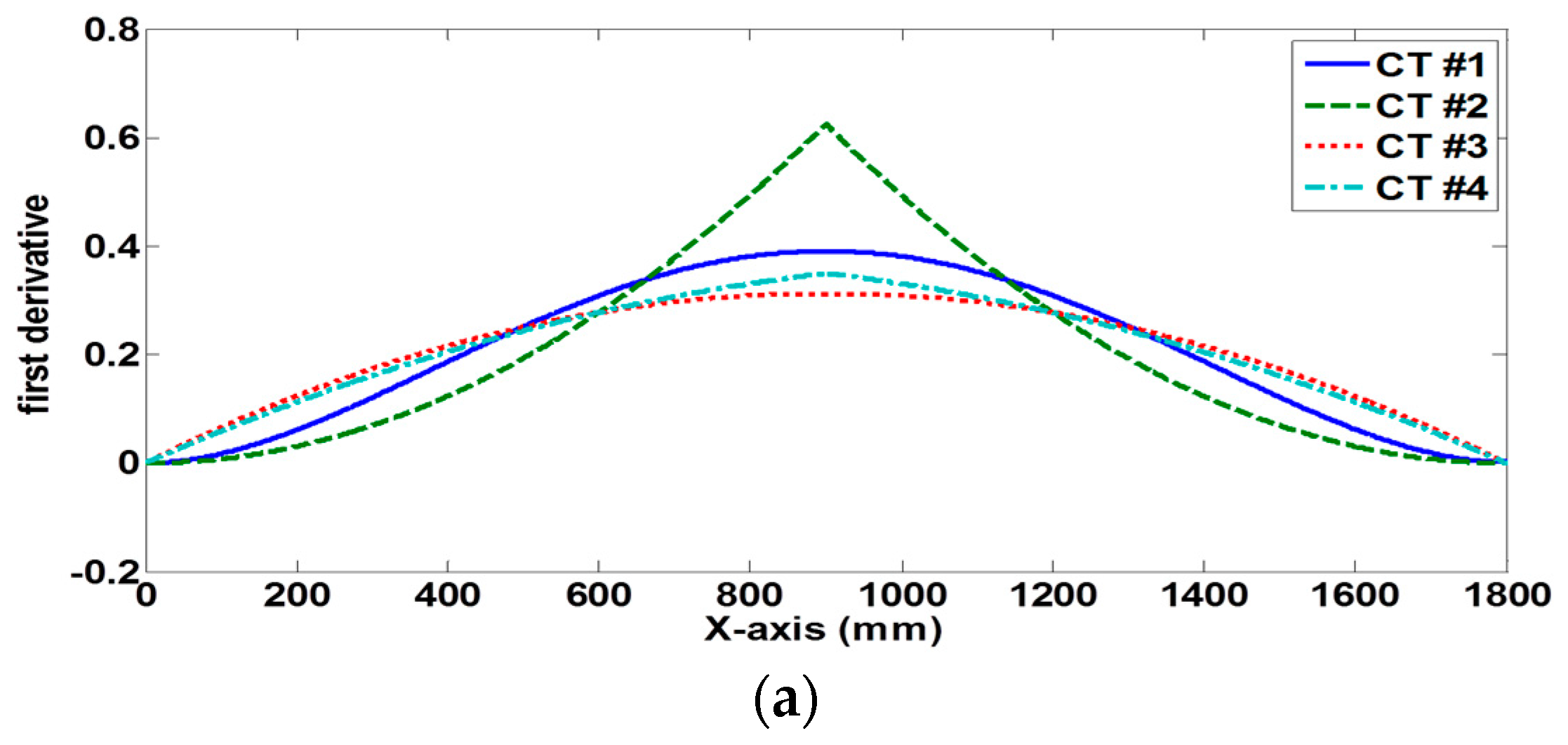
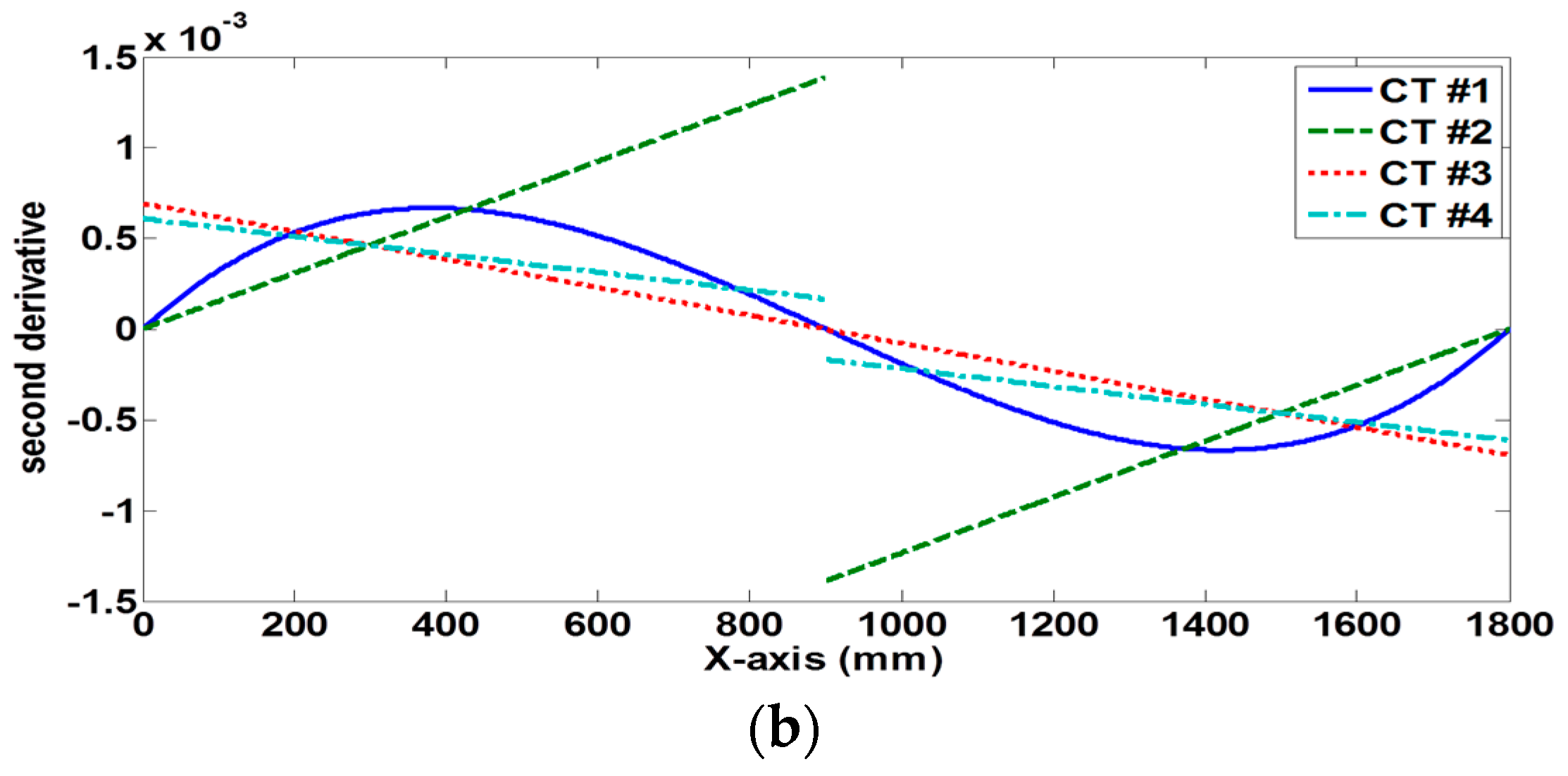
- The first and the second derivatives of different contraction wall shape equations could provide a hint for qualitatively comparing the flow characteristics at the contraction exits.
- The octagonal cross-sectional shape of a wind tunnel shows a better fluid mechanics performance in terms of the thinner boundary layer, a lower axial velocity standard deviation within the core region at the contraction exit, and a lower pressure drop along the contraction.
- From the aspect of an engineering application, a wind tunnel contraction with an octagonal cross-sectional shape has not only better flow performance than that with a circular or square cross-sectional shape but also the lower difficulty of manufacturing and cost according to our experience. Moreover, as compared to the circular cross-sectional shape, the octagonal cross-sectional shape has a larger cross-sectional area to result in a smaller blockage ratio within the test section under the same hydraulic diameter circumstance. An octagonal cross-sectional shape is recommended as a design candidate of wind tunnel contraction.
Author Contributions
Conflicts of Interest
Abbreviations
| CT | contraction |
| Hi | half height of contraction entrance |
| Ho | half height of contraction exit |
| L | length of contraction portion |
| Vex | exit axial velocity |
| Xm | equal to xm/L |
| x | x coordinate |
| xm | location of inflection point |
| y | y coordinate |
References
- International Organization for Standardization. Meteorology—Wind Measurements—Part 1: Wind Tunnel Test Methods for Rotating Anemometer Performance; ISO 17713-1: 2007(E); BSI: London, UK, 2007. [Google Scholar]
- ASTM International. Standard Test Method for Determining the Performance of a Cup Anemometer or Propeller Anemometer; D5096-02; ASTM: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Chun, S. Air Speed Measurement Standards Using Wind Tunnels, Wind Tunnels and Experimental Fluid Dynamics Research; InTech: Rijeka, Croatia, 2011; pp. 173–197. [Google Scholar]
- Terao, Y.; Choi, Y.M.; Gutkin, M.; Jian, W.; Shinder, I.; Yang, C.-T. Final Report on the APMP Air Speed Key Comparison (APMP.M.FF-K3). Metrologia 2010, 47, 1–31. [Google Scholar] [CrossRef]
- Moonen, P.; Blocken, B.; Roels, S.; Carmeliet, J. Numerical modeling of the flow conditions in a closed-circuit low-speed wind tunnel. J. Wind Eng. Ind. Aerodyn. 2006, 94, 699–723. [Google Scholar] [CrossRef]
- Lastra, M.R.; Oro, J.M.F.; Vega, M.G.; Marigorta, E.B.; Morros, C.S. Novel design and experimental validation of a contraction nozzle for aerodynamic measurement in a subsonic wind tunnel. J. Wind Eng. Ind. Aerodyn. 2013, 118, 35–43. [Google Scholar] [CrossRef]
- Calautit, J.K.; Chaudhry, H.N.; Hughes, B.R.; Sim, L.F. A validated design methodology for a closed-loop subsonic wind tunnel. J. Wind Eng. Ind. Aerodyn. 2014, 125, 180–194. [Google Scholar] [CrossRef]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: Cambridge, UK, 1953; pp. 68–75. [Google Scholar]
- Hussain, A.K.M.F.; Ramjee, V. Effects of the axisymmetric contraction shape on incompressible turbulent flow. J. Fluids Eng. 1976, 98, 58–68. [Google Scholar] [CrossRef]
- Metha, R.D.; Bradshaw, P. Design rules for small low speed wind tunnels. Aeronaut. J. 1979, 83, 443–449. [Google Scholar]
- Yeh, T.T.; Hall, J.M. Airspeed Calibration Service; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2007; pp. 250–279.
- Hernández, M.A.G.; Lόpez, A.I.M.; Jarzabek, A.A.; Perales, J.M.P.; Wu, Y.; Sun, X.X. Design Methodology for a Quick and Low-Cost Wind Tunnel. In Wind Tunnel Designs and Their Diverse Engineering Applications; InTech: Rijeka, Croatia, 2013; pp. 3–28. [Google Scholar]
- Su, Y. Flow analysis and design of three-dimensional wind tunnel contractions. AIAA J. 1991, 29, 1912–1920. [Google Scholar]
- Bell, J.H.; Mehta, R.D. Contraction Design for Small Low-Speed Wind Tunnels; NASA Ames Research Center: Moffett Field, CA, USA, 1988.
- Fang, F.; Chen, J.C.; Hong, Y.T. Experimental and analytical evaluation of flow in a square-to square wind tunnel contraction. J. Wind Eng. Ind. Aerodyn. 2001, 89, 247–262. [Google Scholar] [CrossRef]
- Bouriga, M.; Taher, R.; Morency, F.; Weiss, J. Numerical investigation of secondary flows in a constant-width wind-tunnel contraction. Aeronaut. J. 2015, 119, 613–630. [Google Scholar] [CrossRef]
- Bradshaw, P.; Pankurst, R.C. The design of low-speed wind tunnels. Prog. Aerosp. Sci. 1964, 5, 1–69. [Google Scholar] [CrossRef]
- Mehta, R.D. Aspects of the Design and Performance of Blower Wind Tunnel Component. Ph.D. Thesis, Department of Aeronautics, Imperial College, University of London, London, UK, 1978. [Google Scholar]
- Mentor, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 23, 1335–1342. [Google Scholar] [CrossRef]
- Bouriga, M.; Lemyre-Baron, J.; Morency, F.; Weiss, J. Preliminary experimental and numerical investigations of the flow in the contraction of a boundary layer wind tunnel. Trans. Can. Soc. Mech. Eng. 2014, 38, 517–532. [Google Scholar]
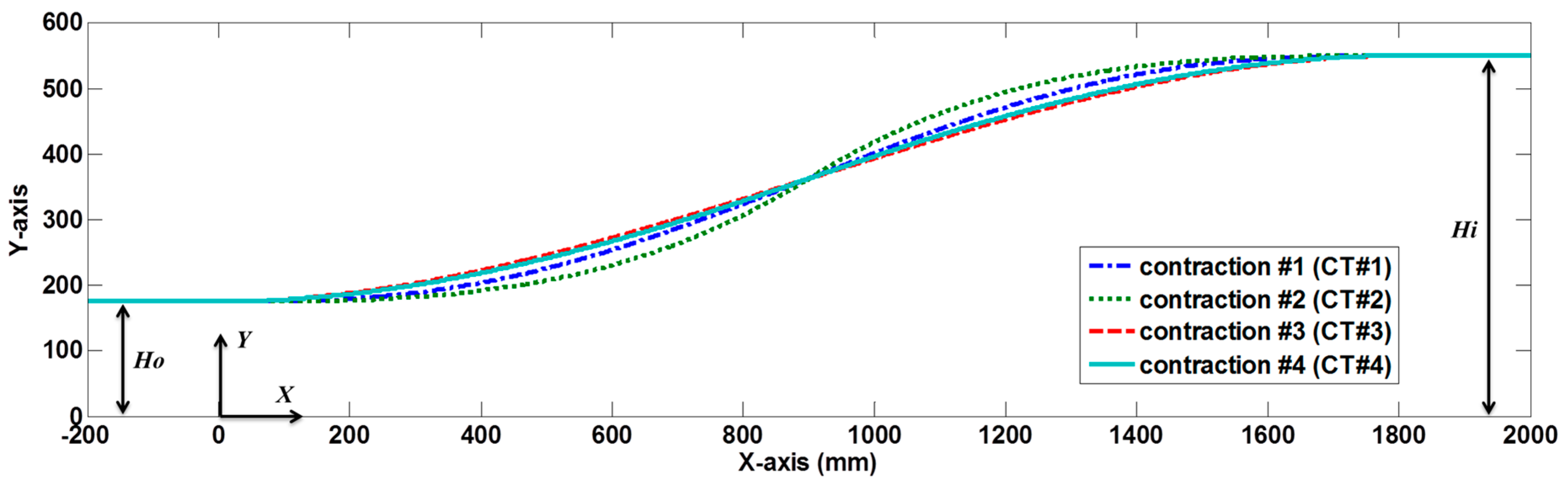


| Contraction Case | Original Equation | Adopted Equation |
|---|---|---|
| CT #1 [14] | ||
| CT #2 [15] | ||
| CT #3 | ||
| CT #4 [12] |
| Case | Entrance | Exit |
|---|---|---|
| Vex = 6 m/s | uniform velocity profile = 0.608 m/s | gauge pressure = 0 |
| turbulent intensity = 40% | turbulent intensity = 1% | |
| hydraulic diameter = 1100 mm | hydraulic diameter = 350 mm | |
| Vex = 60 m/s | uniform velocity profile = 6.075 m/s | gauge pressure = 0 |
| turbulent intensity = 20% | turbulent intensity = 0.5% | |
| hydraulic diameter = 1100 mm | hydraulic diameter = 350 mm |
| Case | Cross-Sectional Shape | ||
|---|---|---|---|
| Circle | Square | Octagon | |
| CT #1 | 72 Pa | 71 Pa | 65 Pa |
| CT #2 | 80 Pa | 78 Pa | 70 Pa |
| CT #3 | 63 Pa | 58 Pa | 58 Pa |
| CT #4 | 64 Pa | 65 Pa | 59 Pa |
| Component | Pressure Drop (Pa) | Percentage |
|---|---|---|
| honeycomb | 12 | 2.9% |
| 5 screen meshes | 160 | 39.3% |
| contraction | 64 | 15.6% |
| test section | 79 | 19.3% |
| diffuser | 37 | 9.0% |
| 4 turning corners | 57 | 13.9% |
| total | 409 | 100% |
| Case | Cross-Sectional Shape | |||
|---|---|---|---|---|
| Circle | Square | Octagon | ||
| Vex = 6 m/s | CT #1 | 0.014 m/s | 0.014 m/s | 0.012 m/s |
| CT #2 | 0.018 m/s | 0.016 m/s | 0.012 m/s | |
| CT #3 | 0.013 m/s | 0.012 m/s | 0.010 m/s | |
| CT #4 | 0.012 m/s | 0.012 m/s | 0.010 m/s | |
| Vex = 60 m/s | CT #1 | 0.072 m/s | 0.064 m/s | 0.051 m/s |
| CT #2 | 0.097 m/s | 0.073 m/s | 0.052 m/s | |
| CT #3 | 0.064 m/s | 0.052 m/s | 0.042 m/s | |
| CT #4 | 0.059 m/s | 0.054 m/s | 0.045 m/s | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kao, Y.-H.; Jiang, Z.-W.; Fang, S.-C. A Computational Simulation Study of Fluid Mechanics of Low-Speed Wind Tunnel Contractions. Fluids 2017, 2, 23. https://doi.org/10.3390/fluids2020023
Kao Y-H, Jiang Z-W, Fang S-C. A Computational Simulation Study of Fluid Mechanics of Low-Speed Wind Tunnel Contractions. Fluids. 2017; 2(2):23. https://doi.org/10.3390/fluids2020023
Chicago/Turabian StyleKao, Yi-Huan, Zhou-Wei Jiang, and Sheng-Cyuan Fang. 2017. "A Computational Simulation Study of Fluid Mechanics of Low-Speed Wind Tunnel Contractions" Fluids 2, no. 2: 23. https://doi.org/10.3390/fluids2020023
APA StyleKao, Y.-H., Jiang, Z.-W., & Fang, S.-C. (2017). A Computational Simulation Study of Fluid Mechanics of Low-Speed Wind Tunnel Contractions. Fluids, 2(2), 23. https://doi.org/10.3390/fluids2020023






