Reply to “Comment on Tailleux, R. Neutrality Versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32.”

Abstract

McDougall, Groeskamp and Griffies (MGG) strongly criticise all aspects of Tailleux (2016) that challenge the current conventional wisdom about the use of neutral density concepts for studying and parameterising lateral ocean stirring and mixing. However, their claim that most of Tailleux (2016)’s results or conclusions are incorrect is easily shown to originate: (1) from mistakingly confusing Tailleux’s Eulerian arguments for Lagrangian ones; (2) from their irrational belief that only one particular kind of quasi-material surface is somehow endorsed by Nature and hence relevant to the description of stirring and mixing—namely the locally-defined neutral tangent planes—stating at one point: “why should the ocean care about human constructed density variables”? MGG appear to overlook the simple fact that solutions of the Navier–Stokes equations—which synthesise our ideas about how Nature works—never require the introduction of any form of quasi-material or quasi-neutral density variable. This implies that the empirical isopycnal/isentropic stirring property is necessarily an emergent property of the Navier–Stokes equations, and hence that all forms of isopycnal surfaces—both neutral and not—are necessarily all human constructs. To establish the relevance of any particular construct to the actual ocean, an explicit model of stirring is needed to elucidate the nature of the dynamical/energetics constraints on lateral stirring. Even in the simplest model of stirring, neutral stirring represents only one possible mode out of a continuum of stirring modes responsible for lateral stirring in the ocean, without any evidence that it should dominate over the other ones. To help clarify the issues involved, it is proposed to regard the rigorous study of ocean stirring and mixing as relying on at least five distinct stages, from defining a model of stirring to constructing physically-based mixing parameterisations in numerical ocean models.

1. Preliminaries

My eminent colleagues Trevor J. McDougall, Sjoerd Groeskamp and Stephen M. Griffies (MGG thereafter) take issue with several aspects of [1], which they believe to be both “provocative” and having “the potential to cause unnecessary confusion on the topic of the direction (MGG use the singular here and thus implicitly assume that lateral stirring occurs in a single possible direction. There is no physical basis for such a claim, which is disproved by all published theoretical models of stirring, such as that first considered by Eckart [2] or that based on the discrete view of stirring analysed in [1] and in the present response) of lateral (MGG actually used `neutral’ in place of `lateral’; this is either an oversight or a deliberate attempt to mislead the reader into thinking that the two terms are interchangeable, which is not the case) mixing in the ocean”. MGG’s view, however, appears to be in sharp contrast with that of other reviewers—see Appendix A. MGG’s comment represents an exciting opportunity to further exchange views about the physics of lateral stirring and of neutral density concepts, which have puzzled a large majority of oceanographers for over 30 years. MGG’s comment appears to be primarily prompted by their strong objections to my attempts at reformulating their qualitative argument in mathematical form and alleged proof that lateral stirring only occurs in neutral tangent planes. My point is that it will remain impossible for anybody in the oceanographic community to assess the validity of MGG’s arguments until these arguments are put in a proper mathematical form with clearly stated and testable hypotheses. The fact that MGG find that my attempt at mathematically formalising their “proof” represents in itself major progress towards clarifying it, since it establishes what [3] is not about by ruling out [1]’s Eulerian interpretation of their qualitative arguments. As discussed below, however, it is unclear that the alternative—namely, a Lagrangian interpretation of MGG’s “proof”—really makes more sense.

Before responding to the specifics of MGG, let me first remark that the introduction of any material or quasi-material density variable is not a priori required to solve the non-averaged form of the Navier–Stokes equations (NANSE). Indeed, the NANSE describe irreversible mixing of heat and salt in terms of isotropic Laplacian operators, not rotated ones. As a result, the empirically-based property that tracers appear to be stirred primarily along isentropic/isopycnal “stirring surfaces” is necessarily an emergent property of the NANSE. Other well-known and important emergent properties of the NANSE in the context of the climate system are El-Niño, the various monsoon circulation systems, the Madden–Julian Oscillation, the stratospheric bi-annual oscillation, sudden stratospheric warmings, various types of waves (e.g., internal-gravity waves and Rossby waves), tropical cyclones, midlatitude storms, to name but a few. Unless they occur at sub-grid scales, emergent properties are a priori most useful to test and validate models. For instance, climate modellers would never seriously consider enforcing El-Niño to occur in their climate models by artificially forcing zonal movements of the Pacific warm pool; climate modellers want their models to simulate El-Niño for the right reasons. In other words, enforcing an emergent property into a model as a way to improve agreement with observations is rarely regarded as good practice, so one should have a full understanding of the physics of the problem before attempting to do so; in particular, one should assess whether the emergent property considered is in principle “resolvable” by models, or is an “unresolvable” one occurring at sub-grid scale and hence in need of parameterisation. Whether the isopycnal-stirring emergent property should be regarded as resolvable or unresolvable by numerical ocean models is poorly understood. So far, it has generally been assumed that it should be enforced in coarse resolution numerical ocean models by means of [4]’s rotated diffusion tensor, owing to the widespread belief (e.g., [5]) that this is essential to eliminate the western boundary spurious upwelling that [6] observed to occur in early ocean models mixing separately in the horizontal and vertical directions and having no parameterisation of meso-scale eddies. Whether any actual evidence exists to support such a claim is unclear, however; in fact, Boning, et al. and Lazar, et al. [7,8] strongly suggest that it is the introduction of a meso-scale eddy parameterisation like that proposed by [9]—rather than the use of rotated diffusion per se—that gets rid of the Veronis effect. Rotated diffusion tensors, however, are rarely employed, if ever, in eddy-resolving ocean models, suggesting that oceanographers view the “isopycnal stirring” emergent property as one that ocean models can only reproduce correctly when resolving eddies. If further confirmed, the possibility that the Veronis effect may in fact have little to do with the particular details of the diffusion tensor would, however, support the idea that the “isopycnal stirring” emergent property could in fact be resolvable at much coarser resolution than usually assumed. For this reason, it seems essential to examine the logic and rationale behind enforcing the “isopycnal-stirring” emergent property in ocean models, owing to the numerous consequences that our failure to fully understand the physics of the problem could have on the trust we place in the validity and accuracy of our models. Assessing the validity of MGG’s various claims and assertions is obviously an essential step towards that goal.

2. Buoyancy, Locally-Referenced Potential Density, Lagrangian Energetics, and Transience

Most of MGG’s Section 1 “Overarching comments on Tailleux (2016)” is concerned with the proper interpretation of equations $\mathbf{d}·\delta \mathbf{x}=0$ and $\mathbf{d}·\delta \mathbf{x}\ne 0$, which I introduced in [1] as an attempt to translate into mathematical form the rhetorical arguments underlying [3]’s alleged “proof” that one should accept—based on their Figure 1—that lateral stirring takes place exclusively in neutral tangent planes. Based on [3]’s arguments—which MGG believe that I misunderstood or misinterpreted—I assumed that the kind of displacement $\delta \mathbf{x}$ considered by [3] referred to a Eulerian one, as this is required in order to interpret the quantity $b=-\mathbf{d}·\delta \mathbf{x}=-g({\rho }_p-{\rho }_e)/{\rho }_0$ as the standard buoyancy force that plays such a central role in the evidence given by [3]; moreover, I believe that in absence of any qualifier, most oceanographers would naturally interpret the term “displacement” as referring to a Eulerian one; this seems further vindicated by the fact the parcel illustrated in [3]’s Figure 1 appears to move laterally in a regular Cartesian coordinate system, not a Lagrangian one. However, we now learn from MGG’s comment that [3] apparently intended their displacement to be interpreted as a Lagrangian displacement conserving its locally-referenced potential density (LRPD). Although this is certainly a most welcome clarification, it just seems to make [3]’s argument even more puzzling and confusing. Indeed, saying that an adiabatic and isohaline infinitesimal displacement conserves its LRPD, and saying that such a parcel motion takes place on the locally-defined neutral tangent plane are generally understood to be equivalent statements. Therefore, MGG’s thought experiment in which a fluid parcel conserving its LRPD is envisioned to leave its neutral tangent plane and experience a restoring buoyancy force seems to be one that is supposed to be impossible by the very definition of LRPD. Attributing this impossibility as MGG do to the smallness of observed viscous dissipation rates therefore appears to be misleading at best. MGG should focus on improving the mathematical formulation and clarity of their argument; most importantly, they should state as precisely as possible what exactly is assumed, what is deduced. Otherwise, their reductio ad absurdum is at great risk of being no more than an absurdum probationem!

In order to help the reader appreciate the widely different implications of the Eulerian versus Lagrangian interpretation of $\delta \mathbf{x}$, it is useful to describe both types of displacement in terms of the mathematically ambiguous locally-referenced potential density ${\rho }_{\Theta }^l$ introduced by MGG (In the original version of [1], I pointed out that the concept of LRPD—being usually defined as a variable being equal at every point to in-situ density, yet having no term proportional to the pressure gradient in its gradient—was a mathematically impossible concept, to which Prof. McDougall, in his second review, responded: Regarding the use of Locally referenced potential density (LRPD), Remi and I are in agreement on this, and I apologize that my remarks in the first review were not clearer. We agree that the neutral tangent plane is the same as the plane of constant potential density whose reference pressure is the fixed local value. In recent years I have tried not to use a symbol such as ${\rho }_{\Theta }^l$ for LRPD because it implies that it is a well-defined variable, which it is not. Despite Prof. McDougall’s criticism, the mathematically incorrect LRPD makes a forceful re-appearance in MGG’s comment, being a central part of their argument. This is not to say, however, that a mathematically rigorous definition of LRPD is impossible. As far as I can judge, a rigorous definition of LRPD can be achieved by defining it locally as a purely material variable $\gamma (S,\theta )$ that is as neutral as feasible in some sense. In practice, this can be done either by means of a local version of [10]’s approach, or by locally constructing $\gamma$ directly in $(S,\theta )$ space as proposed by [1]. However, because this rigorous definition of LRPD then depends on what one means by “as neutral as feasible”’, whose definition requires the introduction of some arbitrary human-imposed cost function, it follows that any rigorous definition of LRPD must be non-unique, contrary to what the mathematically incorrect definition might suggest. In other words, the concept of LRPD is in reality significantly more ambiguous and imprecise than what MGG would have us believe.), viz.,

$$\left(\mathrm{Eulerian}-\mathrm{Adiabatic}\mathrm{and}\mathrm{isohaline}\right)-\mathbf{d}·\delta {\mathbf{x}}_E=-\frac{g\delta t}{{\rho }_0}\frac{\partial {\rho }_{\Theta }^l}{\partial t}=\mathrm{Buoyancy},$$

(1)

$$\left(\mathrm{Lagrangian}\right)-\mathbf{d}·\delta {\mathbf{x}}_L=-\frac{g\delta t}{{\rho }_0}\frac{D{\rho }_{\Theta }^l}{Dt}=\mathrm{Diabatic}.$$

(2)

Thus, Equation (1) makes it clear that $\mathbf{d}·\delta {\mathbf{x}}_E\ne 0$ implies transience and the deformation of whatever material surface $\gamma (S,\theta )$ one chooses to regard the fluid parcel as belonging to, not diapycnal mixing. In the Lagrangian interpretation, however, Equation (2) shows that $\mathbf{d}·\delta {\mathbf{x}}_L\ne 0$ should not be interpreted as the existence of a non-zero buoyancy force, but as the presence of diapycnal mixing. Accordingly, a non-neutral displacement in the Eulerian interpretation (1) used in [1] just means transience and/or a fluid displacement taking place in a material surface that is non-neutral; this obviously does not imply diapycnal mixing by definition, whereas diapycnal mixing is required in the Lagrangian interpretation (2) implicit in MGG’s comments. Since the Eulerian nature of all the interpretations made in [1] is made explicit in pages 3 and 6 of my paper, I find it difficult to understand how MGG could have mistaken it for a Lagrangian interpretation. Therefore, there is absolutely no reason for MGG to write: Inexplicably, Tailleux (2016) asserts that while individual motions are diabatic, their average is adiabatic. This is incorrect. Rather, if individual motions are diabatic, then the average of many such motions exhibits dianeutral diffusion. In fact, in the Eulerian interpretation, the non-neutrality of Eulerian displacements ${\mathbf{d}}^{\left(i\right)}·\delta {\mathbf{x}}_E^{\left(i\right)}\ne 0$ never implies dianeutral diffusion. The correct way to interpret [1]’s result for the sum of non-neutral displacements is therefore as follows:

$$\sum _{i=1}^N{\mathbf{d}}^{\left(i\right)}·\dot{\delta }{\mathbf{x}}_E^{\left(i\right)}=\frac{g\delta t}{{\rho }_0}\sum _{i=1}^N{\left(\frac{\partial {\rho }_{\Theta }^l}{\partial t}\right)}^{\left(i\right)}\approx N\overline{\mathbf{d}}·\overline{\delta {\mathbf{x}}_E}\approx 0,$$

(3)

which states that the sum of adiabatic non-neutral displacements is approximately neutral. Here, the assumption for this result to hold is that each Eulerian temporal derivative $\partial {\rho }_{\Theta }^l/\partial t$ behaves as a random variable with zero mean (which is plausible but arguably difficult to prove). In contrast, MGG appear to insist on interpreting the term “non-neutral” as always implying diabatism and dianeutral diffusion—which is only true in their Lagrangian interpretation of the term—regardless of how others may choose to interpret it. Given the infinite number of non-neutral stirring surfaces $\gamma (S,\theta )=\mathrm{constant}$, MGG should inform us of their recommended terminology to describe adiabatic and isohaline stirring taking place on the latter to avoid semantics being used as a tool for confusing, rather than clarifying, the issues debated.

Another important longstanding point of confusion clarified by MGG pertains to the question of whether neutral surfaces should be best regarded as a “thermodynamic” or “dynamical” concept. The question arises because neutral surfaces are commonly described as surfaces along which fluid parcel exchanges experience no restoring buoyancy force, which may—at least superficially—appear as a dynamical constraint, since the concept of buoyancy is rooted in the momentum equations. However, MGG appear to say that one should regard neutral surfaces as a purely thermodynamic concept defined as surfaces of constant LRPD, and hence that the zero buoyancy property should not be regarded as a constraint but rather as a consequence of their thermodynamic definition. MGG’s admission that their views on lateral stirring in the ocean exclude any form of dynamical information to rely exclusively on thermodynamic information makes it difficult to understand why this would make their approach superior to those proposed by [1,11], whose first-principles theories are able to incorporate both types of information. MGG’s idea that stirring in the ocean can be understood without exploiting any form of dynamical information seems at odds with all of the literature on the subject stemming from [2] seminal approach to stirring and mixing.

3. What Does the Ocean Care about? Human Versus Nature, Local Versus Global

Apart from the Eulerian versus Lagrangian points of contention discussed above, MGG raise a number of interesting issues pertaining to the Human versus Nature approach to lateral stirring surfaces that seems to underscore—if needed—the irrational basis of neutral density theory as it is currently formulated or advocated in [3]. To make my case, I am providing a rebuttal to a number of representative comments raised by MGG about the issue, using boldface for my responses, before attempting to clarify the overall problematic by re-situating the Human versus Nature controversy in the context of the rigorous study of stirring and mixing in Section 3.2.

3.1. Rebuttal (in Boldface) of Representative Comments about the Human Versus Nature Controversy

• “Tailleux (2016) asserts that `adiabatic and isohaline parcel exchanges can only be meaningfully defined on material surfaces of the form $\gamma (S,\theta )=\mathrm{constant}$’. We disagree with this statement.” The fact remains that stirring surfaces are by definition the ones that are invariant upon adiabatic and isohaline parcel exchanges; this constrains them to being defined in terms of material functions of S and $\theta$ alone, whether MGG agree or not. MGG fail to realise this because their construction of LRPD is mathematically incorrect. Mathematically, the only correct way to define LRPD is as the material function $\gamma (S,\theta )$, maximising neutrality locally in some sense. This can be done either by following a local version of [10]’s approach or by following [1]’s suggestion to minimise the Jacobian term $\partial (\gamma ,\rho )/\partial (S,\theta )$ in the vicinity of the point considered. Whether to regard $\gamma (S,\theta )$ as local or global depends solely on the investigator’s intention to use it as a local or global descriptor of stirring. In neutral density theory, this distinction would be between LRPD and [12]’s globally-defined empirical neutral density ${\gamma }^n$. How these distinctions enter the problem is further clarified below as one goes from Stages 1–3 to Stage 4. “There is no fundamental reason that the ocean should oblige in this regard. Rather, we oceanographers should examine ocean mixing in terms of known physical processes that occur at the in-situ pressure of the mixing.” These are rhetorical arguments, not scientific ones. On the other hand, I think that one should first define the particular problem one is trying to solve, then formulate a mathematically well-posed problem to study it, and finally use the tools that one deems appropriate to solve it. Ideally, one should attempt to formulate testable hypotheses in a way that others can understand and scrutinise. This is the basis of the scientific method. In contrast, MGG seem to be asserting that they can make definitive statements about ocean stirring without considering any particular model of stirring, or that it is somehow possible to claim that there is one and only one possible kind of stirring surface endorsed by Nature based only on the equation of state from seawater, the consideration of a single one-dimensional fluid parcel trajectory, and observations that viscous dissipation rates are small in some unspecified sense. How can this possibly be enough information to say anything meaningful about turbulent ocean stirring?
• “…then Tailleux (2016) incorrectly asserts that the globally defined $\gamma (S,\theta )$ variable must have some significance to the issue of local mixing processes and that we should attempt to minimize the extra unintended mixing across the iso-surfaces of $\gamma (S,\theta )$. There is no reason for the ocean to pay special attention to an arbitrary variable $\gamma (S,\theta )$ of our construction.” The relevance of my $\gamma (S,\theta )$ to the local and global descriptions of stirring is justified by the fact that $\gamma$ is constructed so that the energy cost of all adiabatic and isohaline parcel exchanges taking place on iso-$\gamma$ surfaces satisfies $\mathrm{\Delta }E\le 0$, which characterises lateral stirring in the ocean according to the simple model of stirring considered by [1]. As mentioned previously, solving the NANSE does not require the introduction of any density variable, so MGG are obviously right than there is no reason for the ocean to pay special attention to an arbitrary variable $\gamma (S,\theta )$ of our construction. I find it therefore baffling that MGG should think that their own construction— which is no more than a particular subcase of the more general class of variables considered by [1]—is the only non-arbitrary density variable somehow “endorsed” by Nature—a belief that is obviously more mystical than rational.
• “Rather than attempting to impose human-conceived, globally-defined $\gamma (S,\theta )$ variable as a new anthropogenic constraint on ocean mixing dynamics, we instead look to ocean physics for inspiration regarding ocean mixing. The relevant $\gamma (S,\theta )$ function to be considered when local mixing processes are considered is the locally-defined potential density ${\rho }_{\Theta }^l(S,\theta )$. The reference pressure of this potential density variable is the local in-situ pressure of this potential density variable at which the mixing is occurring and ${\rho }_{\Theta }^l(S,\theta )$ is clearly not a globally-defined variable.” What MGG think is the right approach is well known; asserting it once more does not help us understand why they think they can crack the ocean turbulence problem from just musing about the equation of state for seawater, a single one-dimensional fluid parcel trajectory, and observations of viscous dissipation rates, or why they think that LRPD is less arbitrary than any other material or non-material density variable.
• “Tailleux (2016) prefers to imagine that the ocean mixes along a $\gamma (S,\theta )$ surface, but why this would be the case in doing so the ocean would automatically delete a real physical process, thermobaricity, that occurs in the ocean?” As said above, the irreversible mixing of heat and salt in the NANSE is represented in terms of (isotropic) Laplacian operators, not rotated ones. I therefore consider that the idea that the ocean mixes heat and salt separately along some Nature-endorsed isopycnal and diapycnal directions has no physical basis. On the other hand, we may always decide—if we find it useful as seems to be the case in the ocean—to decompose mixing into isopycnal and diapycnal components in terms of some density-like material function $\gamma (S,\theta )$ of our choice. I [1] have discussed the physics that should inform this choice, which is different from MGG’s view. Contrary to what MGG or [13] assert, it is perfectly possible for a variable $\gamma (S,\theta )$ to represent thermobaricity, as this is the case of [14]’s thermodynamic neutral density ${\gamma }^T$, owing to its use of a reference pressure $p_r(S,\theta )$ that is itself a material function. Moreover, ${\gamma }^T$ was found to be the most accurate material approximation of ${\gamma }^n$ and of its gradient ever constructed, much better than the previous attempt by [15], which suggests that it can reproduce all of what ${\gamma }^n$ does (apart from non-material behaviour).
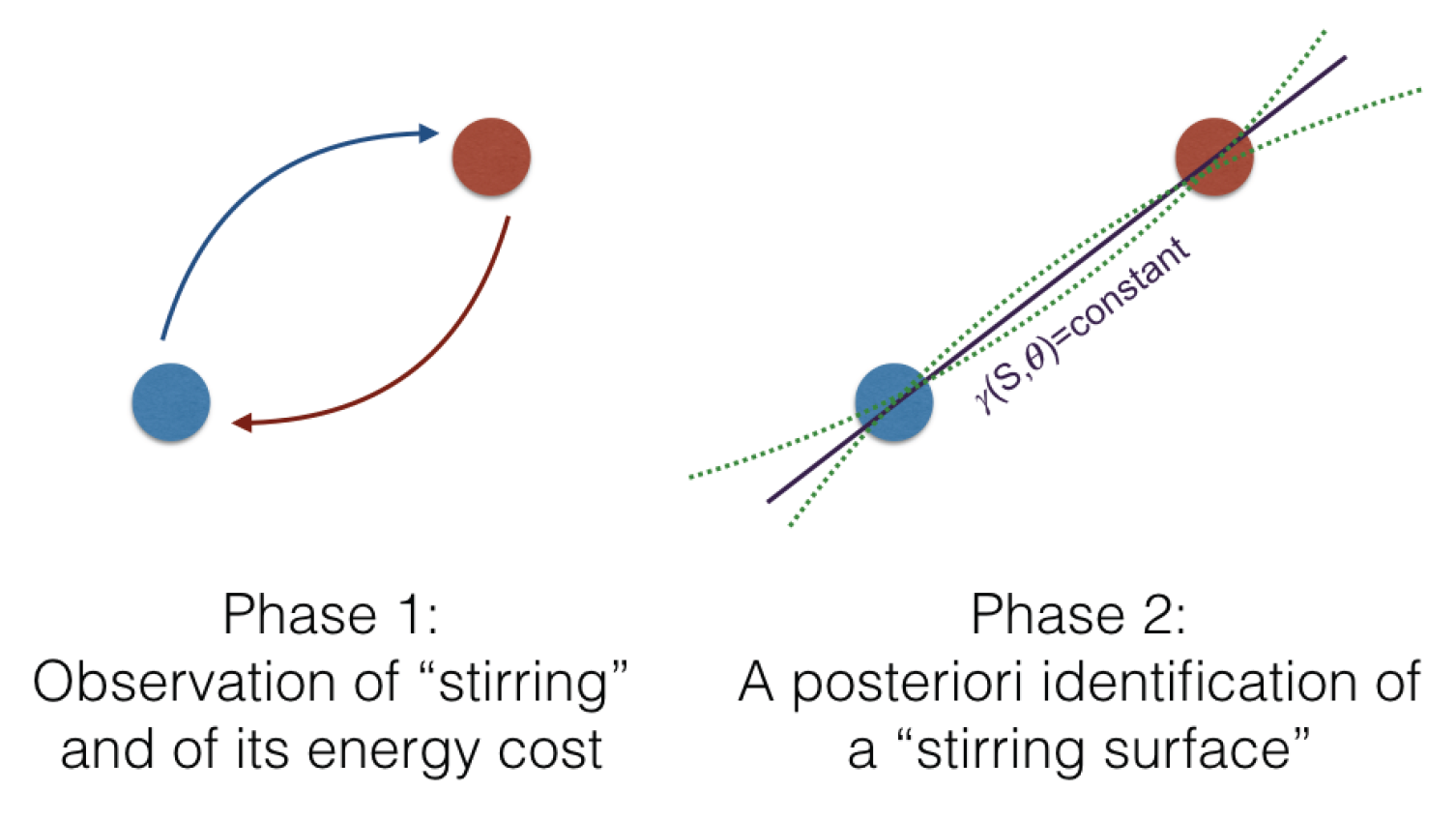
• “This dispersion mechanism appears to be a new mixing mechanism, but it relies on the unphysical demand that the ocean mix along an anthropogenically chosen $\gamma (S,\theta )$ surface.” No, it does not. The dispersion mechanism exists independently of any anthropogenically chosen $\gamma (S,\theta )$ surface. As explained below, the $\gamma$-chosen surface is constructed after the fact. The way it works is as follows: two fluid parcels swap position in the ocean. Then, anthropos invents a material surface $\gamma$ that fits the data and declares that the two parcels have exchanged position on such a surface. Fluid parcels are never aware of how anthropos chooses to explain their behaviour. This process is schematically illustrated in Figure 1.

3.2. The Five Stages of a Rigorous Study of Stirring and Mixing, from Observations to Parameterisations

As the points raised by MGG are somewhat subtle, it seems useful to try to formulate a notional “operational” protocol for the rigorous study of stirring and mixing, from the identification of a suitable model of stirring to the parameterisation of turbulent heat and salt fluxes in numerical ocean models. To that end, I identified five key stages, which I tried to make as transparent as possible. My hope is that by making it explicit, this protocol can be criticised by others and potentially improved through successive refinements.

• The first stage consists of introducing a model of stirring. Among the models available, the most comprehensive and detailed is probably that first discussed by [2]. For the present purposes, it is sufficient to use the simpler model used by [1] that regards stirring as a general permutation of a discretised version of the ocean conserving $\theta$ and S, of which the building blocks are pairwise permutations of fluid parcels. This model aims to formalise what one means by “stirring” in the context of the problem considered and facilitate the communication of one’s ideas to other investigators in the field by defining clearly the particular hypotheses made.
• The second stage consists of introducing a notional observing system capable of recording the thermodynamic properties $(S_i,{\theta }_i,p_i)$ and geographical locations $(x_i,y_i,z_i)$ of each fluid parcel making up the pairwise permutations defining “stirring events”. At the end of the observing phase, a preliminary classification of the various observed permutations into “vertical stirring” and “lateral stirring” categories could be attempted based on the ratio $\left|\mathrm{\Delta }z\right|/{(\mathrm{\Delta }{x}^2+\mathrm{\Delta }{y}^2)}^{1/2}$ for instance, or any other criterion deemed appropriate.
• The third stage consists of introducing stirring surfaces by fitting the data, as illustrated in the right panel of Figure 1. The simplest fit assumes a linear function of S and $\theta$,

  $$\gamma (S,\theta )=b\left[S-S_1-\frac{\mathrm{\Delta }S}{\mathrm{\Delta }\theta }(\theta -{\theta }_1)\right]+{\gamma }_0,$$

  (4)

  where $\mathrm{\Delta }S=S_2-S_1$ and $\mathrm{\Delta }\theta ={\theta }_2-{\theta }_1$, where b and ${\gamma }_0$ are arbitrary constants. Of course, more complex (nonlinear) functions could also be used, as illustrated in right panel of Figure 1, but this is not warranted. Equation (4) is a local descriptor and a human construct. Each locally defined material surface $\gamma (S,\theta )=\mathrm{constant}$ can be characterised in terms of its energy cost

  $$\mathrm{\Delta }E={\left(\frac{\partial \gamma }{\partial S}\right)}^{-1}\frac{\partial (\nu ,\gamma )}{\partial (S,\theta )}\mathrm{\Delta }\theta \mathrm{\Delta }p,$$

  (5)

  and is seen to be controlled by the Jacobian term $J_n=\partial (\nu ,\gamma )/\partial (S,\theta )$, where $\nu =1/\rho$. As shown by [1], all permutations with negative energy cost $\mathrm{\Delta }E\le 0$ appear to conform to our a priori expectations of lateral stirring. Neutral surfaces $(\mathrm{\Delta }E\approx 0)$ are only one out of a continuum of surfaces involved in lateral stirring and not the only one, contrary to what MGG claim.
• In the fourth stage, we now seek a globally defined material density variable $\gamma (S,\theta )$, as previously undertaken by [10,12,16] for instance. The aim is to go from a $(S,\theta )$ representation of water masses to a density/spiciness $(\gamma ,\xi )$ representation, where $\xi (S,\theta )$ is meant to parameterise spiciness. We note that if in-situ density $\rho =\rho (S,\theta ,p)=\widehat{\rho }(\gamma ,\xi ,p)$ is regarded as a function of $(\gamma ,\xi ,p)$, then the neutral vector is given by

  $$\mathbf{N}=-\frac{g}{\rho }\left(\nabla \rho -\frac{1}{c_s^2}\nabla p\right)=-\frac{g}{\rho }\left(\frac{\partial \widehat{\rho }}{\partial \gamma }\nabla \gamma +\frac{\partial \widehat{\rho }}{\partial \xi }\nabla \xi \right).$$

  (6)
  As noted by [1], the sign and amplitude of the partial derivative of $\widehat{\rho }$ with respect to spiciness $\partial \widehat{\rho }/\partial \xi$ control both the degree of non-neutrality of $\gamma$ and the energy cost $\mathrm{\Delta }E$ of adiabatic and isohaline parcel exchanges. All globally-defined variables $\gamma$ capable of enforcing the constraint $\mathrm{\Delta }E\le 0$ for all possible locally-defined adiabatic and isohaline parcel exchanges can claim relevance to the description of lateral stirring in the ocean. Note that such an approach does not assume that mixing occurs along iso-$\gamma$ surfaces, because—as stated earlier—irreversible mixing of heat and salt is described by isotropic Laplacian diffusion, not rotated diffusion. Rather, the goal is to find a density variable $\gamma (S,\theta )$ that can be useful to work in an isopycnal coordinate system. A priori, the number of such variables is infinite, which implies that the concepts of “isopycnal” and “diapycnal” are fundamentally non-unique and different for each variable $\gamma$, raising the question of which particular density variable $\gamma$ measurements of “diapycnal” and “isopycnal” mixing actually pertain to.
• In the fifth stage, we seek to parameterise the turbulent heat and salt fluxes ${\mathbf{F}}_{\theta }$ and ${\mathbf{F}}_S$ in terms of rotated diffusion tensors:

  $$-{\mathbf{F}}_{\theta }={\mathsf{\Psi }}_{\gamma }\times \nabla \theta +\left[K_i^{\gamma }(\mathbf{I}-\mathbf{d}{\mathbf{d}}^T)+K_T^{\gamma }\mathbf{d}{\mathbf{d}}^T\right]\nabla \theta ,$$

  (7)

  $$-{\mathbf{F}}_S={\mathsf{\Psi }}_{\gamma }\times \nabla S+\left[K_i^{\gamma }(\mathbf{I}-\mathbf{d}{\mathbf{d}}^T)+K_S^{\gamma }\mathbf{d}{\mathbf{d}}^T\right]\nabla S,$$

  (8)

  where $\mathbf{d}=\nabla \gamma /|\nabla \gamma |$ is the unit vector defining the diapycnal direction, while $K_i^{\gamma }$ is the isopycnal turbulent mixing, $K_S^{\gamma }$ and $K_T^{\gamma }$ are turbulent diapycnal mixing coefficients for heat and salt respectively, and ${\mathsf{\Psi }}_{\gamma }$ is the meso-scale eddy potential defining skew-diffusion (e.g., [17]). A simple mathematical analysis reveals that the way to express ${\mathbf{F}}_S$ and ${\mathbf{F}}_{\theta }$ as per (7) and (8) is non-unique, and that the choice of $\mathbf{d}$ is a priori arbitrary; however, each choice of $\mathbf{d}$ entails different values of ${\mathsf{\Psi }}_{\gamma }$, $K_i^{\gamma }$, $K_S^{\gamma }$, and $K_T^{\gamma }$ that are functions of the variable $\gamma$ chosen. While $\mathbf{d}$ can be specified in terms of the neutral vector, as is currently the most common practice, it is also a priori possible to construct $\mathbf{d}$ based on a globally-defined $\gamma$, provided that the turbulent mixing coefficients are modified appropriately. Owing to the non-uniqueness and apparent arbitrariness of $\mathbf{d}$ and $\gamma$, a key question is how best to specify the $\gamma$-dependent turbulent mixing coefficients. Without a suitable theoretical framework explaining how to link such coefficients to microstructure measurements, the only practical option must arguably involve inverse methods such as that based on the adjoint (e.g., [18]). In any case, there is a priori no particular reason to think that observations of “vertical” and “lateral” mixing relate to the neutral directions because—as acknowledged by MGG and explained in [1]—finite amplitude neutral trajectories require implicit diabatic sources of heat and salt to keep them neutral. As a result, the turbulent diapycnal diffusivitities associated with the use of the neutral directions must necessarily contain a “fictitious” part resulting from the existence of these hidden diabatic sources; these remain poorly understood, however, and most often overlooked in the literature.

4. Conclusions

I have shown that MGG’s claim that most of my results and conclusions are incorrect has no merit, for being primarily due to: (1) mistaking my Eulerian arguments for Lagrangian ones; (2) MGG’s irrational belief that the neutral tangent planes are somehow endorsed by Nature as being the only ones relevant to the local description of lateral stirring in the ocean. As MGG acknowledge in their comment, their views about lateral stirring appear to solely rely on the use of the equation of state for in-situ density, on the consideration a single one-dimensional fluid directory, and on the observed “smallness” of viscous dissipation rates; in particular, they insist that their approach does not rely on dynamical or energetics arguments rooted in the momentum equations, which they seem to regard as ultimately responsible for introducing confusion about the directions of lateral stirring in [1]. Yet, despite the fact that their views about lateral stirring do not appear to rely on any particular model of stirring, such as that first discussed by [2] or the discrete view of stirring used in [1], MGG nevertheless claim to be able to make definitive statements about the nature of lateral stirring and stirring surfaces, which is at odds with all published literature on the subject.

I find it difficult upon reading [3] or MGG’s comment not to be reminded of Hans Christian Andersen’s tale “The Emperor’s New Clothes”. Indeed, MGG and [3], like the weavers of Andersen’s tale, assert to the oc`eanographic community (the Emperor) that they have proven that lateral stirring occurs solely in neutral tangent planes (the new clothes). For the past ten years or so, the belief in the validity of such a “proof” has been used as justification for labelling as incorrect all rigorous/first principles attempts at proposing alternative constructions of density variables. Thus, using specially “tailored” metrics, McDougall et al. [15,19] challenged the usefulness/validity of [16]’s orthobaric density or of material surfaces (supported by [10] or [14]). Based on my understanding of the problem, however, I believe that MGG’s proof is actually “invisible”, and easily refuted by simple and rigorous considerations.