Abstract
In this paper we discuss the deformation of a flexible fiber clamped to a spherical body and immersed in a flow of fluid moving with a speed ranging between 0 and 50 cm/s by means of three dimensional numerical simulation developed in COMSOL . The effects of flow speed and initial configuration angle of the fiber relative to the flow are analyzed. A rigorous analysis of the numerical procedure is performed and our code is benchmarked against well established cases. The flow velocity and pressure are used to compute drag forces upon the fiber. Of particular interest is the behavior of these forces as a function of the flow speed and fiber orientation. The Vogel exponents, which characterize the rate of bending of a fiber in a flow, are found for the various configurations examined here and seem to display interesting variations. These exponents are then compared with our previously studied two-dimensional models.
1. Introduction
The subject of fluid structure interaction (FSI) is very complex and involves the coupled interaction of fluid flows with solid bodies, rigid and elastic. In this paper we analyze a simple version of such a problem by investigating the forces upon flexible fibers attached to a basal body and held in different configurations. This three dimensional investigation was conducted at low Reynolds numbers (between 0 and 9000) and is an extension of our previous two-dimensional study [1].
While our study remains at a more fundamental level, applications for this problem are plentiful. The modeling of unmanned air vehicles (UAV), for instance, is a very important and well studied FSI problem corresponding to aerodynamic flows. One key objective in these problems is the optimal design of the aircraft (rigid-body) through minimization of the forces acting on it. Additionally, FSI has several medical applications; numerical studies have been done to analyze airflow in human vocal folds. Specifically, the modeling of the interaction between air and vocal chords when talking is important planning vocal surgeries, and in voice rehab. Understanding the dynamics of elastic structures and their interaction with fluids can greatly advance the medical industry [2,3].
The terminal configuration, including velocity and orientation, of a rigid body in a fluid flow is a well studied problem for over a century and continues to be explored (see for instance, [4,5,6,7,8,9,10]). The classical problem of the terminal orientation of a body itself is a difficult problem which is compounded by the addition of flexibility [11,12,13,14,15,16]. The current paper is a part of our ongoing contribution to the broader subject of terminal configurations in fluid-solid interaction and aims to extend the results of our previous work [1]. Experimental and numerical studies have revealed that deformable bodies in a flow reconfigure their orientations in order to reduce drag. An important metric for the bending behavior is the drag exponent or “Vogel exponent” [17,18] which indicates the rate at which drag force on the body varies with the velocity, given by the expression where according to previous studies. The current paper considers flexible fibers, attached to a basal body, submerged in a flow with speeds 0–50 cm/s. The effect of fiber length and orientation, upon the bending behavior are examined.
The paper is structured as follows. In Section 2 we describe the numerical setup we use for our analysis. As part of this setup, we first perform a benchmark of the methods we use to make sure they can reproduce classical results (Section 2.2.1). We choose a simplified three dimensional problem—the flow around a ball-and use the drag coefficient to gauge our numerical calculations. We then perform a convergence study to determine the optimal mesh density that will be used in the main study (Section 2.2.2). In Section 3 we describe the results of our analysis of the ball and fiber system and offer conclusions and plans for future work in Section 4.
2. Three Dimensional Numerical Simulations
In this section we describe the numerical setup we use in our analysis. The system under investigation is the ball-fiber system shown in Figure 1 where the ball is rigid and the fiber is flexible. This system is placed at the center of a box-like domain containing the fluid, as shown in Figure 1.
Figure 1.
The geometry of the problem and meshing in the domain and around the ball-fiber system.
Fluid flows in the channel and interacts with the ball and fiber system. The elastic fiber bends under the load and, at small Reynolds numbers, it reaches a final/equilibrium configuration. We simulate numerically this interaction and bending, and perform measurements of the drag force and final bending angle of the fiber. In the following sections we describe the numerical approach we use for these simulations.
2.1. Governing Equations
Navier-Stokes and linear elasticity equations model the structural deformation of flexible fibers in a flow. In a three dimensional setup, we model the steady-state solution of the problem, since we are strictly concerned with the steady drag force and final bending angle of the fiber. We are, therefore, considering the following system of equations:
where is the incompressible fluid velocity field, T is time, is the density of the fluid, is the density of the solid, μ is the dynamic viscosity, is the external volume force on the fluid and is the force per unit volume on the fiber. At the channel inlet, the flow is taken to be fully developed and parabolic while at the chancel outlet, zero pressure conditions are imposed. The Cauchy stress tensor for the solid material, σ, is given by [19]
where , and . Here , , , , ϵ and stand for the displacement of the fiber, stiffness tensor, stress tensor, initial stress tensor, strain tensor and initial strain tensor, respectively and : represents the double dot product between the two tensors [20]. In the special case of a homogeneous isotropic media, like the one considered in our study, σ reduces to the simple form
where K is the bulk modulus and is the shear modulus of the material.
2.2. Numerical Setup
We use COMSOL for our numerical simulations. This multiphysics software uses a fluid-structure interaction module which includes laminar flow and structural mechanics governing both Navier-Stokes and linear elasticity equations. More specifically, COMSOL uses the finite element method to solve the equations. For choice of finite element basis functions we use P1 + P1 (linear velocity and pressure elements) with consistent stabilization [21]. The discretization of the displacement field for the solid is given by quadratic elements. We used the arbitrary Lagrangian-Eulerian (ALE) technique [21] to describe the deforming geometry (moving mesh) with Winslow smoothing [22]. A fully-coupled solver is used with Newton’s method for the nonlinear solver and MUMPS for the direct linear solver. We first benchmark the code using the classical problem of the flow around a sphere. Then we run convergence tests on the ball and fiber system to ensure the method is converging. The following sections describe these preliminary tests.
2.2.1. Flow Around a Sphere
Three dimensional flow around a sphere was used as a benchmark for the main model [23]. We are primarily concerned with choosing the numerical parameters (e.g., finite element mesh density) which result in accurate solutions to the Navier-Stokes Equations. Our study analyzes mesh elements ranging from 5000 to 310,000 and determines the optimal mesh for the ball and fiber model. The primary source of comparison was the total drag force on the sphere which is described mathematically through the well-known formula
where are the drag force, density of the fluid, radius of the sphere, drag coefficient, and terminal velocity, respectively. The drag coefficients of many objects have been both experimentally and numerically computed. The theoretical drag curve indicates how the increase in Reynolds number affects the drag coefficient [24,25]. As a balance between computational time and velocity, parameters were chosen for a Reynolds number of 15,000. For stability, we chose the velocity to be slightly higher than the maximum velocity used in the ball and fiber experiment.
For this comparison of drag coefficients we used Pa· s, m/s, and kg/m. The radius of the ball is m. Here the diameter of the sphere was used as the characteristic length m. We first calculate the drag coefficients for a fixed Reynolds number based on formulas reported in the literature [24,26,27,28]. We then compute the relative error in drag coefficients using the formula
where and represent the drag coefficients computed in this paper and the papers cited above respectively. The relative error is then plotted as a function of mesh density in Figure 2.
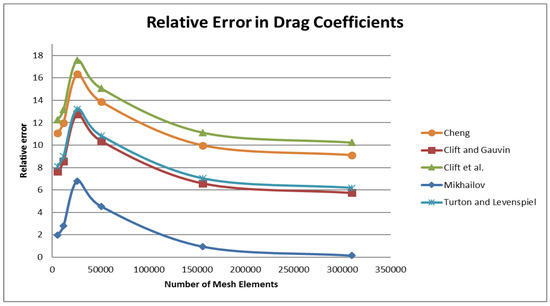
Figure 2.
Relative error for drag coefficients for varying number of mesh elements computed using formulas in Cheng [24], Clift and Gauvin [26], Clift et al. [26], Mikhailov [27], Turton and Levenspiel [28].
In Table 1 we give further numerical details for the relative error with respect to the formula given by Mikhailov [27].

Table 1.
Numerical values of the relative error for drag coefficients with respect to Mikhailov [27].
The results of this section show that the numerical method we use can accurately reproduce results published in the literature for the classical flow past a sphere problem. This motivates the use of this numerical procedure for the main focus of this paper, the ball and fiber system.
2.2.2. Convergence Study for Ball and Fiber System
This section describes the convergence study performed for optimal choice of mesh density for the ball and fiber system. Three settings governed the meshing of the fluid environment: (1) A master size defining global properties; (2) free tetrahedral meshing for the flow domain without the fiber; and (3) free tetrahedral meshing for only the sphere and fiber. We choose a ”custom” mesh with the parameters detailed in Table 2.

Table 2.
Custom mesh parameters chosen for Master size in mesh.
According to [29], to increase performance, it is desirable to: (i) lower the minimum element size and the resolution of curvature; (ii) raise the resolution of narrow regions and increase the maximum element growth rate. This explains the use of certain parameters in the custom mesh given in Figure 2. The mesh governing the ball and fiber is chosen using the predefined “extra fine” setting in COMSOL. This gives a good refinement near the object to ensure that sharp corners are taken into account. We ran a mesh study on the size of the mesh in the flow domain without the ball and fiber. This parameter sweep runs through four predefined settings with the number of elements ranging from 21,000 to 74,000. Table 3 shows us the measured drag at a maximum velocity of m/s run for each setting of mesh densities. We also calculated the relative error using the formula
and the results are included in the third column in Table 3.

Table 3.
Mesh Study for ball and fiber.
Based on these results we select the number of mesh points 48,493 as our optimal choice for the mesh.
2.2.3. Parametric Study
After the preliminary numerical tests, we perform our simulations of the ball and fiber immersed in a flow of water with the parameters described below. Based on the benchmark and convergence studies performed in the previous sections, we choose for the discretization of velocity elements and 48,493 mesh points for the algorithm. The system of Equations (1)–(3) are solved with the following boundary conditions: (i) the no-slip boundary conditions are imposed on all faces of the flow domain and on all boundaries of the ball and fiber; (ii) zero pressure conditions are held at the outlet; (iii) the sphere is fixed, while the fiber is free to bend; (iv) the tip of the fiber has an imposed boundary load given by
where is force per unit volume on the fiber.
The fiber is considered to be linearly elastic with isotropic material properties Pa, and kg/m being the Young’s modulus, Poisson’s ratio, and density, respectively. Two different angles were computed for flow speeds ranging from 0.009 m/s to 0.4510 m/s, chosen based on the two-dimensional simulations and physical experiments reported in our earlier study [1]. Simulations were conducted for both 2 cm and 4 cm fibers.
3. Results
In this section, we describe the numerical solutions generated with COMSOL. Additionally, we discuss similar results to the two-dimensional simulations performed in [1] such as deformation angles, drag and Vogel exponents. The change in the drag force on the ball and fiber system with the flow speed is depicted in Figure 3.
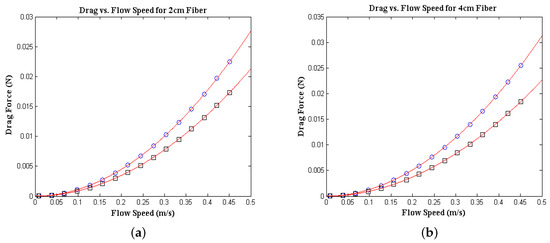
Figure 3.
These plots show the change of drag force as a function of velocity and are computed for angles of (◯) and (□) for fibers of lenghts (a) 2 cm and (b) 4 cm.
The graphs show the change in the drag force for fibers of lengths 2 and 4 cm respectively. We notice that an increase in fiber length leads to a significant increase in drag force. The red lines in the figure represent exponential least squares fits, i.e.,
The drag coefficients and Vogel exponents [17], α, for the parameter range examined in this study are summarized in Table 4. We can see from this table that the Vogel exponents are much closer to the standard inertial drag model with . The flexible body appears to be much stiffer, and bends less due to the properties of the solid such as the bulk modulus.

Table 4.
Summary of least squares fit of Drag to Velocity.
We also examined the average bending behavior of the fibers by computing the deflection angle of the line connecting the points of suspension and free ends of the fiber. Spherical coordinates are used as the reference frame. The Cauchy number (Ca), defines the ratio of inertial to elastic forces in the system and is given by where ρ is the density of the fluid, U is the characteristic velocity and K is the bulk modulus of the fiber which is taken to be 4 GPa (based on our previous experiments with Nylon fibers). Gosselin et al. [13] note that the drag on a flexible rectangular plate can be seen to depend on an appropriate scaling of , defined by (where is the drag coefficient) such that for the flexible plate transitions to a reconfigured state. As in our previous studies, we use a simple rescaling of the Cauchy number, to bring it to the same scale as in previous work. The initial coordinates were calculated using the coordinates of the center of the sphere. That is, for the 90 degree case, we have , , and . For the 45 degree case a geometrical argument was used to deduce , , and . The coordinates of the tip of the fiber, denoted were measured using an averaging probe around the boundary representing the tip of the fiber. Our coordinate system is denoted by , where φ is the measure of the angle from the vertical and θ is the measure of the angle in the plane. Typically, the bending in the direction, φ, is that being compared to the 2-dimensional results. Here and , where .
We can see from Figure 4 that an increase in fiber length corresponds to an increase in bending. Furthermore, for higher , the difference between the deformation angles among varying fiber lengths increases. For of approximately 50, the difference between the 4 cm and 2 cm fibers in initial configuration of 45 degrees is around . Additionally, the difference in the 90 degree case seems more significant. The difference among fiber lengths seem to vary about in this case. If we compare among the two images we see that, qualitatively, the different configuration angles produce similar deformation. Although, the difference is subtle, it appears that the 90 degree configuration changes with modified Cauchy number at a faster rate. The fiber represented here is merely a prototype to model different scenarios, in which bending may be more prominent. For example, the hair that lines the skin is much thinner than the fiber used, and thus has different structural properties. We expect that these type of fibers should bend more. For the two-dimensional study, we used a fiber of different length and resulted in significant bending [1].
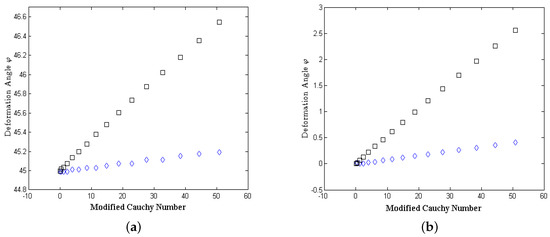
Figure 4.
The φ Deformation is considered to be measured in the plane (up and down). These angles are measured for (a) and (b) configuration angles for fiber lengths of 2 cm (◇) and 4 cm (□).
One main goal in computations is to reduce the dimensionality of the problem to make the modeling easier. It is important to check the validity of this reduction, however. In this section we compare the simulations in two and three dimensions. The results of the two-dimensional simulations were reported in our previous paper [1]. In the two-dimensional experiments, we see the Vogel exponents to be significantly smaller than those of the three dimensional problem, for the same geometric setup and parameter values. In 2-D we see Vogel exponents ranging from to , however, in 3-D we see that the Vogel exponents follow closer to the exponents of a rigid body. Specifically, we have found that the exponents range from to .
The deformation in the plane was measured (φ) in both two and three dimensions. We found no significant percentage increase in bending between the slowest flow speed of m/s and fastest flow speed of m/s. We measured the initial configurations of and for both the 2 cm and 4 cm fibers. For the 2 cm fiber the percentage increase in bending is rather small. Specifically, for we see an increase of about in 2-D versus an increase of approximately for 3-D. The initial configuration shows an percentage increase of approximately for the 2-D fiber versus an increase of approximately for the 3-D fiber.
The 4 cm fiber bends much more, but shows no significant difference between two and three dimensions. For the initial configuration of we have an percentage increase of about for 2-D fiber and for 3-D fiber. For the initial configuration of we see an increase of approximately for the 2-D fiber and for the 3-D fiber. More accurate calculations and relative percentage differences are seen in Table 5 and Table 6.

Table 5.
Percentage increase in 2 cm fiber length bending at m/s relative to m/s for initial configurations of and for both 2-D and 3-D simulations.

Table 6.
Percentage increase in 4 cm fiber length bending at m/s relative to m/s for initial configurations of and for both 2-D and 3-D simulations.
4. Conclusions
In summary, this paper examines the configurations of flexible fibers in a flow field by means of a three dimensional numerical simulation using COMSOL. Our investigations reveal that the length and initial orientation of the fiber can cause significant changes to the reconfiguration patterns and forces experienced. The Vogel exponents are also computed and in three dimensions, are seen to be much higher than the values obtained by us previously in the two dimensional study [1] and those obtained in the literature. This apparent discrepancy may be attributed to the relatively low flow speeds and high stiffness of the fiber employed in the current calculations which were chosen to match our previous two-dimensional work. A more thorough study of the effect of stiffness, geometric variations of the basal body, initial configuration of the fiber and flow speed will be conducted in the future; in particular, we plan to investigate the flapping regime of the fiber in three dimensions.
Author Contributions
This work was performed while Ryan Allaire was a graduate student at Montclair State University as part of his MS Thesis. Both authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allaire, R.; Guerron, P.; Nita, B.; Nolan, P.; Vaidya, A. On the equilibrium configurations of flexible fibers in a flow. Int. J. Nonlinear Mech. 2014, 69, 157–165. [Google Scholar] [CrossRef]
- Hasnedlová, J.; Feistauer, M.; Horáček, J.; Kosík, A.; Kučera, V. Numerical Simulation of Fluid-Structure Interaction of Compressible Flow and Elastic Structure. Computing 2013, 95, 343–361. [Google Scholar] [CrossRef]
- Huang, L.; Quinn, S.J.; Ellis, P.D.; Williams, J.E. Biomechanics of snoring. Endeavour 1995, 19, 96–100. [Google Scholar] [CrossRef]
- Camassa, R.; Chung, B.J.; Howard, P.; McLaughlin, R.M.; Vaidya, A. Vortex Induced Oscillations of Cylinders at Low and Intermediate Reynolds Numbers; Sequeira, A., Rannacher, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 135–145. [Google Scholar]
- Fields, S.B.; Klaus, M.; Moore, M.G.; Nori, F. Chaotic dynamics of falling disks. Nature 1997, 388, 252–254. [Google Scholar] [CrossRef]
- Galdi, G.P.; Vaidya, A. Translational Steady fall of Symmetric Bodies in Navier-Stokes Liquid, with Application to Particle Sedimentation. J. Math. Fluid Mech. 2001, 3, 183–211. [Google Scholar] [CrossRef]
- Kirchoff, G. Uber die Bewegung enines Rotationskorpers in einer flussigkeit. J. Reine Angew. Math. Soc. 1869, 71, 237–281. [Google Scholar]
- Leal, L.G. Particle Motion in a Viscous Fluid. Annu. Rev. Fluid Mech. 1980, 12, 435–476. [Google Scholar] [CrossRef]
- Tanabe, Y.; Kaneko, K. Behavior of falling paper. Phys. Rev. Lett. 1994, 73, 1372–1376. [Google Scholar] [CrossRef] [PubMed]
- Willmarth, W.W.; Hawk, N.E.; Galloway, A.J.; Roos, F.W. Aerodynamics of oscillating disks and a right-circular cylinder. J. Fluid Mech. 1967, 27, 177–207. [Google Scholar] [CrossRef]
- Alben, S.; Shelley, M.; Zhang, J. Drag reduction through self-similar bending of a flexible body. Nature 2002, 420, 479–481. [Google Scholar] [CrossRef] [PubMed]
- Alben, S.; Shelley, M.; Zhang, J. How flexibility induces streamlining in a two-dimensional flow. Phys. Fluids 2004, 16, 1694–1713. [Google Scholar] [CrossRef]
- Gosselin, F.; de Langre, E.; Machado-Almeida, B.A. Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 2010, 650, 319–341. [Google Scholar] [CrossRef]
- Shelley, M.J.; Zhang, J. Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 2011, 43, 449–465. [Google Scholar] [CrossRef]
- Schouveiler, L.; Eloy, C.; Le Gal, P. Flow-induced vibrations of high mass ratio flexible filaments freely hanging in a flow. Phys. Fluids 2005, 17, 047104. [Google Scholar] [CrossRef]
- Zhu, L. Viscous flow past a flexible fibre tethered at its center pint: Vortex shedding. J. Fluid Mech. 2007, 587, 217–234. [Google Scholar] [CrossRef]
- Vogel, S. Drag and flexibility in sessile organisms. Am. Zool. 1984, 24, 37–44. [Google Scholar] [CrossRef]
- Vogel, S. Drag and reconfiguration of broad leaves in high winds. J. Exp. Bot. 1989, 40, 941–948. [Google Scholar] [CrossRef]
- Slaughter, W.S. The linearized Theory of Elasticity; Birkhauser: Basel, Switzerland, 2002. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: Berlin, Germany, 1998. [Google Scholar]
- Donea, J.; Huerta, A. Finite Element Methods for Flow Problems; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Winslow, A. Numerical solution of the quasilinear Poisson equations in a nonuniform triangle mesh. J. Comp. Phys. 1967, 2, 149–172. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cheng, N. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Drag of a Sphere. Available online: https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html (accessed on 13 September 2015).
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Mikhailov, M.D.; Freire, A.P. The drag coefficient of a sphere: An approximation using Shanks transform. Powder Technol. 2013, 237, 432–435. [Google Scholar] [CrossRef]
- Turton, R.; Levenspiel, O. A short note on the drag correlation for spheres. Powder Technol. 1986, 47, 83–86. [Google Scholar] [CrossRef]
- Griesmer, A. Size Parameters for Free Tetrahedral Meshing in COMSOL Multiphysics. Available online: https://www.comsol.com/blogs/size-parameters-free-tetrahedral-meshing-comsol-multiphysics/ (accessed on 30 January 2014).
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).