Hydrodynamic Performance and Cavitation Characteristics of an Integrated Pump-Gate

Abstract

The integrated pump-gate is a hydraulic facility that integrates a pumping station and a gate, playing a vital role in urban drainage systems, flood control, and other scenarios. Although integrated pump-gates are widely used, their internal flow presents different forms depending on the application scenarios, such as backflow, vortices, and cavitation. These effects markedly influence the pump’s hydraulic performance, operational stability, and overall reliability. This study investigates the cavitation characteristics and internal flow fields within the complex geometry of the integrated pump-gate and numerically simulates the cavitation phenomenon using the SST turbulence model. Specifically, the influence of the impeller, guide vanes, and structural supports on the cavitation performance and internal flow state was analyzed. The results show that the geometric characteristics of the impeller’s leading edge significantly influence the cavitation structure. Regarding cavitation performance, NPSH_c was determined to be 5.3 m. At the leading edge of the guide vanes, cavitation usually occurs at the axial diffusion position of the flow channel, and the degree of cavitation is affected by the relative position of the guide vanes and the impeller blades. The structural supports and protrusions significantly affect the vortex structures in the flow field, with protrusion-induced vortex clusters dominating the guide vane region.

1. Introduction

With the acceleration of urbanization, urban waterlogging has become an increasingly severe issue. As a new type of hydraulic facility, integrated pump gates are widely applied in urban flood control, drainage and water regulation, as shown in Figure 1. Compared with traditional separate pumping stations and gate systems, integrated pump gates combine the functions of pumping and gating into a single system, featuring a small footprint, short construction period, and simplified operation and maintenance. These advantages make integrated pump gates an effective solution for urban flood management. However, the operating environment of the pump gate system is complex, especially the internal flow, cavitation and vortex phenomena inside the pump, which put forward high requirements for hydraulic performance and structural stability.

The cavitation and vortex phenomena within pumps have been a major focus of research [1]. Regarding the geometric design, Xie et al. [2] optimized the inlet and outlet horn configurations of integrated pump-gates using CFD simulations, demonstrating that appropriate inlet horn geometry can effectively mitigate flow separation and suppress vortex formation. Similarly, Li et al. [3] investigated how the geometric dimensions of pumps (installation height and spacing of pumps) affect hydraulic performance, indicating that reasonable installation height can effectively improve reflux vortices. Zhang et al. [4] further studied the influence of intake vortices on the performance of axial flow pumps, pointing out that intake vortices can cause changes in the blade flow angle and generate cavitation. Guo et al. [5] investigated the influence of inlet guide vanes on the cavitation performance of an axial flow pump. Their results confirmed the beneficial effect of positive inlet guide vane angles on cavitation performance, and they pointed out that as NPSH_a decreases from a high value, the cavitation volume initially expands in the circumferential direction.

During impeller operation, tip leakage induced by the clearance strongly influences cavitation behavior and is therefore an indispensable consideration in the study of cavitation in the blades of integrated pump gates. Additionally, flow instability within the tip clearance is a primary factor responsible for clogging and operational instability. Tan et al. [6] and Kim et al. [7] conducted a detailed study on how the tip clearance affects the performance of axial flow pumps. The backflow induced by the tip clearance contributes significantly to efficiency degradation and is one of the main causes of reduced performance in axial flow pumps. Consistent with this, Fan et al. [8] analyzed the cavitation-induced energy loss in mixed-flow pumps, indicating that high entropy production zones within the impeller are typically located in the blade tip clearance and along the suction surface. Similarly, Boulon et al. [9] found through experiments that a larger tip clearance significantly increases the risk of cavitation in leakage vortices. Higashi et al. [10] further examined the effects of variations in cavitation number, angle of attack, and clearance size on the characteristics of tip cavitation. More importantly, the influence of the complex leakage vortices it causes on the flow in the main channel. Shi et al. [11,12] studied the leakage flow at the blade tip of axial flow pumps and the interaction mechanism between leakage vortices and cavitation. The results show that slight cavitation can promote the development of tip leakage vortices, and the changes in blade load caused by cavitation also have a certain influence on the morphology of tip leakage vortices. From the perspective of vortex-blade interaction, Al-Obaidi [13] revealed that the tip leakage vortex (TLV) actively modulates the pressure difference across blade surfaces. Consistent with these findings, Yu et al. [14] conducted a study on how the impeller clearance affects cavitation performance. The research found that as the clearance increases, the backflow vortex behind the impeller becomes more significant, and the cavitation phenomenon also becomes more severe.

Besides geometry, operational conditions also play a critical role. According to He et al. [15], high flow rates optimize the radial force distribution but deteriorate flow stability, leading to chaotic spectral behaviors. Liu et al. [16] compared the pump-gate’s cavitation characteristics in forward versus reverse rotation, indicating that strong cavitation vortex structures appeared on both the suction and pressure surfaces of the impeller in the reverse operation mode. In addition, Liu et al. [17] investigated the cavitation characteristics of a water-jet pump under valley and peak conditions, revealing that the tip leakage vortex is significantly more pronounced in the peak condition compared to the valley condition. Long et al. [18] conducted experiments and CFD analysis to study the cavitation in water jet pumps, revealing that the cavitation vortex structure is closely related to the design of the impeller and the operation mode. Jiao et al. [19] conducted cavitation simulations and experimental studies under low-head conditions. The results indicate that the vortex structures are primarily concentrated on the pressure side at low heads, whereas they extend toward the suction side at high heads. Zheng et al. [20] conducted numerical simulations and experimental investigations on cavitation in the hump region of an axial-flow pump. The results indicate that the formation of perpendicular cavitation vortices and the resulting asymmetric passage blockage are considered the primary causes of performance deterioration. Furthermore, they analyzed the flow characteristics of different airfoils under varying cavitation conditions and found that cavitation primarily manifests as tip and sheet cavitation. It was observed that with increasing cavitation intensity, the sheet cavitation region progressively develops axially from the blade tip to the outlet and extends radially from the shroud to the hub, eventually covering nearly the entire blade surface [21]. Wang et al. [22] studied the vortex structure in cloud cavitation flows and simulated the vortex structure under different cavitation numbers, proposing to reduce the occurrence of cavitation through optimized design. In addition, the spatiotemporal evolution of axial-flow pump cavitation exhibits a rich variety of forms when the number of guide vanes and impeller blades is unequal [23,24], and cloud cavitation is particularly destructive and readily induces intense noise and vibrations [25].

While most existing studies focus on macroscopic design or flow conditions, structural details are often overlooked. Although the energy dissipation of axial-flow pump cavitation occurs mainly through turbulent dissipation, wall surface irregularities also have a significant impact on cavitation and flow structures [26]. In light of this, another detail frequently overlooked in engineering practice—namely the inevitable diffusion-shaped flow passage design—warrants in-depth exploration. Currently, the specific influence mechanism of diffusion-shaped flow passages on “geometrically induced” cavitation in integrated pump-gates remains unsystematically understood.

This study aims to bridge this gap by incorporating common influencing factors such as tip clearance to accurately simulate the pump’s real-world operating conditions. Furthermore, to comprehensively reveal the cavitation characteristics and vortex structures, this study explicitly accounts for the potential effects of support components and structural protrusions during actual operation. Through detailed analysis, this work aims to provide a theoretical basis for the future research and design optimization of integrated pump-gates.

2. Numerical Calculation Method

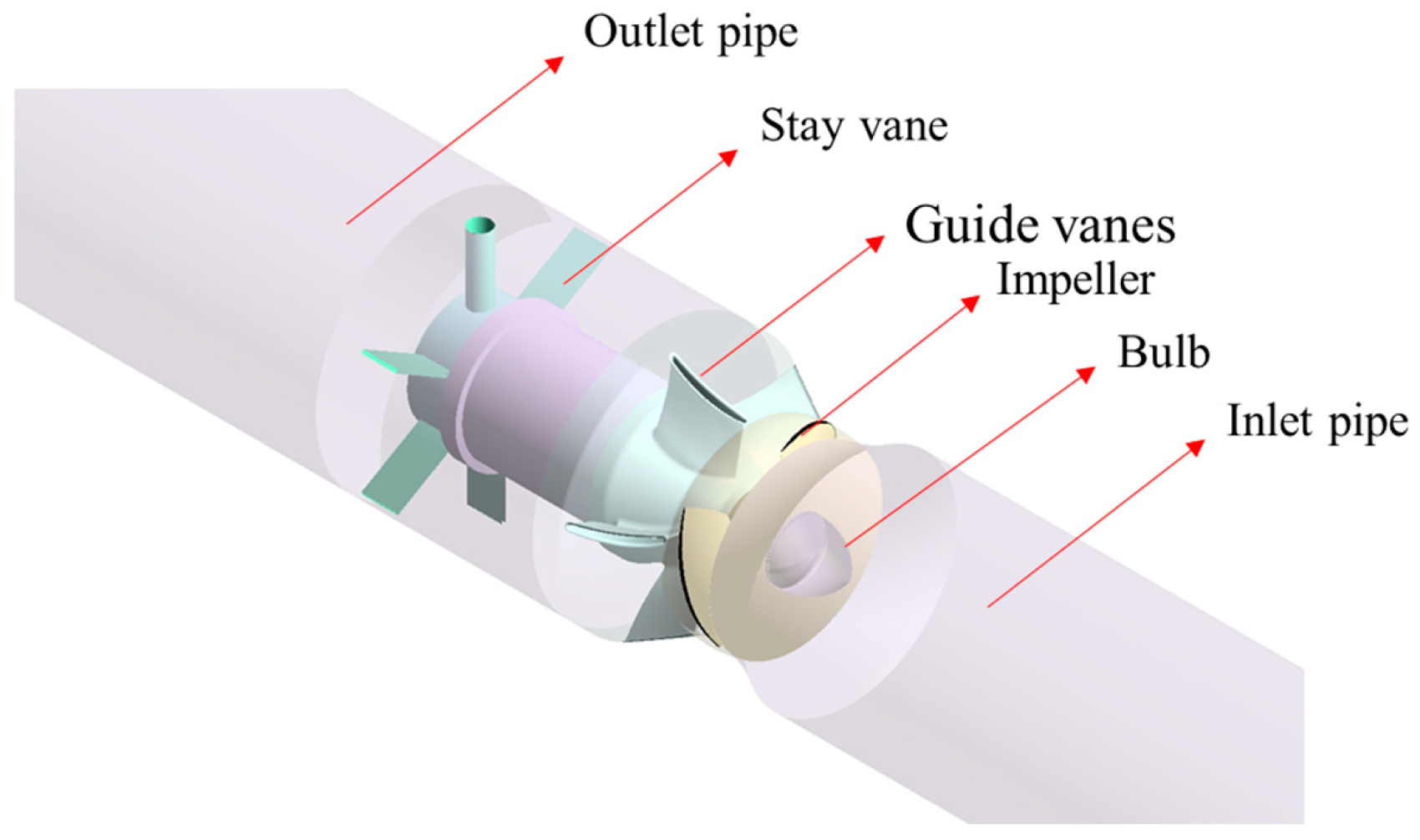
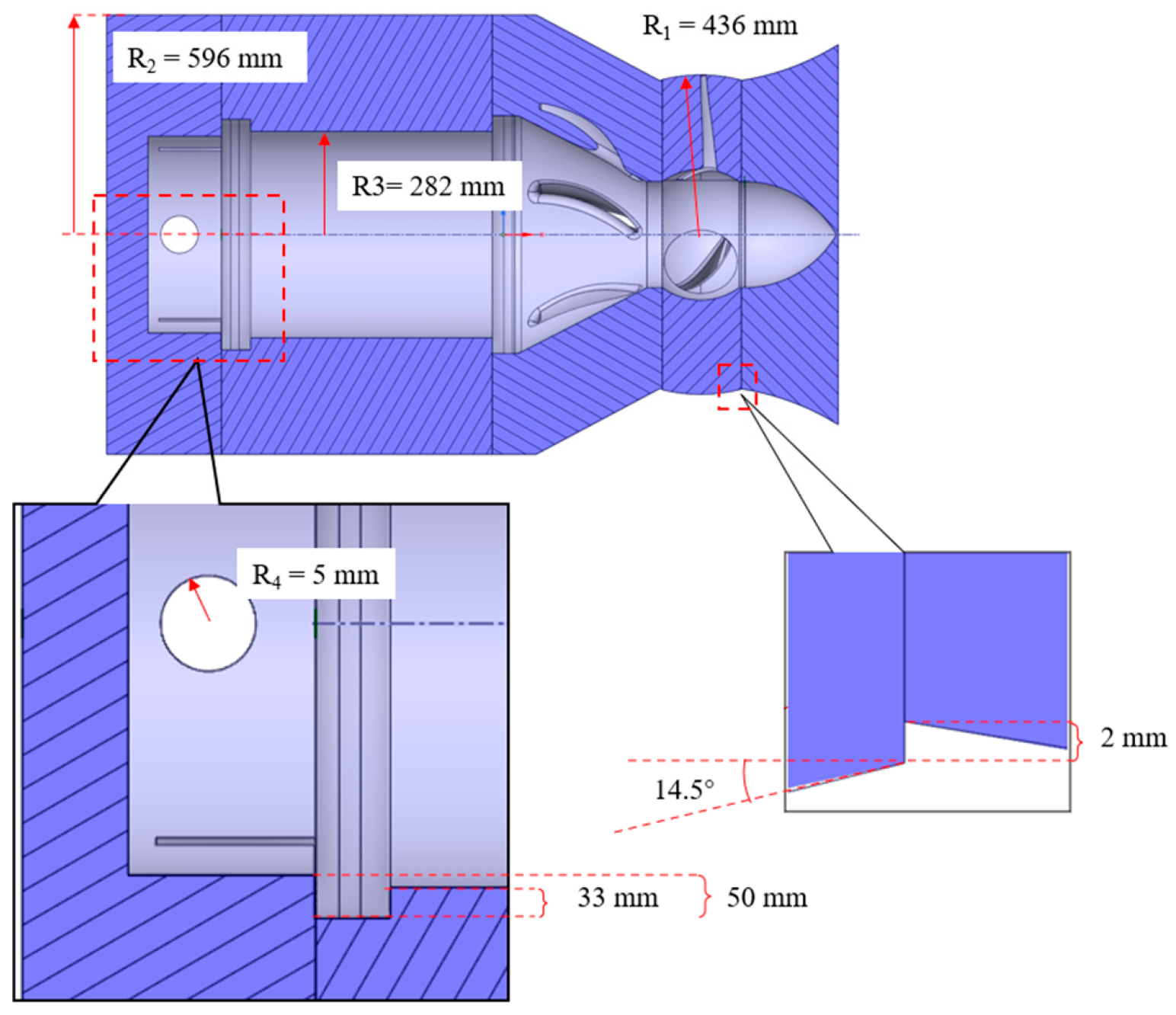
2.1. Geometric Models

The focus of this study is an integrated pump gate system. To conduct a detailed analysis of its cavitation characteristics and internal flow features, a computational model was established. This model includes a bell-shaped inlet pipe, impeller, guide vanes and outlet pipe. At the upstream of the impeller is the bulb, and the downstream of the guide vanes features support vanes. It can significantly reduce the vibration generated during the operation of the pump body. A schematic representation of the computational model is shown in Figure 2.

The detailed geometric features of the model are illustrated in Figure 3. The diffusion-shaped flow passages are primarily located at the impeller inlet and the inlet region of the guide vanes. The main design parameters are listed in

Table 1. Main design parameters of the integrated pump-gate.

Parameters	Unit	Value
Head	m	2.3
Rotational Speed	r/min	485
Blade number of impeller		3
Number of guide vanes		5
Mass flow rate	m3/h	3040
Tip clearance diameter	mm	2

.

To characterize the flow regime and ensure the applicability of the turbulence model, the Reynolds number Re is defined based on the impeller diameter R₁ and rotational speed n:

$$Re={\displaystyle \frac{\pi n{R_1}^2}{60v}}$$

(1)

where v is the kinematic viscosity of water (0.893 $\times$ 10⁻⁶ m²/s). In this study, the calculated Re is approximately 2.16 $\times$ 10⁷, indicating a fully developed turbulent flow.

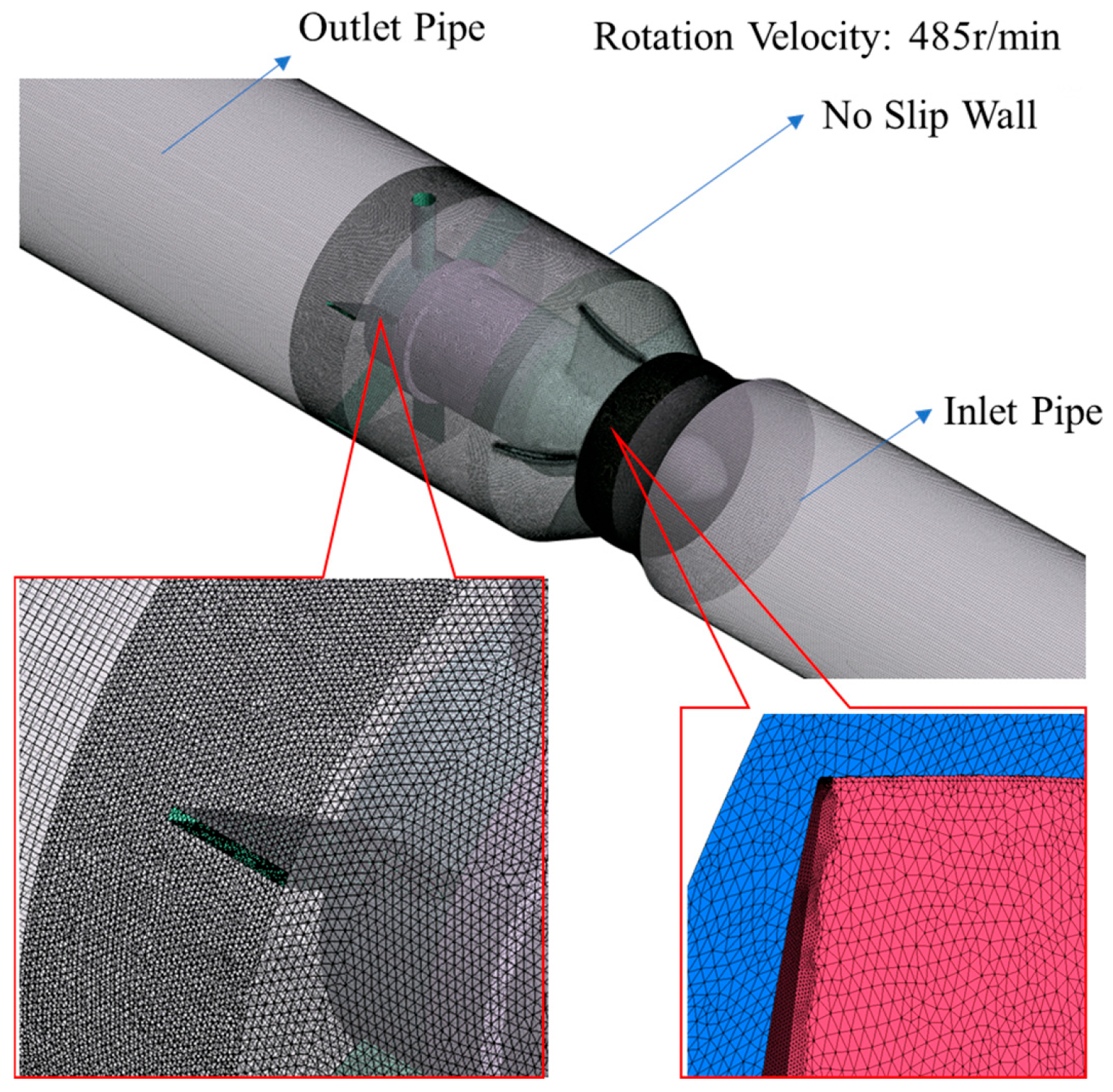
2.2. Mesh Generation

In fluid simulations, mesh generation discretizes the computational domain for numerical solution. A high-quality mesh is essential for ensuring both accuracy and efficiency, as it determines whether CFD simulations can effectively capture flow characteristics while optimizing computational resources. Based on the hydraulic model, the five fluid domains were discretized, and unstructured meshing was performed using ANSYS Meshing. The resulting mesh is displayed in Figure 4.

2.3. Governing Equations

The fluid motion is governed by the conservation of mass and momentum, which are mathematically expressed in Equations (2) and (3).

$${\displaystyle \frac{\partial \mathsf{\rho }}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left(\mathsf{\rho }{\mathrm{u}}_{\mathrm{i}}\right)}{\partial {\mathrm{x}}_{\mathrm{i}}}}=0$$

(2)

$${\displaystyle \frac{\partial \mathsf{\rho }\overline{{\mathrm{u}}_{\mathrm{i}}}}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left(\mathsf{\rho }\overline{{\mathrm{u}}_{\mathrm{i}}}\overline{{\mathrm{u}}_{\mathrm{j}}}\right)=-{\displaystyle \frac{\partial \stackrel{\mathrm{-}}{\mathrm{p}}}{\partial {\mathrm{x}}_{\mathrm{i}}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left(\mathsf{\mu }{\displaystyle \frac{\partial \overline{{\mathrm{u}}_{\mathrm{i}}}}{\partial {\mathrm{x}}_{\mathrm{j}}}}-\mathsf{\rho }\overline{{\mathrm{u}}_{\mathrm{i}}^{\mathrm{\prime }}{\mathrm{u}}_{\mathrm{j}}^{\mathrm{\prime }}}\right)+{\mathrm{f}}_{\mathrm{i}}$$

(3)

where x_i and x_j represent the Cartesian components, expressed in meters; ū_i and ū_j stand for the Reynolds-averaged velocity components in the same directions, in m s⁻¹; t is the elapsed time, in seconds; ρ signifies the fluid density, in kg m⁻³; $\overline{p}$ represents the mean static pressure, in pascals; μ represents the dynamic viscosity, in Pa s; and f_i accounts for the body-force component, in newtons.

2.4. Turbulence and Cavitation Model

This study adopts the SST k-ω model to close the RANS equations. This turbulence model is renowned for its superior fidelity in resolving boundary layer detachment induced by strong adverse pressure gradients. Its reliability in incompressible flow regimes has been well-documented across extensive literature. This study adopts the Schnerr-Sauer cavitation model to close the mass transfer equation. In the Schnerr-Sauer cavitation model, the bubble number density n₀ is a critical parameter governing cavitation inception. Considering the water quality in the experiment, n₀ is set to 1 $\times$ 10¹¹ in this study to better accurately reproduce the experimental cavitation patterns.

2.5. Boundary Conditions

The computational methodology employed in this study is similar to that used in a previous investigation of integrated pump-gates [15]. However, unlike the previous investigation that concentrated on pressure fluctuations and radial forces, this paper presents a dedicated analysis of the cavitation performance. Numerical simulations of the integrated pump-gate model were conducted using ANSYS CFX 2024 R1. The working fluid was clear water at 25 °C. Simulations were performed under varying flow rates at rotational speeds of 485 r/min. A total pressure inlet and a mass flow outlet were selected. All solid surfaces were treated as no-slip walls.

For the steady-state calculation, the interface between the rotating and stationary domains was modeled using the Frozen Rotor approach. The converged steady-state result was then used to initialize the transient simulation. In the unsteady simulation, the Transient Rotor-Stator model was applied to the interfaces to capture the rotor-stator interaction. The time step was set to 3.44 $\times$ 10⁻⁴ s. The convergence criterion was set to 10⁻⁴.

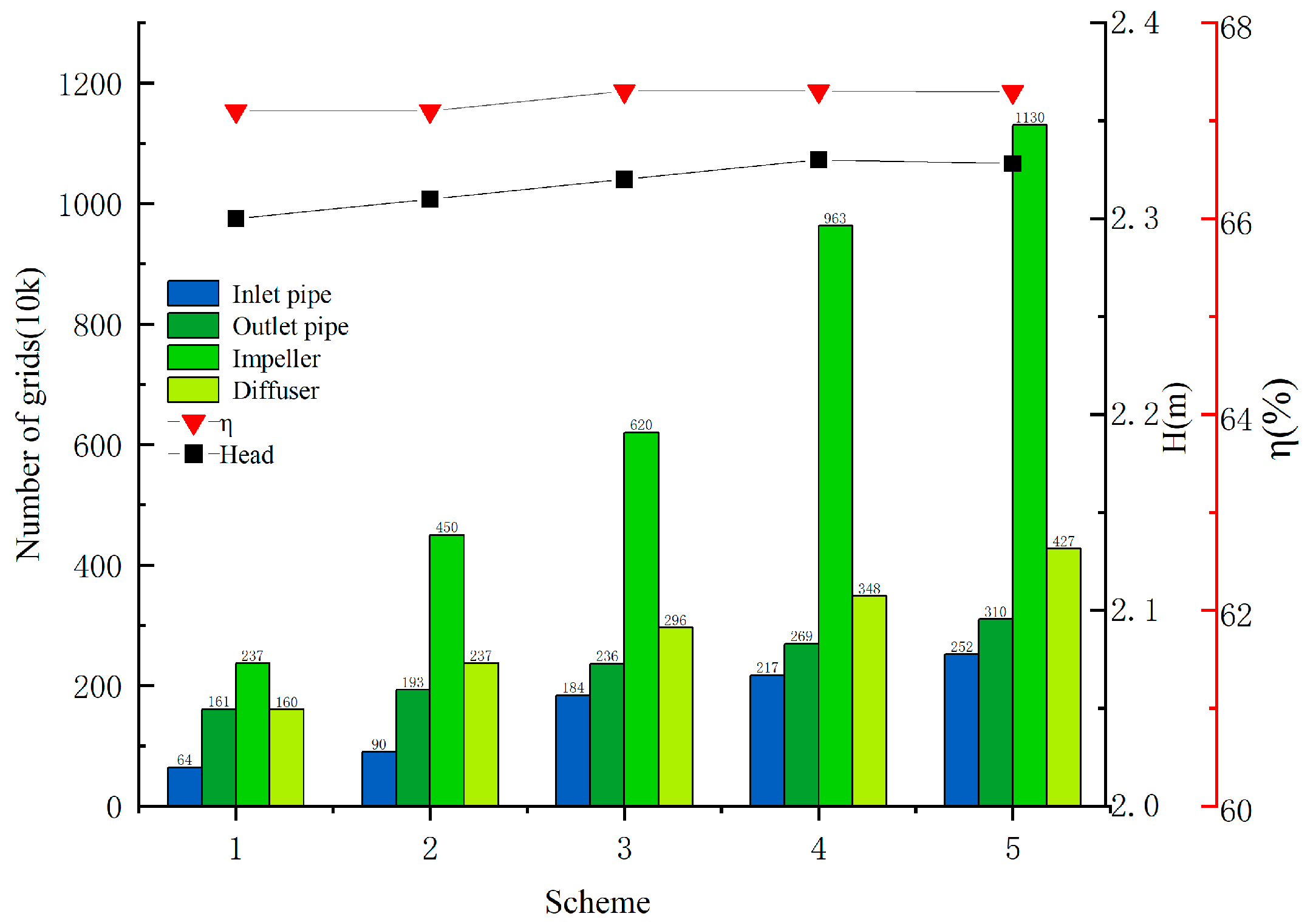
2.6. Grid-Independence

Considering the small-scale backflow at positions such as the blade top clearance of the impeller, in order to improve the simulation stability of numerical simulation in cross-scale flow as much as possible, this study adopts ANSYS mesh for meshing and conducts a large amount of local encryption at the blade top clearance position. Five sets of grid schemes were adopted for performance simulation, and the external characteristics of the pump were obtained as shown in Figure 5. Considering the need to analyze the internal flow field in the subsequent cavitation simulation, under the condition of stable external characteristics, the scheme with as many grids as possible was selected to clearly display the internal flow details of the water body at the impeller and guide vane positions. After comprehensive consideration, scheme 4 was selected as the optimal mesh for the subsequent simulations.

3. Cavitation Characteristics and Coherent Vortical Structures

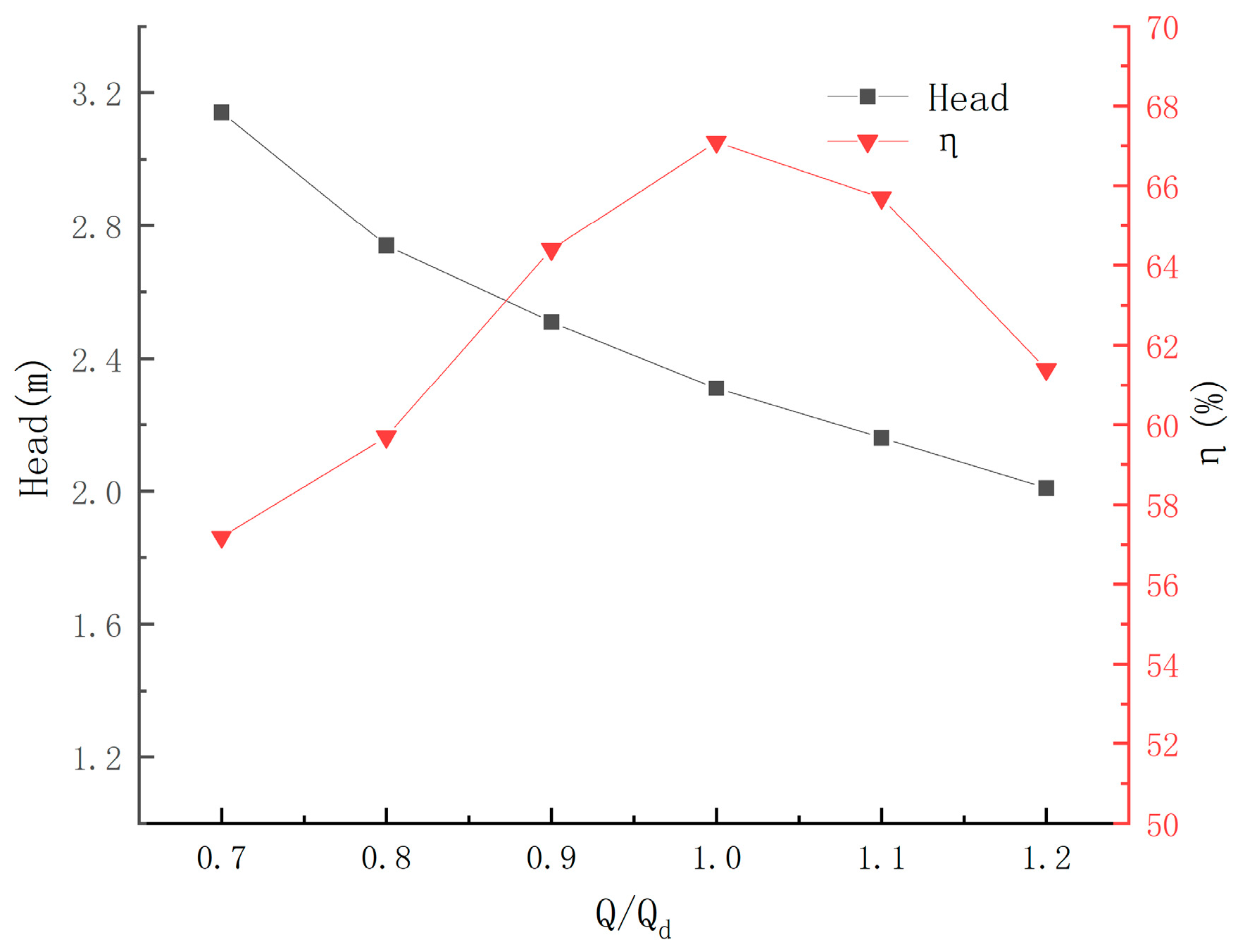
3.1. Hydraulic Performance Test Results

The performance of the integrated pump gate under multiple working conditions was calculated based on the white outlet flow rate, as shown in Figure 6. At the rated flow rate, the pump head reached 2.31 m, which was close to the optimal efficiency point.

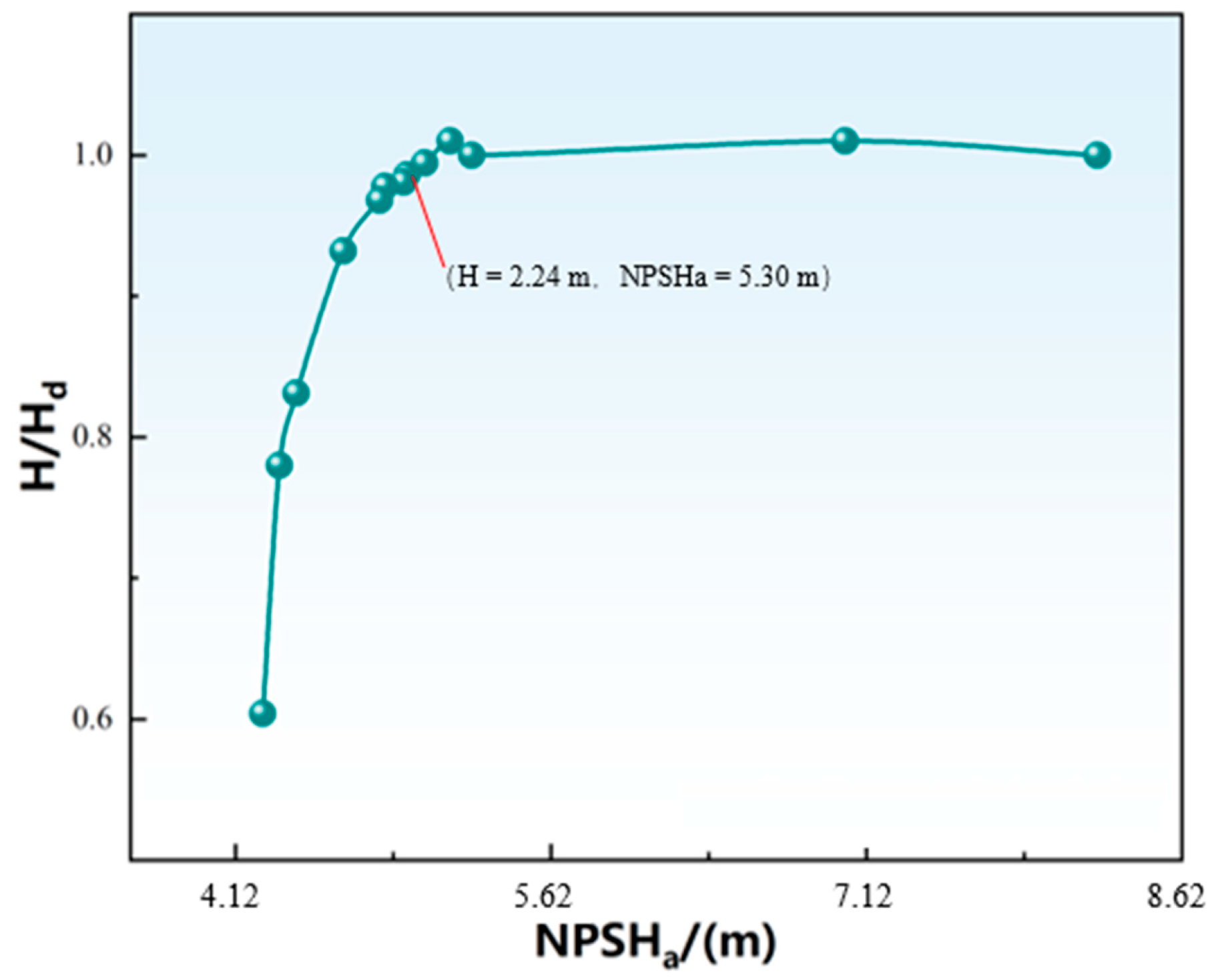
3.2. Cavitation Performance Curve and Inception Characteristics

Cavitation simulation of the pump was performed by reducing the inlet pressure. According to the 3% head drop criterion, the critical NPSH (NPSH_c) is defined as the NPSH at which the pump head drops by 3%. The NPSH_a at different operating points is shown in Figure 7. When NPSH_a = 5.30 m, the pump head decreased from 2.32 m to 2.25 m, and the critical net positive suction head (NPSH_c) was finally determined to be 5.30 m, indicating that the pump had good cavitation performance during operation.

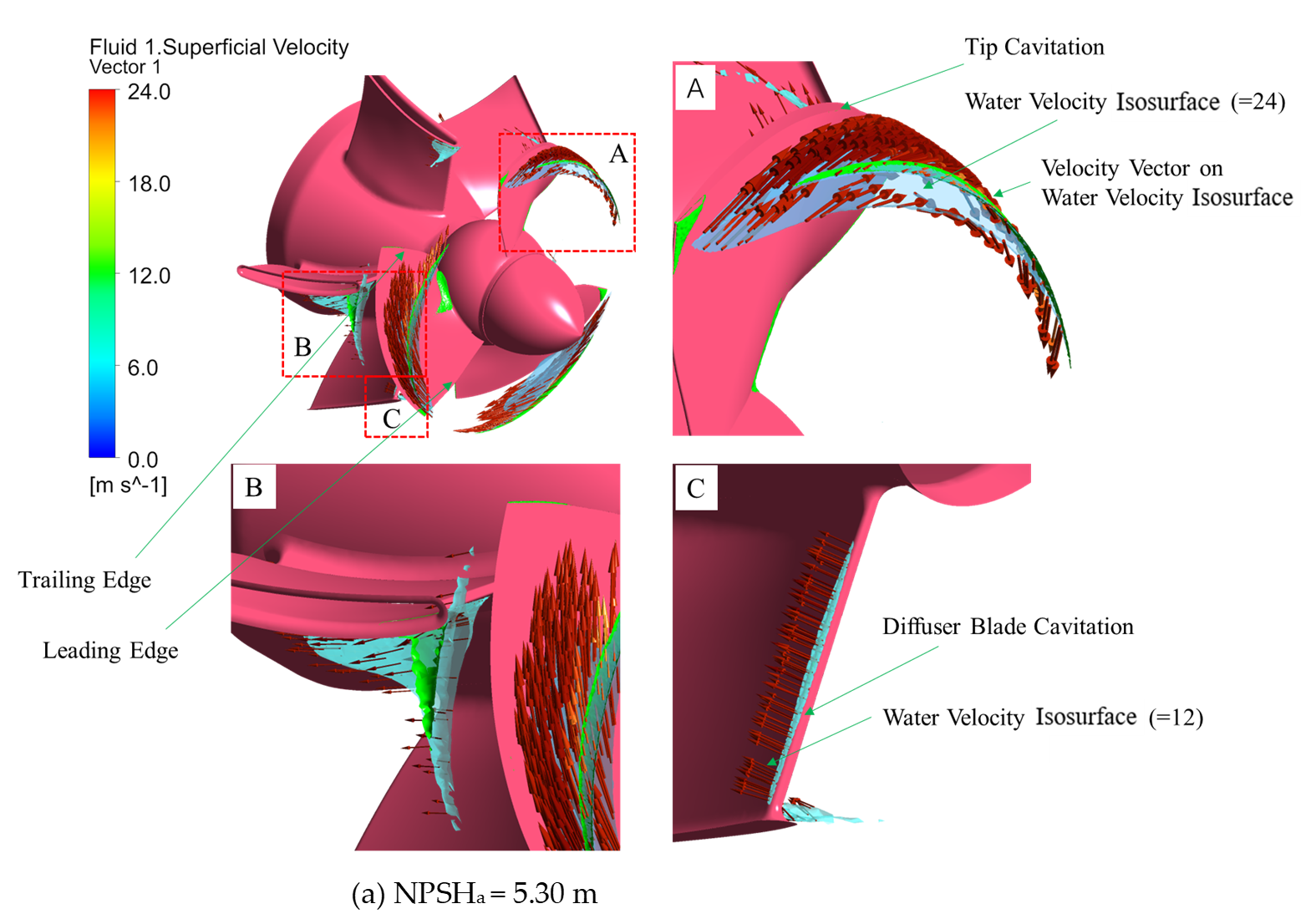
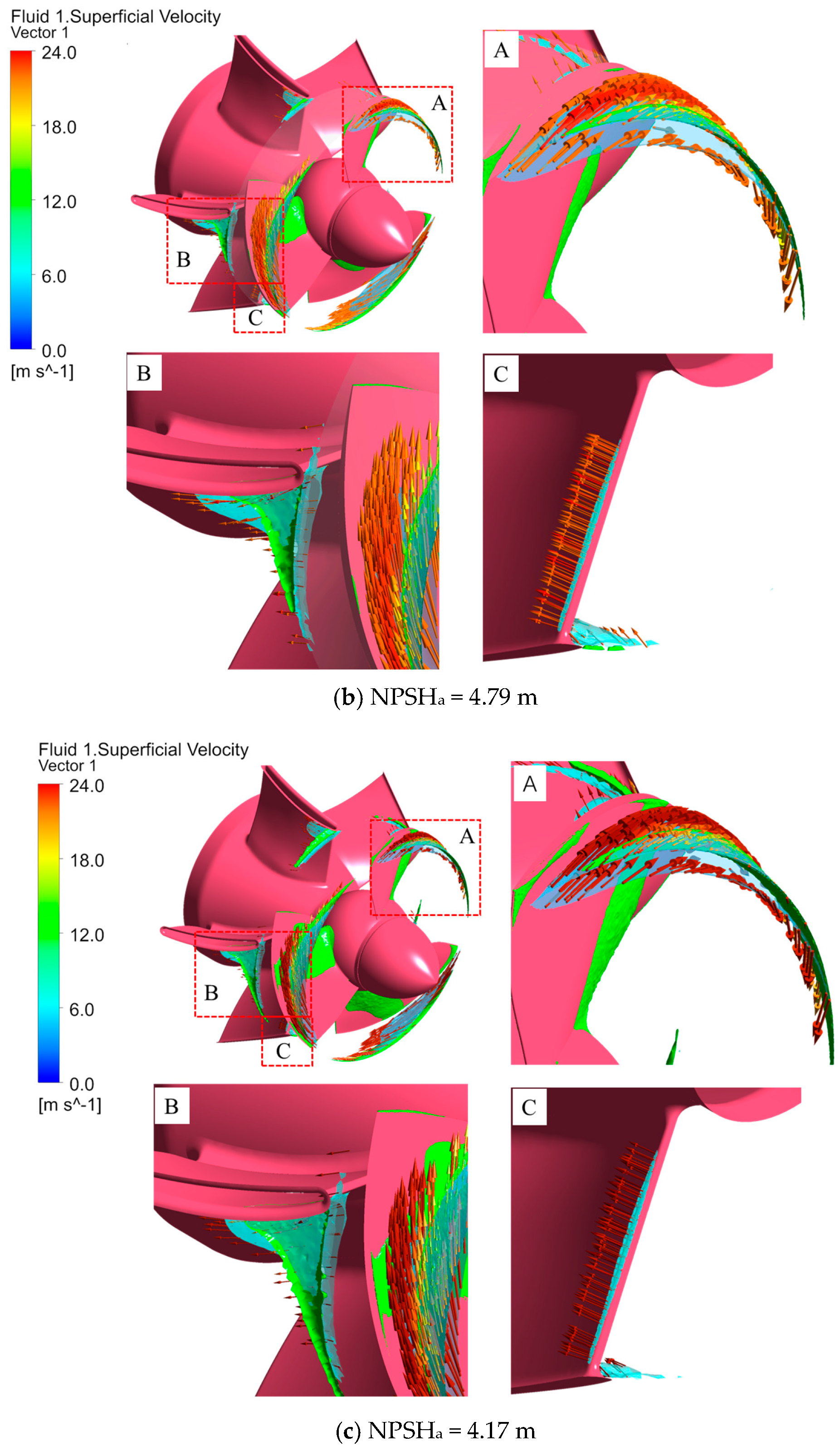
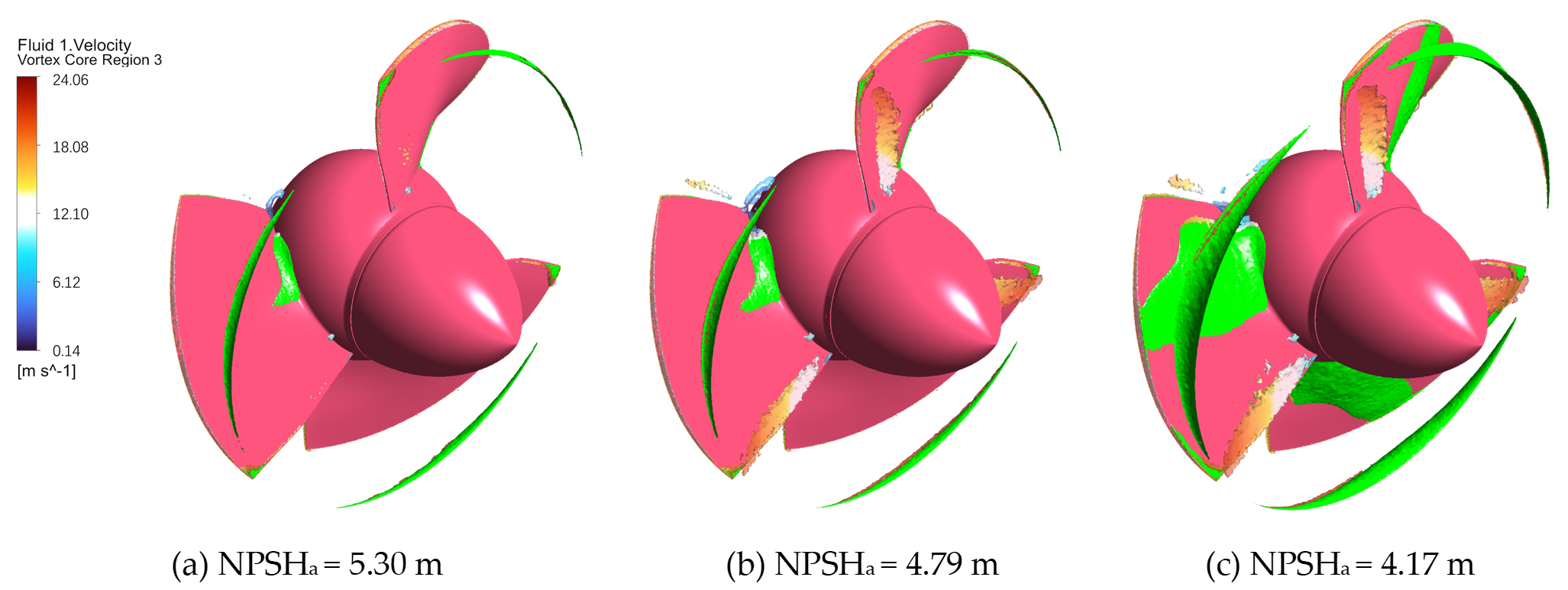
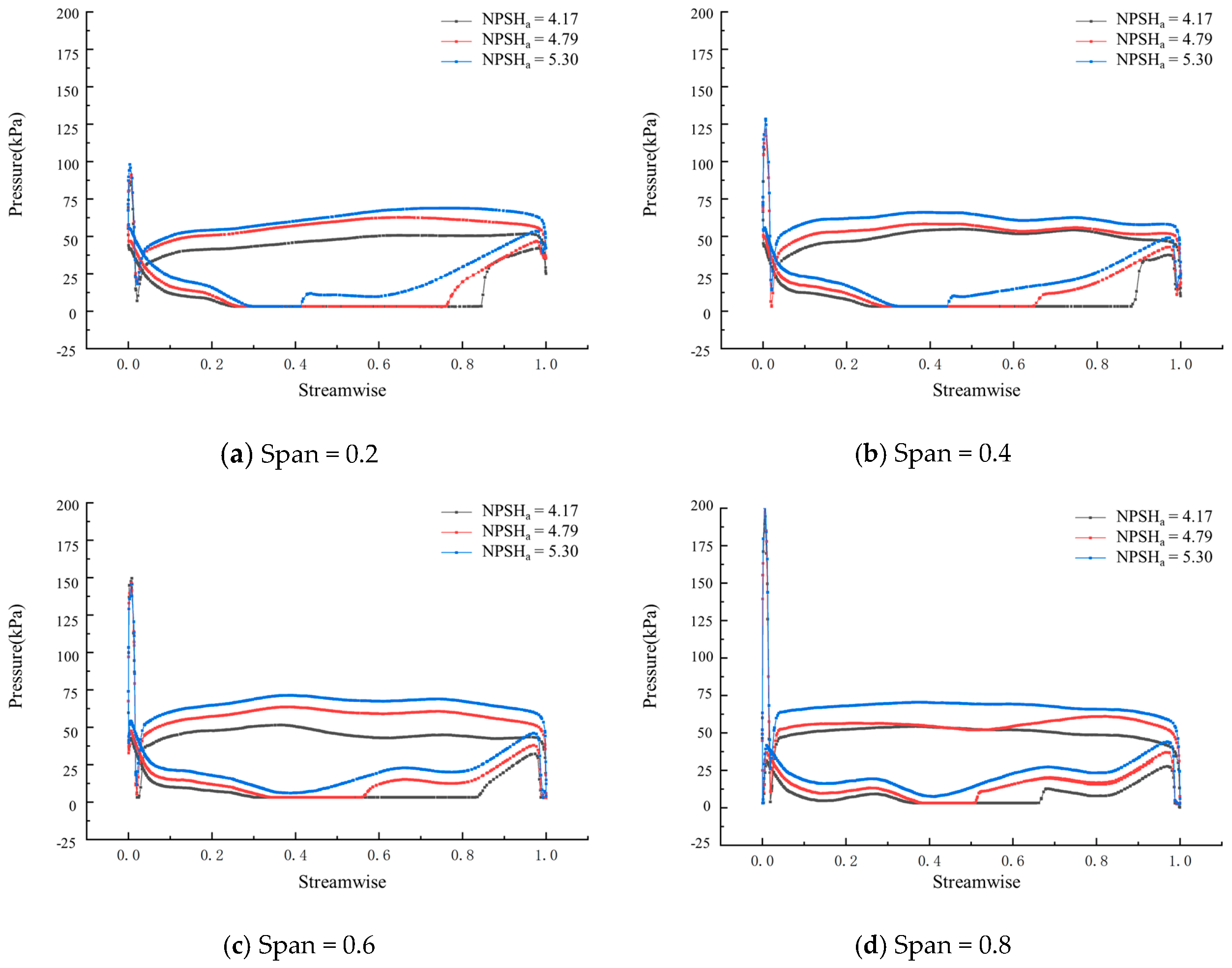
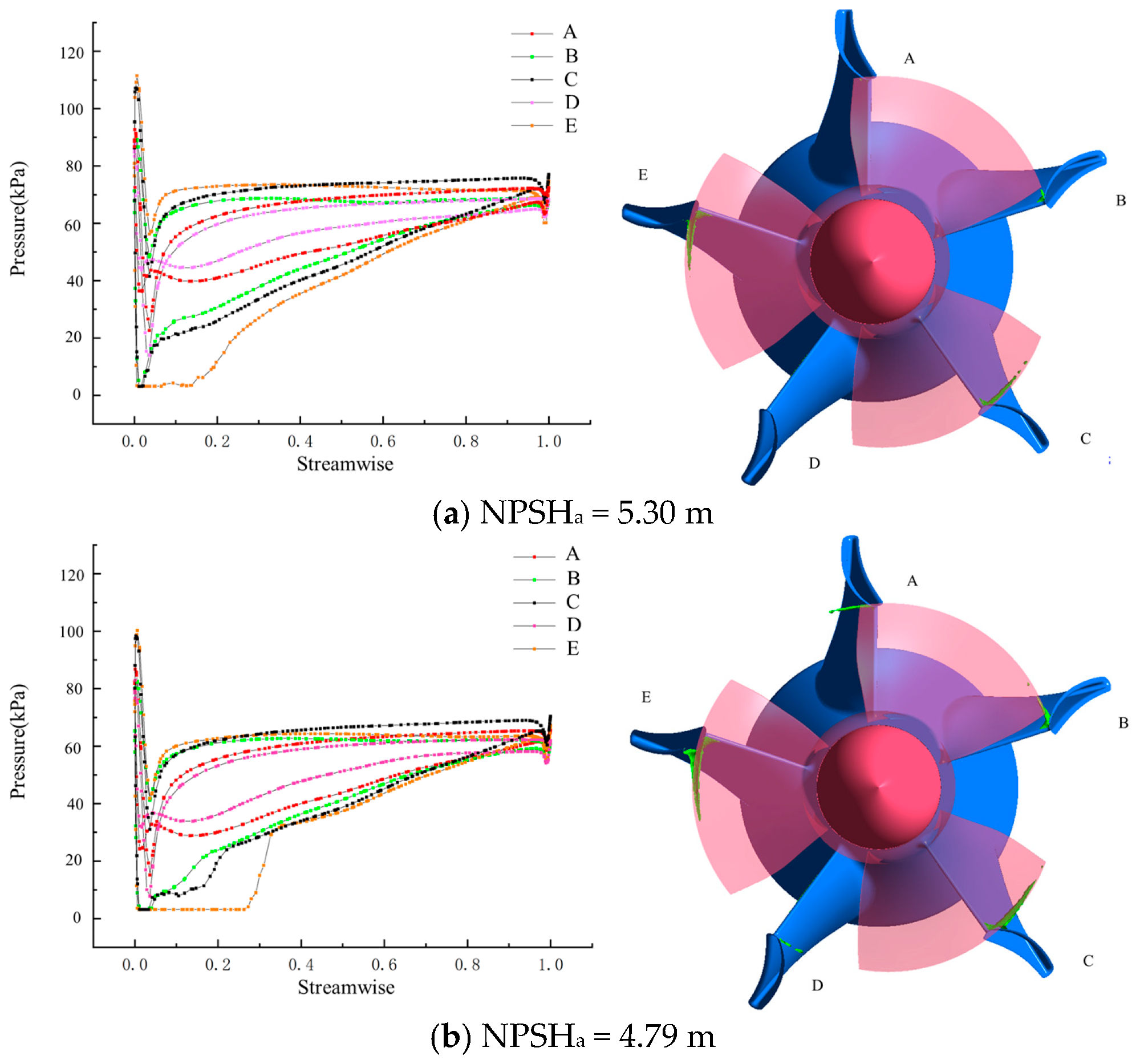
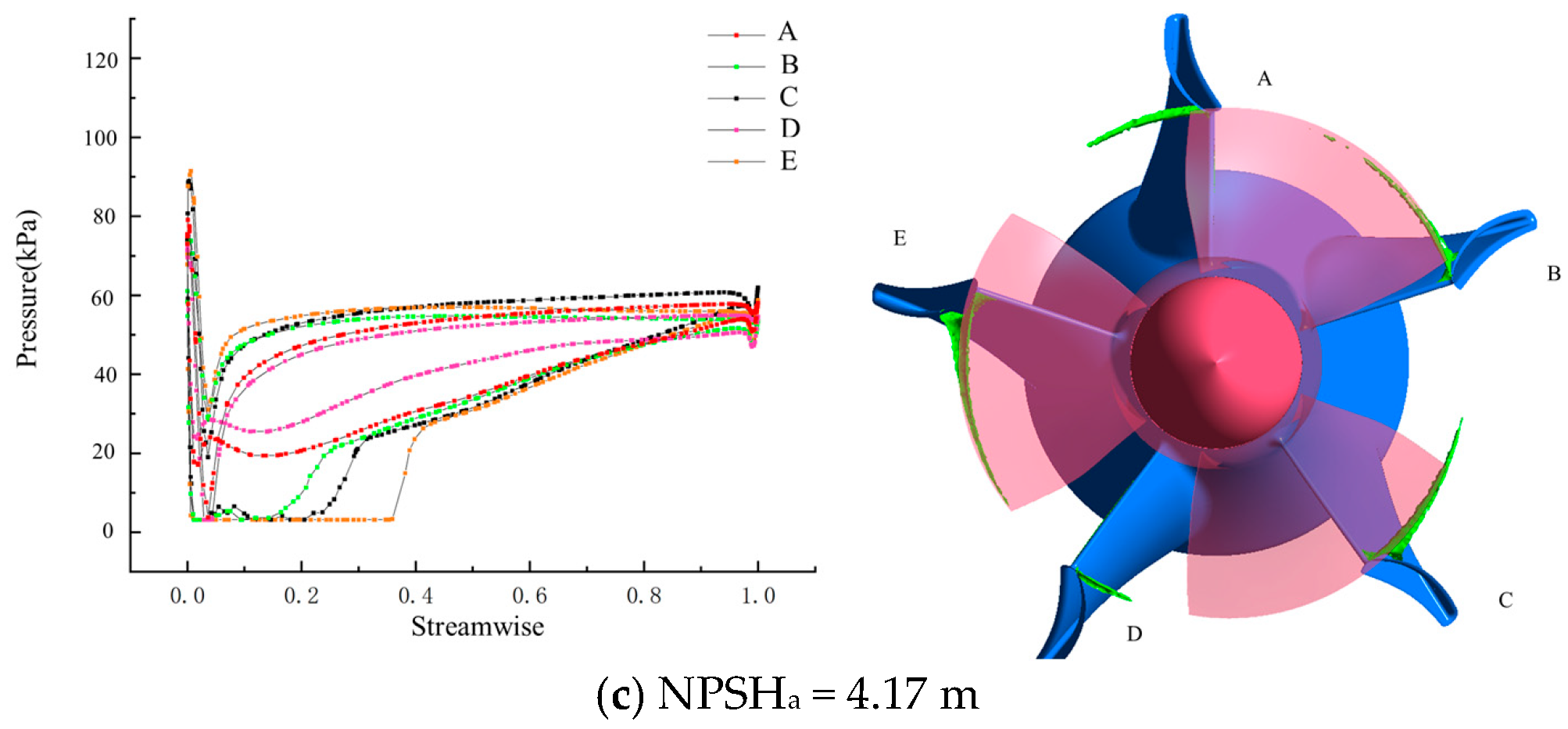
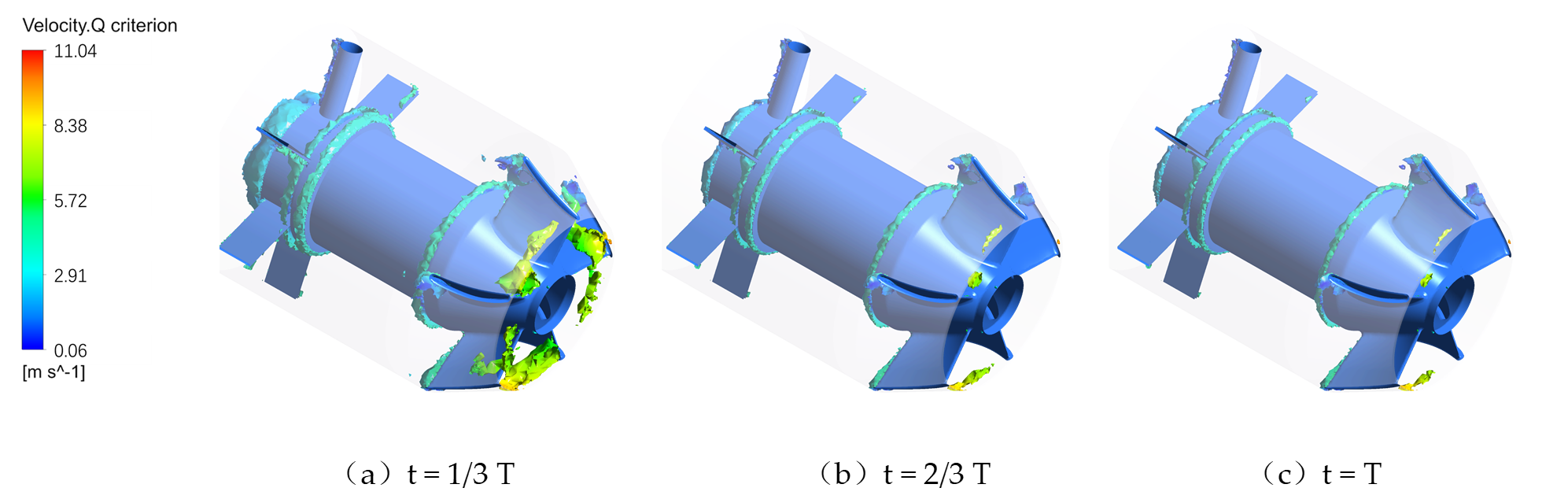
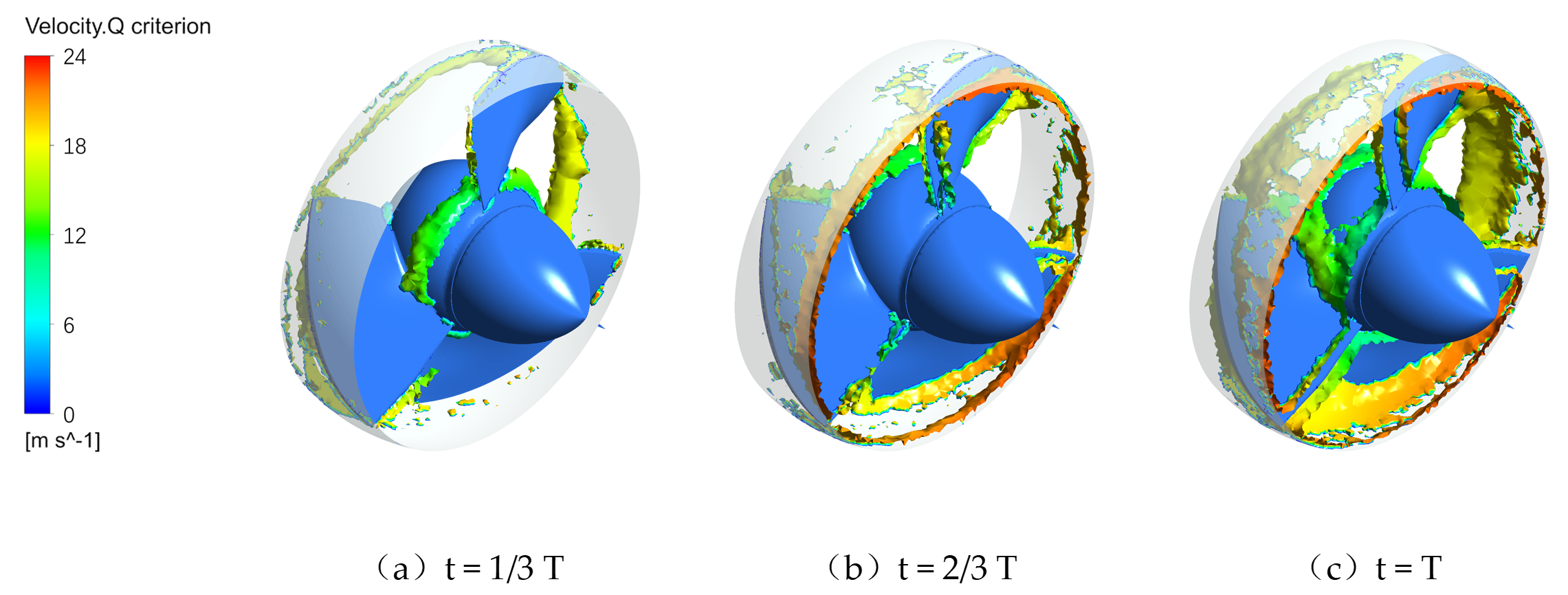
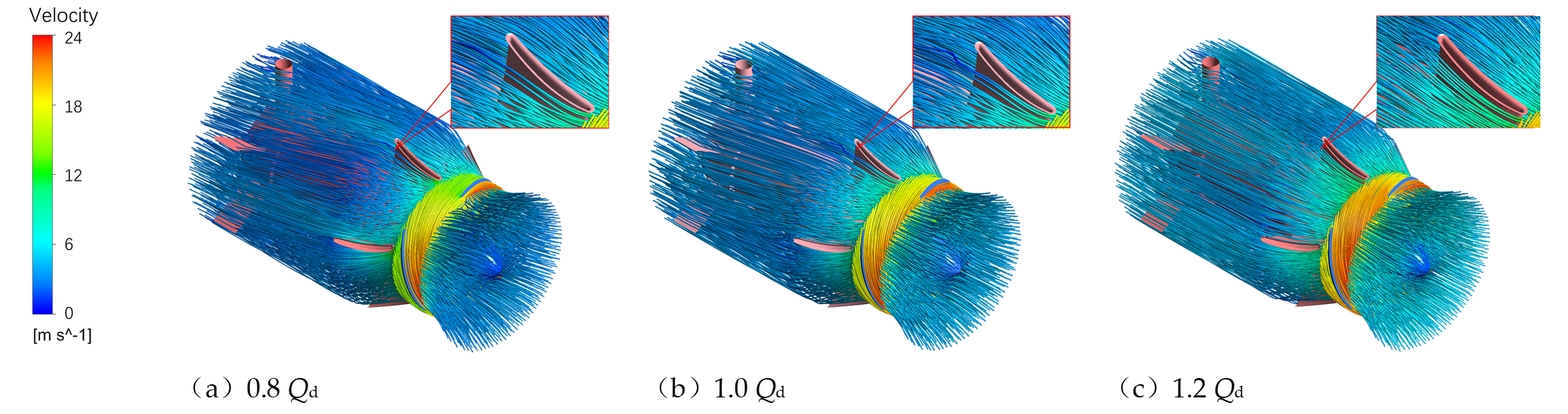
3.3. Cavitation Distribution and Its Coupling with Local Flow Topology

To further examine the pump’s flow behavior under cavitation and analyze the cavitation spatial features at different inlet pressures, the vapor volume isosurfaces and velocity characteristics of the impeller and guide vanes flow channel space were analyzed and compared when NPSHa = 5.30, 4.79, 4.17, as shown in Figure 8. The green part is the isosurface with a vapor volume fraction of 0.2, and the blue transparent areas of the impeller and guide vanes are the isosurfaces with liquid water velocities of 24 and 12 m/s, respectively. Mark the flow direction characteristics on the velocity isosurface using vectors.

At the leading edge of the impeller blade, the isosurface with a velocity of 24 m/s completely encloses the area where the volume fraction of cavitation is greater than 20%. This indicates that due to the occurrence of cavitation, the velocity field of the fluid in this area is significantly affected. Its velocity characteristics have good similarity in the circumferential direction and remain along the rotation direction until the tip of the blade begins to dissipate. Its starting section is located a certain distance ahead of the tip of the adjacent impeller blade along the circumferential direction. At the junction of the radial diffusion position of the guide vane flow channel and the leading edge of the guide vane, the cavitation region and the velocity isosurface have similar characteristics. In zone C, the cavitation isosurfaces on the guide vane leading edge form bands and are encompassed by the velocity isosurfaces. The isosurfaces extend radially from the leading edge of the vanes near the hub to the rim position.

Based on the isosurface distribution characteristic of a vapor volume fraction of 0.2, the cavitation morphology in this integrated pump gate presents a significant “geometrically induced” characteristic rather than a single blade airfoil cavitation. In the impeller inlet leading edge and blade-tip periphery (zone A), no typical narrow and long leakage vortex cavitation band driven only by the blade tip gap leakage was observed. Instead, a large range of cavitation bubble groups adhering to the flow channel wall and extending towards the suction surface of the blade were observed. The physical root cause of this phenomenon lies in the specific geometric features of the impeller inlet region marked in Figure 3, characterized by a 14.5° diffusion-shaped flow passage and a 2 mm backward-facing step. When the high-speed inflow passes through this protrusion, the wall boundary layer undergoes forced separation, forming a low-pressure recirculation zone behind the protruding step. Since the local pressure in this zone falls below the saturated vapor pressure, cavitation occurs in the fluid before it enters the impeller to do work. The generated cavitation bubbles are sucked to the blade’s leading edge and periphery, forming the dispersed cavitation distribution observed.

When NPSH_a = 4.17 m, compared with NPSH_a = 5.30 m, the cavitation area at the leading edge of the guide vanes remains largely unchanged in both shape and position. The position of the cavitation area at the leading edge of the impeller remains largely unchanged, but there is a tendency for the cavitation area to expand outward. Cavitation that occurs at the middle position of the impeller exhibits a clear development trend along both the tail edge and the tip of the blade. The isosurface with a vapor volume fraction of 0.2 has already shown inconsistency in the shape of the isosurface with the same velocity. For instance, in the cavitation zone B, the velocity isosurface at the front end of the guide vanes remains basically stable under different total inlet pressures. However, the cavitation zone expands significantly as the pressure decreases. When NPSHa = 4.17 m, the cavitation vapor isosurface is basically coincident with the velocity isosurface, but this phenomenon is not obvious at NPSHa = 5.30 m.

By comparing the cavitation at the top of the impeller blades under three different pressures, it can be found that when NPSHa = 5.30 m, no obvious cavitation develops at the blade tip clearance position. However, when NPSHa = 4.79 m, cavitation begins to appear at the blade tip clearance position, and as the inlet pressure decreases, the cavitation at the blade tip clearance gradually approaches the cavitation area at the impeller hub position. When NPSHa = 4.17 m, the two cavitation zones have become interconnected. Notably, during this process, the cavitation area of the blade tip clearance does not show a significant trend of expanding along the clearance direction, whereas cavitation at the junction of the blade leading edge and tip clearance exhibits a pronounced extension along the blade tip clearance.

As shown in Figure 9, it is the isosurface of an integrated pump gate with a vapor volume fraction of 0.2 (the green part in the figure). The isosurfaces other than the green ones are the isosurfaces of the vortex structure based on the Q criterion. When NPSH_a = 5.30 m, it can be seen that the vortex clusters are mainly concentrated in the blade top clearance, the blade front end, and the blade tail edge, especially near the hub. As the total inlet pressure increases, the vortex intensity at the leading edge and tail edge of the blade gradually increases, but no obvious cavitation area still appears. As the total inlet pressure continues to decrease, the cavitation area shows a clear trend of expanding outward. Specifically, the cavitation area at the blade tip mainly extends backward along the blade tip gap, and the cavitation area at the position where the water flow channel at the leading edge of the impeller diffuses steadily expands outward. The gap between the blade and the hub, on the one hand, extends towards the blade tail edge, and on the other hand, expands towards the shroud. During this process, the vortex structure of the impeller remains basically stable.

To analyze the flow characteristics along the radial direction, the dimensionless blade height, referred to as Span, is introduced. It is defined as:

$$Span={\displaystyle \frac{r-r_h}{r_h-r_s}}$$

(4)

where r is the radial coordinate, r_h is the hub radius, and r_s is the shroud radius. Consequently, Span = 0 represents the hub surface, and Span = 1 represents the shroud surface. Similarly, the dimensionless streamwise position, referred to as Streamwise, is defined to characterize the flow from the blade inlet to the outlet:

$$Streamwise={\displaystyle \frac{l}{c}}$$

(5)

where l is the distance from the blade leading edge along the chord line, and c is the chord length. Thus, Streamwise = 0 corresponds to the leading edge (LE), and Streamwise = 1 corresponds to the trailing edge (TE).

Figure 10 shows the pressure distribution of the impeller blades with four different extension distances of Span ratios of 0.2, 0.4, 0.6, and 0.8. The horizontal axis represents the chordwise position along the blade surface (0: leading edge, 1: trailing edge). The vertical axis represents the pressure indicated by the blade. When NPSH_a = 5.30 m, cavitation is negligible on the side close to the rim, and the cavitation area is concentrated on the side close to the hub. When NPSH_a is lower than 4.79, a distinct cavitation area also appears on the side close to the rim. Furthermore, by observing the blade pressure load in a certain spread direction under the rated net positive suction head (NPSH_a), Cavitation is mainly observed at the mid-span of the blade, as well as in a very small range near the leading and trailing edges of the blade. With the decrease in NPSH_a, cavitation begins to appear at the leading and trailing edges of the blade, but there is no obvious trend of expansion along the flow direction. The cavitation area in the middle of the blade continuously expands towards both ends as NPSH_a keeps decreasing. In the range of Streamwise = 0.8 to 0.95, the surface pressure of the suction surface of the blade always remains at a relatively large value, and there is no significant difference in the surface pressure of the pressure surface at this position compared with other regions, which proves that the working capacity of the blade at this position is poor.

In the above analysis, the cavitation of the impeller guide vanes was discussed as a whole. Due to the trumpet-shaped guide vanes in the guide vane basin, local cavitation occurred. In this study, a steady-state numerical simulation was conducted using a frozen rotor model. Due to the inconsistent number of blades of the impeller and guide vanes, the relative positional relationship between the two blades shows diversity. This phenomenon also reflects from the side the possibility that cavitation occurs during actual operation and strong pressure pulsation is generated at a certain moment due to the change in the relative position of the impeller guide vanes. The pressure distribution characteristics of the five guide vanes when Span = 0.9 were extracted, respectively, as shown on the left side of Figure 11, and on the right side are the isosurfaces of the guide vanes with a vapor volume fraction of 20 and the blade codes.

From the pressure diagram, it can be seen that the pressure on the back of blade D shows a significant difference compared with other blades. This might be due to the obvious misalignment of this guide vane blade with the impeller blade, while the circumferential positions of the other four blades have a higher degree of overlap with the impeller blade, showing a strong consistency on the pressure diagram. By comparing the pressure distribution of the blades under different NPSH_a, it can be observed that the difficulty of cavitation in blade D and blade A is relatively high, while the regions of the other three blades below the saturated vapor pressure show strong volatility under different NPSH_a.

3.4. Unsteady Flow Characteristics of Integrated Pump Gates

The internal vortex structures of the integrated pump gate at different times were extracted to analyze their spatio-temporal distribution characteristics. The three-dimensional vortex structures of the guide vane and impeller basins were analyzed, respectively, as shown in Figure 12 and Figure 13. Figure 12 and Figure 13 present the pressure distribution at three typical instants within one rotation cycle, corresponding to 1/3 T, 2/3 T, and T, where T = 0.124 s is the period of impeller rotation. It can be seen from the figure that the dominant unsteady characteristics of the flow field are instead controlled by the dynamic and static interference (RSI) effect. Meanwhile, the vortex structure at the sudden change in the radial radius of the flow channel exhibits significant periodic pulsation characteristics. In addition, there are obvious vortices at the front end of the guide vanes. There may be a strong correlation with the dynamic and static interference between the impeller and the guide vanes. When the Wake Core of the blade sweeps to the front end of the guide vanes, the high vorticity fluid carried by the wake is rectified by the rear guide vanes and the vortex energy is strengthened. The radial continuity of the vortex structure is disrupted.

As shown in Figure 13, the vortex structure in the impeller inlet region does not form a typical isolated tip leakage vortex rotating with the blades. Instead, it appears as an almost closed circumferential shear vortex ring attached to the outer wall of the flow channel. This distinct flow topology reflects the hydrodynamic effect of the sudden increase in the radial radius of the inlet section, including the 2 mm protrusion and the guide vane-shaped channel. As fluid passes through this region, the boundary layer separates, forming a high-vorticity free shear layer. Before entering the rotating impeller, this shear layer evolves into a macroscopic vortex band along the outer edge of the blade tips. High turbulent kinetic energy regions (yellow/orange isosurfaces in the figure) are mainly concentrated in this peripheral ring, indicating that the geometrically induced vortex is significantly stronger than the airfoil vortices near the blades and may be an important source of flow blockage and hydraulic loss at the impeller inlet.

By comparing the vortex structures at three different time instances, it can be seen that, although the blades are in geometrically symmetric positions, the shape and intensity distribution of the peripheral vortex ring exhibit noticeable unsteady pulsations. This is caused by the high-speed rotating blades periodically cutting through the stationary inlet shear layer. Each time a blade passes through the shear layer, the velocity potentials in the rotating and stationary reference frames superimpose, amplifying the Kelvin-Helmholtz instability within the shear layer. The vortex clusters undergo local fragmentation, stretching, and reorganization. As illustrated at the middle time snapshot, the vortex structures become more fragmented and turbulent kinetic energy increases. This forced pulsation from blade rotation not only alters the local steam intake angle at the blade tip but also subjects the tip region to very high-frequency impact loads, which underlie the previously mentioned “non-blade cavitation” phenomenon that fluctuates sharply over time.

In addition to the annular vortices near the shroud at the impeller inlet, concentrated vortex structures are also observed near the hub and at the blade roots, as shown in Figure 14. In particular, the hub vortex clusters, while showing some changes in region and shape over time, maintain a relatively stable intensity and do not dissipate periodically like the vortices at the blade leading edge. Although the temporal periodicity of the impeller vortex structures does not fully match the blade rotation frequency, the overall vortex distribution exhibits good spatial symmetry.

A comparison of the three-dimensional streamline distributions at 0.8 Q_d and 1.2 Q_d shows that the flow rate has a notable effect on the flow quality in the guide vane outlet region. At the partial load condition of 0.8 Q_d, a low-velocity stagnation zone appears near the trailing edge of the guide vanes, accompanied by irregular streamlines, suggesting local momentum loss due to flow separation. By contrast, at the overload condition of 1.2 Q_d, the streamlines are smooth and uniform, with no large-scale separation structures, indicating improved flow compliance. The guide vanes also contribute to reducing the residual swirl (vorticity) of the fluid leaving the impeller, helping the flow transition into a stable axial pattern and providing favorable conditions for the downstream passage.

In the outlet passage, the interaction between the fluid and the support structures demonstrates good hydraulic compatibility. At 1.2 Q_d, the sheet-like support blades with streamlined profiles align closely with the main flow direction, allowing the streamlines to bypass smoothly without causing noticeable blockage or wake formation. In contrast, at 0.8 Q_d, the incoming flow is observed to continuously impinge on the surface of the support blades. For the asymmetrical cylindrical cable conduit, minor local separation occurs on the leeward side, but this disturbance dissipates quickly. This rapid reattachment is assisted by the guide vanes’ rectification effect and the strong mainstream transport at 1.2 Q_d, enabling the flow to resume axial motion after bypassing the cylinder. These observations suggest that the local separation caused by the cylinder is spatially limited and has minimal influence on the overall downstream flow uniformity.

4. Conclusions and Discussion

This study investigates the cavitation and internal flow characteristics of integrated pump-gate axial flow pumps under complex operating conditions. Based on the SST k − ω turbulence model, numerical simulations and flow field analyses were conducted, focusing on the influence of the impeller, guide vane diffusion channels, and pump body support components on cavitation morphology, vortex structures, and hydraulic stability. The aim is to identify the critical regions and dominant mechanisms responsible for flow instability, providing a basis for subsequent structural optimization and engineering applications.

Regarding cavitation performance, the pump’s critical operating condition was determined using a “3% head drop” criterion, yielding an NPSH_c of 5.30 m. The results indicate that the pump exhibits good anti-cavitation capability within the investigated range of speed and flow rates. As the inlet pressure decreases, the cavitation area generally expands. However, the initial positions and primary distribution of cavitation remain spatially stable, suggesting that the cavitation-sensitive regions are closely linked to the geometric configuration.

In terms of cavitation mechanisms, cavitation at the impeller inlet shows a clear “geometrically induced” characteristic: The flow channel expansion and step structure at the impeller shroud induce the formation of a local low-pressure zone, followed by a low-pressure recirculation region. This triggers cavitation prior to the fluid entering the impeller. The cavitation at this location exhibits a band-like geometric characteristic and shows no obvious tendency to merge with the cavitation regions on the blade surfaces. Cavitation at the leading edge of the guide vanes mainly occurs in axially diffusion-sensitive areas of the flow channel, appearing as a band-like attachment along the circumferential direction, reflecting the combined effects of diffusion-induced low pressure and incoming flow conditions. Analysis of the guide vanes’ cavitation performance indicates that the flow domain and vane angle have a significant influence on cavitation, and the cavitation behavior may also be affected by the relative positions of the impeller blades and guide vane blades, as their spatial relationship alters local flow characteristics and thus affects cavitation development.

Regarding vortex structures and unsteadiness, the vortex in the impeller inlet region does not take the form of a typical isolated tip leakage vortex but rather resembles a circumferential shear vortex ring attached to the outer wall. Under the influence of rotational and static interference, it exhibits clear periodic pulsation and reorganization. Periodic vortex intensification tends to occur near geometric discontinuities in the diffusion section and at the leading edge of the guide vanes, indicating that unsteady flow characteristics within the device are influenced by multiple factors.

In summary, cavitation and hydraulic instability in integrated pump gates exhibit pronounced “geometric sensitivity.” Key risk areas include the diffusion region upstream of the impeller shroud, the low-pressure regions near the impeller leading edge and blade tips, and the diffusion-sensitive sections of the guide vanes. Subsequent collaborative optimization can be applied to the inlet transition, the local profile and clearance of the blade leading edge, the guide vane inlet matching, and the arrangement of support components, aiming to further improve flow uniformity and operational stability.