Characterizing the Internal Flow Behavior of Spray Pulsating Operation in Internal-Mixing Y-Jet Atomizers

Abstract

The production of a stable and uniform spray is a primary concern in fuel atomization applications, such as in fluid catalytic cracking reactors, directly affecting the process quality and gas emissions. However, depending on nozzle geometry and operating conditions, undesired pulsed spray behavior may occur. This phenomenon originates from the internal multiphase flow interaction in Y-jet nozzles and leads to unstable sprays. Understanding the formation of spray pulsations is challenging due to limited internal flow visualization in the nozzle and the fast dynamics involved. Accordingly, this work elucidates the mechanisms of the pulsed spray formation through 3D transient numerical multiphase simulations inside a mixing chamber. The model is validated against internal pressure measurements and applied to investigate the internal mixing behavior across several operating conditions. Results show that the liquid-to-gas momentum flux ratio governs the internal flow regimes. A higher liquid momentum flux obstructs the gas flow, leading to periodic spray bursts when the gas overcomes the liquid back pressure. The simulations also reveal self-sustained oscillatory flow patterns and cyclic transitions between gas penetration and liquid accumulation, which produce periodic pressure fluctuations and nozzle discharge pulsations. The findings offer valuable guidance for optimizing nozzle operation and geometry to suppress pulsation and improve atomization performance.

1. Introduction

Heavy oil processing is directly associated with energy generation systems, such as in power plants, combustion processes, and fluid catalytic cracking (FCC) units [1]. In such applications, the oil is dispersed in the form of a spray to increase the specific liquid surface area and thus enhance heat and mass transfer phenomena. For instance, in FCC units, crude oil is dispersed inside the reactor and subsequently converted through catalytic cracking into valuable petrochemical products such as jet fuel, diesel, gasoline, and hydrocarbons [2]. Consequently, understanding and improving oil atomization carries significant environmental and economic importance in fuel production.

The category of heavy oils encompasses a wide range of high-viscosity fuels, including residual oils and naphtha, which are challenging to atomize effectively and require specially designed nozzles for these industrial processes. In this context, specific strategies have been employed to facilitate the dispersion of such viscous liquids, such as oil pre-heating [3] and using a dispersing medium, typically compressed air or superheated steam, to assist in atomization [4].

The use of auxiliary gas in twin-fluid atomizers offers advantages in the nozzle operation compared with single-fluid atomizers, such as lower operating pressures for efficient atomization of viscous liquids [5]. Further atomization improvement, i.e., droplet size reduction, is achieved by optimizing the nozzle geometry and tailoring the operating conditions [6,7]. These measures contribute to achieving an acceptable gas emission level and proper plant operation [8,9,10].

Typical atomizers used in industrial power plants include the T-jet and Y-jet nozzles. They are classified as internal-mixing nozzles and are particularly well-suited for atomizing viscous liquids at high operating loads because they use a high-speed gas stream and promote an intense gas–liquid mixing within the nozzle chamber. This design is preferred for use in fluid catalytic cracking units in comparison with other twin-fluid atomizers, such as effervescent atomizers, because they feature a simple geometry, offer easy and cheap maintenance, and are less prone to clogging due to coke formation from the contact of heavy oil with steam.

In internal-mixing nozzles, shear-driven atomization is the dominant breakup mechanism in comparison with pressure atomization or impact. The high-velocity gas stream interacts with the surface of the relatively slow-moving liquid, inducing Kelvin–Helmholtz instabilities and forming surface waves that detach from the bulk liquid, producing ligaments and then primary droplets.

A key feature distinguishing these two nozzle designs is the impingement angle between the gas and the liquid injection ports. In T-jet nozzles, the liquid enters perpendicularly (at a 90° angle) to the central gas stream, while in Y-jet nozzles, the inlets of the fluids converge at a smaller angle. As the gas flows into the mixing chamber, it exerts an additional shear force on the liquid stream, pushing it toward the nozzle outlet and promoting liquid disintegration.

The liquid penetration into the mixing chamber and its interaction with the gas stream are governed by the liquid-to-gas momentum ratio ($\mathrm{\Phi }$) defined in Equation (1):

$$\mathrm{\Phi }={\left({\displaystyle \frac{{\dot{M}}_L}{{\dot{M}}_G}}\right)}^2\left({\displaystyle \frac{{\rho }_G}{{\rho }_L}}\right){\left({\displaystyle \frac{D_G}{D_L}}\right)}^2\sin \alpha ={\left({\displaystyle \frac{1}{GLR}}\right)}^2\left({\displaystyle \frac{{\rho }_G}{{\rho }_L}}\right){\left({\displaystyle \frac{D_G}{D_L}}\right)}^2\sin \alpha ,$$

(1)

where $GLR$ is the gas-to-liquid mass flow rate ratio, and ${\rho }_G$ and ${\rho }_L$ are the gas and liquid densities, respectively, calculated at the respective fluid inlet port diameter, represented by $D_G$ and $D_L$ for gas and liquid. $\alpha$ represents the port angle of the Y-jet configuration.

The $\mathrm{\Phi }$ magnitude represents the relative injection force of the liquid compared to that of the gas stream [11,12]. This parameter is decisive for the local liquid distribution in different regions of the spray, as, for instance, measured with a patternator device [13]. This spray characteristic directly impacts the spatial distribution of droplet sizes and velocities [14]. Spray regions with lower liquid mass flux typically present smaller droplet sizes because of the velocity difference between the gas and the liquid, inducing further liquid breakup [12].

The parameter $\mathrm{\Phi }$ was initially formulated for Y-jet nozzles with two inlet ports to the mixing chamber (one central gas port and an angled lateral liquid injection) [15]. When the liquid jets have lower momentum than the gas ($\mathrm{\Phi }<$ 1), the liquid jet is deflected toward the chamber walls, forming an annular flow pattern characterized by a thicker liquid film on the same side as its inlet. In this regime, the gas stream occupies the central region of the mixing chamber, promoting limited interaction with the liquid, which remains mostly attached to the walls [16].

A momentum ratio in the range 1 $<\mathrm{\Phi }<$ 3 implies equivalent gas and liquid forces, indicating that the liquid penetrates further into the mixing chamber center. Consequently, the gas interaction with the liquid is not limited to the free surface of the liquid film attached to the wall (as for $\mathrm{\Phi }<$ 1) but implies more intense mixing and shear stress imposed by the high-speed gas jet, creating a relatively finer spray. However, under certain conditions, this regime can occasionally lead to an oscillatory two-phase flow behavior, because the liquid restricts the region available for the gas jet expansion when it flows from the gas inlet port to the mixing chamber. This gas obstruction causes a pressure buildup and liquid accumulation inside the mixing chamber, which eventually leads to the abrupt ejection of a liquid chunk from the mixing chamber, characterizing the pulsed spray formation [5,17].

This pulsation process repeats periodically during the atomization process, and the frequency is dependent on the nozzle geometry and operating conditions. However, this unstable nozzle operation is detrimental to the atomization process because it produces a broad variation in droplet size and velocity, and it provides uneven liquid distribution in the spray. Such irregularities compromise the subsequent catalytic cracking reaction in FCC units, which may form undesired byproducts, in addition to adversely affecting the temperature distribution inside the reactor.

Further increasing the momentum ratio $\mathrm{\Phi }>$ 3 results in a liquid jet with enough momentum to gradually cross the entire mixing chamber cross-section. In these cases, the blocking effect on the gas becomes more evident because it is deflected to the internal chamber edges and must flow around the liquid column. This regime is characteristic of low $GLR$ and forms a continuous central liquid core.

Some studies have characterized the effect of the pulsed nozzle operation on the spray development [18]. In Barbieri et al. [19], two main spray oscillation patterns that correlate with the internal-mixing chamber pressure have been observed. At high $GLR$ and, consequently, low internal pressure, typically corresponding to $\mathrm{\Phi }<$ 1, the spray center emerging from the nozzle consists of a fine liquid mist. Here, liquid ligaments and droplets locally detach from the spray core due to the collapse of gas bubbles. Conversely, at low $GLR$, higher internal pressures intensify the bubble collapse, expelling liquid lumps from the nozzle and causing the characteristic pulsed spray motion observed in Y-jet nozzles.

Understanding the internal gas–liquid interaction in Y-jet nozzles is essential for mitigating pulsed spray behavior, which can be achieved through appropriate modifications in the nozzle design or operating conditions. Accordingly, the aim of this work is to elucidate the onset and evolution of the pulsed spray operation in a specific design of the internal-mixing Y-jet nozzle. To achieve this, a detailed numerical simulation of the internal mixing process is validated against experimental pressure measurements obtained inside the nozzle. The simulations are used to describe, both quantitatively and qualitatively, the interaction dynamics between the liquid and gas streams within the mixing chamber, using water and air as working fluids. Based on the flow patterns obtained numerically, recommendations are proposed to suppress or eliminate pulsed spray formation and improve nozzle performance.

2. Experimental Pressure Acquisition

The experimental methodology presented in this section describes how pressure is acquired from inside the mixing chamber. The results are used to validate the numerical simulations presented in the subsequent section. A detailed description of the experimental facility and operating conditions is given in [19], and only relevant information regarding the nozzle construction and pressure sensors positioning is provided in this work.

The typical atomizer layout used for the steam-assisted oil atomization in the FCC reactors is shown in Figure 1a. It features a central lance for the gas flow, with an internal diameter of 35 mm in the case of this study, while the liquid flows through an annular section, with an outer diameter of 90 mm, up to reaching the Y-jet nozzle at the atomizer tip, which is highlighted by the red dashed circle.

The internal-mixing Y-jet nozzle design consists of two liquid inlet ports positioned 180° apart, as depicted in Figure 1b. Upon entering the mixing chamber, the two liquid jets impinge and are further disrupted by the high-speed central gas stream coming from above. The nozzle geometry features a liquid-to-gas impingement angle $\alpha$ = 72°, a mixing chamber length $L_m$ = 34.3 mm, and an opening angle $\beta$ = 10°, resulting in an outlet diameter $D_m$ = 15.2 mm. The gas supply channel has a minimum diameter $D_G$ = 3.6 mm at the throat, and the liquid channels have a minimum diameter $D_L$ = 5.5 mm.

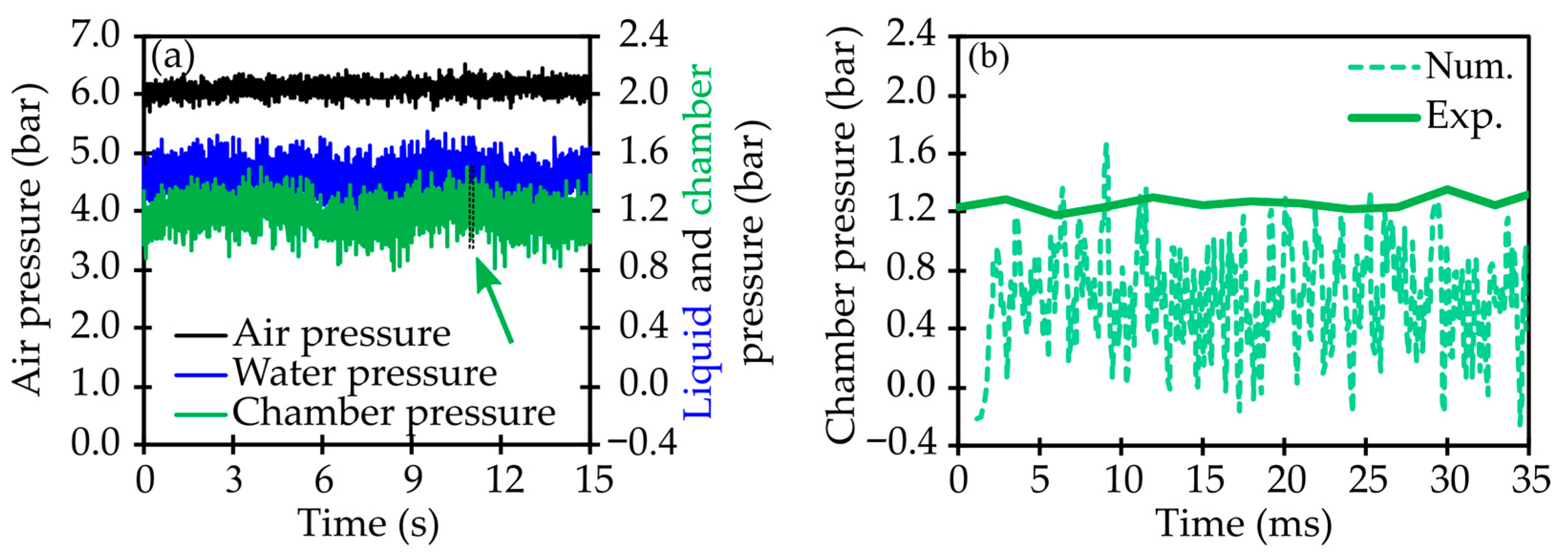
Important details about the internal mixing process can be derived from the internal pressure signal. For this, the nozzle has a central internal pressure monitoring point ($p_m$), as indicated by the green marker in Figure 1b, which is located at $z/D_G$ = 0.375. This pressure sensor (PT5404 from company IFM with a pressure range from 0 to 10 bar and inaccuracy < 0.5%) enables the measurement of the static pressure from the mixing chamber centerline with an acquisition frequency of 333 Hz. This point is aligned with, and is directly downstream from, the gas inlet port. It is intentionally positioned to acquire the chamber pressure in the pre-impingement region, characterized by a predominant single-phase gas flow. This enables the determination of whether a choked gas flow condition is achieved at the minimum area region in the experiments. Additionally, the gas and liquid injection pressures ($p_G$ and $p_L$, respectively), are obtained from pressure sensors before their injection into the atomizer.

In this work, the experiments are conducted using water and air as working fluids. The compressed air is supplied at room temperature (21 ± 2 °C) and has its flow rate measured with the flowmeter OPTISWIRL 4200 from the company Krohne, which has an operating range of 0–650 kg/h and uncertainty of 1%. The air injection remains constant in all experiments at an absolute pressure of 7 bar, which is measured before reaching the nozzle with a PI2204 pressure sensor from the company IFM, with a range of 0 to 11 bar and a precision of 0.01 bar. The water is supplied by a centrifugal pump, and the operating condition is measured using a flowmeter (OPTISONIC 3400 C from Krohne, with a range of 0 to 8000 kg/h and an uncertainty in the measurements < 0.5%) and a pressure sensor (PT5404 from company IFM, with a pressure range from 0 to 10 bar and inaccuracy < 0.5%). The different operating conditions are obtained by varying the liquid mass flow rate while the gas injection remains constant.

3. Numerical Methodology

The numerical simulations aim to explore the mixing state promoted by the interaction of the gas and liquid phases within the internal mixing chamber. This characterization is challenging in the real facility due to the use of opaque materials when manufacturing the nozzle, such as metal. The simulations represent, and are compared with, air-assisted atomization experiments using water as the liquid. In the pre-processing stage, the geometry of the nozzle cavity (Figure 2a) is discretized into control volumes using the software ANSYS ICEM-CFD version 19.2. A sketch of the numerical mesh used to represent the fluid inlets and the mixing chamber consists of a rectangular geometry, as shown in Figure 2b.

The structured mesh presents a greater refinement in the central nozzle region, specifically at the gas inlet and in the impingement region between the gas and liquid streams, with elements measuring 0.1–0.3 mm, as highlighted in Figure 2b. These elements increase in size towards the nozzle outlet, reaching a maximum of 1.6 mm. Figure 2c indicates the nozzle dimensions in the numerical simulation, which are based on the nozzle geometry in Figure 1b.

The pre-processing stage includes setting the boundary conditions and determining the numerical model solution strategy, which is performed using the finite volume method [20,21] in the software ANSYS Fluent version 19.2.

The numerical modeling of the internal multiphase flow in Y-jet atomizers assumes the continuum hypothesis, incompressible flow of the liquid phase, compressible gas flow, and no chemical reaction. The gas and liquid phases are not interpenetrating, and the interface between them in the flow is tracked with the VOF (Volume of Fluid) approach, developed by [22].

The use of the VOF approach matches the main aim of this work, representing the overall spray behavior inside the nozzle and characterizing the interaction between the liquid and the gas streams within the nozzle cavity. The primary breakup in the nozzle cavity and droplet formation would require very fine meshes or other numerical approaches, such as LES or adaptive mesh refinement, which are more computationally expensive. In this work, a high-order interface reconstruction (Geo-Reconstruction scheme) is used to represent the interface and match the focus on the gas and liquid interaction inside the nozzle.

Accordingly, the multiphase flow can be represented by the mass conservation equation (Equation (2)) and by the linear momentum conservation equation (Equation (3)):

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho \mathit{v}\right)=0,$$

(2)

$${\displaystyle \frac{\partial \left(\rho \mathit{v}\right)}{\partial t}}+\nabla ·\left(\rho \mathit{v}\mathit{v}\right)=-\nabla p+\nabla ·\left[{\mu }_{eff}\left(\nabla \mathit{v}+\nabla {\mathit{v}}^T\right)\right]+\rho \mathit{g}+\mathit{F},$$

(3)

where $\mathit{v}$ is the velocity vector, $\rho$ is the fluid density, $p$ is the static pressure, $\mathit{g}$ is the gravity vector, and ${\mu }_{eff}$ is the effective viscosity defined as the sum of the molecular viscosity $\left(\mu \right)$ and the turbulent viscosity $\left({\mu }_T\right)$, according to Equation (4):

$${\mu }_{eff}=\mu +{\mu }_T.$$

(4)

The surface tension $\mathit{F}$ is modeled with the Continuum Surface Force (CSF) model. The fluids share the same transport equations in the VOF model and, as they are not interpenetrating, in each control volume, the phase volume fractions are equal to unity, as shown in Equation (5):

$$\sum _{q=1}^n{f}_{v,q}=1,$$

(5)

with $f_{v,q}$ as the volume fraction of component $q$. $f_{v,q}$ equals 0 means that the control volume is empty of the $q^{th}$ component, and $f_{v,q}$ of unity represents a control volume full of the $q^{th}$ component, while 0 $<f_{v,q}<$ 1 indicates that the control volume contains the interface of the $q^{th}$ component with one or more other components.

A continuity equation for $f_{v,q}$ represents the temporal and spatial evolution of the volume fraction without source term and mass transfer, according to Equation (6):

$${\displaystyle \frac{\partial \left(f_{v,q}{\rho }_q\right)}{\partial t}}+\mathbf{\nabla }·\left(f_{v,q}{\rho }_q{\mathit{v}}_q\right)=0,$$

(6)

with ${\rho }_q$ as the density of the $q^{th}$ phase and ${\mathit{v}}_q$ as the velocity vector of the $q^{th}$ phase.

The density and molecular viscosity in Equations (2)–(4) are defined using the mixture rule, accounting for the phase volume fraction in each control volume. For a two-phase system, as the case of this study represented by indexes 1 and 2, and with the known volume fraction of phase 2, $\rho$ and $\mu$ are given by Equations (7) and (8), respectively. The solution of the continuity equation for the volume fraction allows for tracking the interface between the two phases:

$$\rho =f_{v2}{\rho }_2+\left(1-f_{v2}\right){\rho }_1,$$

(7)

$$\mu =f_{v2}{\mu }_2+\left(1-f_{v2}\right){\mu }_1.$$

(8)

The turbulence modeling relies on the Boussinesq hypothesis, which assumes that the Reynolds tensor in the Navier–Stokes equations is a linear function of the strain rate with the turbulent viscosity as the coefficient. The numerical investigation presented in this work calculates the turbulent viscosity using the Shear-Stress-Transport (SST) k-ω model. This model, proposed by [23], which is based on a k-ε and k-ω blending, is applied to describe the turbulent fluid flow in the inner and outer parts of the boundary layer for a wide Reynolds number range [21]. This model assumes the eddy viscosity hypothesis and addresses the turbulent viscosity as an effective viscosity, as shown in Equation (4). This is a reasonable alternative to more expensive approaches, such as LES or DNS, matching the main objective of this work.

Table 1. Numerical setup of the internal flow numerical simulations.

Condition	Configuration
Temporal approach	Transient
Gravity	9.81 m/s2 in Z-direction
Multiphase model	VOF (Volume of Fluid)
Turbulence model	k-ω SST
Gas phase (air)	Density: Ideal gas Viscosity: 1.789 × 10−5 kg/(m·s) Compressible fluid
Air inlet	Mass flow inlet: 48 kg/h at 7 bar and 300 K Turbulent intensity: 5% Turbulent viscosity ratio: 10
Liquid phase (water)	Density: 998.2 kg/m3 Viscosity: 1.01 × 10−3 kg/(m·s) Surface tension: 0.072 N/m Incompressible fluid
Water inlet	Constant velocity magnitude in m/s Turbulent viscosity: 5% Turbulent viscosity ratio: 10
Outlet	Pressure outlet with a gauge pressure of 0 Pa
Pressure-velocity coupling	SIMPLE
Discretization	Pressure: PRESTO! Gradient: Least Squares Cell-Based Momentum and density: Second-order upwind Volume fraction: Geo-Reconstruction Turbulent kinetic energy: First-order upwind Specific dissipation rate: First-order upwind Energy: Second-order upwind
Residuals	1 × 10−5 for all variables except energy (1 × 10−6)
Time step	Adaptative with a lower limit of 10−7 and an upper limit of 10−3 s
Global Courant number	1

shows the standard simulation configuration. The simulations represent air as a compressible gas phase following the ideal law. It is injected into the gas inlet boundary condition (Figure 2a) at an absolute pressure of 7 bar, corresponding to the air-assisted experiments. Water is the liquid phase, and its inlets are set to a constant velocity magnitude depending on the evaluated condition. An outlet boundary condition of prescribed pressure equal to 0 Pa is specified at the domain outlet. All walls are characterized as no-slip conditions. An adaptive time step (1 $\times$ 10⁻⁷ s $<\mathrm{\Delta }t<$ 1 $\times$ 10⁻³ s) is used. The simulations are processed using ANSYS Fluent version 19.2 software, while the post-processing is carried out in CFD-Post 19.2.

Although the VOF is commonly used with incompressible or weakly compressible problems, the gas flow, especially after the gas inlet port, has compressible effects. At this point, it is important to consider modeling the gas as a compressible fluid with the energy equation enabled in this work, as presented in Table 1.

The numerical solution uncertainty associated with the grid element size is quantified using the GCI (grid convergence index) methodology detailed in [24]. Three meshes with different refinements have been produced to evaluate the liquid height inside the mixing chamber and the chamber pressure along the nozzle length near the internal wall as local variables. The GCI of the liquid height is lower than 3.5% along the nozzle length, while the static pressure shows a GCI generally lower than 10%. Accordingly, the intermediate mesh with approximately 85,000 elements is used for further internal flow simulation studies. This is a crucial step to ensure simulation accuracy. A more detailed analysis of the GCI method for the meshes is presented in Appendix A.

4. Results and Discussion

4.1. Comparison with Experimental Data

The performance of the simulations in representing the experimental conditions is analyzed regarding the pressure along the nozzle cavity. In Figure 3, the solid lines represent the axial profile of the mean static pressure in the mixing chamber averaged over their respective entire simulation period of 0.04~0.05 s in each GLR. The hatched area corresponds to the pressure temporal fluctuation. The triangular markers represent the internal chamber static pressure obtained experimentally at the pressure acquisition point under the corresponding experimental condition. In this plot, the error bars also represent the measured signal’s temporal fluctuation.

The intermittent process associated with the pulsatile liquid ejection results in a significant pressure signal fluctuation. In this situation, the pressure increases significantly when there is a nozzle cross-section restriction and decreases when the liquid portion inside the nozzle is ejected. The condition of GLR = 0.024 represents an operation at a very high momentum ratio $\mathrm{\Phi }$ for the experiments, which features a significant fluctuation of $p_m$. This condition can be adequately represented by the simulation, in which there is an average static pressure of 1.35 bar obtained experimentally and 1.38 bar obtained numerically in the pre-impingement position.

Increasing the GLR to 0.034 induces a reduction in the internal mixing chamber pressure, which is observed both experimentally and in the simulation. The pressure reduction in the numerical simulation is more remarkable in the numerical result, because it constrains less of the space available for the gas flow. Consequently, the liquid is pressed more intensely to the internal chamber walls in the numerical simulations than in the experiments in this condition. This behavior could be verified by imaging the internal flow in the real nozzle, but this is out of the scope of this work. The momentum ratio $\mathrm{\Phi }$ reduction causes the liquid to penetrate less into the nozzle cavity and exert a weaker constraint on the gas expansion upon entering the mixing chamber.

The higher pressure $p_m$ obtained when lowering the GLR leads to more intense pressure fluctuations, which can affect the air and the water streams, as illustrated in Figure 4 at GLR = 0.024 ($\mathrm{\Phi }\cong$ 1.47). In Figure 4a, the air pressure is read on the left ordinate axis while the liquid and the mixing chamber pressures are read on the right ordinate axis.

Pressure fluctuations occur at different time scales in Figure 4a, with the main variations in the order of milliseconds. However, a remarkable feature of the experiments at very low GLR is observed between 6 and 9 s, when the pressure drops substantially to approximately 0.8 bar. Simultaneously, the liquid pressure experiences a slight decrease while the gas pressure increases. This atomizer’s performance at low GLR has been consistently observed experimentally across different Y-jet nozzles [19] and is attributed to the larger liquid momentum relative to the gas momentum.

According to Barbieri et al. (2023) [19], in these cases, the liquid injection into the mixing chamber temporarily obstructs the gas flow. Once the gas overcomes this constraint, it forcefully expels a liquid lump from the mixing chamber, leading to more frequent gas bubble explosions and the detachment of liquid ligaments and droplets. Under these conditions, especially at even lower GLR, intermittent nozzle operation and pulsatile spray formation become more intense, resulting in unstable performance.

A short time interval ($\mathrm{\Delta }t$ = 35 ms) of the experimental mixing chamber pressure signal, as indicated by the arrow in Figure 4a, is compared to the chamber pressure signal obtained from the simulations in Figure 4b. The numerical data is represented as a dashed green line from the beginning of the simulation, while the experimental data is the continuous green line. The gap in the numerical data between 16.7 ms and 19.3 ms in Figure 4b corresponds to a period where data has not been acquired during the simulations.

Despite the static pressure below 0.4 bar at the start of the simulation, there is evidence of a significant pressure fluctuation between 0.8 and 2.8 bar after 5 ms. A similar $p_m$ value of 0.8 bar is also observed in the experiments in Figure 4a between 6 and 9 s, although the fluctuations appear less frequent. This discrepancy is likely due to the difference in data acquisition frequencies—approximately 12,500 Hz in the simulations versus 333 Hz in the experiments. A closer acquisition frequency between the experiments and simulations would be necessary to capture the same transient phenomena.

Increasing the GLR to 0.034 by reducing the liquid flow rate results in a more stable air-assisted atomization, as shown in Figure 5a. Two main fluctuation time scales are observed, particularly in the liquid and mixing chamber pressure signals: one with a period of several seconds and a more frequent fluctuation occurring on the millisecond scale. In this operating condition, the liquid imposes a weaker limitation on the gas expansion within the nozzle cavity, preventing the significant pressure drop observed in Figure 4a.

The corresponding numerical results in Figure 5b indicate lower pressure values than the experiments, with the static pressure at the pre-impingement stage ranging mainly between 0 and 1.2 bar. In contrast, the experimental data shows a mean pressure of approximately 1.18 bar.

A variation in the liquid physical properties would directly affect how the liquid is disrupted by the gas, since they are coupled with inertial and aerodynamic forces. A lower surface tension would contribute to destabilizing the liquid surface because of the reduction in the cohesion forces between the liquid molecules. Consequently, the kinetic energy of the gas would encounter a reduced liquid resistance to breakup. The increase in the liquid viscosity, on the other hand, would suppress the growth of liquid instability, because the liquid would resist internal shear deformation, absorbing the turbulent and aerodynamic energy of the gas. As a result, larger ligaments and a coarser spray would be expected with liquids of higher viscosity than water. A deeper investigation of this topic requires further numerical and experimental examination but is out of the scope of this work.

4.2. Analysis of the Pressure Temporal Development

The influence of the pulsatile flow pattern on the pressure temporal evolution within the nozzle cavity among all simulated conditions is shown in Figure 6. As the GLR decreases, achieved by increasing the liquid mass flow rate at a constant air mass flow rate, both the average chamber pressure and the magnitude of pressure fluctuations increase.

The frequency analysis of these fluctuations is depicted in Figure 7a and reveals a dominant peak in each spectrum, which increases in amplitude as the GLR reduces. The peak frequencies also decrease with GLR, as shown in Figure 7b. For example, at GLR = 0.009, its highest amplitude indicates that pressure fluctuations are most intense under this condition. Compared to the other cases, its highest frequency demonstrates that increasing the liquid mass flow rate promotes a more frequent blocking of the nozzle cavity cross-section, leading to the pulsed spray flow pattern.

4.3. Characterization of the Liquid Volume Fraction, Velocity, and Pressure Fields

The pressure oscillation and its relationship with the internal flow development is further explored by considering the simulation results. The snapshot time sequence in Figure 8 represents the initial atomization stage inside the nozzle cavity. In this case, the air flow rate of 48 kg/h and the liquid flow rate of 2000 kg/h are started simultaneously, corresponding to $GLR$ = 0.024.

Figure 8a shows the multiphase flow evolution inside the nozzle cavity, represented by the liquid volume fraction between 1 and 6 ms after starting the simulation. Due to the ratio between the air inlet pressure and the atmospheric pressure inside the chamber being greater than 1.89, the gas develops a choked flow condition at the beginning of the simulation, as shown in Figure 8b in the velocity profile. The static pressure field in Figure 8c is also evidence of the occurrence of pressure gradients typical of the choked condition.

Upon contact with the gas at t = 2 ms, the liquid interacts with it and changes the pressure and velocity fields inside the nozzle, pushing the gas to the mixing chamber center, as shown in Figure 8b,c. The liquid injection with a momentum larger than the gas ($\mathrm{\Phi }$ = 1.47) advances towards the nozzle cavity center and partially blocks the gas flow. In addition to altering the velocity profiles, the obstruction of the nozzle cavity cross-section by the liquid increases the static pressure in the pre-impingement region, as demonstrated in Figure 8c at t = 3 ms, which, in this case, ends up detaching liquid ligaments from the liquid jets. This behavior evidences the onset of the typical pulsatile spray flow inside the internal mixing chamber observed in Y-jet nozzles, which certainly influences the spray development and the droplets’ size and velocity after exiting the nozzle.

After the ejection of these liquid lumps, the pressure in the impingement region drops (Figure 8c at t = 4 ms) and new instabilities appear in the liquid film, forming liquid projections towards the nozzle center. These liquid lumps extend towards the nozzle cavity in the middle and limit the gas flow again. This cycle repeats as the simulation progresses, as shown in Figure 9, considering a time interval of 30 < t < 35 ms after the simulation starts, leading to a pulsating spray flow.

The snapshots also show a more concentrated liquid region close to the nozzle’s internal walls, while the gas occupies the nozzle center, except when the liquid lumps are expelled. The three-dimensional flow model indicates an asymmetrical liquid ligament projection to the chamber center, which can lead to an alternating liquid ejection.

Increasing $\mathrm{\Phi }$ to 11.51 causes a more intense gas flow restriction imposed by the liquid, as shown in Figure 10 for $GLR$ = 0.009. The Figure shows instantaneous snapshots of liquid volume fraction (Figure 10a), flow velocity (Figure 10b), and pressure inside the nozzle (Figure 10c) at 48 < t < 53 ms after the start of the simulation. As the liquid jets have a higher momentum than the gas, they advance further toward the nozzle cavity center in comparison with $\mathrm{\Phi }$ = 1.47, even impinging at t = 50 ms in Figure 10a, for example. Consequently, there is a significant pressure increase in the pre-impingement region until the gas overcomes the resistance to its flow imposed by the liquid. When it happens at t = 52 ms and t = 53 ms, there is a liquid ejection in the direction of the nozzle outlet and a pressure reduction in the pre-impingement region, with the propagation of a pressure wave along the nozzle. This pressure propagation is also noticeable at t = 48 ms and t = 49 ms, which is caused by the ejection of a liquid lump prior to this time step.

The volume fraction, flow velocity, and pressure field snapshots in Figure 10 are remarkably similar between the instants t = 50 ms and t = 51 ms. This behavior indicates that the whole liquid ejection mechanism, with pressure release followed by its buildup, happens at least once within this interval of 1 ms. This process is investigated with greater temporal resolution in Figure 11, which shows instantaneous snapshots at every 0.1 ms within 51.1 ≤ t ≤ 51.6 ms after the start of the simulation.

The high-pressure region forming at t = 51 ms in Figure 10 is followed by the release of a liquid mass along with the pressure relief at t = 51.1 ms in Figure 11, which propagates along the nozzle cavity at t = 51.2 ms. As the channel is cleared again for the flow, the multiphase mixture, especially the gas, shows an increase in velocity, notably in the nozzle medial portion. Still at t = 51.2 ms, however, a constriction of the nozzle cross-section is again formed in the pre-impingement region, which extends to t = 51.3 ms. The gas, blocked by the liquid, increases the pressure in this nozzle region, and there is a significant flow velocity reduction in the intermediate nozzle region. This culminates in liquid ejection when the gas overcomes the resistance imposed by the liquid, releasing the pressure in the pre-impingement region at t = 51.4 ms. In lower GLR conditions, as exemplified in Figure 10 and Figure 11, the pulsatile movement is more intense than in high GLR conditions, and the obstruction of the nozzle cavity cross-section, depending on the liquid momentum, is crucial for characterizing the different flow patterns.

5. Conclusions

Liquid atomization using Y-jet nozzles constitutes a fundamental role in the oil refining process. Understanding the operation of this nozzle configuration is essential for optimizing energy use, enhancing process efficiency, and reducing environmental impact by minimizing raw material consumption.

Achieving stable atomization is critical for the proper design of the refining facilities and for ensuring consistent product standards. The formation of pulsed sprays, however, is highly sensitive to the operating conditions. This study identified the mechanisms responsible for pulsed spray formation and clarified the role of gas–liquid interactions within the nozzle’s mixing chamber.

When the liquid jets enter the mixing chamber, they impose back pressure on the gas stream. Increasing the liquid-to-gas momentum ratio, i.e., reducing the gas-to-liquid mass flow ratio GLR, limits the space available for gas expansion within the chamber and escalates the internal pressure, resulting in the power-law relation between $p_m/p_G$ and GLR. This typical Y-jet nozzle operation causes high pressures in the nozzle cavity, especially in the pre-impingement region, which is associated with a liquid recirculation that can partially block the gas flow into the mixing chamber. Upon overcoming the obstruction established by the liquid jets, the gas stream promotes a sudden liquid mass removal from the nozzle, creating an oscillatory spray formation. As the flow develops in an expanding nozzle cavity, the pressure reduces along the nozzle cavity up to reaching the atmospheric pressure from outside the nozzle. Furthermore, at lower momentum ratios $\mathrm{\Phi }$, the liquid projections alternately detach in the impingement region, while at a high momentum ratio, the flow develops more symmetrically.

The numerical model has been validated with experimental pressure measurements inside the nozzle. The comparison of the pressure magnitude agreed with the measurement values, and pressure signal oscillations have been measured and captured numerically, which are associated with the intense mixing within the nozzle. The frequency at which these oscillations occur depends on the operating conditions and decreases with the GLR. As the momentum ratio $\mathrm{\Phi }$ increases, more intense pressure fluctuations are observed.

These findings emphasize the importance of selecting appropriate GLR values that balance atomization efficiency and stability for specific industrial applications. A comprehensive investigation of the multiphase flow dynamics can inform the design of more efficient atomizers and guide the definition of operational windows that suppress pulsed behavior while maintaining effective atomization.