Digital Twins: A Solution Under the Standard k-ε Model in Industrial CFD, to Predict Ideal Conditions in a Sugar Dryer
Abstract
1. Introduction
2. Materials and Methods
2.1. Dryer Technical Parameter Specification
2.2. Methodology
2.2.1. Technical Parameters Specifications
2.2.2. Mathematical Model
2.2.3. Numerical Implementation
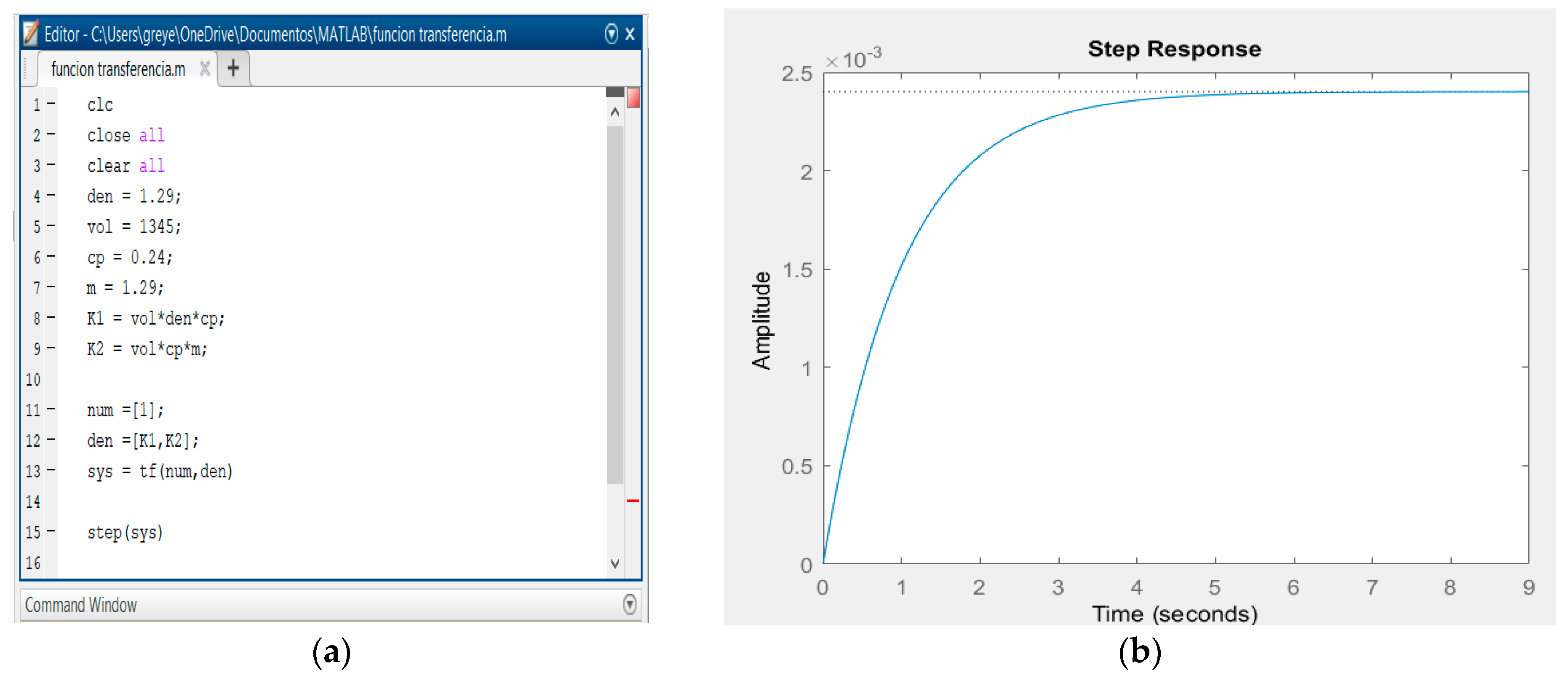
2.2.4. Transfer Function in MATLAB R2017
2.2.5. Simulation Studies
2.2.6. Validation and Analysis
2.3. Mathematical Model of the Technologic System
2.4. Standard k-ε Method Used in Industrial CFD
2.5. Turbulence Model Selection
3. Results
3.1. Experimental Determination of the Transfer Function in Matlab R2015
3.2. Experimental Analysis of Centrifuge Dryer in CFD2015
3.2.1. Testing in Actual Conditions
3.2.2. Experimentation for the Prediction of Ideal Conditions
3.3. Experimental Data and CFD Model Validation
3.3.1. Experimental Data Under Real Conditions
3.3.2. Validación del Modelo CFD
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, M.; Srivastava, R.; Fuenmayor, E.; Kuts, V.; Qiao, Y.; Murray, N.; Devine, D. Applications of Digital Twin across Industries: A Review. Appl. Sci. 2022, 12, 5727. [Google Scholar] [CrossRef]
- Segovia, M.; Garcia-Alfaro, J. Design, Modeling and Implementation of Digital Twins. Sensors 2022, 22, 5396. [Google Scholar] [CrossRef] [PubMed]
- Menon, D.; Anand, B.; Chowdhary, C.L. Digital Twin: Exploring the Intersection of Virtual and Physical Worlds. IEEE Access 2023, 11, 75152–75172. [Google Scholar] [CrossRef]
- Bamunuarachchi, D.; Georgakopoulos, D.; Banerjee, A.; Jayaraman, P.P. Digital Twins Supporting Efficient Digital Industrial Transformation. Sensors 2021, 21, 6829. [Google Scholar] [CrossRef]
- Deng, M.; Menassa, C.C.; Kamat, V.R. From BIM to Digital Twins: A Systematic Review of the Evolution of Intelligent Building Representations in the AEC-FM Industry. J. Inf. Technol. Constr. 2021, 26, 58–83. [Google Scholar] [CrossRef]
- Leng, J.; Wang, D.; Shen, W.; Li, X.; Liu, Q.; Chen, X. Digital Twins-Based Smart Manufacturing System Design in Industry 4.0: A Review. J. Manuf. Syst. 2021, 60, 119–137. [Google Scholar] [CrossRef]
- Wu, J.; Zuo, R. Intelligent Computation Offloading Based on Digital Twin-Enabled 6G Industrial IoT. Appl. Sci. 2024, 14, 1035. [Google Scholar] [CrossRef]
- Guerrero-Hernandez, V.; Reyes-Morales, G.; Jacome-Onofre, P.; Ortega Moody, J.A.; Matacapan-Toto, F.A.; Martínez Herrera, M.A. Integration of an Industrial Control to a Digital Twin at the Industrial Level. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Spain, 19–21 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar]
- Lopes, P.V.; Silveira, L.; Guimaraes Aquino, R.D.; Ribeiro, C.H.; Skoogh, A.; Verri, F.A.N. Synthetic Data Generation for Digital Twins: Enabling Production Systems Analysis in the Absence of Data. Int. J. Comput. Integr. Manuf. 2024, 37, 1252–1269. [Google Scholar] [CrossRef]
- González-Herbón, R.; González-Mateos, G.; Rodríguez-Ossorio, J.R.; Domínguez, M.; Alonso, S.; Fuertes, J.J. An Approach to Develop Digital Twins in Industry. Sensors 2024, 24, 998. [Google Scholar] [CrossRef]
- Hu, Y.; Taha, O.W.; Yang, K. Fault Detection in Active Magnetic Bearings Using Digital Twin Technology. Appl. Sci. 2024, 14, 1384. [Google Scholar] [CrossRef]
- Molinaro, R.; Singh, J.-S.; Catsoulis, S.; Narayanan, C.; Lakehal, D. Embedding Data Analytics and CFD into the Digital Twin Concept. Comput. Fluids 2021, 214, 104759. [Google Scholar] [CrossRef]
- Dixon, A.G.; Partopour, B. Computational Fluid Dynamics for Fixed Bed Reactor Design. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 109–130. [Google Scholar] [CrossRef] [PubMed]
- Haringa, C. An Analysis of Organism Lifelines in an Industrial Bioreactor Using Lattice-Boltzmann CFD. Eng. Life Sci. 2023, 23, e2100159. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Wutz, J.; Waterkotte, B.; Heitmann, K.; Wucherpfennig, T. Computational Fluid Dynamics (CFD) as a Tool for Industrial UF/DF Tank Optimization. Biochem. Eng. J. 2020, 160, 107617. [Google Scholar] [CrossRef]
- Nidhul, K.; Yadav, A.K.; Anish, S.; Arunachala, U.C. Efficient Design of an Artificially Roughened Solar Air Heater with Semi-Cylindrical Side Walls: CFD and Exergy Analysis. Sol. Energy 2020, 207, 289–304. [Google Scholar] [CrossRef]
- Jaszczur, M.; Młynarczykowska, A.; Demurtas, L. Effect of Impeller Design on Power Characteristics and Newtonian Fluids Mixing Efficiency in a Mechanically Agitated Vessel at Low Reynolds Numbers. Energies 2020, 13, 640. [Google Scholar] [CrossRef]
- Yamini, O.A.; Movahedi, A.; Mousavi, S.H.; Kavianpour, M.R.; Kyriakopoulos, G.L. Hydraulic Performance of Seawater Intake System Using CFD Modeling. J. Mar. Sci. Eng. 2022, 10, 988. [Google Scholar] [CrossRef]
- Zhang, C.; Bounds, C.P.; Foster, L.; Uddin, M. Turbulence Modeling Effects on the CFD Predictions of Flow over a Detailed Full-Scale Sedan Vehicle. Fluids 2019, 4, 148. [Google Scholar] [CrossRef]
- Mani, M.; Dorgan, A.J. A Perspective on the State of Aerospace Computational Fluid Dynamics Technology. Annu. Rev. Fluid Mech. 2023, 55, 431–457. [Google Scholar] [CrossRef]
- Zhao, Y.; Akolekar, H.D.; Weatheritt, J.; Michelassi, V.; Sandberg, R.D. RANS Turbulence Model Development Using CFD-Driven Machine Learning. J. Comput. Phys. 2020, 411, 109413. [Google Scholar] [CrossRef]
- Didane, D.H.; Bajuri, M.N.A.; Manshoor, B.; Boukhari, M.I. Performance Investigation of Vertical Axis Wind Turbine with Savonius Rotor Using Computational Fluid Dynamics (CFD). CFD Lett. 2022, 14, 116–124. [Google Scholar] [CrossRef]
- Park, D.; Go, J.S. Design of Cyclone Separator Critical Diameter Model Based on Machine Learning and CFD. Processes 2020, 8, 1521. [Google Scholar] [CrossRef]
- Nakhaei, M.; Lu, B.; Tian, Y.; Wang, W.; Dam-Johansen, K.; Wu, H. CFD Modeling of Gas–Solid Cyclone Separators at Ambient and Elevated Temperatures. Processes 2020, 8, 228. [Google Scholar] [CrossRef]
- Ngo, S.I.; Lim, Y.-I. Multiscale Eulerian CFD of Chemical Processes: A Review. ChemEngineering 2020, 4, 23. [Google Scholar] [CrossRef]
- Acharya, T.; Casimiro, L. Evaluation of Flow Characteristics in an Onshore Horizontal Separator Using Computational Fluid Dynamics. J. Ocean Eng. Sci. 2020, 5, 261–268. [Google Scholar] [CrossRef]
- Kuang, S.; Zhou, M.; Yu, A. CFD-DEM Modelling and Simulation of Pneumatic Conveying: A Review. Powder Technol. 2020, 365, 186–207. [Google Scholar] [CrossRef]
- Yi, H.; Kim, M.; Lee, D.; Park, J. Applications of Computational Fluid Dynamics for Mine Ventilation in Mineral Development. Energies 2022, 15, 8405. [Google Scholar] [CrossRef]
- Pramadhony; Kaprawi, S.; Dewi, P.; Muhammad, S.; Sugianto. The Effects of the Exhaust Fan Position to Indoor Air Pollution Distribution in Enclosed Parking Garage. CFD Lett. 2023, 15, 123–138. [Google Scholar] [CrossRef]
- Kim, R.; Hong, S.; Norton, T.; Amon, T.; Youssef, A.; Berckmans, D.; Lee, I. Computational Fluid Dynamics for Non-Experts: Development of a User-Friendly CFD Simulator (HNVR-SYS) for Natural Ventilation Design Applications. Biosyst. Eng. 2020, 193, 232–246. [Google Scholar] [CrossRef]
- Martins, J.R.R.A. Aerodynamic Design Optimization: Challenges and Perspectives. Comput. Fluids 2022, 239, 105391. [Google Scholar] [CrossRef]
- Atmaca, M.; Ezgi, C. Three-Dimensional CFD Modeling of a Steam Ejector. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 2236–2247. [Google Scholar] [CrossRef]
- Tutar, M.; Üstün, C.E.; Campillo-Robles, J.M.; Fuente, R.; Cibrián, S.; Arzua, I.; Fernández, A.; López, G.A. Optimized CFD Modelling and Validation of Radiation Section of an Industrial Top-Fired Steam Methane Reforming Furnace. Comput. Chem. Eng. 2021, 155, 107504. [Google Scholar] [CrossRef]
- Langrish, T.A.G.; Harrington, J.; Huang, X.; Zhong, C. Using CFD Simulations to Guide the Development of a New Spray Dryer Design. Processes 2020, 8, 932. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Editorial: Recent Trends in Computational Fluid Dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
- Srinavin, P.; Laloon, K.; Wongwuttasatien, T.; Patra, S.; Padungthon, S. Drying process optimization and kinetic study of sugarcane filter cake using a pilot-scale rotary dryer. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Palacios-Bereche, M.C.; Palacios-Bereche, R.; Ensinas, A.V.; Gallego, A.G.; Modesto, M.; Nebra, S.A. Brazilian sugar cane industry–A survey on future improvements in the process energy management. Energy 2022, 259, 124903. [Google Scholar] [CrossRef]
- Mkwananzi, T.; Mandegari, M.; Görgens, J.F. Disturbance Modelling through Steady-State Value Deviations: The Determination of Suitable Energy Indicators and Parameters for Energy Consumption Monitoring in a Typical Sugar Mill. Energy 2019, 176, 211–223. [Google Scholar] [CrossRef]
- Huang, S.; Chen, Q.; Cheng, Y.; Xian, J.; Tai, Z. Supersonic Combustion Modeling and Simulation on General Platforms. Aerospace 2022, 9, 366. [Google Scholar] [CrossRef]
- Sankalp, S.S.; Sharma, V.; Singh, A.; Salian, A.S.; Srinivas, G. Computational Analyses of Tail Fin Configurations for a Sounding Rocket. Aerosp. Syst. 2022, 5, 233–246. [Google Scholar] [CrossRef]
- Kulshreshtha, A.; Gupta, S.K.; Singhal, P. FEM/CFD Analysis of Wings at Different Angle of Attack. Mater. Today Proc. 2020, 26, 1638–1643. [Google Scholar] [CrossRef]
- Rajanna, M.R.; Johnson, E.L.; Codoni, D.; Korobenko, A.; Bazilevs, Y.; Liu, N.; Lua, J.; Phan, N.; Hsu, M.C. Finite Element Methodology for Modeling Aircraft Aerodynamics: Development, Simulation, and Validation. Comput. Mech. 2022, 70, 549–563. [Google Scholar] [CrossRef]
- Kamal, M.N.F.; Ishak, I.A.; Darlis, N.; Maruai, N.M.; Jamian, R.; Rashid, R.A.; Samiran, N.; Hassan, N.N.M. Flow Structure Characteristics of the Simplified Compact Car Exposed to Crosswind Effects Using CFD. J. Adv. Res. Appl. Sci. Eng. Technol. 2022, 28, 56–66. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, H.; Wang, M.; Miao, C.; Wu, Y.; Li, Q. Design and Investigation of a Dynamic Auto-Adjusting Ejector for the MED-TVC Desalination System Driven by Solar Energy. Entropy 2022, 24, 1815. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, T.; Lv, H.; Zhou, W.; Zhang, C. Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage. World Electr. Veh. J. 2021, 12, 118. [Google Scholar] [CrossRef]
- Tan, L.; Yuan, Y. Computational Fluid Dynamics Simulation and Performance Optimization of an Electrical Vehicle Air-Conditioning System. Alex. Eng. J. 2022, 61, 315–328. [Google Scholar] [CrossRef]
- Fertahi, S.D.; Belhadad, T.; Kanna, A.; Samaouali, A.; Kadiri, I. CFD Investigation of Fin Design Influence on Phase Change Material Melting for Solar Thermal Energy Storage. e-Prime—Adv. Electr. Eng. Electron. Energy 2023, 6, 100306. [Google Scholar] [CrossRef]
- Ngadi, Z.; Lahlaouti, M.L. CFD Modeling of Petcoke Co-Combustion in a Real Cement Kiln: The Effect of the Turbulence-Chemistry Interaction Model Applied with K-ϵ Variations. Int. Rev. Appl. Sci. Eng. 2022, 13, 148–163. [Google Scholar] [CrossRef]
- Saini, A.K.; Radu, T.; Paritosh, K.; Kumar, V.; Pareek, N.; Tripathi, D.; Vivekanand, V. Bioengineered Bioreactors: A Review on Enhancing Biomethane and Biohydrogen Production by CFD Modeling. Bioengineered 2021, 12, 6418–6433. [Google Scholar] [CrossRef]
- Antara, I.G.F.B.; Sucipta, M.; Astawa, K.; Wirawan, I.K.G.; Sukrawa, M. CFD Simulation of Photovoltaic Thermal PV/T) Cooling System with Various Channel Geometries. J. Heat Mass Transf. Res. 2024, 11, 297–306. [Google Scholar] [CrossRef]
- Villalobos-Lara, A.D.; Castillo, B.; Rivera, F.F.; Vazquez-Arenas, J. Model Accounting for the Cr(III) Electroprecipitation Kinetics in an Electrochemical Reactor Based on CFD and Mass Transport Contributions. J. Electroanal. Chem. 2023, 928, 117057. [Google Scholar] [CrossRef]
- Savarese, M.; Cuoci, A.; De Paepe, W.; Parente, A. Machine Learning Clustering Algorithms for the Automatic Generation of Chemical Reactor Networks from CFD Simulations. Fuel 2023, 343, 127945. [Google Scholar] [CrossRef]
- Rezaeimanesh, M.; Asghar Ghoreyshi, A.; Peyghambarzadeh, S.M.; Hassan Hashemabadi, S. A Coupled CFD Simulation Approach for Investigating the Pyrolysis Process in Industrial Naphtha Thermal Cracking Furnaces. Chin. J. Chem. Eng. 2022, 44, 528–542. [Google Scholar] [CrossRef]
- Jamil, Q.; Rana, K.B.; Matoh, L. A CFD Study on Optimization of Mass Transfer and Light Distribution in a Photocatalytic Reactor with Immobilized Photocatalyst on Spheres. Water 2024, 16, 1828. [Google Scholar] [CrossRef]
- Zohdi, T.I. A Digital Twin Framework for Machine Learning Optimization of Aerial Fire Fighting and Pilot Safety. Comput. Methods Appl. Mech. Eng. 2021, 373, 113446. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Li, Y. Instability of the Realizable k—ε Turbulence Model beneath Surface Waves. Phys. Fluids 2020, 32, 115108. [Google Scholar] [CrossRef]
- Ioannidis, G.; Li, C.; Tremper, P.; Riedel, T.; Ntziachristos, L. Application of CFD Modelling for Pollutant Dispersion at an Urban Traffic Hotspot. Atmosphere 2024, 15, 113. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Y.; Ooka, R.; Flageul, C.; Kim, Y.; Kikumoto, H.; Wang, Z.; Sartelet, K. Modeling of Street-Scale Pollutant Dispersion by Coupled Simulation of Chemical Reaction, Aerosol Dynamics, and CFD. Atmos. Chem. Phys. 2023, 23, 1421–1436. [Google Scholar] [CrossRef]
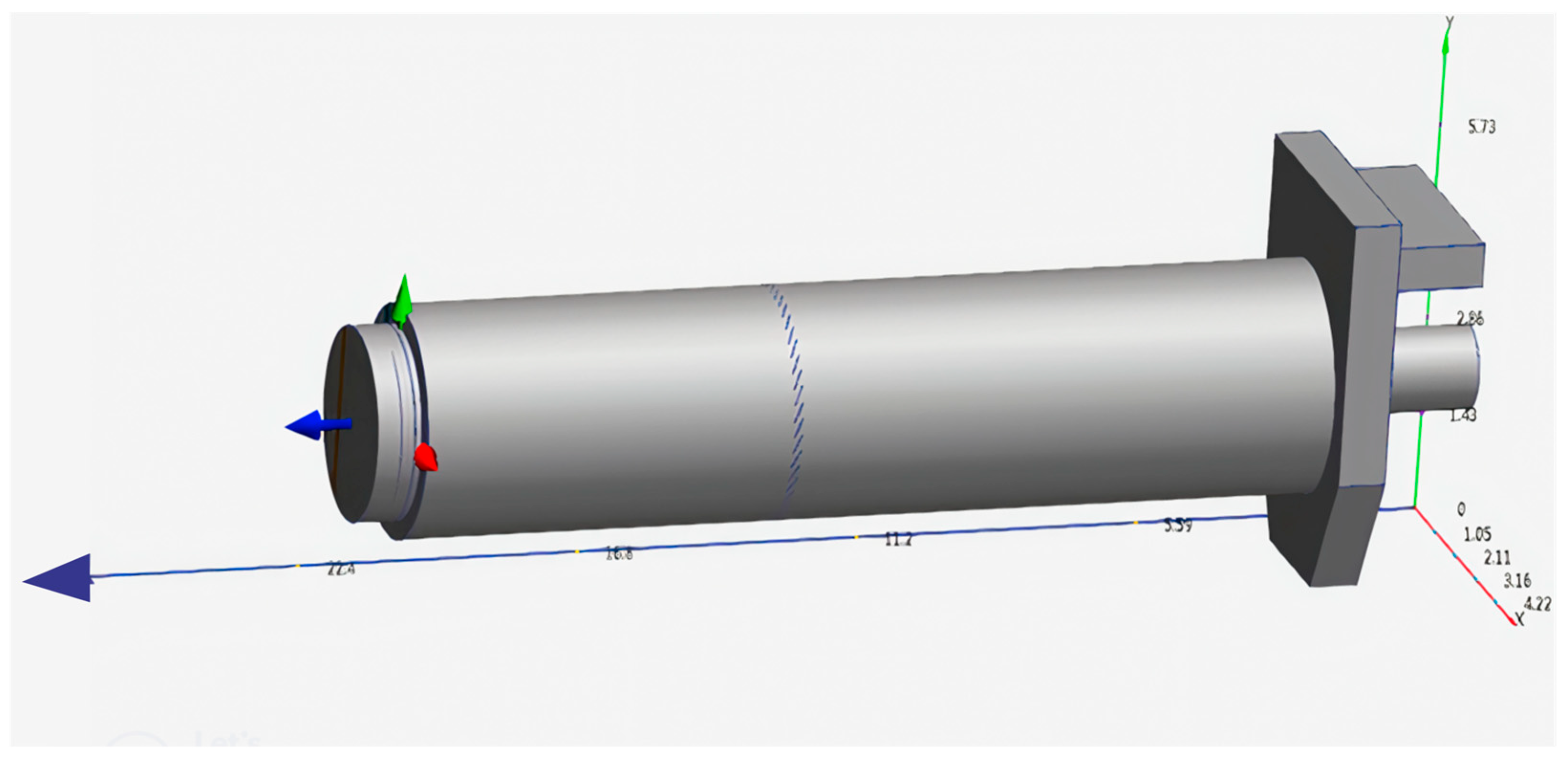

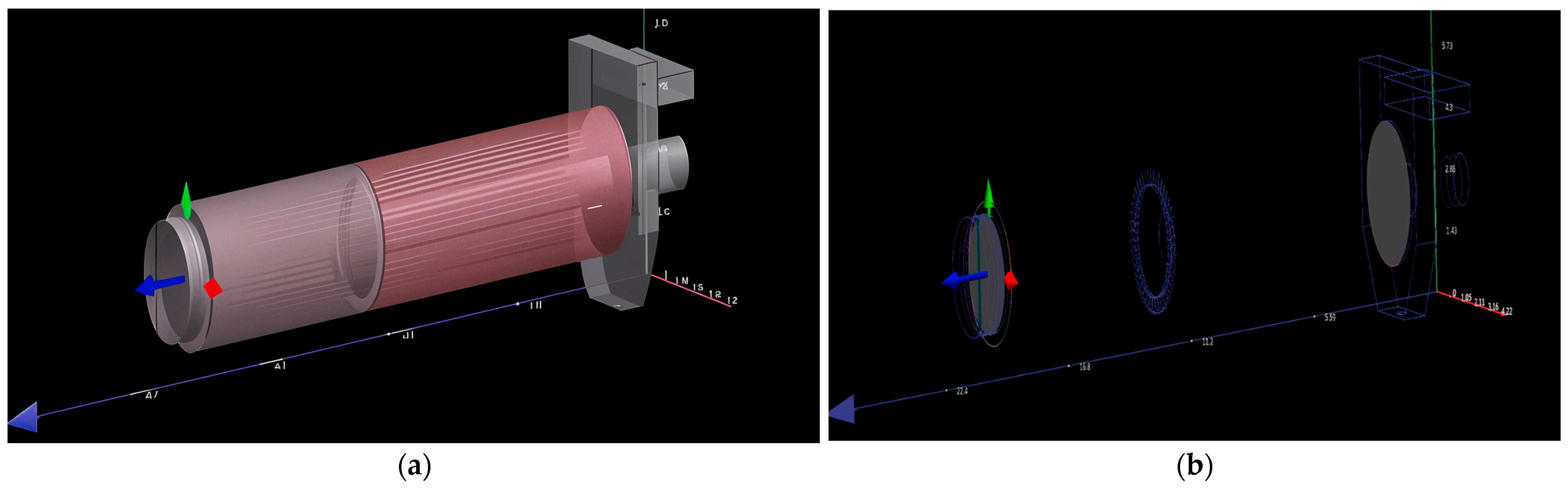
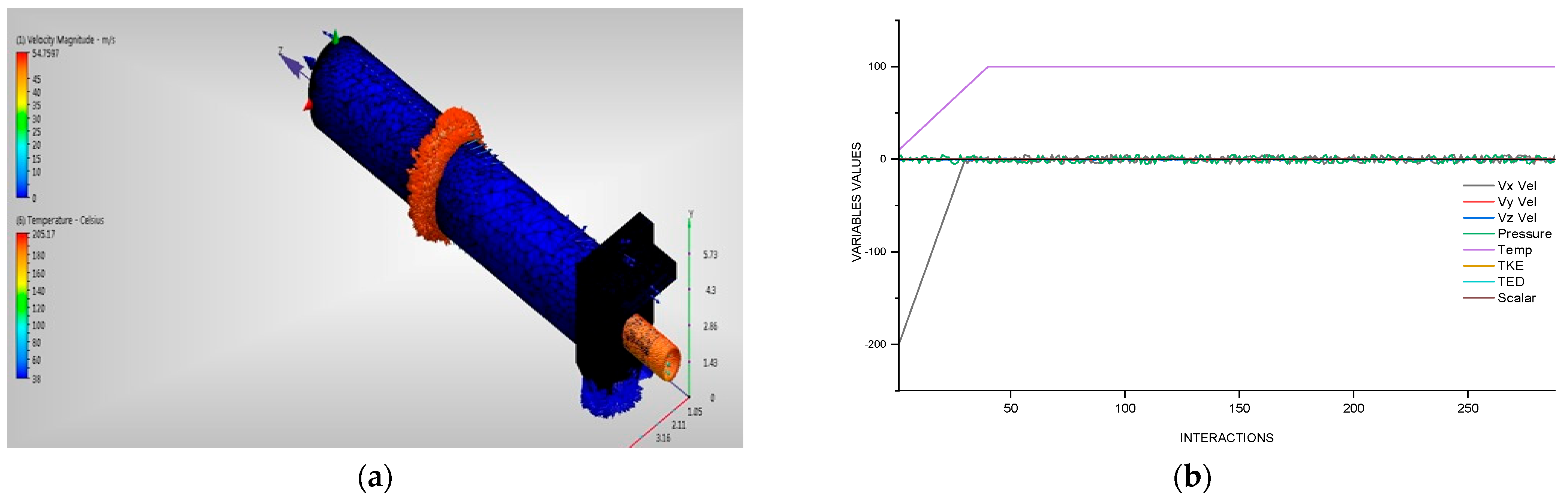


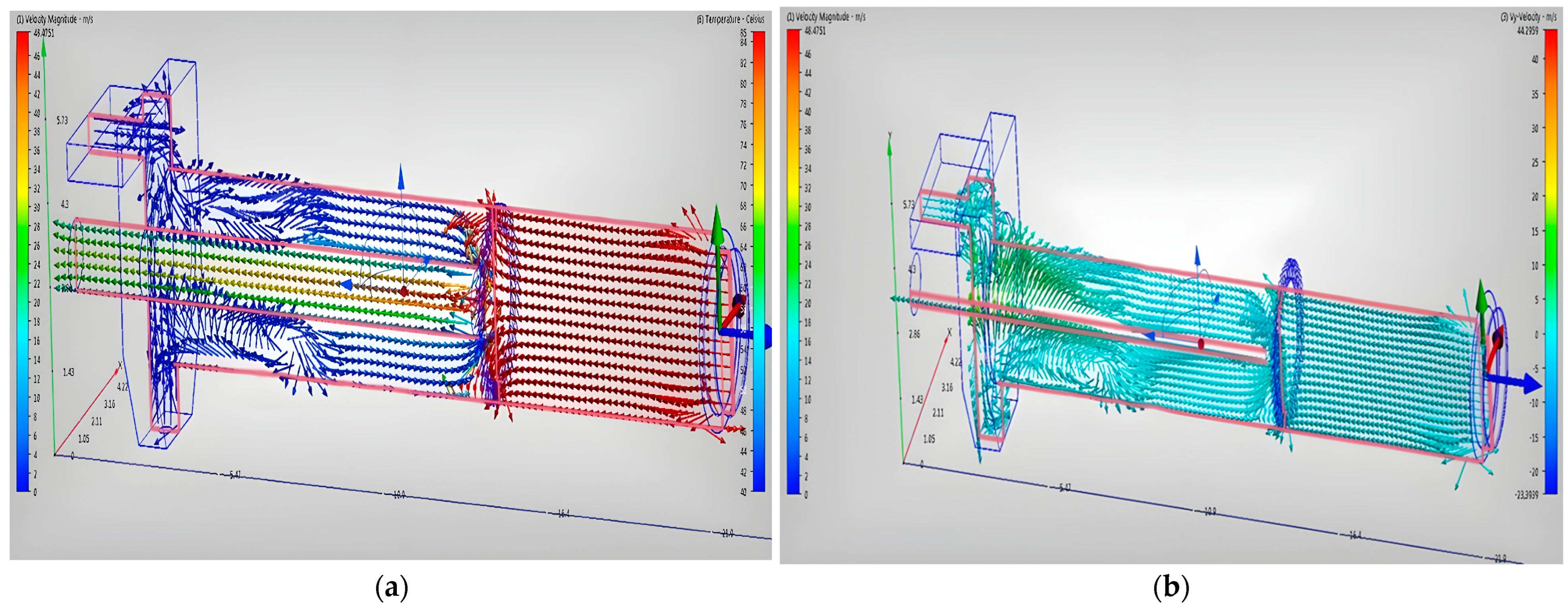
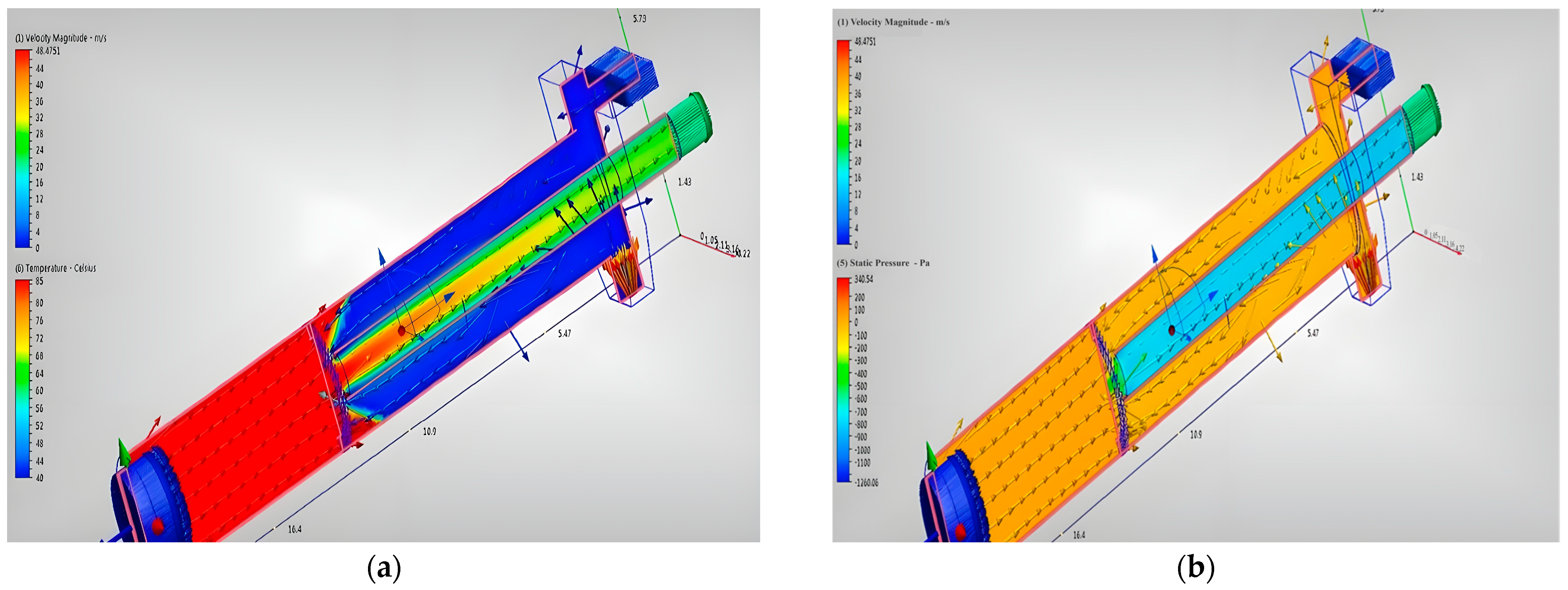
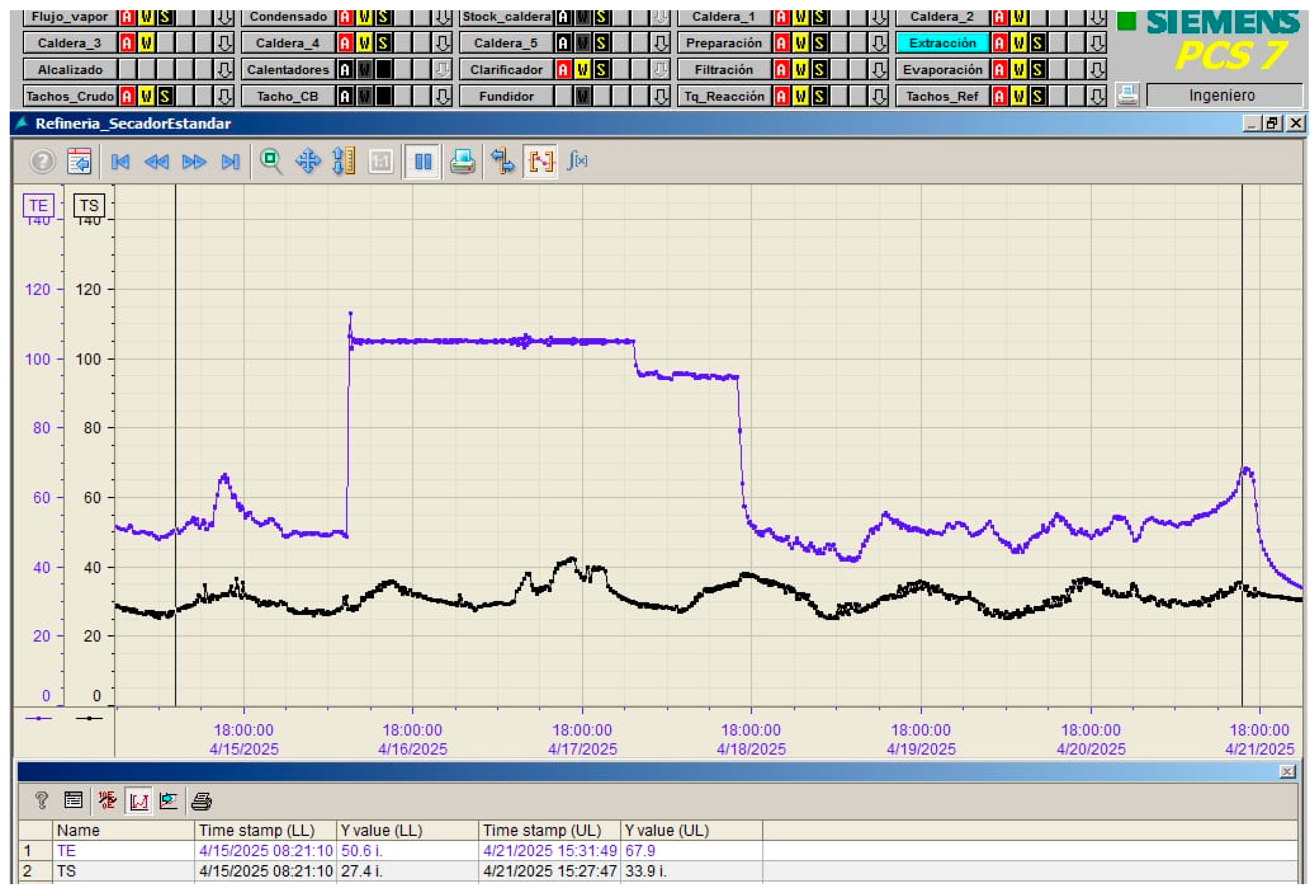
| Classification | Measurement Unit |
|---|---|
| Central tube cooling section | |
| Inner diameter | 13.116 m |
| Length | 11.8872 m |
| Outer diameter | 120.142/10.16 cm |
| Design conditions | |
| Initial air temperature | 299.15 °K (26 °C) |
| Initial sugar temperature | 313.15–315.35 °K (40–42.22 °C) |
| Final air temperature | 416.48 °K (143.33 °C) |
| Final sugar temperature | 310.26 °K (37.11 °C) |
| Operating conditions | |
| Sugar inlet temperature | 299.15 °K (49 °C) |
| Sugar inlet humidity | 1.9% |
| Sugar outlet temperature | 316.15 °K (43 °C) |
| Residence time | 20 min |
| Air radiator | |
| Air flow | 26,000 CFM |
| Mass flow | 53,070.30729 kg/h |
| Pressure drops | 11.69548 Pa |
| Air inlet temperature | 277.55 °K (4.44 °C) |
| Air outlet temperature | 416.15 °K (143 °C) |
| Maximum pressure | 103,421 Pa |
| Maximum temperature | 423.15 °K (150 °C) |
| Steam flow | 3611.50244994 kg/h |
| Air fan | |
| Air flow capacity | 47,407 CFM |
| Power | 74,570 Watts |
| Speed | 790 RPM |
| Dryer inclination | 1.5 degrees |
| Date 2025 | TE Real (°C) | TS Real (°C) |
|---|---|---|
| 16/04 | 100 | 38 |
| 17/04 | 100 | 42 |
| 18/04 | 95 | 39 |
| Date 2025 | TE CFD (°C) | TE Real (°C) | Error (%) | TS CFD (°C) | TS Real (°C) | Error (%) |
|---|---|---|---|---|---|---|
| 16/04 | 97 | 100 | −3.0 | 40 | 38 | 2.0 |
| 17/04 | 97 | 100 | −3.0 | 40 | 42 | 2.0 |
| 18/04 | 97 | 95 | 2.0 | 40 | 39 | 1.0 |
| Industrial Areas | Typical Applications | Advantages k-ε Model | Challenges and Limitations |
|---|---|---|---|
| Aerospace [40,41,42,43] | Supersonic combustion in aerospace vehicles, missiles with wing and tail-fin configuration, wing designs, and aerodynamics of cubicopters. | Robustness, computational efficiency, ability to simulate separate flows | Difficulty in accurately predicting flow separation in adverse conditions |
| Automotive [44,45,46,47] | Aerodynamic design of compact cars, dynamic self-adjusting ejector, hydrogen leakage in batteries, and vehicle air conditioning systems. | Versatility, ability to simulate internal and external flows | Limitations in predicting turbulence near walls in complex geometries |
| Energy [48,49,50,51] | Vibration analysis in a reactor, combustion in a cement kiln, bioreactor design, and ventilation in mining. | Robustness, ability to simulate combustion flows | Difficulty in capturing the interaction between turbulence and chemistry in combustion processes |
| Chemical processes [52,53,54,55] | Reactor design, mixer design, and pipeline flow analysis. | Computational efficiency, ability to simulate multiphase flows | Limitations of turbulence prediction in flows with high anisotropy |
| Environmental [56,57,58,59] | Simulation of pollutant dispersion and flow modelling in water bodies. | Versatility, ability to simulate flows in complex geometries | Difficulty in capturing the influence of turbulence on mass transfer phenomena |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero-Hernández, V.; Reyes-Morales, G.; Bastián Lima, V.A.; Ortega-Moody, J.; Bertel, Q.R.Q.; Rodríguez, G.A.; Sánchez, B.E.G.; Ceballos-Díaz, C.; Herazo, L.C.S. Digital Twins: A Solution Under the Standard k-ε Model in Industrial CFD, to Predict Ideal Conditions in a Sugar Dryer. Fluids 2025, 10, 146. https://doi.org/10.3390/fluids10060146
Guerrero-Hernández V, Reyes-Morales G, Bastián Lima VA, Ortega-Moody J, Bertel QRQ, Rodríguez GA, Sánchez BEG, Ceballos-Díaz C, Herazo LCS. Digital Twins: A Solution Under the Standard k-ε Model in Industrial CFD, to Predict Ideal Conditions in a Sugar Dryer. Fluids. 2025; 10(6):146. https://doi.org/10.3390/fluids10060146
Chicago/Turabian StyleGuerrero-Hernández, Verónica, Guillermo Reyes-Morales, Violeta Alejandra Bastián Lima, Jorge Ortega-Moody, Quelbis Román Quintero Bertel, Gerardo Aguila Rodríguez, Blanca Estela González Sánchez, Claudia Ceballos-Díaz, and Luis Carlos Sandoval Herazo. 2025. "Digital Twins: A Solution Under the Standard k-ε Model in Industrial CFD, to Predict Ideal Conditions in a Sugar Dryer" Fluids 10, no. 6: 146. https://doi.org/10.3390/fluids10060146
APA StyleGuerrero-Hernández, V., Reyes-Morales, G., Bastián Lima, V. A., Ortega-Moody, J., Bertel, Q. R. Q., Rodríguez, G. A., Sánchez, B. E. G., Ceballos-Díaz, C., & Herazo, L. C. S. (2025). Digital Twins: A Solution Under the Standard k-ε Model in Industrial CFD, to Predict Ideal Conditions in a Sugar Dryer. Fluids, 10(6), 146. https://doi.org/10.3390/fluids10060146










