Weakly Nonlinear Instability of a Convective Flow in a Plane Vertical Channel
Abstract
1. Introduction
- A weakly nonlinear approach is used in the paper in the limit of small Prandtl numbers to investigate the behavior of the most unstable perturbation. The asymptotic expansion is constructed in the neighborhood of the critical point where the Grashof number is slightly larger than the critical value.
- The amplitude evolution equation for the most unstable mode is derived from the equations of motion in contrast with many other studies where a phenomenological approach is used (the form of the amplitude equation is assumed without derivation). It is shown that the amplitude evolution equation is the complex Ginzburg–Landau equation (CGLE). The formulas for the calculations of the coefficients of the equation are derived in the paper. It is shown that the coefficients depend on the solutions of the linear stability problem, the corresponding adjoint problem, and three boundary value problems, which are obtained using the expansion procedure.
- The formulas for the coefficients of the CGLE do not change and are the same for different convective flows between two parallel vertical planes. These flows include (a) flows due to heat sources of constant or variable density; (b) flows due to a temperature difference between the walls of the channel or the superposition of cases (a) and (b). In all these cases, the same CGLE derived in the present paper can be used. The input data for the calculation of the coefficients of the CGLE are as follows: (1) the velocity profile obtained from the solution of the steady state Navier–Stokes equations under the Boussinesq approximation, and (2) the corresponding critical values of the parameters of the linear stability problem.
- To illustrate the procedure, we perform calculations for the case of heat sources of constant density. The results show that the CGLE correctly predicts the type of bifurcation (supercritical bifurcation) in agreement with experimental data. This means that when the base flow becomes linearly unstable, a new laminar flow with a more complicated structure sets in. In addition, the CGLE also predicts the existence of periodic solutions for some values of the parameters also in agreement with experimental data.
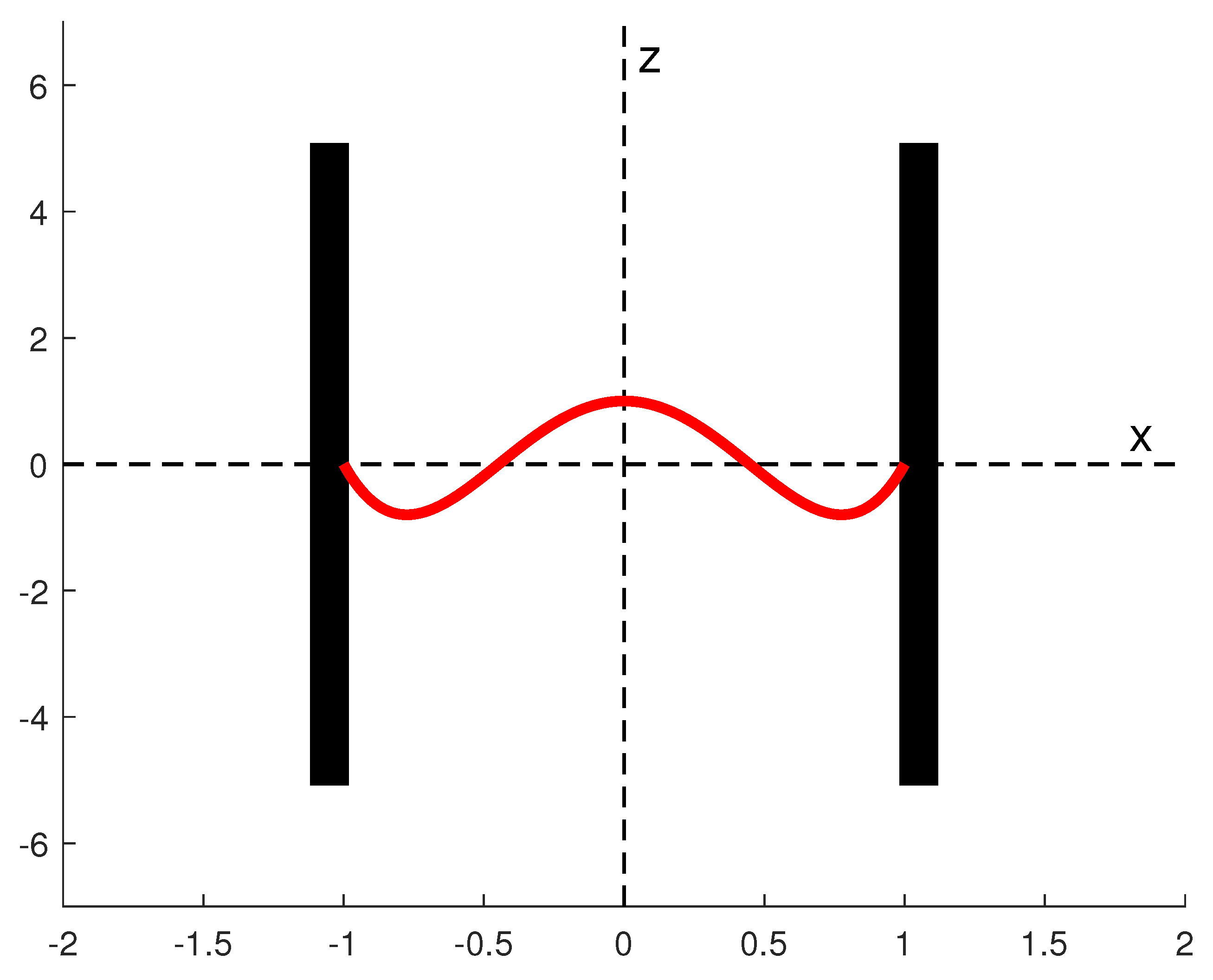
2. Mathematical Formulation of the Problem
3. Linear Stability Analysis
4. Weakly Nonlinear Stability Analysis
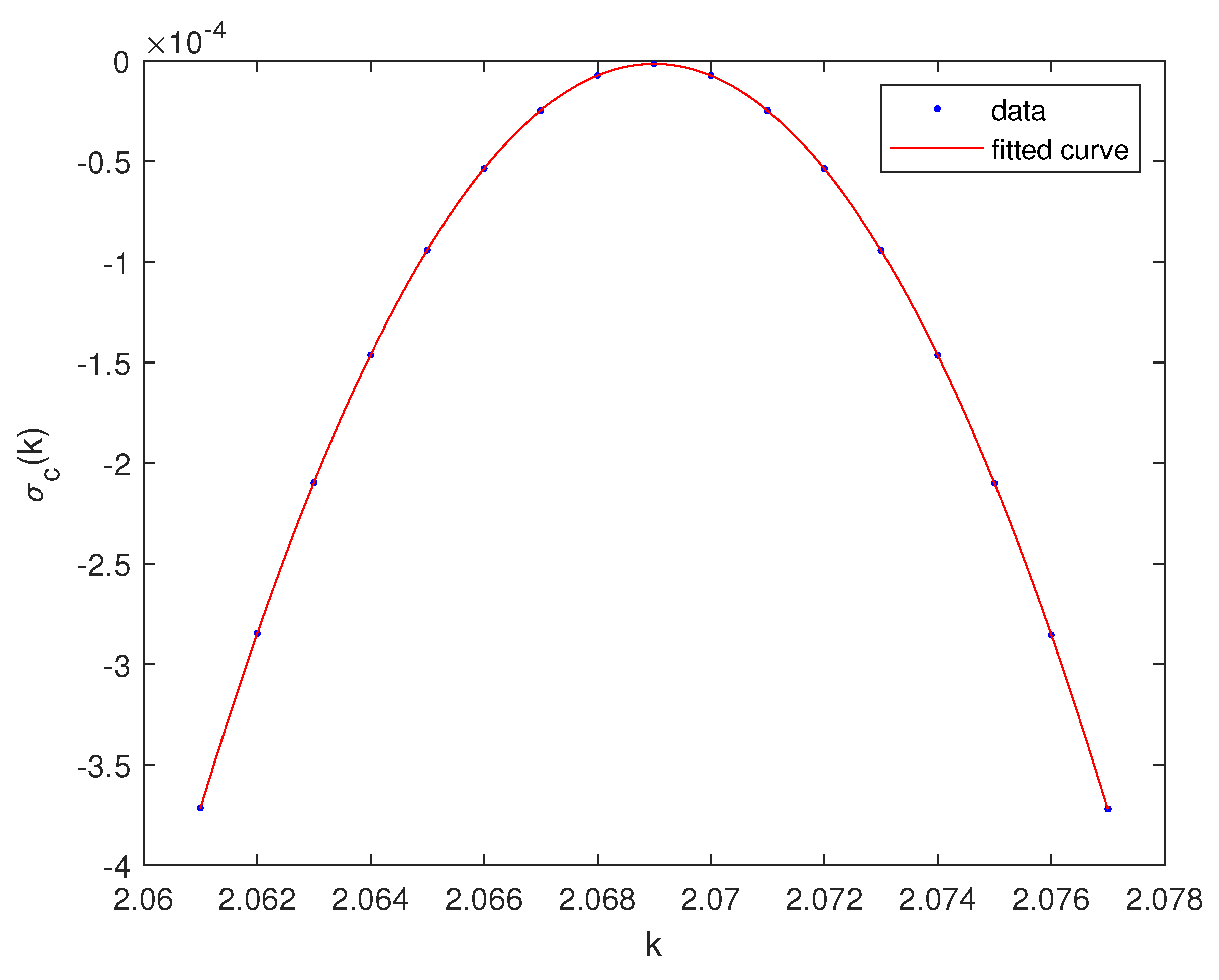
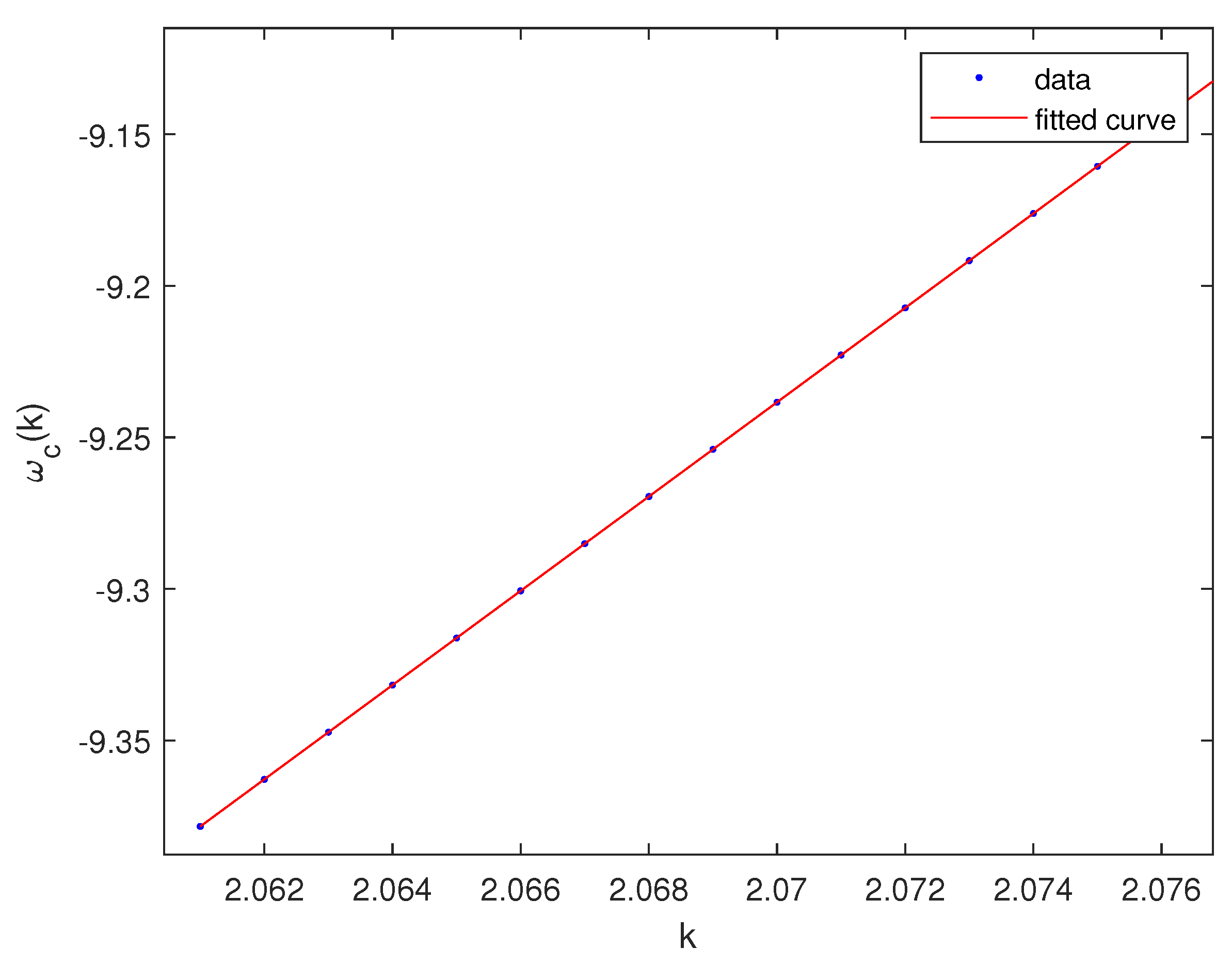
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richard, Y. Physics of mantle convection. In Treatise of Geophysics; Elsevier: New York, NY, USA, 2015; Volume 7, pp. 23–71. [Google Scholar]
- Hudoba, A.; Molokov, S. Linear stability of buoyant convective flow in a vertical channel with internal heat sources and a transverse magnetic field. Phys. Fluids 2016, 28, 114103. [Google Scholar] [CrossRef]
- Lewandowski, W.M.; Ryms, M.; Kosakowski, W. Thermal biomass conversion: A review. Processes 2020, 8, 516. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kalis, H.; Marinaki, M.; Strautins, U.; Zake, M. On numerical simulation of electromagnetic field effects in the combustion process. Math. Model. Anal. 2018, 23, 327–343. [Google Scholar] [CrossRef]
- Schmid, P.J.; Henningson, D.S. Stability and Transition in Shear Flows. Springer: New York, NY, USA, 2001. [Google Scholar]
- Stewartson, K.; Stewart, J.T. A non-linear instability theory for a wave system in plane Poiseuille flow. J. Fluid Mechnanics 1971, 48, 529–545. [Google Scholar] [CrossRef]
- Kolyshkin, A.A.; Ghidaoui, M.S. Stability analysis of shallow wake flows. J. Fluid Mechnanics 2003, 494, 355–377. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Kolyshkin, A.A. A quasi-steady appraoch to the instability of time-dependent flows in pipes. J. Fluid Mechnanics 2002, 465, 301–330. [Google Scholar] [CrossRef]
- Gershuni, G.Z.; Zhukhovitskii, E.M.; Iakimov, A.A. Two kinds of instability of stationary convective motion induced by internal heat sources. J. Appl. Math. Mech. 1973, 37, 544–548. [Google Scholar] [CrossRef]
- Takashima, M. The stability of natural convection in a vertical fluid layer with internal heat generation. J. Phys. Soc. Jpn. 1983, 52, 2364–2370. [Google Scholar] [CrossRef]
- Takashima, M. The stability of natural convection due to internal heat sources in a vertical fluid layer. Fluid Dyn. Res. 1990, 6, 15–23. [Google Scholar]
- Shikhov, V.M.; Yakushin, V.I. Stability of convective motion caused by inhomogeneously distributed internal heat sources. Fluid Dyn. 1977, 12, 457–461. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Exchange in Chemical Kinetics; Princeton: Princeton, NJ, USA, 1955. [Google Scholar]
- Eremin, E.A. On the stability of steady convective motion generated by internal heat sources. Fluid Dyn. 1983, 18, 438–441. [Google Scholar] [CrossRef]
- Gritsans, A.; Kolyshkin, A.; Sadyrbaev, F.; Yermachenko, I. On the stability of a convective flow with nonlinear heat sources. Mathematics 2023, 11, 3895. [Google Scholar] [CrossRef]
- Boussinesq, J. Théory Analytique de la Chaleur; Gauthier-Villars: Paris, France, 1903. [Google Scholar]
- Spiegel, E.A.; Veronis, G. On the Boussinesq approximation for a compressible fluid. Astrophys. J. 1960, 131, 442–447. [Google Scholar] [CrossRef]
- Mihailjan, J.M. A rigorous exposition of the Boussinesq approximation applicable to a thin layer of luid. Astrophys. J. 1962, 136, 1126–1133. [Google Scholar] [CrossRef]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Convective Stability of Incompressible Fluids; Ketter Publications: Jerusalem, Israel, 1976. [Google Scholar]
- Gray, D.D.; Giorgini, A. The validity of the Boussinesq approximation for liquids and gases. Int. J. Heat Mass Transf. 1976, 19, 545–551. [Google Scholar] [CrossRef]
- White, D., Jr.; Johns, L.E. The Frank-Kamenetskii transformation. Chem. Eng. Sci. 1987, 42, 1849–1851. [Google Scholar] [CrossRef]
- Squire, H.B. On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. 1933, A142, 621–628. [Google Scholar]
- Gershuni, G.Z.; Zhukhovitskii, E.M.; Iakimov, A.A. On the stability of plane-parallel convective motion due to internal heat sources. Int. J. Heat Mass Transf. 1974, 17, 717–726. [Google Scholar] [CrossRef]
- Zvillinger, D. Handbook on Differential Equations; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Le Gal, P.; Ravoux, J.F.; Floriani, E.; Dudok de Wit, T. Recovering coefficients of the complex Ginzburg-Landau equation from experimental spatio-temporal data: Two examples from hydrodynamics. Phys. D Nonlinear Phenom. 2003, 174, 114–133. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Applications, 2nd ed.; Elsevier: New York, NY, USA, 2014. [Google Scholar]
- Suslov, S.A.; Paolucci, S. Stability of non-Boussinesq convection via the complex Ginzburg-Landau model. Fluid Dyn. Res. 2004, 35, 159–203. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Krekhov, A.P. An introduction to the Ginzburg-Landau theory of phase transitions and nonequilibrium patterns. Phys. Rep. 2015, 572, 1–42. [Google Scholar] [CrossRef]
- Aranson, I.S.; Kramer, L. The world of complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Kozlov, V.G. Experimental investigation of stability of convective motion of a fluid due to internal heat sources. Fluid Dyn. 1978, 13, 503–507. [Google Scholar] [CrossRef]
- Khan, A.; Bera, P. Waekly nonlinear stability analysis of non-isothermal parallel flow in a vertical porous annulus. Int. J. Non-Linear Mech. 2024, 160, 104630. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Kolyshkin, A.A.; Liang, J.H.; Chan, F.C.; Li, Q.; Xu, K. Linear and nonlinear analysis of shallow wakes. J. Fluid Mech. 2006, 548, 309–340. [Google Scholar] [CrossRef]
- Couairon, A.; Chomaz, J.-M. Primary and secondary nonlinear global instability. Phys. D 1999, 132, 428–456. [Google Scholar] [CrossRef]

| 0 | 1719.11 | 2.07 | 0 |
| 0.05 | 1641.22 | 2.06 | 4.53 |
| 0.1 | 1572.65 | 2.05 | 8.52 |
| 0.2 | 1451.35 | 1.96 | 15.58 |
| N | |
|---|---|
| 20 | 1719.105329719 |
| 30 | 1719.518187156 |
| 40 | 1719.518187156 |
| 50 | 1719.518187156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budkina, N.; Koliskina, V.; Kolyshkin, A.; Volodko, I. Weakly Nonlinear Instability of a Convective Flow in a Plane Vertical Channel. Fluids 2025, 10, 111. https://doi.org/10.3390/fluids10050111
Budkina N, Koliskina V, Kolyshkin A, Volodko I. Weakly Nonlinear Instability of a Convective Flow in a Plane Vertical Channel. Fluids. 2025; 10(5):111. https://doi.org/10.3390/fluids10050111
Chicago/Turabian StyleBudkina, Natalja, Valentina Koliskina, Andrei Kolyshkin, and Inta Volodko. 2025. "Weakly Nonlinear Instability of a Convective Flow in a Plane Vertical Channel" Fluids 10, no. 5: 111. https://doi.org/10.3390/fluids10050111
APA StyleBudkina, N., Koliskina, V., Kolyshkin, A., & Volodko, I. (2025). Weakly Nonlinear Instability of a Convective Flow in a Plane Vertical Channel. Fluids, 10(5), 111. https://doi.org/10.3390/fluids10050111





