A Review of Diffuse Interface-Capturing Methods for Compressible Multiphase Flows

Abstract

This paper discusses in detail the classification, historical development, and application of diffuse interface-capturing models (DIMs) for compressible multiphase flows. The work begins with an overview of the development of DIMs, highlighting important contributions and key moments from classical studies to contemporary advances. The theoretical foundations and computational methods of the diffuse interface method are outlined for the full models and the reduced models or sub-models. Some of the difficulties encountered when using DIMs for multiphase flow modelling are also discussed.

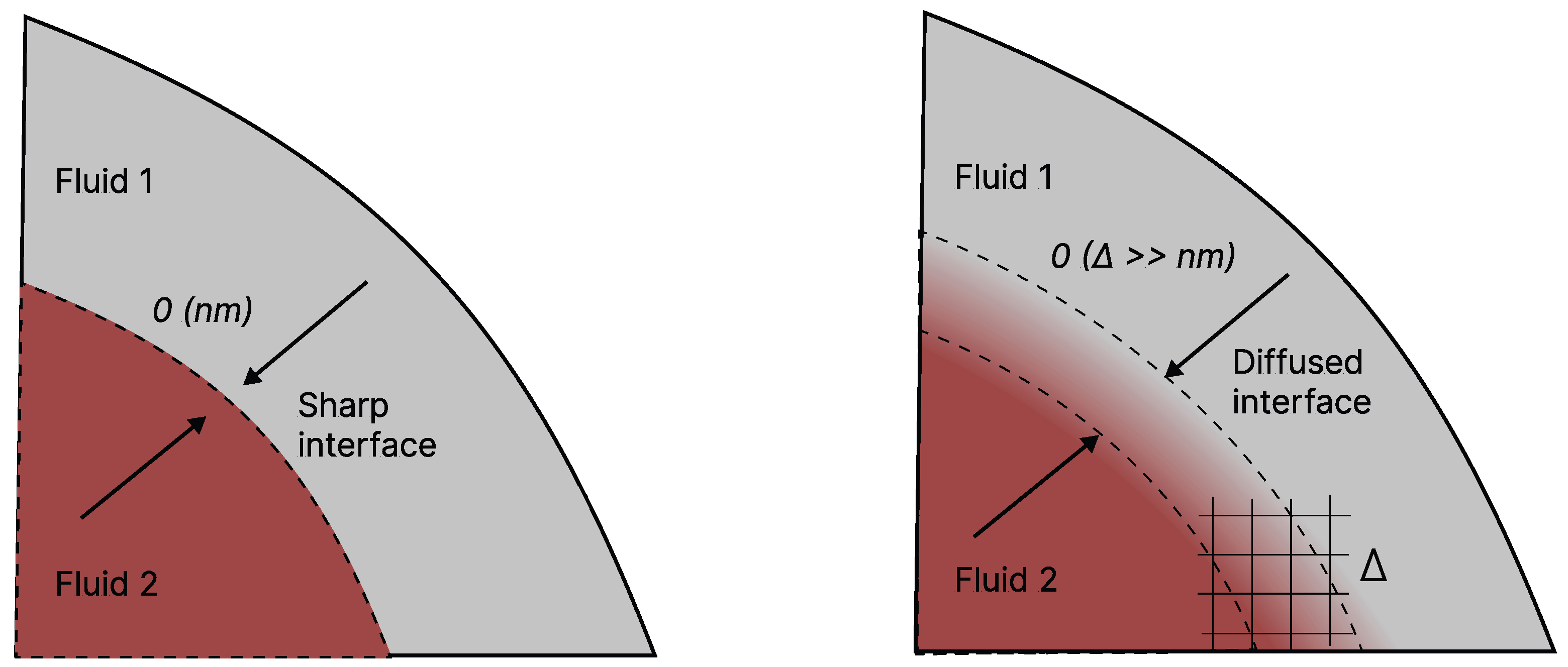
1. Introduction

Compressible multiphase flow occurs both in nature and across various industrial processes, from chemical manufacturing and aerospace engineering to environmental science. This type of flow occurs when fluids—often gases—experience significant density changes due to variations in pressure and temperature.

In nature, examples of compressible multiphase flow include gas explosions in mines, underwater volcanic eruptions, and hurricanes. In industrial contexts, they occur in processes like fuel injection in internal combustion engines (ICEs) and jet engines, desalination in a nuclear reactor, and underwater motion of high-speed projectiles, where gas and liquid phases interact under high-pressure conditions.

Single-phase compressible flows are ubiquitous in CFD and primarily characterised by a discontinuous wave in the form of shock waves and solved using the Euler or Navier–Stokes equations. Compressible multiphase flows, on the other hand, are characterised by not just shock waves but a new form of discontinuity in the form of contact waves at the interface. The wide application of compressible multiphase flow in science and engineering has led to much work being devoted to solving and understanding the models of the interfacial interactions between fluids. The interface of compressible multiphase flows frequently has a different thermodynamic property than the two interacting fluids and can obey different equations of state (EoSs). The numerical modelling of the material interface of compressible multiphase flows requires the Euler or Navier–Stokes equation for each fluid coupled with extra equation(s) for the interface. The complexity of the physics involved in the phase change of the mixture, the high gradients of flow variables, the choice of numerical discretisation to capture these phenomena, and obtaining experimental results for validation are several factors that make the numerical modelling of such flows challenging.

When numerically modelling compressible multiphase flow, two parameters are of interest and importance: how that interface is being treated and the location or position of the material interface between the two fluids. The location of the constantly changing interface must first be identified and then treated either as a sharp boundary or as a diffuse zone. The traditional approach to treating the interface between two fluids is to consider the interface to be infinitely sharp, i.e., with a thickness of zero. The material interface in the flow between the fluids is treated as an infinitely thin free boundary. The physical internal structure of such an interface is not considered or resolved. This assumption is reasonable and straightforward in many cases since the interface thickness of such a flow is infinitesimal, on the order of a few Angstroms ($1={10}^{-10}$ m). These methods described above in which the interface is advected and regarded as a sharp discontinuity are often regarded generally as “Sharp Interface Models” (SIM) (Figure 1).

Locating the position of the interface has two common approaches. The interface can be tracked using a Langragian moving mesh or captured on a fixed Eulerian grid. The Lagrangian models deform with each fluid’s particle and interface motion. They are commonly used for dispersed flow. The physical properties such as mass, velocity, temperature, and position of the single particles are tracked. This can be cumbersome, especially for a complex geometry and three-dimensional cases. This is because tracking the interface often leads to large deformations due to re-meshing. To circumvent this problem, sharp interface-capturing methods used for advecting the interface are the Volume of Fluid (VoF), level set (LS) and the Ghost Fluid Method (GFM). Coupled with the momentum, energy, and volume species equations for each phase, the interface, treated as a free boundary, is supplemented with boundary conditions and equations. Many works have been conducted to improve on their significant drawbacks: low-speed flows, low density–viscosity ratios, and mass-conservation errors [1,2,3,4]. In a wide range of situations, the interface is treated as a free boundary, while its tracked/captured motion is sufficient and reasonable. These methods of tracking/capturing the interface, while the interface is featured as a sharp boundary, are regarded, in this paper, as sharp interface-tracking/capturing methods. In many works in the literature, the terms “Sharp Interface” (SI) and “Sharp Interface Model/Method” (SIM) are commonly used to describe computational approaches that treat the interface between different phases as a distinct, sharp boundary. This characterisation encompasses both interface tracking methods, which explicitly follow the interface’s position using computational elements like grids or markers, and certain interface-capturing methods designed to maintain a sharp interface representation within a fixed computational grid. Consequently, “Sharp Interface” can refer to both tracking and capturing models that treat the interface as a sharp boundary, irrespective of whether the interface is explicitly tracked or reconstructed (Figure 2). In flows involving changes in the topology of the interface, the structural composition of the interface plays a critical role. In situations where the interface is involved, the physical mechanisms that act on the interface may be of a scale similar to the thickness of the interface that separates the two fluids in contact. This can lead to a deformation of the interface and changes in the topology, such as the merging of bubbles or the breakup of liquid droplets, underwater explosions, etc. Assuming a zero thickness for the interface can lead to errors in calculating the interfacial forces and the mass transfer rates. In such cases, the interface may have a finite thickness due to the interfacial tension effects or thermal diffusion, and neglecting this thickness can be erroneous.

To accurately capture the internal structure of the interface, another approach for treating the interface is to capture the interface as diffuse zones. This method provides a smooth representation of the interface, taking into account the interfacial thickness and the associated physical mechanisms. These methods are referred to in many works in the literature as the “Diffuse Interface” or “Diffuse Interface Models” (DI or DIMs). In Diffuse Interface Models, the two fluids are assumed to have different densities, viscosities, and other physical properties but are allowed to mix across the interface zone. They are built upon the averaging procedures of the local conservation and thermodynamic laws. The average values of volume fraction and thermodynamic quantities like the fluids’ momentum, energy, and pressure are determined by solving a set of equations on a fixed Eulerian grid. The solution of the conserved quantities then evolves across all computational cells via numerical discretisation, resulting in numerical or artificial diffusion across multiple grids without the need to explicitly track or reconstruct them, as in the SIM. In this review, we employ the abbreviation DIM, standing for “diffuse interface-capturing model”, to denote methods where the diffuse interface is not explicitly tracked. Instead, its evolution is implicitly resolved as a component of the governing equations’ solution. In order to understand the dynamics of phase transitions and the behaviour of materials at interfaces, it is crucial to compute internal energies and temperatures at the interfaces in an accurate and efficient manner. The diffuse interface-capturing model (DIM) has gained popularity over the last few decades due to advancements in computational power, which have allowed for more efficient and accurate simulations of multiphase, multicomponent and multispecies systems. An overview of Sharp Interface Models and diffuse interface-capturing models is presented in Figure 2. Diffuse interface-capturing models offer several key advantages over SIM, in that:

• They simplify the handling of complex deforming interfaces by treating them as transition regions with varying material properties rather than sharply defined boundaries.
• The computational efficiency is improved by eliminating the need for explicit interface tracking, which is particularly beneficial in large-scale and complex simulations.
• They are capable of accurately capturing discontinuities such as shock and contact waves, which are essential in compressible flow simulations.
• They provide flexibility in handling abrupt variations in thermodynamic properties across interfaces.
• They minimise spurious numerical oscillations, leading to more stable and reliable simulations.

Historically, the concept of interfaces separating multiphase flows traces back at least two centuries, with foundational ideas proposed by Young, Gauss, and Laplace in the early 19th century [5]. Initially conceptualised as zero-thickness boundaries, interfaces were assumed to represent free boundaries subject to surface tension, with physical parameters such as capillarity described by the Young–Laplace equation [6]. The evolution of this concept in the late 19th century led to the consideration of interfaces as thin layers with non-zero thickness (i.e., a diffuse zone), where strong gradients of some physical properties take place, a notion articulated by Poisson and Clausius (1831) [7], Maxwell (1876) [8], and Gibbs (1878) [9,10].

Gibbs’ seminal work [9] on the equilibrium of heterogeneous substances in 1878 laid the groundwork for subsequent advancements, with Rayleigh (1892) [11] and van der Waals (1893) [12] developing gradient theories for predicting interface thickness. However, challenges persisted in accurately estimating interface thickness due to the inability of accounting for non-equilibrium effects 1959 [13]. Nonetheless, pioneering contributions by Ono and Hillert (1956) [14] in the mid-20th century marked a significant milestone in the development of diffuse interface-capturing models.

The categorisation of DIMs into Phase Field Models (PFMs) and Multi-Fluid Models (MFMs) serves as a foundational framework for understanding their diverse methodologies and applications [15,16,17,18]. From the above historical perspective, all DIMs, in general, treat the interface as a volumetric region or thin layer. The PFM, rooted in the Cahn–Hilliard equation [13], conceptualises interfaces as transition layers and is excellent at capturing intricate interface topologies with varying shapes and complexities [5], such as immiscible liquids geometrically constrained to a small-scale (microfluidics) and turbulent two-phase flows, and can also capture phenomena such as coalescence, break-up, and phase separation. Its key features are interface motion and thickness estimation. For further insights into the PFMs, the reader is referred to [19,20]. Conversely, MFMs treat interfaces as diffuse surfaces, allowing for artificial mixing between phases, albeit with potential trade-offs in accurately representing intricate interface structures, but they are advantageous in terms of computational cost. The individual phase has its distinct fluid and governing equations. The interface is represented as a transition region between the fluids, and its thickness is usually taken as a small but finite value.

Most of these models in the category of MFMs have their fundamentals from the Volume of Fluid (VoF) methods developed by Hirts and Nicols [21]. The most complete set of MFMs is the Baer–Nunziato [22] seven-equation model. It consists of two mass conservation equations, two momentum equations, two energy equations, and one additional equation that describes the topology of the flow, such as advection or convection.

The original Baer–Nunziato model has a significant number of waves, which can make it computationally expensive and difficult to use. It may also be sensitive to numerical relaxation techniques. To address these problems, simplified versions of the Baer–Nunziato model have been created, using equilibrium assumptions to lessen the number of waves and improve the model’s computational efficiency.

The Baer–Nunziato equations are simplified by assuming thermodynamic equilibrium between the two phases, which allows for the elimination of some of the non-equilibrium terms in the equations. This reduces the number of waves in the system and makes the model more stable and easier to solve numerically. The equilibrium assumptions used in these models may include assumptions about temperature and pressure equilibrium, as well as assumptions about the mass transfer rates between the two phases.

Several simplified versions of the full Baer–Nunziato model have been developed due to its non-conservative nature, and these reduced models are now widely used in practical engineering applications. Some of the most commonly used simplified models include the Kapila et al. model [23], the Allaire et al. model [24], the Saurel et al. model [25], the Murrone et al. model [26], and the Abgrall et al. model [27].

The “ideal” MFM for solving a compressible multiphase system is strictly hyperbolic, fully conservative, and follows thermodynamic laws [28]. However, it is often challenging to develop a model that meets all three criteria simultaneously, and trade-offs may need to be made between accuracy and computational efficiency.

In recent years, much work has been performed to improve existing models and develop new models that better satisfy the “ideal” mathematical conditions. This includes the development of new numerical methods and algorithms that are better suited to solving the complex equations governing multiphase flows. Efforts have also been made to incorporate more accurate thermodynamic models and equations of state into the models to improve their accuracy [29,30,31,32].

The Baer–Nunziato model’s non-conservative nature makes it a non-equilibrium because there is a total disequilibrium of velocity and pressure between the two phases in contact.

The reduced or sub-models of the full seven equations in the Baer–Nunziato (B-N) model [22] are obtained via asymptotic expansions, wherein physical properties like pressure, velocity, and temperature are assumed to reach equilibrium between phases. To the best of the authors’ knowledge, Saurel and Abgrall (1999) [25] were the pioneers in developing such sub-models for the Baer–Nunziato equations, extending the approach to compressible multiphase flow. After their work, various other models have emerged, categorised based on equilibrium assumptions or relaxation techniques applied to the non-equilibrium Baer–Nunziato equations. Given that each phase (indexed by k) possesses distinct pressures ($p_k$), temperatures ($T_k$), velocities ($v_k$), and chemical potentials (${\mu }_k$), different relaxation methods have been utilised to attain mixture–phase equilibrium. These methods include relaxation towards mechanical equilibrium (where velocity and pressure approach equilibrium at interfaces), thermal equilibrium (minimising heat transfer between phases), velocity equilibrium, pressure equilibrium, or combinations thereof (e.g., mechanical and thermal equilibrium). Each relaxation technique is tailored to suit specific compressible multiphase flow cases, researcher requirements, and computational constraints. The number of equations in existing reduced models varies from four (4) to six (6), contingent upon the relaxation strategies employed. These sub-models have proven effective in addressing compressible multiphase flow challenges, with the advantage of incorporating additional physics such as surface tension, heat conduction, viscous stresses, and gravitational effects to tackle specific flow conditions.

The mechanical equilibrium models proposed by Allaire and Massoni (2002) [24], Guillard and Murrone (2005) [26], and Kapila (2009) [23] have garnered significant attention in many works in the literature. Saurel’s six-equation model (1999) [25], which considers velocity equilibrium, is also notable in this context. Additionally, Romenski (2019) [28] introduced a newer seven-equation model.

In the subsequent sections, a chronological model hierarchy will be presented through the categorisation of the full models and the sub-models based on the specific numerical relaxation methodologies or procedures employed (Figure 3). The high-order methods used for enhancing accuracy in diffuse models are reviewed in detail. The challenges associated with DIM application in compressible multiphase flow and the most recent applications of these models in the current literature are also examined. Furthermore, the interface-sharpening techniques used in reducing the numerical diffusion and improving the interface resolution are explored. This paper aims to provide an updated overview with a particular focus on the recent developments while offering guidance for new researchers entering the field of diffuse frameworks (Figure 4).

Noteworthy contributions from various authors who have extensively reviewed this domain are also acknowledged [10,16,27,33,34]. One of the first reviews in this direction is Saurel’s 2018 [34] review, which examines the formulation and implementation of diffuse models for compressible multiphase flows with material interfaces. It specifically details the Saurel seven-equation, Saurel six-equation, and Kapila five-equation models, along with some of their applications.

Another significant review is Maltsev (2022) [33], which focuses on high-order schemes for handling discontinuities within the diffuse realm. It details the recent advancements of these numerical schemes and further discusses their application to multi-species and multicomponent flows within the diffuse framework, using the finite volume, discontinuous Galerkin, and lattice Boltzmann methods.

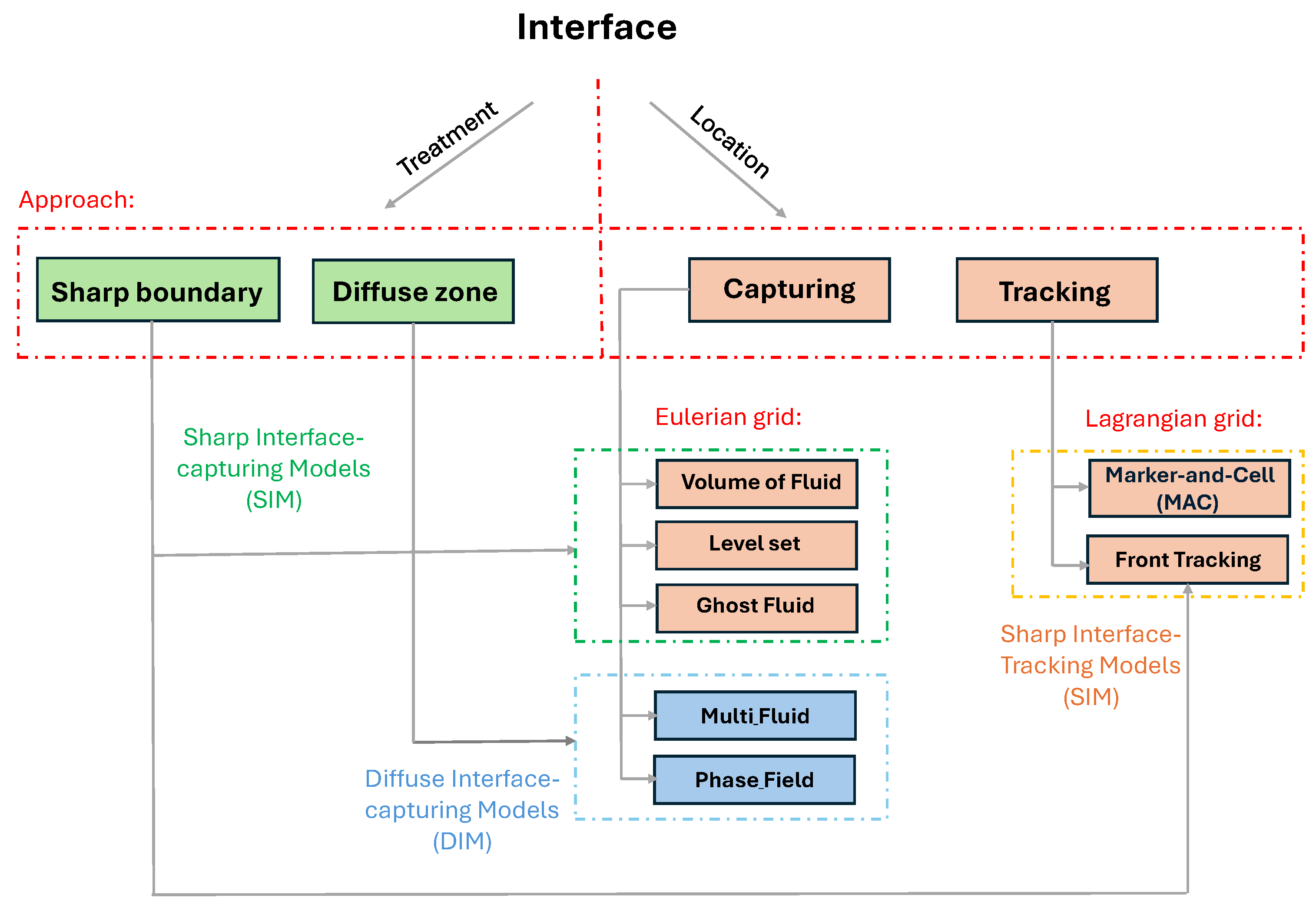
2. Total Non-Equilibrium Models

The most comprehensive forms of the diffuse model for multi-fluids are represented by total non-equilibrium models. These models consist of seven sets of hyperbolic partial differential equations (PDEs), wherein each fluid phase is characterised by its own pressure ($p_k$), temperature ($T_k$), velocity ($u_k$), and other physical parameters. They are referred to as non-equilibrium models due to the complete lack of equilibrium between the physical variables (such as pressure, temperature, velocity, and chemical compositions) assumed across the two distinct phases.

The set of seven equations comprises two mass equations, two energy equations, two momentum equations, and one equation for each phase to delineate the volume fraction or topology of the interface. Examples of models falling into this category include the Baer–Nunziato seven equations [22], the Saurel–Abgrall seven equations [25], and the Romenski seven equations [28] (Figure 5).

While these total non-equilibrium models are capable of accurately describing a wide range of multiphase flows, they come with significant computational costs and complexity due to the non-conservative source terms present in them, which are expressed as differential or algebraic expressions representing interfacial forces within the fluid.

Saurel–Abgrall, employing ensemble averaging procedures as outlined by Drew and Passmann [35], developed a seven-equation model based on the full Baer–Nunziato equations by disregarding dissipative terms. Romenski, on the other hand, proposed an alternative set of equations to address the non-conservative nature of Baer–Nunziato models. His approach yielded another set of seven conservative equations, which are hyperbolic (non-symmetric) and can be expressed in divergent forms [36], unlike the seven equations of Saurel–Abgrall and Baer–Nunziato that are hyperbolic but non-symmetric (Figure 5). Each of these models will be discussed subsequently.

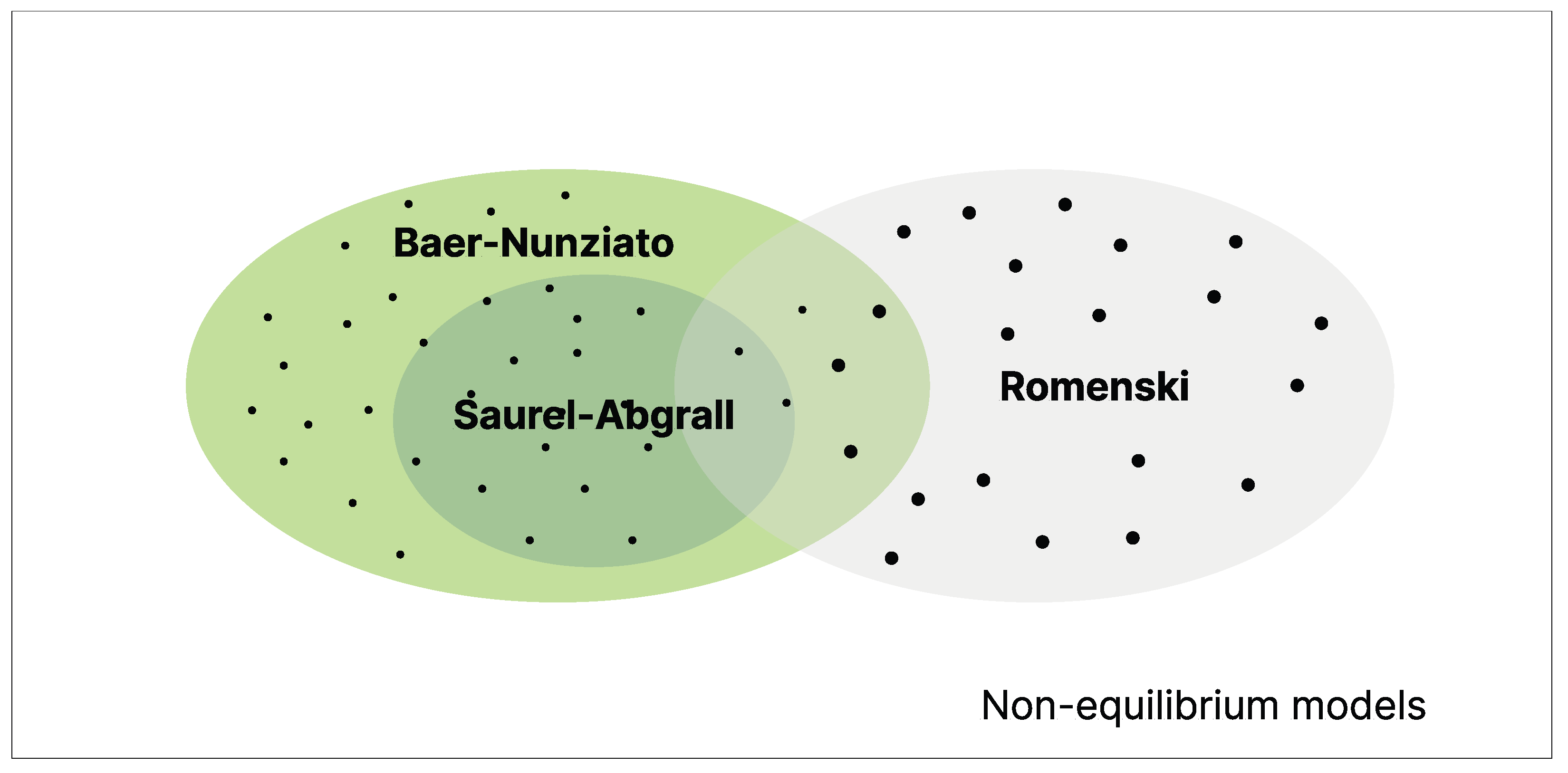
2.1. Baer–Nunziato Non-Equilibrium Model

The Baer–Nunziato (B-N) model stands as the foundation for numerous methodologies within the Multi-Fluid Model (MFM) category of diffuse interface methods. Originating from Baer and Nunziato’s seminal work in 1986, this hyperbolic set of seven equations was initially derived to solve the deflagration to detonation transition in explosive materials (DDT). Over time, its applicability has expanded to encompass a broad spectrum of compressible multiphase flows. It represents one of the most versatile full non-equilibrium multiphase flow models within this domain.

The equations consist of the conservation principles governing mass, momentum, and energy for each phase k, alongside equations describing interfacial area and phase change processes. These conservation equations, formulated for each phase, incorporate terms to account for interfacial momentum and energy exchange on an Eulerian grid system. However, a prominent challenge inherent to this model is its non-conservative nature as mentioned previously. In its original formulation, expressing it in either conservative or divergent form remains elusive, complicating the definition of a discontinuous solution like shock waves and contacts.

The seven equations, consists of the two mass conservation Equations (2) and (3), the two momentum Equations (4) and (5), the two energy Equations (6) and (7), and an additional equation describing volume fraction dynamics (1). Each phase is delineated and characterised by distinct thermodynamic properties, including pressure, velocity, temperature, and chemical potential.

A revised rendition of the classic Baer–Nunziato seven-equation model, introduced by Lund et al. [37,38], incorporates considerations for mass exchange and heat transfer. This revised version explicitly incorporates relaxation processes as source terms on the right-hand side (RHS) of the equations for two-phase flow:

2.1.1. Volume Advection

The equation governing the advection of volume fraction (${\alpha }_1$) is expressed as follows:

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+{\overrightarrow{u}}_k·\nabla {\alpha }_1=\Psi ,$$

(1)

where $\Psi$ represents the source term associated with volume transfer.

2.1.2. Mass Conservation

The mass conservation equations for each phase are given by

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1\right)+\nabla ·\left({\alpha }_1{\rho }_1{\overrightarrow{u}}_1\right)=\Phi ,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2\right)+\nabla ·\left({\alpha }_2{\rho }_2{\overrightarrow{u}}_2\right)=-\Phi ,\hfill \end{array}$$

(3)

where $\Phi$ denotes the source term related to mass transfer.

2.1.3. Momentum Conservation

The momentum conservation equations for each phase are formulated as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{u}_1\right)+\nabla ·\left({\alpha }_1({\rho }_1{\overrightarrow{u}}_1+p_1)\right)-p_I·\nabla {\alpha }_1=\Lambda ,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2{u}_2\right)+\nabla ·\left({\alpha }_2({\rho }_2{\overrightarrow{u}}_2+p_2)\right)-p_I·\nabla {\alpha }_1=-\Lambda ,\hfill \end{array}$$

(5)

where $\Lambda$ represents the source term associated with the momentum transfer.

2.1.4. Energy Balance

The energy balance equations for each phase are expressed as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{E}_1\right)+\nabla ·\left({\alpha }_1{\overrightarrow{u}}_1\left({\rho }_1{E}_1+p_1\right)\right)-p_I{u}_I·\nabla {\alpha }_1=\Gamma ,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2{E}_2\right)+\nabla ·\left({\alpha }_2{\overrightarrow{u}}_2\left({\rho }_2{E}_2+p_2\right)\right)+p_I{u}_I·\nabla {\alpha }_1=-\Gamma ,\hfill \end{array}$$

(7)

where $\Gamma$ denotes the source term associated with the energy transfer.

The subscripts 1 and 2 represent the phases k, and ${\alpha }_k$ represent the volume fraction of each phase, respectively. The variables ${\rho }_k$, ${\overrightarrow{u}}_k$, $p_k$, and $E_k$ represent the density, velocity vector, pressure, and total energy per unit mass of each phase, respectively. They must satisfy the saturation constraint ${\alpha }_1+{\alpha }_2=1$. $p_I$ and $u_I$ represent the interfacial pressure and velocity, respectively, and are expressed as

$$p_I={\alpha }_1{p}_1+{\alpha }_2{p}_2,$$

(8)

$$u_I={\displaystyle \frac{{\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2}{{\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2}}.$$

(9)

The source terms $\Psi$, $\Phi$, $\Lambda$, and $\Gamma$ are dependent on the relaxation coefficients $\mathcal{J}$, $\mathcal{K}$, $\mathcal{L}$, and $\mathcal{M}$, respectively, which control the rate at which equilibrium is reached. These relaxation coefficients are functions of the pressures, chemical potentials, velocities, and temperatures of the two-phase flow:

$$\begin{array}{cc}\hfill & \Psi =\mathcal{J}(p_1-p_2),\hfill \\ \hfill & \Phi =\mathcal{K}({\mu }_1-{\mu }_2),\hfill \\ \hfill & \Lambda =\mathcal{K}({\mu }_1-{\mu }_2)+\mathcal{L}(u_1-u_2),\hfill \\ \hfill & \Gamma =(\mu +{\displaystyle \frac{1}{2}}{v}^2)\mathcal{K}({\mu }_1-{\mu }_2)+p\mathcal{J}(p_1-p_2)+\mathcal{M}(T_1-T_2).\hfill \end{array}$$

(10)

And they can be succinctly expressed in vector form as follows:

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+\nabla ·\mathbf{F}\left(\mathbf{Q}\right)+\mathbf{H}\left(\mathbf{Q}\right)·\nabla {\alpha }_1=\mathbf{S}\left(\mathbf{Q}\right),$$

(11)

where $\mathbf{Q}$ represents the evolution variables, $\mathbf{F}$ determines the flux of the system, $\mathbf{H}$ and $\mathbf{S}$ denote the non-conservative quantities, and $\mathbf{S}$ encompasses all source terms, while $\mathbf{H}$ remains a zero vector in this context:

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_1{\rho }_1\\ {\alpha }_1{\rho }_1{u}_1\\ {\alpha }_1{\rho }_1{E}_1\\ {\alpha }_2{\rho }_2\\ {\alpha }_2{\rho }_2{u}_2\\ {\alpha }_2{\rho }_2{E}_2\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1{\overrightarrow{u}}_k\\ {\alpha }_1{\rho }_1{\overrightarrow{u}}_1\\ {\alpha }_1{\rho }_2{\overrightarrow{u}}_2\\ {\alpha }_1({\rho }_1{\overrightarrow{u}}_1+p_1)\\ {\alpha }_2({\rho }_2{\overrightarrow{u}}_2+p_2)\\ {\alpha }_1{\overrightarrow{u}}_1\left({\rho }_2{E}_1+p_1\right)\\ {\alpha }_1{\overrightarrow{u}}_2\left({\rho }_2{E}_2+p_2\right)\end{array}\right],\mathbf{H}=\left[\begin{array}{c}0\\ 0\\ 0\\ -p_k\\ p_k\\ -p_k{u}_k\\ p_k{u}_I\end{array}\right]$$

(12)

$$\mathbf{S}=\left[\begin{array}{c}\Psi \\ \Phi \\ -\Phi \\ -\Lambda \\ \Lambda \\ \Gamma \\ -\Gamma \end{array}\right].$$

(13)

The Baer–Nunziato model embodies a hierarchy of sub-models for two-phase flow, influenced by relaxation processes categorised into four types:

• Velocity Relaxation (u-Relaxation): As the relaxation coefficient $\mathcal{L}$ tends to infinity, momentum transfer between phases leads to velocity equilibrium ($u_1\equiv u_2$).
• Pressure Relaxation (p-Relaxation): With $\mathcal{J}$ approaching infinity, volume transfer occurs between phases, resulting in pressure equilibrium ($p_1\equiv p_2$).
• Thermal Relaxation (T-Relaxation): As $\mathcal{M}$ tends to infinity, heat exchange between phases establishes thermal equilibrium ($T_1\equiv T_2$).
• Chemical Relaxation ($\mu$-Relaxation): As $\mathcal{K}$ approaches infinity, mass transfer between phases ensures chemical equilibrium.

These relaxation mechanisms govern the rate at which equilibrium is attained, and are dependent on the pressures, chemical potentials, velocities, and temperatures within the two-phase flow system.

2.2. Saurel–Abgrall Non-Equilibrium Model

In 1999, Saurel and Abgrall introduced a modified version of Baer and Nunziato’s model, tailored specifically for immiscible two-phase flow applications, employing Drew’s ensemble averaging procedure [35]. Unlike the Baer–Nunziato model, the Saurel–Abgrall model characterises pressure and velocity at the interface differently.

The numerical approximation of non-conservative terms becomes challenging when dealing with discontinuous functions, such as those encountered in shock waves and interfaces. Solving the Riemann problem for the S-A equations is difficult due to the lack of orderliness in the seven waves generated. Several authors [27,39,40,41,42,43,44,45] have made significant improvements and contributions to this model.

The original Saurel–Abgrall model consists of seven equations, although numerous simplified sub-models with fewer equations exist depending on the application. These equations form a hyperbolic system that describes the conservation of mass, momentum, and energy in each phase, along with the evolution of the interface between the phases. The seven-equation model is expressed below as presented in the paper [41]:

2.2.1. Volume Advection

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+{\overrightarrow{u}}_I·\nabla {\alpha }_1& =\mathcal{J}(p_1-p_2)\hfill \end{array}$$

(14)

2.2.2. Mass Conservation

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \left({\alpha }_1{\rho }_1\right)}{\partial t}}+\nabla ·\left({\alpha }_1{\rho }_1{\overrightarrow{u}}_1\right)& =0\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \left({\alpha }_2{\rho }_2\right)}{\partial t}}+\nabla ·\left({\alpha }_2{\rho }_2{\overrightarrow{u}}_2\right)& =0\hfill \end{array}$$

(16)

2.2.3. Momentum Conservation

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{u}_1\right)+\nabla ·\left({\alpha }_1({\rho }_1{\overrightarrow{u}}_1+p_1)\right)-p_k·\nabla {\alpha }_1=\mathcal{L}(u_2-u_1)\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2{u}_2\right)+\nabla ·\left({\alpha }_2{\overrightarrow{u}}_2({\rho }_2+p_2)\right)+p_k·\nabla {\alpha }_1=\mathcal{L}(u_2-u_1)\hfill \end{array}$$

(17)

2.2.4. Energy Balance

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{E}_1\right)+\nabla ·\left({\alpha }_1{\overrightarrow{u}}_1({\rho }_1{E}_1+p_1)\right)-p_k{u}_1·\nabla {\alpha }_1={\overline{u}}_I\mathcal{L}(u_2-u_1)-\mathcal{K}{\overline{p}}_I(p_1-p_2)\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2{E}_2\right)+\nabla ·\left({\alpha }_2{\overrightarrow{u}}_2({\rho }_2{E}_2+p_2)\right)-p_k{u}_k·\nabla {\alpha }_1=-{\overline{u}}_I\mathcal{L}(u_2-u_1)+{\overline{p}}_1\mathcal{J}(p_1-p_2)\hfill \end{array}$$

(18)

In compact vector form,

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+\nabla ·\mathbf{F}\left(\mathbf{Q}\right)+\mathbf{H}\left(\mathbf{Q}\right)·\nabla {\alpha }_1={\mathbf{S}}_v\left(\mathbf{Q}\right)+{\mathbf{S}}_p\left(\mathbf{Q}\right)$$

(19)

The vector of conserved variables $\mathbf{Q}$, flux tensor $\mathbf{F}$, and velocity field vector $\mathbf{u}$ are defined as

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_1{\rho }_1\\ {\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_1{\rho }_1{E}_1\\ {\alpha }_2{\rho }_2\\ {\alpha }_2{\rho }_2\mathbf{u}\\ {\alpha }_2{\rho }_2{E}_2\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1{\mathbf{u}}_I\\ {\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_1{\rho }_1{\mathbf{u}}^2+{\alpha }_1{p}_1\\ {\alpha }_1\mathbf{u}(E_1+p_1)\\ {\alpha }_2{\rho }_2\mathbf{u}\\ {\alpha }_2{\rho }_2{\mathbf{u}}^2+{\alpha }_2{p}_2\\ {\alpha }_2\mathbf{u}(E_2+p_2)\end{array}\right],\mathbf{H}\left(\mathbf{Q}\right)=\left[\begin{array}{c}-u_k\\ 0\\ p_k\\ u_k{p}_k\\ 0\\ -p_k\\ -u_k{p}_I\end{array}\right].$$

(20)

The source terms for velocity relaxation ${\mathbf{S}}_v$ and pressure relaxation ${\mathbf{S}}_p$ are expressed as

$$\begin{array}{cc}\hfill {\mathbf{S}}_v& =\left[\begin{array}{c}\mathcal{J}(p_1-p_2)\\ 0\\ 0\\ \mathcal{J}{p}_1(p_1-p_2)\\ 0\\ 0\\ \mathcal{J}{p}_1(p_1-p_2)\end{array}\right],\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mathbf{S}}_p& =\left[\begin{array}{c}0\\ 0\\ -\mathcal{L}(u_1-u_2)\\ -\mathcal{L}{u}_k(u_1-u_2)\\ 0\\ \mathcal{L}(u_1-u_2)\\ -\mathcal{L}{u}_k(u_1-u_2)\end{array}\right].\hfill \end{array}$$

(22)

To provide closure to the Saurel–Abgrall seven equations, in addition to the volume fraction constraint of both phases ${\alpha }_1+{\alpha }_2=1$ and the equation of state for each phase, the interfacial velocities and interfacial pressure are symmetric for both phases and are defined as

$$u_k=\overline{{\mathrm{u}}_I}+sgn(\nabla ·\left({\alpha }_1\right)){\displaystyle \frac{p_2-p_1}{Z_1+Z_2}},$$

(23)

$$p_k=\overline{{\mathrm{p}}_I}+sgn(\nabla ·{\alpha }_1){\displaystyle \frac{Z_1{Z}_2}{Z_1+Z_2}}(u_2-u_1).$$

(24)

where $\overline{{\mathrm{u}}_I}$ and $\overline{{\mathrm{p}}_I}$ are the interface velocity and volume average pressure, respectively, ${\mathrm{Z}}_{\mathrm{k}}={\rho }_{\mathrm{k}}{\mathrm{c}}_{\mathrm{k}}$ represents the acoustic impedance of each phase $\mathrm{k}$, and $\mathcal{J}$ and $\mathcal{L}$ control the relaxation rates towards mechanical equilibrium.

2.3. Romenski Seven-Equation Model

The seven-equation model, proposed by Romenski, offers a conservative and hyperbolic formulation, distinct from the Baer–Nunziato (B-N) and Saurel–Abgrall (S-A) models. The Symmetric Hyperbolic and Thermodynamically Compatible (SHTC) Romenski model provides conservative equations appropriate for diffuse systems based on a thermodynamically compatible formalism system and extended irreversible thermodynamic rules. Unlike Baer–Nunziato and Saurel–Abgrall equations, Romenski’s equations feature differences in interfacial pressure definitions, especially noticeable in multidimensional cases where phase momentum equations are interconnected with lift forces related to phase vorticities.

The Romenski model has been adapted under certain conditions, applied in compressible multiphase problems by various authors [28,36,46,47]. These equations are expressed in terms of mixture parameters of state, but Romenski and Toro [36] reformulated the model in terms of individual phases under isentropic conditions, which is the standard for the Baer–Nunziato models and sub-models. The Romenski seven-equation model in terms of individual phases is presented in one dimension for simplicity [36]:

$$\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2\right)=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\alpha }_1{\rho }_1{u}_1^2+{\alpha }_2{\rho }_2{u}_2^2+{\alpha }_1{p}_1+{\alpha }_2{p}_2\right)=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left(\left({\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2\right)\alpha \right)+{\displaystyle \frac{\partial }{\partial x}}\left(\left({\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2\right)\alpha \right)=-\Phi \hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\alpha }_1{\rho }_1{u}_1\right)=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left(u_1-u_2\right)+{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{u_1^2}{2}}-{\displaystyle \frac{u_2^2}{2}}+e_1+{\displaystyle \frac{p_1}{{\rho }_1}}-e_2-{\displaystyle \frac{p_2}{{\rho }_2}}\right)=-\Pi \hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{e}_1+{\alpha }_2{\rho }_2{e}_2+{\displaystyle \frac{u_1^2}{2}}+{\displaystyle \frac{u_2^2}{2}}\right)+\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial x}}\left({\alpha }_1{\rho }_1{u}_1\left(e_1+{\displaystyle \frac{p_1}{{\rho }_1}}+{\displaystyle \frac{u_1^2}{2}}\right)+{\alpha }_2{\rho }_2{u}_2\left(e_2+{\displaystyle \frac{p_2}{{\rho }_2}}+{\displaystyle \frac{u_2^2}{2}}\right)\right)=0.\hfill \end{array}\right.$$

(25)

The source terms on the right-hand side are expressed as

$$\Phi =-{\displaystyle \frac{1}{\tau }}\left(p_1-p_2\right),\Pi =-\kappa {\displaystyle \frac{\left({\alpha }_1{\rho }_1{\alpha }_2{\rho }_2\right)}{{\rho }^2}}(u_1-u_2),$$

(26)

where $\tau$ represents the pressure relaxation parameter, and $\kappa$ is the coefficient of interfacial friction, both functions of the mixture’s state parameters.

The interfacial speed ($u_I$) and pressure ($p_I$) follow the same definitions as in the Baer–Nunziato model:

$$\begin{array}{cc}\hfill u_I& ={\displaystyle \frac{{\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2}{{\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2}},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill p_I& ={\displaystyle \frac{{\alpha }_1{\rho }_1{p}_2+{\alpha }_2{\rho }_2{p}_1}{{\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2}}.\hfill \end{array}$$

(28)

In one dimension, the Romenski model can be compactly expressed in vector format:

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\mathbf{F}\left(\mathbf{Q}\right)=\mathbf{S}\left(\mathbf{Q}\right),$$

(29)

where $\mathbf{Q}$ is the vector of conserved variables, $\mathbf{F}$ represents the flux tensor, and $\mathbf{S}$ denotes the source terms:

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2\\ {\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2\\ ({\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2)\alpha \\ {\alpha }_1{\rho }_1\\ u_1-u_2\\ {\alpha }_1{\rho }_1{e}_1+{\alpha }_2{\rho }_2{e}_2+{\displaystyle \frac{p_1}{{\rho }_1}}+{\displaystyle \frac{u_1^2}{2}}\end{array}\right]$$

(30)

$$F=\left[\begin{array}{c}{\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2\\ {\alpha }_1{\rho }_1{u}_1^2+{\alpha }_2{\rho }_2{u}_2^2+{\alpha }_1{p}_1+{\alpha }_2{p}_2\\ ({\alpha }_1{\rho }_1{u}_1+{\alpha }_2{\rho }_2{u}_2)\alpha \\ {\alpha }_1{\rho }_1{u}_1\\ {\displaystyle \frac{u_1^2}{2}}-{\displaystyle \frac{u_2^2}{2}}+e_1+{\displaystyle \frac{p_1}{{\rho }_1}}-e_2-{\displaystyle \frac{p_2}{{\rho }_2}}\\ {\alpha }_1{\rho }_1{u}_1(e_1+{\displaystyle \frac{p_1}{{\rho }_1}}+{\displaystyle \frac{u_1^2}{2}})+{\alpha }_2{\rho }_2{u}_2(e_2+{\displaystyle \frac{p_2}{{\rho }_2}}+{\displaystyle \frac{u_2^2}{2}})\end{array}\right]$$

(31)

$${\mathbf{S}}_v=\left[\begin{array}{c}0\\ 0\\ -\Phi \\ -\Pi \\ 0\\ 0\end{array}\right]$$

(32)

3. Mechanical Equilibrium Model

The mechanical equilibrium model, often termed the “one pressure, one velocity” model, assumes that the momentum, energy, and mass transfer between different phases of a fluid reach equilibrium due to differences in their thermodynamic properties. This model maintains a single pressure and a single velocity for all the components of the fluid. In a two-dimensional space with dimensions x and y, the model provides velocity components and pressure for each component at multi-material interfaces. It is represented as

$$\begin{array}{cc}\hfill p_1& =p_2\equiv p\hfill \\ \hfill {\mathbf{u}}_1& ={\mathbf{u}}_2\equiv \mathbf{u}\hfill \\ \hfill {\mathbf{v}}_1& ={\mathbf{v}}_2\equiv \mathbf{v}\hfill \end{array}$$

(33)

This is enforced through the isobaric assumption of the Baer–Nunziato (B-N) equations. Due to the pressure differences between interacting components or phases, volume transfer is assumed.

Mechanical phase equilibrium is achieved when two phases or fluids interact. With mechanical equilibrium implemented, the full seven Baer–Nunziato equations are mostly reduced to five-equation models, making them simpler to solve numerically. These models are tailored for treating interfaces of non-miscible fluids in non-reacting flows, such as liquid–gas mixtures and flows involving free surfaces or pure interfaces. Note that this model only assumes mechanical equilibrium in the fluid; each phase remains in thermal disequilibrium, as there is no heat exchange between the two phases. Popular models in this category include those proposed by Allaire et al. (2002) and Kapila et al. (2001).

These equations consist of two continuity equations for each phase of the fluid, one momentum equation, and one energy equation. An additional non-conservative advection equation for the volume fraction is coupled with the equations. Models in this category have the same four conservative equations, presented below in Equation (34), with slightly varying formulations in the non-conservative advection equation for the volume fraction, which determine the position of the material interface between the two fluids.

Four equations for a two-phase flow:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \left({\alpha }_1{\rho }_1\right)}{\partial t}}+\nabla ·\left({\alpha }_1{\rho }_1\mathbf{u}\right)=0\hfill \\ {\displaystyle \frac{\partial \left({\alpha }_2{\rho }_2\right)}{\partial t}}+\nabla ·\left({\alpha }_2{\rho }_2\mathbf{u}\right)=0\hfill \\ {\displaystyle \frac{\partial \left(\rho \mathbf{u}\right)}{\partial t}}+\nabla ·(\rho \mathbf{u}\otimes \mathbf{u})+\nabla p\hfill & =0\hfill \\ {\displaystyle \frac{\partial \left(\rho E\right)}{\partial t}}+\nabla ·\left((\rho E+p)\mathbf{u}\right)\hfill & =0\hfill \end{array}\right.$$

(34)

where subscripts 1 and 2 represent the fluid’s component, $\alpha$ is the volume fraction of each component, $\rho$ is the density, $\mathbf{u}=(u,v,w)$ is the velocity, p is the pressure, and E is the total specific energy.

The advection equation for the volume fraction in Allaire’s five-equation model is

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+\mathbf{u}·\nabla {\alpha }_1=0$$

(35)

In Kapila’s five-equation model, it is represented as

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+\mathbf{u}·\nabla {\alpha }_1=K\nabla ·\mathbf{u}$$

(36)

Tiwari recast the Kapila model’s advection equation into conservative form as

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+\nabla ·\left({\alpha }_1\mathbf{u}\right)=K\nabla ·\mathbf{u}$$

(37)

where the K term in the advection equation is defined as

$$K={\displaystyle \frac{{\alpha }_1{\rho }_1{c}_2^2}{{\alpha }_2{\rho }_1{c}_1^2+{\alpha }_1{\rho }_2{c}_2^2}}$$

(38)

The Wood’s speed of sound in the original Kapila et al. model is represented by

$${\displaystyle \frac{1}{\rho c^2}}={\displaystyle \frac{{\alpha }_1}{{\rho }_1{c}_1^2}}+{\displaystyle \frac{{\alpha }_2}{{\rho }_2{c}_2^2}}$$

(39)

where the speed of sound for each phase is defined as

$$c_1=\sqrt{{\displaystyle \frac{{\gamma }_1}{{\rho }_1}}\left(p+p_{c,1}\right)},c_2=\sqrt{{\displaystyle \frac{{\gamma }_2}{{\rho }_2}}\left(p+p_{c,2}\right)}$$

(40)

The mixture speed of sound used in Allaire et al.’s five-equation model is derived from the SG-EoS as in Equation (41):

$$c=\sqrt{{\displaystyle \frac{\gamma (p+{\pi }_{\infty })}{\rho }}}$$

(41)

The equations are expressed in a non-conservative form, but a quasi-conservative approach is adopted by reformulating the advection equation in Equations (42) and (43) to handle the numerical challenges while preserving accuracy:

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+\nabla ·f=\left({\alpha }_1\right)\nabla ·\mathbf{u}$$

(42)

$${\displaystyle \frac{\partial {\alpha }_1}{\partial t}}+\nabla ·\mathbf{f}=\left({\alpha }_1+K\right)\nabla ·\mathbf{u}$$

(43)

These models generally express a non-linear system of partial differential equations (PDEs) in two-phase fluid as shown in Equation (44), where Q is the vector of conserved variables, F represents the flux tensor, and $\mathbf{u}$ is the velocity field. The S-vector includes all source terms, in this case, a zero vector:

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+\nabla ·\mathbf{F}\left(\mathbf{Q}\right)+\mathbf{H}\left(\mathbf{Q}\right)\nabla ·u=\mathbf{S}\left(\mathbf{Q}\right)$$

(44)

Allaire et al.’s five-equation model presented in vector form is given by

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ \rho \mathbf{u}\\ \rho E\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1\mathbf{u}\\ {\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_2{\rho }_2\mathbf{u}\\ \rho {\mathbf{v}}^2+p\\ \mathbf{u}(\rho E+P)\end{array}\right],\mathbf{H}=\left[\begin{array}{c}-{\alpha }_1\\ 0\\ 0\\ 0\\ 0\end{array}\right].$$

(45)

Kapila et al.’s five-equation model presented in vector form is given by

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ \rho \mathbf{u}\\ \rho E\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1\mathbf{u}\\ {\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_2{\rho }_2\mathbf{u}\\ \rho {\mathbf{u}}^2+p\\ \mathbf{u}(\rho E+P)\end{array}\right],\mathbf{H}=\left[\begin{array}{c}-{\alpha }_1-\mathbf{K}\\ 0\\ 0\\ 0\\ 0\end{array}\right].$$

(46)

The density, momentum, kinetic energy, and internal energy of the mixture are expressed as follows:

$$\begin{array}{cc}\hfill \rho & ={\left(\alpha \rho \right)}_1+{\left(\alpha \rho \right)}_2=\sum _{k=1}^N{\left(\alpha \rho \right)}_k:\mathrm{mixture}\mathrm{density}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill \rho \mathbf{u}& =({\left(\alpha \rho \right)}_1+{\left(\alpha \rho \right)}_2))\mathbf{u}=\sum _{k=1}^N{\left(\alpha \rho \right)}_k\mathbf{u}:\mathrm{mixture}\mathrm{momentum}\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill \rho e_{\mathrm{K}}& ={\displaystyle \frac{{\rho }_k{\mathbf{u}}^2}{2}}:\mathrm{mixture}\mathrm{kinetic}\mathrm{energy}\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill \rho e_{\mathrm{I}}& ={\left(\alpha \rho \right)}_1{e}_1+{\left(\alpha \rho \right)}_2{e}_2=\sum _{k=1}^N{\left(\alpha \rho e\right)}_k:\mathrm{mixture}\mathrm{internal}\mathrm{energy}\hfill \end{array}$$

(50)

The total energy is given by

$$\rho E_{\mathrm{T}}=({\left(\alpha \rho \right)}_1{e}_1+{\left(\alpha \rho \right)}_2{e}_2+\sum _{k=1}^N{\displaystyle \frac{{\rho }_k\mathbf{u}·\mathbf{u}}{2}})$$

(51)

To determine the internal energy and solve the equations, the stiffened equation of state (EoS) is applied to both components of the fluid:

$$p_k=({\gamma }_k-1){\rho }_k{e}_k-{\gamma }_k{p}_{c,k},k=1,2$$

(52)

Using the stiffened EoS, the internal energy is expressed as

$$\rho e_k={\displaystyle \frac{p+{\gamma }_k{p}_{c,k}}{{\gamma }_k-1}}$$

(53)

and the total energy as

$$\rho E=\sum _{k=1}^N{\alpha }_k\left({\displaystyle \frac{p+{\gamma }_k{p}_{c,k}}{{\gamma }_k-1}}+{\displaystyle \frac{{\rho }_k\mathbf{u}·\mathbf{u}}{2}}\right)$$

(54)

4. Velocity Equilibrium or Pressure-Disequilibrium Model

Saurel et al. [34] highlighted a significant challenge encountered in the application of Wood’s speed of sound (39) utilised in the Kapila five-equation model, namely its non-monotonic behaviour, along with the non-conservative nature of the K term in the advection equation. To address this issue, Saurel [48] proposed a six-equation model and introduced a monotonic mixture speed of sound known as the monotonic frozen speed of sound.

The Saurel six-equations models, stemming from the Saurel–Abgrall seven-equations framework discussed earlier, is referred to as pressure disequilibrium models. Assuming that the velocities of the two interacting fluids are in equilibrium (i.e., $u_1=u_2\equiv u$), this approach yields a single-velocity, compressible, two-phase flow model with two pressures for the mixture phase. The set of six equations comprises conservation laws for mass, momentum, and energy for both phases, along with an equation for the volume fraction of one of the phases.

Further enhancements were made by Zein [41], who introduced heat transfer into the original six-equation model. In its fundamental form, devoid of mass and heat transfer considerations, the model can be expressed as follows:

$$\begin{array}{cc}\hfill \mathbf{Phase}\mathbf{1}:& \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}{\alpha }_1+\mathbf{u}·\nabla {\alpha }_1=\mu (p_1-p_2)\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1\right)+\nabla ·\left({\alpha }_1{\rho }_1\mathbf{u}\right)=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_1{\rho }_1{E}_1\right)+\nabla ·\left({\alpha }_1\mathbf{u}\left({\rho }_1{E}_1+p_1\right)\right)=-\mu {\overline{p}}_I\left(p_1-p_2\right)\hfill \\ \\ \hfill \mathbf{Phase}\mathbf{2}:& \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2\right)+\nabla ·\left({\alpha }_2{\rho }_2\mathbf{u}\right)=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}{\alpha }_1{\rho }_1{E}_1+\nabla ·{\alpha }_1({\rho }_1{E}_1+p_1\mathbf{u})=0\hfill \\ \hfill & {\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_2{\rho }_2{E}_2\right)+\nabla ·\left({\alpha }_2\mathbf{u}\left({\rho }_2{E}_2+p_2\right)\right)=\mu {\overline{p}}_I\left(p_1-p_2\right)\hfill \end{array}$$

(55)

These models, which can generally be expressed as a non-linear system of PDE in a two-phase fluid, are presented below:

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+\nabla ·\mathbf{F}\left(\mathbf{Q}\right)+\mathbf{H}\left(\mathbf{Q}\right)\nabla \mathbf{u}=\mathbf{S}\left(\mathbf{Q}\right)$$

(56)

where $\mathbf{Q}$ is the vector of conserved variables, $\mathbf{F}$ represents the flux tensor, and $\mathbf{u}$ is the velocity field. The $\mathbf{S}$ and $\mathbf{H}$ terms are non-conservative quantities which include all of the source terms:

$$\begin{array}{cc}\hfill \mathbf{Q}& =\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ \rho \mathbf{u}\\ {\alpha }_1{\rho }_1{E}_1\\ {\alpha }_2{\rho }_2{E}_2\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1\mathbf{u}\\ {\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_2{\rho }_2\mathbf{u}\\ \rho \mathbf{u}\otimes \mathbf{u}+p\mathbf{I}\\ {\alpha }_1{\rho }_1{E}_1\mathbf{u}\\ {\alpha }_2{\rho }_2{E}_2\mathbf{u}\end{array}\right],\hfill \\ \hfill \mathbf{H}& =\left[\begin{array}{c}-{\alpha }_1\\ 0\\ 0\\ \mathbf{0}\\ {\alpha }_1{p}_1\\ {\alpha }_2{p}_2\end{array}\right],\mathbf{S}=\left[\begin{array}{c}\mu (p_1-p_2)\\ 0\\ 0\\ 0\\ -\mu p_k(p_1-p_2)\\ \mu p_k(p_1-p_2)\end{array}\right]\hfill \end{array}$$

(57)

Interfacial pressure is expressed in the same way as Saurel’s seven equations and corresponds to the mixture total pressure:

$$p_I={\displaystyle \frac{Z_1{p}_1+Z_2{p}_2}{Z_1+Z_2}}$$

(58)

The variable $Z_{\mathrm{k}}$ denotes the acoustic impedance of phase $\mathrm{k}$, where ${\rho }_{\mathrm{k}}$ represents the density of the phase and ${\mathrm{c}}_{\mathrm{i}}$ is the speed of sound in that particular phase. The mechanical equilibrium state is reached at the end of the relaxation processes controlled by the pressure relaxation term $\mu >0$.

As $\mu \to +\infty$, the six equations in the presence of pressure relaxation converge to the Kapila five-equation models. The speed of sound of the mixture is defined to be monotonic and given as

$$c^2=\sum _{k=1}^2{\displaystyle \frac{{\alpha }_k{\rho }_k{c}_k^2}{\rho }}$$

(59)

The mixture’s energy equation is the sum of the internal energies of the two fluids or phases:

5. Thermal and Mechanical Equilibrium Model by Abgrall et al.

The four-equation model proposed by Abgrall [27] establishes thermal and mechanical equilibrium among the interacting fluids within the mixture, leveraging the seven-equation framework of Baer–Nunziato. This formulation, which is considered the most basic model in the DIM category, consists of four equations: one for the conservation of mass for each phase k and another for the momentum and internal energy of the mixture. For temperature, velocity fields, and pressure, the two phases are assumed to be homogeneous. This simplicity facilitates the incorporation of additional physical phenomena, such as viscosity, surface tension, and phase changes, via source terms. Demou et al. [49] extend this model by introducing viscosity, thermal conductivity, surface tension, and gravity effects, enhancing its applicability to scenarios like nucleate boiling flow and phase changes.

$$\mathrm{Four}\mathrm{equations}:\left\{\begin{array}{cc}\hfill {\displaystyle \frac{\partial \left({\alpha }_1{\rho }_1\right)}{\partial t}}+\nabla ·\left({\alpha }_1{\rho }_1\mathbf{u}\right)& =\Gamma \hfill \\ \hfill {\displaystyle \frac{\partial \left({\alpha }_2{\rho }_2\right)}{\partial t}}+\nabla ·\left({\alpha }_2{\rho }_2\mathbf{u}\right)& =-\Gamma \hfill \\ \hfill {\displaystyle \frac{\partial \left(\rho \mathbf{u}\right)}{\partial t}}+\nabla ·(\rho \mathbf{u}\otimes \mathbf{u})+\nabla p& =0\hfill \\ \hfill {\displaystyle \frac{\partial \left(\rho E\right)}{\partial t}}+\nabla ·\left((\rho E+p)\mathbf{u}\right)& =0\hfill \end{array}\right.$$

(60)

where the subscripts 1 and 2 represent the phases, $\alpha$ is the volume fraction of each phase or component, $\rho$ is the mixture density, $\mathbf{u}=(u,v,w)$ is the mixture velocity, p is the mixture pressure, E is the mixture total specific energy, and $\Gamma$ are the source terms which are zero if additional physics such as mass transfer are not included. The energy of the mixture is given as $E=e+{\displaystyle \frac{1}{2}}{\mathbf{u}}^2$ with the internal energy $e={\alpha }_1{e}_1+{\alpha }_2{e}_2$. The speed of sound is the Wood’s speed of sound, given as

$$c_{\mathrm{wood}}=\sqrt{\rho \left({\displaystyle \frac{{\alpha }_1}{{\rho }_1{c}_1^2}}+{\displaystyle \frac{{\alpha }_2}{{\rho }_2{c}_2^2}}\right)}$$

(61)

where $\rho ={\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2$. In a non-linear system of PDEs, the Abgrall equation can be written as presented below:

$${\displaystyle \frac{\partial \mathbf{Q}}{\partial t}}+\nabla ·\mathbf{F}\left(\mathbf{Q}\right)+\mathbf{H}\left(\mathbf{Q}\right)\nabla ·\mathbf{u}=\mathbf{S}\left(\mathbf{Q}\right).$$

(62)

where $\mathbf{Q}$ is the vector of conserved variables, $\mathbf{F}$ is a flux tensor, $\mathbf{u}$ is the velocity field, and $\mathbf{H}$ and $\mathbf{S}$ are non-conservative quantities. Here, $\mathbf{S}$ is a zero vector.

In a compact matrix–vector form, the four equations are given by

$$\mathbf{Q}=\left[\begin{array}{c}{\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ \rho \mathbf{u}\\ \rho E\end{array}\right],\mathbf{F}=\left[\begin{array}{c}{\alpha }_1{\rho }_1\mathbf{u}\\ {\alpha }_2{\rho }_2\mathbf{u}\\ \rho {\mathbf{u}}^2+p\\ \mathbf{u}(\rho E+p)\end{array}\right],\mathbf{H}=\left[\begin{array}{c}\Gamma \\ \Gamma \\ 0\\ 0\end{array}\right].$$

(63)

6. Choice of Equation of State (EoS)

To close the hyperbolic system of equations within diffuse models (DIMs), the thermodynamic properties of compressible multiphase fluids are expressed as functions of physical parameters such as pressure, temperature, density, specific internal energy, and specific entropy.

Various equations of state (EoSs) are employed in numerical simulations of DIM, particularly for modelling liquid–gas flows or mixtures. Common EoSs include the Ideal Gas, Stiffened Gas, Noble–Abel Stiffened Gas (NASG), van der Waals, and Tait EoSs (refer to Table 1). These EoSs are specified for each phase and integrated into the DIM equations as additional closure systems. Among them, the Stiffened Gas EoS stands out for its widespread use in modelling compressible multicomponent flow due to its capability to describe immiscible fluids effectively [50,51,52,53,54,55,56]. This EoS accounts for attractive and repulsive molecular effects, making it popular in compressible multiphase flow simulations [27].

The DIM framework allows for the use of different EoSs for each phase, such as employing the Stiffened Gas EoS for the gas phase and Tait’s EoS for the liquid phase. This flexibility becomes necessary when distinct EoSs are required for both fluid phases.

6.1. Ideal Gas EoS

The Ideal Gas EoS is particularly useful when one of the interacting fluids is an inert gas. In this case, the pressure of the fluid is straightforwardly expressed as

$$p_k=({\gamma }_k-1){\rho }_k{e}_k,$$

(64)

where ${\gamma }_k$ represents the adiabatic specific heat ratio for the gas under consideration.

6.2. Tait’s EoS

Tait’s EoS, also known as the isentropic stiffened gas EoS, finds frequent use in compressible multiphase flow simulations involving liquids such as water [3,4,57,58]. This EoS relates the fluid’s pressure to its density alone, expressed as $p=p\left(\rho \right)$. It offers accurate estimation of low pressures, particularly in regions where cavitation occurs [3]. Tait’s EoS is suitable for fluid pressures up to 2000 MPa [3] and is represented by

$$p_k=\left(\gamma -1\right)\rho e-\gamma \left(\mathrm{B}-\mathrm{A}\right).$$

(65)

Here, constants A and B, along with $\gamma$, are chosen based on the specific fluid under consideration.

6.3. Van der Waals Gas EoS

The van der Waals equation is advantageous for computing pressure in compressible multiphase flow scenarios involving phase transitions, such as boiling flows. It is expressed as

$$p={\displaystyle \frac{\gamma -1}{1-\rho b}}(\rho e-\pi +a{\rho }^2)-(\pi +a_k{\rho }^2),$$

(66)

where a represents a constant characterising the attractive forces between gas molecules, b represents the specific co-volume, and $\pi$ denotes the osmotic pressure. The values of these constants vary depending on the specific gas and its conditions.

6.4. Stiffened Gas EoS

The Stiffened Gas EoS, introduced by Harlow and Amsden [59], is extensively used to describe the thermodynamic properties of liquids, gases, and solids in compressible multiphase flow simulations. It is typically expressed as pressure for each phase or fluid, given by

$$p_k=({\gamma }_k-1){\rho }_k{e}_k-{\gamma }_k{\pi }_{\infty ,k},$$

(67)

where ${\pi }_{\infty ,k}$ represents a reference pressure for each phase, and ${\gamma }_k$ is the adiabatic index specific to each phase.

For the mixture, the EoS is represented as

$$\begin{array}{cc}\hfill \xi & ={\displaystyle \frac{1}{\gamma -1}}=\sum _k{\displaystyle \frac{{\alpha }_k}{{\gamma }_k-1}},\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\pi }_{\infty }\gamma }{\gamma -1}}& =\sum _k{a}_k{\displaystyle \frac{{\pi }_{\infty ,k}{\gamma }_k}{{\gamma }_k-1}},\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill p& =(\gamma -1)\rho e-\gamma {\pi }_{\infty }.\hfill \end{array}$$

(70)

6.5. Noble–Abel Stiffened Gas (NASG) EoS

The Noble–Abel Stiffened Gas EoS, a hybrid of the Noble–Abel and Stiffened Gas equations, accounts for both thermal and compressibility effects in fluids. This EoS, introduced by Le Métayer and Saurel [60], has demonstrated potential for compressible multiphase flows and considers factors such as thermal agitation and short-distance repulsion [60,61,62,63]. It is expressed as

$$p_k({\rho }_k,e_k)=({\gamma }_k-1){\displaystyle \frac{{\rho }_k(e_k-q_k)}{(1-{\rho }_k{b}_k)}}-{\gamma }_k{\pi }_{\infty k},$$

(71)

where $(\gamma -1)(e-q)$ represents thermal agitation and $1-{\rho }_k{b}_k$ accounts for short-distance repulsion.

6.6. Mie–Grüneisen EoS

The Mie–Grüneisen equation of state (EoS) provides a general EoS framework for modelling compressible multiphase flow. Despite its incompleteness, as it only considers the Grüneisen coefficient as a function of density, it remains widely used.

The Mie–Grüneisen equation of state (EoS) can be expressed in its general form as follows:

$$p_k\left({\rho }_k{e}_k\right)={\Gamma }_k\left({\rho }_k\right)[{\rho }_k{e}_k-\rho e_{ref}\left({\rho }_k\right)]+p_{ref}\left({\rho }_k\right).$$

(72)

Here, $p_{ref}\left(\rho \right)$ and $e_{ref}\left(\rho \right)$ represent the pressure and internal energy of a reference state chosen along a pressure–volume (p-V) reference curve. The Grüneisen coefficient $\Gamma (\rho ,e)$ is defined as

$$\Gamma (\rho ,e)={\displaystyle \frac{\partial p}{\rho \partial e}}.$$

(73)

This equation is commonly extended to various complete equations of state (EoSs) such as the Ideal Gas, Tait, Stiffened Gas, van der Waals, and NASG EoSs, which are expressed in the form of the Mie–Grüneisen EoS as follows:

Ideal Gas:

$$\left\{\begin{array}{c}\Gamma \left(\rho \right)=\gamma -1\hfill \\ p_{ref}\left(\rho \right)=0\hfill \\ e_{ref}\left(\rho \right)=0\hfill \end{array}\right.$$

(74)

Tait:

$$\left\{\begin{array}{c}\Gamma \left(\rho \right)=\gamma -1\hfill \\ p_{ref}\left(\rho \right)=-\gamma (B-A)\hfill \\ e_{ref}\left(\rho \right)=0\hfill \end{array}\right.$$

(75)

Stiffened Gas:

$$\left\{\begin{array}{c}\Gamma \left(\rho \right)=\gamma -1\hfill \\ p_{ref}\left(\rho \right)=-{\gamma }_k{\pi }_k\hfill \\ e_{ref}\left(\rho \right)=0\hfill \end{array}\right.$$

(76)

Van der Waals:

$$\left\{\begin{array}{c}\Gamma \left(\rho \right)={\displaystyle \frac{\gamma -1}{1-b\rho }}\hfill \\ p_{ref}\left(\rho \right)=-a{\rho }^2\hfill \\ e_{ref}\left(\rho \right)=-a\rho \hfill \end{array}\right.$$

(77)

NASG:

$$\left\{\begin{array}{c}\Gamma \left(\rho \right)={\displaystyle \frac{\gamma -1}{1-b\rho }}\hfill \\ p_{ref}\left(\rho \right)=-{\gamma }_k{\pi }_k\hfill \\ e_{ref}\left(\rho \right)=0\hfill \end{array}\right.$$

(78)

Table 1. Summarised overview of the EoSs commonly used for compressible multiphase flow using the diffuse models.

EoS	Used in	Equations
Ideal Gas	[48]	$p_k=({\gamma }_k-1){\rho }_k{e}_k$
Tait	[3,4,57,58]	$p_k=({\gamma }_k-1){\rho }_k{e}_k-\gamma (B-A)$
van der Waals	[58,64]	$p_k={\displaystyle \frac{(\gamma -1)}{(1-\rho b)}}(\rho e-\pi +a{\rho }^2)-(\pi +a_k{\rho }^2)$
Stiffened Gas	[52,54,55,56,65,66,67]	$p_k=({\gamma }_k-1){\rho }_k{e}_k-{\gamma }_k{\pi }_{\infty ,k}$
NASG	[60,61,62,63,64,68,68]	$p_k({\rho }_k,e_k)=({\gamma }_k-1){\displaystyle \frac{{\rho }_k(e_k-q_k)}{(1-{\rho }_k{b}_k)}}-{\gamma }_k{\pi }_{\infty k}$
Mie–Gruneisen	[69,70,71,72]	$p_k\left({\rho }_k{e}_k\right)={\Gamma }_k\left({\rho }_k\right)[{\rho }_k{e}_k-\rho e_{\mathrm{ref}}\left({\rho }_k\right)]+p_{\mathrm{ref}}\left({\rho }_k\right)$

Table 1. Summarised overview of the EoSs commonly used for compressible multiphase flow using the diffuse models.

EoS	Used in	Equations
Ideal Gas	[48]	$p_k=({\gamma }_k-1){\rho }_k{e}_k$
Tait	[3,4,57,58]	$p_k=({\gamma }_k-1){\rho }_k{e}_k-\gamma (B-A)$
van der Waals	[58,64]	$p_k={\displaystyle \frac{(\gamma -1)}{(1-\rho b)}}(\rho e-\pi +a{\rho }^2)-(\pi +a_k{\rho }^2)$
Stiffened Gas	[52,54,55,56,65,66,67]	$p_k=({\gamma }_k-1){\rho }_k{e}_k-{\gamma }_k{\pi }_{\infty ,k}$
NASG	[60,61,62,63,64,68,68]	$p_k({\rho }_k,e_k)=({\gamma }_k-1){\displaystyle \frac{{\rho }_k(e_k-q_k)}{(1-{\rho }_k{b}_k)}}-{\gamma }_k{\pi }_{\infty k}$
Mie–Gruneisen	[69,70,71,72]	$p_k\left({\rho }_k{e}_k\right)={\Gamma }_k\left({\rho }_k\right)[{\rho }_k{e}_k-\rho e_{\mathrm{ref}}\left({\rho }_k\right)]+p_{\mathrm{ref}}\left({\rho }_k\right)$

7. High-Order Methods for Diffuse Models

High-order methods for solving hyperbolic conservation laws have become a fundamental framework of computational fluid dynamics (CFD) in recent decades, both for compressible multiphase flows and single flows. These schemes have garnered significant attention in literature due to their ability to handle the intricate interactions between fluids and the contact discontinuity occurring at their interfaces. Critical to their effectiveness is their ability to accurately resolve interfaces while mitigating excessive diffusion, especially in regions where solutions transition smoothly or near discontinuities such as shocks or fluid interfaces. While some may argue that high-order schemes are computationally expensive, the reality is that they often offer superior accuracy with fewer computational elements compared to lower-order methods. A numerical method is typically classified as being of order k if the error decreases proportionally to $\Delta t^k$, allowing for more precise solutions with smaller time steps. High-order methods, defined as those with an accuracy order of at least three, have been extensively applied in both single-phase and multiphase flows to capture discontinuities efficiently. In compressible multiphase flow simulations using the diffuse models, common high-order methods used include the Discontinuous Galerkin (DG) [67,73,74] and ADER-Discontinuous Galerkin (ADER-DG) [75] within finite element frameworks, and Weighted Essentially Non-Oscillatory (WENO) [52,54,76], and its variants WENO-Z [77], WENO-JS, WEN0-UP, Central Weighted Essentially Non-Oscillatory (CWENO) [65,66], Targeted Essentially Non-oscillatory (TENO) [78], Multidimensional Optimal Order Detection (MOOD) [79], and Monotone Upstream-Centred Scheme for Conservation Law (MUSCL) [80,81,82,83,84,85] within finite volume and finite difference frameworks. A hybrid Discontinuous Galerkin (DG)–Finite Volume (FV) method has also recently been employed [86,87] to incorporate the advantages of both models. This approach involves switching between a DG method and an FV method based on specific criteria or conditions. Depending on the flow characteristics and the required degree of accuracy, each of the aforementioned approaches offers distinct advantages. Finite-volume WENO, TENO, or CWENO schemes have proven to be efficient for solving compressible multiphase flows, although they are more computationally intensive than finite-difference schemes, which are limited to uniform meshes or smooth curvilinear coordinates. Accuracy in capturing discontinuities and ensuring appropriate flux directionality is achieved by combining approximate Riemann solvers, such as HLL or HLLC, with WENO, TENO, or CWENO schemes. To address issues like artificial smearing at interfaces, a notable weakness in diffuse models, various techniques have been developed in conjunction with high-order methods. These include the Anti-diffusion Interface Sharpening (ADIS) technique, THINC (Tangent of Hyperbola for Interface Cap -turing) interface sharpening technique, and Total Variation Diminishing (TVD) limiter technique. These techniques aim to enhance the accuracy and resolution of interfaces by controlling diffusion effects and limiting numerical oscillations. These hybrid techniques maintain the sharpness for the moving interface using the high-order schemes for smooth regions, while the non-polynomial reconstruction is used for discontinuities such as shockwave and contact wave. Chiapolino et al. [88] and Pandare et al. [89] used the MUSCL schemes with limiters for compressible two-phase flows on hybrid unstructured grids for the six-equation single-pressure model. Price et al. [69], Faucher et al. [90], and Cheng et al. [84] have also expanded the DIM to unstructured meshes. In the diffuse interface finite-volume framework, one of the earliest applications of unstructured mesh to compressible multiphase flow was by Dumbser (2013) [91] for a reduced version of the seven-equation Baer–Nunziato models using WENO schemes. Tsoutsanis et al. [79] took a similar approach, employing Multidimensional Optimal Order Detection (MOOD) for the five-equation model on an unstructured mesh. The paper of Tsoutsanis et al. presented a thorough extension of the Multidimensional Optimal Order Detection (MOOD) framework within the context of simulating compressible multicomponent flows on unstructured meshes using the diffuse models (DIM) with a five-equation model and employing the high-order CWENO spatial discretisation, to effectively balanced computational efficiency with improved non-oscillatory behaviour compared to traditional WENO variants. Importantly, the relaxed MOOD enhancement of the CWENO method significantly improved the robustness of the overall numerical framework. Li et al. [78] introduced a novel hybrid scheme, TENO-THINC. This scheme combines the TENO scheme for smooth regions with the THINC scheme for non-smooth regions, resulting in improved resolution of physical discontinuities and material interfaces. The method, applied to a reduced five-equation formulation of the diffuse interface model, demonstrates robustness in extreme simulations with high density and pressure ratios. Numerical tests from the paper show that TENO-THINC outperforms standard TENO and WENO-JS schemes in terms of robustness and dissipation. Either by finite difference or finite volume techniques, an exact or approximate solution to the Riemann problem of DIM equations is needed as a reference solution to verify the accuracy of our numerical method. Numerical simulations of compressible multiphase flows pose significant computational challenges, particularly when resolving Riemann problems resulting from the reconstruction of Diffuse Interface Models (DIMs). Various approximate solvers, such as the Roe Solver [92], HLL solvers [93], and the HLLC solver [94], have been employed to address these challenges. Among these, the HLLC solver, which accounts for phase velocities and sound speeds, is preferred for scenarios with low densities and pressures common in compressible multiphase flows. However, achieving an exact Riemann solution for DIM remains complex [95,96]. Several approaches have been proposed to tackle this complexity. Tokareva and Toro [97] introduced an HLLC-type approximate Riemann solver for the Baer–Nunziato model, later refined by Lochon et al. [98]. Hennessey et al. [99] improved upon this solver by incorporating reactive flow dynamics. Andrianov and Warnecke [100] presented an inverse procedure for constructing exact solutions to the Riemann problem for the homogeneous Baer–Nunziato model, while Thein [46] provided exact solutions for the Romenski seven-equation model. For the six-equation model, Saurel–Abgrall [42] developed the HLLC scheme, overcoming the dissipative nature of earlier methods. Similarly, for mechanical equilibrium models, Coralic and Colonius [54] and Li et al. [101] utilised the HLLC solver, while Tian and Toro [102] developed an HLLC-type solver for the five-equation model. Also, Deledicque and Papalexandris [103] presented an exact Riemann solver for compressible two-phase flow models containing non-conservative products. While the discontinuous finite element method is advantageous for unstructured or distorted meshes, finite volume higher-order schemes, such as Weighted Essentially Non-Oscillatory (WENO) schemes, offer robustness in the presence of strong shocks at a lower computational cost. WENO schemes, often combined with HLL or HLLC solvers, effectively capture complex flow phenomena, including bubble dynamics and shock/bubble interactions, with high-order accuracy. Variants like WENO-Z, WENO-JS, WENO-UP, CWENOZ, and CWENO further enhance accuracy by minimising numerical oscillations across interfaces which is common with the traditional WENO schemes. WENO schemes and their variants show promise in accurately simulating compressible multiphase flows across a wide range of scenarios. The

Table 2. High-order methods for diffuse interface-capturing models in compressible multiphase/multicomponent flows.

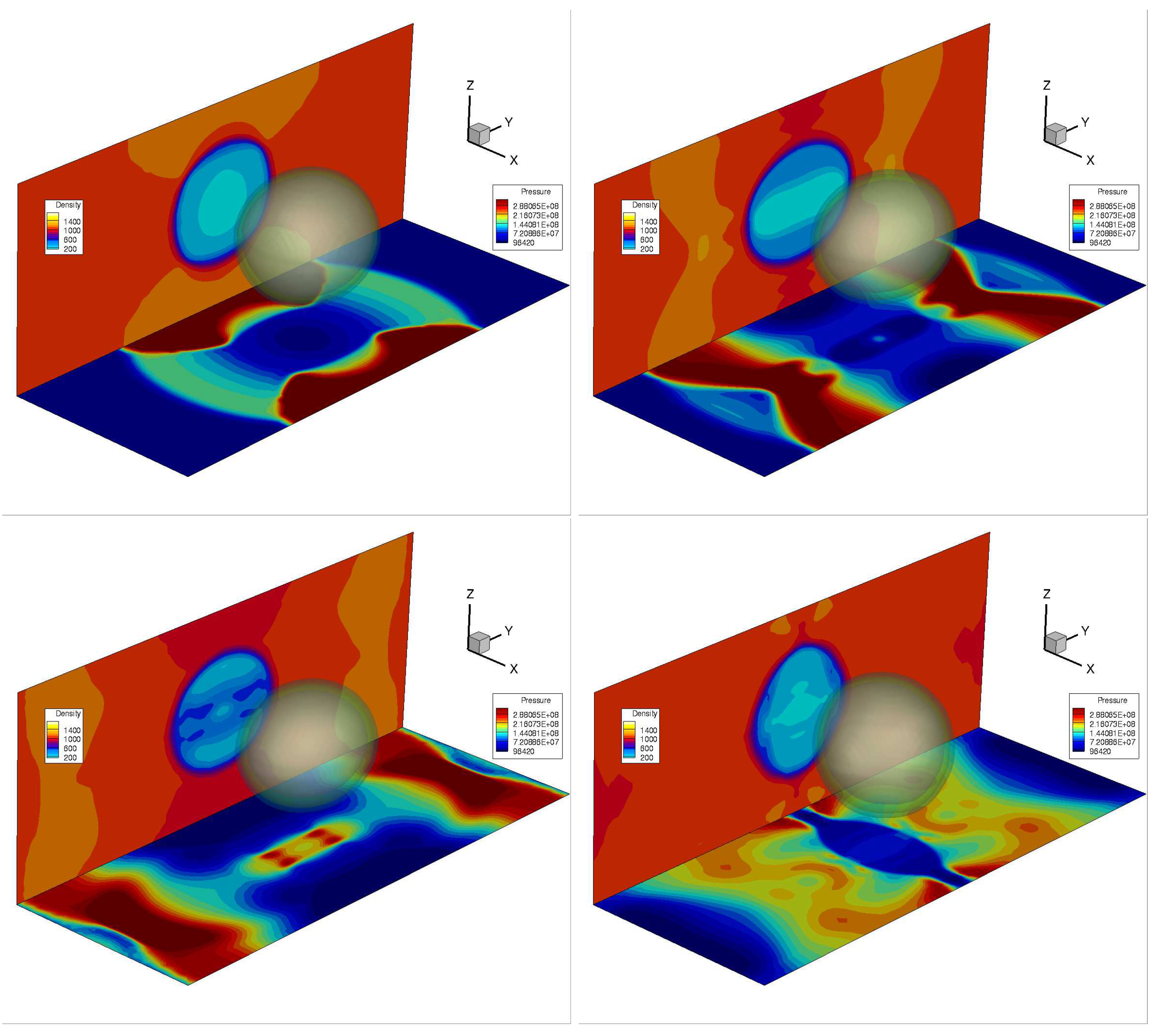
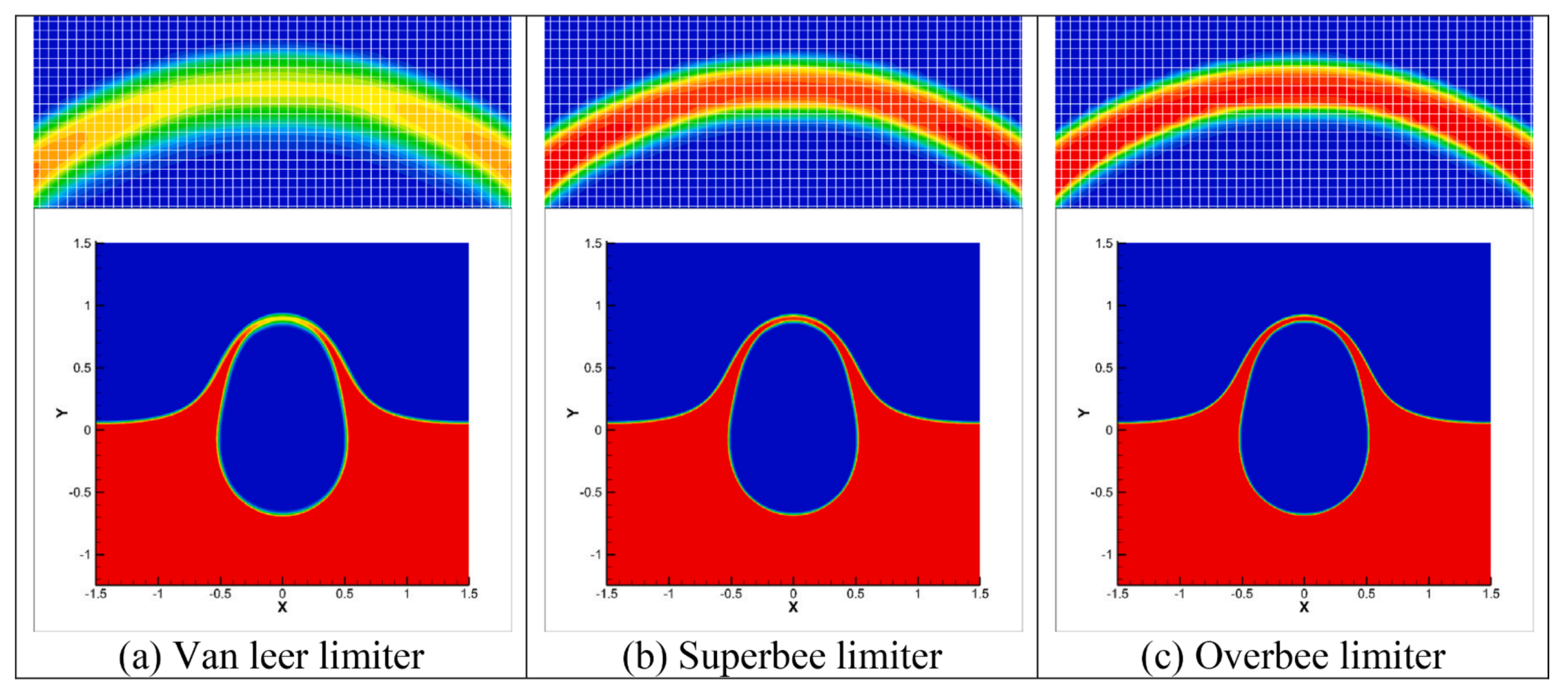
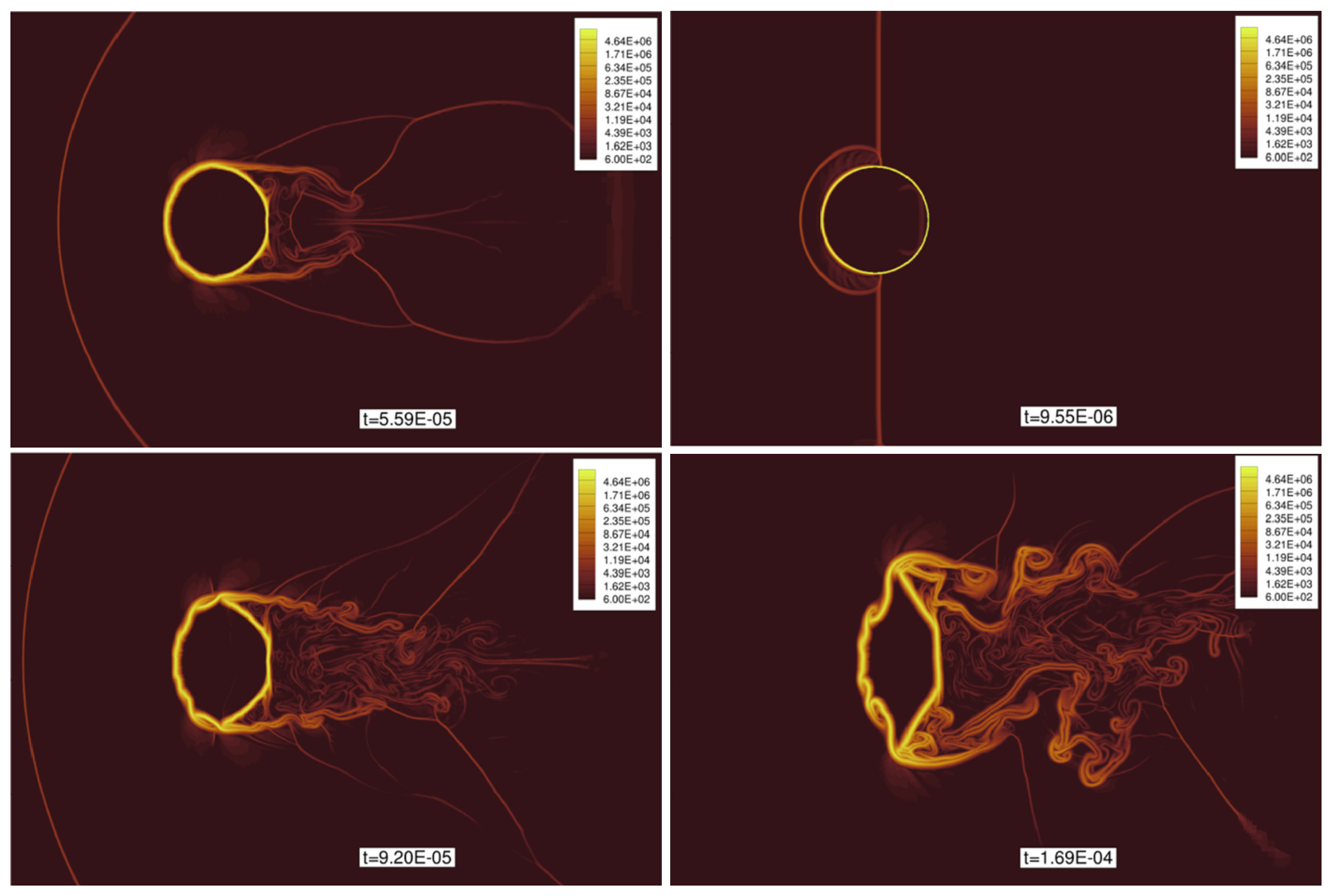
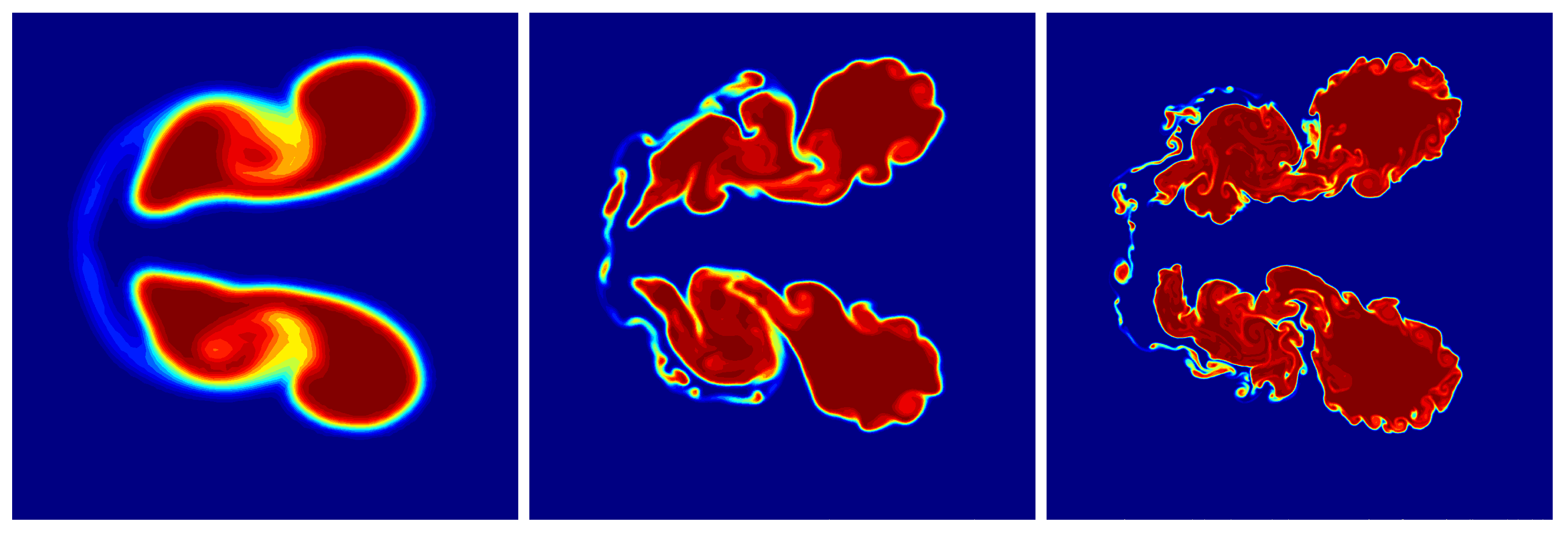
High-Order Method	Framework	Literature
DG	Finite Element	[67,73,104]
ADER-DG	Finite Element	[75]
WENO	Finite Volume/Finite Difference	[53,54,91,105,106,107]
WENO-Z, WENO-JS	Finite Volume/Finite Difference	[52,76,77]
CWENO	Finite Volume/Finite Difference	[65,66]
TENO	Finite Volume/Finite Difference	[78]
MOOD	Finite Volume/Finite Difference	[79]
MUSCL	Finite Volume/Finite Difference	[52,56,80,81,83,84,85,108]
WENO-DG, MUSCL-DG	Hybrid DG-FV	[86,87,109]
LBM	Lattice Boltzmann	[110]

below summarises the application of various high-order methods in diffuse models for compressible multiphase flow:

8. Methods for Minimising Numerical Smearing in Compressible Multiphase Flow

Numerical smearing at interfaces poses a significant challenge in the accurate simulation of compressible multiphase flows using diffuse models (DIMs). To mitigate this issue, several techniques have been developed, each offering unique advantages and applications. Here, an overview of these methods is presented, as well as their utilisation across different DIM formulations.

8.1. Anti-Diffusion Interface Sharpening (ADIS) Technique

The ADIS technique, pioneered by Kokh and Lagoutiere [111], is a post-processing step commonly employed alongside high-order methods such as Weighted Essentially Non-Oscillatory (WENO) schemes [112,113]. By introducing an anti-diffusion term into the volume–fraction equation, the ADIS technique effectively controls interface smearing. The evolution of the anti-diffusion correction is governed by a pseudo-time parameter t, and the technique utilizes a positive diffusion coefficient D:

$${\displaystyle \frac{\partial \alpha }{\partial t}}=-\nabla ·(D\nabla \alpha )$$

(79)

where t is a pseudo-time to evolve the anti-diffusion correction and $D>0$ is an anti-diffusion coefficient.

8.2. THINC Interface Sharpening Technique

The Tangent of Hyperbola for Interface Capturing (THINC) technique, introduced by Shyue and Xiao [83,112], is integrated with the MUSCL schemes to reduce numerical smearing and oscillations at interfaces. This approach interpolates volume fractions as a pre-processing step while maintaining other variables with MUSCL interpolations [51,114,115,116]. By controlling interface sharpness through a hyperbolic tangent function, THINC effectively sharpens interfaces, particularly in mixture zones. The interpolation function for one-dimensional cases is given by

$$\alpha \left(x\right)=0.5\left\{1+{\sigma }_{i}tanh\left[\beta \left({\displaystyle \frac{x-x_{i-1/2}}{\Delta x}}\right)-{\tilde{x}}_o\right]\right\}$$

(80)

where ${\sigma }_i$ is the sign function of the volume fraction, $\Delta x_i$ is the grid resolution, and $\beta$ is a flexible user’s parameter to vary the thickness and slope, where $\beta \approx 2-3.5$.

The interface position is determined below as

$${\tilde{x}}_o={\displaystyle \frac{1}{2\beta }}ln\left[{\displaystyle \frac{-1+exp\left(\beta \left(1+{\sigma }_i-2{\overline{\alpha }}_i\right)/{\sigma }_i\right)}{1-exp\left(\beta \left(1-{\sigma }_i-2{\overline{\alpha }}_i\right)/{\sigma }_i\right)}}\right]$$

(81)

where ${\overline{\alpha }}_i$ is given as

$${\overline{\alpha }}_i={\displaystyle \frac{1}{\Delta x_i}}{\int }_{x_{i-1/2}}^{x_{i+1/2}}{\alpha }_i\left(x\right)dx.$$

(82)

8.3. Limiter Techniques (e.g., TVD and BVD)

Limiter techniques are employed within conventional MUSCL schemes to restrict the steepness of concentration gradients and ensure well-defined interfaces. These techniques, such as Total Variation Diminishing (TVD), Superbee, Overbee, and Ultrabee limiters, maintain interface sharpness by constraining the gradient of scalar variables. By considering various criteria, including interface distance, curvature, and pressure gradient, limiter functions effectively minimize numerical smearing.

8.4. Interface Compression Technique

The interface compression technique, inspired by methods developed for incompressible flow, addresses numerical smearing by representing interfaces with high accuracy. This technique, proposed by Shukla et al. [81,82], modifies the advection equation to balance the interface thickness and diffusion. By utilising a characteristic regularisation rate and interface normal vector, the interface compression technique ensures sharp and well-defined interfaces:

$${\displaystyle \frac{\partial \alpha }{\partial t}}+\mathbf{u}·\nabla \alpha ={\mathcal{U}}_o\mathbf{n}·\nabla \left[{ϵ}_b|\nabla \alpha |-\alpha (1-\alpha )\right],$$

(83)

where $\left({ϵ}_b\right|\nabla \alpha \left|\right)$ is the interface balance function and $\left(\alpha \right(1-\alpha \left)\right)$ is the diffusion function, which are used to maintain the interface thickness. The symbol ${ϵ}_b$ denotes the thickness of the interface, which is chosen independently and chosen to be greater than the minimum grid size $\Delta x_{min}$. The symbol ${\mathcal{U}}_o$ represents the characteristic regularisation rate, and the symbol $\mathbf{n}$ represents the interface normal vector, which can be expressed as

$$\mathbf{n}=\nabla \alpha /\left|\nabla \alpha \right|,$$

(84)

and $\alpha$ is determined as a function x by

$$\alpha \left(x\right)=0.5\left[1+tanh\left({\displaystyle \frac{s\left(x\right)}{2{ϵ}_b}}\right)\right].$$

(85)

where $s\left(x\right)$ is the normal coordinate to the interface.

Ongoing research focuses on refining these methods and selecting the most suitable approach for specific compressible multiphase flow simulations. A comparative analysis could provide valuable insights into the advantages and limitations of each technique under various conditions, guiding further developments in interface sharpening strategies.

The

Table 3. Overview of methods for minimising numerical smearing in compressible multiphase flow using diffuse models (DIMs). U: Used; NYU: Not Yet Used (to the best of the author’s knowledge).

Methods	5-eqn. DIM	6-eqn. DIM	7-eqn. DIM
Anti-diffusion	U [51,111]	U [111,113]	NYU
THINC	U [58,64,114,117,118]	U [115]	NYU
Limiter Techniques (e.g., TVD, BVD)	U [56,88,119,120]	NYU	NYU
Interface Compression	U [81,82,121,122]	NYU	NYU

below summarises the application of various interface sharpening techniques across different DIM formulations.

9. Selected Test Cases Used for Verification and Validation of DIM Methods

In this final section, recent applications of diffuse models (DIMs) are discussed briefly in the context of selected test cases that have been meticulously chosen by authors to verify and validate the performance of DIMs. Underwater explosion test cases serve as common benchmarks for evaluating the diffuse interface-capturing models (used in [4,51,52,76,82,86,112,119,120,123,124,125,126,126]), particularly in understanding the effect of rapid pressure drop in certain regions of the fluid on the surrounding structure or surface. This is significant because the damage caused by cavitation on a nearby structure during such an explosion is substantial. These test cases are simulated using different boundaries including free surface, rigid body or wall, and enclosed cylinders. They are particularly effective for assessing DIMs algorithms because they induce cavitation at extremely low pressures, which can lead to the non-convergence of the numerical method.

To solve the convergence problems during cavitation, a single-fluid cavitation model must be incorporated into the DIMs. A variety of approaches exist in the literature, examples being the cut-off model, vacuum model [127], isentropic model [3], Schmidt model [128], and modified Schmidt. A detailed review of the cavitation models can be found in [3,4,57]. However, because the mass and heat transfer factors that are inherent in compressible two-phase flows are not included in the one-fluid model, it is unable to capture detailed thermodynamic processes during phase transition.

This constraint is addressed by extending simplified diffuse interface-capturing models with five or six equations [45,51,129,130,131] to include source terms in energy and mass conservation equations, which allows the transfer of mass and heat. This method called two-fluid cavitation avoids non-physical pressure events in cavitation regions. However, it has an increased computational cost, particularly for seven-equation models that are not in equilibrium.

To enforce mechanical and thermal equilibrium, researchers frequently use simplified DIMs, such as the four- or five-equation interface-capturing models. The versatility of current DIMs with phase transitions was demonstrated by Jun et al. [68], who expanded a phase transition model used by Chiapolino et al. [85,88] to investigate cavitation in underwater explosion cases.

Among these DIMs with phase transitions are the six-equation model by Pelanti and Shyue [51,130], the five-equation model by Saurel et al. [131], the five-equation model by Martelot et al. [129], and the six- and seven-equation models by Zein et al. [45]. Boiling, condensation, and other thermodynamic processes involving liquid-to-vapour and vapour-to-liquid transitions can be captured by these models. The work by Adebayo et al. [125] is one of the more recent applications of DIMs for underwater explosion (UNDEX) test scenarios. To examine the material interface between the bubbly gas and the free surface of the air-water medium, they used the central-weighted essentially non-oscillatory (CWENO) method to model an underwater explosion close to a free surface. Figure 6 shows numerical Schlieren visualisations for density gradients that show the process at various points in time. The high-pressure air bubble initially explodes, and the resulting shock wave spreads outward towards the interface. Upon reaching the air-water interface, the shock wave reflects into the water. In the same study, Adebayo et al. [125] investigated the fluid-structure interaction of an explosive, modelled as a pressurised bubble, within a cylindrical water-filled enclosure. Using a three-dimensional set-up, gravitational effects were accounted for to analyse shock wave propagation and cavitation dynamics within the confined structure (Figure 7). The 3D contour plot in Figure 7 depicts the formation of a low-pressure region surrounding the expanding bubble, while a high-pressure field generates shock waves propagating toward the cylinder walls. As time progresses, these shock waves reflect off the walls and traverse back through the fluid domain, interacting with the evolving bubble dynamics.

In another recent study by Van Guyen et al. [119] (Figure 8), three compressive limiters were utilised alongside a monotonic upstream-centred scheme for conservation laws (MUSCL) to preserve a sharp air–water interface, thereby minimising numerical smearing. The numerical framework presents a conceptually simple yet robust and versatile numerical procedure. Notably, simulations utilising the Van Leer flux limiter resulted in a significantly diffused interface, while simulations employing the superbee and overbee flux limiters successfully captured sharp interface profiles on the same grid size.

Tsoutsanis et al. [79] expanded the application of the high-order, Multidimensional Optimal Order Detection (MOOD)-CWENO framework to simulate a test case involving a shock wave interacting with a cylindrical water column on unstructured meshes. Utilising the five-equation model, the results, illustrated in Figure 9, show the typical flow structures such as the transmitted wave, expansion wave, Mach stem, and recirculation zone. The simulation captures the formation of transverse jets and the associated Richtmyer–Meshkov instability when water is forced into an air cavity as depicted in Figure 9.

Another highly significant test case extensively utilised within the realm of Diffuse Interface Models is the helium bubble shock experiment, investigated in both two- and three-dimensional configurations. This test case is founded upon the experimentation of Haas and Sturtevant (1997) [132]. It involves subjecting a helium bubble to a high-pressure shock wave generated by a shock tube. This particular problem has been thoroughly explored by researchers such as Tsoutsanis et al. (2021) [65], Wang et al. (2020) [133], Coralic et al. (2014) [54], and Johnsen et al. (2006) [134]. The results of Tsoutsanis et al. [65] in Figure 10 where the high-order CWENO technique was utilised highlight the emergence of Kelvin–Helmholtz instabilities at the helium bubble interface with increasing 2D grid resolution (Figure 10). However, the resolution in the 3D setup (Figure 11) proves inadequate for capturing these instabilities.

10. Conclusions

This paper provides a comprehensive and current overview of recent advances in the domain of diffuse interface-capturing models (DIMs), which are becoming more and more prominent in solving compressible multiphase flow cases. It also gives a historical background, showing how these models evolved while fusing early contributions with more recent uses. This perspective is particularly significant for ongoing research, as it necessitates the need for refining existing models, formulating new approaches that align more closely with the mathematical principles governing ideal multiphase flow systems, and enhancing numerical methodologies, algorithmic frameworks, and thermodynamic modelling for greater accuracy and computational efficiency.