Tabulated Chemistry Models for Numerical Simulation of Combustion Flow Field
Abstract
1. Introduction
2. Applicability to Various Fuels
3. Consideration of Flow and Chemical Properties
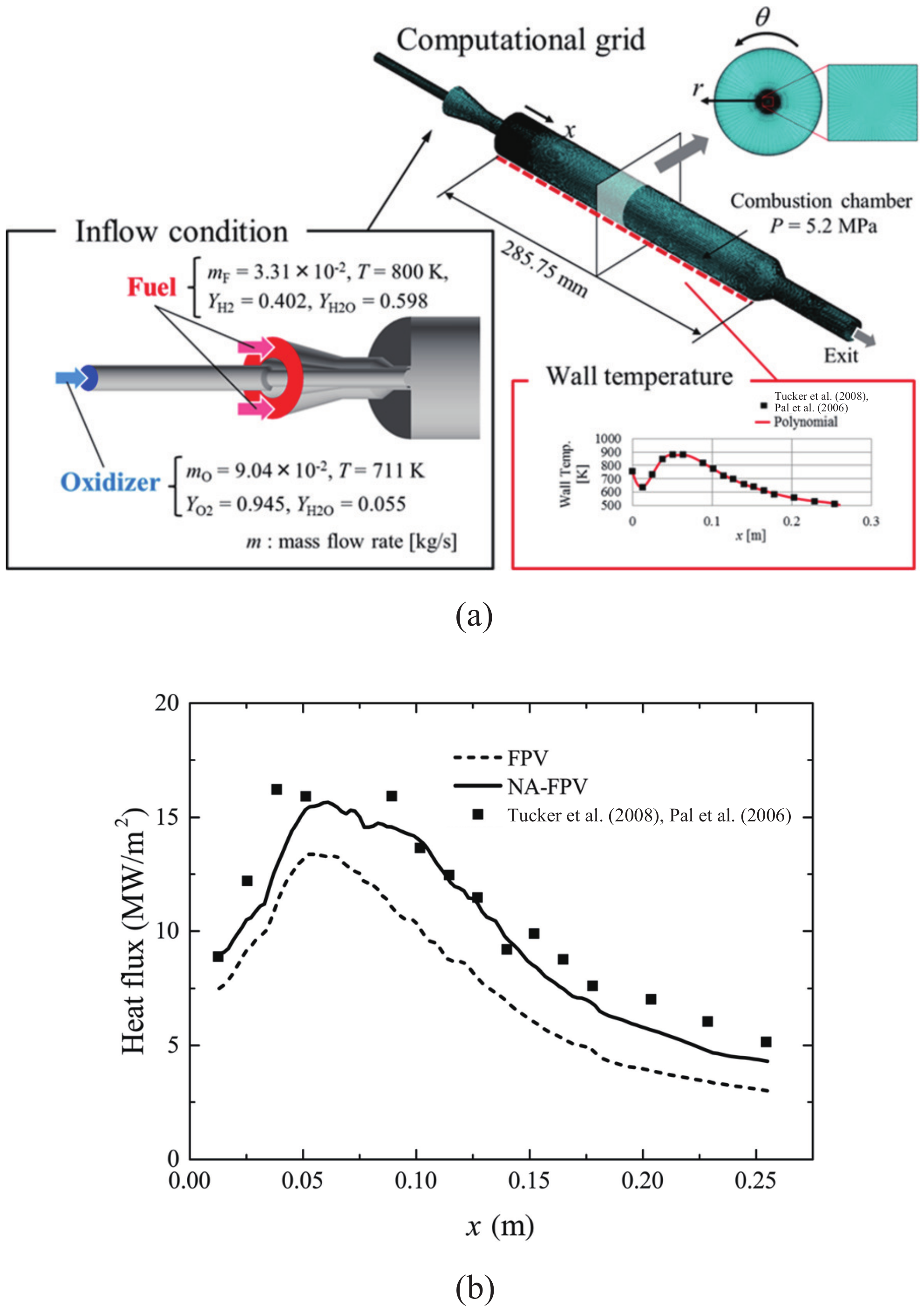
3.1. Effect of Adiabaticity in the Flow Field
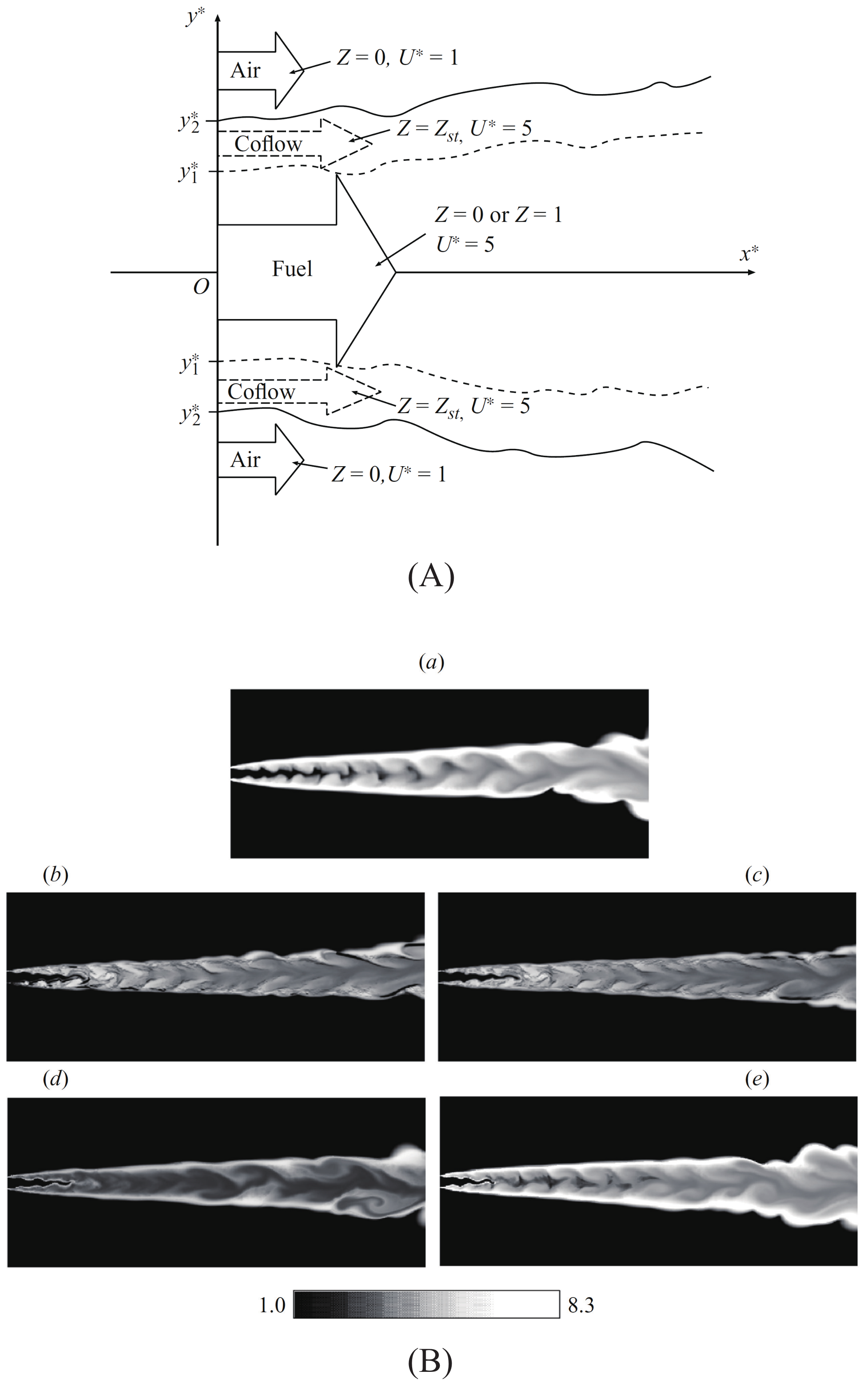
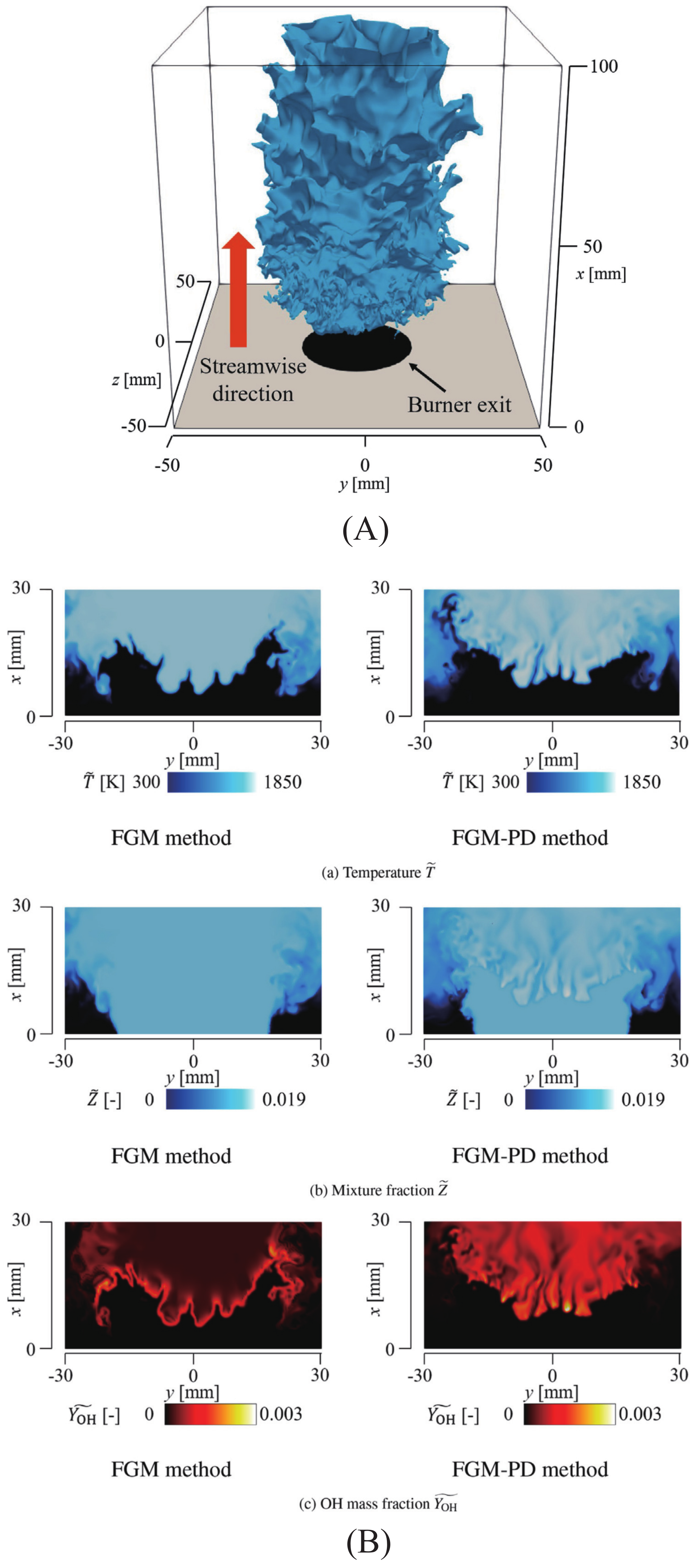
3.2. Effect of Diffusivity of Chemical Species
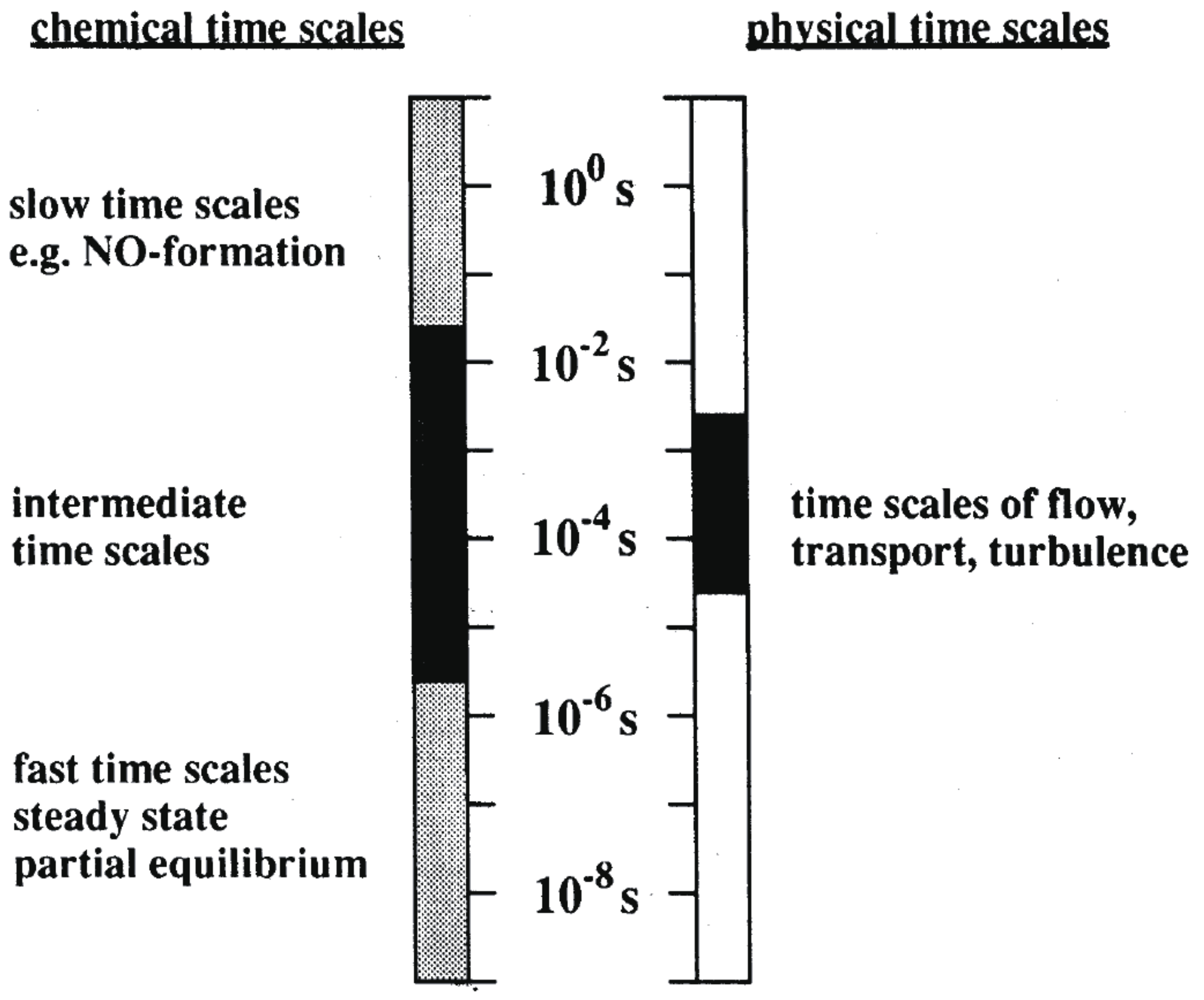
4. Applicability to Relatively Slow Reactions
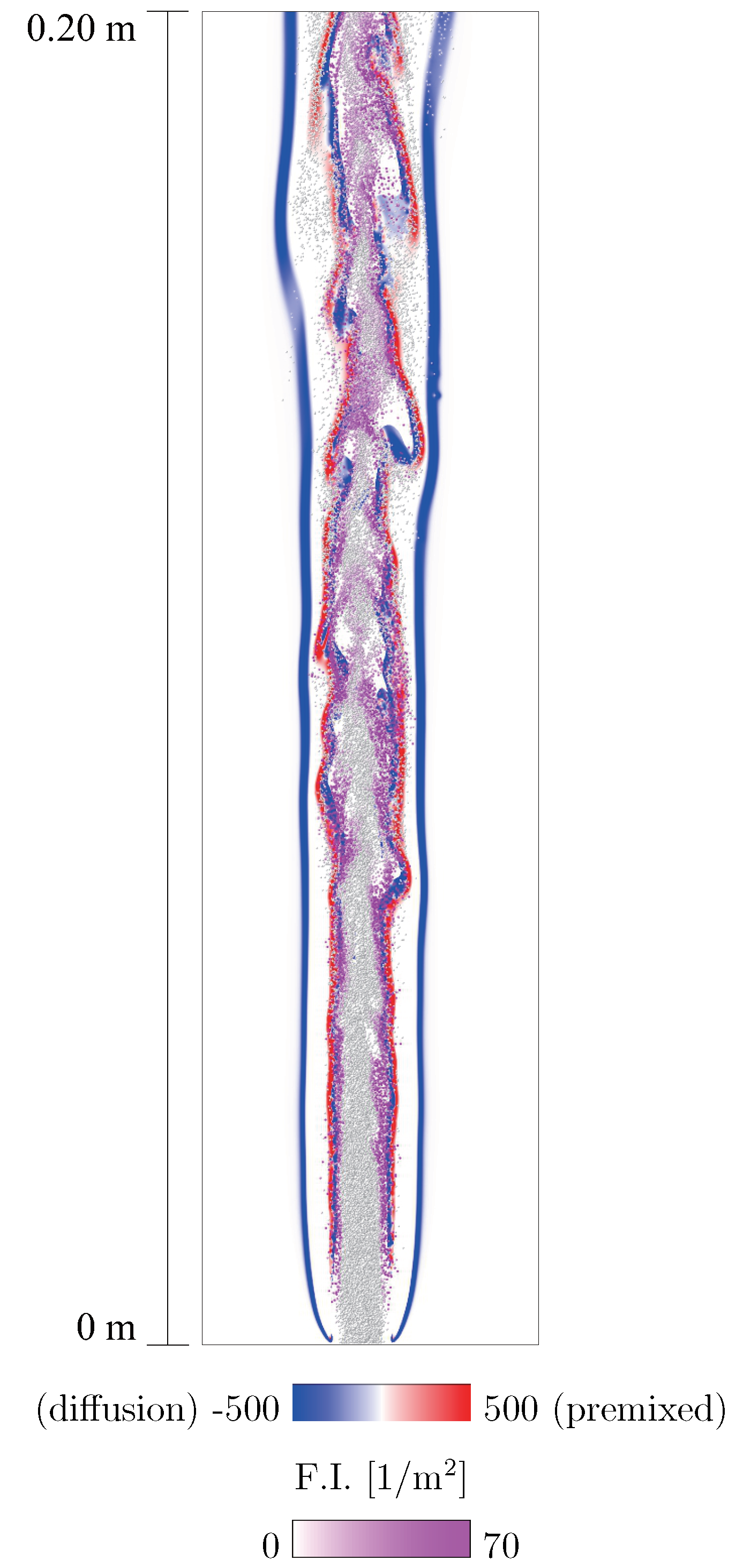
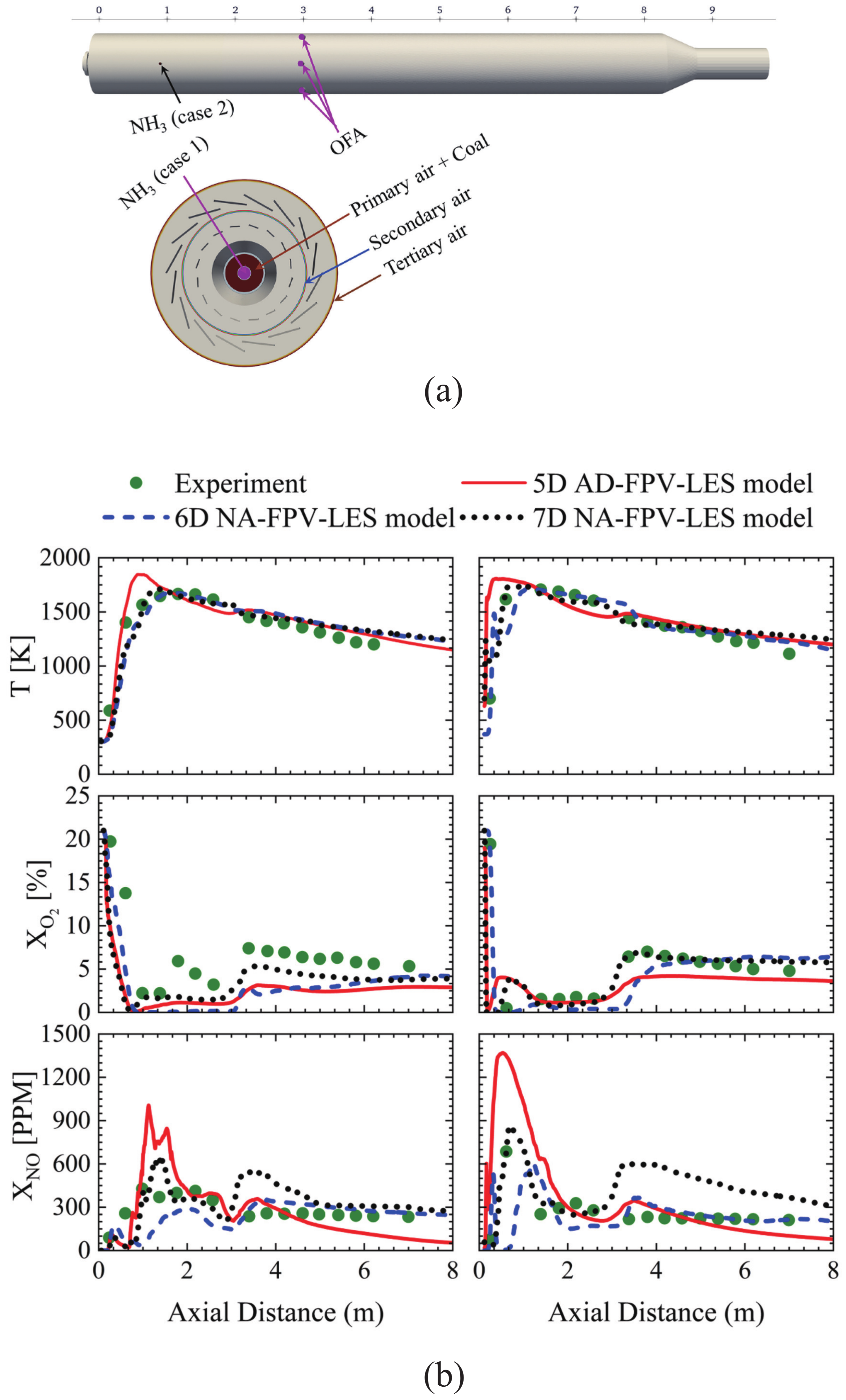
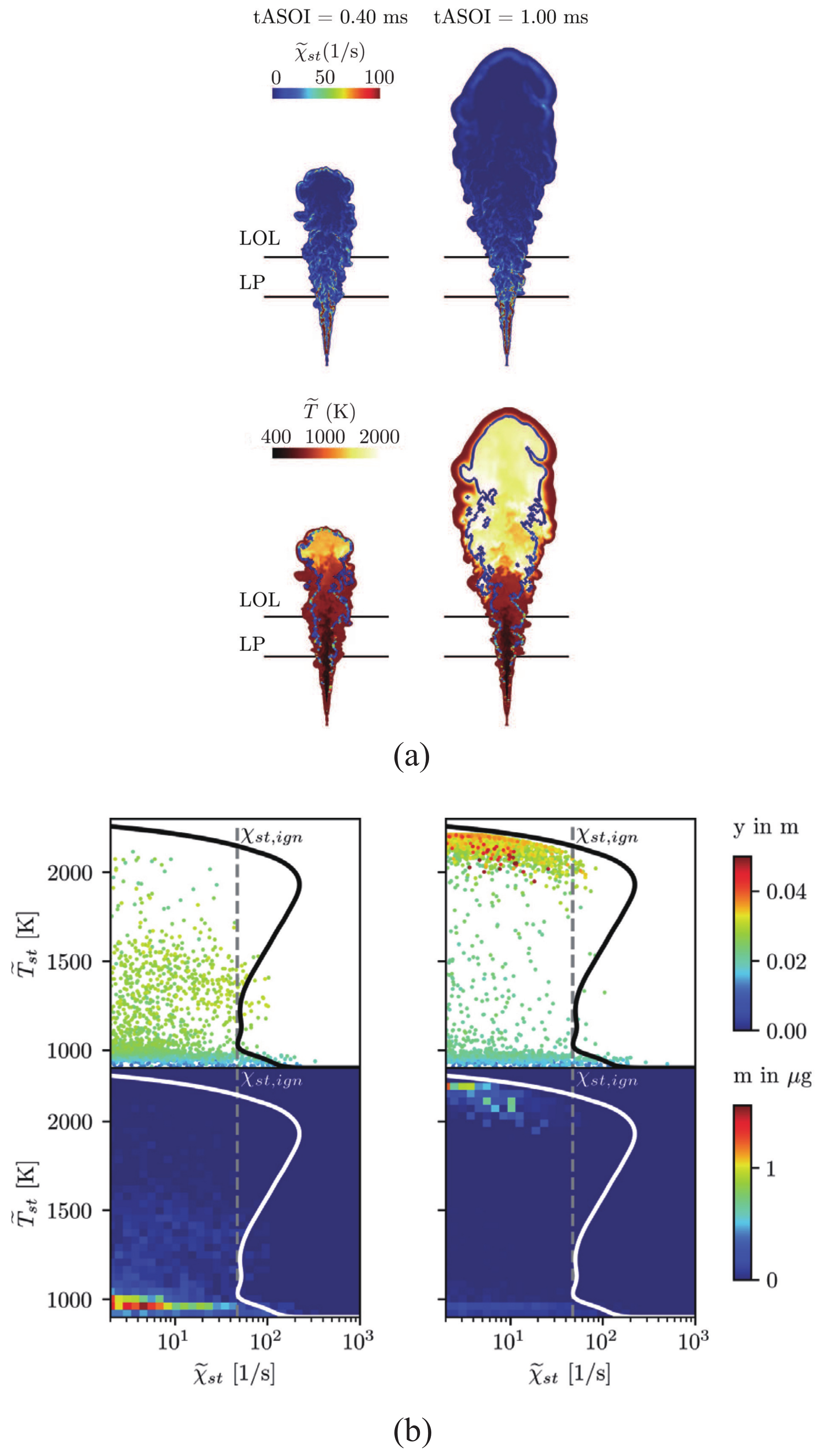
5. Consideration of Non-Stationary Phenomena
6. Summary
- The flamelet/progress-variable (FPV) method has been successfully applied to a wide range of combustor scales, from laboratory experiments to practical applications, as well as across various fuel types, establishing itself as a critical tool for combustion analysis.
- By taking into account fluid dynamics and reaction kinetics factors, such as the non-adiabatic effect of the combustion field and the preferential diffusion of chemical species, FPV methods are able to analyze combustion phenomenon under a wide range of conditions.
- Attempts to reproduce basic phenomena such as ignition and extinction of the flame are also leading to progress in elucidating the fundamental physical phenomena.
Funding
Conflicts of Interest
References
- Yamashita, H.; Shimada, M.; Takeno, T. A numerical study on flame stability at the transition point of jet diffusion flames. Symp. (Int.) Combust. 1996, 26, 27–34. [Google Scholar] [CrossRef]
- Hara, T.; Muto, M.; Kitano, T.; Kurose, R.; Komori, S. Direct numerical simulation of a pulverized coal jet flame employing a global volatile matter reaction scheme based on detailed reaction mechanism. Combust. Flame 2015, 162, 4391–4407. [Google Scholar] [CrossRef]
- Hwang, S.M.; Kurose, R.; Akamatsu, F.; Tsuji, H.; Makino, H.; Katsuki, M. Application of optical diagnostics techniques to a laboratory-scale turbulent pulverized coal flame. Energy Fuels 2005, 19, 382–392. [Google Scholar] [CrossRef]
- van Oijen, J.A.; de Goey, L.P.H. Modelling of premixed laminar flames using flamelet-generated manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef]
- Gupta, H.; Teerling, O.J.; van Oijen, J.A. Effect of progress variable definition on the mass burning rate of premixed laminar flames predicted by the Flamelet Generated Manifold method. Combust. Theory Model. 2021, 25, 631–645. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Pitsch, H. Flamemaster: A C++ Computer Program for 0D Combustion and 1D Laminar Flame Calculations. 1998. Available online: https://www.itv.rwth-aachen.de/downloads/flamemaster (accessed on 28 January 2025).
- Ma, T.; Gao, Y.; Kempf, A.M.; Chakraborty, N. Validation and implementation of algebraic LES modelling of scalar dissipation rate for reaction rate closure in turbulent premixed combustion. Combust. Flame 2014, 161, 3134–3153. [Google Scholar] [CrossRef]
- Ruan, S.; Swaminathan, N.; Isono, M.; Saitoh, T.; Saitoh, K. Simulation of premixed combustion with varying equivalence ratio in gas turbine combustor. J. Propuls. Power 2015, 31, 861–871. [Google Scholar] [CrossRef]
- Chen, Z.X.; Ruan, S.; Swaminathan, N. Large eddy simulation of flame edge evolution in a spark-ignited methane-air jet. Proc. Combust. Inst. 2017, 36, 1645–1652. [Google Scholar] [CrossRef]
- Ghiasi, G.; Doan, N.A.K.; Swaminathan, N.; Yennerdag, B.; Minamoto, Y.; Tanahashi, M. Assessment of SGS closure for isochoric combustion of hydrogen-air mixture. Int. J. Hydrogen Energy 2018, 43, 8105–8115. [Google Scholar] [CrossRef]
- Swaminathan, N.; Bai, X.-S.; Brethouwer, G.; Haugen, N.E.L.; Fureby, C.; Brethouwer, G. (Eds.) Advanced Turbulent Combustion Physics and Applications; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Rieth, M.; Clements, A.G.; Rabaçal, M.; Proch, F.; Stein, O.T.; Kempf, A.M. Flamelet LES modeling of coal combustion with detailed devolatilization by directly coupled CPD. Proc. Combust. Inst. 2017, 36, 2181–2189. [Google Scholar] [CrossRef]
- Mayrhofer, M.; Koller, M.; Seemann, P.; Bordbar, H.; Prieler, R.; Hochenauer, C. MILD combustion of hydrogen and airean efficient modelling approach in CFD validated by experimental data. Int. J. Hydrogen Energy 2022, 47, 6349–6364. [Google Scholar] [CrossRef]
- Wen, J.; Hu, Y.; Nishiie, T.; Iino, J.; Masri, A.; Kurose, R. A flamelet LES of turbulent dense spray flame using a detailed high-resolution VOF simulation of liquid fuel atomization. Combust. Flame 2022, 237, 111742. [Google Scholar] [CrossRef]
- Kong, F.; Li, T.; Cheng, C.; Shan, C.; Xu, B. Modeling of spray flame in gas turbine combustors with LES and FGM. Fuel 2022, 325, 124756. [Google Scholar] [CrossRef]
- Kasuya, H.; Iwai, Y.; Itoh, M.; Morisawa, Y.; Nishiie, T.; Kai, R.; Kurose, R. Les/flamelet/ANN of oxy-fuel combustion for a supercritical CO2 power cycle. Appl. Energy Combust. Sci. 2022, 12, 100083. [Google Scholar] [CrossRef]
- Albrecht, B.; Zahirovic, S.; Bastiaans, R.; van Oijen, J.A.; de Goey, L.P.H. A premixed flamelet-PDF model for biomass combustion in a grate furnace. Energy Fuels 2008, 22, 1570–1580. [Google Scholar] [CrossRef]
- Sakib, A.H.M.N.; Farokhi, M.; Birouk, M. Evaluation of flamelet-based partially premixed combustion models for simulating the gas phase combustion of a grate firing biomass furnace. Fuel 2023, 333, 126343. [Google Scholar] [CrossRef]
- Baba, Y.; Kurose, R. Analysis and flamelet modelling for spray combustion. J. Fluid Dyn. 2008, 612, 45–79. [Google Scholar] [CrossRef]
- Watanabe, J.; Yamamoto, K. Flamelet model for pulverized coal combustion. Proc. Combust. Inst. 2015, 35, 2315–2322. [Google Scholar] [CrossRef]
- Peters, N. Laminar diffusion flamelet models in non-premixed turbulent combustion. Prog. Energy Combust. Sci. 1984, 10, 319–339. [Google Scholar] [CrossRef]
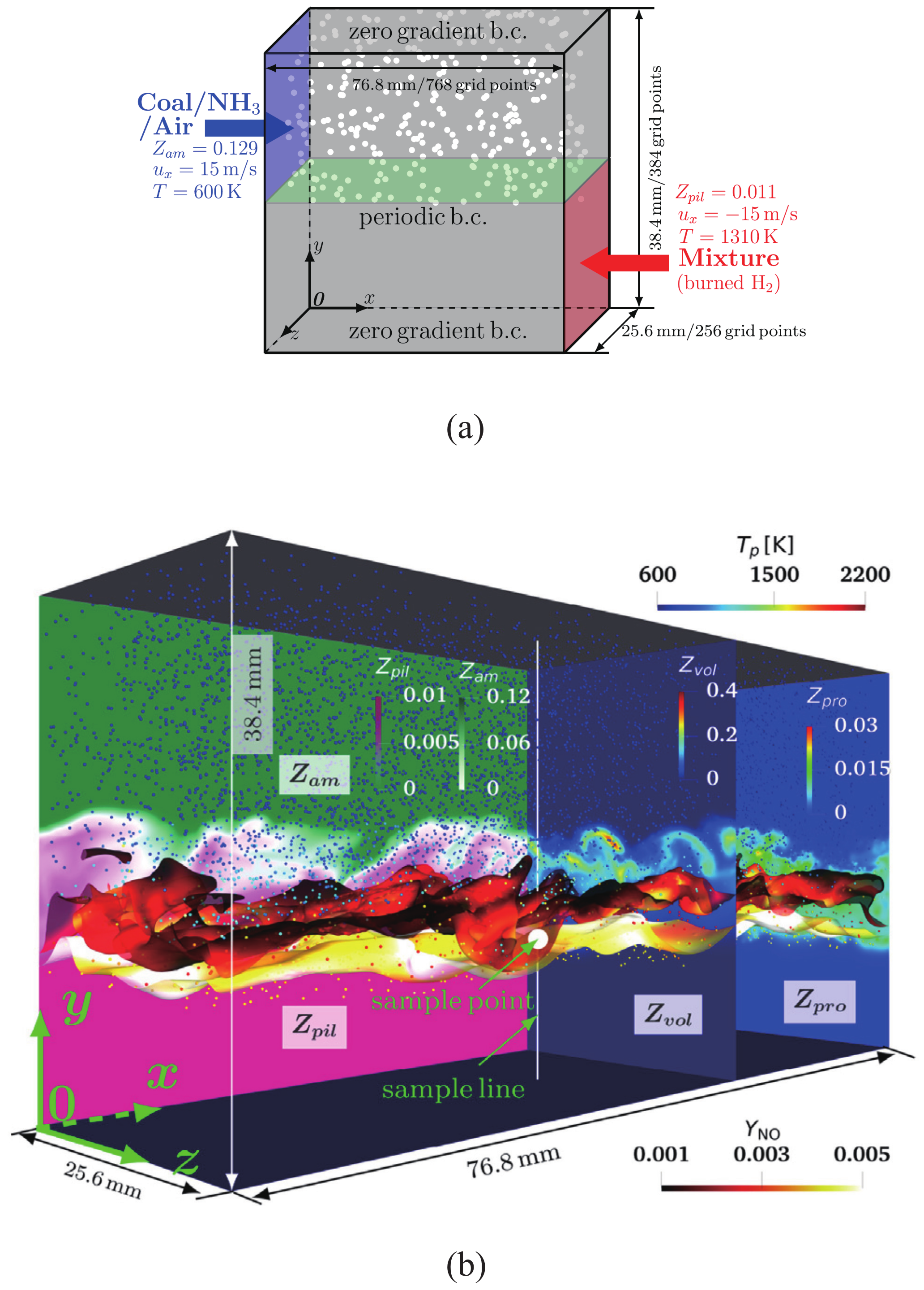
- Wen, X.; Shamooni, A.; Zirwes, T.; Stein, O.T.; Kronenburg, A.; Hasse, C. Carrier-phase direct numerical simulation and flamelet modeling of NOx formation in a pulverized coal/ammonia co-firing flame. Combust. Flame 2024, 269, 113722. [Google Scholar]
- Wen, X.; Luo, K.; Jin, H.; Fan, J. Large eddy simulation of piloted pulverised coal combustion using extended flamelet/progress variable model. Combust. Theory Model. 2017, 21, 925–953. [Google Scholar]
- Meller, D.; Lipkowicz, T.; Rieth, M.; Stein, O.T.; Kronenburg, A.; Hasse, C.; Kempf, A.M. Numerical analysis of a turbulent pulverized coal flame using a flamelet/progress variable approach and modeling experimental artifacts. Energy Fuels 2021, 35, 7133–7143. [Google Scholar] [CrossRef]
- Proch, F.; Kempf, A.M. Modeling heat loss effects in the large eddy simulation of a model gas turbine combustor with premixed flamelet generated manifolds. Proc. Combust. Inst. 2015, 35, 3337–3345. [Google Scholar]
- Kishimoto, A.; Moriai, H.; Takenaka, K.; Nishiie, T.; Adachi, M.; Ogawara, A.; Kurose, R. Application of a nonadiabatic flamelet/progress-variable approach to Large-eddy simulation of H2/O2 combustion under a pressurized condition. J. Heat Transf. 2017, 139, 124501-1. [Google Scholar] [CrossRef]
- Yadav, S.; Yu, P.; Tanno, K.; Watanabe, H. Multi-stream FPV-LES modeling of ammonia/coal co-firing on a semi-industrial scale complex burner with pre-heated secondary, tertiary, and staged combustion air. Combust. Flame 2024, 270, 113729. [Google Scholar]
- Tucker, P.; Menon, S.; Merkle, C.; Oefelein, J.; Yang, V. Validation of high-fidelity CFD simulations for rocket injector design. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008. [Google Scholar]
- Pal, S.; Marshall, W.; Woodward, R.; Santoro, R. Wall heat flux measurements for a uni-element GO2/GH2 shear coaxial injector. In Proceedings of the Third International Workshop on Rocket Combustion Modeling, Paris, France, 13 March 2006. [Google Scholar]
- Pitsch, H.; Peters, N. A consistent Flamelet formulation for non-premixed combustion considering differential diffusion effects. Combust. Flame 1998, 114, 26–40. [Google Scholar]
- Donini, A.; Bastiaans, R.J.M.; van Oijen, J.A.; de Goey, L.P.H. Differential diffusion effects inclusion with flamelet generated manifold for the modeling of stratified premixed cooled flames. Proc. Combust. Inst. 2015, 35, 831–837. [Google Scholar]
- Smooke, M.D. Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane-Air Flames: A Topical Volume; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Altantzis, C.; Frouzakis, C.E.; Tomboulides, A.G.; Matalon, M.; Boulouchos, K. Hydrodynamic and thermodiffusive instability effects on the evolution of laminar planar lean premixed hydrogen flames. J. Fluid Mech. 2012, 700, 329–361. [Google Scholar]
- Kai, R.; Tokuoka, T.; Nagao, J.; Pillai, A.L.; Kurose, R. LES flamelet modeling of hydrogen combustion considering preferential diffusion effect. Int. J. Hydrogen Energy 2023, 48, 11086–11101. [Google Scholar]
- Ihme, M.; Schmitt, C.; Pitsch, H. Optimal artificial neural networks and tabulation methods for chemistry representation in LES of a bluff-body swirl-stabilized flame. Proc. Combust. Inst. 2009, 32, 1527–1535. [Google Scholar]
- Honzawa, T.; Kai, R.; Hori, K.; Seino, M.; Nishiie, T.; Kurose, R. Experimental and numerical study of water sprayed turbulent combustion: Proposal of a neural network modeling for five-dimensional flamelet approach. Energy AI 2021, 5, 100076. [Google Scholar] [CrossRef]
- Masri, A.R. Web Site for the Sydney Swirl Flame Series. 2006. Available online: http://www.aeromech.usyd.edu.au/thermofluids (accessed on 28 January 2025).
- Wen, X.; Berger, L.; vom Lehn, F.; Parente, A.; Pitsch, H. Numerical analysis and flamelet modeling of NOx formation in a thermodiffusively unstable hydrogen flame. Combust. Flame 2023, 253, 112817. [Google Scholar] [CrossRef]
- Wick, A.; Attili, A.; Bisetti, F.; Pitsch, H. DNS-driven analysis of the Flamelet/Progress Variable model assumptions on soot inception, growth, and oxidation in turbulent flames. Combust. Flame 2020, 214, 437–449. [Google Scholar] [CrossRef]
- Maas, U.; Pope, S.B. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Combust. Flame 1992, 88, 239–264. [Google Scholar] [CrossRef]
- Wen, X.; Debiagi, P.; Stein, O.T.; Kronenburg, A.; Kempf, A.M.; Hasse, C. Flamelet tabulation methods for solid fuel combustion with fuel-bound nitrogen. Combust. Flame 2019, 209, 155–166. [Google Scholar] [CrossRef]
- Ihme, M.; Pitsch, H. Modeling of radiation and nitric oxide formation in turbulent nonpremixed flames using a flamelet/progress variable formulation. Phys. Fluids 2008, 20, 055110. [Google Scholar] [CrossRef]
- Wan, J.; Guo, J.; Wei, Z.; Jiang, X.; Liu, Z. Large eddy simulation of NO formation in non-premixed turbulent jet flames with flamelet/progress variable approach. J. Therm. Sci. 2024, 33, 2399–2412. [Google Scholar] [CrossRef]
- Pitsch, H.; Ihme, M. An unsteady/flamelet progress variable method for les of nonpremixed turbulent combustion. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit Meeting Papers, Reno, NV, USA, 10–13 January 2005; p. 2004-557. [Google Scholar]
- Ihme, M.; See, Y.C. Prediction of autoignition in a lifted methane/air flame using an unsteady flamelet/progress variable model. Combust. Flame 2010, 157, 1850–1862. [Google Scholar]
- Bajaj, C.; Ameen, M.; Abraham, J. Evaluation of an unsteady flamelet progress variable model for autoignition and flame lift-off in diesel jets. Combust. Sci. Technol. 2013, 185, 454–472. [Google Scholar]
- Sun, Z.; Gierth, S.; Pollack, M.; Hasse, C.; Scholtissek, A. Ignition under strained conditions: Unsteady flamelet progress variable modeling for diesel engine conditions in the transient counterflow configuration. Combust. Flame 2021, 240, 111841. [Google Scholar] [CrossRef]
- Gierth, S.; Haspel, P.; Scholtissek, A.; Sun, Z.; Popp, S.; Hasse, C. Evaluation of the unsteady flamelet progress variable approach in Large Eddy Simulations of the ECN Spray A. Sci. Technol. Energy Transit. 2022, 77, 5. [Google Scholar] [CrossRef]
- Pickett, L.M. Engine Combustion Network, Sandia National Laboratory. 2013. Available online: https://ecn.sandia.gov (accessed on 28 January 2025).



| Species | Value |
|---|---|
| 0.97 | |
| 1.11 | |
| 0.83 | |
| 1.39 | |
| 0.70 | |
| 0.73 | |
| 1.10 | |
| 0.30 | |
| 1.10 | |
| 1.12 | |
| 1.27 | |
| 1.28 | |
| 1.00 | |
| 1.30 | |
| 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muto, M. Tabulated Chemistry Models for Numerical Simulation of Combustion Flow Field. Fluids 2025, 10, 83. https://doi.org/10.3390/fluids10040083
Muto M. Tabulated Chemistry Models for Numerical Simulation of Combustion Flow Field. Fluids. 2025; 10(4):83. https://doi.org/10.3390/fluids10040083
Chicago/Turabian StyleMuto, Masaya. 2025. "Tabulated Chemistry Models for Numerical Simulation of Combustion Flow Field" Fluids 10, no. 4: 83. https://doi.org/10.3390/fluids10040083
APA StyleMuto, M. (2025). Tabulated Chemistry Models for Numerical Simulation of Combustion Flow Field. Fluids, 10(4), 83. https://doi.org/10.3390/fluids10040083






