An Improved Regularization Scheme for an Extended Lattice Boltzmann Model
Abstract
1. Introduction
2. Numerical Methods
2.1. Thermally Compressible LBM
2.2. Regularization Method for Thermally Compressible LBM
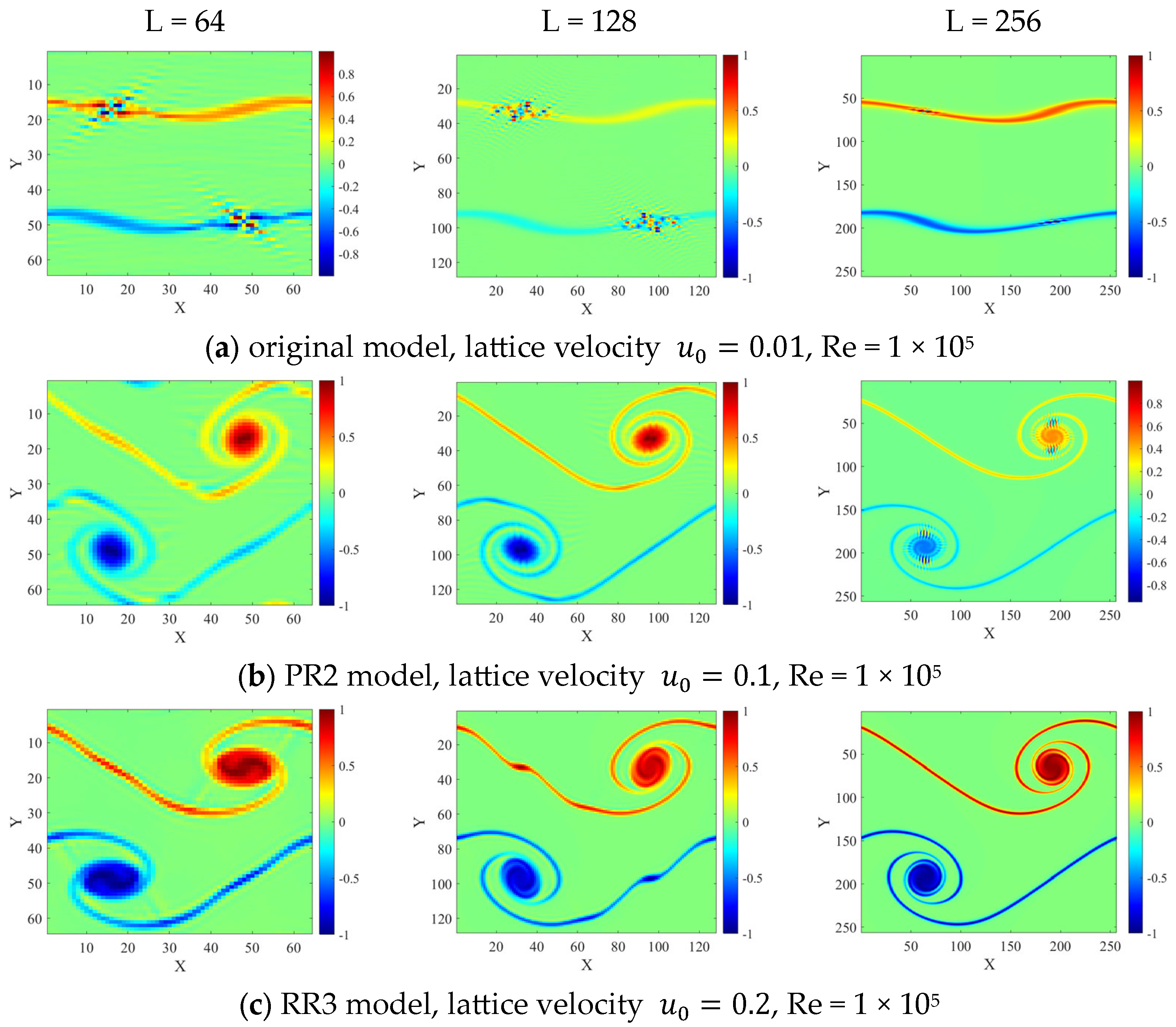
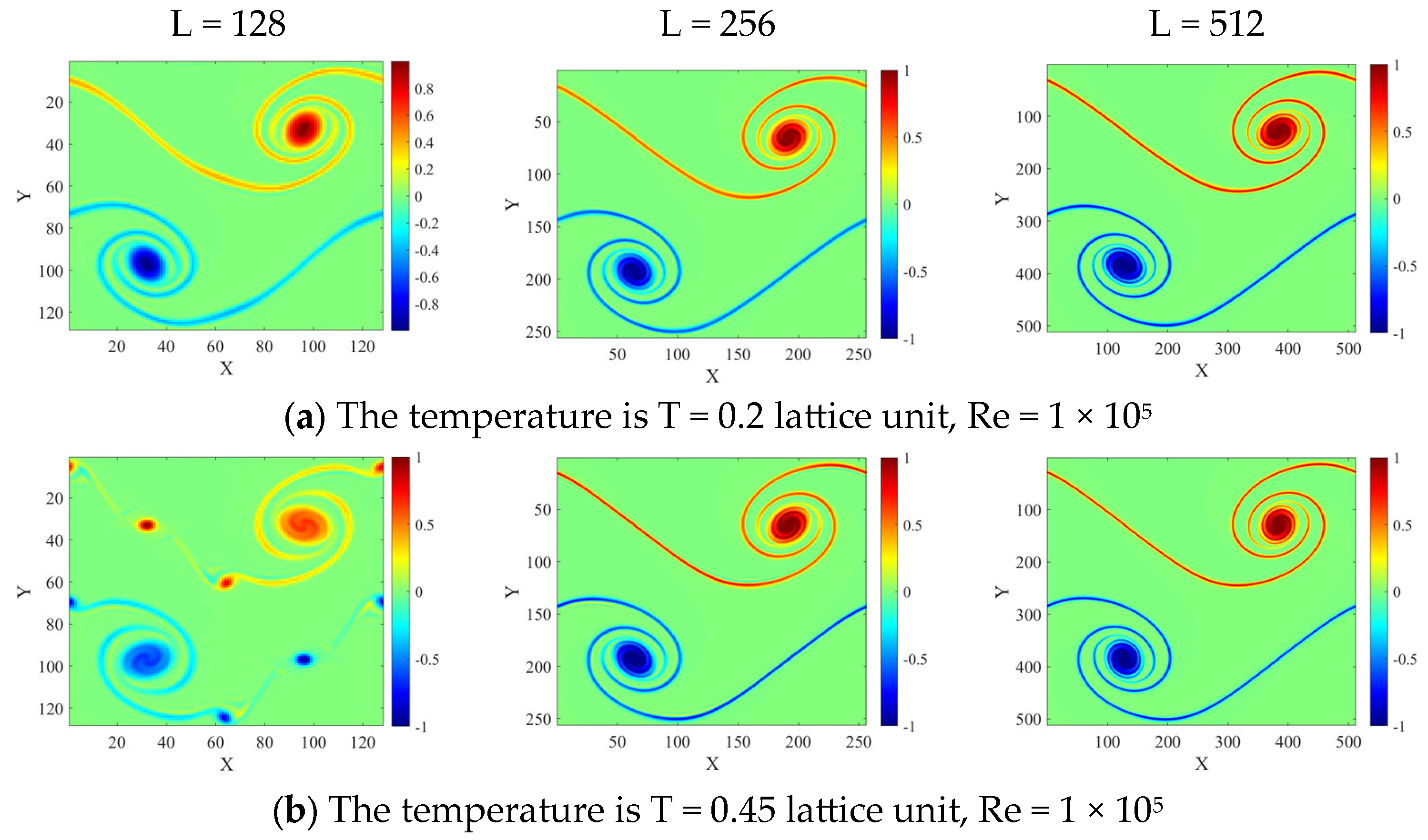
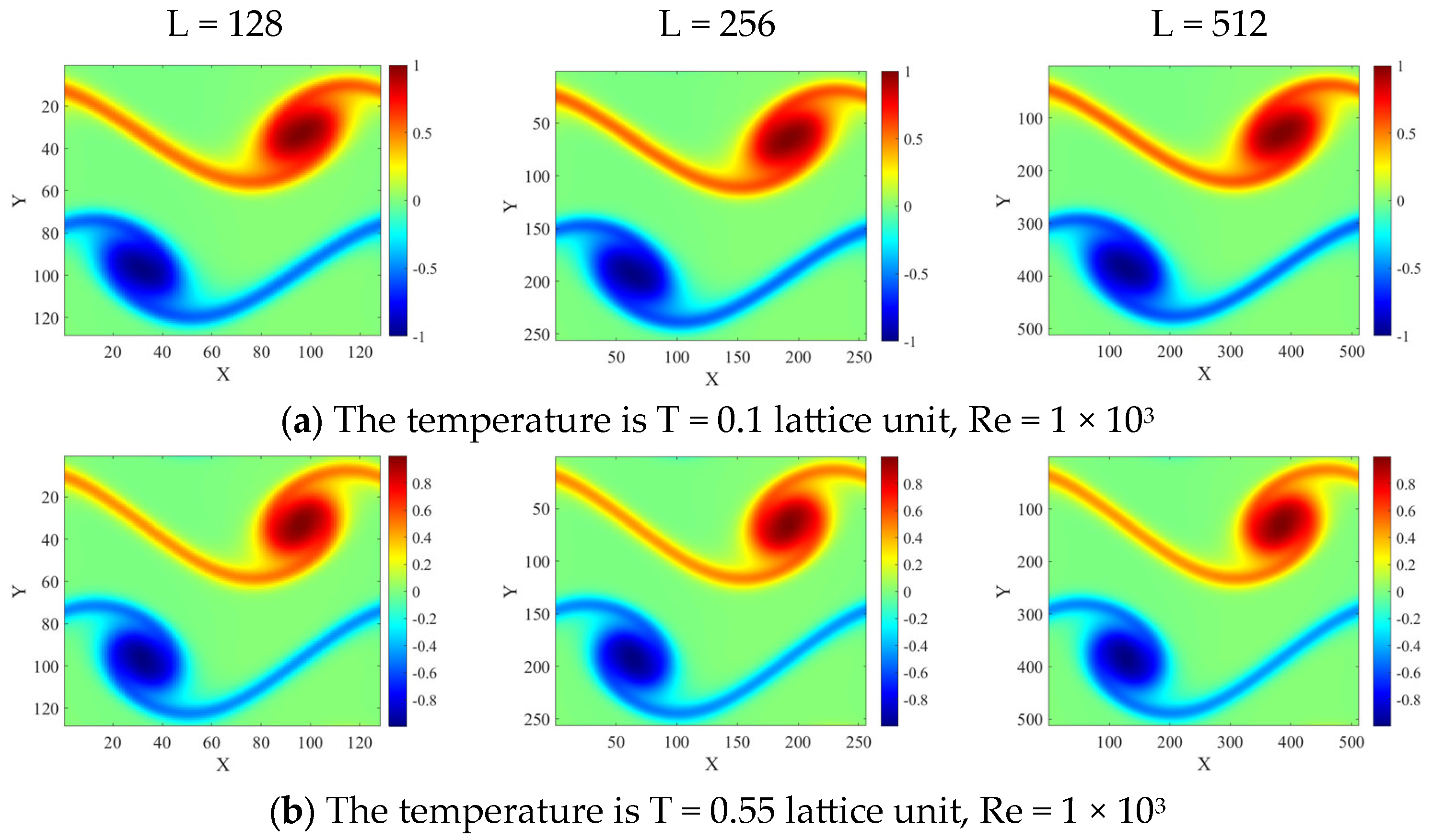
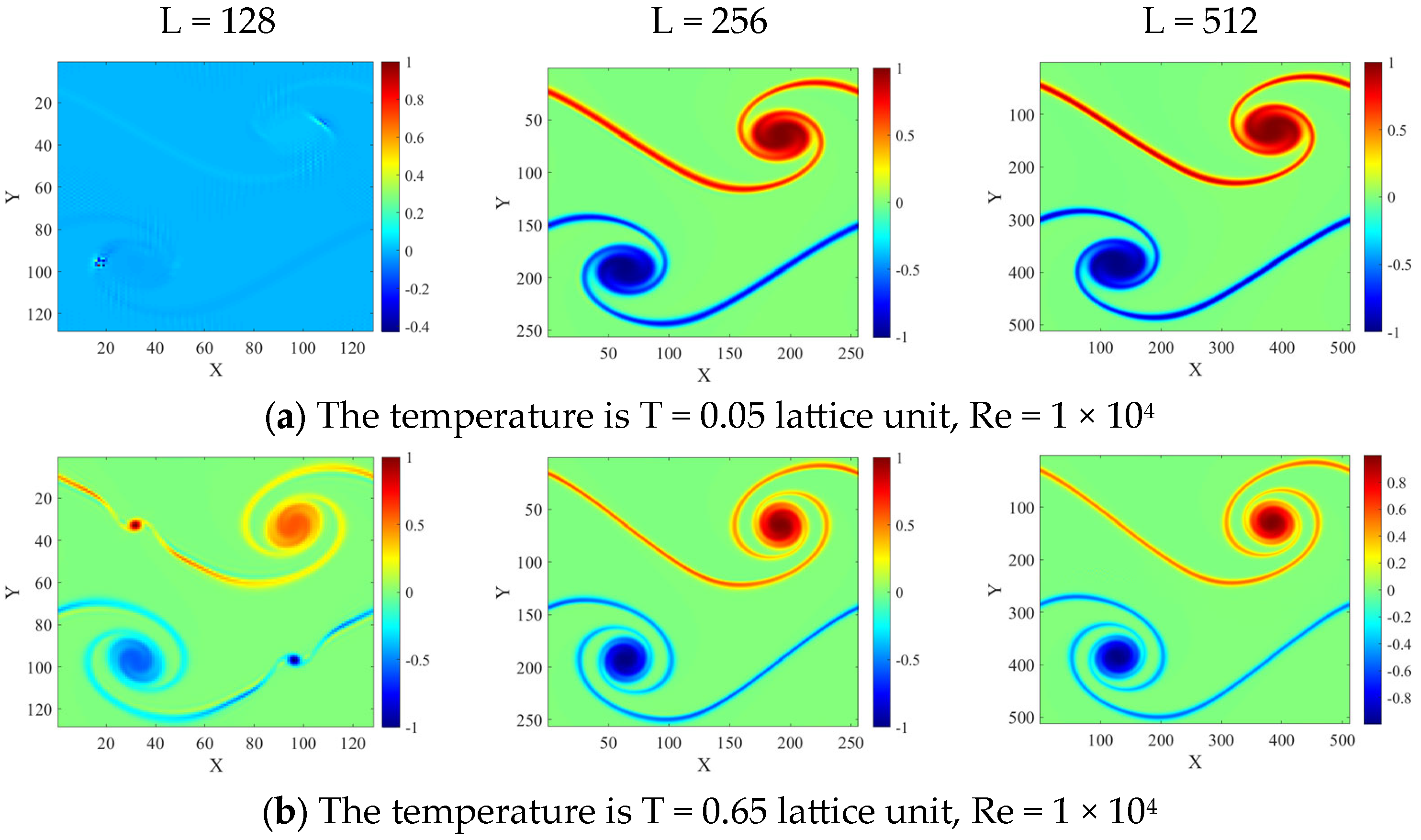
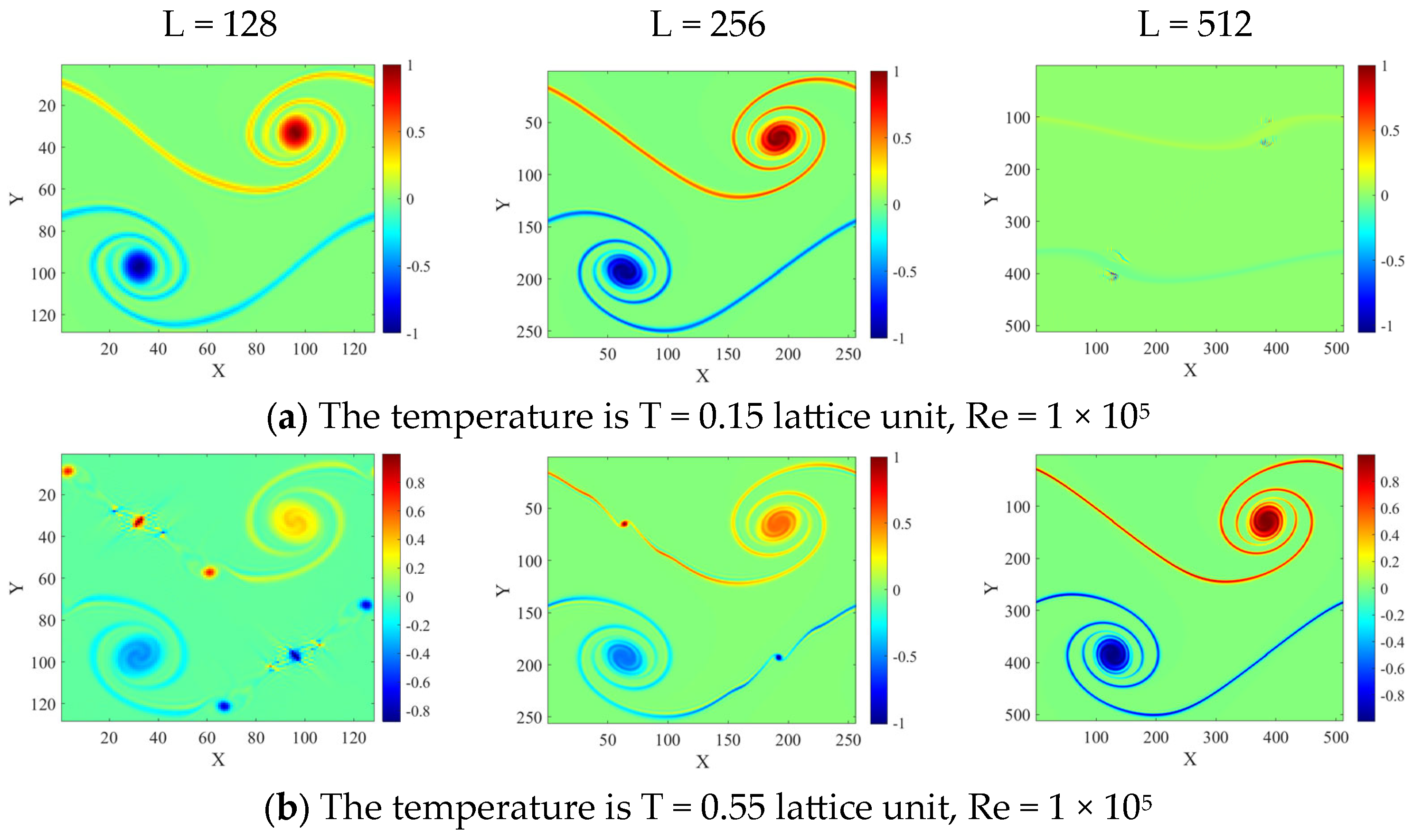
3. Numerical Results
3.1. Galilean Invariance, Isotropy, and Temperature Independence Tests
3.2. Stability Tests
3.2.1. Flow at Lattice Reference Temperature
3.2.2. Flow at Temperature Deviating from the Lattice Reference Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LBM | Lattice Boltzmann method |
| CFD | Computational fluid dynamics |
| BGK | Bhatnagar–Gross–Krook |
References
- Dorschner, B.; Bösch, F.; Chikatamarla, S.S.; Boulouchos, K.; Karlin, I.V. Entropic multi-relaxation time lattice Boltzmann model for complex flows. J. Fluid Mech. 2016, 801, 623–651. [Google Scholar] [CrossRef]
- Wagner, A.J. Thermodynamic consistency of liquid-gas lattice Boltzmann simulations. Phys. Rev. E 2006, 74, 056703. [Google Scholar] [CrossRef]
- Tölke, J.; De Prisco, G.; Mu, Y. A lattice Boltzmann method for immiscible two-phase Stokes flow with a local collision operator. Comput. Math. Appl. 2013, 65, 864–881. [Google Scholar] [CrossRef]
- Montessori, A.; Prestininzi, P.; La Rocca, M.; Falcucci, G.; Succi, S.; Kaxiras, E. Effects of Knudsen diffusivity on the effective reactivity of nanoporous catalyst media. J. Comput. Sci. 2016, 17, 377–383. [Google Scholar] [CrossRef]
- Sawant, N.; Dorschner, B.; Karlin, I.V. Consistent lattice Boltzmann model for reactive mixtures. J. Fluid Mech. 2022, 941, A62. [Google Scholar] [CrossRef]
- Bocanegra Cifuentes, J.A.; Borelli, D.; Cammi, A.; Lomonaco, G.; Misale, M. Lattice Boltzmann Method Applied to Nuclear Reactors—A Systematic Literature Review. Sustainability 2020, 12, 7835. [Google Scholar] [CrossRef]
- Bocanegra, J.A.; Misale, M.; Borelli, D. A systematic literature review on Lattice Boltzmann Method applied to acoustics. Eng. Anal. Bound. Elem. 2024, 158, 405–429. [Google Scholar] [CrossRef]
- Sharma, K.V.; Straka, R.; Tavares, F.W. Current status of Lattice Boltzmann Methods applied to aerodynamic, aeroacoustic, and thermal flows. Prog. Aerosp. Sci. 2020, 115, 100616. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. A Review on the development of lattice Boltzmann computation of macro fluid flows and heat transfer. Alex. Eng. J. 2015, 54, 955–971. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Complex States of Flowing Matter; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Springer: Cham, Switzerland, 2017; Volume 10, pp. 4–15. [Google Scholar]
- Saadat, M.H.; Hosseini, S.A.; Dorschner, B.; Karlin, I.V. Extended lattice Boltzmann model for gas dynamics. Phys. Fluids 2021, 33, 046104. [Google Scholar] [CrossRef]
- Shan, X.; Yuan, X.F.; Chen, H. Kinetic theory representation of hydrodynamics: A way beyond the Navier–Stokes equation. J. Fluid Mech. 2006, 550, 413–441. [Google Scholar] [CrossRef]
- Chikatamarla, S.S.; Karlin, I.V. Lattices for the lattice Boltzmann method. Phys. Rev. E 2009, 79, 046701. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Shan, X. Temperature-scaled collision process for the high-order lattice Boltzmann model. Phys. Rev. E 2019, 100, 013301. [Google Scholar] [CrossRef]
- Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Entropic lattice Boltzmann model for gas dynamics: Theory, boundary conditions, and implementation. Phys. Rev. E 2016, 93, 063302. [Google Scholar] [CrossRef]
- Wilde, D.; Krämer, A.; Reith, D.; Foysi, H. Semi-Lagrangian lattice Boltzmann method for compressible flows. Phys. Rev. E 2020, 101, 053306. [Google Scholar] [CrossRef]
- Prasianakis, N.I.; Karlin, I.V. Lattice Boltzmann method for simulation of compressible flows on standard lattices. Phys. Rev. E 2008, 78, 016704. [Google Scholar] [CrossRef]
- Prasianakis, N.I.; Karlin, I.V.; Mantzaras, J.; Boulouchos, K.B. Lattice Boltzmann method with restored Galilean invariance. Phys. Rev. E 2009, 79, 066702. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B.; Zhao, T.S. Thermal lattice Boltzmann equation for low Mach number flows: Decoupling model. Phys. Rev. E 2007, 75, 036704. [Google Scholar] [CrossRef]
- Feng, Y.; Sagaut, P.; Tao, W. A three dimensional lattice model for thermal compressible flow on standard lattices. J. Comput. Phys. 2015, 303, 514–529. [Google Scholar] [CrossRef]
- Saadat, M.H.; Bösch, F.; Karlin, I.V. Lattice Boltzmann model for compressible flows on standard lattices: Variable Prandtl number and adiabatic exponent. Phys. Rev. E 2019, 99, 013306. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Darabiha, N.; Thévenin, D. Compressibility in lattice Boltzmann on standard stencils: Effects of deviation from reference temperature. Philos. Trans. R. Soc. A 2020, 378, 20190399. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Acoustic and thermal properties in two and three dimensions. Phys. Rev. E 2003, 68, 036706. [Google Scholar] [CrossRef]
- Wissocq, G.; Sagaut, P.; Boussuge, J.F. An extended spectral analysis of the lattice Boltzmann method: Modal interactions and stability issues. J. Comput. Phys. 2019, 380, 311–333. [Google Scholar] [CrossRef]
- D’Humieres, D. Generalized Lattice-Boltzmann Equations. Rarefied Gas Dyn. Theory Simul. 1992, 159, 450–458. [Google Scholar]
- Wissocq, G.; Coreixas, C.; Boussuge, J.F. Linear stability and isotropy properties of athermal regularized lattice Boltzmann methods. Phys. Rev. E 2020, 102, 053305. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B. Lattice Boltzmann method with regularized pre-collision distribution functions. Math. Comput. Simul. 2006, 72, 165–168. [Google Scholar] [CrossRef]
- Coreixas, C.; Wissocq, G.; Puigt, G.; Boussuge, J.F.; Sagaut, P. Recursive regularization step for high-order lattice Boltzmann methods. Phys. Rev. E 2017, 96, 033306. [Google Scholar] [CrossRef]
- Jacob, J.; Malaspinas, O.; Sagaut, P. A new hybrid recursive regularised Bhatnagar–Gross–Krook collision model for lattice Boltzmann method-based large eddy simulation. J. Turbul. 2018, 19, 1051–1076. [Google Scholar] [CrossRef]
- Saadat, M.H.; Dorschner, B.; Karlin, I. Extended lattice Boltzmann model. Entropy 2021, 23, 475. [Google Scholar] [CrossRef]









| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| Original | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | diverges |
| PR2 | 0.010 | 0.010 | 0.010 | 0.010 | diverges | diverges | diverges |
| RR3 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | −2.116 |
| RR4 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | −1.160 |
| T/ | 0.1 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 |
| Original | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | diverges |
| PR2 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | diverges |
| RR3 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
| RR4 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, Y.; Gao, H. An Improved Regularization Scheme for an Extended Lattice Boltzmann Model. Fluids 2025, 10, 101. https://doi.org/10.3390/fluids10040101
Zhang Z, Li Y, Gao H. An Improved Regularization Scheme for an Extended Lattice Boltzmann Model. Fluids. 2025; 10(4):101. https://doi.org/10.3390/fluids10040101
Chicago/Turabian StyleZhang, Zhihong, Yijin Li, and Haobu Gao. 2025. "An Improved Regularization Scheme for an Extended Lattice Boltzmann Model" Fluids 10, no. 4: 101. https://doi.org/10.3390/fluids10040101
APA StyleZhang, Z., Li, Y., & Gao, H. (2025). An Improved Regularization Scheme for an Extended Lattice Boltzmann Model. Fluids, 10(4), 101. https://doi.org/10.3390/fluids10040101





