Transonic Aerodynamic Performance Analysis of a CRM Joined-Wing Configuration †
Abstract
1. Introduction
2. Materials and Methods
2.1. JW Design Methodology
2.2. JW Geometries
2.3. Computational Domain and Mesh Generation
2.3.1. CFD Solver
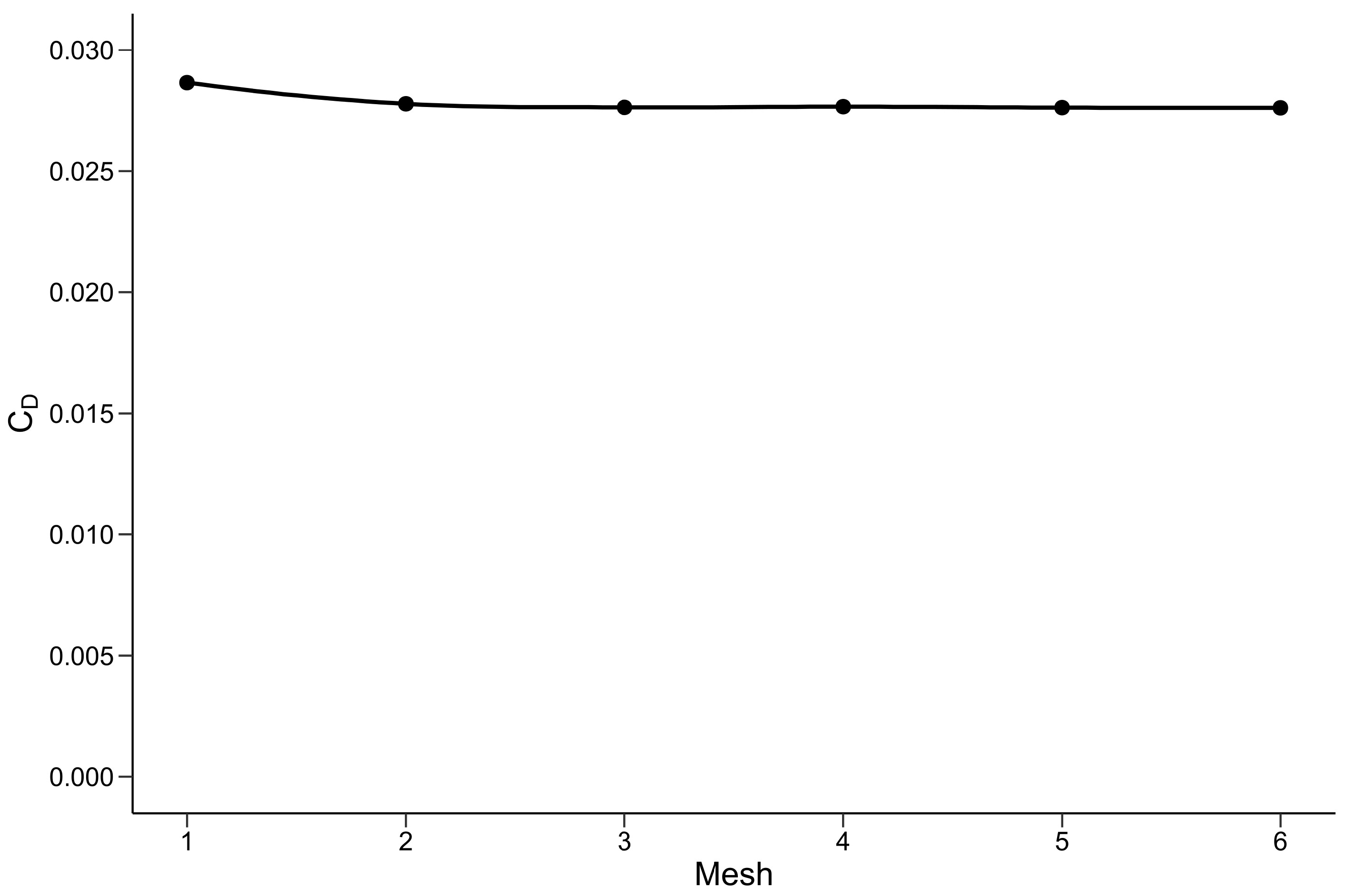
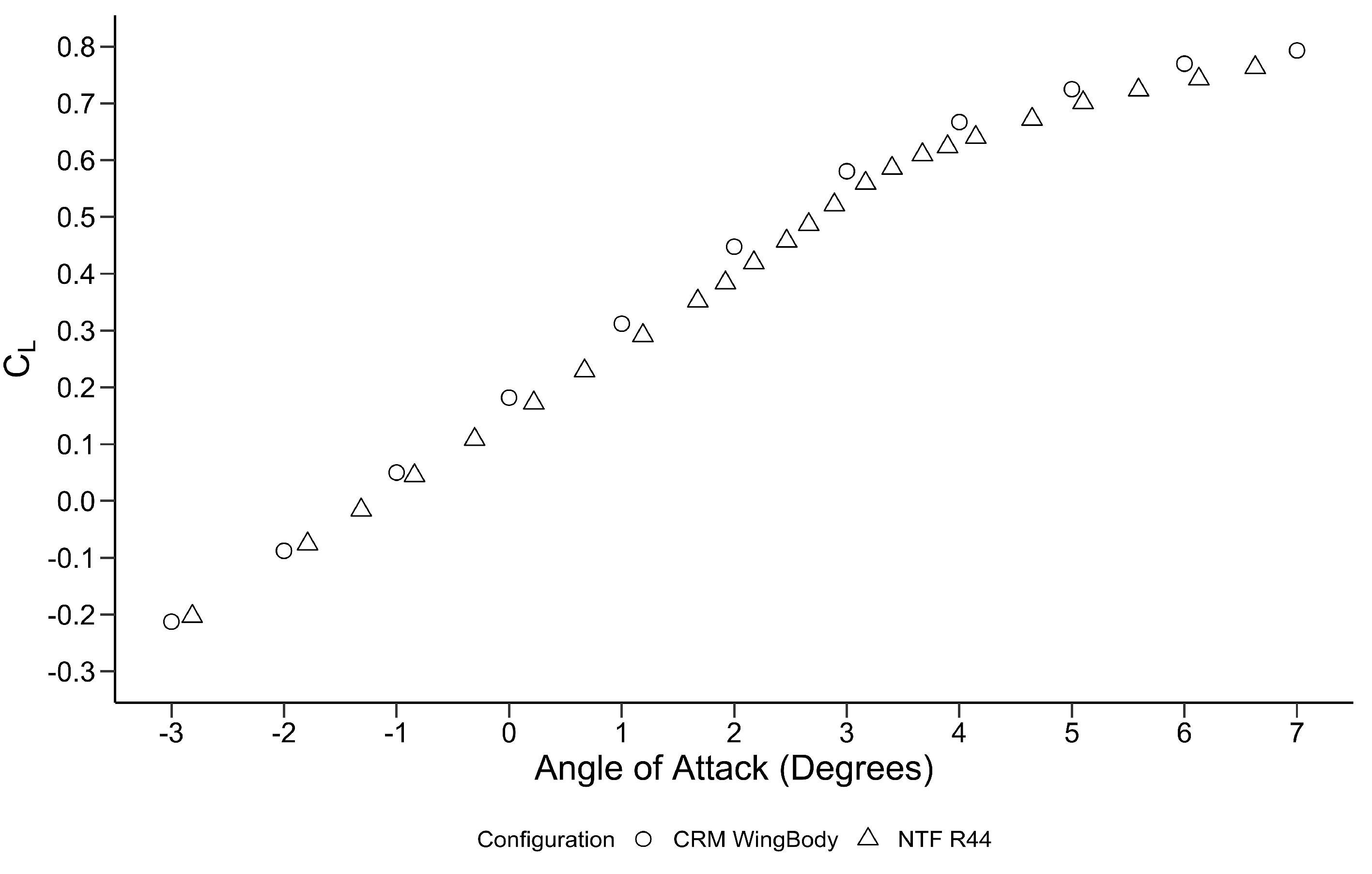
2.3.2. Validation of Numerical Approach
3. Transonic Flow Results for JW Configurations and Discussions
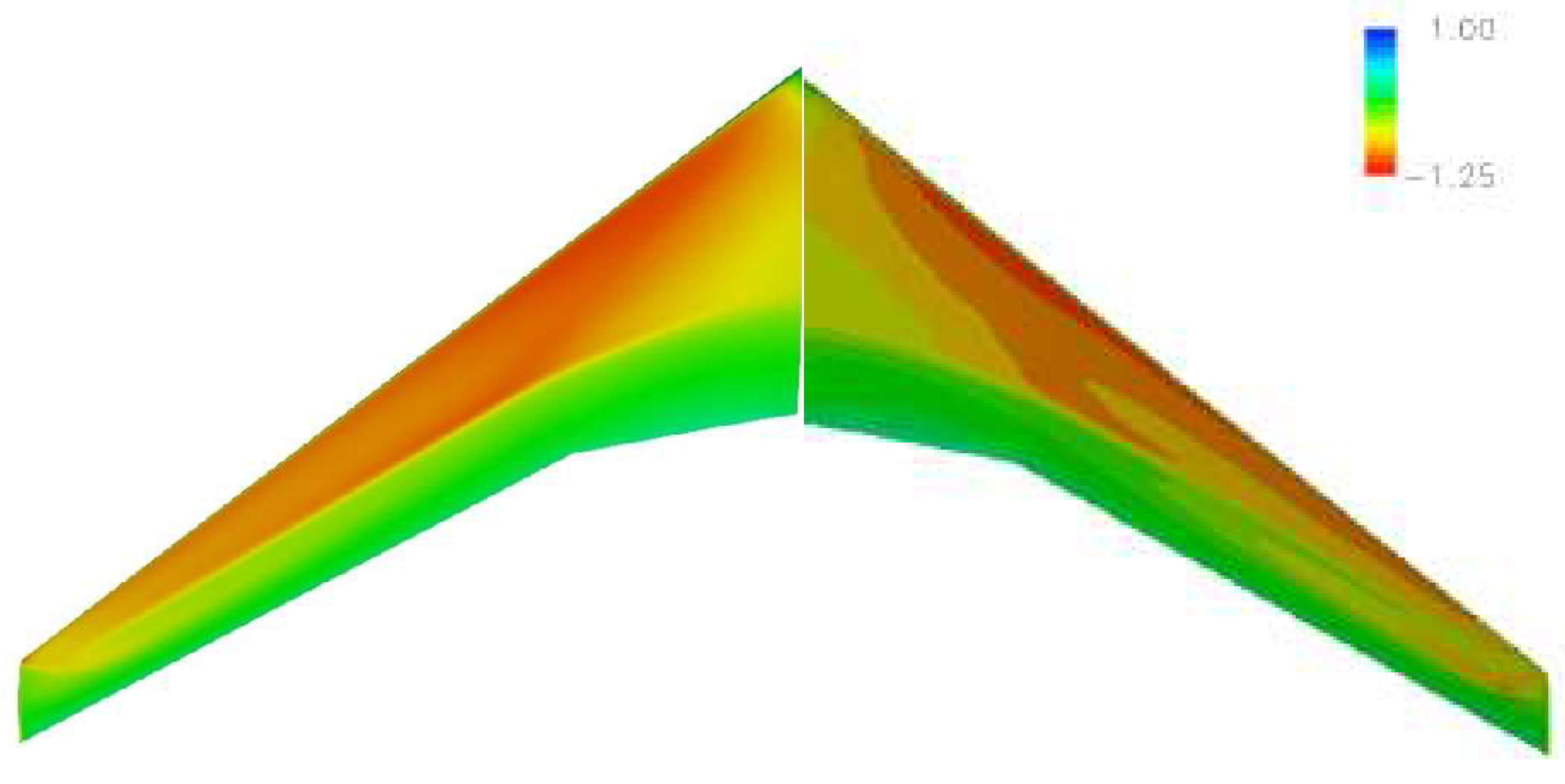
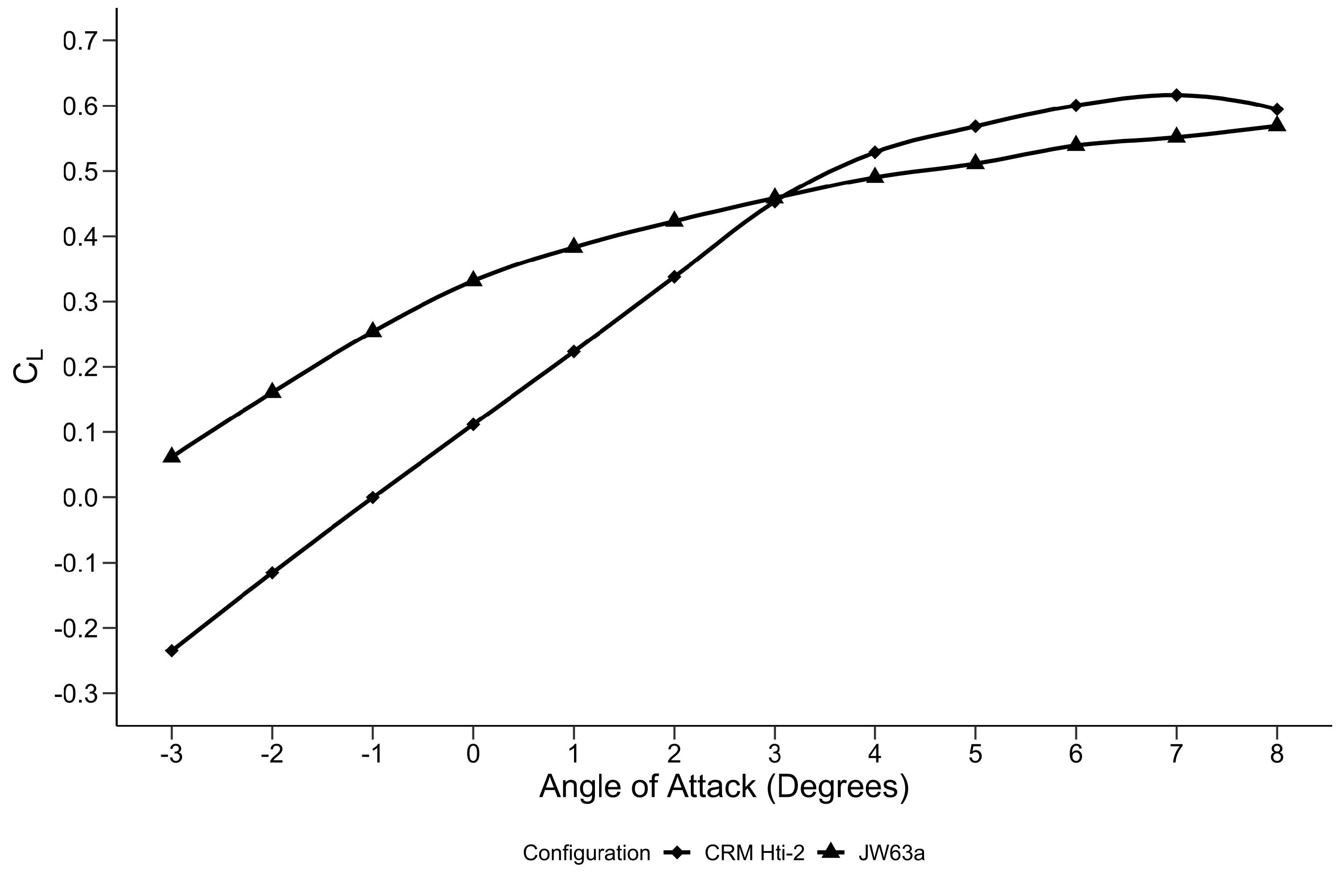
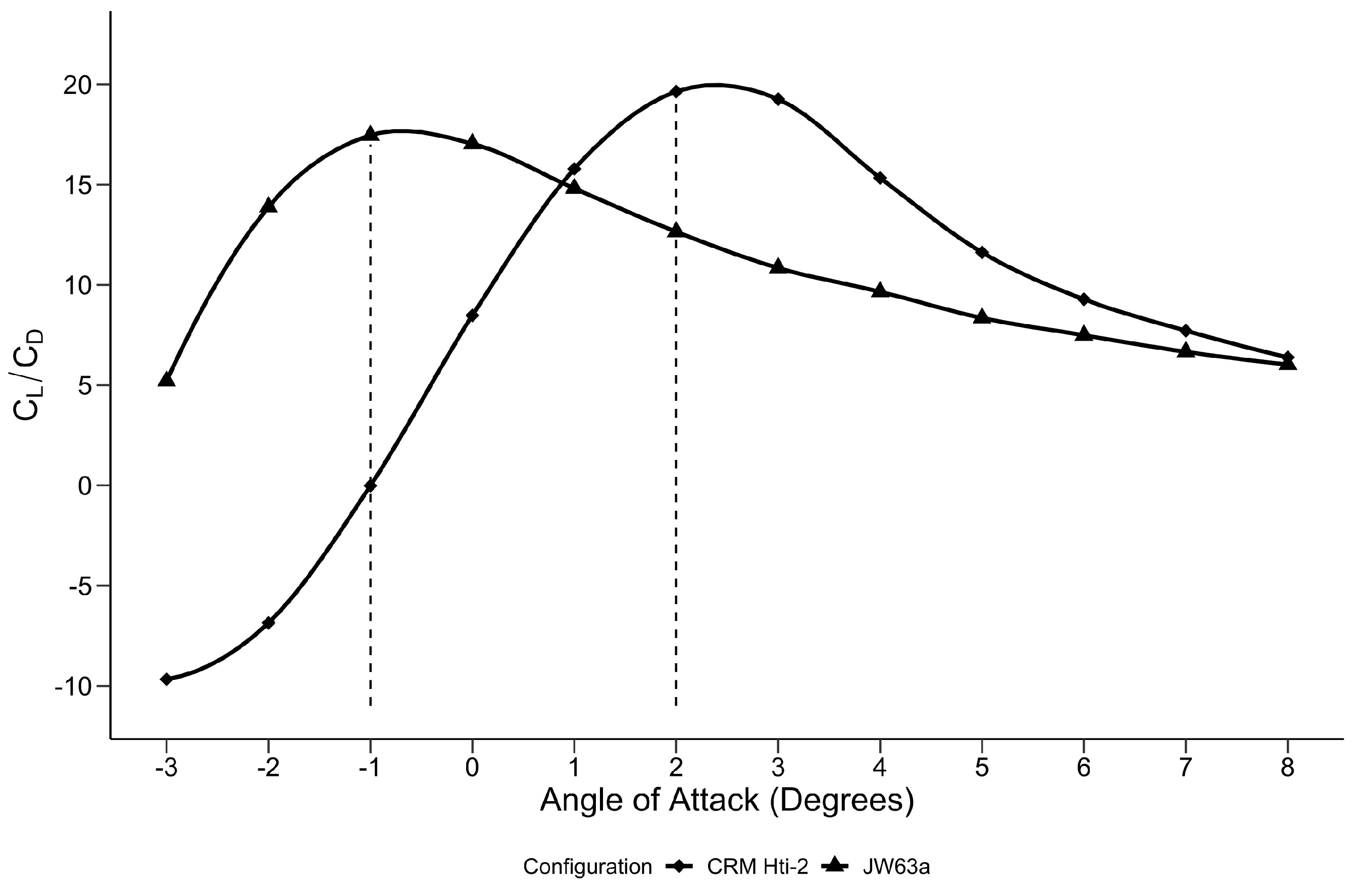
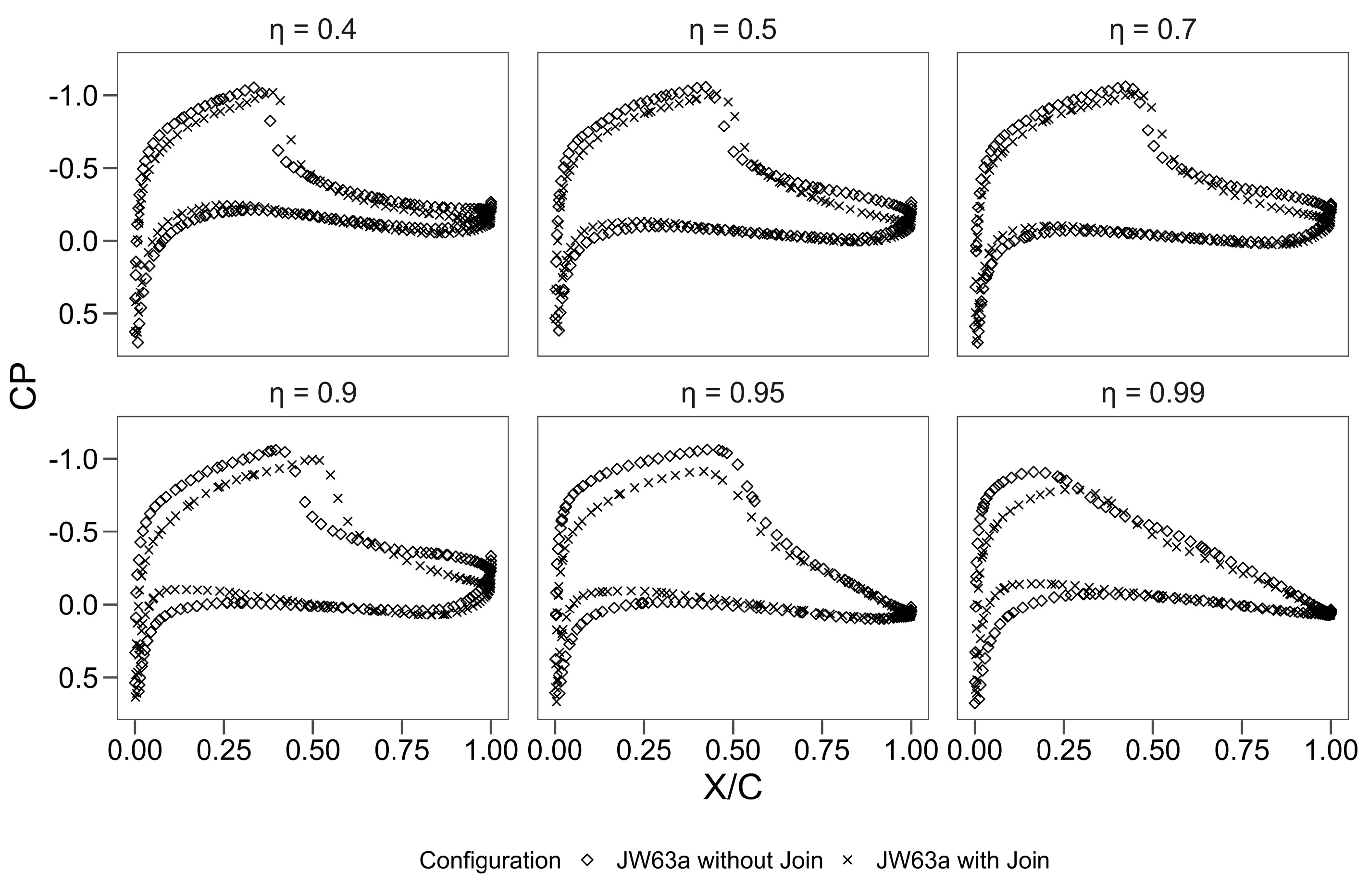
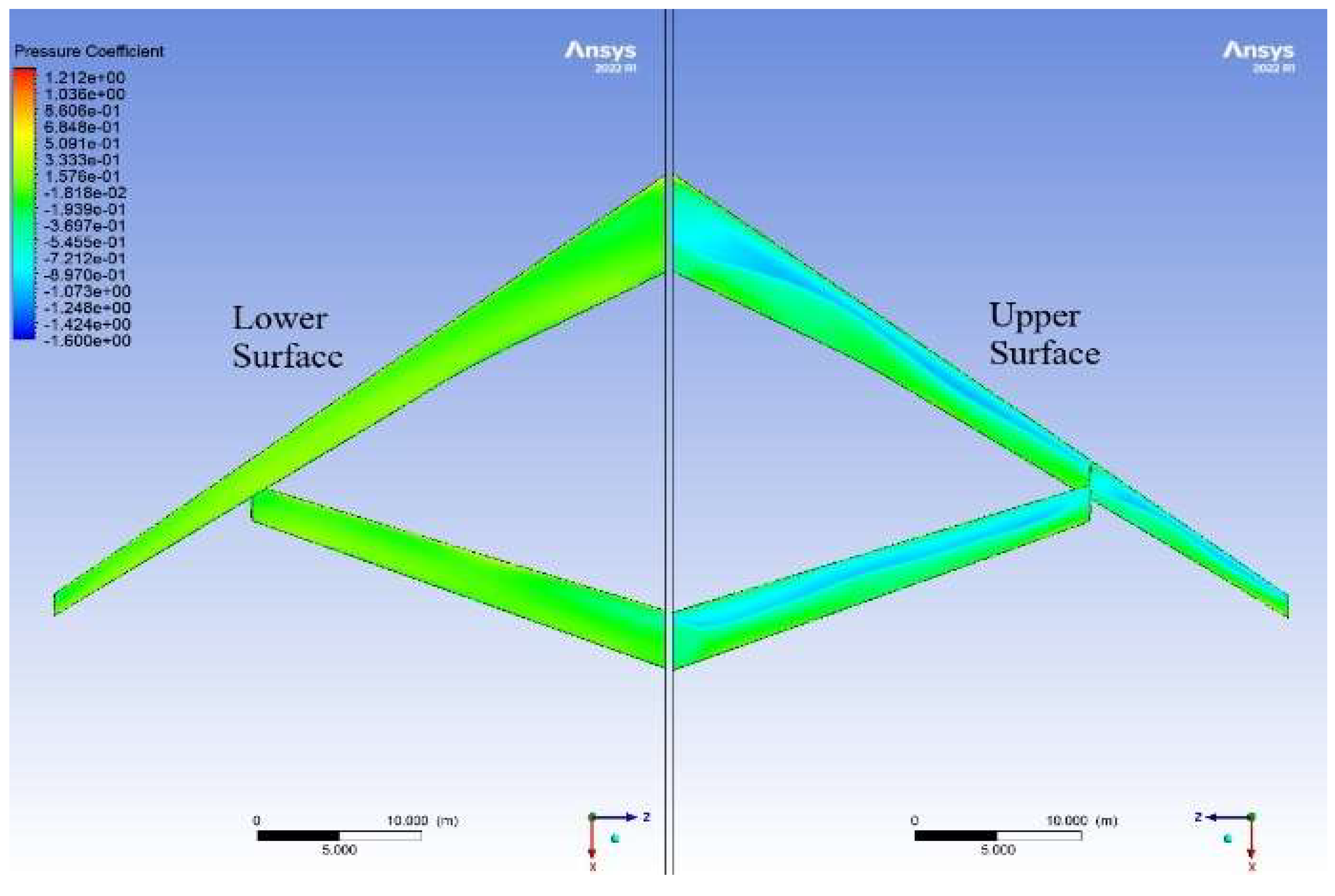
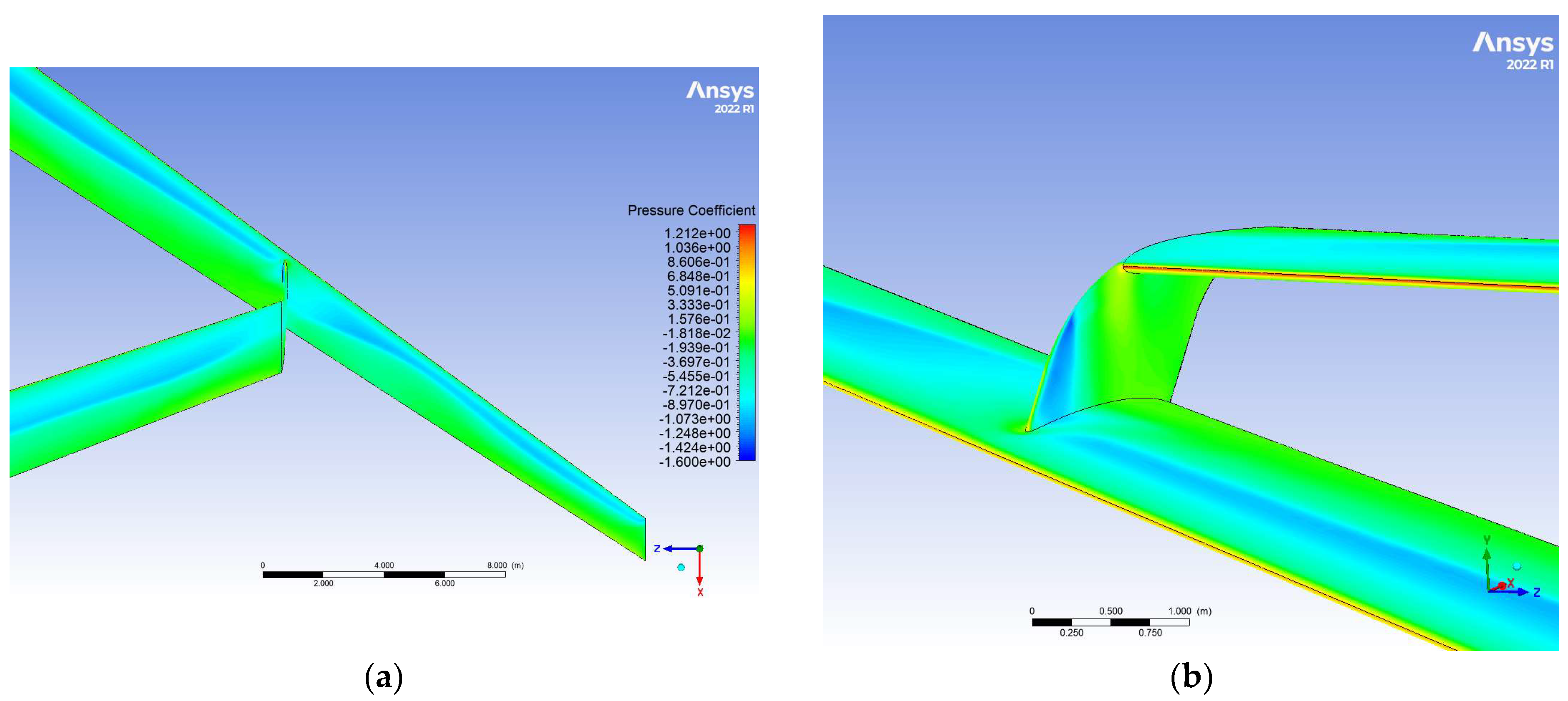
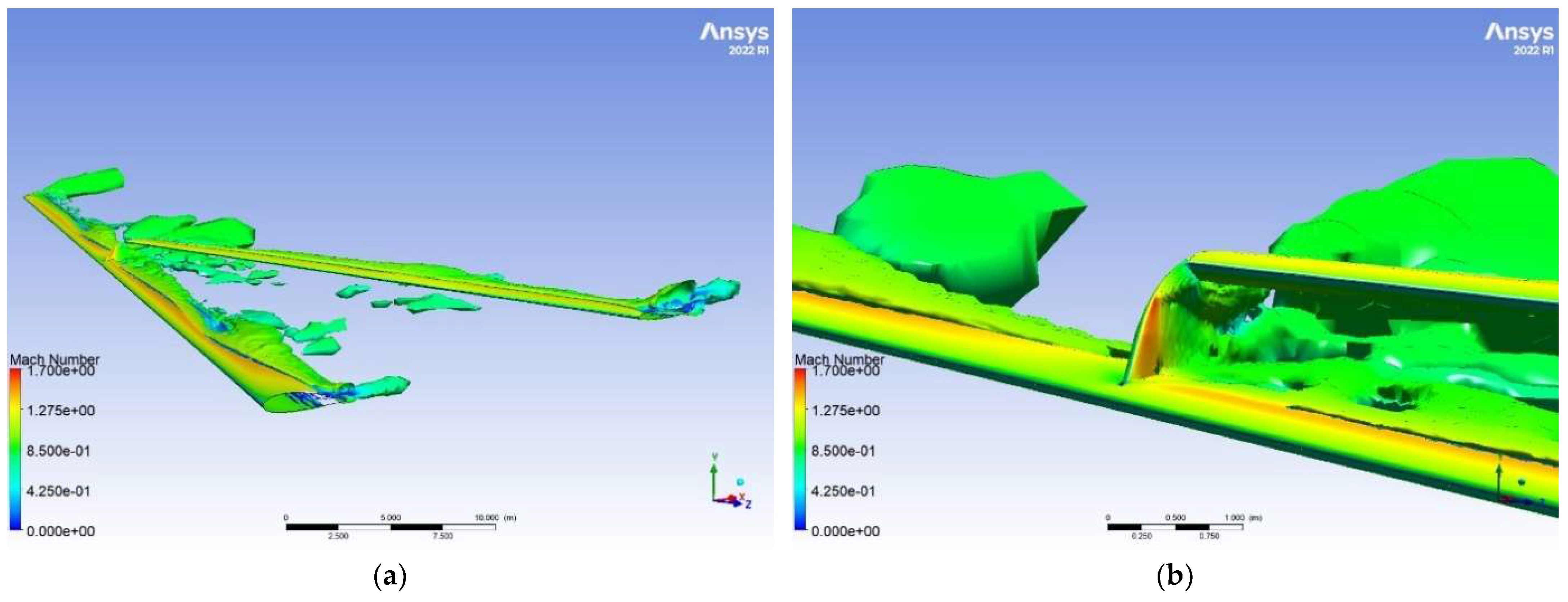
3.1. Initial Joined–Wing Configuration (JW63a)
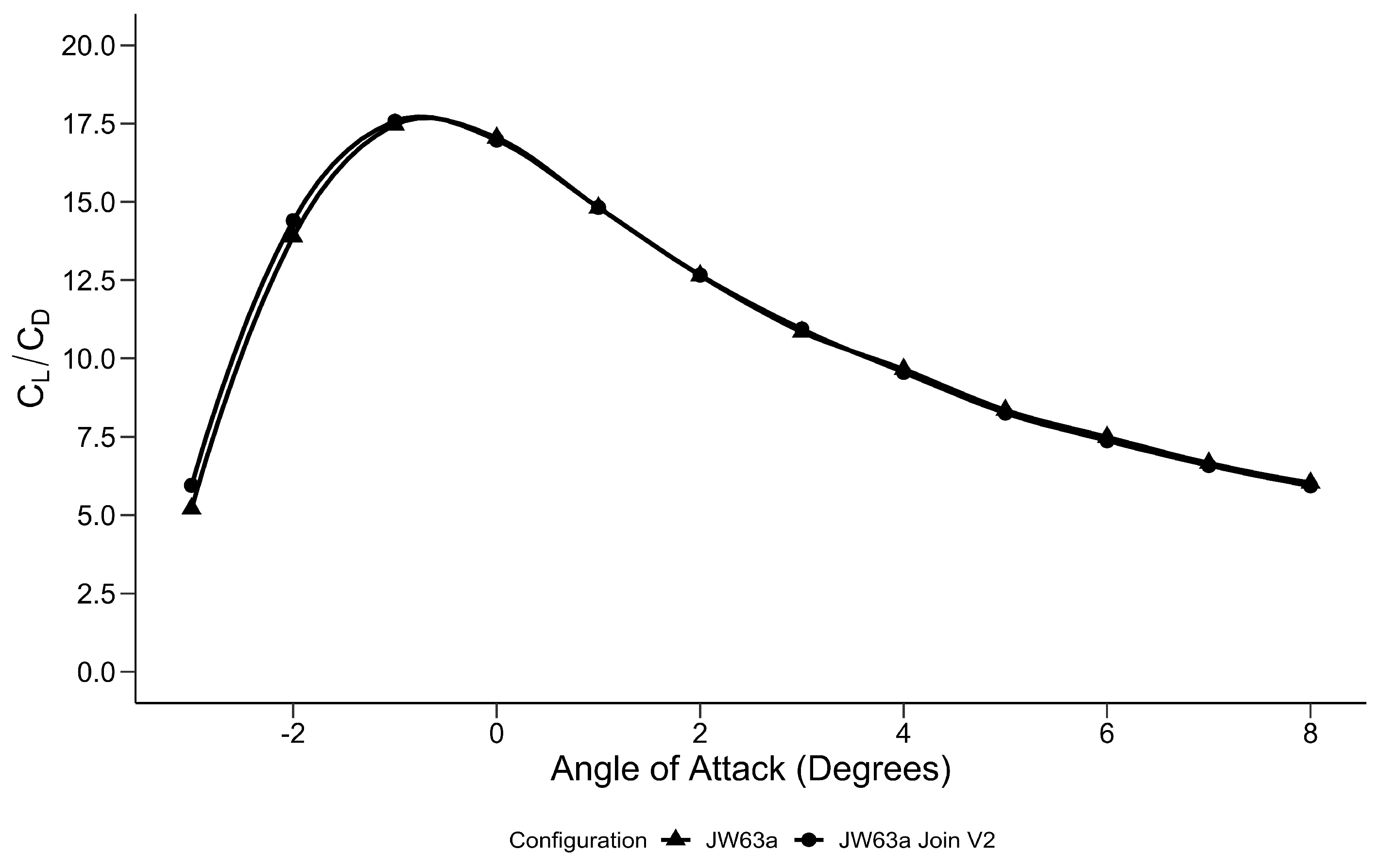
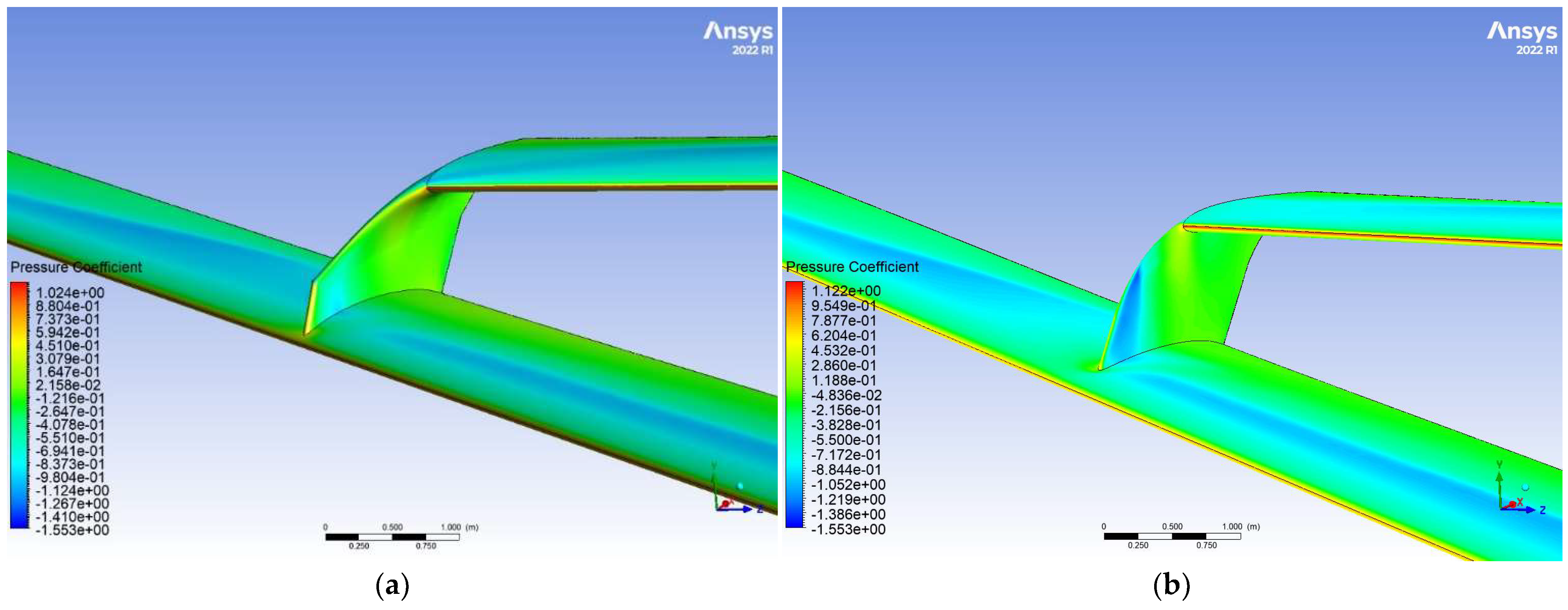
3.2. Vertical Fin Optimisation—Variant 2 (v2)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kapania, R.K.; Schetz, J.A.; Durham, F.D.; Malik, W.; Segee, M.C.; Gupta, R. Multidisciplinary Design Optimization and Cruise Mach Number Study of Truss-Braced Wing Aircraft. 2018. Available online: https://www.researchgate.net/publication/330364934_Multidisciplinary_Design_Optimization_and_Cruise_Mach_Number_Study_of_Truss-Braced_Wing_Aircraft (accessed on 5 November 2024).
- Maldonado, D.; Hunter, C.; Housman, J.A.; Viken, S.A.; Piotrowski, M.G.H.; McMillin, S.N.; Kiris, C.C.; Milholen, W.E. Improvements in Simulating a Mach 0.80 Transonic Truss-Braced Wing Configuration using the Spalart-Allmaras and k-ω SST Turbulence Models. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; pp. 1–31. [Google Scholar] [CrossRef]
- Harrison, N.A.; Beyar, M.D.; Dickey, E.D.; Hoffman, K.; Gatlin, G.M.; Viken, S.A. Development of an efficient mach=0.80 transonic truss-braced wing aircraft. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Weil Brenner, M.; Trepanier, J.; Tribes, C.; Petro, E. Conceptual Design Framework for Blended Wing Body Aircraft. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, Indiana, 17–19 September 2012. [Google Scholar] [CrossRef]
- Trac-pho, J. Conceptual Design of a Blended Wing Body Airliner; San José State University: San Jose, CA, USA, 2022. [Google Scholar]
- Cipolla, V.; Frediani, A.; Abu Salem, K.; Binante, V.; Rizzo, E.; Maganzi, M. Preliminary transonic CFD analyses of a PrandtlPlane transport aircraft. Transp. Res. Procedia 2018, 29, 82–91. [Google Scholar] [CrossRef]
- Prandtl, L. Induced Drag of Multiplanes. In Technische Berichte; 1924; Volume III, no. 7. Available online: https://ntrs.nasa.gov/citations/19930080964 (accessed on 5 November 2024).
- Munk, M. The Minimum Induced Drag of Aerofoils; TR121; 1923. Available online: https://ntrs.nasa.gov/citations/19930091456 (accessed on 5 November 2024).
- Wolkovitch, J. The joined wing—An overview. J. Aircr. 1986, 23, 161–178. [Google Scholar] [CrossRef]
- Jemitola, P.O.; Fielding, J.P. Box wing aircraft conceptual design. In Proceedings of the 28th Congress International Council of the Aeronautical Sciences 2012, ICAS 2012, Brisbane, Australia, 23–28 September 2012; Volume 1, pp. 570–579. [Google Scholar]
- Djojodihardjo, H.; Foong, K.E. Conceptual Design and Aerodynamic Study of Joined-Wing Business Jet Aircraft. 2014. Available online: https://www.researchgate.net/publication/254862073_Conceptual_Design_and_Aerodynamic_Study_of_Joined-Wing_Business_Jet_Aircraft (accessed on 5 November 2024).
- Sahana, D.S.; Aabid, A. CFD Analysis of Box Wing Configuration. Int. J. Sci. Res. 2016, 5, 706–709. [Google Scholar] [CrossRef]
- Smith, S.C.; Stonum, R.K. Experimental Aerodynamic Characteristics of a Joined-Wing Research Aircraft Configuration. Nasa Technol. Memo. 1989. Available online: https://ntrs.nasa.gov/api/citations/19890014914/downloads/19890014914.pdf (accessed on 5 November 2024).
- Sivaji, R. Aerodynamic Analysis of the Joined-Wing Configuration of a High-Altitude, Long Endurance (HALE) Aircraft; University of Cincinnati: Cincinnati, OH, USA, 2004. [Google Scholar]
- Jemitola, P.; Okonkwo, P. Review of Structural Issues in the Design of a Box Wing Aircraft. J. Aerosp. Eng. Mech. Open Access 2019, 3, 161–166. [Google Scholar]
- Galinski, C.; Dziubinski, A.; Surmacz, K.A.; Dziubiński, A.; Kuprianowicz, S.; Surmacz, K.A.; Galiński, C.; Zółtak, J. The joined wing scaled demonstrator results of CFD. In Proceedings of the 29th Congress Internation Council of the Aeronautical Science ICAS 2014, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Jemitola, P.O. Conceptual Design and Optimization Methodology for Box Wing Aircraft; 2012. Available online: https://dspace.lib.cranfield.ac.uk/items/9e23ac4d-1212-4cd2-9305-97f9e34a4d0f (accessed on 5 November 2024).
- Cavallaro, R.; Demasi, L. Challenges, Ideas, and Innovations of Joined-Wing Configurations: A Concept from the Past, an Opportunity for the Future. Prog. Aerosp. Sci. 2016, 87, 1–93. [Google Scholar] [CrossRef]
- Nangia, R.K.; Palmer, M.E.; Point, T.W.; Hyde, L.; Cooper, P.J.E. Aerodynamic—Efficient Configurations & Structural Design Challenges Arising—Joined Wings & Oblique Wings. In Proceedings of the RAeS/CEAS European Air & Space Conference, Manchester, UK, 26–29 October 2009; pp. 26–29. [Google Scholar]
- Kaparos, P.; Papadopoulos, C.; Yakinthos, K. Conceptual design methodology of a box wing aircraft: A novel commercial airliner. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2651–2662. [Google Scholar] [CrossRef]
- Khalid, A.; Kumar, P. Aerodynamic Optimization of Box Wing—A Case Study. Int. J. Aviat. Aeronaut. Aerosp. 2014, 1. [Google Scholar] [CrossRef]
- Khan, F. Preliminary Aerodynamic Investigation of Box-Wing Configurations Using Low Fidelity Codes. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2010; pp. 313–327. [Google Scholar]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6919. [Google Scholar] [CrossRef]
- Rivers, M.B.; Dittberner, A. Experimental Investigations of the NASA Common Research Model. J. Aircr. 2014, 51, 1183–1193. [Google Scholar] [CrossRef]
- Lamar, E. A Vortex-Lattice for of the Mean Method Shapes Drag Trimmed Minimum Vortex with Minimum Vortex Drag; Hampton: Memphis, TN, USA, 1976. [Google Scholar]
- Rivers, M.; Hunter, C. Support System Effects on the NASA Common Research Model. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9–12 January 2012. [Google Scholar] [CrossRef]
- Hanman, P.; Yao, Y.; Bouferrouk, A. Aerodynamics of a CRM Joined-Wing Configuration at Transonic Speeds. In Proceedings of the 57th 3AF International Conference on Applied Aerodynamics, Bordeaux, France, 29–31 March 2023. [Google Scholar]
- Scalabrin, L.C.; de Souza, R.F. Grid assessment using the NASA common research model (CRM) wind tunnel data. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; pp. 1–18. [Google Scholar] [CrossRef][Green Version]
- Krishna, Z.; Gandhar, P.; Balasubramanyam; Varghese, A.; ANSYS Inc.; Zore, K.; Sasanapuri, B.; Parkhi, G.; Varghese, A. Ansys mosaic poly-hexcore mesh for high-lift aircraft configuration. In Proceedings of the 21st AeSI Annual CFD Symposium, Bangalore, India, 8–9 August 2019; pp. 1–11. [Google Scholar]
- ANSYS Inc. Ansys Fluent User’s Guide, 2022R1; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Ansys Inc. ANSYS Fluent Tutorial Guide; ANSYS Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- ANSYS FLUENT 13 User’s Guide Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013; Volume 15317, pp. 724–746.
- Morrison, J.H. 4th AIAA CFD Drag Prediction Workshop. 2009. Available online: https://aiaa-dpw.larc.nasa.gov/Workshop4/ (accessed on 5 November 2024).
- Raymer, D. Aircraft Design: A Conceptual Approach, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992; ISBN 0930403517. [Google Scholar]
- Hue, D.; Chanzy, Q.; Landier, S. DPW-6: Drag Analyses and Increments Using Different Geometries of the Common Research Model Airliner. J. Aircr. 2018, 55, 1509–1521. [Google Scholar] [CrossRef]
- Zilliac, G.; Pulliam, T.; Rivers, M.; Zerr, J.; Delgado, M.; Halcomb, N.; Lee, H. A Comparison of the Measured and Computed Skin Friction Distribution on the Common Research Model. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef][Green Version]

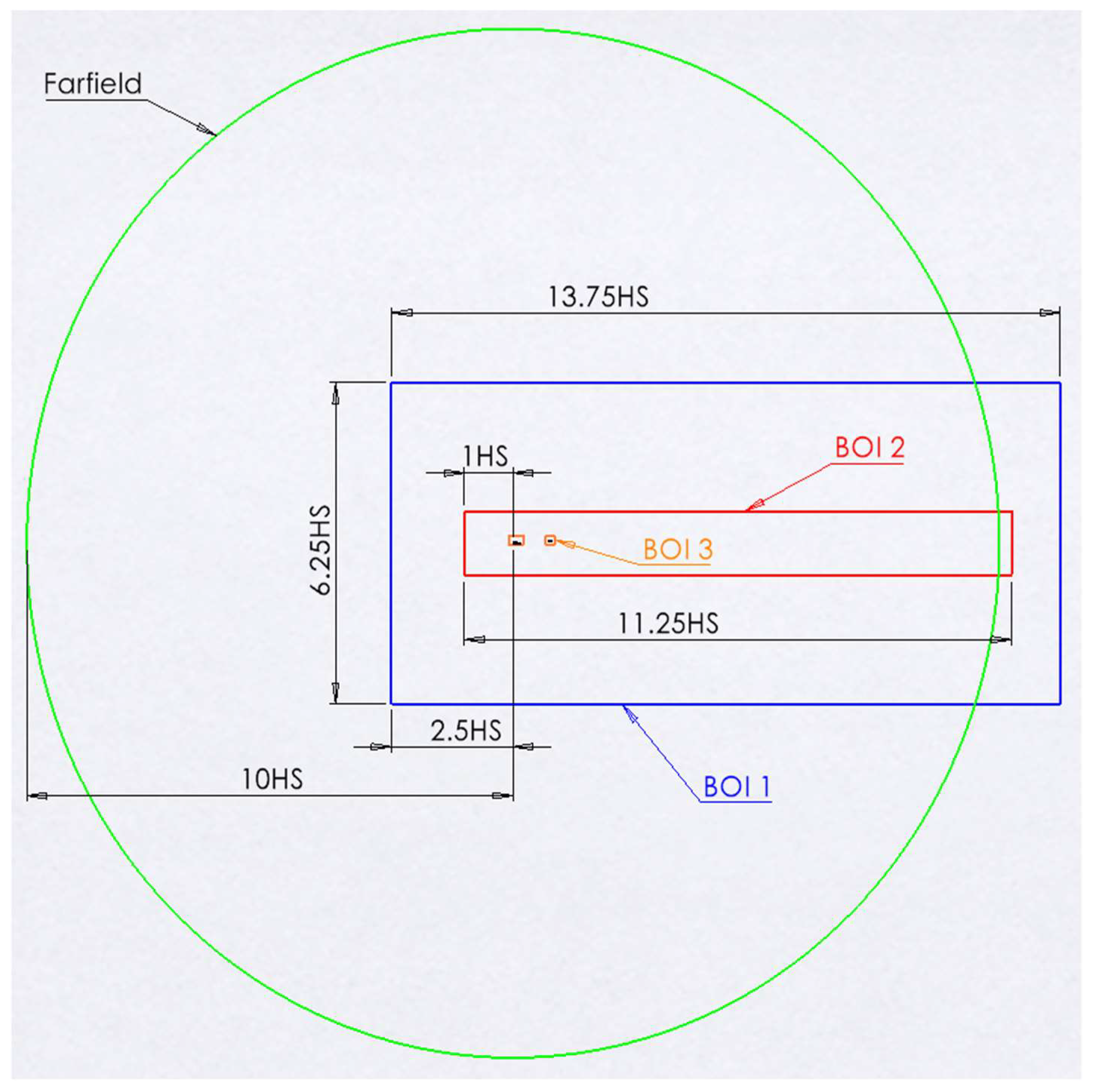











| Variable | Range |
|---|---|
| Half Span (m) | 29.38–40 |
| Root Chord (m) | 6–9 |
| Join Location (η) | 0.4–0.9 |
| Tail Height (Above Main Wing Root) (m) | 2.027–13.739 |
| JW63a Main Wing | JW63a Rear Wing | CRM Main Wing | CRM Horizontal Tail | |
|---|---|---|---|---|
| Half Span (m) | 40 | 28 | 29.38 | 10.668 |
| Root Chord (m) | 7 | 3.94 | 13.49 | 3.94 |
| Vert. Height of aft Root (m) | N/A | 2.027 | N/A | 2.027 |
| Dihedral (Degrees) | 7 | 4.921 | 7 | 7.857 |
| Taper Ratio | 0.2 | 0.6 | 0.2 | 0.6 |
| Joint Location (% Span) | 0.7 | N/A | N/A | N/A |
| AR | 22.21 | 17.78 | 9 | 4.9 |
| Sweep Angle (Degrees) | 35 | −18 | 35 | 37 |
| Mesh | No. Elements (Million) |
|---|---|
| 1 | 2.2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 15 |
| 5 | 22 |
| 6 | 35 |
| Parameter | Value |
|---|---|
| Global Max Volume Size | 16.384 m |
| Body of Influence 1 Volume Size | 5 m |
| Body of Influence 2 Volume Size | 1 m |
| Body of Influence 3 Volume Size | 0.1 m |
| Wing Face Size | 0.1 m |
| Edge Sizing | 0.01 m |
| First Layer Inflation Height | m |
| Number of Cells for Boundary layer | 22 |
| Number of Elements | 13,447,407 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanman, P.; Yao, Y.; Bouferrouk, A. Transonic Aerodynamic Performance Analysis of a CRM Joined-Wing Configuration. Fluids 2025, 10, 27. https://doi.org/10.3390/fluids10020027
Hanman P, Yao Y, Bouferrouk A. Transonic Aerodynamic Performance Analysis of a CRM Joined-Wing Configuration. Fluids. 2025; 10(2):27. https://doi.org/10.3390/fluids10020027
Chicago/Turabian StyleHanman, Paul, Yufeng Yao, and Abdessalem Bouferrouk. 2025. "Transonic Aerodynamic Performance Analysis of a CRM Joined-Wing Configuration" Fluids 10, no. 2: 27. https://doi.org/10.3390/fluids10020027
APA StyleHanman, P., Yao, Y., & Bouferrouk, A. (2025). Transonic Aerodynamic Performance Analysis of a CRM Joined-Wing Configuration. Fluids, 10(2), 27. https://doi.org/10.3390/fluids10020027









