Transient Simulation and Analysis of Runaway Conditions in Pumped Storage Power Station Turbines Using 1D–3D Coupling

Abstract

Pumped-storage power plants play a vital role in power systems by providing peak load regulation, frequency control, and phase modulation services. The safety and stability of these plants critically depend on understanding transient processes during frequent unit start–stop cycles and operational transitions. This study employs 1D–3D coupled numerical simulations to investigate a pump–turbine unit’s external characteristics, pressure pulsations, and internal flow dynamics under turbine runaway conditions. At the runaway rotational speed of 650.9 r/min, large-scale vortices with intensities exceeding 500 s⁻¹ form at the inlet of specific runner blade passages, severely obstructing flow. Concurrently, the tailwater pipe vortex structure transitions from a central spiral pattern to a wall-attached configuration. The concurrent occurrence of these phenomena induces abrupt runner force variations and significant pressure pulsations, primarily comprising high-frequency high-amplitude pulsations at 1× and 2× blade frequency attributable to runner dynamic-static interference; broad-spectrum high-amplitude pulsations resulting from operational transitions; and low-frequency high-amplitude pulsations induced by the tailwater pipe vortex belt.

1. Introduction

Pumped storage power stations, also known as regenerative power plants, operate under both turbine and pumping modes [1]. Compared to conventional hydropower stations, pumped-storage units undergo more frequent start–stop cycles and operational transitions for peak shaving and frequency regulation [2]. These rapid operational changes impose significant impacts on the units themselves, water conveyance systems, and electrical equipment. Transient process analysis is therefore essential to prevent damage to pipeline systems during hydraulic transitions. Since the seminal 1967 work by Streeter and Wylie in Hydraulic Transients, which established the method of characteristics (MOC) for solving transient flow equations and pioneered computer-based unsteady flow solutions [3], advancements in computing technology have substantially enhanced the feasibility and accuracy of turbine transient studies. Chaudhry [4] conducted comprehensive research on hydropower plant transients and systematized computational methodologies. Nicolet et al. [5] employed SIMSEN software to simulate one-dimensional transient conditions including guide vane rejection and load rejection with 15 s linear closure, identifying pressure fluctuations from rigid and elastic water hammer effects to characterize oscillatory modes. The application of three-dimensional computational fluid dynamics (3D CFD) has enabled more intuitive visualization of pump–turbine transient dynamics. While the 1D MOC [6] offers rapid and efficient simulation of unit transients, it only captures external characteristics. Conversely, 3D numerical simulation excels in resolving internal flow behavior but demands substantial computational resources [7]. Consequently, integrated 1D–3D methodologies have gained scholarly traction. Z. Xijun et al. [8] coupled 1D pipe networks with 3D models (spiral case, guide vanes, runner, draft tube) to simulate pump–turbine start–stop transitions, analyzing pressure and flow characteristics in the runner domain. Hao Yan et al. [9] combined 1D cascading dynamics with 3D hydrodynamic computations to track solid particles in feed pipes, validating the consistency between coupled simulations and experimental results. Research on turbine runaway conditions [10] during pump–turbine transients is critically important. During uncontrolled runaway [11,12], the rotational speed surges without power output while the energy dissipation [13] becomes unstable. Extreme centrifugal forces, vibrations [14], and severe pressure fluctuations may ultimately cause catastrophic failures. Furthermore, diverse turbine configurations [15,16] exhibit distinct runaway behaviors [17], necessitating multifaceted investigations. Scholars persistently examine pump–turbine runaway phenomena: Zhenggui et al. numerically and experimentally validated flow patterns during power failure under pumping mode with guide vane rejection, revealing violent flow transitions (smooth–turbulent–smooth–turbulent) in runner and guide vane passages causing significant energy losses. Jialiang Yang et al. [18] employed 1D–3D coupling to simulate ultra-high-head turbine runaway, identifying novel instantaneous flow-induced pressure pulsations that amplify axial force fluctuations. Fu Xilong et al. [19] analyzed runaway cavitation via 1D–3D coupling simulation, finding minor deviations from the experimental data; notably, two-phase flow models yielded pressure/hydraulic fluctuations threefold greater than single-phase models, with delayed severe oscillation onset. S. Liu et al. [20] investigated Kaplan turbine load rejection using variable-speed sliding mesh, revealing intensified vortex-induced pressure fluctuations in draft tube downstream sections. Xiaoxi Zhang et al. [21] coupled 1D conveyance systems with 3D Francis turbine models, demonstrating fracture of the annular pressure distribution at draft tube inlets inducing small vortex ropes that merge into eccentric spiral vortex ropes with growing low-frequency pulsations as operations deviate from the rated conditions. Weilong Guang et al. [22] analyzed labyrinth seal effects on runaway performance, concluding that hybrid seals improve draft tube/runner flow patterns while stepped seals reduce axial thrust. Xiaolong Fu et al. [23] simulated vortex-induced runaway (TRP) in ultra-high-head turbines, linking local blade frequency (BF) at high-pressure inlets to speed/head ratios; design modifications successfully reduced speed surges and transient pressures. Ke et al. [24] simulated two pump–turbines during guide vane closure/rejection transients, identifying dual axial force peaks during runaway from superimposed negative (spiral case) and positive (draft tube) water hammer waves induced by high-speed bypass flows. It is accomplished by means of a 1D–3D coupling method. Di Zhu et al. [25] studied marine pump–turbine stall runaway under varying guide vane openings: 12° openings caused destabilizing vortex growth between the guide vanes and runner, while 12–20° openings showed uniform vortex intensity distributions.

To better investigate the characteristics of pump–turbines under runaway conditions, this study establishes a one-dimensional characteristic-based model of the water conveyance system and surge tank, along with a three-dimensional numerical simulation model of the pump–turbine unit. These models are developed based on in-depth research into the principles and characteristics of transition processes in pumped storage hydropower systems, utilizing the method of characteristics and three-dimensional numerical simulation techniques. Furthermore, user-defined functions (UDFs) [26,27] are implemented on the Fluent platform to achieve customized numerical coupling and data transfer between the one-dimensional and three-dimensional domains. The proposed methodology is applied to simulate and analyze the turbine runaway condition in a pumped storage power station with an extended water conveyance system, examining the pressure pulsation characteristics and internal flow field behavior of the pump–turbine under this specific operational scenario. Compared to simplified approaches that rely solely on direct three-dimensional simulations, the methodology presented in this study offers distinct advantages. In conventional three-dimensional numerical simulations of transient processes, boundary conditions are often defined using experimental data or simplified quantitative approximations—a practice typically adopted to conserve computational resources and reduce simulation time. However, such simplifications are prone to introduce non-negligible errors and fail to accurately represent the complex flow behavior during the transient operation of hydraulic machinery. Although the 1D–3D coupling method has been previously applied to pump–turbines by Fu Xiaolong et al., their research primarily focused on the influence of a “one-pipe–two-unit” configuration on water hammer effects in long penstocks and did not provide a comprehensive description of the coupling methodology. Thus, notable distinctions remain between their work and the present study. Compared to previous studies, the innovation of this paper lies in leveraging FLUENT’s compliable UDF module to achieve simultaneous one-dimensional and three-dimensional calculations and data exchange. Each step is based on the data from the previous step on the overlapping coupling surface, ensuring data accuracy. This approach focuses on the pressure fluctuations and flow field characteristics of pump–turbines under runaway conditions.

2. Theoretical Methods and Numerical Simulation Preprocessing

2.1. Theoretical Method

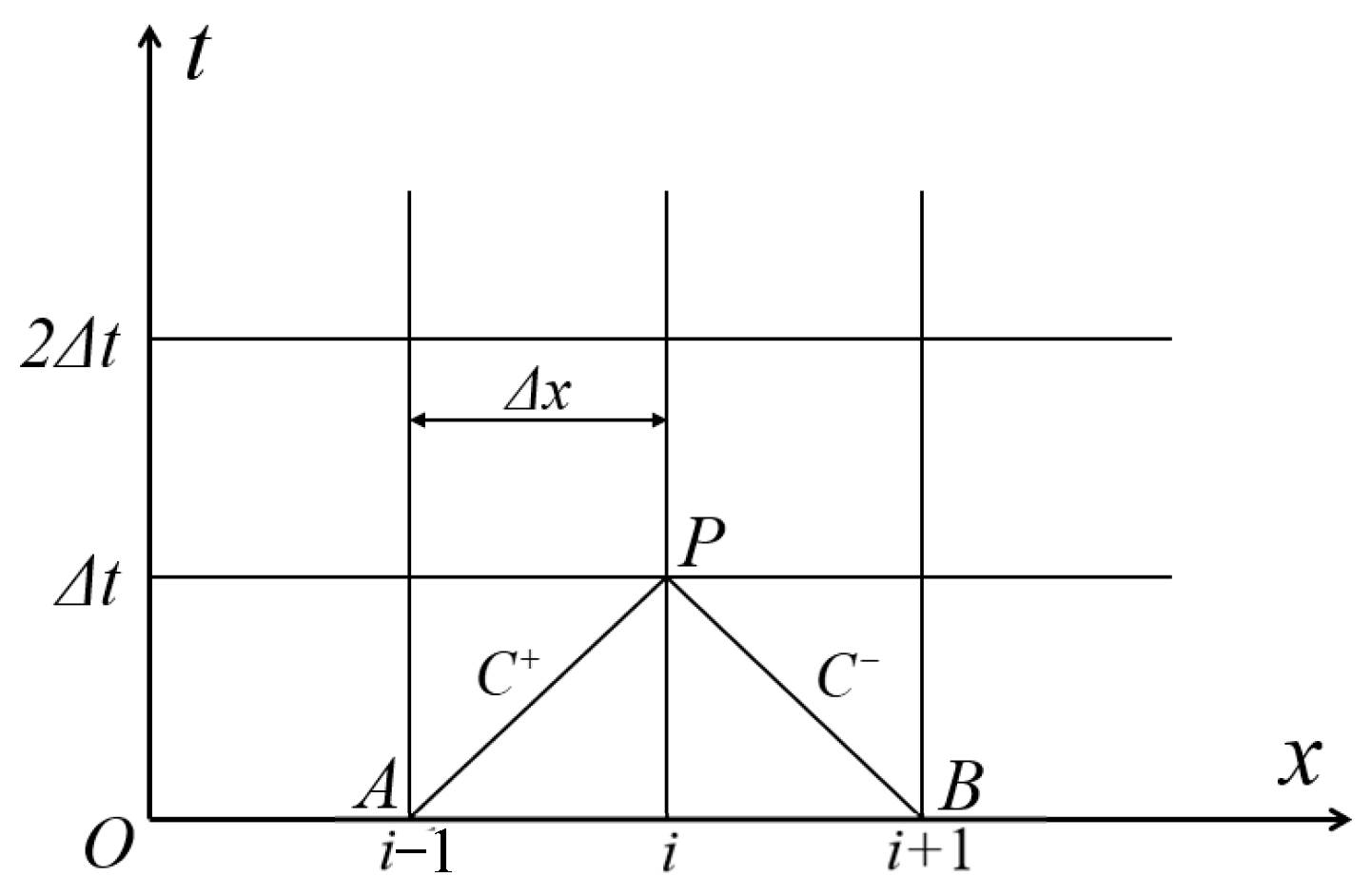
2.1.1. One-Dimensional Characteristic Line Method

The equations of motion and continuity for transient flow are expressed as:

$$L_1=g{\displaystyle \frac{\partial H}{\partial x}}+V{\displaystyle \frac{\partial V}{\partial x}}+{\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{fV\left|V\right|}{2D}}=0,$$

(1)

$$L_2={\displaystyle \frac{\partial H}{\partial t}}+V{\displaystyle \frac{\partial H}{\partial x}}-V\sin \alpha +{\displaystyle \frac{a^2}{g}}{\displaystyle \frac{\partial V}{\partial x}}=0,$$

(2)

where H denotes the head (m), t is the time (s), V represents the cross-sectional average flow velocity (m/s), x indicates the distance along the pipeline axis (m), α signifies the pipeline inclination angle relative to horizontal, g is the gravitational acceleration (m/s²), a denotes the water hammer wave speed (m/s), f is the friction factor, and D designates the pipe diameter (m).

These equations are linearly combined using a parameter λ:

$$V+{\displaystyle \frac{g}{\lambda }}=V+\lambda {\displaystyle \frac{a^2}{g}}={\displaystyle \frac{dx}{dt}},$$

(3)

yielding

$$\lambda \left[{\displaystyle \frac{\partial H}{\partial t}}+{\displaystyle \frac{\partial H}{\partial x}}{\displaystyle \frac{dx}{dt}}\right]+\left[{\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{\partial V}{\partial x}}{\displaystyle \frac{dx}{dt}}\right]+{\displaystyle \frac{fV\left|V\right|}{2D}}-\lambda V\sin \alpha =0.$$

(4)

Applying the chain rule of differentiation:

$${\displaystyle \frac{dH}{dt}}={\displaystyle \frac{\partial H}{\partial t}}+{\displaystyle \frac{\partial H}{\partial x}}{\displaystyle \frac{dx}{dt}},$$

(5)

$${\displaystyle \frac{dV}{dt}}={\displaystyle \frac{\partial V}{\partial t}}+{\displaystyle \frac{\partial V}{\partial x}}{\displaystyle \frac{dx}{dt}},$$

(6)

gives

$$\lambda {\displaystyle \frac{dH}{dt}}+{\displaystyle \frac{dV}{dt}}+{\displaystyle \frac{fV\left|V\right|}{2D}}-\lambda V\sin \alpha =0.$$

(7)

From Equation (3), two specific solutions for λ are derived:

$$\lambda =\pm {\displaystyle \frac{g}{a}},$$

(8)

$${\displaystyle \frac{dx}{dt}}=V\pm a.$$

(9)

Substituting Equation (8) into Equation (7) and combining with Equation (9) yields two sets of ordinary differential equations:

$$C^{+}\left\{\begin{array}{l}{\displaystyle \frac{dH}{dt}}+{\displaystyle \frac{a}{g}}{\displaystyle \frac{dV}{dt}}+{\displaystyle \frac{afV\left|V\right|}{2gD}}-V\sin \alpha =0\\ {\displaystyle \frac{dx}{dt}}=V+a\end{array}\right.,$$

(10)

$$C^{-}\left\{\begin{array}{l}{\displaystyle \frac{dH}{dt}}-{\displaystyle \frac{a}{g}}{\displaystyle \frac{dV}{dt}}-{\displaystyle \frac{afV\left|V\right|}{2gD}}-V\sin \alpha =0\\ {\displaystyle \frac{dx}{dt}}=V-a\end{array}\right..$$

(11)

Along the C⁺ and C⁻ characteristics, the upper expressions are termed compatibility equations, while the lower expressions represent the positive and negative characteristic equations.

Given that the wave speed in pipelines significantly exceeds the flow velocity (a >> V), the V term in the characteristic equations can be neglected. Additionally, the Vsinα term in the compatibility equations is negligible. Thus, the equations simplify to

$$C^{+}\left\{\begin{array}{l}{\displaystyle \frac{dH}{dt}}+{\displaystyle \frac{a}{g}}{\displaystyle \frac{dV}{dt}}+{\displaystyle \frac{afV\left|V\right|}{2gD}}=0\\ {\displaystyle \frac{dx}{dt}}=a\end{array}\right.,$$

(12)

$$C^{-}\left\{\begin{array}{l}{\displaystyle \frac{dH}{dt}}-{\displaystyle \frac{a}{g}}{\displaystyle \frac{dV}{dt}}-{\displaystyle \frac{afV\left|V\right|}{2gD}}=0\\ {\displaystyle \frac{dx}{dt}}=-a\end{array}\right..$$

(13)

The characteristic equations are discretized using the finite difference method established by Streeter and Wylie. For hydraulic transient computation requiring nodal pressure and flow rate evolution, a pipeline of length L is divided into N segments of length Δx. The time step Δt satisfies the Courant condition (Δt = Δx/a). The characteristic grid in the x-t plane is illustrated in Figure 1, where AP and BP represent the positive and negative characteristic lines, respectively.

The compatibility Equation (12) holds along the AP positive characteristic line. Multiply the equation by dt = dx/a, introduce the pipe flow rate Q = AV, and then integrate along this C⁺ characteristic line:

$$H_P-H_A+{\displaystyle \frac{a}{gA}}\left(Q_P-Q_A\right)+{\displaystyle \frac{f}{2gD{A}^2}}{\displaystyle {\int }_A^P\left|Q\right|Qdx=0}.$$

(14)

Neglecting higher-order terms of V yields the first-order approximate integral form:

$${\displaystyle {\int }_A^P\left|Q\right|Qdx=}\left|Q_A\right|Q_A\Delta x.$$

(15)

As first-order friction approximation suffices for most engineering applications, substituting Equation (15) into Equation (14) gives

$$H_P=H_A-{\displaystyle \frac{a}{gA}}\left(Q_P-Q_A\right)-{\displaystyle \frac{f\Delta x}{2gD{A}^2}}\left|Q_A\right|Q_A.$$

(16)

Similarly, integrating compatibility Equation (13) along the BP characteristic line (C⁻) yields

$$H_P=H_B-{\displaystyle \frac{a}{gA}}\left(Q_P-Q_B\right)-{\displaystyle \frac{f\Delta x}{2gD{A}^2}}\left|Q_B\right|Q_B.$$

(17)

Defining B = a/(gA) and R = fΔx/(2gDA²), these equations become

$$C^{+}:H_P=C_P-B{Q}_P,$$

(18)

$$C^{-}:H_P=C_M+B{Q}_P,$$

(19)

where

$$C_P=H_A+B{Q}_A-R\left|Q_A\right|Q_A,$$

(20)

$$C_M=H_B-B{Q}_B+R\left|Q_B\right|Q_B.$$

(21)

For a given pipeline, B and R remain constant. C_p and C_m are determined by conditions at points A and B, respectively. Equations (18) and (19) enable the computation of head H_p and discharge Q_p at the interior node P.

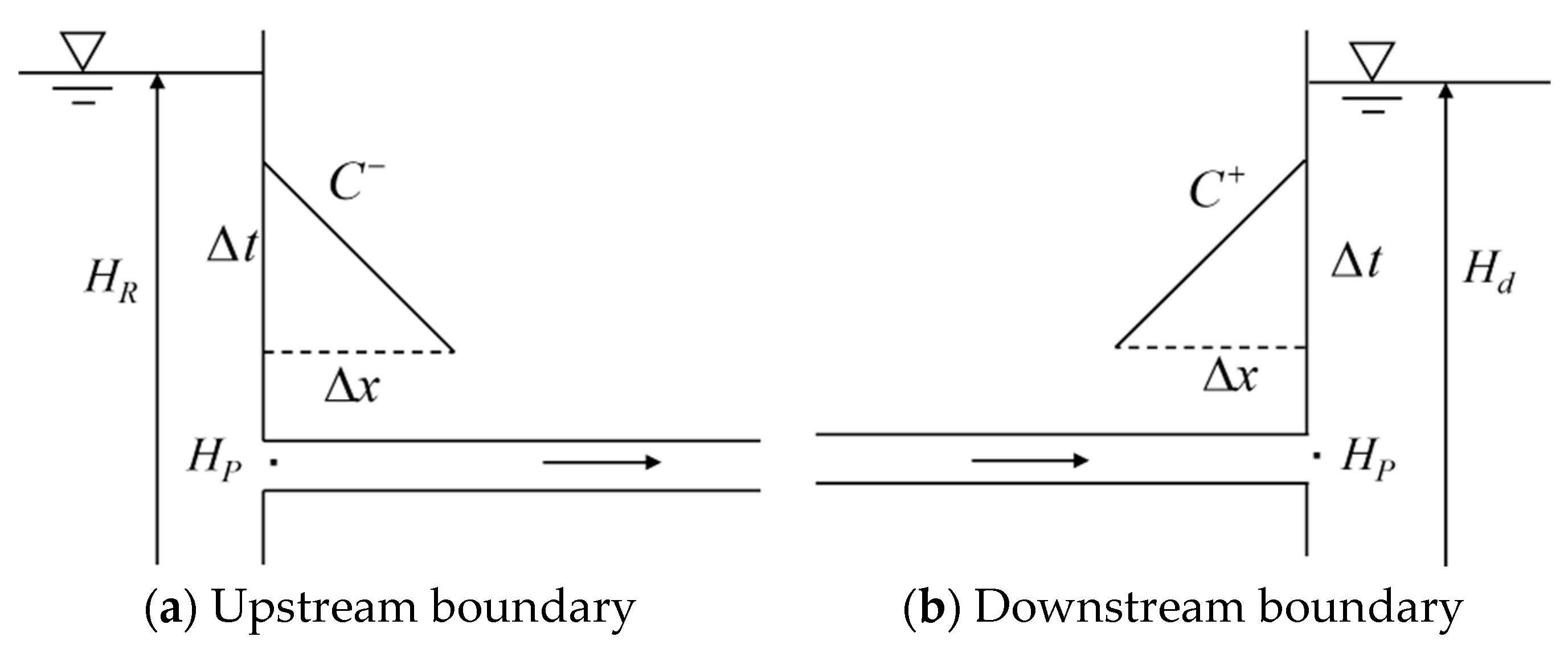
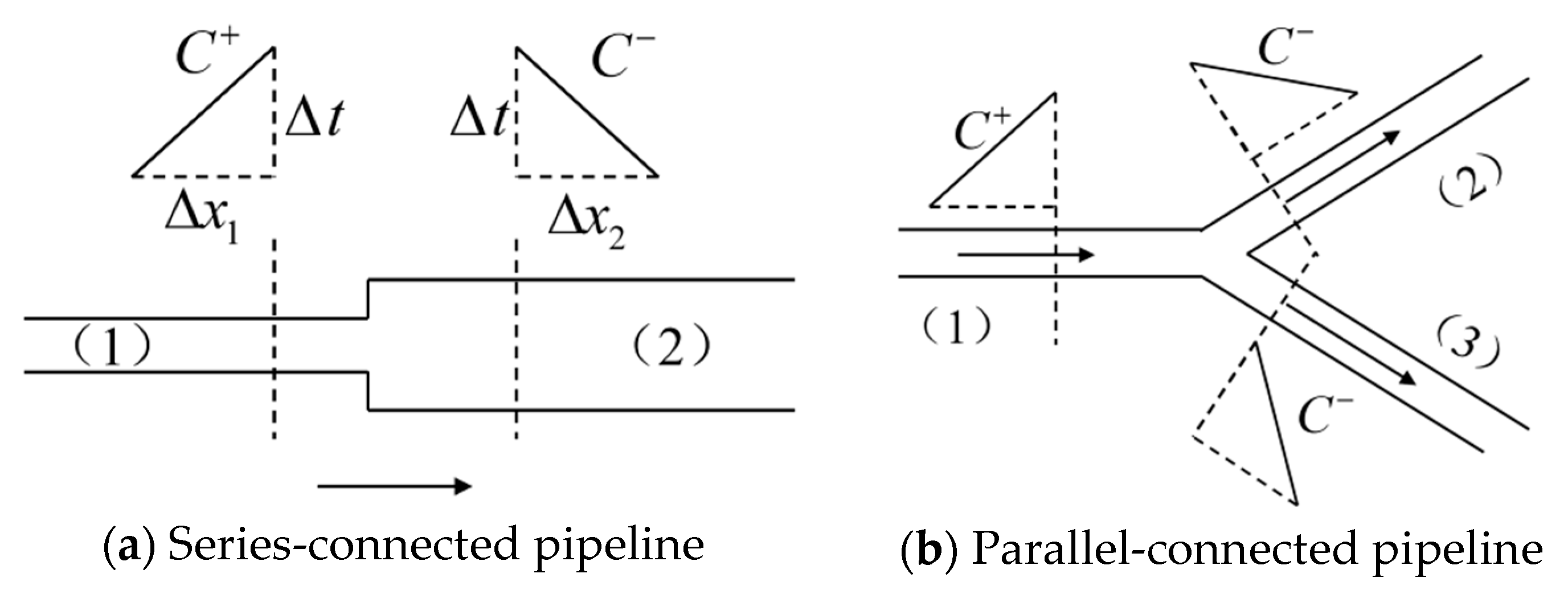
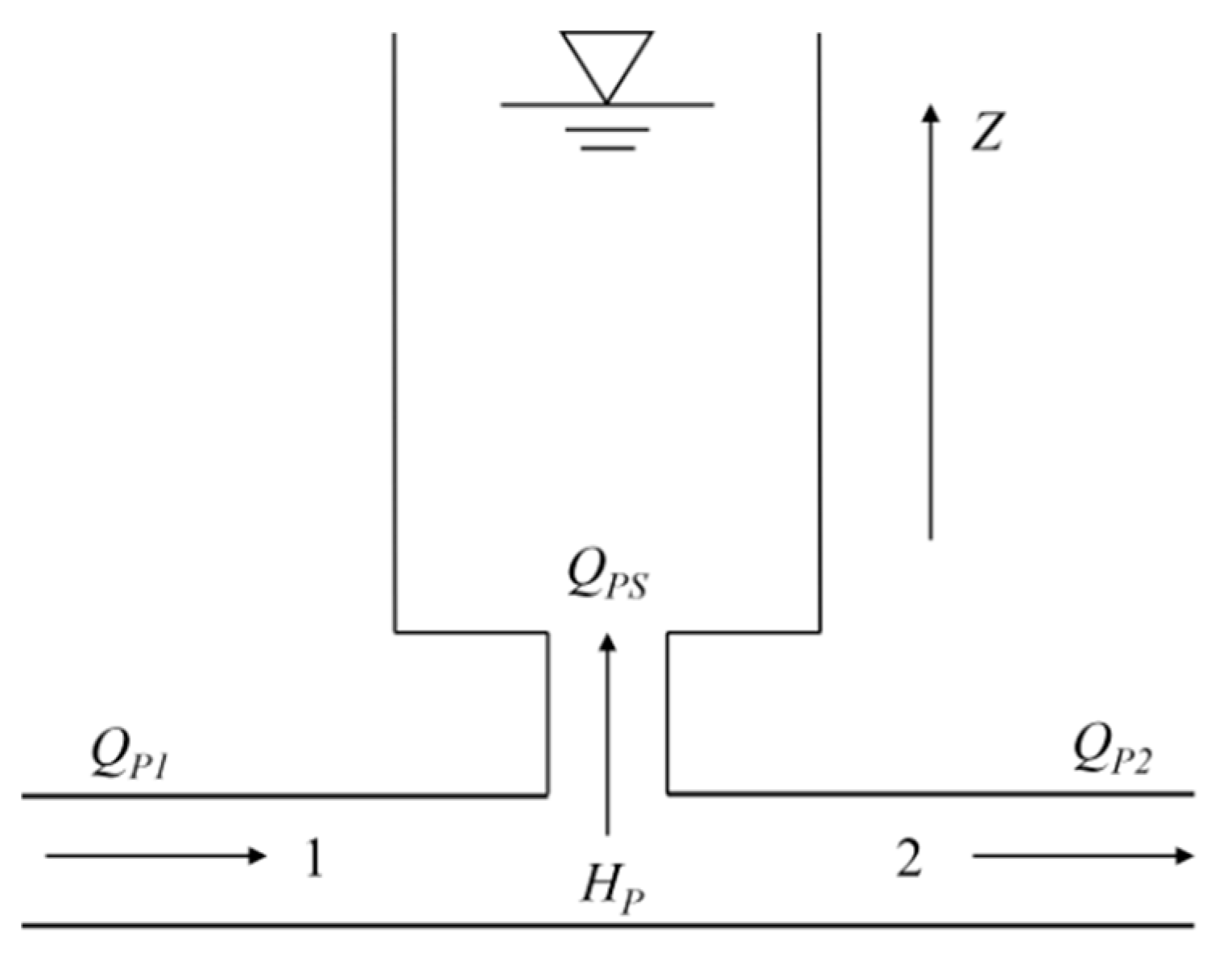
2.1.2. Boundary Condition Theory

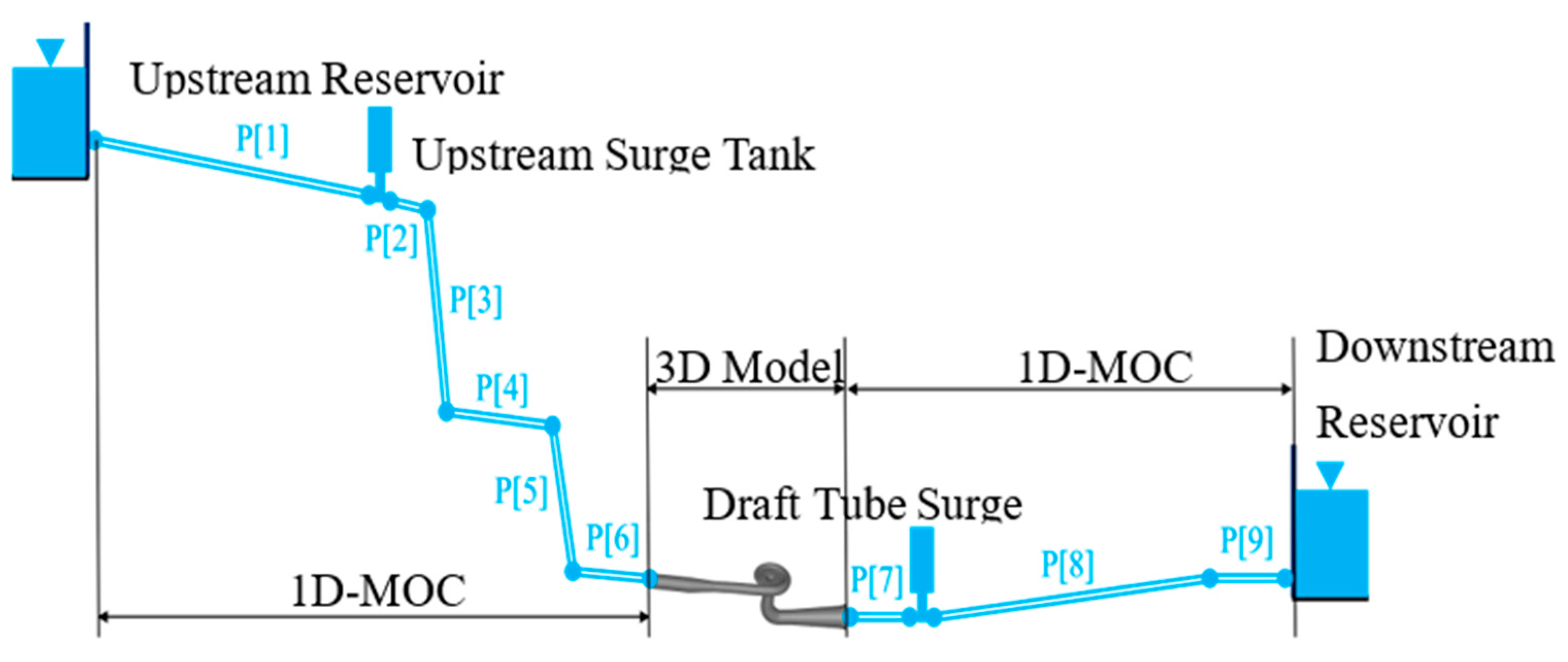
Upstream/Downstream Reservoirs

Water level changes in reservoir boundaries are negligible over short durations. For the upper reservoir, the inlet pressure is treated as constant:

$$H_P=H_R.$$

(22)

Applying the negative characteristic compatibility equation H_p = C_M + BQ_p yields

$$Q_P={\displaystyle \frac{H_R-C_M}{B}}.$$

(23)

For the lower reservoir, outlet pressure is similarly considered constant. We use the positive characteristic compatibility equation:

$$H_P=H_d,$$

(24)

$$Q_P={\displaystyle \frac{C_P-H_d}{B}}.$$

(25)

Figure 2 illustrates these boundary configurations.

Series/Parallel Pipe Junctions

For series-connected pipes with different parameters (Figure 3a), continuity and equal piezometric head (neglecting local losses) govern the junction:

$$\left\{\begin{array}{l}{H}_P=H_{P\left(1,N+1\right)}=H_{P\left(2,1\right)}\\ Q_P=Q_{P\left(1,N+1\right)}=Q_{P\left(2,1\right)}\end{array}\right..$$

(26)

With characteristic equations C⁺ and C⁻ on both pipe segments, the boundary solution is

$$\left\{\begin{array}{l}{H}_P={\displaystyle \frac{B_2{C}_{P1}+B_1{C}_{M2}}{B_1+B_2}}\\ Q_P={\displaystyle \frac{C_{P1}-C_{M2}}{B_1+B_2}}\end{array}\right..$$

(27)

As shown in Figure 3b, this is a parallel boundary condition where one pipe is divided into two pipes. Assuming that the pressure heads at the connection point are equal, according to the continuity equation and the corresponding equations $C^{+}$, $C^{-}$, we have

$$\left\{\begin{array}{l}{H}_{P\left(1,N+1\right)}=C_{P1}-B_1{Q}_{P\left(1,N+1\right)}\\ H_{P\left(2,1\right)}=C_{M2}+B_2{Q}_{P\left(2,1\right)}\\ H_{P\left(3,1\right)}=C_{M3}+B_3{Q}_{P\left(3,1\right)}\\ H_P=H_{P\left(1,N+1\right)}=H_{P\left(2,1\right)}=H_{P\left(3,1\right)}\\ Q_{P\left(1,N+1\right)}=Q_{P\left(2,1\right)}+Q_{P\left(3,1\right)}\end{array}\right..$$

(28)

Solving for discharge, we have

$$H_P={\displaystyle \frac{\frac{C_{P1}}{B_1}+\frac{C_{M2}}{B_2}+\frac{C_{M3}}{B_3}}{\frac{1}{B_1}+\frac{1}{B_2}+\frac{1}{B_3}}}.$$

(29)

Substituting H_P into respective C⁺, C⁻ equations gives the branch flow rates.

Surge Tank Boundary

During hydraulic transient co-simulation of pressurized pipelines, the surge tank constitutes an internal boundary within the piping system. As illustrated in Figure 4, upstream and downstream pipelines are designated as 1 and 2, respectively, with the surge tank water level referenced to an identical piezometric head datum.

Neglecting water inertia and friction losses, we have

$$Z=H_P-K{Q}_{PS}^2,$$

(30)

where H_P = piezometric head at junction (m), Q_ps = surge tank inflow (m³/s), K = throttle orifice impedance coefficient, and Z = water level (m).

During the time period, the hydraulic parameters of the pressure regulating chamber change slightly, and the water level Z of the pressure regulating chamber can be approximated as

$$Z\approx H_P-K\left|Q_S\right|Q_{PS},$$

(31)

$$Z\approx Z_0+{\displaystyle \frac{Q_{PS}+Q_S}{2F}}\Delta t,$$

(32)

where Q_s = initial inflow (m³/s), Z₀ = initial water level (m), and F = cross-sectional area (m²).

Combining the surge tank continuity with characteristic equations $C^{+}$, $C^{-}$, we have

$$Q_{PS}={\displaystyle \frac{H_P-Z_0-\frac{\Delta t}{2F}{Q}_S}{\frac{\Delta t}{2F}+K\left|Q_S\right|}},$$

(33)

$$H_P={\displaystyle \frac{\frac{C_{P1}}{B_1}+\frac{C_{M2}}{B_2}+\frac{Z_0+\frac{\Delta t}{2F}{Q}_S}{\frac{\Delta t}{2F}+K\left|Q_S\right|}}{\frac{1}{B_1}+\frac{1}{B_2}+\frac{1}{\frac{\Delta t}{2F}+K\left|Q_S\right|}}}.$$

(34)

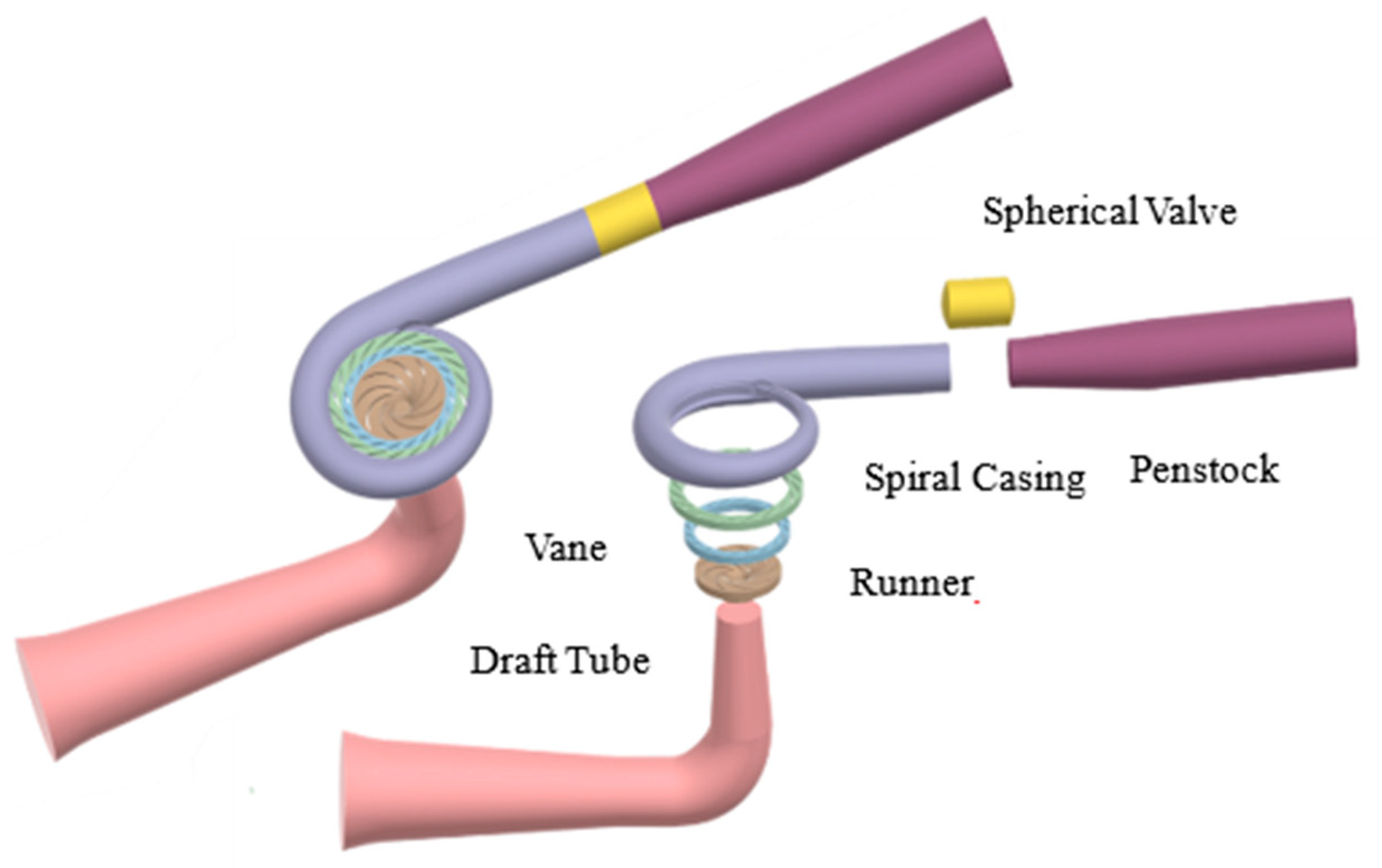
2.2. Model and Mesh Establishment

This study investigates a pump–turbine unit at a pumped-storage power plant using 1D–3D coupling methodology. The upstream/downstream water conveyance systems and surge tank are simulated via the one-dimensional method of characteristics (MOC), the theoretical basis of which is not reiterated here. For the spherical valve and pump-turbine components, three-dimensional numerical simulation is employed. The established 3D computational domain comprises seven sequential hydraulic components: penstock, spherical valve, spiral case, stay vanes, guide vanes, runner, draft tube. The key parameters are listed in

Table 1. Main parameters of the pump–turbine.

Basic Parameters	Symbol	Value
Number of runner blades	Zr	9
Number of guide vanes	Zg	20
Number of stay vanes	Zs	20
Rated head	Hr	540 m
Rotational speed	Nr	500 r/min
Runaway speed	n11r	660 r/min
Rated power	Pr	306 MW

, with the full computational domain illustrated in Figure 5.

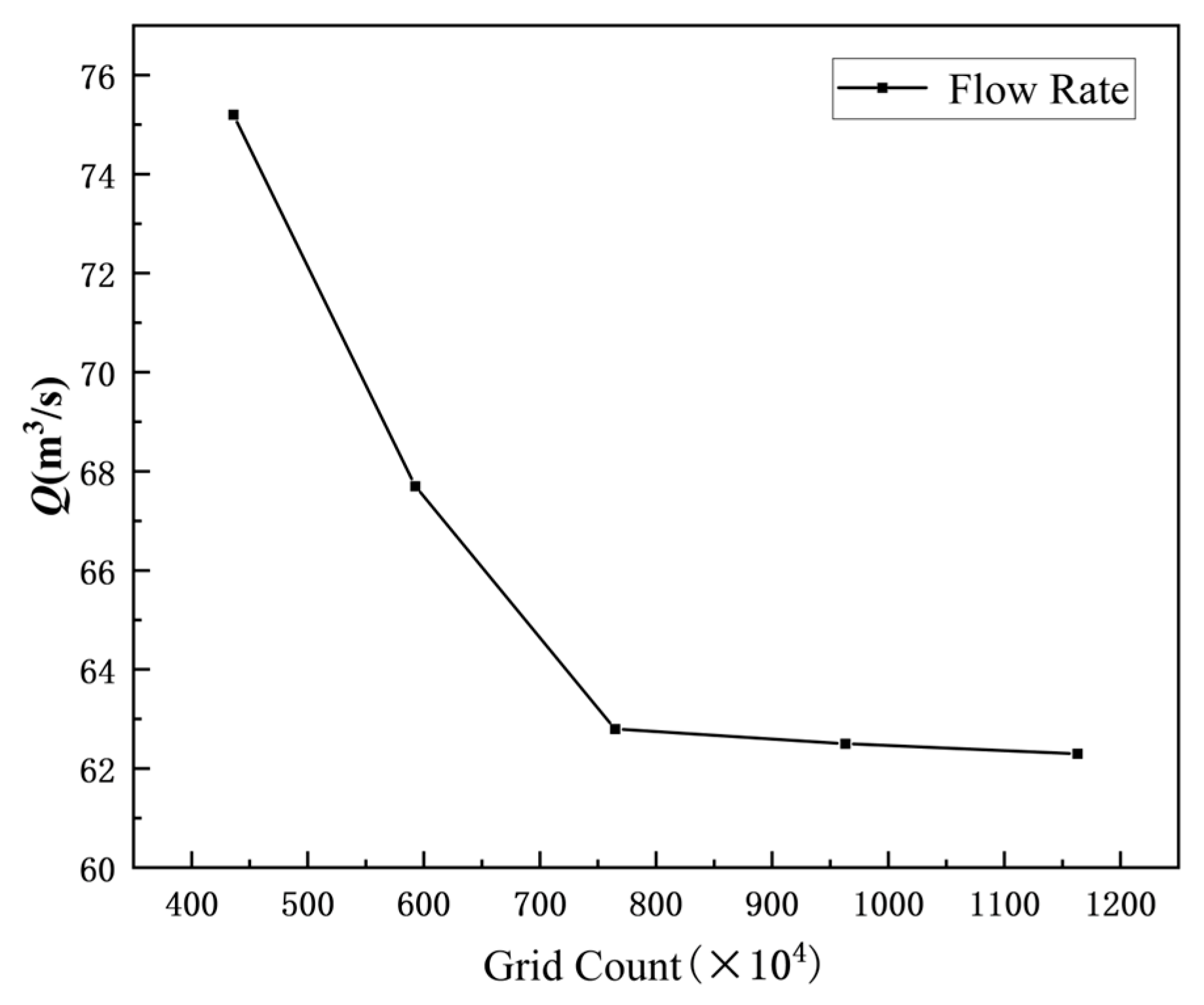
2.3. Grid Generation and Independence Verification

Prior to 3D numerical simulation, the computational domain requires meshing. Tetrahedral grids accommodate complex geometries with minimal simplification, making them suitable for objects with intricate boundaries. They provide relatively uniform grid distribution throughout the domain, enhance numerical accuracy, and allow localized refinement/coarsening to adapt to physical field variations. Consequently, this study employs unstructured grids for domain discretization. Additionally, the implementation of dynamic mesh in the numerical simulation necessitates a refined mesh resolution, with a minimum grid size of 0.003 mm. Figure 6 illustrates the mesh scheme for the pump–turbine components.

For grid independence verification, five mesh configurations ranging from 4.0 to 12.0 million nodes were evaluated. Figure 7 shows the variation in the steady-state flow rate under rated turbine operating conditions versus grid density. To balance computational accuracy and efficiency, the 7.648-million-node mesh was selected for subsequent transient simulations.

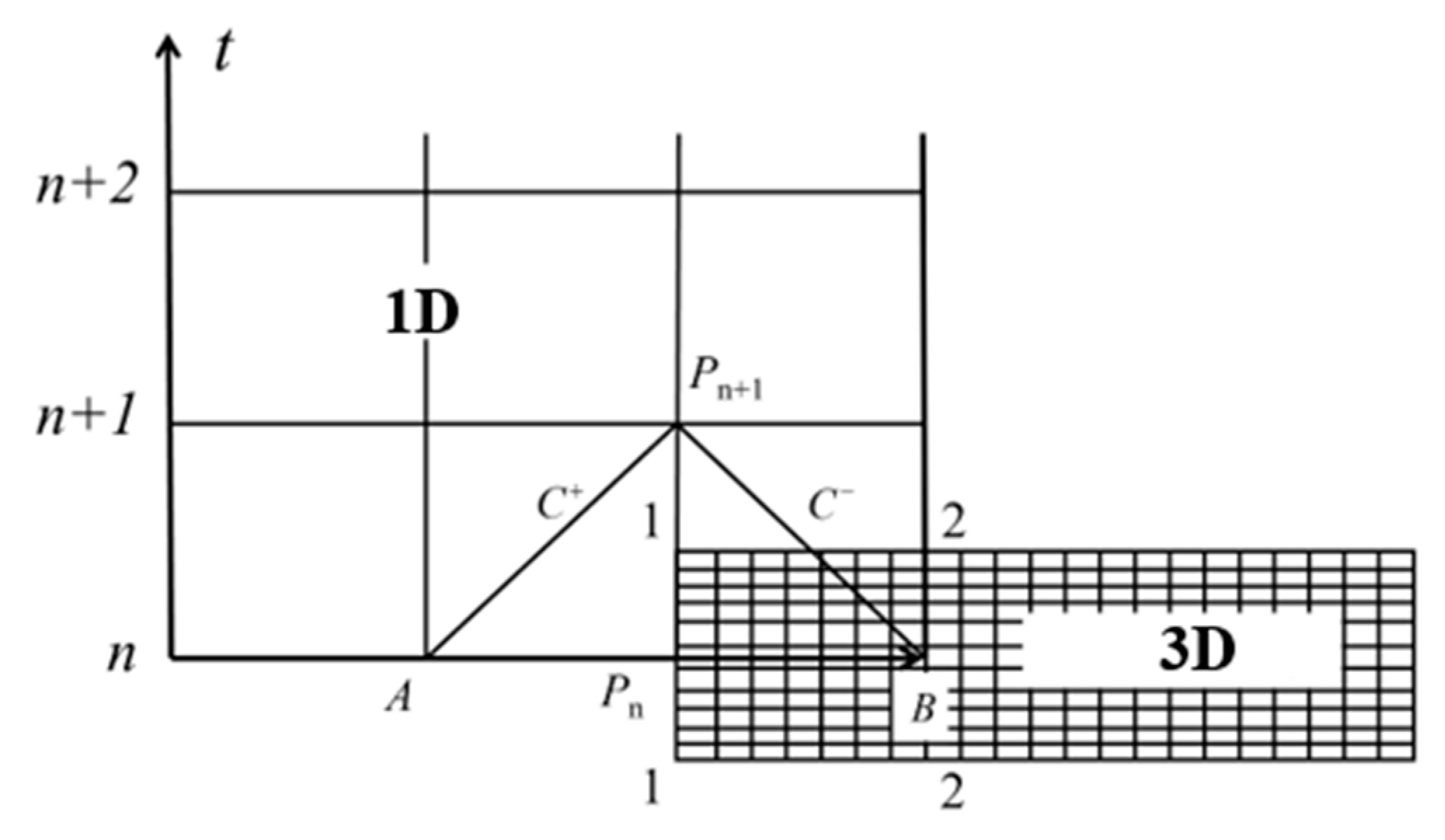
2.4. 1D–3D Coupling Scheme

The term “1D–3D coupling model” refers to the integration of the one-dimensional method of characteristics (MOC) for pipeline systems with three-dimensional numerical simulation techniques. Coupling strategies can generally be classified into two categories: strong coupling and weak coupling. In this study, a bidirectional sequential coupling scheme is employed, whereby one physical field is solved first, and the resulting data are transferred as input conditions to the other field. This bidirectional process enables iterative data exchange and interaction between the 1D and 3D computational domains. Following the coupling frameworks proposed by Zhang Xiaoxi—namely, the interface coupling and partial overlapping methods—the present work adopts the simpler overlapping coupling approach. Schematic diagrams of the coupled model are provided in Figure 8 and Figure 9, while relevant parameters of the 1D water conveyance system are summarized in

Table 2. Parameters of the 1D water conveyance system.

Pipe ID	Friction Loss Coefficient hw	Pipe Diameter D (m)	Pipe Length L (m)	Wave Speed a (m/s)	Inlet Elevation Hin (m)	Outlet Elevation Hout (m)
P[1]	0.0115	6	452.19	1100	703.2	674.42
P[2]	0.013	6	56.2	1100	674.42	672.38
P[3]	0.0115	5.2	274.3	1120	672.38	398.09
P[4]	0.012	5.2	195.92	1120	398.09	394.17
P[5]	0.0123	4.8	292.47	1120	394.17	101.69
P[6]	0.021	4.4	98.42	1120	101.69	94.3
P[7]	0.012	4.8	155.4	1120	83.3	98.6
P[8]	0.0115	6.5	999.27	1100	98.6	165.4
P[9]	0.0119	6.5	122.63	1100	165.4	165.5

. The primary computational procedure of the coupling methodology is outlined as follows; additionally, the coupling methodology in this study is activated exclusively during transient load rejection events and is not employed under steady-state operating conditions.

(1) Establish separate 1D and 3D computational component models. The 1D model comprises upstream and downstream reservoirs, surge tanks, and pipelines. The 3D model includes sections of the pipeline, a spherical valve, spiral casing, stay vanes, guide vanes, runner, and draft tube. (2) Initialize the 1D components using the Method of Characteristics (MOC), and transfer the computed values at the coupling interface to the 3D model. (3) Use the data transferred from the 1D model as boundary conditions to obtain the initial flow field for the 3D numerical simulation. (4) Extract the plane-averaged pressure and flow rate values at the n-th time step from the upstream and downstream overlapping coupling interfaces (Interface 2-2) of the 3D simulation. (5) Transfer the acquired values to the corresponding 1D computational nodes at the overlapping coupling interfaces (Interface 2-2) to serve as boundary conditions for the 1D calculation. (6) Calculate the data for all 1D computational nodes at the (n + 1)-th time step. Transfer the pressure value from the relevant 1D node (P-node) at the (n + 1)-th time step to the upstream and downstream overlapping coupling interfaces (Interface 1-1) to serve as boundary conditions for the 3D simulation. (7) Proceed with the 3D simulation for the (n + 1)-th time step, and return to Step 4, repeating the sequence for subsequent time steps.

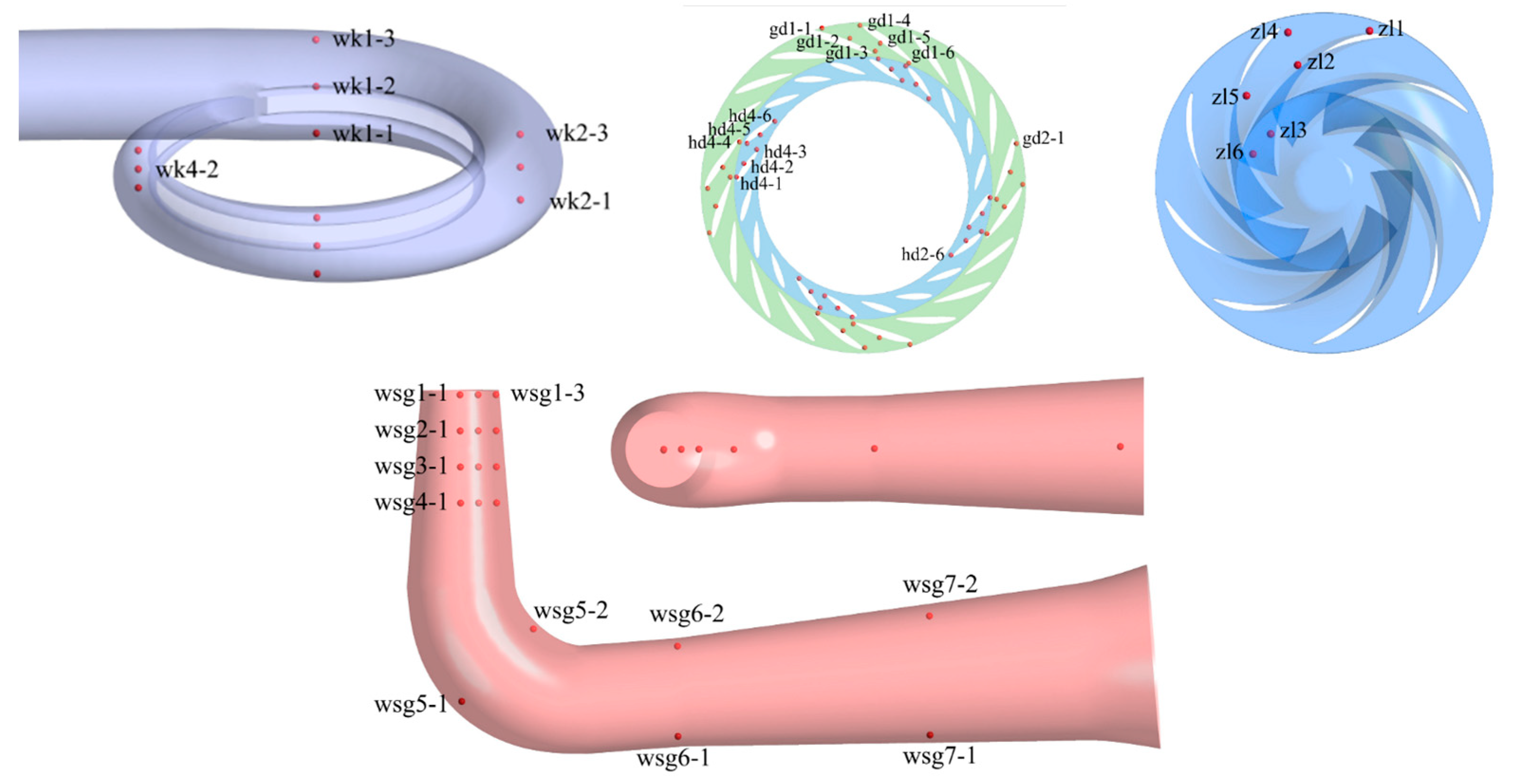
2.5. Setting of Boundary Conditions

This study analyzes flow field evolution during turbine runaway following stable operation under rated turbine conditions of the prototype unit, with steady-state and transient calculations performed in Ansys Fluent 2024 R2. For transient runaway simulation, the SST k-ω model was employed for its superior rotational flow prediction accuracy. The runner domain was configured with Mesh Motion, incorporating a compiled user-defined function (UDF) for rotational speed variation that was activated in the Mesh Motion interface, The motion of the guide vanes was achieved by configuring the built-in dynamic mesh technology in Fluent, with smoothing and remeshing performed at each time step. The custom UDF for 1D–3D coupling was similarly compiled and implemented at pressure boundary conditions. Given rapid runner acceleration during transients, excessive rotation per time step could cause computational instability or floating-point overflow; thus, a time step of 0.001 s was adopted with residual convergence criterion set to 1.0 × 10⁻⁶ and maximum iterations per step limited to 15, enabling stable simulation of the full 68-s transient process. Monitoring points were distributed throughout the flow passage to capture pressure pulsations during the transition.

To facilitate post-simulation analysis of pressure pulsations, monitoring points were strategically positioned throughout the entire flow passage. The locations of these monitoring points are illustrated in Figure 10.

3. Numerical Investigation of the Transient Response During Turbine Runaway

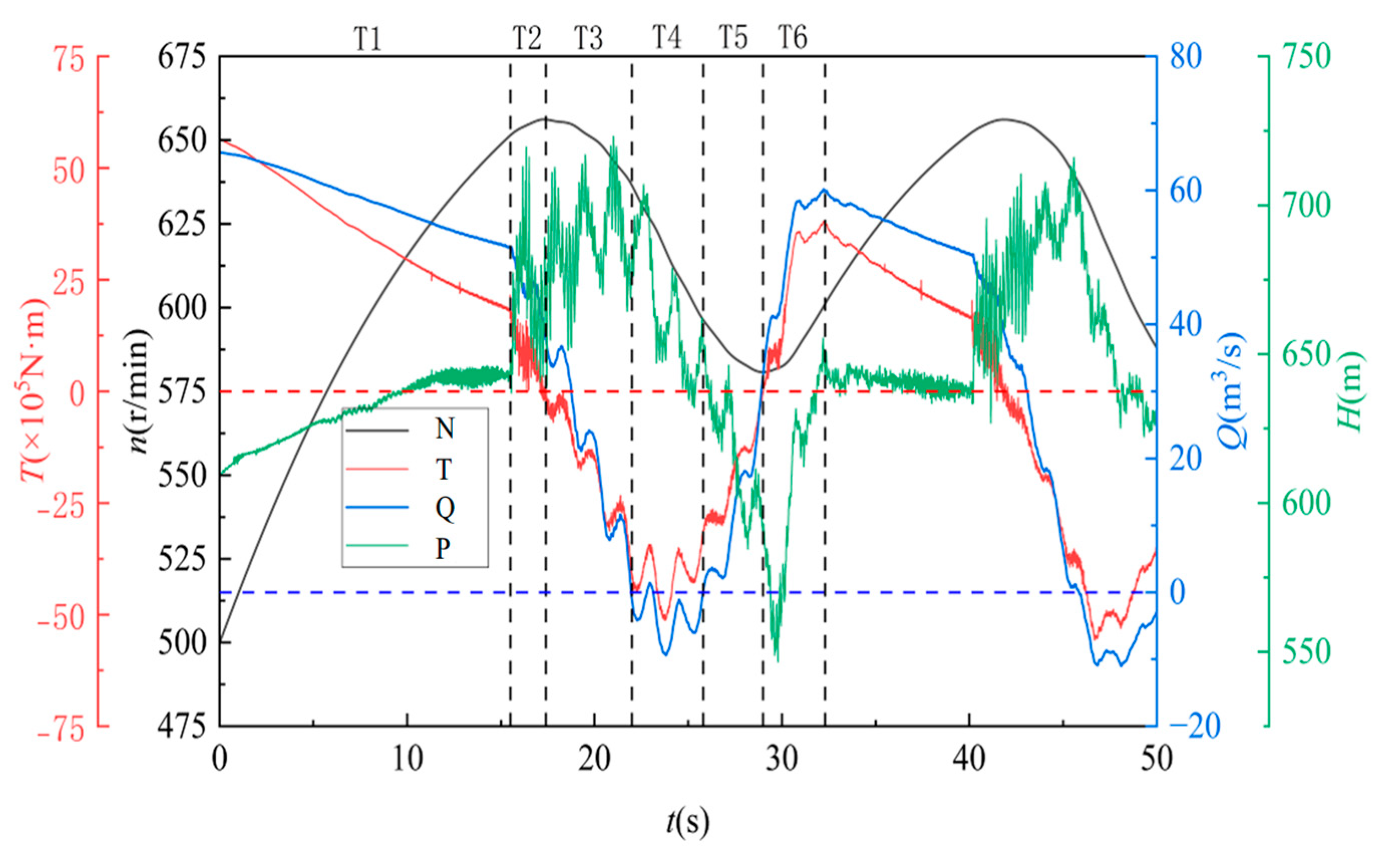
3.1. Analysis of Turbine Runaway External Characteristics

Figure 11 illustrates the temporal evolution of the rotational speed, torque, and flow rate during the complete load-rejection runaway process. The transition comprises six distinct phases (T1–T6): During T1 (turbine mode), positive torque and flow prevail. Post load-rejection, the speed begins to increase, while the runner flow remains stable. T2 sustains turbine operation with the speed ascending to runaway at 656.16 r/min (0.58% deviation from actual 660 r/min), accompanied by rapid pressure surge. T3 enters braking mode: the torque reverses to negative values, the speed declines, the flow decreases, and the unit enters the inverse S-shaped region [28], with periodic pressure oscillations peaking at 722.96 m. T4 (reverse pump mode) exhibits negative flow/torque, persistent periodic oscillations, and speed reduction; the flow reverses polarity at 23.8 s, reaching −9.4 m³/s. T5 re-enters braking mode, maintaining deceleration. T6 resumes turbine operation with positive torque, increasing the speed/flow until stabilization after 32.3 s, followed by recurring flow/torque reduction cycles.

Notably, the second oscillation period demonstrates markedly reduced pressure amplitude compared to the initial inverse S-shaped region operation. This damping effect indicates that the first severe oscillation was amplified by water hammer pressure, whereas subsequent entries into the inverse S-shaped region exhibit attenuated the hydraulic pressure and consequently diminished the oscillation magnitudes.

3.2. Analysis of Pressure Pulsation Characteristics in Turbine Runaway Conditions

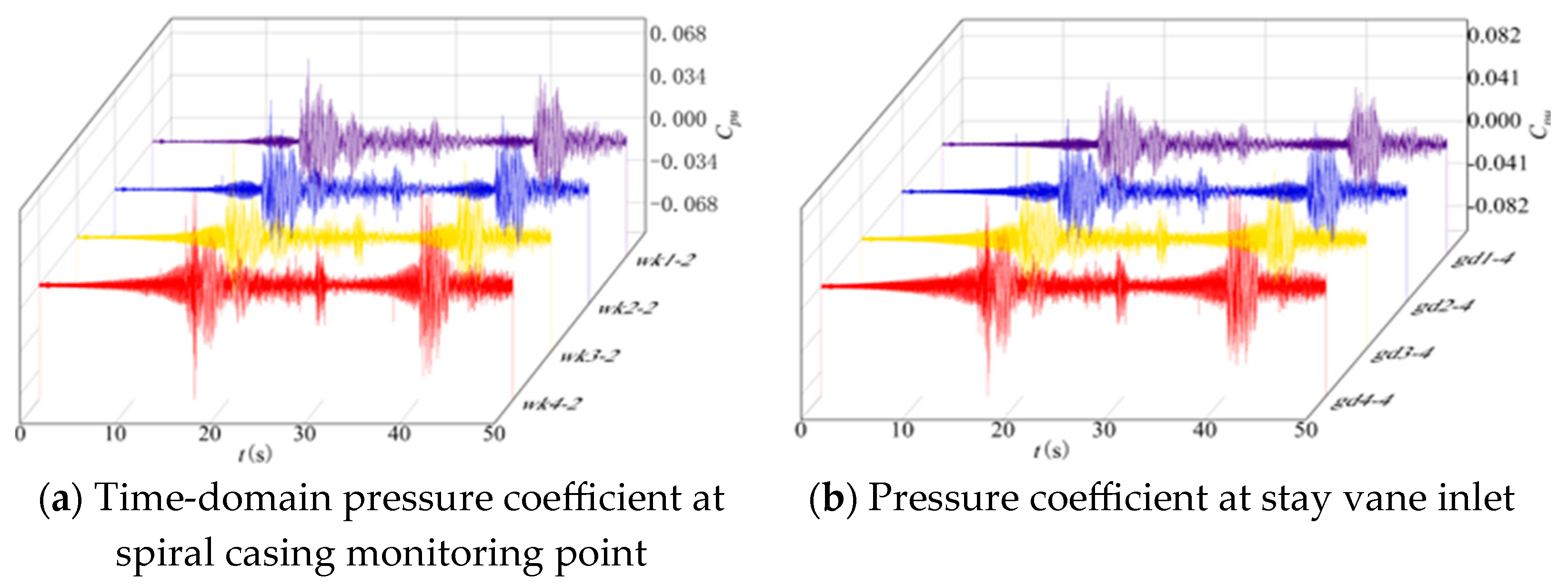
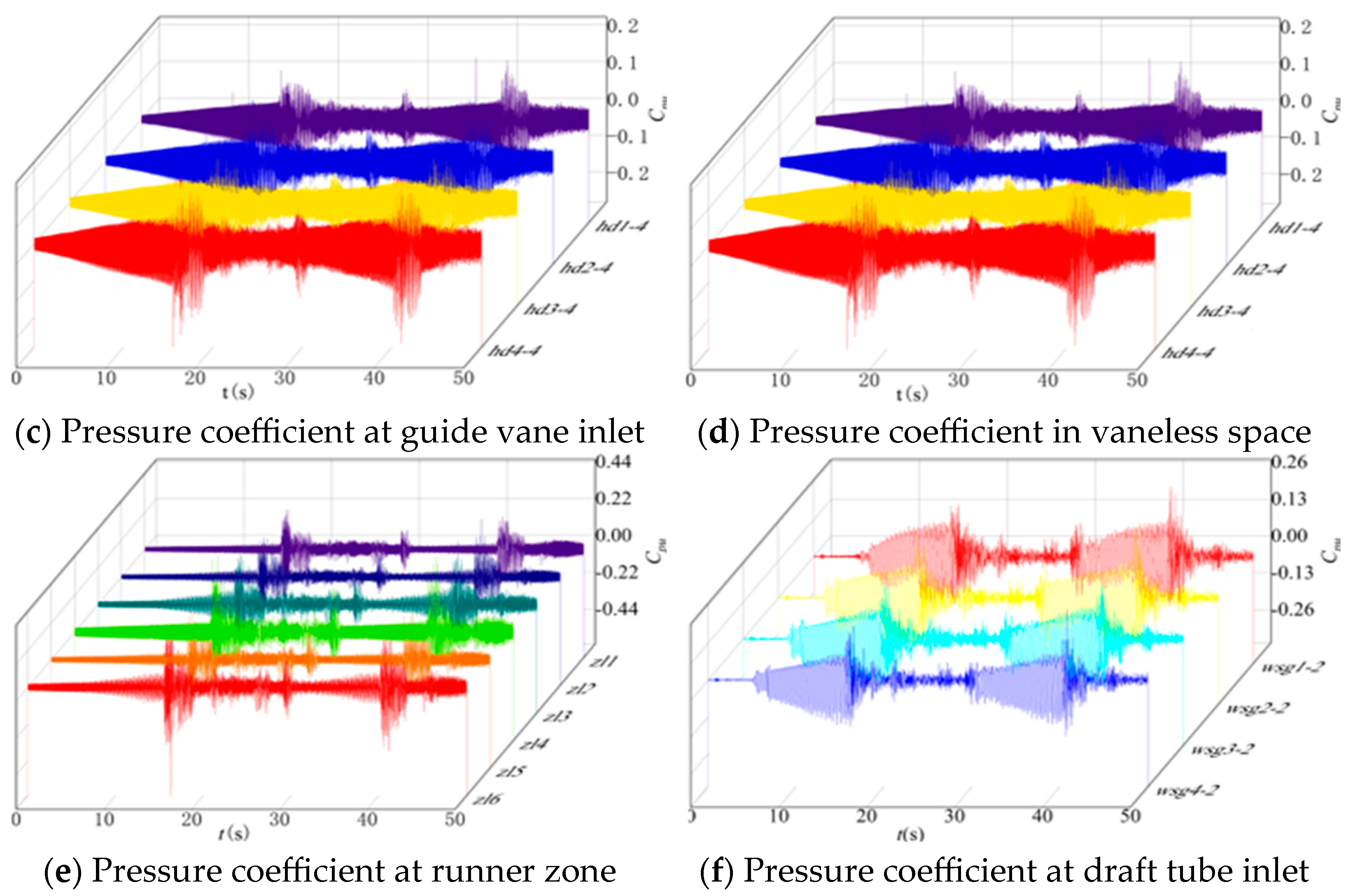
3.2.1. Time-Domain Characteristic Analysis

Figure 12 presents dimensionless pressure coefficient time-domain diagrams for monitoring points throughout the unit. The pressure coefficients vary across regions, yet all exhibit pulsation patterns consistent with runner force and torque characteristics, showing significant pulsations near runner torque zero-crossings at 15.4 s, 29.3 s, and 40 s. Between 21 and 27 s, reduced-amplitude pulsations occur, correlating with previously described external characteristics and runner force variations.

Notably, guide vane inlets and vaneless spaces exhibit the most pronounced pulsation amplitudes throughout the runaway transition. Within the runner domain, the pressure pulsations diminish significantly after flow entry, with fluctuations reconverging near 15.4 s, 29.3 s, and 40 s. At the draft tube, the pulsation amplitudes decrease with the increasing distance from the runner. A distinct pressure coefficient increase occurs at 5 s, coinciding with the flow pattern transition in the draft tube.

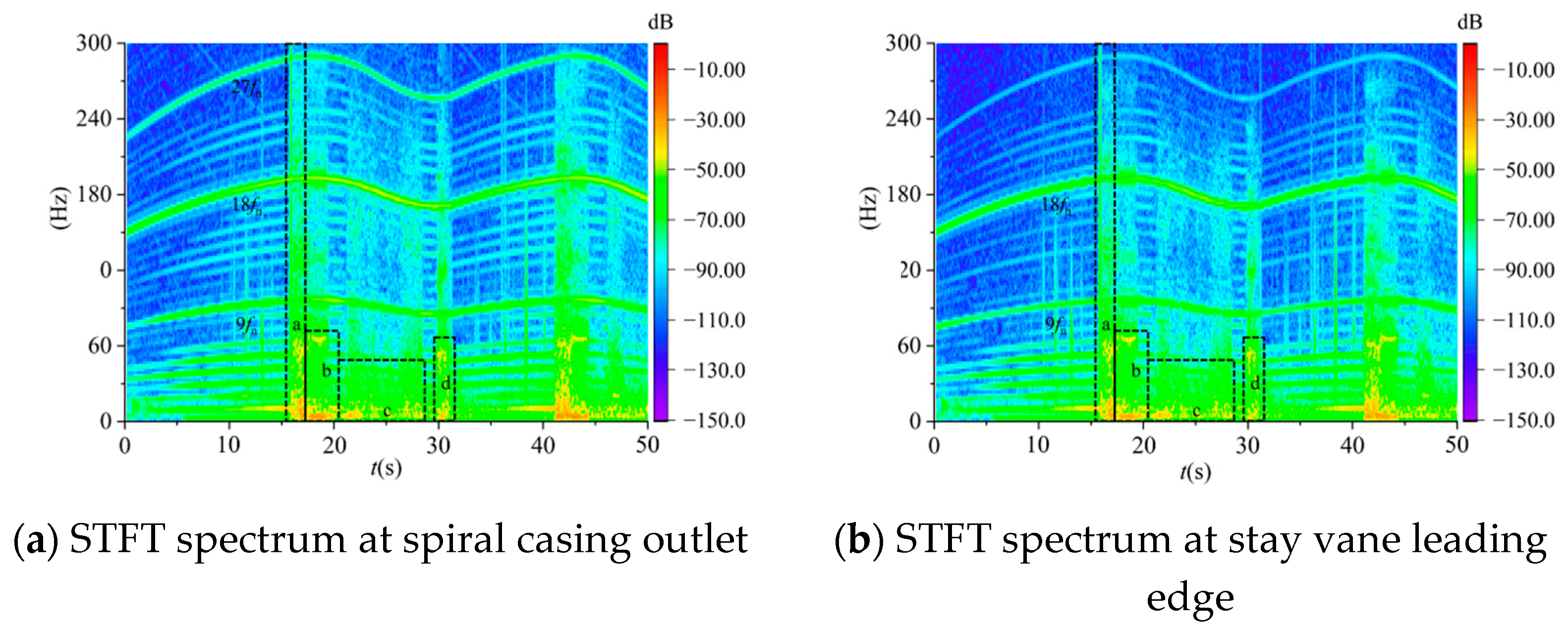
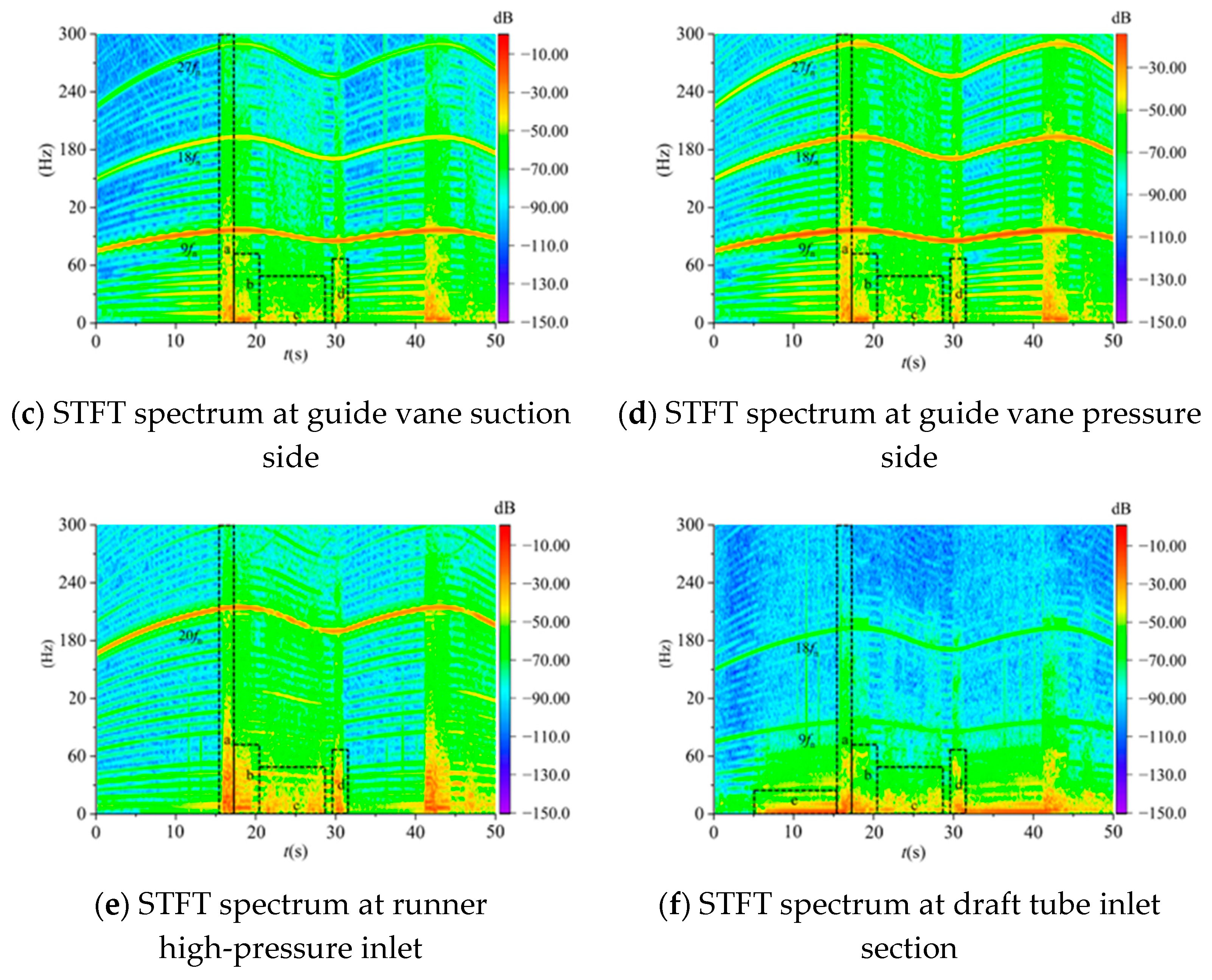
3.2.2. Frequency-Domain Characteristic Analysis

Short-time Fourier transform (STFT) was applied to investigate the frequency compositions and evolution of pressure pulsations at six monitoring points: spiral case outlet, stay vane inlet, guide vane inlet, guide vane outlet, runner high-pressure inlet, and draft tube inlet. Figure 13 presents the dimensionless pressure pulsation STFT results.

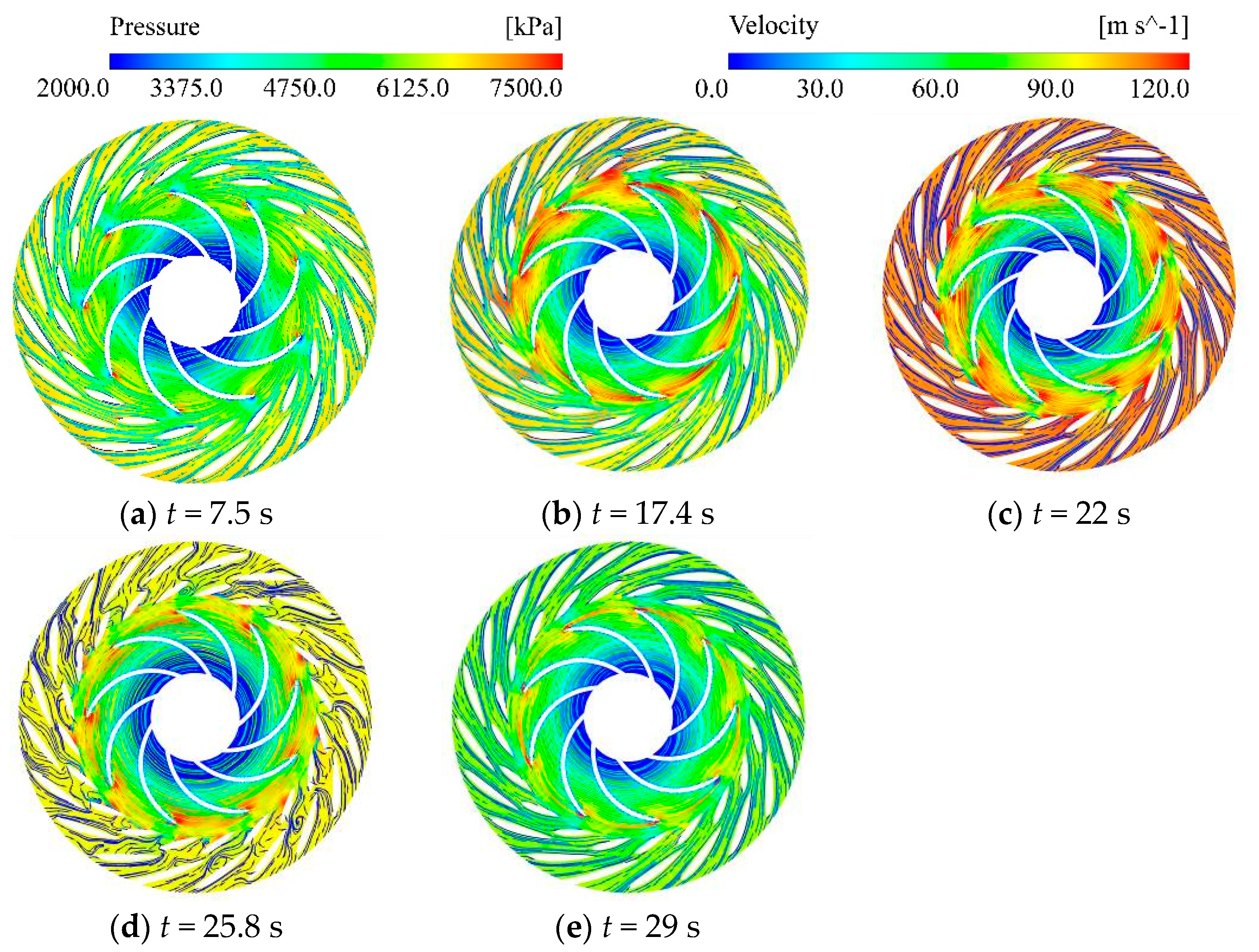
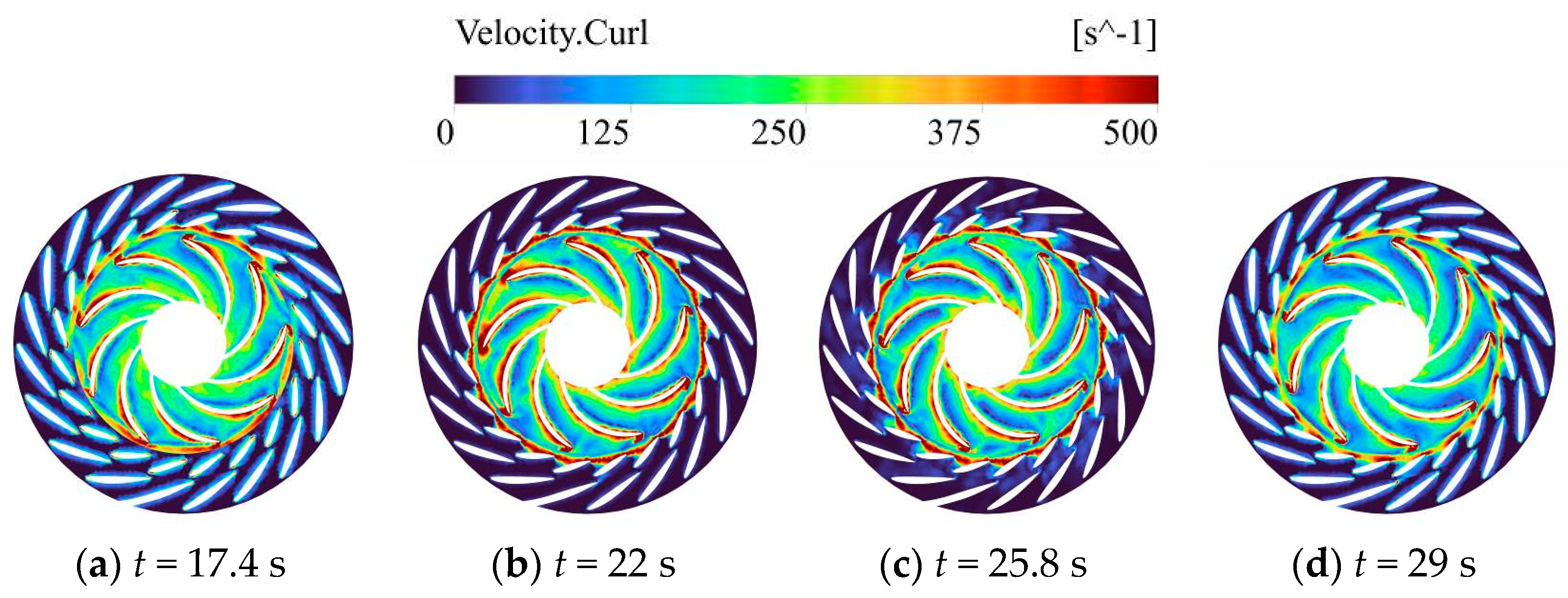
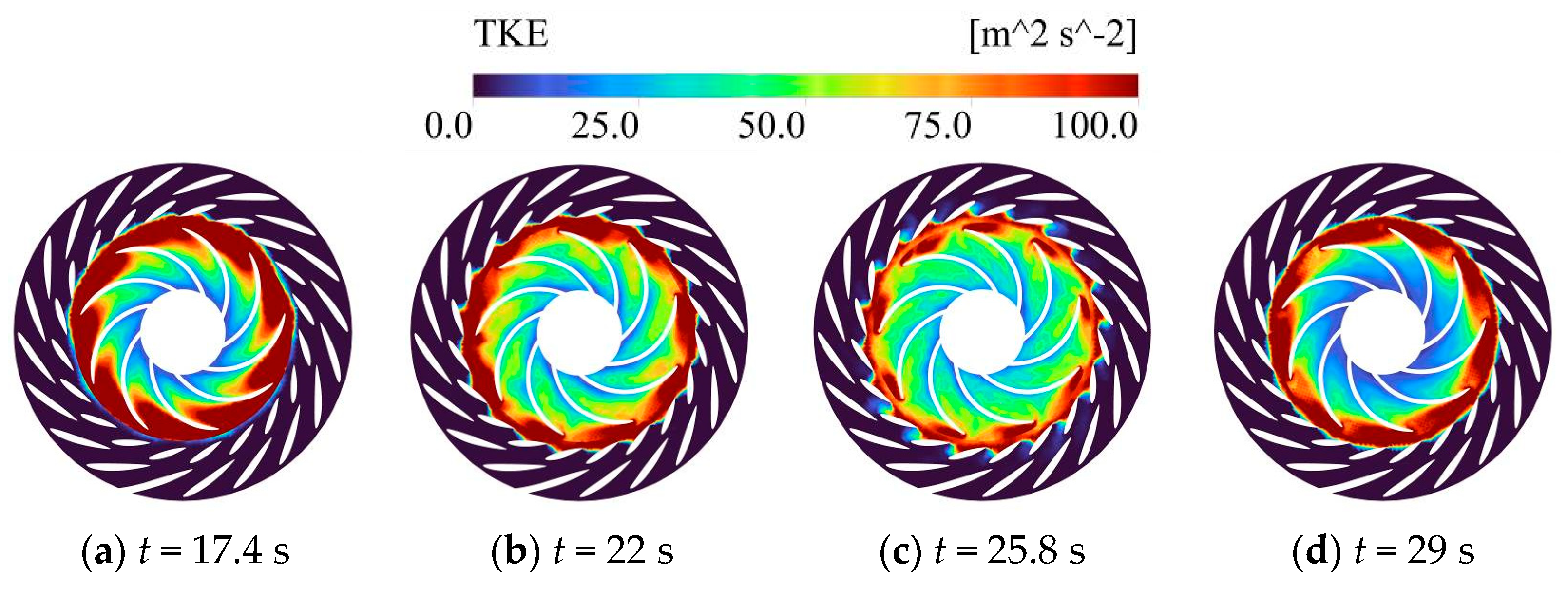
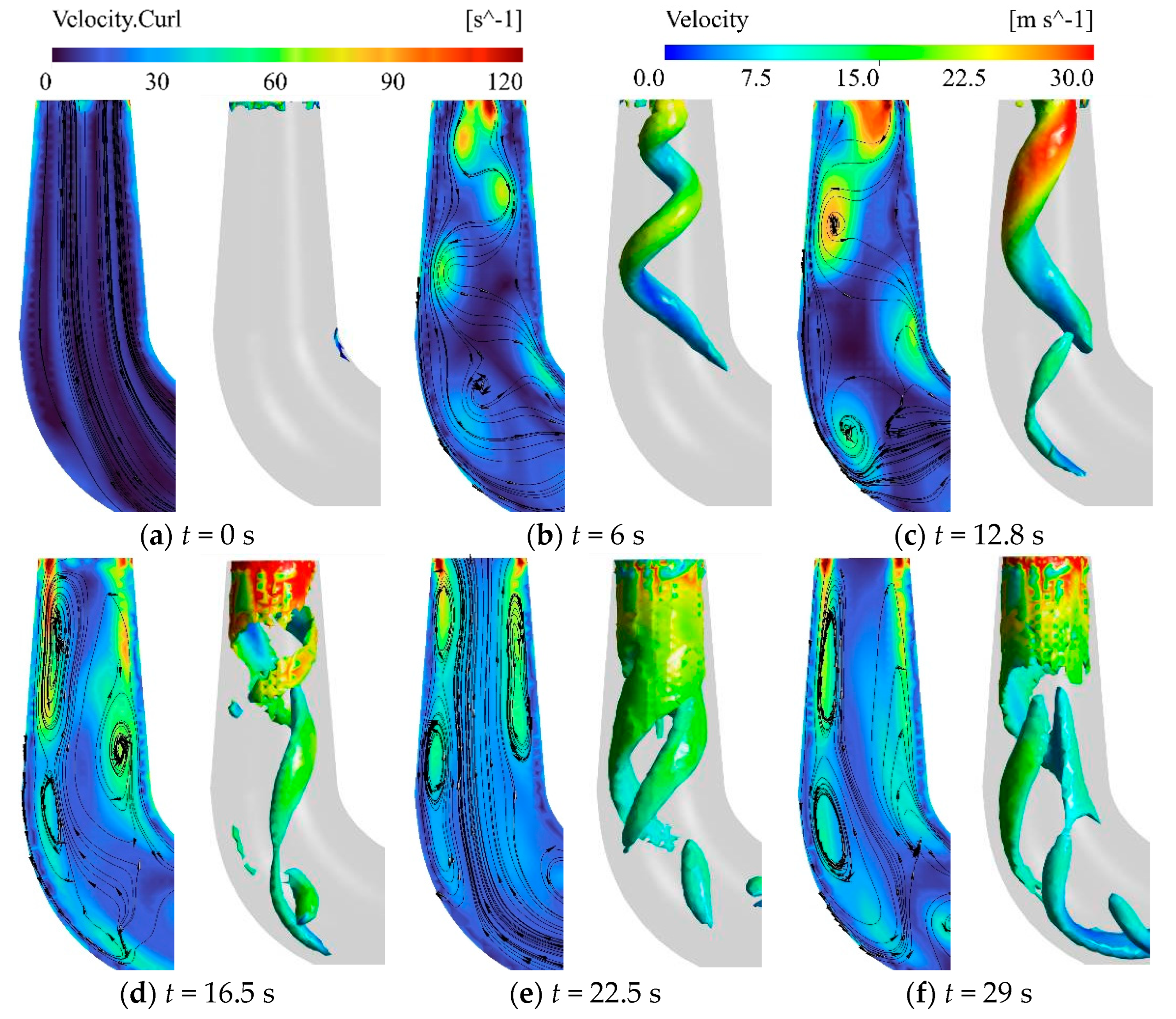
3.3. Internal Flow Field Characteristic Analysis of Turbines Under Runaway Conditions

3.3.1. Internal Flow Characteristics of Double-Row Cascades and Runners

To investigate the instability mechanisms during turbine runaway, seven characteristic instants were selected based on external characteristics and pressure pulsation patterns: initial 7.5 s, region a (significant pulsations), 17.4 s (torque zero-crossing, region b), 22 s (zero-flow, region c), 25.8 s (flow recovery to zero, region c), and 29 s (torque re-zeroing, region d). Figure 14 presents the pressure contours and velocity streamlines at the mid-planes of the double cascade and runner.

At 7.5 s (post load-rejection), the flow patterns remain largely unchanged. By 17.4 s, vortices exceeding 500 s⁻¹ form in the vaneless space near spiral case outlet and runner inlet, coinciding with torque zero-crossing where driving and resisting moments equilibrate. The runner high-pressure zone expands as the high-velocity fluid occupies the entire rotating region, accelerated by runner blade extrusion during flow reduction before being ejected and recirculated via low-pressure zones. At 22 s (zero-flow), fluid exiting the guide vanes encounters runner-inlet high-pressure blockage, colliding with the subsequent flow to form merging high-pressure zones in vaneless space and guide vane outlets. This unstable high-pressure region exerts multidirectional forces on the runner, explaining the torque fluctuations. By 24 s (minimum torque/flow), the high-pressure zone propagates inward while the reverse flow generates vortices in guide/stay vane regions. The backflow vortices generated exhibit a range of scales and varying intensities. These vortices are highly unstable and inherently unsteady. Over time, the periodic shedding and evolution of the backflow vortices interact with the runner rotation, exciting strong low-frequency pressure pulsations. The frequency of such pulsations is typically much lower than the runner rotational frequency (e.g., related to the vortex rope frequency), which can easily induce resonance with the unit or powerhouse foundation structure, leading to significant hazards. When the backflow vortices impinge on the guide vanes or runner blades, they break down into smaller-scale vortical structures, generating high-frequency pressure pulsations. This process may cause local fatigue in components and contribute to structural noise. Furthermore, according to the related studies, cavitation can become particularly severe under load rejection backflow conditions.

Figure 15 and Figure 16, respectively, show the vorticity and turbulent kinetic energy (TKE) distributions at critical instants. At 17.4 s, elongated vortex bands at the runner blade leading edges and guide vane outlets obstruct the flow, causing rapid flow reduction. High TKE regions in the vaneless/runner domains correlate with significant pulsations in region b (17.2–20.5 s). At 22 s, intensified annular vorticity at guide vane outlets extends to vaneless space, further blocking flow. The diminished TKE in the runner corresponds to reduced pulsation amplitudes in region c (20.5–28.5 s). The vortex zones contract at 25.8 s as the flow/torque recover, concentrating near runner inlets and guide vane high-pressure outlets by 29 s.

3.3.2. Internal Flow Characteristics in Draft Tubes

Six characteristic instants during runaway were selected to analyze the draft tube streamline and vortex rope development (Figure 17). The left panels display vorticity contours with streamlines; the right panels depict vortex rope configurations. At t = 0 s (immediate post load-rejection), the flow remains stable without vortex formation. As the runner speed increases, the reduced axial velocity initiates a columnar vortex rope, inducing pressure pulsations that evolve into a helical structure with growing diameter, length, and energy. Concurrently, pulsation amplitudes intensify. The expanding helical vortex approaches draft tube walls, transitioning into a wall-attached vortex rope that breaks the flow symmetry and obstructs the passage, triggering severe pressure pulsations throughout the unit.

Progressive wall-attached vortex development increases the reverse flow toward the runner, causing negative flow (reverse pump mode). The vortex reaches its maximum extent, with secondary attached vortices evolving into mutually spiraling structures. A new columnar vortex forms between them, restoring the flow stability and reducing runner pressure pulsations. Subsequently, gravity diminishes the reverse flow, gradually restoring the positive flow. Increasing downward flow contracts the wall-attached vortex diameter, eventually transitioning back toward an annular vortex configuration. Throughout this process, variations in guide vane openings and flow rates induce continuous changes in the vortex rope within the draft tube. This may generate pressure pulsations with frequencies close to the rotational frequency of the unit, potentially exciting resonant vibrations in the turbine system and thereby compromising operational safety.

4. Conclusions

Through 1D–3D coupled numerical simulations, this study systematically investigated external characteristic variations and pressure pulsation behavior during pump-turbine runaway. Time–frequency analyses elucidated pressure pulsation compositions across hydraulic components, while the flow pattern evolution in the double cascade/runner and draft tube vortex development were correlated with macroscopic characteristics. The key findings are as follows:

(1)

Runaway simulation reveals distinct transitional phases, yielding a predicted runaway speed of 656.16 r/min (0.58% deviation from actual value) and peak pressure of 722.96 m. Attenuated water hammer pressure reduces the periodic oscillation amplitudes during subsequent entries into the inverse S-shaped region.

(2)

The Short-Time Fourier Transform (STFT) analysis identifies the following: high-frequency pulsations at 1×/2× blade passing frequency (runner-induced rotor–stator interference), prevalent throughout the flow passage; broad-spectrum high-amplitude pulsations during operational mode transitions, concentrated near torque turning points; low-frequency high-amplitude pulsations at 1×/2× runner frequency (draft tube vortex ropes), primarily affecting the draft tube domain.

(3)

At 650.9 r/min, large-scale vortices (>500 s⁻¹) obstruct selected runner blade passages, while draft tube vortex ropes transition from central helical structures to wall-attached configurations. Their synergistic effect triggers abrupt runner force variations and intense pressure pulsations.