Numerical and Parametric Investigation of the Influence of Rectangular and Elliptical Phase Change Material Geometries on the Thermal Performance of a Ground-Air Heat Exchanger
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling
Performance Indicator
2.2. Computational Modeling
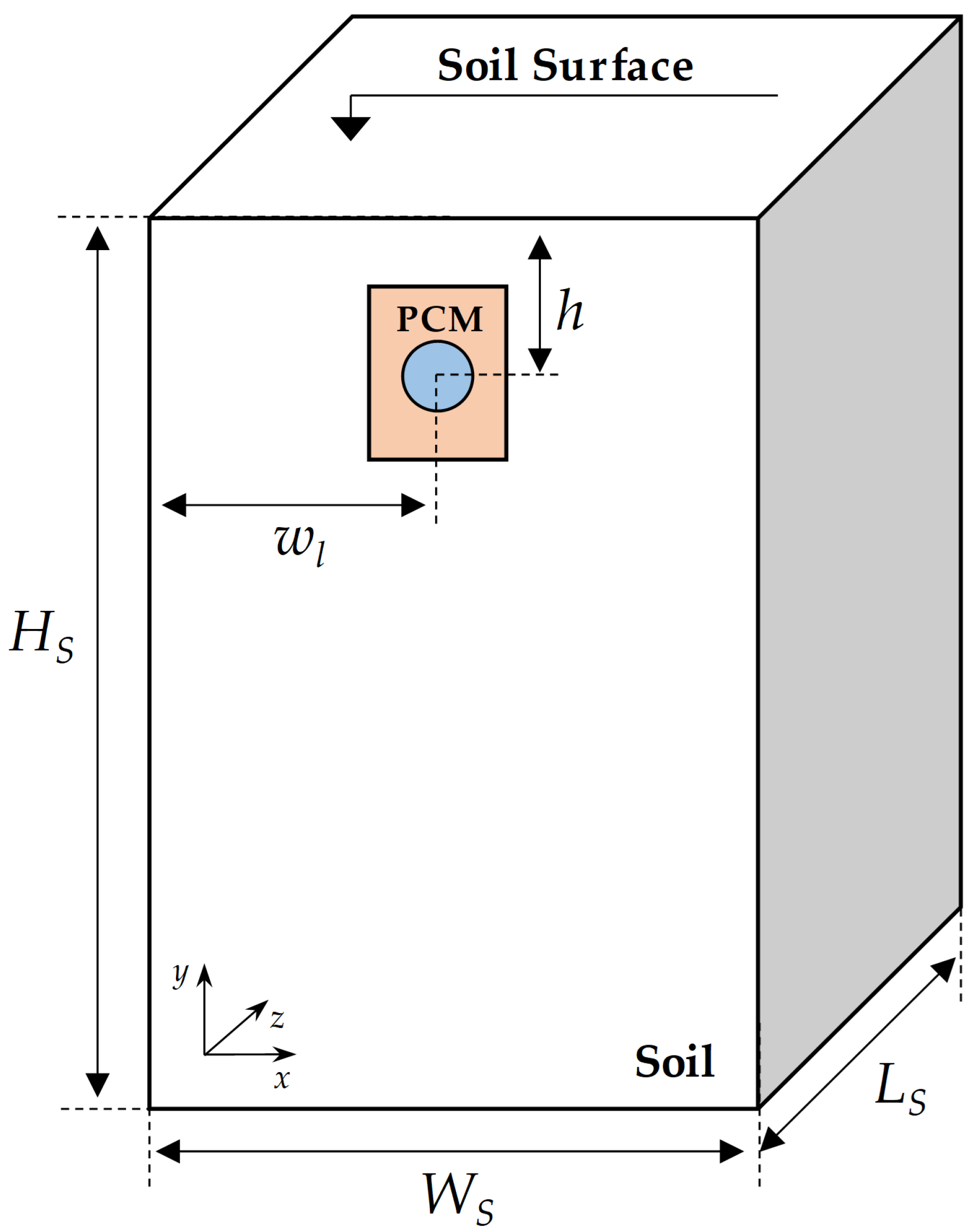
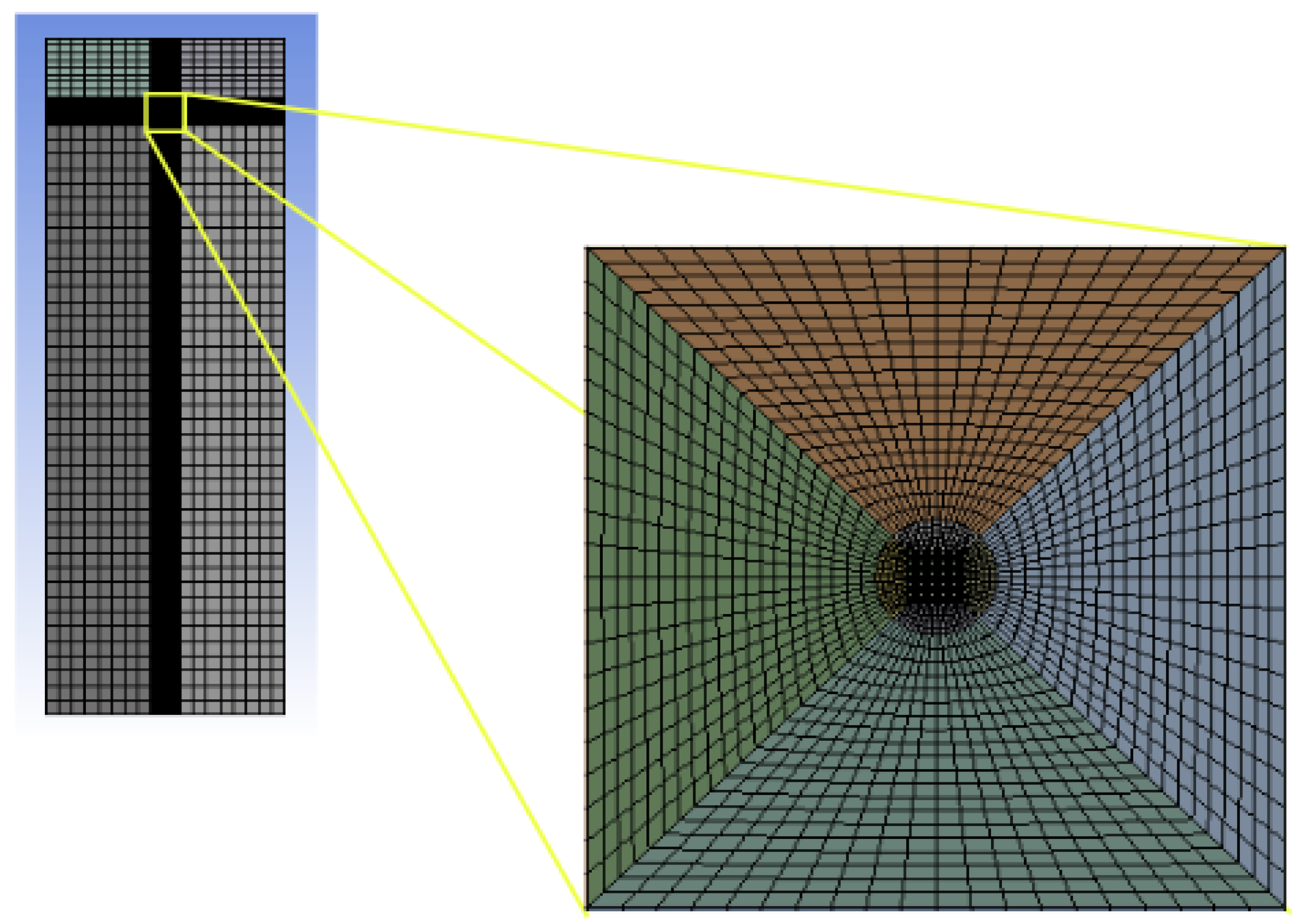
2.2.1. Computational Domain
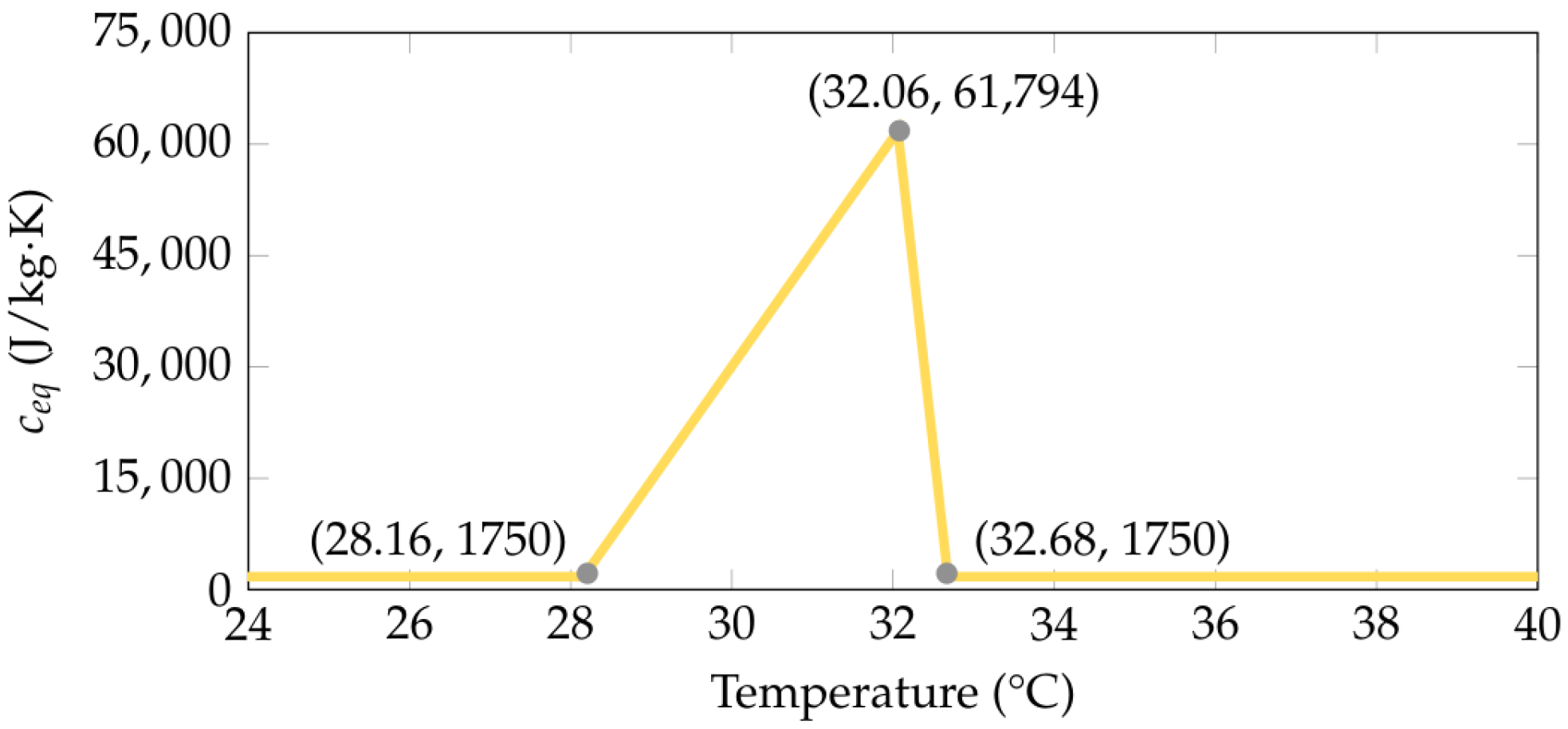
2.2.2. Thermophysical Properties of the Materials
2.2.3. Initial Condition and Boundary Conditions
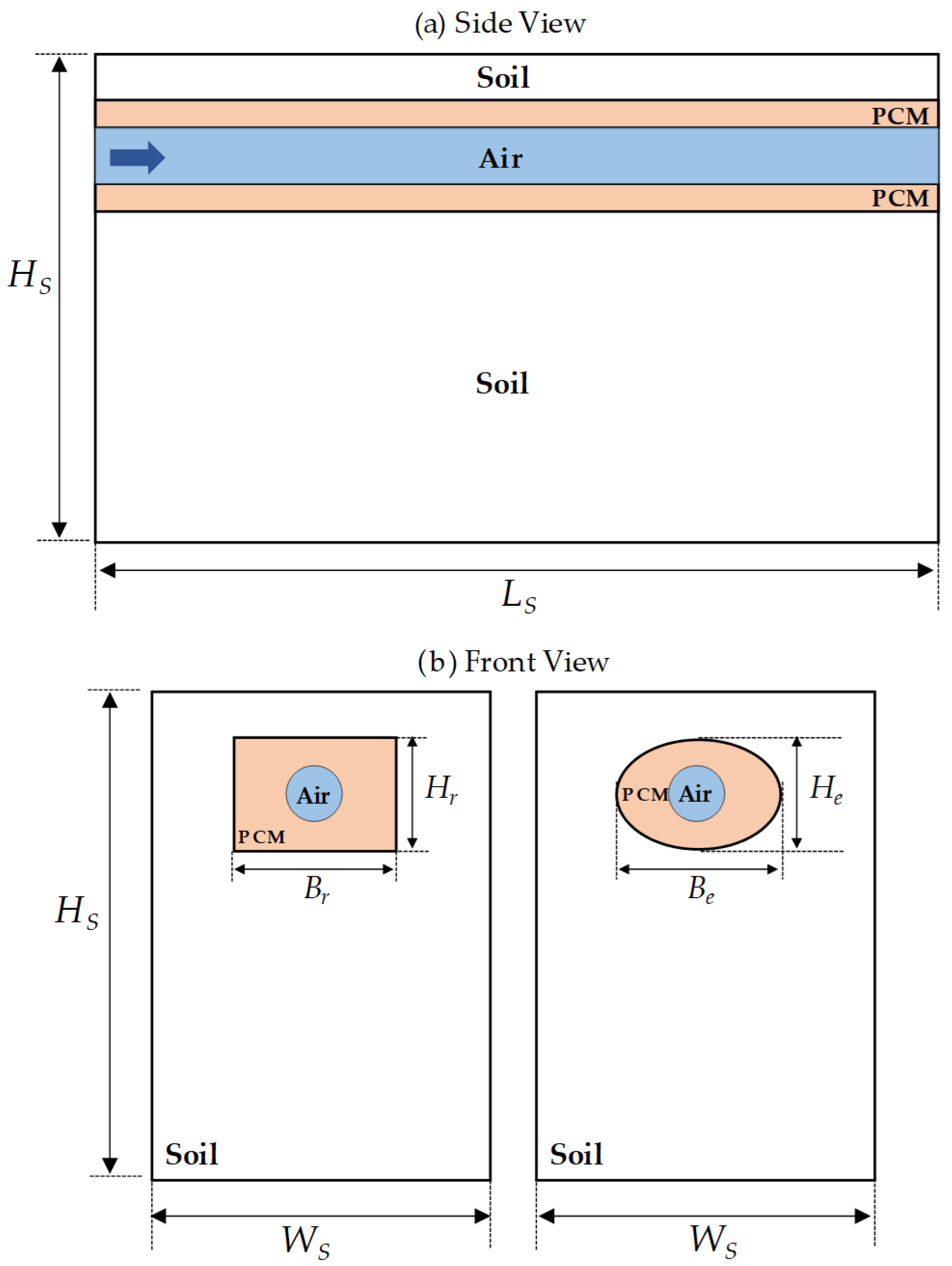
2.2.4. Preliminary Geometric Configurations of PCM
2.2.5. Case Study
3. Numerical Modeling
3.1. Solution Configuration
3.2. Mesh Convergence Study
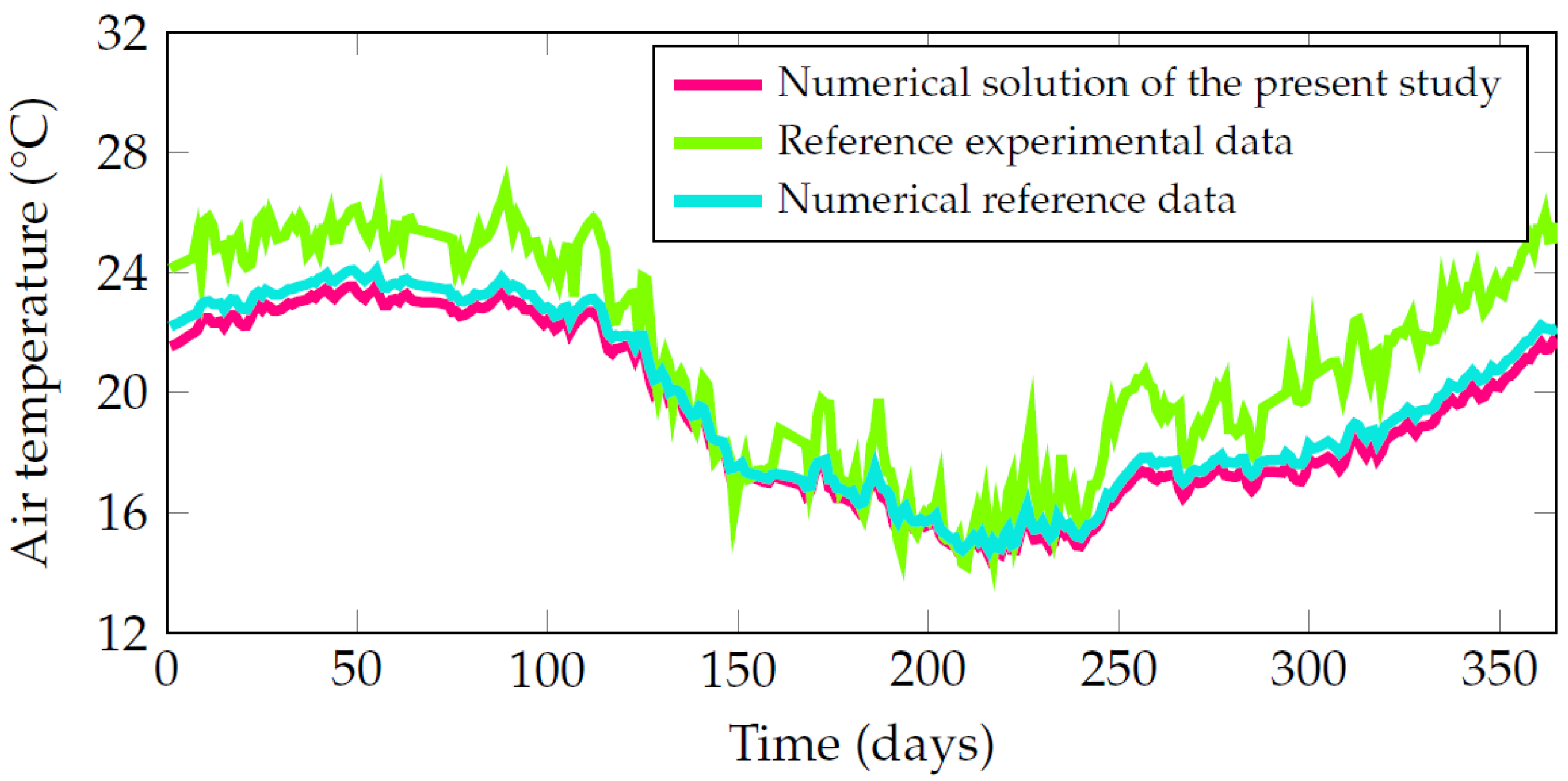
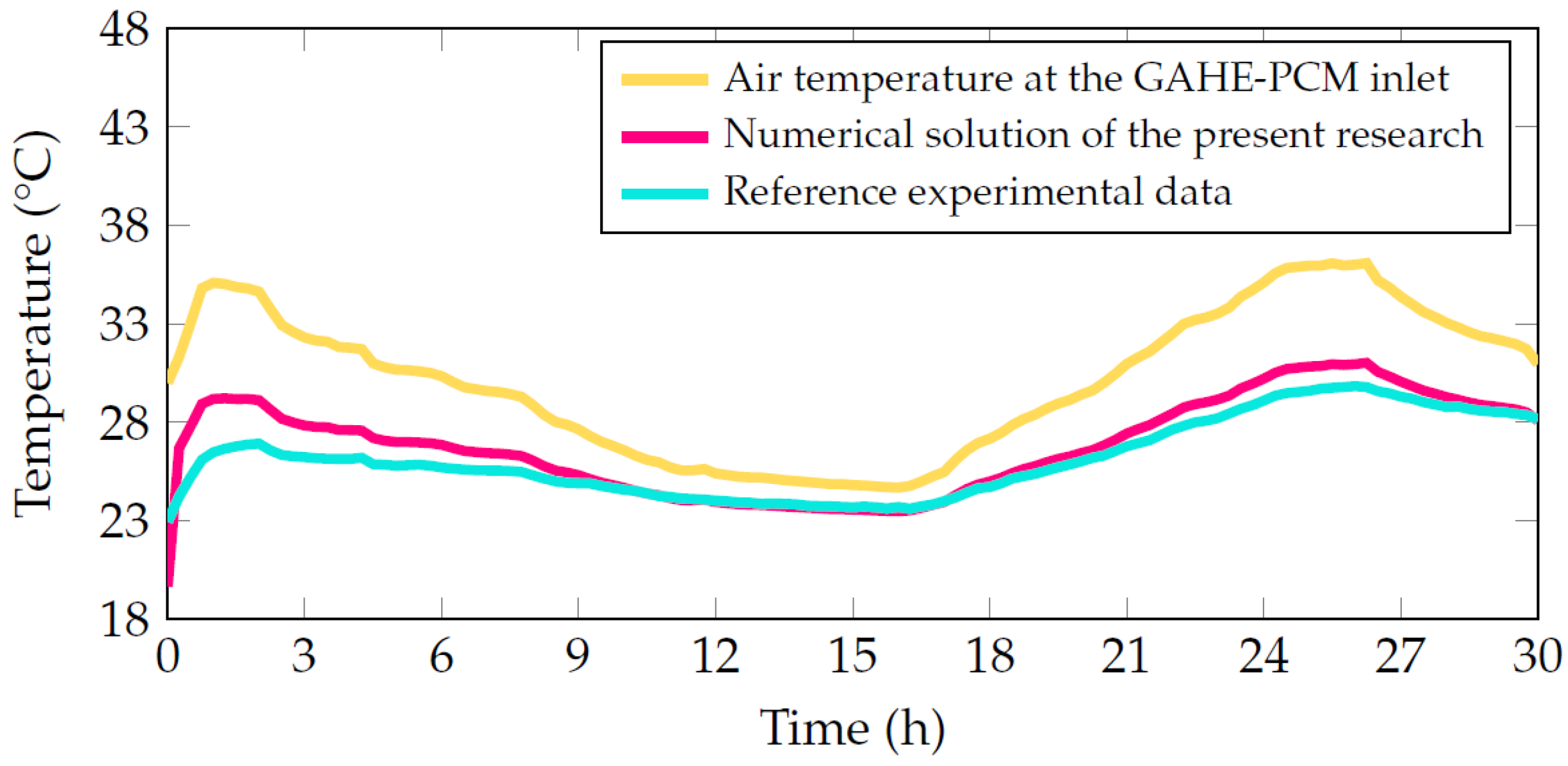
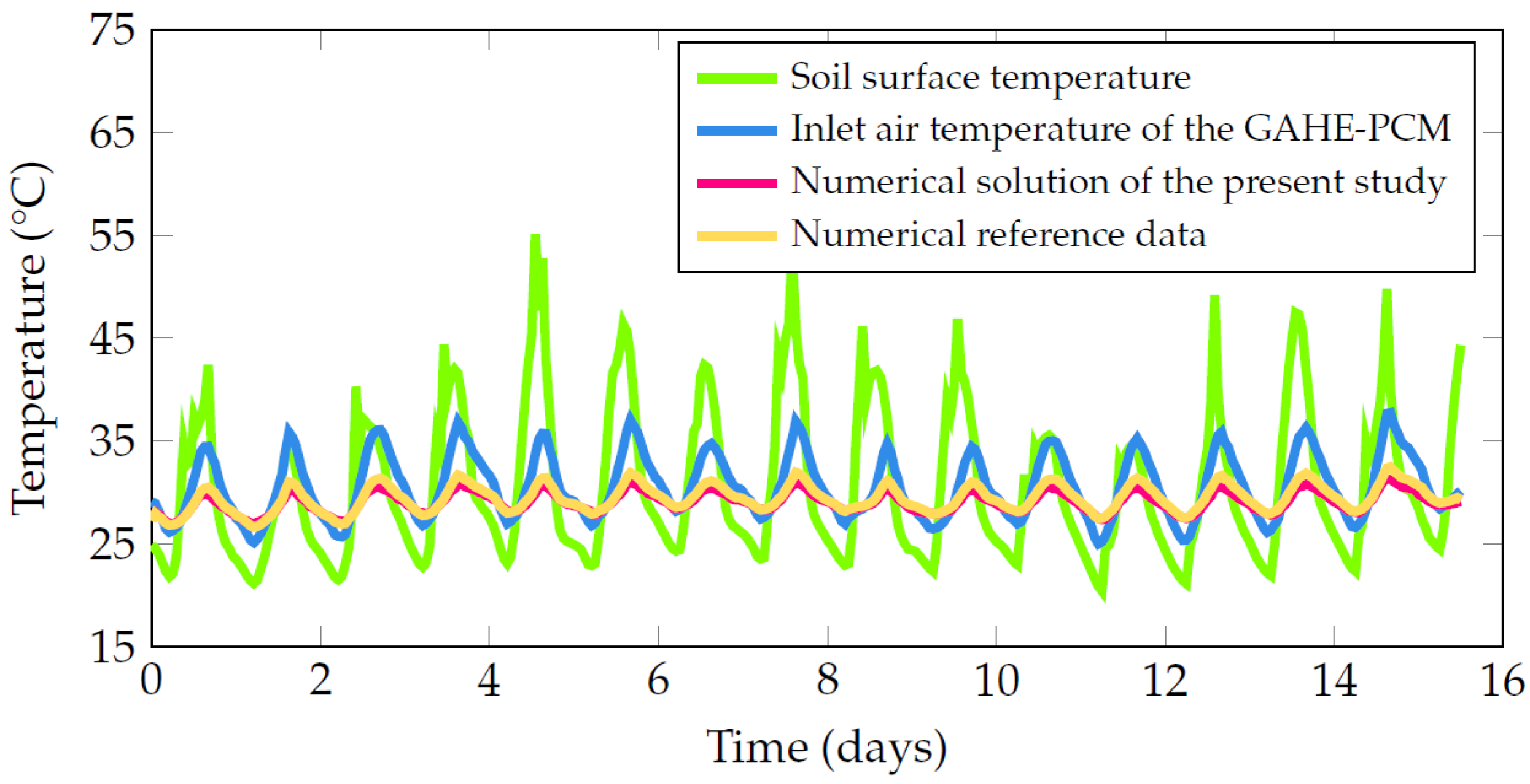
3.3. GAHE Numerical Model Verification and Validation
3.4. Validation and Verification of the GAHE-PCM Computational Model
4. Results
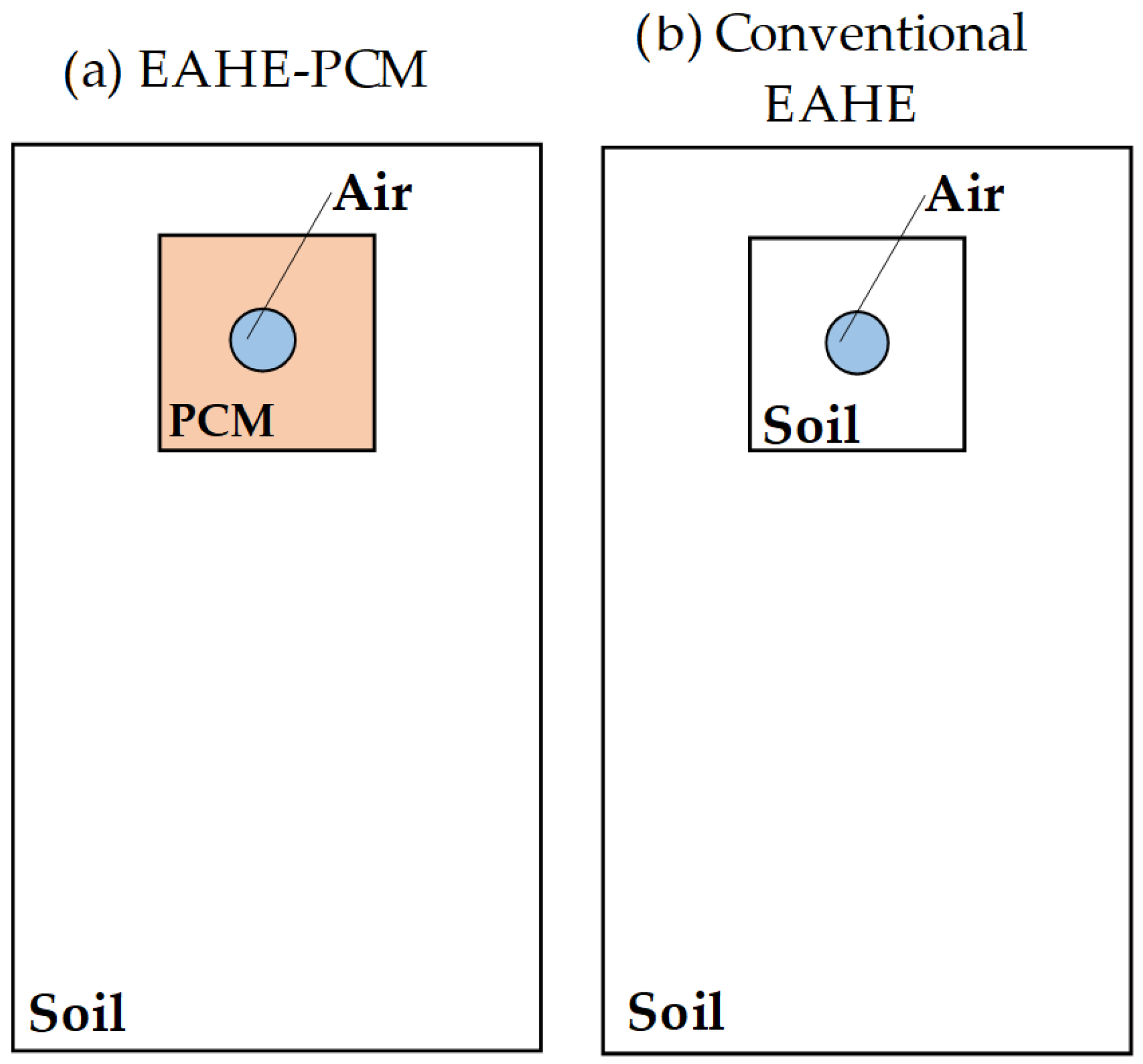
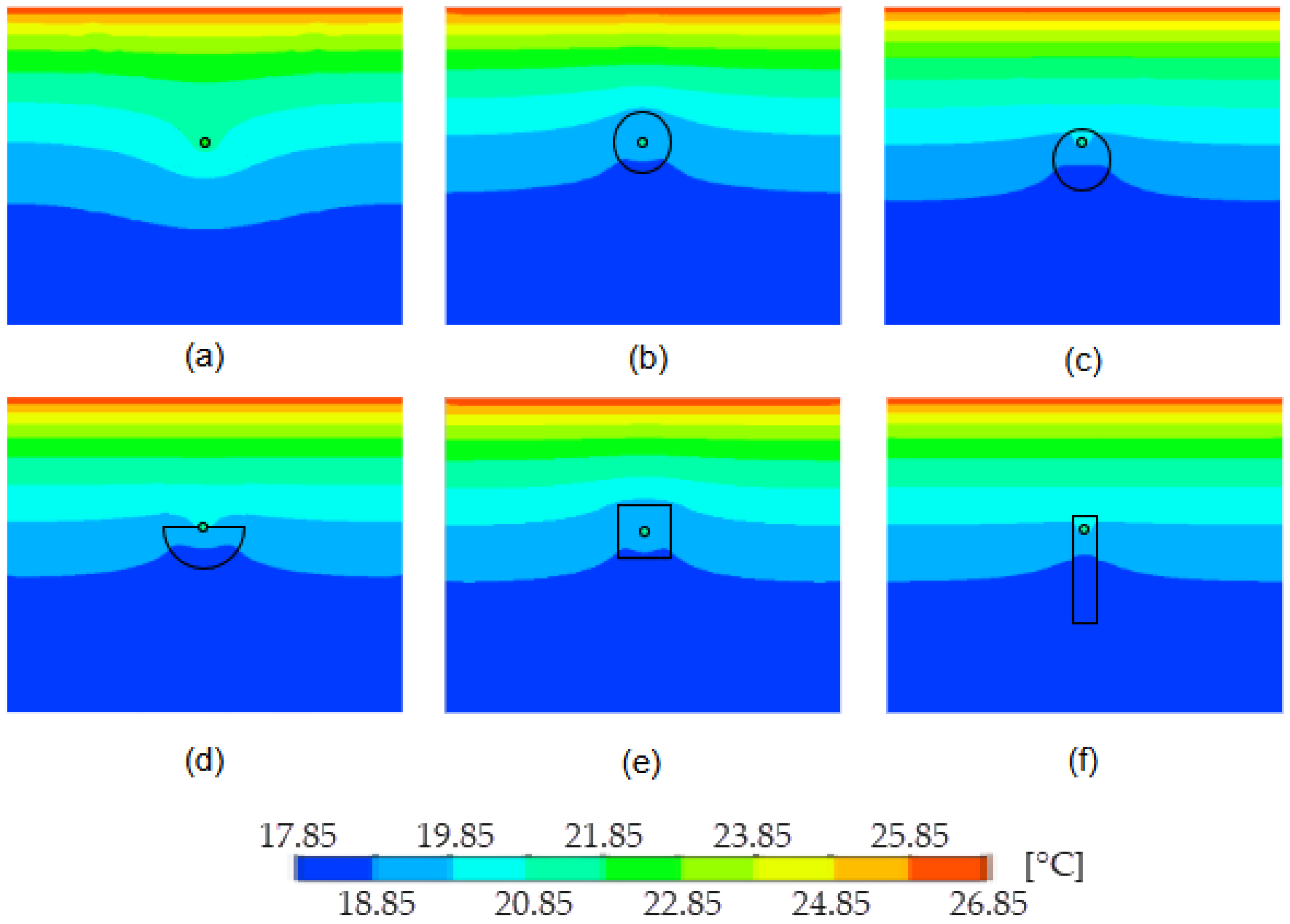
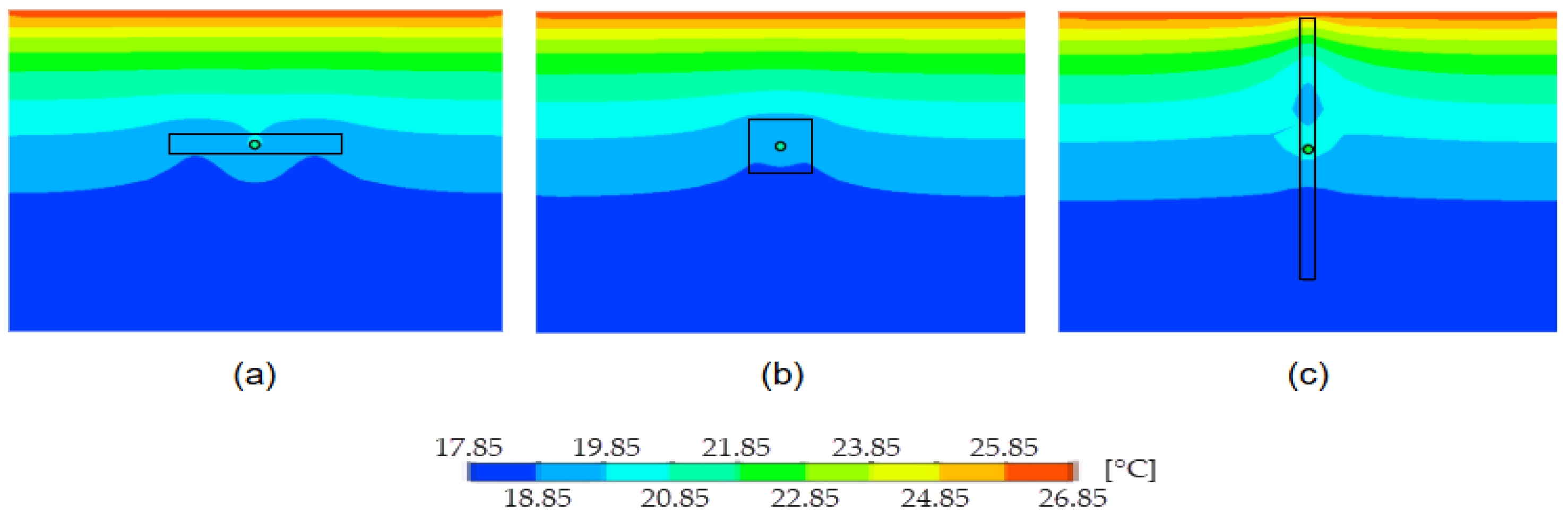
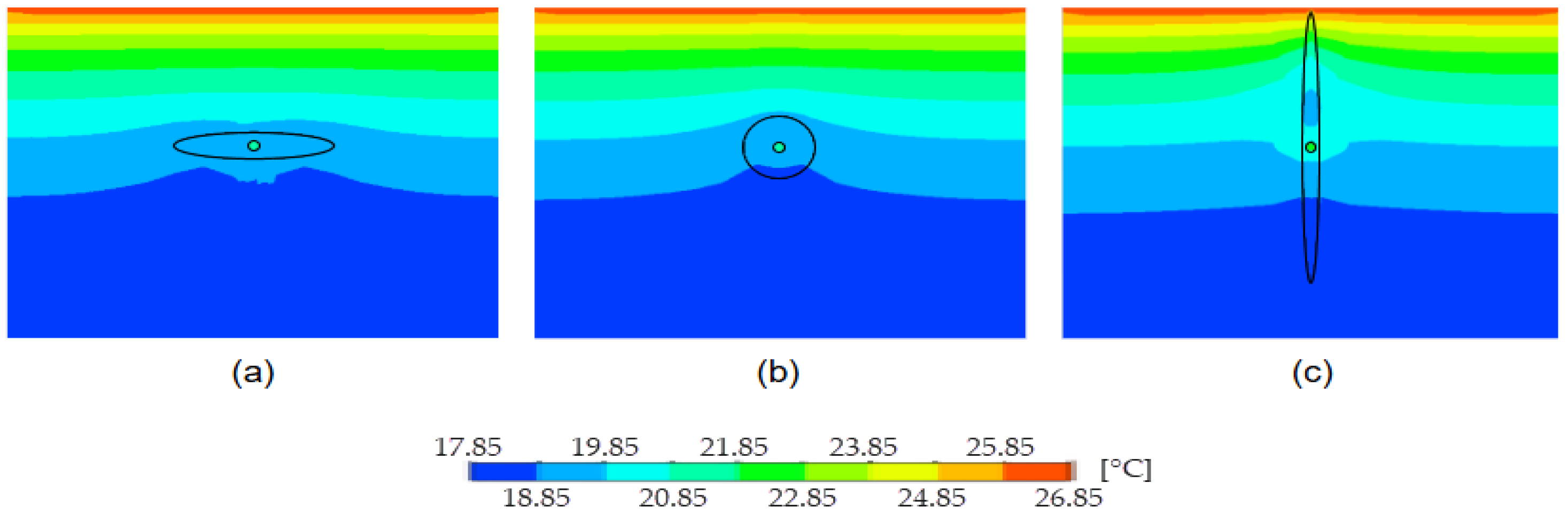
4.1. Influence of Concentric and Eccentric PCM Arrangements on Thermal Potential
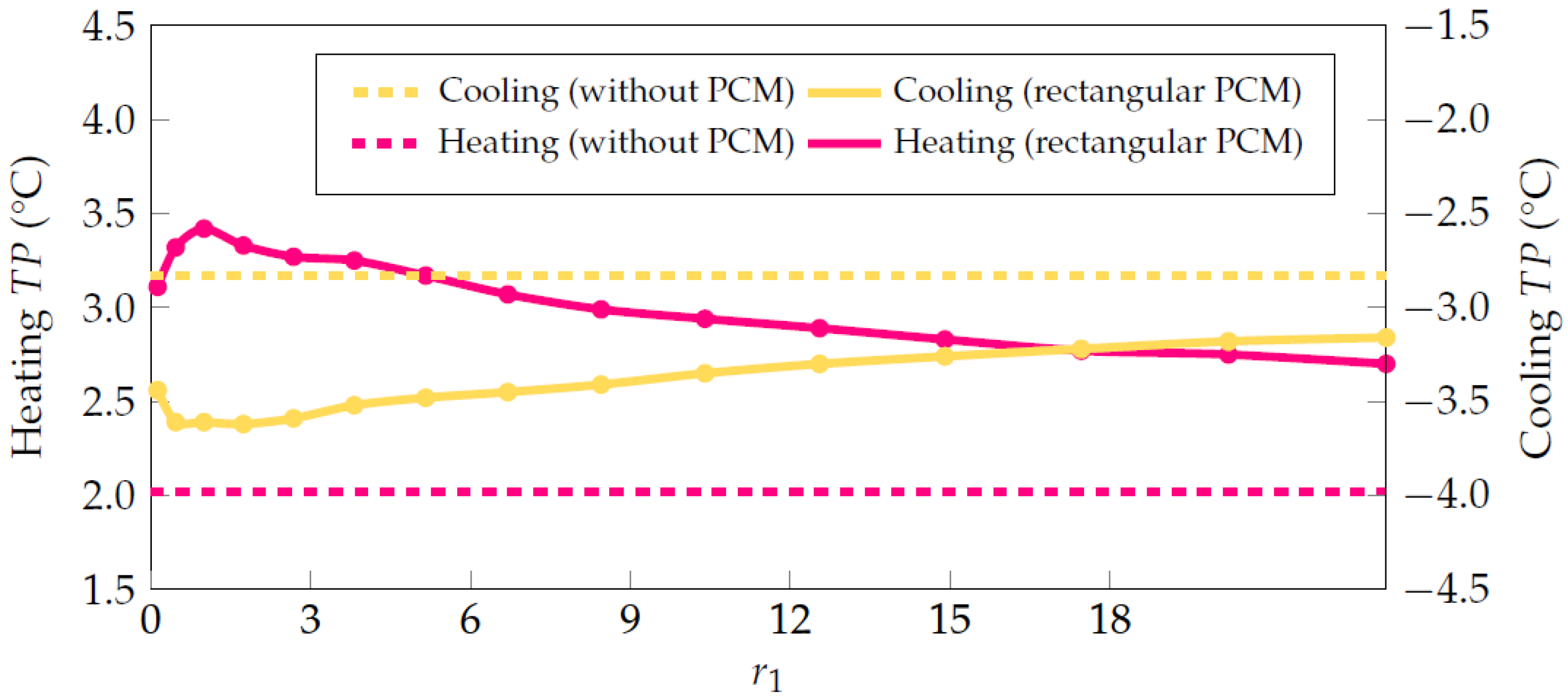
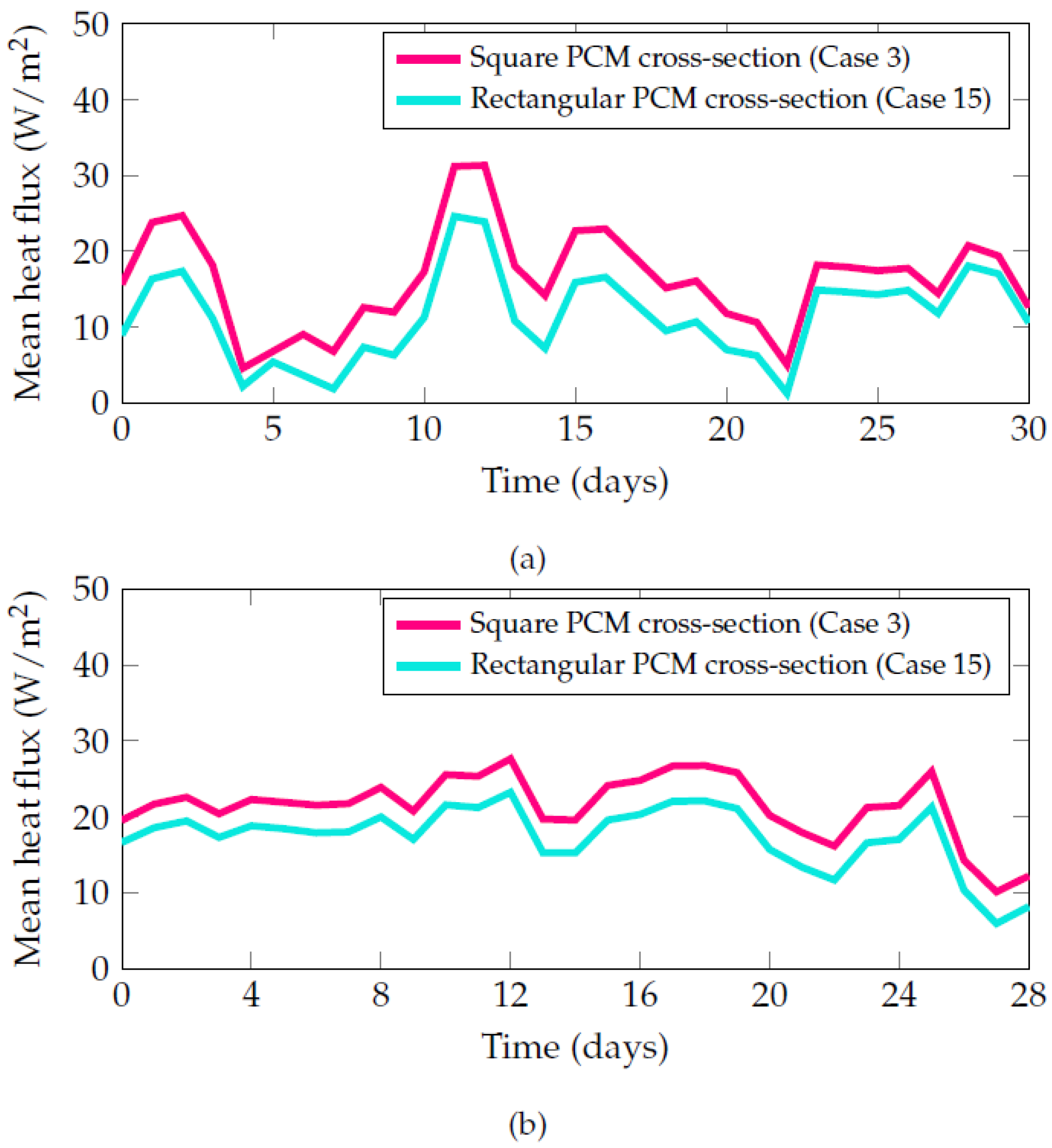
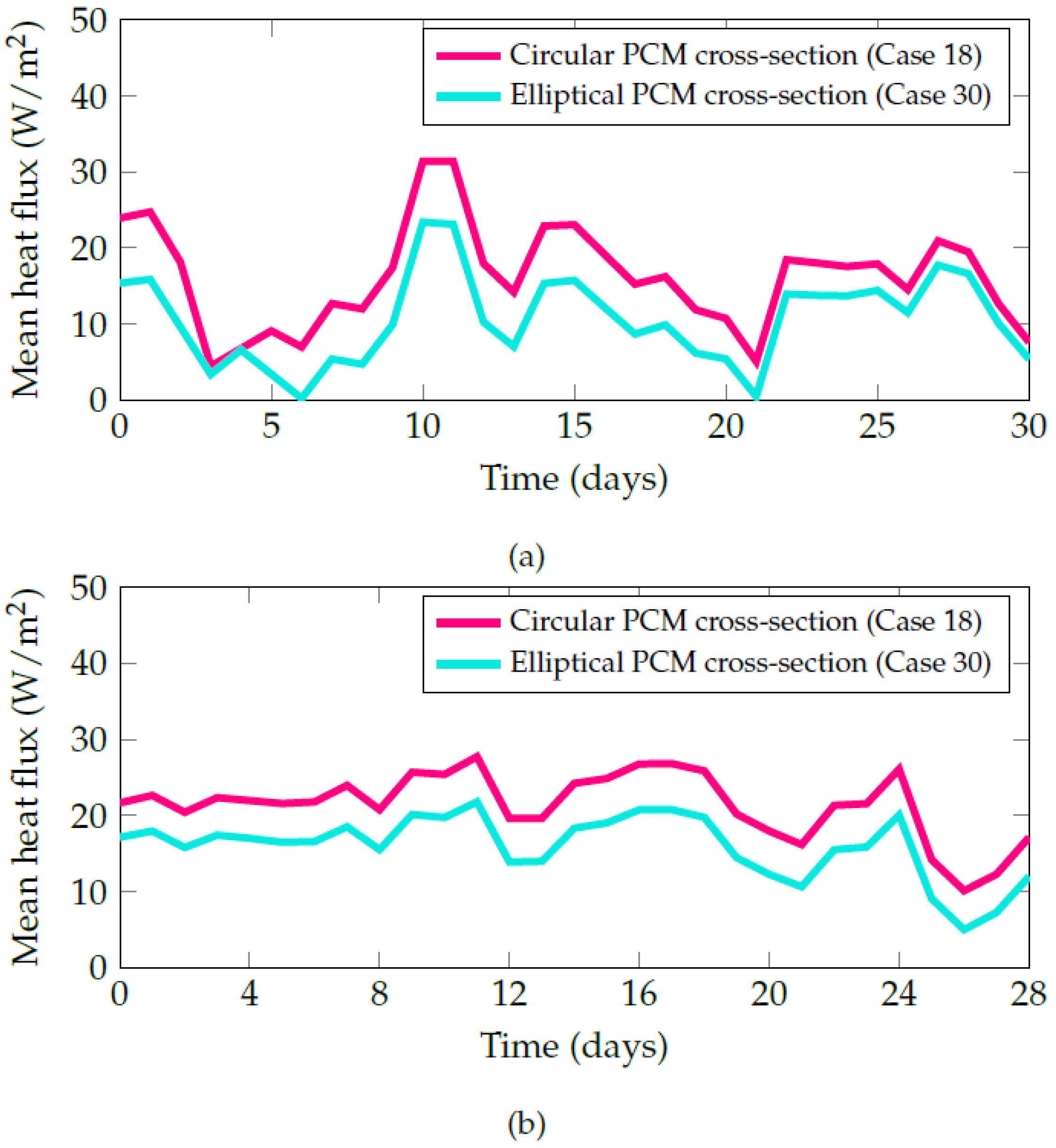
4.2. Rectangular PCM Configuration
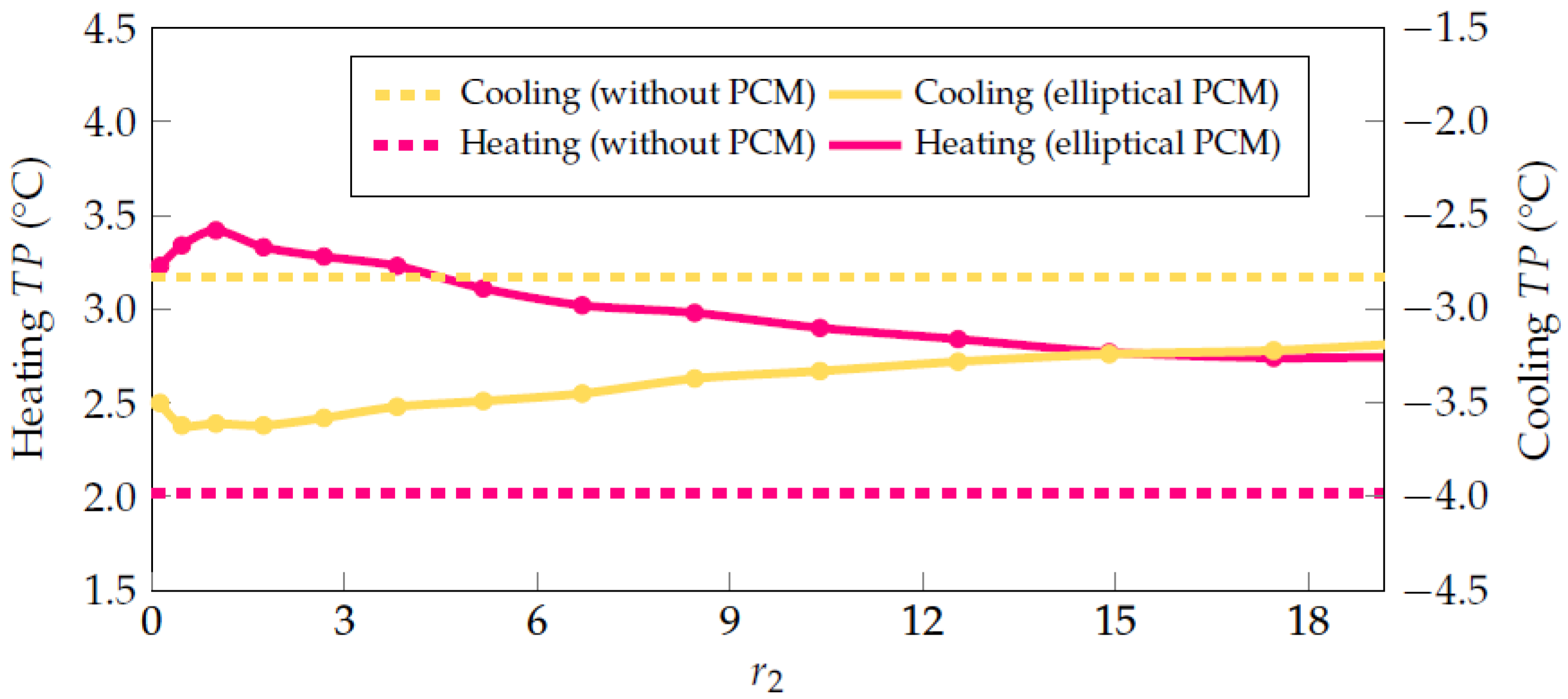
4.3. Elliptical PCM Configuration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency (IEA). Global Energy Review 2025. Available online: https://www.iea.org/reports/global-energy-review-2025 (accessed on 14 May 2025).
- Hegazi, A.A.; Abdelrehim, O.; Khater, A. Parametric optimization of earth-air heat exchangers (EAHEs) for central air conditioning. Int. J. Refrig. 2021, 129, 278–289. [Google Scholar] [CrossRef]
- Guo, X.; Wei, H.; He, X.; Du, J.; Yang, D. Experimental evaluation of an earth–to–air heat exchanger and air source heat pump hybrid indoor air conditioning system. Energy Build. 2022, 256, 111752. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Khan, M.M.K.; Amanullah, M.T.O.; Rasul, M.G.; Hassan, N.M.S. Thermal performance of building-integrated horizontal earth-air heat exchanger in a subtropical hot humid climate. Geothermics 2022, 99, 102313. [Google Scholar] [CrossRef]
- Li, J.; Jimenez-Bescos, C.; Calautit, J.K.; Yao, J. Evaluating the energy-saving potential of earth-air heat exchanger (EAHX) for Passivhaus standard buildings in different climates in China. Energy Build. 2023, 288, 113005. [Google Scholar] [CrossRef]
- Rodrigues, M.K.; Coswig, F.S.; Camargo, K.R.; Isoldi, L.A.; Brum, R.S.; Ramalho, J.V.A.; Vaz, J.; Rocha, L.A.O.; Santos, E.D. Thermal performance simulations of Earth-Air Heat Exchangers for different soils of a coastal city using in-situ data. Sustain. Energy Technol. Assess. 2018, 30, 224–229. [Google Scholar] [CrossRef]
- Brum, R.S.; Ramalho, J.V.A.; Rodrigues, M.K.; Rocha, L.A.O.; Isoldi, L.A.; Dos Santos, E.D. Design evaluation of earth-air heat exchangers with multiple ducts. Renew. Energy 2019, 135, 1371–1385. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Misra, R.; Das Agrawal, G.; Bhardwaj, M.; Jamuwa, D.K. The state of art on the applications, technology integration, and latest research trends of earth-air-heat exchanger system. Geothermics 2019, 82, 34–50. [Google Scholar] [CrossRef]
- Rodrigues, M.K.; Brum, R.S.; Vaz, J.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. Numerical investigation about the improvement of the thermal potential of an earth-air heat exchanger (EAHE) employing the constructal design method. Renew. Energy 2015, 80, 538–551. [Google Scholar] [CrossRef]
- Brum, R.S.; Vaz, J.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. A new computational modeling to predict the behavior of earth-air heat exchangers. Energy Build. 2013, 64, 395–402. [Google Scholar] [CrossRef]
- Jensen-Page, L.; Narsilio, G.A.; Bidarmaghz, A.; Johnston, I.W. Investigation of the effect of seasonal variation in ground temperature on thermal response tests. Renew. Energy 2018, 125, 609–619. [Google Scholar] [CrossRef]
- Naranjo-Mendoza, C.; Wright, A.J.; Oyinlola, M.A.; Greenough, R.M. A comparison of analytical and numerical model predictions of shallow soil temperature variation with experimental measurements. Geothermics 2018, 76, 38–49. [Google Scholar] [CrossRef]
- Badache, M.; Eslami-Nejad, P.; Ouzzane, M.; Aidoun, Z.; Lamarche, L. A new modeling approach for improved ground temperature profile determination. Renew. Energy 2016, 85, 436–444. [Google Scholar] [CrossRef]
- Bansal, V.; Misra, R.; Agarwal, G.D.; Mathur, J. Transient Effect of Soil Thermal Conductivity and Duration of Operation on Performance of Earth Air Tunnel Heat Exchanger. Appl. Energy 2013, 103, 1–11. [Google Scholar] [CrossRef]
- Mathur, A.; Srivastava, A.; Mathur, J.; Mathur, S.; Agrawal, G.D. Transient Effect of Soil Thermal Diffusivity on Performance of EATHE System. Energy Rep. 2015, 1, 17–21. [Google Scholar] [CrossRef]
- Cuny, M.; Lin, J.; Siroux, M.; Magnenet, V.; Fond, C. Influence of coating soil types on the energy of earth-air heat exchanger. Energy Build. 2018, 158, 1000–1012. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- Cao, D.; Shi, B.; Loheide, S.P.; Gong, X.; Zhu, H.H.; Wei, G.; Yang, L. Investigation of the influence of soil moisture on thermal response tests using active distributed temperature sensing (A–DTS) technology. Energy Build. 2018, 173, 239–251. [Google Scholar] [CrossRef]
- Cuny, M.; Lin, J.; Siroux, M.; Fond, C. Influence of Rainfall Events on the of an Earth–Air Heat Exchanger Embedded in a Multilayered Soil. Renew. Energy 2020, 147, 2664–2675. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Misra, R.; Agrawal, G.D. Improving the thermal performance of ground air heat exchanger system using sand-bentonite (in dry and wet condition) as backfilling material. Renew. Energy 2020, 146, 2008–2023. [Google Scholar] [CrossRef]
- Mohammadi, S.A.; Jahangir, M.H. Numerical investigation of the saturating soil layers’ effect on air temperature drops along the pipe of Earth-Air Heat Exchanger systems in heating applications. Geothermics 2024, 123, 103109. [Google Scholar] [CrossRef]
- Mathur, A.; Srivastava, A.; Agrawal, G.D.; Mathur, S.; Mathur, J. CFD analysis of EATHE system under transient conditions for intermittent operation. Energy Build. 2015, 87, 37–44. [Google Scholar] [CrossRef]
- Mathur, A.; Surana, A.K.; Mathur, S. Numerical investigation of the performance and soil temperature recovery of an EATHE system under intermittent operations. Renew. Energy 2016, 95, 510–521. [Google Scholar] [CrossRef]
- Zhou, T.; Xiao, Y.; Huang, H.; Lin, J. Numerical study on the cooling performance of a novel passive system: Cylindrical phase change material-assisted earth-air heat exchanger. J. Clean. Prod. 2020, 245, 118907. [Google Scholar] [CrossRef]
- Maytorena, V.M.; Hinojosa, J.F.; Moreno, S.; Buentello-Montoya, D.A. Thermal performance analysis of a passive hybrid earth-to-air heat exchanger for cooling rooms at Mexican desert climate. Case Stud. Therm. Eng. 2023, 41, 102590. [Google Scholar] [CrossRef]
- Pause, B. Phase change materials and their application in coatings and laminates for textiles. In Smart Textile Coatings and Laminates, 2nd ed.; The Textile Institute Book Series: Greer, SC, USA, 2019; pp. 175–187. [Google Scholar]
- Li, W.; Rahim, M.; Wu, D.; El Ganaoui, M.; Bennacer, R. Dynamic integration of phase change material in walls for enhancing building thermal performance—A novel self-adaptive method for moving PCM layer. Energy Convers. Manag. 2024, 308, 118401. [Google Scholar] [CrossRef]
- Anter, A.G.; Sultan, A.A.; Hegazi, A.A.; El Bouz, M.A. Thermal performance and energy saving using phase change materials (PCM) integrated in building walls. J. Energy Storage 2023, 67, 107568. [Google Scholar] [CrossRef]
- NematpourKeshteli, A.; Iasiello, M.; Langella, G.; Bianco, N. Increasing melting and solidification performances of a phase change material-based flat plate solar collector equipped with metal foams, nanoparticles, and wavy wall-Y-shaped surface. Energy Convers. Manag. 2023, 291, 117268. [Google Scholar] [CrossRef]
- Algarni, S. Evaluation and optimization of the performance and efficiency of a hybrid flat plate solar collector integrated with phase change material and heat sink. Case Stud. Therm. Eng. 2023, 45, 102892. [Google Scholar] [CrossRef]
- Faraji, H.; Çagatay, Y.; Arshad, A.; Arıcı, M.; Choukairy, K.; El Alami, M. Passive thermal management strategy for cooling multiple portable electronic components: Hybrid nanoparticles enhanced phase change materials as an innovative solution. J. Energy Storage 2023, 70, 108087. [Google Scholar] [CrossRef]
- Motevalizadeh, M.; Rooberahan, A.; Namaghi, M.S.; Mohammadi, M.; Passandideh-Fard, M.; Sardarabadi, M. Cooling enhancement of portable computers processor by a heat pipe assisted with phase change materials. J. Energy Storage 2022, 56, 106074. [Google Scholar] [CrossRef]
- Itani, M.; Bachnak, R.; Ghaddar, N.; Ghali, K. Evaluating performance of hybrid PCM-fan and hybrid PCM-desiccant vests in moderate and hot climates. J. Build. Eng. 2019, 22, 383–396. [Google Scholar] [CrossRef]
- Mneimneh, F.; Moussalem, C.; Ghaddar, N.; Ghali, K.; Omeis, I. Experimental study on the effectiveness of the PCM cooling vest in persons with paraplegia of varying levels. J. Therm. Biol. 2020, 91, 102634. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Xiao, Y.; Liu, Y.; Lin, J.; Huang, H. Research on cooling performance of phase change material-filled earth-air heat exchanger. Energy Convers. Manag. 2018, 177, 210–223. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, Y.; Ma, Y.; Peng, Y.; Wang, Y. Parametric study on the thermal performance of phase change material-assisted earth-to-air heat exchanger. Energy Build. 2021, 238, 110811. [Google Scholar] [CrossRef]
- Maytorena, M.; Moreno, S.; Hinojosa, J.F. Effect of operation modes on the thermal performance of EAHE systems with and without PCM in summer weather conditions. Energy Build. 2021, 250, 111278. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, Z.; Yang, T.; El Mankibi, M.; Roccamena, L.; Sun, Y.; Sun, P.; Li, S.; Zhang, G. Experimental and numerical study of a vertical earth-to-air heat exchanger system integrated with annular phase change material. Energy Convers. Manag. 2019, 186, 433–449. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, P.; Li, S.; Yu, Z.; El Mankibi, M.; Roccamena, L.; Yang, T.; Zhang, G. Enhancing a vertical earth-to-air heat exchanger system using tubular phase change material. J. Clean. Prod. 2019, 237, 117763. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, P.; Xie, M.; Zhou, Y.; He, Y.; Zhang, G.; Chen, D.; Li, S.; Yan, Z.; Qin, D. Multivariant optimization and sensitivity analysis of an experimental vertical earth-to-air heat exchanger system integrating phase change material with Taguchi method. Renew. Energy 2021, 173, 401–414. [Google Scholar] [CrossRef]
- Ouzzane, M.; Bady, M. Investigation of an innovative Canadian well system combined with a frozen water/PCM heat exchanger for air-cooling in hot climate. Appl. Therm. Eng. 2022, 213, 118737. [Google Scholar] [CrossRef]
- Vielma, G.A.; Rodrigues, M.K.; Rocha, L.A.O.; Dos Santos, E.D.; Brum, R.S.; Isoldi, L.A. Computational modeling of an earth–air heat exchanger integrated with phase change materials: A case study performed for the Viamão City, Rio Grande do Sul State, Brazil. Defect Diffus. Forum 2023, 427, 85–94. [Google Scholar] [CrossRef]
- Ren, Z.; Ren, Y.; Zhou, T.; Wang, T.; Gao, X.; Yang, Z.; Xiong, Q.; Chen, S.; Xiao, Y. Investigating the dynamic thermal performance of a novel PCM to earth-air heat exchanger: Developing numerical model and comparing thermal performance. J. Build. Eng. 2024, 97, 110718. [Google Scholar] [CrossRef]
- Vielma, G.A.; Rodrigues, M.K.; Rocha, L.A.O.; Dos Santos, E.D.; Brum, R.S.; Isoldi, L.A. Numerical analysis of phase change material parameters on the behavior of a ground-air heat exchanger. Defect Diffus. Forum 2024, 436, 103–115. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, H.; Xiao, Y.; Chao, L. Performance improvement of the phase change material-assisted earth-air heat exchanger in summer. Appl. Therm. Eng. 2024, 248, 123325. [Google Scholar] [CrossRef]
- Cao, H.; Zeng, C.; He, J.; Lü, X.; Yuan, Y. Experimental investigation on energy and resilience performance of spherical PCM-assisted EAHE system for underground buildings. Appl. Therm. Eng. 2025, 270, 126267. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Canada Flintridge, CA, USA, 2006. [Google Scholar]
- Fox, R.; McDonald, A.; Mitchell, J.W. Fox and McDonald’s Introduction to Fluid Mechanics, 10th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Brum, R.S.; Rocha, L.A.O.; Vaz, J.; Dos Santos, E.D.; Isoldi, L.A. Development of simplified numerical model for evaluation of the influence of soil-air heat exchanger installation depth over its thermal potential. Int. J. Adv. Renew. Energy Res. 2012, 1, 505–514. [Google Scholar]
- Rodrigues, M.K.; Vaz, J.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. A full approach to Earth-Air Heat Exchanger employing computational modeling, performance analysis and geometric evaluation. Renew. Energy 2022, 191, 535–556. [Google Scholar] [CrossRef]
- Vaz, J.; Sattler, M.A.; Dos Santos, E.D.; Isoldi, L.A. Experimental and numerical analysis of an earth-air heat exchanger. Energy Build. 2011, 43, 2476–2482. [Google Scholar] [CrossRef]
- Phase Change Energy Solutions. BioPCM Q20 Tunable Physical and Chemical Properties. Available online: https://phasechange.com/wp-content/uploads/2020/08/BioPCM-Data-Sheet-Q20.pdf (accessed on 13 March 2025).
- Campbell, K.R.; Sailor, D.J. Phase change materials as thermal storage for high performance homes. In Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, IMECE 2011 (Parts A and B), Denver, CO, USA, 11–17 November 2011; The American Society of Mechanical Engineers: New York, NY, USA, 2011. [Google Scholar]
- Höhne, G.W.H.; Cammenga, H.K.; Eysel, W.; Gmelin, E.; Hemminger, W. The temperature calibration of scanning calorimeters. Thermochim. Acta 1990, 160, 1–12. [Google Scholar] [CrossRef]
- Vielma, G.A.; Colonico, Z.; Rodrigues, M.K.; Rocha, L.A.O.; Dos Santos, E.D.; Brum, R.S.; Isoldi, L.A. Influence of the Thickness of the Phase Change Material on the Thermal Performance of a Ground-Air Heat Exchanger. In Proceedings of the XII Regional Meeting on Applied and Computational Mathematics of Rio Grande do Sul (XII ERMAC-RS), Porto Alegre, RS, Brazil, 2–4 July 2025. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
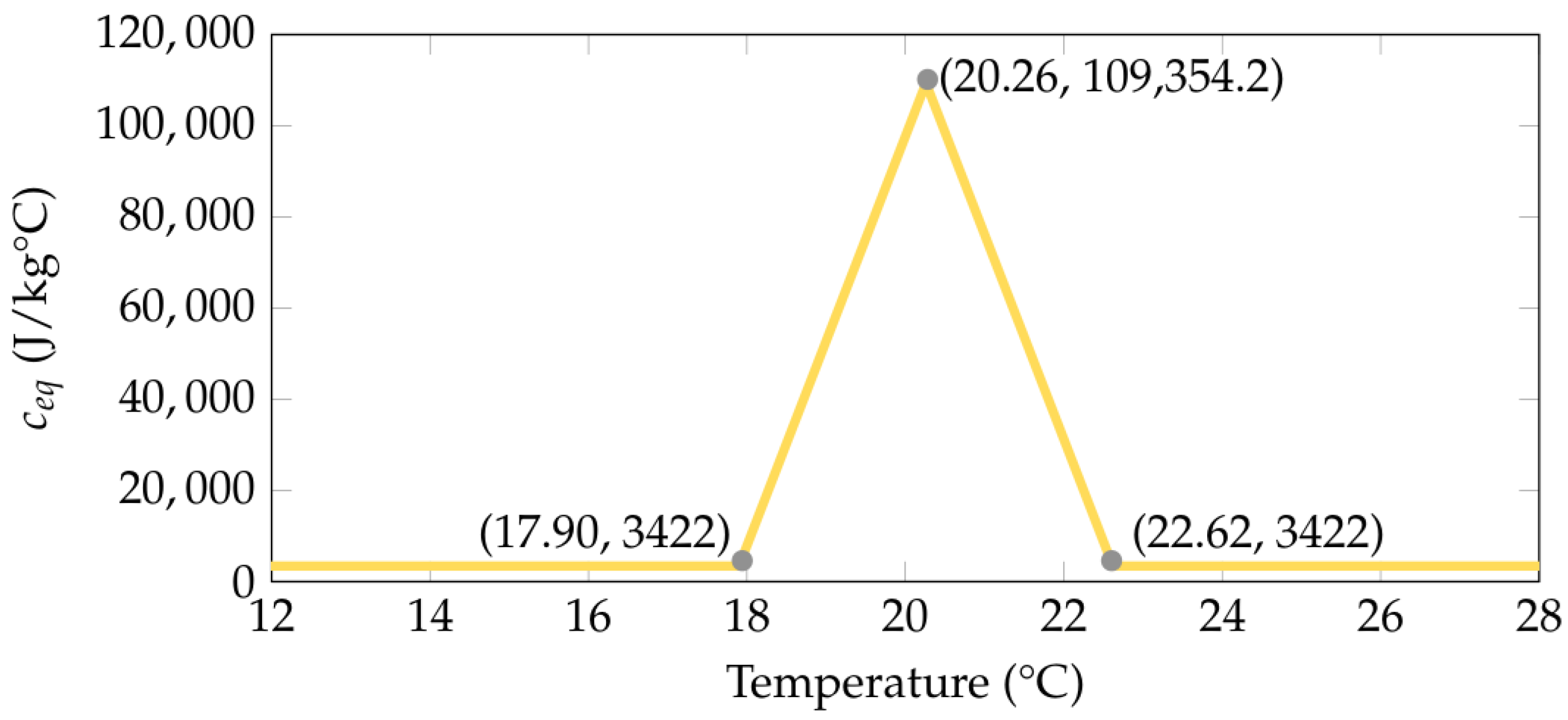
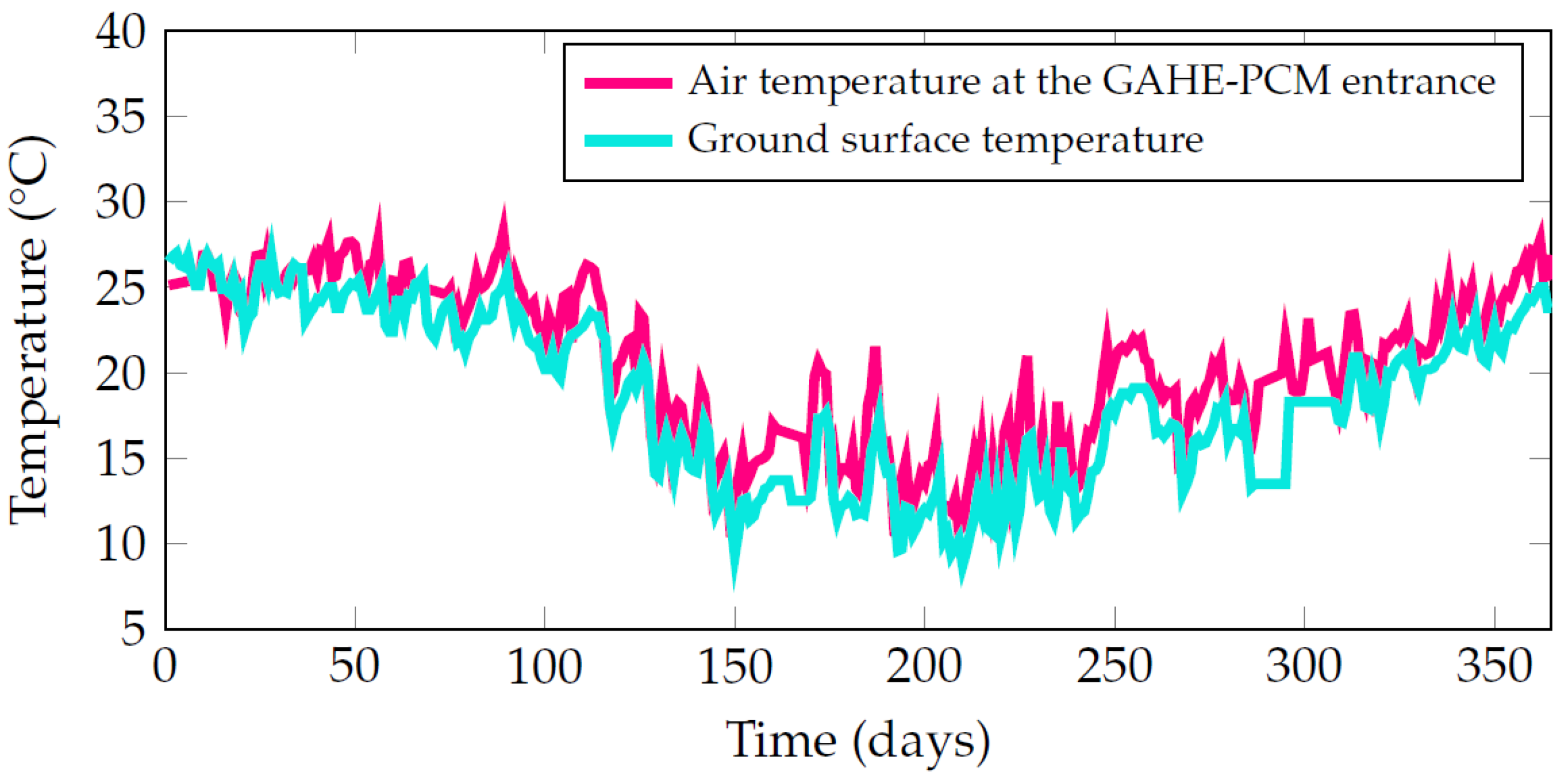
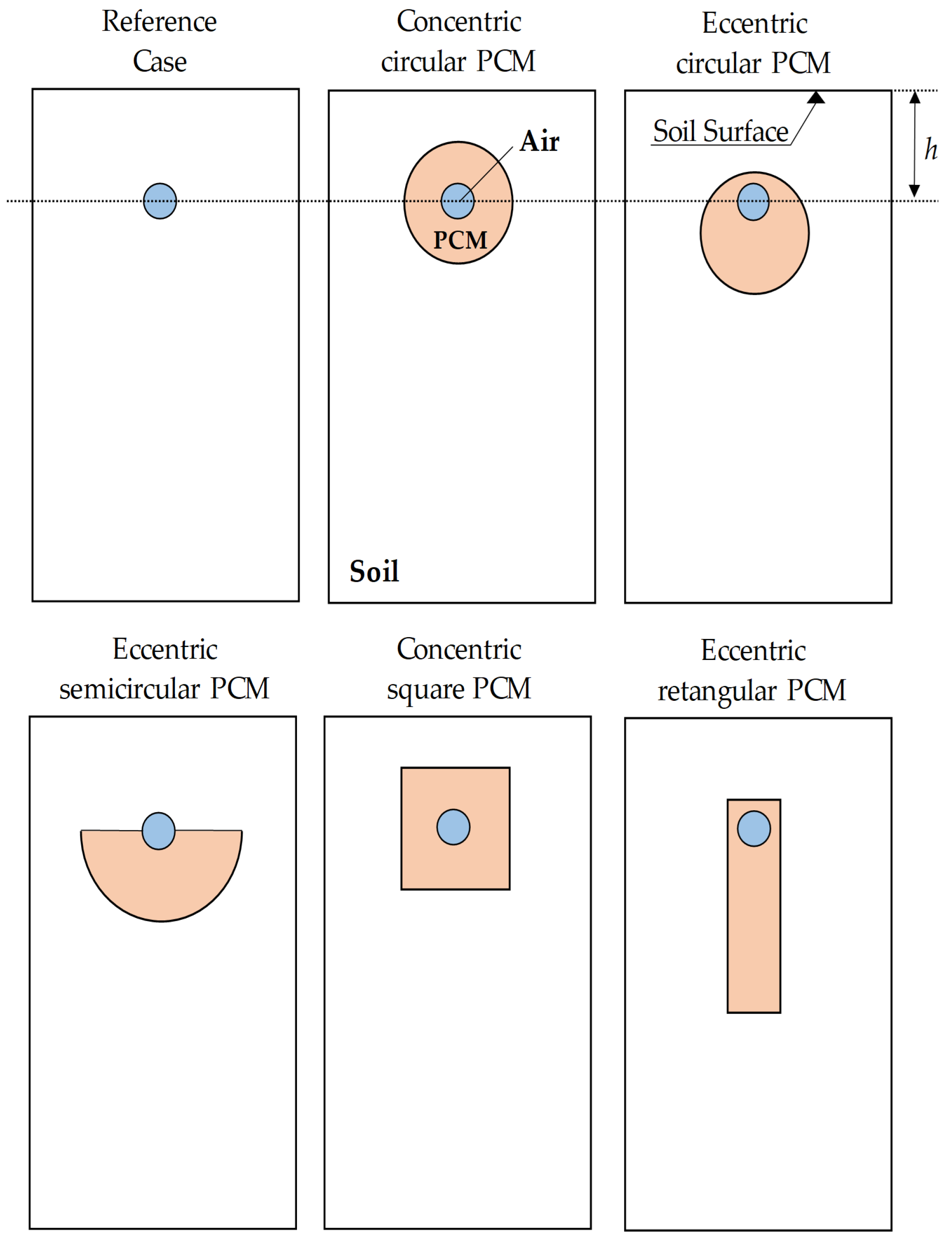
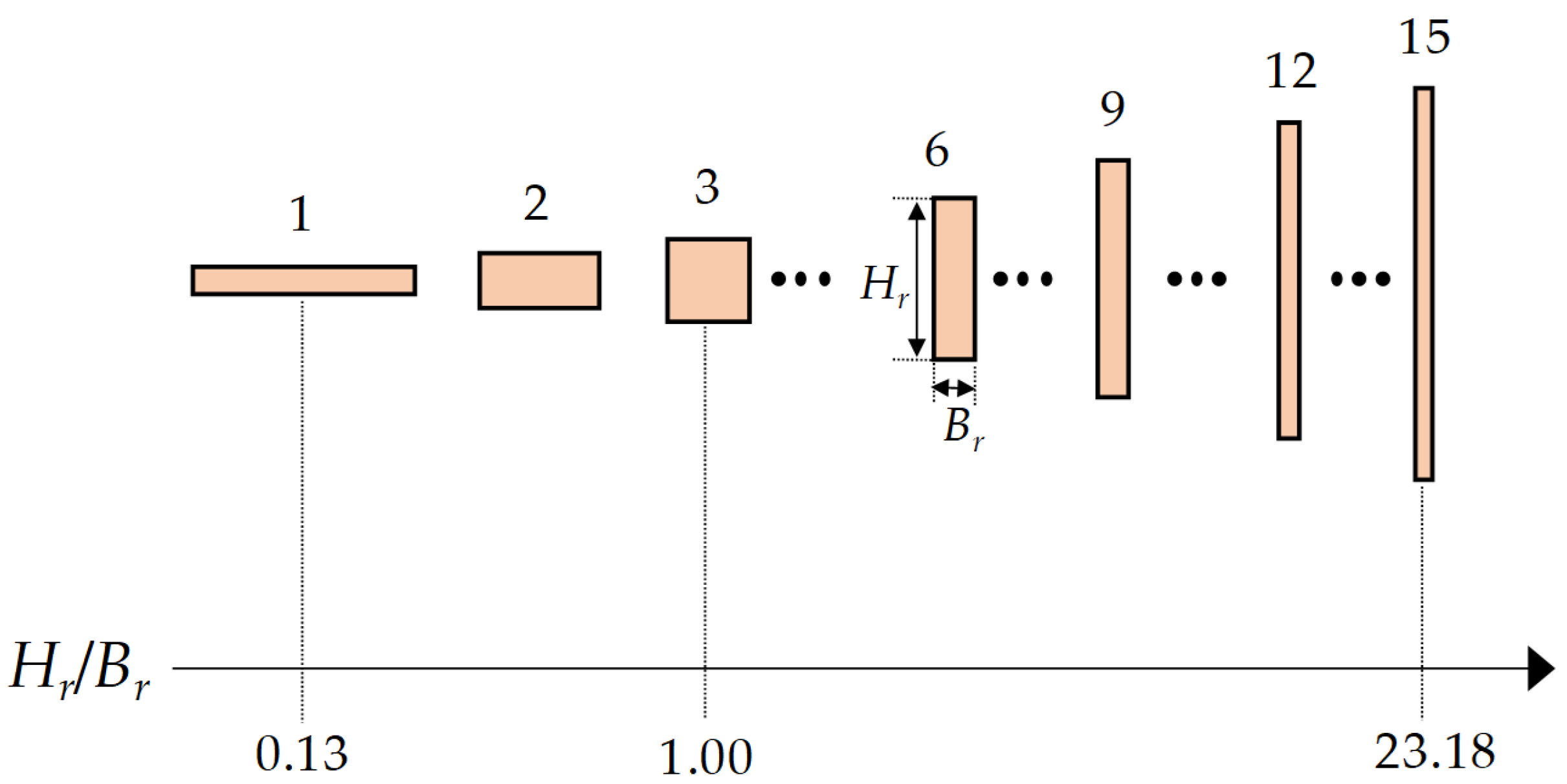
| Materials | (kg/m3) | k (W/m·K) | (J/kg·K) | (kg/(m·s)) |
|---|---|---|---|---|
| Soil | 1800 | 2.1 | 1780 | — |
| Air | 1.160 | 0.0242 | 1010 | 1.798 × |
| BioPCM Q20 | 1400 | 2.5 | 3422 | — |
| Case | (m) | (m) | |
|---|---|---|---|
| 1 | 1.73 | 0.23 | 0.13 |
| 2 | 0.92 | 0.43 | 0.47 |
| 3 | 0.63 | 0.63 | 1.00 |
| 4 | 0.48 | 0.83 | 1.74 |
| 5 | 0.38 | 1.03 | 2.68 |
| 6 | 0.32 | 1.23 | 3.82 |
| 7 | 0.28 | 1.43 | 5.16 |
| 8 | 0.24 | 1.63 | 6.70 |
| 9 | 0.22 | 1.83 | 8.45 |
| 10 | 0.20 | 2.03 | 10.40 |
| 11 | 0.18 | 2.23 | 12.55 |
| 12 | 0.16 | 2.43 | 14.90 |
| 13 | 0.15 | 2.63 | 17.46 |
| 14 | 0.14 | 2.83 | 20.22 |
| 15 | 0.13 | 3.03 | 23.18 |
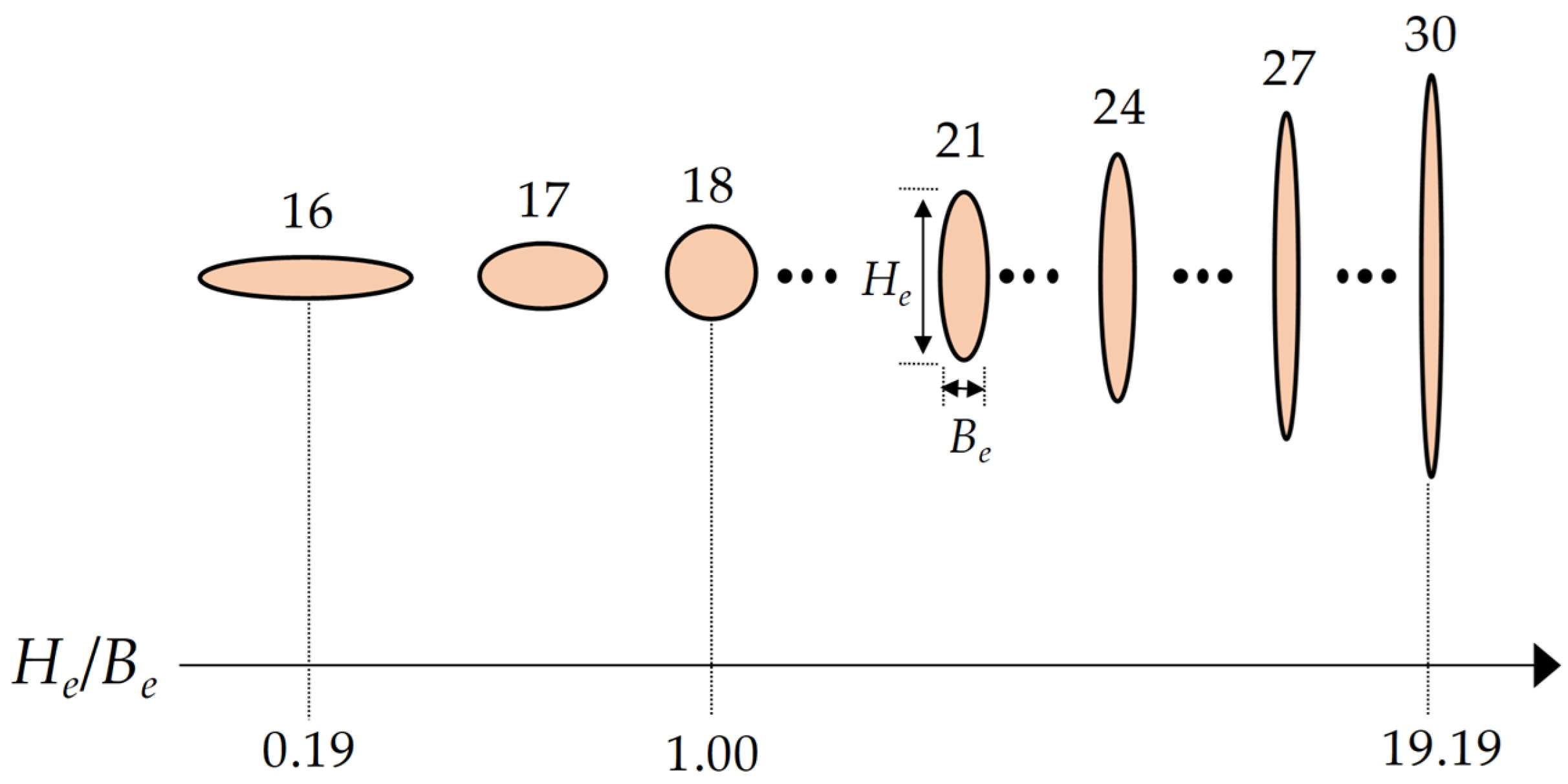
| Case | (m) | (m) | |
|---|---|---|---|
| 16 | 1.63 | 0.31 | 0.19 |
| 17 | 0.99 | 0.51 | 0.52 |
| 18 | 0.71 | 0.71 | 1.00 |
| 19 | 0.55 | 0.91 | 1.64 |
| 20 | 0.45 | 1.11 | 2.44 |
| 21 | 0.38 | 1.31 | 3.40 |
| 22 | 0.33 | 1.51 | 4.52 |
| 23 | 0.29 | 1.71 | 5.80 |
| 24 | 0.26 | 1.91 | 7.24 |
| 25 | 0.24 | 2.11 | 8.83 |
| 26 | 0.22 | 2.31 | 10.59 |
| 27 | 0.20 | 2.51 | 12.50 |
| 28 | 0.19 | 2.71 | 14.57 |
| 29 | 0.17 | 2.91 | 16.80 |
| 30 | 0.16 | 3.11 | 19.19 |
| Mesh | Number of Nodes | Number of Volumes | Average Temperature at Duct Outlet (°C) | Absolute Relative Difference |
|---|---|---|---|---|
| 130,866 | 125,000 | 19.7375 | 0.000435 | |
| 459,853 | 444,800 | 19.7461 | 0.000099 | |
| 746,586 | 726,000 | 19.7442 |
| Mesh | Number of Nodes | Number of Volumes | Pressure at Duct Inlet (Pa) | Absolute Relative Difference |
|---|---|---|---|---|
| 130,866 | 125,000 | 36.35574 | 0.000808 | |
| 459,853 | 444,800 | 36.32635 | 0.000020 | |
| 746,586 | 726,000 | 36.32563 |
| Time Step (s) | Number of Volumes | Average Temperature at Duct Outlet (°C) | Absolute Relative Difference |
|---|---|---|---|
| 1800 | 444,800 | 19.7464 | 0.000015 |
| 3600 | 444,800 | 19.7467 | 0.000005 |
| 7200 | 444,800 | 19.7468 |
| Parameter | Vaz et al. [54] | Rodrigues et al. [53] | Present Study |
|---|---|---|---|
| Type of study | Experimental | Numerical | Numerical |
| Domain dimensions | Not applicable | 10 × 15 × 25.77 m | Same as Rodrigues et al. [53] |
| Number of ducts | 3 | 3 | 1 |
| Burial depth | 1.60 m (A, B) 0.50 m (C) | Same as Vaz et al. [54] | 1.60 m |
| Duct diameter | 110 mm (A, B) 100 mm (C) | Same as Vaz et al. [54] | 110 mm |
| Soil properties | Derived from experimental calibration | Same as Vaz et al. [54] | Same as Rodrigues et al. [53] |
| Inlet air velocity | 3.30 m/s (A) 3.60 m/s (B) 2.50 m/s (C) | Same as Vaz et al. [54] | 3.30 m/s |
| Inlet air temperature | Measured experimentally (annual cycle) | Averaged daily values from Vaz et al. [54] | Same as Rodrigues et al. [53] |
| Ground surface temperature | Measured experimentally (annual cycle) | Averaged daily values from Vaz et al. [54] | Same as Rodrigues et al. [53] |
| Simulation period | 1 year of monitoring | 2 years (1 year stabilization) | Same as Rodrigues et al. [53] |
| Materials | (kg/m3) | k (W/m·K) | (J/kg·K) | (kg/(m·s)) |
|---|---|---|---|---|
| Air | 1.165 | 0.0267 | 1005 | 1.9 × |
| Moist sand | 1452 | 0.76 | 1150 | — |
| Chongqing soil | 1800 | 1.1 | 860 | — |
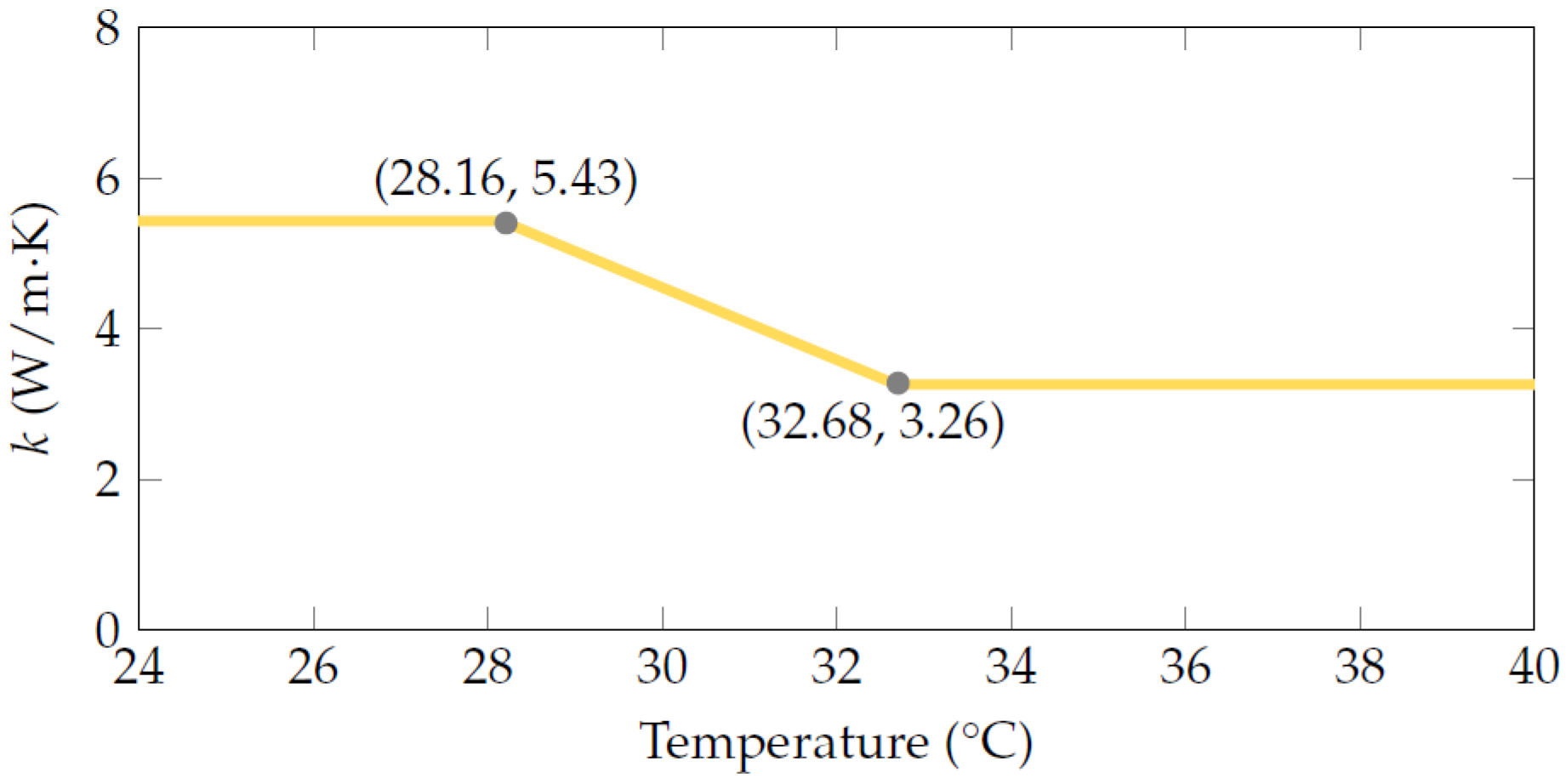
| CA–PA/EG | 904.5 | 5.43/3.26 | 1750 | — |
| Case | Annual Average Heating TP (°C) | Increase (%) | Annual Average Cooling TP (°C) | Increase (%) |
|---|---|---|---|---|
| Reference | 2.02 | — | −2.83 | — |
| Concentric configurations | ||||
| Circular concentric | 3.42 | 69.31 | −3.61 | 27.56 |
| Square concentric | 3.42 | 69.31 | −3.61 | 27.56 |
| Eccentric configurations | ||||
| Circular eccentric | 3.36 | 66.34 | −3.57 | 26.15 |
| Semicircular eccentric | 3.27 | 61.88 | −3.51 | 24.03 |
| Rectangular eccentric | 3.10 | 53.47 | −3.48 | 22.97 |
| Case | Annual Average Heating TP (°C) | Improvement (%) | Annual Average Cooling TP (°C) | Improvement (%) |
|---|---|---|---|---|
| Reference | 2.02 | — | −2.83 | — |
| 1 | 3.11 | 53.96 | −3.44 | 21.55 |
| 2 | 3.32 | 64.36 | −3.61 | 27.56 |
| 3 | 3.42 | 69.31 | −3.61 | 27.56 |
| 4 | 3.33 | 64.85 | −3.62 | 27.92 |
| 5 | 3.27 | 61.88 | −3.59 | 26.86 |
| 6 | 3.25 | 60.89 | −3.52 | 24.38 |
| 7 | 3.17 | 56.93 | −3.48 | 22.97 |
| 8 | 3.07 | 51.98 | −3.45 | 21.91 |
| 9 | 2.99 | 48.02 | −3.41 | 20.49 |
| 10 | 2.94 | 45.54 | −3.35 | 18.37 |
| 11 | 2.89 | 43.07 | −3.30 | 16.61 |
| 12 | 2.83 | 40.10 | −3.26 | 15.19 |
| 13 | 2.77 | 37.13 | −3.22 | 13.78 |
| 14 | 2.75 | 36.14 | −3.18 | 12.37 |
| 15 | 2.70 | 33.66 | −3.16 | 11.66 |
| Case | Annual Average Heating TP (°C) | Increase (%) | Annual Average Cooling TP (°C) | Increase (%) |
|---|---|---|---|---|
| Reference | 2.02 | — | −2.83 | — |
| 1 | 3.23 | 59.90 | −3.50 | 23.67 |
| 2 | 3.34 | 65.35 | −3.62 | 27.92 |
| 3 | 3.42 | 69.31 | −3.61 | 27.56 |
| 4 | 3.33 | 64.85 | −3.62 | 27.92 |
| 5 | 3.28 | 62.38 | −3.58 | 26.50 |
| 6 | 3.23 | 59.90 | −3.52 | 24.38 |
| 7 | 3.11 | 53.96 | −3.49 | 23.32 |
| 8 | 3.02 | 49.50 | −3.45 | 21.91 |
| 9 | 2.98 | 47.52 | −3.37 | 19.08 |
| 10 | 2.90 | 43.56 | −3.33 | 17.67 |
| 11 | 2.84 | 40.59 | −3.28 | 15.90 |
| 12 | 2.77 | 37.13 | −3.24 | 14.49 |
| 13 | 2.74 | 35.64 | −3.22 | 13.78 |
| 14 | 2.74 | 35.64 | −3.17 | 12.01 |
| 15 | 2.66 | 31.68 | −3.12 | 10.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vielma Vivas, G.A.; Colonico Reyes, Z.; Razera, A.L.; Rocha, L.A.O.; dos Santos, E.D.; Brum, R.d.S.; Isoldi, L.A. Numerical and Parametric Investigation of the Influence of Rectangular and Elliptical Phase Change Material Geometries on the Thermal Performance of a Ground-Air Heat Exchanger. Fluids 2025, 10, 311. https://doi.org/10.3390/fluids10120311
Vielma Vivas GA, Colonico Reyes Z, Razera AL, Rocha LAO, dos Santos ED, Brum RdS, Isoldi LA. Numerical and Parametric Investigation of the Influence of Rectangular and Elliptical Phase Change Material Geometries on the Thermal Performance of a Ground-Air Heat Exchanger. Fluids. 2025; 10(12):311. https://doi.org/10.3390/fluids10120311
Chicago/Turabian StyleVielma Vivas, Giovanni Antonio, Zurisaday Colonico Reyes, Andre Luis Razera, Luiz Alberto Oliveira Rocha, Elizaldo Domingues dos Santos, Ruth da Silva Brum, and Liércio André Isoldi. 2025. "Numerical and Parametric Investigation of the Influence of Rectangular and Elliptical Phase Change Material Geometries on the Thermal Performance of a Ground-Air Heat Exchanger" Fluids 10, no. 12: 311. https://doi.org/10.3390/fluids10120311
APA StyleVielma Vivas, G. A., Colonico Reyes, Z., Razera, A. L., Rocha, L. A. O., dos Santos, E. D., Brum, R. d. S., & Isoldi, L. A. (2025). Numerical and Parametric Investigation of the Influence of Rectangular and Elliptical Phase Change Material Geometries on the Thermal Performance of a Ground-Air Heat Exchanger. Fluids, 10(12), 311. https://doi.org/10.3390/fluids10120311









