Vortex Dynamics Effects on the Development of a Confined Turbulent Wake

Abstract

In the present work, the turbulent wake of a circular cylinder in a confined flow environment at a blockage ratio of 14% is experimentally investigated in a wind tunnel consisting of a parallel test section followed by a constant-area distorting duct, under subcritical Re inlet conditions. The initial stage of wake development, extending from the bluff body to the end of the parallel section, is analyzed, with the use of hot-wire anemometry and laser-sheet visualization. The near field reveals partial similarity to unbounded wakes, with the principal difference being a modification of the Kármán vortex street topology, attributed to altered vortex dynamics under confinement. Further downstream, the mean and fluctuating velocity distributions of the confined wake gradually evolve toward channel-flow characteristics. To elucidate this transition, wake measurements are systematically compared with channel flow data obtained in the same configuration under identical inlet conditions and with reference channel-flow datasets from the literature. Experimental results show that a vortex-transportation mechanism exists due to confinement effect, resulting in the progressive crossing and realignment of counter-rotating vortices toward the tunnel centerline. Although wake flow characteristics are preserved, suppression of classical periodic shedding is clearly depicted. Furthermore, it is shown that the confined near-wake spectral peak persists up to x₁/d~60 as in the free case and then vanishes as the spectra broadens. Coincidentally, the confined wake exhibits a narrower halfwidth than its free wake counterpart, while a centerline shift of the shed vortices is observed. Farfield wake-flow maintains strong anisotropy, while a weaker downstream growth of the streamwise integral scale is observed when compared to channel flow. Together, these findings explain how confinement reforms the nearfield topology and reorganizes momentum transport as the flow evolves to channel-like flow.

1. Introduction

Vortex streets forming in the wakes of bluff bodies, first systematically described by von Kármán, remain a cornerstone problem in fluid dynamics because they capture the essential processes of shear-layer instability, vortex roll-up, and large-scale coherent structure formation [1,2,3]. Wake flows are inherently complex, arising from the coupled dynamics of boundary-layer separation, free shear-layer development, and the periodic shedding of vortices into the near wake. This alternating shedding produces a highly organized yet unsteady flow field that imposes significant fluctuating forces on the generating body, leading to vortex-induced vibrations, acoustic emissions, and, under certain conditions, structural failure [4,5]. As a result, a vast body of research has focused on understanding the dynamics of unsteady separated wakes and their downstream evolution, as well as on devising passive and active flow control strategies to mitigate these adverse effects [6,7,8].

Despite extensive progress in the study of free wakes, establishing a clear connection between nearfield vortex shedding and the evolution of far-field turbulence remains a persistent challenge. In particular, the degree to which the downstream momentum field retains a signature of the initial shedding dynamics is still not fully resolved. Addressing this question is essential not only for advancing fundamental turbulence research but also for informing strategies of active and passive flow control [9,10,11,12,13].

A related but less systematically explored configuration is the wake developing in the presence of confining plane boundaries. Such bounded wakes are of both fundamental and practical relevance, arising in mixing and combustion processes within ducts, as well as in marine and aerodynamic applications. The presence of walls modifies the dynamics compared to unbounded wakes in two key ways: (i) by constraining the lateral spread of the wake through an irrotational condition, and (ii) by introducing additional vorticity associated with growing wall boundary layers. The resulting confined wake structure is therefore more intricate than its free counterpart, as it emerges from the combined influence of body-generated vorticity and wall-induced shear layers [4,5,14,15,16].

Only a limited number of experimental investigations have examined wake flows in the presence of a single confining boundary, with emphasis on how confinement modifies key aerodynamic and hydrodynamic parameters compared to unbounded cases [4,5,14]. These studies report systematic variations in lift and drag coefficients, stagnation point location, base pressure, Strouhal number, and surface pressure distributions, as well as the suppression or persistence of vortex shedding, depending on the body–wall distance and the thickness of the approaching boundary layer. Complementary numerical work [15] addressed the case of a circular cylinder placed between two parallel walls at a high blockage ratio (20%) under laminar Poiseuille inflow. Simulations revealed significant alterations of the near-wake topology, not only when the body was positioned close to a wall but also when it was located symmetrically at the channel centerline. Across both experimental and numerical studies, a consistent finding is that confinement effects become increasingly pronounced as the gap between the bluff body and the confining boundary decreases [16].

More recent investigations have advanced the understanding of confined wakes by focusing on how wall proximity alters vortex dynamics and near-wake organization. These studies have clarified the role of confinement in modifying pressure distributions, altering velocity coherence, and influencing the onset or suppression of vortex shedding [17,18,19,20,21,22,23]. While these contributions have provided valuable insight into the mechanisms governing confined wakes, a systematic characterization of how nearfield formation dynamics condition the far-wake structure under confinement requires further investigation.

Although the influence of confinement on bluff-body wakes has been recognized, most prior investigations have been restricted to laminar regimes, moderate blockage ratios, or single-wall configurations. Consequently, the behavior of turbulent wakes under strong confinement remains insufficiently understood. In particular, the mechanistic link between nearfield modifications of the Kármán vortex street and the redistribution of momentum in the far field has not been systematically resolved [13,18,20,23]. This unresolved coupling between initial vortex formation and downstream wake development constitutes a critical gap in our current understanding of confined turbulence. The present study addresses this gap through an experimental characterization of a turbulent wake generated by a circular cylinder at a blockage ratio of 14% in a parallel-duct configuration. Using multi-sensor hot-wire anemometry, three-dimensional momentum field data are obtained from the nearfield region to the far downstream domain. These measurements are directly contrasted with channel flow experiments conducted under identical inflow conditions and further contextualized against canonical free-wake and fully developed channel-flow data available in the literature [24,25,26]. This approach enables a systematic assessment of how confinement alters vortex dynamics across successive stages of wake evolution.

Beyond classical cylinder wakes, applied flow control studies have shown that the effect of targeted actuation on shedding and momentum transfer reshapes aerodynamic configurations. Pulse jet excitation used on supercritical airfoils at low and high frequencies leads to a delay of separation and modifies wake shedding frequency and drag [27]. Furthermore, studies on an aircraft scale showed that tangential/discrete jet blowing in a vertical tail B777-200 increases lateral force effectiveness while reducing mass flow demand relative to continuous slots [28]. A study of high-lift systems flow control showed that a modulated pulsative jet vortex generator in a single-slotted flap suppresses or reorganizes vortex rejection in the near wake [29]. Marine hydrodynamic application studies, such as toroidal propellers, reveal the existence of efficiency gains and altered vortex merging pathways when compared to conventional propellers, highlighting the coupling between actuator and geometry design [30]. A recent work by Abdolahipour [31] reviewed thoroughly flow separation control developments on aerodynamic surfaces, highlighting the dominant roles of actuation frequency and momentum coefficient in flow separation control. Comparison of passive measures to active actuation techniques (steady/pulsed blowing or suction, synthetic Zero Net Mass Flux jets, plasma, and acoustic forcing) highlighted the close linkage between actuator physics and changes in aerodynamic properties such as lift, drag, flow reattachment, and wake organization. Numerical studies [32] of powered nacelles in widebody aircraft documented the effect of propulsion jets on shifting vortex position/strength and the intensification of wake mixing without changing the overall circulation. Thus, further evidence of controlled vortex remodeling was applicable. The aforementioned works depict the importance of the present study’s focus on constraint-induced vortex transportation and reorganization, and the resulting turbulent structure.

The novelty of this work lies in its extensive analysis the phenomenon of vortex transposition, under subcritical Re conditions (1.9 × 10³ < Re < 1.5 × 10⁴), that takes place in the nearfield the vortex street to the downstream emergence of channel-like behavior, illuminating aspects of the physical and turbulent flow mechanisms that still need better understanding for modeling this kind of flows. This is achieved through hot-wire anemometry and laser-sheet visualization that enable the identification and quantitative study of the formed counter-rotating vortices that cross the symmetry plane and then realign towards the centerline of the flow under wall-induced strain (blockage 14%). Downstream flow evolution study illuminates the topological evolution of the confined Kármán street via spectral and turbulent statistical analysis that are compared with co-measured channel flow quantities under identical inlet flow conditions. The provision of both qualitative and quantitative analysis through examination of the detailed vortex topology and momentum transfer under strong confinement provides new perspectives that are significant for modeling of confined mixing, combustion, and marine hydrodynamics, where the interplay between vortex dynamics and wall-bounded constraints critically shapes flow development.

2. Materials and Methods

The experiments were conducted in an open-circuit, variable-speed wind tunnel with a freestream turbulence intensity of approximately 0.5%. The facility consists of two main parts of equal length: a parallel test section and a constant-area distorting duct, as shown schematically in Figure 1a. The parallel section is 810 mm long, with cross-sectional dimensions of 42 × 208 mm² (vertical × horizontal). The circular cylinder wake generator was positioned 60 mm downstream of the channel entrance, with its axis normal to the flow and spanning the horizontal dimension of the section. Two cylinders of 3 mm and 6 mm in diameter were tested, corresponding to blockage ratios of 7% and 14%, respectively. After an initial development length of 125 diameters (based on the 6 mm cylinder) under undisturbed conditions, the wake entered the distorting duct. The lateral dimensions of this duct varied exponentially with streamwise distance, with the exit cross-section expanding to 20 × 434 mm².

Wake measurements covered the Reynolds number (Re) range (based on the cylinder diameter d) of 1.9 × 103 ≤ Re_d ≤ 1.5 × 104, which lies within the subcritical Re_d regime. Some additional measurements were taken in the absence of the cylinder (channel flow) at Re_h = 15,630, with h = 21 mm being the channel half height. Here, three-dimensional quantitative wake and channel flow data for Re_d = 4300 and Re_h = 15,630, respectively, both obtained with the same freestream centerline velocity U_r = 11.25 m/s, are presented. Additionally, qualitative results for the confined wake at Re_d = 760, which also lies in the turbulent regime, are presented, all carried out with the larger cylinder.

Qualitative description of the flow structures, especially on a larger scale, was obtained by flow visualization. A clear perception of local flow dynamics, especially in the near field, was obtained by applying the laser sheet illumination method. A Coherent, USA, 2 W argon-ion laser, in combination with a mirror and a cylindrical lens, illuminated the vertical symmetry plane of the channel. Flow visualization was conducted using magnesium dioxide particles with a mean diameter of 10 μm, injected into the azimuthal symmetry plane of the rig from two holes drilled in the settling chamber’s upper and lower walls. Sequences of the flow motion were recorded using a video camera located successively in several streamwise positions with its line of sight perpendicular to the illuminated domain of interest.

Flow field measurements were performed with TSI hot-wire sensors in X configurations with a wire diameter of 5 μm. Overheat ratio was set to 1.8, resulting in operating sensor temperatures of 250 °C, thereby minimizing the effect of small ambient temperature variations on the acquired measurements. Cross-checks between X-wire and single-wire sensors in the channel reference case, together with systematic downstream trends and visualization observations, indicate that any bias caused by the sensor’s presence is less than the reported uncertainties and does not alter the conclusions about turbulence transfer and momentum redistribution under confinement. Continuous monitoring of the temperature inside the wind tunnel, during calibration and data acquisition, showed differences of less than 1–2 °C. No gain was used for the anemometer outputs; instead, a constant DC value was subtracted to shift signals in the range 0–1 V, thus exploiting the maximum resolution of the A/D converter. These adjustments resulted in a 50 kHz sensor frequency response. The anemometer output was low-pass filtered at a cut-off frequency f_c = 3.8 kHz to prevent aliasing and then discretized in a 12-bit A/D converter for subsequent data processing in a computer. At each measurement position, a time series of 256 k samples was acquired. Mean and turbulent flow-field data were recorded at a sampling rate of 600 Hz. Higher sampling frequencies, up to 5 kHz, were used for calculating autocorrelation functions and power spectral densities. Statistical convergence was verified by comparing datasets collected at different sampling frequencies, which yielded identical mean and RMS values within ±0.5%.

The X-wires were calibrated at the entrance of the wind tunnel in the absence of the cylinder under identical inlet conditions with the presented measurements. Furthermore, wall and core flow measurements via single boundary layer and X probes were also conducted with no cylinder presence. These additional measurements, providing also a frame of reference to check consistency with the X-wire, were performed at the exit of the first duct and at the entrance and exit of the distorting section [33].

The coordinate system used is presented in Figure 1b with its origin defined at the cylinder axis and the bottom wall. The x₁ axis is along the main flow direction, the x₂ axis is along the vertical direction (often called transverse), and the x₃ (spanwise) axis is perpendicular to the former two. Due to the symmetry of the profiles with respect to the tunnel centerline (located at x₂/h = 1), all measurements are presented in the lower half of the tunnel.

All calibration techniques reported in the literature—such as the Collis and Williams correlation, King’s law, lookup tables, and polynomial regression models—were applied concurrently to verify repeatability in correlating measured Voltage (Ε) and corresponding calibration velocity (U); the agreement between resulting datasets was consistently excellent. In the present investigation, calibration was performed using a fourth-degree polynomial fit, which accurately captured the nonlinear behavior of the hot-wire response.

$$U=A_0+A_{1}E+A_2{E}^2+A_3{E}^3+A_4{E}^4$$

(1)

The polynomial coefficients A₀–A₄ were calculated via a least-squares regression method. Calibration residuals contributed a nonlinearity uncertainty of approximately 1.5% (Type B). Additional sources included temperature drift and overheat-ratio stability (≈0.5%) and probe yaw/pitch misalignment (±2°, ≈0.3%). The digitization error of the 12-bit converter (0–1 V input range) was negligible, while finite wire length contributed ≈ 1.5% to the RMS velocity uncertainty.

Combining all sources yields the following estimated relative uncertainties: ≈1.7% for mean velocities $U$, ≈2.5% for turbulence intensities $u^{\prime }$, and ≈4–5% for Reynolds shear and normal stress components. These uncertainty levels are sufficiently small to ensure that the conclusions regarding mean-flow and Reynolds-stress distributions remain unaffected, as spatial variations in the measured quantities exceed 5–10%.

3. Results

The qualitative visualization findings, statistical mean, turbulent flow field, and spectral analysis are discussed in this section.

3.1. Flow Visualization Study

The Reynolds number of the flow visualization experiment was 760, well below the Reynolds number range of the conducted measurements, but certainly within the turbulent regime. This choice was dictated by limitations in the recording speed of the video hardware used and the relative ease in the interpretation of visualization results obtained in a low-speed flow. Differences in flow physics arise with increasing Reynolds number, the most important being, at least as the nearfield coherent motion is concerned, the variations with Re_d of the formation region length [10,11], as well as of the streamwise distance over which the constant periodicity of the shed Kármán street prevails [1,9]. However, these aspects of the motion do not affect the basic mechanisms of the coherent motion, which are of primary interest here. These include, in principle, the topography of the confined vortex street and its “overall signature” on the flow as imprinted in the attained quantitative data distributions.

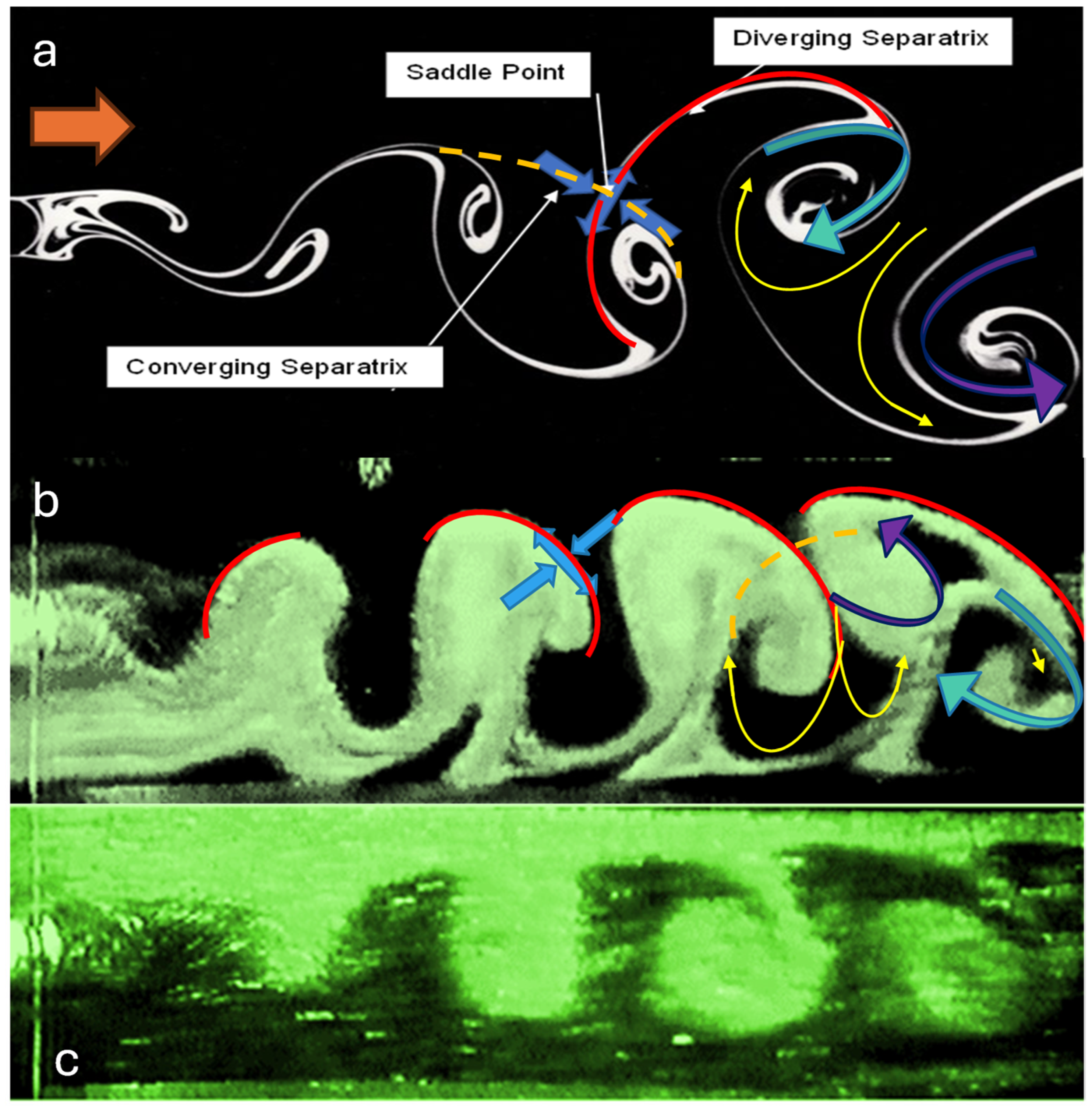
The topology of the near wake region (x₁/d = 0–26) was examined initially. A general view of the confined flow configuration in this region is shown in Figure 2b,c. For comparison, the early development of an unbounded wake is depicted in Figure 2a. In the confined case, the pictures presented in this figure visualize the nearfield coherent motion under different seeding conditions. Figure 2b shows aspects of the motion originating from the lower part of the channel, while Figure 2c tracks the evolution of the upper flow zone. Organized motions of intermediate scale (longitudinal vortices with vorticity principally along the x₁ and x₂ axes), but of substantial dynamical significance, positioned between successive Kármán vortices with mainly spanwise (x₃) vorticity, can also be seen in Figure 2b and especially in Figure 3. Figure 2 offers a qualitative appreciation of the intense mass and momentum exchange taking place between the two sides of the wake. At the borders of the bright regions and very close to the centreline, regions of concentrated vorticity, namely the Kármán vortices, elliptical in shape, are visible as they are convected downstream, especially in the right-hand part of all the pictures.

In Figure 2a,b, some topological aspects of the free and the presently studied confined wake have been included. These are the converging and diverging separatrices—often referred to as rib or braid regions—connecting consecutive counter-rotating spanwise structures and the saddle points formed at their intersections. The sense of rotation of the spanwise motion of the bounded and unbounded vortex street is also illustrated. Additionally, the motion of initially irrotational fluid towards its entrainment by the Kármán vortices is indicated by yellow arrows. The downstream increase in the spatial relationship between spanwise structures and ribs is prevalent from the examination of the evolving flow in Figure 2. In the unbounded configuration, successive separatrices remain parallel to each other since no flow constraint exists in the lateral direction. This is not the case in the presence of a wall restricting the lateral spread of the wake, as in the present situation. Observation of the downstream evolution of a diverging separatrix (denoted by a continuous red line in Figure 2b) shows that this line has the “right” orientation—as in the free case—in the vicinity of the bluff body. Subsequently, it is gradually tilted in the clockwise direction due to the existing lateral extent limitation. Further downstream, the diverging separatrices of the confined flow grow parallel to each other in the “reverse sense” relative to the free case.

Because of the topological modification described above, the major characteristic of the confined wake is the observed transposition of vortices. Kármán vortices initially form at the expected position in the suction region of the body; that is, clockwise and counterclockwise eddies originate from the upper and lower surfaces of the cylinder, respectively. Further downstream, an upward movement of counterclockwise vortices with positive circulation to the upper midplane of the flow is observed. Simultaneously, countermotion of eddies with negative vorticity across the symmetry axis towards the lower half of the street takes place [35]. The sequence of events shown in Figure 4 presents the evolution of the motion of a negative vortex from its stage of formation (Figure 4a) to a downstream distance (Figure 4c), where it has already crossed the horizontal symmetry axis.

The approach of the wake vortices to the walls possessing the same sign of vorticity provides a mechanism for their survival. The flow clearly “adapts” itself in the confined environment where it develops. If this topological change in the near wake did not occur, cancellation of vorticity between the street vortices and the wall layers would have happened, probably resulting in the eventual inhibition of the vortex street. The modified topology of the confined Kármán street is also evident in the visualization results as well as in the contours of coherent vorticity of Nakagawa et al. [34], who studied the near wake of a rectangular cylinder at a blockage ratio of 20%.

Figure 5 and Figure 6 show aspects of the bounded wake motion further downstream. A rather well-arranged periodic system of vortices is presented in Figure 5, which visualizes the region x₁/d = 0–65. A varying degree of order of the Kármán vortices from left to right is presented in Figure 6, where the illustrated region of development is x₁/d = 26–76. The above pictures indicate qualitatively the destruction of the periodic flow regime initially formed behind the body. The succeeding structure is similar in form to the preceding one but more random in character and of larger scale.

3.2. Mean and Turbulent Field Study

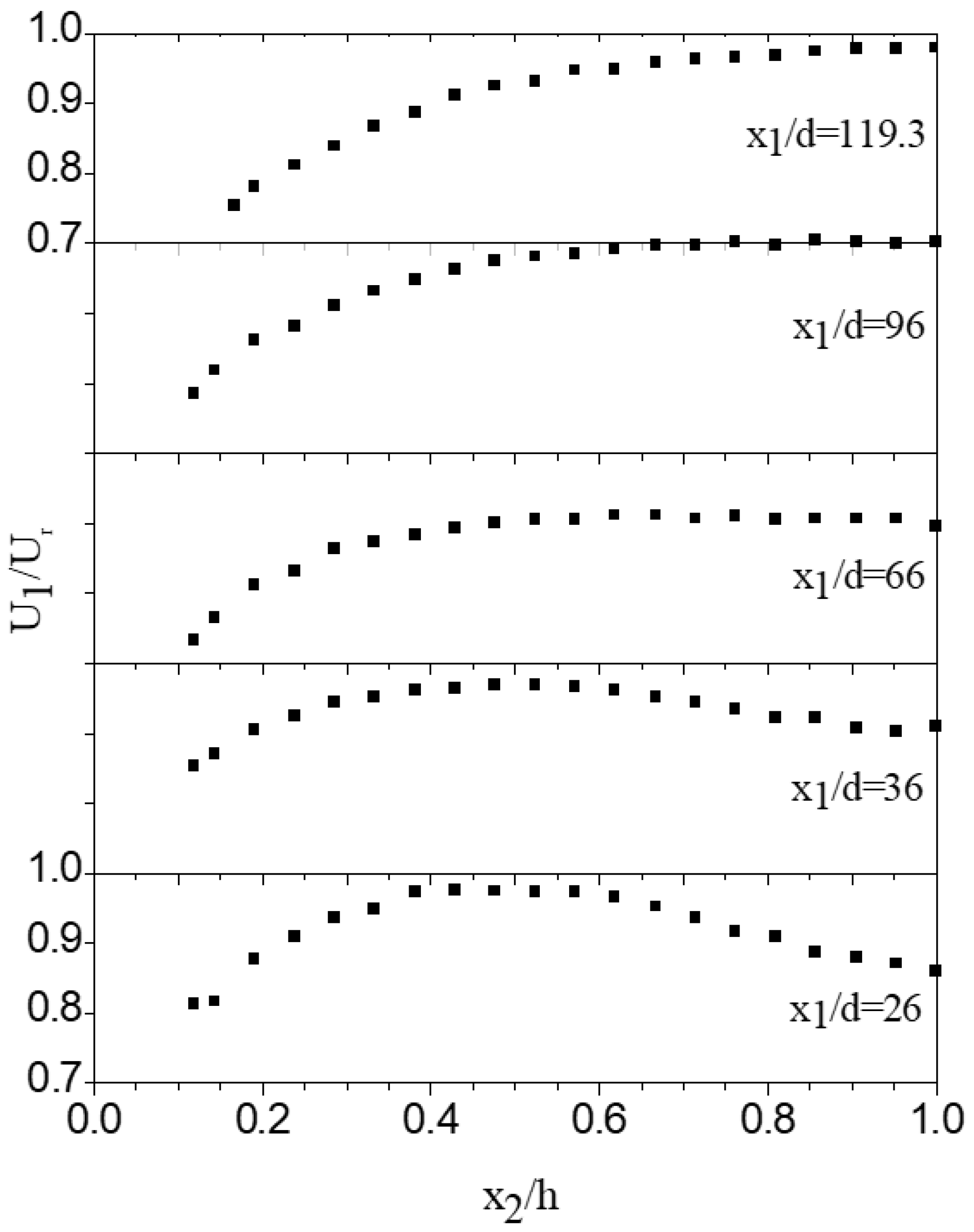
Transverse mean velocity distributions at various downstream positions along the experimental facility are presented in nondimensional form in Figure 7. The local mean velocities have been normalized with the axial reference velocity U_r. The obtained nearfield mean profiles are qualitatively similar in form to those commonly observed in free wakes, though the velocity deficit region appears more “compressed” in the vertical direction in the present flow. 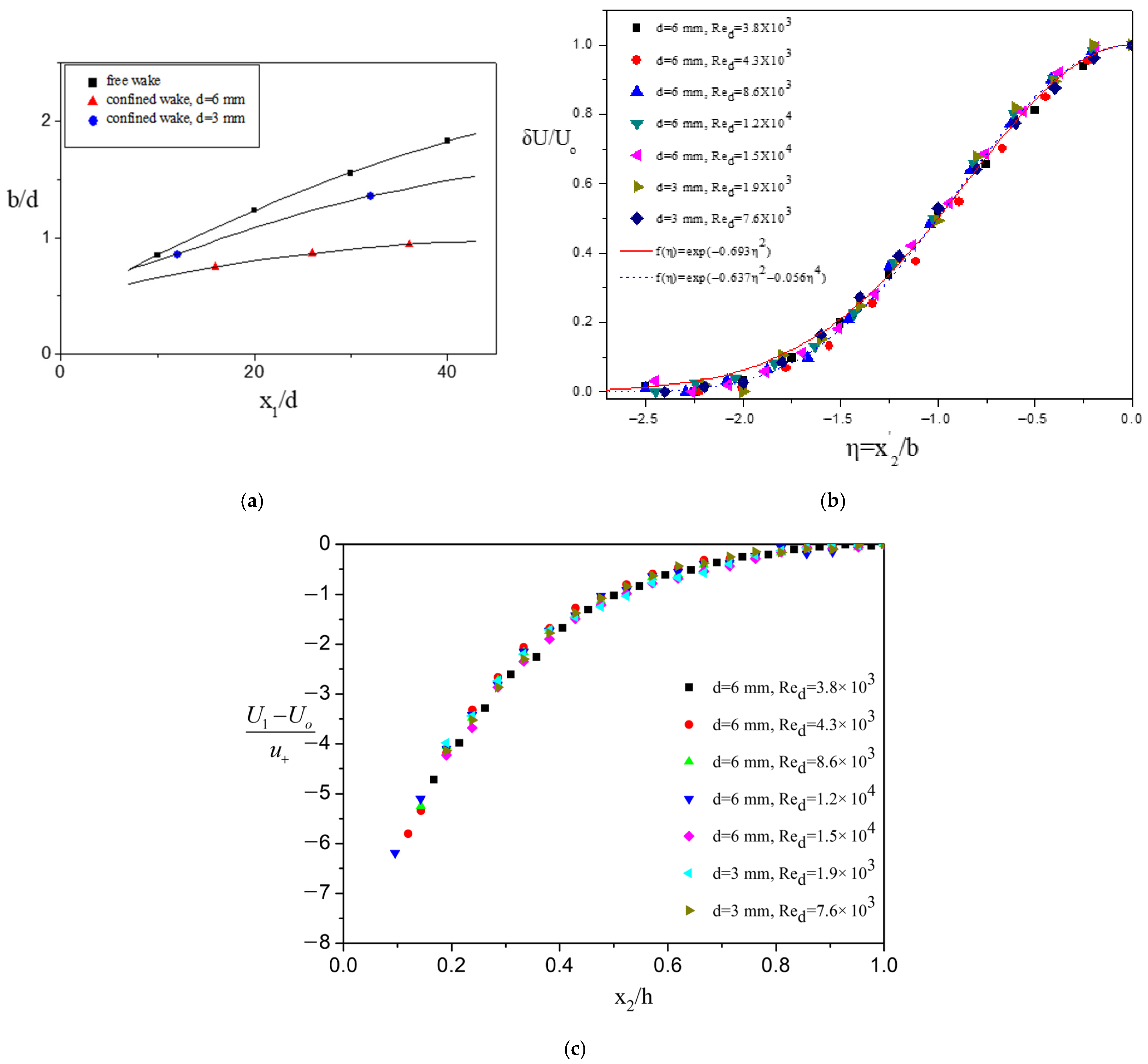Examination of Figure 8a, where the spreading rates of the unrestricted and the presently studied confined wake are shown, confirms this behavior. According to the data of this figure, the wake halfwidth of the present study, in the near region where velocity deficit profiles exist, increases as b ∝ x₁^0.46 and b ∝ x₁^0.24 behind the 3 and the 6 mm in diameter cylinder, respectively, as compared to the free wake growth of b ∝ x₁^0.5.

The initially observed “velocity deficit” distributions do not persist indefinitely. For x₁/d > 60, the mean velocity distributions differ markedly from those attained in the near wake region. The alteration of the mean profiles can be explained by the observed vortex street reversal. Consequently, the velocity induced in the core flow region by the two rows of counter-rotating vortices with mainly spanwise vorticity lies in the same direction as the mean flow celerity. Figure 6, for example, clearly demonstrates this.

Additionally, Figure 8b presents early confined wake profiles obtained in the Reynolds number range examined here (1.9 × 10³ ≤ Re_d ≤ 1.5 × 10⁴) at x₁/d = 36 and 56. Fully developed free wake mean deficit distributions are also included in this figure for comparison. The latter are represented by the exponential functions f(η) = exp(−0.693 η²) traditionally used to describe the mean velocity profile, and f(η) = exp(−0.637 η²–0.056 η⁴) proposed by Wygnanski et al. [9], to achieve better agreement with measurements at the outer edges of the wake. Here, δU is the local velocity deficit, U_o is the maximum deficit at the center of the wake, and η ≡ $x_2^{\prime }$/b is the dimensionless transverse distance from the centerline. (The notation is introduced to distinguish the transverse wake coordinate from x_2, originally defined in Figure 1b). The present early core flow data agree relatively well with the free wake profiles. However, they demonstrate a possible trend of acceleration relative to the free case. This result can be seen in conjunction with Figure 8a, where it is observed that the confined wake halfwidth is narrower than its unbounded counterpart. Hence, the velocity field induced by the spanwise structures in that region increases the translational flow velocity near the symmetry axis and gradually alters the initial deficit profile. In Figure 8c, the distant confined wake mean velocity data are shown for the whole Reynolds number range under study.

As with the early deficit field, self-similarity is observed in the distant “channel flow” region. The same is true also for the various Reynolds stress distributions at the same measurement stations, not presented here.

In accordance with the wake profile “destruction” previously described, the mean flow field becomes subsequently nearly uniform at the core in the transverse direction, as shown in Figure 7. At the same time, this uniform region decreases in lateral extent along the intermediate stations of the parallel flow section because of boundary layer growth and increases with streamwise development of the deformation rate of eddies with spanwise vorticity. Gradually, this zone shrinks to a small region around the symmetry axis close to the exit of the first duct. In general, the attained mean velocity distributions resemble those of a channel flow for x₁/d ≥ 60.

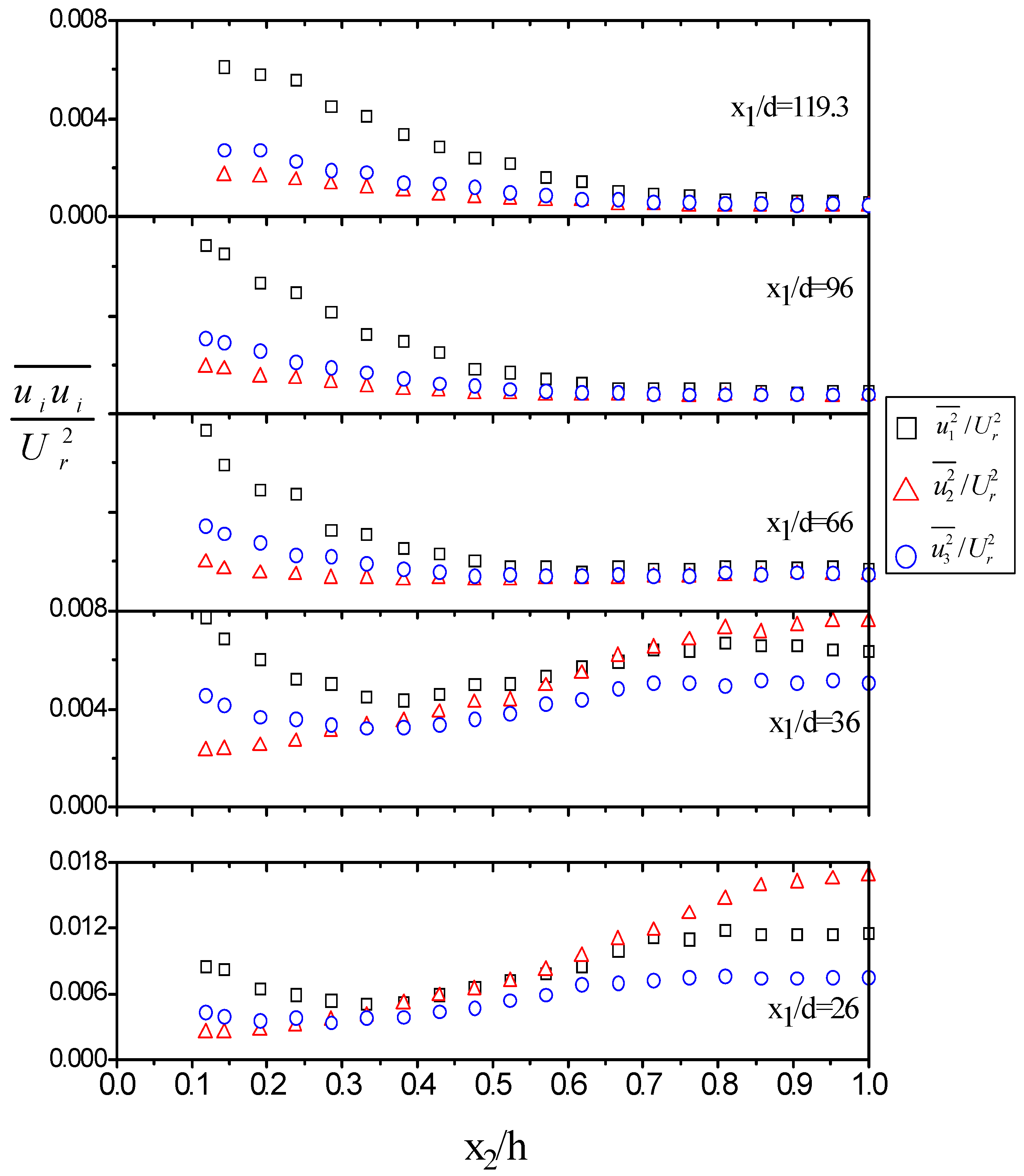
Figure 9 shows transverse distributions of the intensity components, $u_1^2$, $\overline{u_2^2}$ and $\overline{u_3^2}$, normalized by the reference velocity U_r in the range x₁/d = 26–119.3. The turbulence action is concentrated mainly at the core near the cylinder, with $\overline{u_2^2}$ being initially the largest, as is commonly observed in wake flows. As with the mean field, there is a close resemblance of the fluctuating motion to the free wake case in the near region. In the remaining part of the parallel flow section, the attained distributions become progressively uniform but not isotropic at the central zone and strongly non-uniform close to the walls. In general, mean shearing prevailing in the vertical direction leads to transverse distributions with $\overline{u_1^2}$> $\overline{u_3^2}$>$\overline{u_2^2}$ in regions where ∂U₁/∂x₂ ≠ 0, with the latter inequality being stronger the higher the mean shear rate.

The normalized Reynolds shear stress $\overline{u_1{u}_2}$/$U_r^2$ distributions are shown in Figure 10. These profiles exhibit the familiar antisymmetric form throughout. Except for the initial “wake-like” distributions near the cylinder (up to x₁/d ≈ 60), the remaining profiles vary essentially linearly in regions where ∂U₁/∂x₂ ≠ 0. Since the mean shear rate ∂U₁/∂x₂ is positive in the lower halfplane of the flow for x₁/d ≥ 66, the quantity is negative throughout this region. The Reynolds shear stress, defined as τ = −ρ$\overline{u_1{u}_2}$, is thus positive without exception in the same region.

The alteration of the mean velocity and the turbulent stress profiles after x₁/d ≈ 60, previously observed, raises the question of what remains of the wake effect at the end of the straight section. Moreover, to gain an understanding of the distant structure, its resemblance to the free wake and fully developed channel flow configurations needs to be examined. To clarify the above, measurements of the momentum field were carried out at the exit of the parallel duct in the absence of the bluff-body under identical inlet flow conditions with the preceding wake ones. These supplementary measurements do not correspond to the fully developed channel flow situation, due to the insufficient length of the parallel duct. However, since only fully developed channel data exist in the literature, in the following, the present channel measurements are compared with related experimental fully developed data, expecting imperfect agreement with the latter. In this comparison, and for the reasons stated above, confined wake data are also included.

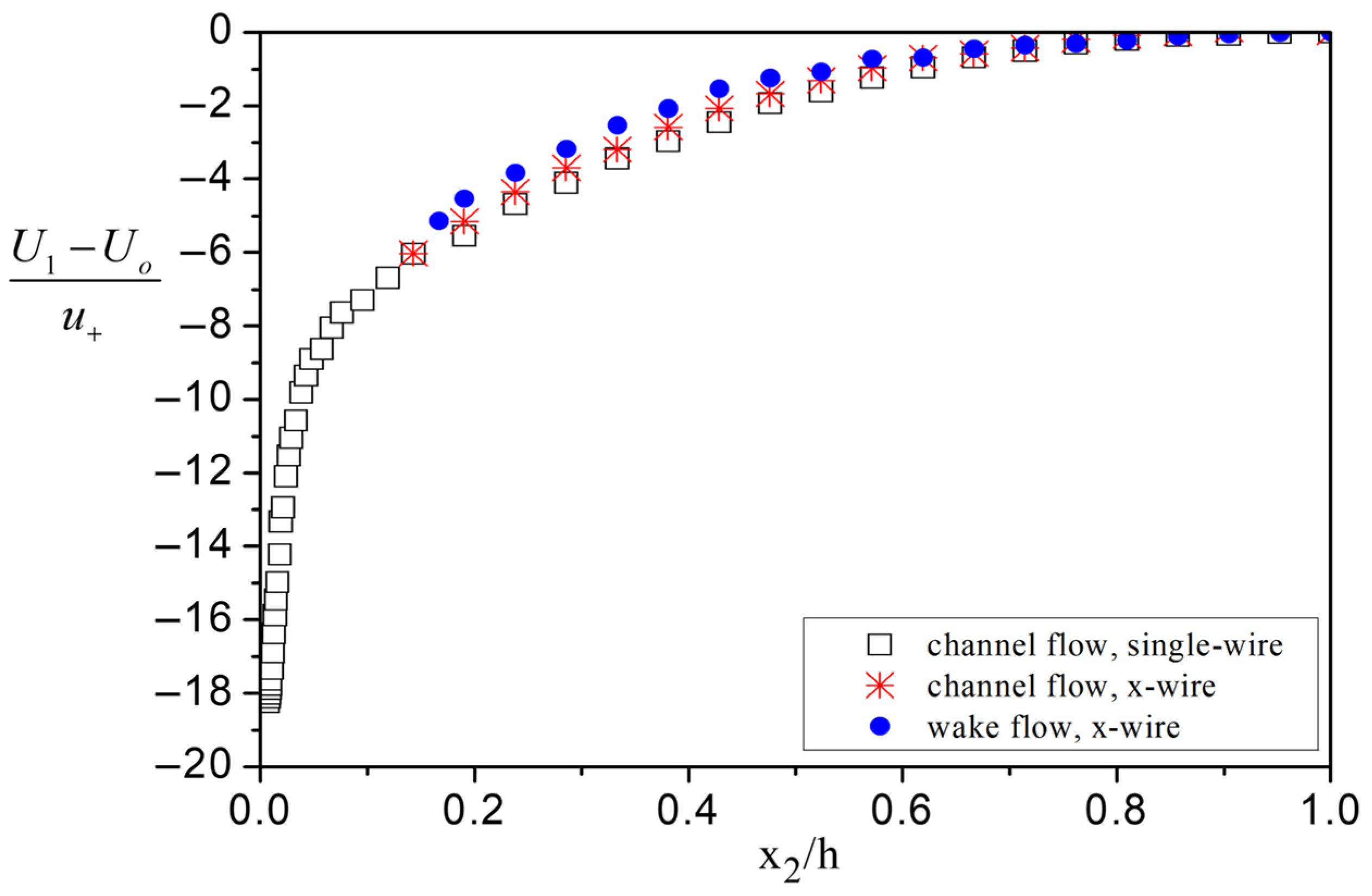
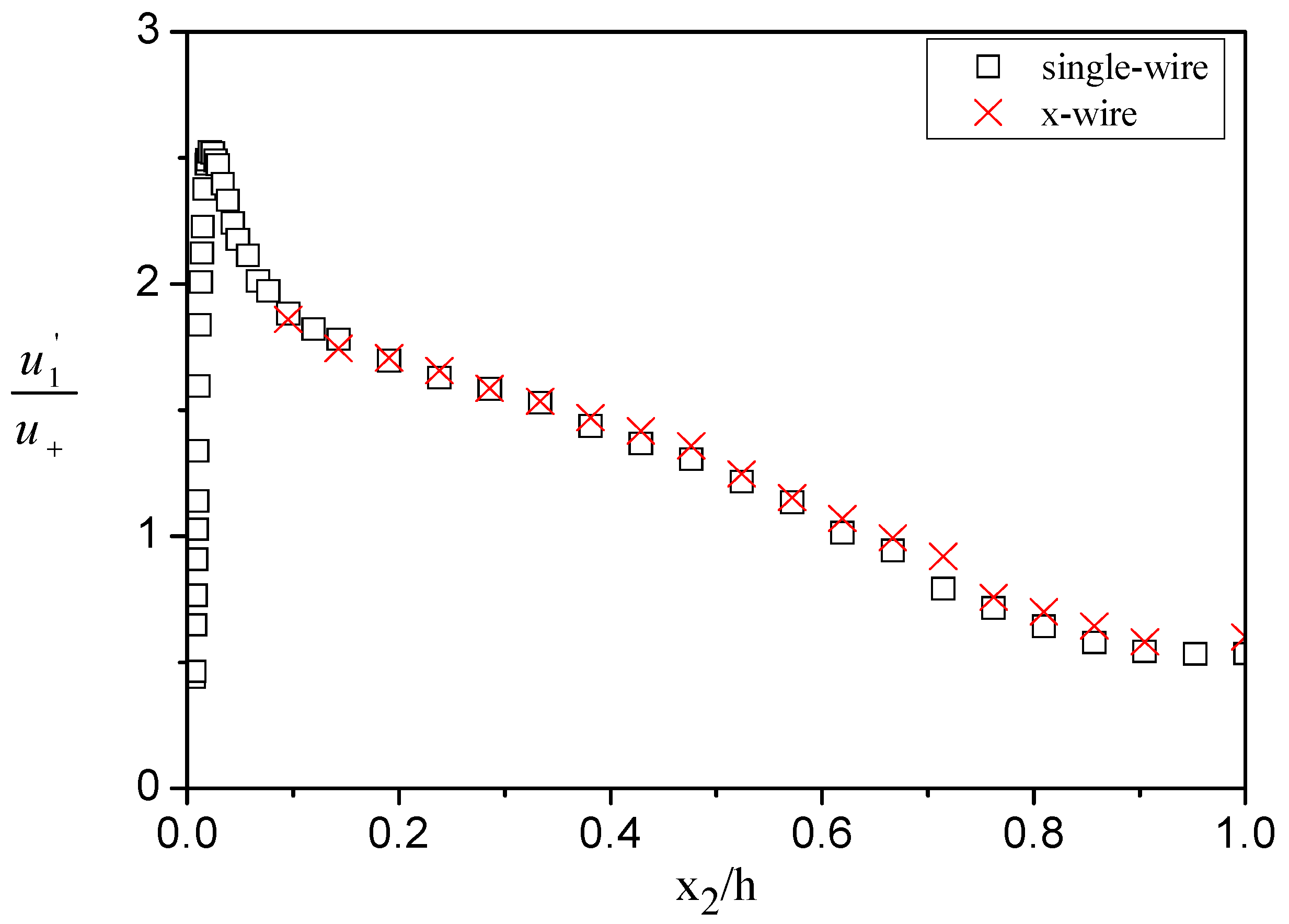
Figure 11 presents mean velocity profiles for channel and wake flow, normalized by the friction velocity and expressed in outer variables, at the farthest measuring station in the parallel section (x₁/d = 119.3). The friction velocity u₊ was estimated following the procedure described by Djenidi et al. [36], based on the assumption of a power law velocity distribution, and is applicable for boundary layer, pipe, and channel flow configurations. As mentioned above, channel flow measurements were obtained using both an X-probe and a single boundary layer type wire, the latter used as a reference probe. It is evident from the examination of Figure 11 and Figure 12—where the RMS distribution of the longitudinal velocity component for channel flow is shown—that the two probes provide nearly identical descriptions of the mean and the fluctuating field. Thus, the accuracy of the x-wire measurements is certified. Regarding the streamwise component for channel flow, data from the single-wire probe are presented in all related graphs. The mean confined wake profile (Figure 11) appears more uniform than the channel distribution in the common range of measurements, due to the “homogenizing” effect of the spanwise wake eddies at the core zone.

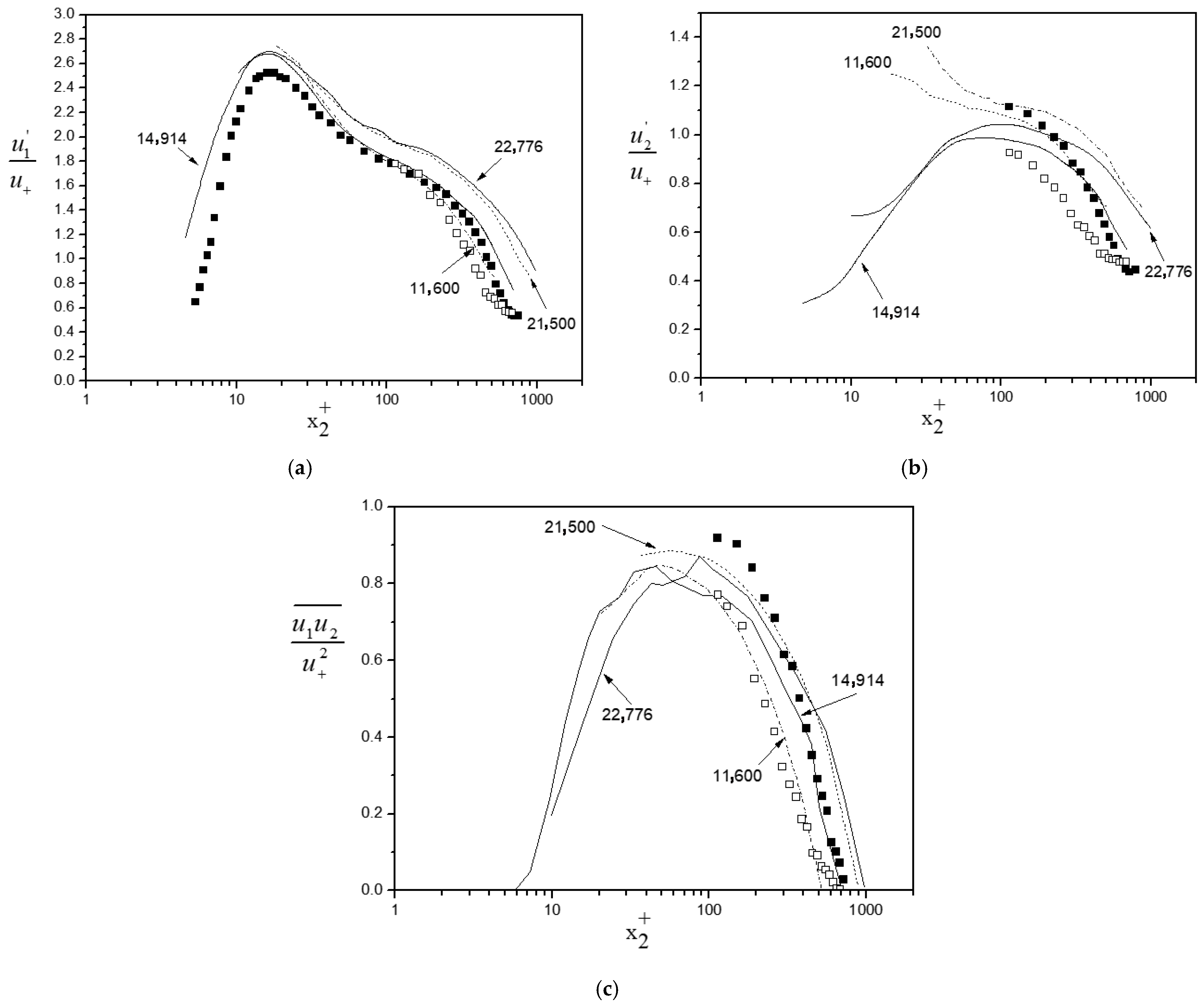
Figure 13 demonstrates the RMS distributions of the streamwise and transverse components (Figure 13a,b) and the shear stress profile (Figure 13c) for the present channel and confined wake flow, all expressed in inner variables. Experimental results for fully developed channel flow from Wei and Willmarth [24], obtained at Re_h = 14,914 and 22,776, and Antonia et al. [25], at Re_h = 11,600 and 21,500, are also included in Figure 13. The above choice of Reynolds numbers was dictated by the fact that they were the closest to Re_h = 15,630 of the present channel flow case. The Reynolds number dependence on the dimensionless fully developed turbulent statistics is quite evident in this figure. To avoid overcrowding of the figure, the referenced measurements have been omitted and are represented by a family of curves passing through the original data.

In all graphs presented in Figure 13, the present channel results exhibit relatively better agreement with the Re_h = 14,914 case of the Wei and Willmarth experiment due to the closer proximity in Reynolds number, especially for $x_2^{+}$ ≥ 300 ($x_2^{+}$ ≡ x₂u₊/ν, where ν is the kinematic viscosity and the superscript + denotes normalization by the wall variables). Since the present channel flow is not fully developed, the agreement with the literature data is only qualitative, especially for u₁. The streamwise component shows a faster trend towards the fully developed stage in relation to the other moments presented in Figure 13. In contrast, the observed deviations are largest for u₂, indicating a much slower trend for the normal fluctuations. Therefore, the deviations of $\overline{u_1{u}_2}$ from the corresponding fully developed curves are also substantial. Regarding the confined wake measurements, also included in Figure 13, it is observed that the corresponding profiles differ appreciably from the present and the referenced channel flow data. This indicates that they represent a quantitative macroscopic signature resulting from a different flow structure. Turbulent flow field statistics reveal a less “canonical” channel flow. This is clearly seen in Figure 13, where comparison of Reynolds stress values between channel and wake flow illustrates a ratio value near 1.0 at the wall proximity ($x_2^{+}$ = 100), and then increases monotonically towards the channel core ($x_2^{+}$ = 650) where values of 7.0 are observed. Ratio values of 1.0 reflect the effect of wall confinement, while larger values indicate a progressive loss of organized vortex coupling and transition toward channel-like turbulence.

Additional insight into the present confined wake and channel flow dynamics is provided by the examination of measured spectra and correlations, derived from both configurations. Figure 14 and Figure 15 present axial and transverse component spectra and the corresponding autocorrelation coefficients ρ₁₁ and ρ₂₂, respectively, measured at several distances from the cylinder. The variation in the above distributions from the vicinity of the generating obstacle towards the end of the parallel section can thus be seen for the bounded wake case.

Channel flow spectra and autocorrelations obtained close to the exit of the parallel section are also included in these figures. To compare the various wake and channel spectra, all taken at the same x₂ position (x₂/h = 0.71), the spectral densities ${\phi }_{u_1}$ and ${\phi }_{u_2}$ of u₁ and u₂, respectively, have been normalized.

$${\displaystyle \frac{{\int }_0^{\infty }{\phi }_{u_1}d\left(k_{1}h\right)}{\overline{u_1^2}}}=1,{\displaystyle \frac{{\int }_0^{\infty }{\phi }_{u_2}d\left(k_{1}h\right)}{\overline{u_2^2}}}=1,$$

(2)

Normalization is such that the energy content variation of each component with wavenumber band can be observed due to variations in flow development and configuration. Here k₁ = ω/U_r is the wavenumber in the x₁ direction, ω is the radian frequency, and $\overline{u_1^2}$, $\overline{u_2^2}$ are the local mean square values. No attempt is made here to find out if some scaling law exists (presumably in outer variables since we consider measured spectra close to the centerline). In fact, no scaling exists because we are dealing with wake spectra at various stages of flow development and channel spectra as well.

Fluctuations in a wide k₁h range are observed in all measured wake spectra, providing evidence that different scales coexist in the flow. The nearfield spectra (x₁/d = 36 and 56) demonstrate definite high intensity peaks at k₁h ≈ 0.8 in the present coordinates, specifically intense in u₂ corresponding to the vortex shedding or Kármán frequency for the Reynolds number examined in this case. This is in accordance with Bevilaqua’s [37] suggestion that velocity fluctuations due to a vortex street are more readily detected in the cross-wake (u₂) component. This behavior, also noticeable in Figure 15b, constitutes an essential feature of the vortex shedding process immediately downstream of the bluff-body, where the spectral density of the velocity fluctuations is characterized by high-quality peaks quite different in nature from those of many other unstable flows.

The constant periodicity of the large-scale motion near the cylinder is seen to prevail up to about x₁/d = 60 in the present case. A direct measure of the rapid destruction of the Kármán vortex street is provided by observing the evolution of the spectral peak with downstream distance. The confined wake spectral distributions of the velocity fluctuations in the present study follow quite similar behavior regarding the evolution of the shedding frequency with free wake flows. Cimbala et al. [10] report that the Kármán street shed in the wake of a circular cylinder does not persist indefinitely but rather decays exponentially with downstream distance. They found experimentally that the decay is rapid, such that velocity fluctuations at the Kármán frequency are lost in ‘background noise’ at a distance between 100 and 150 diameters at Re_d = 150. They also state that the decay is even faster in turbulent wakes where the small-scale motion is more prevalent. Ferré and Giralt [11] point out that the large-scale motions detected in the near wake are Kármán vortices, the periodic activity of which is lost beyond the 60 diameters. The same estimate for the longitudinal distance over which the initial periodicity terminates also comes out from Taneda’s [1] earlier experiments.

Further downstream (x₁/d = 119.3, Figure 14), but also in all measured spectra beyond the 60 diameters not presented here, no sign of periodicity is observed in the measured wake spectral densities. The u₁ component spectral densities reach maxima at lower k₁h values, indicating that the greatest portion of its energy content is favorably distributed to larger scales. The secondary vortex street, which evolves after the original Kármán street has largely decayed, is more diffuse in character and of larger scale. As with the free wake, in the present confined case, the far structure shows no preference for any frequency or scale. A broad band of fluctuations is visible in the related spectra, the center of the band shifting to lower wavenumbers (larger scales) as the flow evolves downstream. The transverse u₂ component spectra show maxima, in general, far from the origin. This happens because the corresponding correlation often becomes negative for small time delays τ (Figure 15b), which in turn means backflow (due to u₂) along the x₁ direction. It should be noted that the k₁h ≈ 0.8 value corresponds to a vortex shedding frequency of f_s ≈ 420 Hz measured in the original spectral distributions, which are presented here in normalized form in Figure 14, as discussed above. This vortex shedding frequency value yields a Strouhal number St ≈ 0.2, as is the case with free wakes in the subcritical Reynolds number range (300 < Re < 3.0 × 10⁵). This is also the case for all the conducted confined wake experiments within the range 1.9 × 10³ < Re < 1.5 × 10⁴ and blockage ratios of 7% and 14%.

The channel flow spectra at x₁/d = 119.3 are smoother for both velocity components than their wake counterparts and more favorably distributed on the larger scale. On the other hand, the wake spectra possess relatively more energy in the inertial and the dissipative wavenumber bands. Figure 15a clearly demonstrates the difference in scale of the energy-containing part of the motion in the two different flow cases. From the autocorrelation functions, the integral scales L_11,1 of the u₁ component along the x₁ direction have been computed. Hence, a typical length scale of the coherent motion can be derived from the correlation plots of Figure 15a. For the confined wake and for x₁/d = 36, 56, and 119.3, L_11,1 =1.35 d, 1.63 d, and 2.44 d, respectively, while for channel flow at x₁/d = 119.3, L_11,1 =3.0 h.

4. Discussion

The turbulent wake of a circular cylinder under wall confinement was investigated, for the case of a 14% blockage in the subcritical Re region, through three-dimensional velocity measurements and flow visualization along the parallel duct of a wind tunnel. The confined wake exhibited continuous downstream evolution dominated by large-scale coherent structures, with the macroscopic characteristics of the velocity field reflecting the underlying vortex topology. Flow visualization in the parallel section confirmed the presence of a vortex shedding pattern analogous to a Kármán street, but with a key modification: confinement induced an inversion of the shed vortices’ relative positioning. In the nearfield and up to x₁/d ≈ 60, the initial periodic flow pattern persisted. The succeeding flow pattern was similar in form to the original Kármán street shed behind the body, but more irregular and larger in scale, signaling the breakdown of the periodical nature of the preceding structure.

Velocity measurements demonstrated that nearfield distributions resembled those of free wakes, though compressed in shape due to lateral constraints. A near-wake shedding peak at St ≈ 0.2 is evident and persists up to x₁/d ≈ 60, beyond which the spectra become broadband as periodicity collapses. Beyond x₁/d ≈ 60, the mean and fluctuating velocity profiles began to approach those of channel flows. However, detailed comparisons with both present channel measurements and canonical channel-flow data revealed that the confined wake remained a distinct flow configuration, governed by its own dynamics. This is documented by the fact that although it exhibited channel-like features, its mean and statistical distributions retained signatures of the initial vortex formation process.

The confined wake exhibits a narrower halfwidth growth than the free wake case, which follows a power law distribution b $\propto$ x₁ⁿ with n $\approx$ 0.5. Instead, for the 3 cm cylinder case (7% blockage), n is about 0.46, while for the 6 cm cylinder case (14% blockage), n is about 0.24. Autocorrelation analysis depicts that the streamwise integral scale L_11,1 increases downstream from approximately 1.35 d to 2.44 d, while the corresponding value of the free channel case is about 3.0 h. The contradiction between the simultaneous approach of the mean field measurements to the lag presented in higher-order moments clarifies why the flow is not yet canonical channel flow, despite the uniformity of U₁. The results support the conclusion that a confined wake does not evolve independently toward a canonical channel state but rather adapts to its bounded environment while preserving imprints of its nearfield dynamics. This mechanistic link between vortex formation and far-field development highlights confinement as a controlling factor in wake evolution.

Future studies should extend these findings to a broader range of Reynolds numbers and blockage ratios, as well as explore the role of wall boundary-layer characteristics. The quantitative metrics of the present work offer benchmark data for validating CFD predictions of the transition from wake-like to channel-like behavior under strong confinement. Therefore, it could strengthen the fundamental understanding of confined wakes and inform applications in confined mixing, combustion, and marine hydrodynamics where wake–wall interactions are critical.