Vortex Stability in the Thermal Quasi-Geostrophic Dynamics

Abstract

The stability of a circular vortex is studied in the thermal quasi-geostrophic (TQG) model. Several radial distributions of vorticity and buoyancy (temperature) are considered for the mean flow. First, the linear stability of these vortices is addressed. The linear problem is solved exactly for a simple flow, and two stability criteria are then derived for general mean flows. Then, the growth rate and most unstable wavenumbers of normal-mode perturbations are computed numerically for Gaussian and cubic exponential vortices, both for elliptical and higher mode perturbations. In TQG, contrary to usual QG, short waves can be linearly unstable on shallow vorticity profiles. Linearly, both stratification and bottom topography (under specific conditions) have a stabilizing role. In a second step, we use a numerical model of the nonlinear TQG equations. With a Gaussian vortex, we show the growth of small-scale perturbations during the vortex instability, as predicted by the linear analysis. In particular, for an unstable vortex with an elliptical perturbation, the final tripolar vortices can have a turbulent peripheral structure, when the ratio of mean buoyancy to mean velocity is large enough. The frontogenetic tendency indicates how small-scale features detach from the vortex core towards its periphery, and thus feed the turbulent peripheral vorticity. We confirm that stratification and topography have a stabilizing influence as shown by the linear theory. Then, by varying the vortex and perturbation characteristics, we classify the various possible nonlinear regimes. The numerical simulations show that the influence of the growing small-scale perturbations is to weaken the peripheral vortices formed by the instability, and by this, to stabilize the whole vortex. A finite radius of deformation and/or bottom topography also stabilize the vortex as predicted by linear theory. An extension of this work to stratified flows is finally recommended.

1. Introduction

Vortices are an essential feature of planetary fluid flows. Their stability is often studied using the rotating shallow water (RSW) model with one or several homogeneous layers (i.e., with a mean vertical stratification [1,2,3,4,5,6]). In particular, these studies showed that vortices with horizontally or vertically sheared velocity profiles can be sensitive to barotropic or baroclinic instabilities. In their nonlinear evolution, strongly unstable vortices break into several fragments. Only for weakly unstable vortices does the perturbation stabilize nonlinearly, leading to a vortex multipole. Vortex stability has also been studied in the quasi-geostrophic model, a subset of the RSW equations, valid for low-frequency dynamics [7,8,9]. These studies also showed that very unstable vortices would break irreversibly into dipoles, while weakly unstable vortices could rearrange as rotating multipoles. Note that the quasi-geostrophic model is still the subject of many studies, in particular for its dependence upon latitude, numerical modeling and data-driven approach [10,11,12].

However, neither the RSW model nor the usual quasi-geostrophic model are appropriate in the presence of a mean horizontal stratification. In particular, such a stratification occurs in the presence of ocean–atmosphere interaction, and is found in the upper ocean layer (the so-called ocean mixed layer). In this layer, the wind and the heat fluxes induced both high-frequency and low-frequency motions. The low-frequency motions have equilibrated horizontal pressure gradient and Coriolis acceleration, and are called balanced motions. In this class of motions lie the quasi-geostrophic motions mentioned below. The high-frequency motions equilibrate this pressure gradient by their relative acceleration or by their turbulent fluxes of momentum. They are unbalanced motions. It has been shown that such unbalanced motions are important at submesoscale in the ocean (i.e., for scales of motion ranging about from 1 to 20 km horizontally) and at the mesoscale in the atmosphere (scales about 10 times larger). In these cases, unbalanced fluid waves can affect balanced flow dynamics [13,14,15,16,17]. High-frequency motions are represented in the RSW model but they are filtered out in the QG model.

To address the dynamics of the upper ocean, an extension of RSW models to horizontally inhomogeneous layers was derived by Ref. [18]. This model was called ILPE (Inhomogeneous Layer Primitive Equation model)—or TRSW (Thermal Rotating Shallow-Water model) for the specific case of the $I{L}^0$ model—in subsequent papers. The IL0 model is a horizontally inhomogeneous-layer shallow-water model, in which the horizontal velocity is not allowed to vary vertically [19]. In his 1993 paper, P. Ripa showed [18] that the pseudo-energy or the pseudo-momentum of flow could not be ascertained to be sign-definite for general flows and therefore that no general criterion for formal stability could be obtained in the ILPE model. This in no way restricts the usefulness of the ILPE nor of the TRSW model. Indeed, they were used to model the upper ocean dynamics [20,21,22] and were also developed to improve their numerical scheme and to include moisture for application to the atmosphere [23,24,25,26,27,28,29].

As the TRSW model equations are difficult to handle, several authors derived a low-Rossby number (low-frequency) version of these equations, called TQG (thermal quasi-geostrophy). Indeed, although they can be influenced by high-frequency motions, balanced motions evolve on longer time-scales. In particular, oceanic vortices can last for several weeks or several months, while the period of high-frequency waves is shorter than a day. Retaining only the balanced motions also allows for a simplification of the equations by which pressure anomaly, with respect to rest, and horizontal velocities, are all represented by a single variable: the streamfunction. This allows for more detailed calculations of vortex dynamics compared to the shallow-water model.

Firstly, P. Ripa derived a low-frequency approximation of the ILPE model that he called ILQG [30]. The equations of this model are called thermal quasi-geostrophic (TQG) equations, which were derived and studied by Refs. [31,32]. A numerical analysis of the TQG equations was achieved by Ref. [33] and this model has been extended to include stochastic effects [34]. Ref. [35] derived a criterion for the nonlinear saturation of thermal instabilities in this model.

The RSW model with an inhomogeneous layer was used by Ref. [36] to study rodons—rotating ellipsoidal vortices—and circular vortices. They determined the radial profile of thickness and the energy of these vortices, and studied their stable or unstable evolutions numerically. They provided a stability condition for vortices with solid-body rotation. More recently, flow solutions were obtained, in a TRSW model, for eastward-propagating vortex dipoles near the Equator [37]. They assessed the steady or unsteady nonlinear evolution of these dipoles with a numerical model. Ref. [38] studied numerically the stability of jets and vortices in the TRSW model and showed that small-scale features appear as the instability develops. The complexity of the TRSW model renders difficult any analytical work on jet or vortex stability. Therefore, we use the TQG model here to analyze the instability of circular vortices for which the radial profiles of streamfunction and of temperature are initially prescribed. After recalling the model equations (Section 2), we provide analytical solutions for linear stability in a vortex core, and then a general stability criterion for circular flows (Section 3). We also compute the growth rates and unstable waves for several velocity and buoyancy distributions numerically. In Section 4, we use a numerical model to classify the nonlinear regimes of thermally unstable vortices in the TQG dynamics. We analyze the finite-time evolution of these vortices with a Fourier analysis and the frontogenesis function. Finally, we conclude this study.

2. Model

2.1. Equations

2.1.1. The Thermal Quasi-Geostrophic (TQG) Model

We mostly follow the notations introduced by Ref. [33] to express the two equations of the thermal quasi-geostrophic model as

$$\begin{array}{ccc}\hfill {\partial }_t\omega +\mathbf{u}·\nabla \omega & =& \mathbf{u}·\nabla b-{\mathbf{u}}_{{\mathbf{h}}_{\mathbf{1}}}·\nabla b,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\partial }_{t}b+\mathbf{u}·\nabla b& =& 0,\hfill \end{array}$$

(2)

where

$$\omega =\left({\nabla }^2-{\displaystyle \frac{1}{R_d^2}}\right)\psi +f,$$

(3)

is the potential vorticity, ${\nabla }^2=\Delta$ is the Laplacian, $\psi$ is the streamfunction, and $R_d=\sqrt{gH}/f$ is the deformation radius, which will be varied here. Note that $R_d$ was taken as unity by [33]. We recall that the radius of deformation is related to the rigidity (or not) of the free surface. When it is infinite, the surface is a rigid lid. Otherwise, the surface is free. In these notations, g is gravity, H is the maximal thickness of the fluid layer at rest, and f is the Coriolis parameter, chosen constant here. Since f is constant, it does not intervene directly since $\omega$ is differentiated in the dynamical equations. That is why we do not include f explicitly in $\omega$ any further. In Equations (1) and (2), b is the buoyancy. In the upper ocean, buoyancy depends linearly on temperature via the equation of state, assuming no other active tracer; that is, $b=g{\beta }_T(T-T_0)$, where ${\beta }_T$ is the thermal expansion coefficient and $T_0$ is the reference temperature. All variables ($\omega ,\psi ,b$) depend only on the horizontal coordinates being vertically averaged.

In the equations above, the velocities are given by the following relations:

$$\begin{array}{ccc}\hfill \mathbf{u}& =& \mathbf{k}\times \nabla \psi ,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\mathbf{u}}_{{\mathbf{h}}_{\mathbf{1}}}& =& \mathbf{k}\times \nabla h_1,\hfill \end{array}$$

(5)

where $h_1$ is the bottom height above the maximal depth (of the fluid at rest) and $\mathbf{k}$ the vertical unit vector.

2.1.2. The One-Layer, Reduced Gravity Quasi-Geostrophic (QG) Model

In our study, we will compare the TQG properties for vortex (in)stability with the equivalent properties in the one-layer quasi-geostrophic (QG) model and in the two-dimensional (2D) incompressible flow model. Here, we remind the reader of the equations for these two models.

The quasi-geostrophic model describes homogeneous incompressible flows with a free-surface, in rapidly rotating environments (e.g., on planet Earth). The horizontal velocity $\mathbf{u}$ derives from a streamfunction as in the equation above. This streamfunction $\psi$ is related to the free-surface elevation $\eta$ via $\psi =g\eta /f_0$, where $f_0$ is the Coriolis parameter. On Earth, $f_0=2\mathsf{\Omega }sin\left(\varphi \right)$ with $\mathsf{\Omega }$ as the rotation rate of the Earth and $\varphi$ as the latitude.

The QG dynamics are governed by the vorticity equation

$${\partial }_t\omega +\mathbf{u}·\nabla \omega =0,$$

with

$$\omega =\left({\nabla }^2-{\displaystyle \frac{1}{R_d^2}}\right)\psi .$$

Since the fluid is homogeneous, there is no temperature variation. Only barotropic instability (horizontal shear) can occur in this model. In this model, the presence of a vortex stretching (the second term in the vorticity above) is known to reduce barotropic instability (e.g., [39]).

2.1.3. The Two-Dimensional Incompressible (2D) Flow Model

The two-dimensional incompressible flow model describes fluids with vanishingly small thickness (e.g., experimentally, fluid flows in a soap film). Here, we consider a horizontal 2D model. The horizontal velocity derives from a streamfunction due to the incompressibility condition in two dimensions. The flow evolution is governed by its vorticity equation

$${\partial }_t\omega +\mathbf{u}·\nabla \omega =0,$$

with

$$\omega ={\nabla }^2\psi$$

Since the fluid is homogeneous, there is no temperature variation. Only barotropic instability (horizontal shear) can occur in this model. There is no vortex stretching in this model so that 2D flows correspond to QG with infinite $R_d$. Note that Rayleigh friction has not been added here [40].

2.2. Flow and Buoyancy Distributions

As we study vortices here, the mean velocity and buoyancy distributions are chosen to be circular, and thus dependent on the radius r only, $\overline{\psi }\left(r\right),\overline{b}\left(r\right)$.

In particular, to derive simple analytical solutions in Section 3.1, we will use

$$\overline{\psi }\left(r\right)={\mathsf{\Omega }}_0{\displaystyle \frac{r^2}{2}},\overline{b}\left(r\right)=B_0{\displaystyle \frac{r^2}{2}},$$

which is an acceptable form for the core of oceanic vortices; see for instance Ref. [41]. We define $\overline{V}=d\overline{\psi }/dr$, the tangential velocity of the mean flow (its radial component is null), and $\overline{\mathsf{\Omega }}=\overline{V}/r$, the corresponding mean rotation rate. Bottom topography will be included only locally in this study.

For the derivation of the linear instability criterion (in Section 3.2 and Section 3.3), a general form of these functions will be kept. Finally, for the numerical study of both linear and nonlinear evolutions of unstable vortices (Section 3.4 and Section 4), Gaussian or power-exponential profiles of mean streamfunction and buoyancy will be considered.

Power exponential vortices have the following profile of vorticity and of buoyancy:

$$\begin{array}{ccc}\hfill \overline{\omega }\left(r\right)& =& {\omega }_0\left[1-{\displaystyle \frac{\alpha }{2}}{(r/r_0)}^{\alpha }\right]exp(-{(r/r_0)}^{\alpha }),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \overline{B}\left(r\right)& =& B_{0}exp(-{(r/r_0)}^{\alpha }),\hfill \end{array}$$

(7)

where ${\omega }_0=2V_0/r_0$, with $V_0$ being the vortex azimuthal velocity and $r_0$ its radius. $B_0$ is the vortex buoyancy.

For the linear instability analysis, angular normal modes will be used:

$${\psi }^{\prime }(r,\theta ,t)=\varphi \left(r\right)exp\left[il(\theta -ct)\right],b^{\prime }(r,\theta ,t)=b\left(r\right)exp\left[il(\theta -ct)\right],$$

where l is the angular mode (or azimuthal mode), and the complex value of $c=c_r+i{c}_i$ contains the phase speed of the perturbation (the real part of c) and the growth rate of the perturbation ($l{c}_i$). With such perturbations, the linearized equations of vorticity and of buoyancy are

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c){\omega }^{\prime }-\overline{\mathsf{\Omega }}{b}^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d}{dr}}(\overline{\omega }-\overline{b})& =& 0,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c)b^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d\overline{b}}{dr}}& =& 0,\hfill \end{array}$$

(9)

in the absence of bottom topography ($h_1=0$).

2.3. Linear and Nonlinear Numerical Models

In Section 3.4, when using normal-mode perturbations and when discretizing the radius over N grid points ($r_1\dots r_N$), the linear Equations (40) and (41) become a $2N\times 2N$ matrix system, in $\varphi$ and b. This system is solved by diagonalization, with c being the eigenvalue and $X(\varphi \left(r_1\right)\dots \varphi \left(r_N\right),b\left(r_1\right)\dots b\left(r_N\right))$ being the corresponding eigenvector. We thus obtain $AX=cBX$, where the A and B matrices depend on $\overline{\mathsf{\Omega }},\overline{\omega },\overline{b}$.

In Section 4, the numerical simulations with the system of nonlinear Equations (1) and (2) will be carried out with a pseudo-spectral code of these equations, on a bi-periodic horizontal grid. The number of grid points is 512 horizontally. The code uses a mixed Euler-leapfrog scheme in time which is conservative in vorticity and buoyancy, and which does not separate odd and even solutions in time-steps. The horizontal derivatives are performed in spectral space, using fast Fourier transforms to recover physical variables. Very weak bi-harmonic viscosity is added to Equations (1) and (2), which does not alter the physical results (tests have been performed with different small values of viscosity).

3. Linear Stability

3.1. A Simple Analytical Solution

Firstly, we look for an analytical solution to Equations (40) and (41); this is possible only for simple mean streamfunction and buoyancy profiles. Here, we choose such profiles, which are realistic for the core of vortices. It is not possible to solve analytically the problem for the whole vortex, but in the core resides most of the mean kinetic (or potential) energy, which feeds the perturbation.

Choosing

$$\overline{\psi }\left(r\right)={\mathsf{\Omega }}_0{\displaystyle \frac{r^2}{2}},\overline{b}\left(r\right)=B_0{\displaystyle \frac{r^2}{2}},\overline{\mathsf{\Omega }}={\mathsf{\Omega }}_0,{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\overline{b}}{dr}}=B_0$$

and inserting these expressions into Equations (40) and (41) (with flat bottom dynamics) leads to

$$\begin{array}{ccc}\hfill ({\mathsf{\Omega }}_0-c){\omega }^{\prime }-{\mathsf{\Omega }}_0{b}^{\prime }-{\psi }^{\prime }\left({\displaystyle \frac{1}{r}}{\displaystyle \frac{d\overline{\omega }}{dr}}-B_0\right)& =& 0,\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill ({\mathsf{\Omega }}_0-c)b^{\prime }-B_0{\psi }^{\prime }& =& 0.\hfill \end{array}$$

(11)

The mean potential vorticity is $\overline{\omega }={\mathsf{\Omega }}_0(2-r^2/\left(2R_d^2\right))$ and therefore

$${\displaystyle \frac{1}{r}}{\displaystyle \frac{d\overline{\omega }}{dr}}=-{\displaystyle \frac{{\mathsf{\Omega }}_0}{R_d^2}}.$$

(12)

With this, the linear equations are

$$\begin{array}{ccc}\hfill ({\mathsf{\Omega }}_0-c){\omega }^{\prime }-{\mathsf{\Omega }}_0{b}^{\prime }+{\psi }^{\prime }\left({\displaystyle \frac{{\mathsf{\Omega }}_0}{R_d^2}}+B_0\right)& =& 0,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill ({\mathsf{\Omega }}_0-c)b^{\prime }-B_0{\psi }^{\prime }& =& 0.\hfill \end{array}$$

(14)

The last step relates ${\omega }^{\prime }$ and ${\psi }^{\prime }$. We recall that these two variables are related by the equation

$${\omega }^{\prime }={\nabla }^2{\psi }^{\prime }-{\psi }^{\prime }/R_d^2$$

with

$${\psi }^{\prime }(r,\theta ,t)=\varphi \left(r\right)exp\left[il(\theta -ct)\right],$$

in general.

This leads to

$${\omega }^{\prime }={\displaystyle \frac{d^{2}phi}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\varphi }{dr}}-{\displaystyle \frac{l^2/r^2}{\varphi }}$$

Calculating the algebraic relation between the two variables is achieved by considering eigen-functions of the Laplacian operator in polar coordinates:

$${\psi }^{\prime }(r,\theta ,t)={\psi }_l{J}_l(r/R_d)exp\left[il(\theta -ct)\right],$$

(15)

This use of a single wave is possible because the system is linear with constant coefficients.

This solution is known to have a Laplacian

$${\nabla }^2{\psi }^{\prime }=-{\psi }^{\prime }/R_d^2$$

which, added to the vortex stretching $-{\psi }^{\prime }/R_d^2$, leads to ${\omega }^{\prime }=-2{\psi }^{\prime }/R_d^2$ (for simplicity, we have not specified here that we take the real part of the expression above; therefore, ${\psi }_l$ is complex).

Similarly, we set

$$b^{\prime }(r,\theta ,t)=b_l{J}_l(r/R_d)exp\left[il(\theta -ct)\right].$$

(16)

This provides a $2\times 2$ homogeneous system in ${\psi }_l,b_l$ whose determinant must vanish. This determinant is

$$D=(2c-{\mathsf{\Omega }}_0)({\mathsf{\Omega }}_0-c)-c{B}_0{R}_d^2=0.$$

(17)

Instability will occur in such a vortex core if

$$\Delta ={({\mathsf{\Omega }}_0-B_0{R}_d^2)}^2-4{\mathsf{\Omega }}_0{B}_0{R}_d^2<0.$$

(18)

Thus, a necessary condition for instability in this case is ${\mathsf{\Omega }}_0{B}_0>0$.

We can analyze condition $\Delta <0$ more fully. Setting $X={\mathsf{\Omega }}_0,Y=B_0{R}_d^2$, this condition can also be written as $(X-Y+2\sqrt{XY})(X-Y-2\sqrt{XY})<0$. Some short algebra indicates that this is possible only if $X-Y<2\sqrt{XY}$ and $X-Y+2\sqrt{XY}>0$, that is, $|X-Y|<2\sqrt{XY}$.

When adding topography to the problem, we can choose a parabolic seamount ${\overline{h}}_1={\mathsf{\Omega }}_1{r}^2/2$, so that ${\overline{V}}_1/r={\mathsf{\Omega }}_1$. Then, we have a new condition for instability:

$$\Delta ={({\mathsf{\Omega }}_0-B_0{R}_d^2)}^2-4({\mathsf{\Omega }}_0-{\mathsf{\Omega }}_1)B_0{R}_d^2<0.$$

(19)

Since ${\mathsf{\Omega }}_1>0$, a seamount stabilizes the flow if $B_0>0$, and conversely.

3.2. Stability Criterion

After this first simple solution, we look for a general stability criterion for TQG vortices. Now we do not choose a specific form of $\overline{\psi }$, nor of $\overline{b}$ any more. Equation (40) could be amenable to a Rayleigh-type criterion by multiplying it by ${\psi }^{\prime *}$ (the complex conjugate of ${\psi }^{\prime }$), but then the coupled term in ${\psi }^{\prime *}{b}^{\prime }$ should be eliminated; this implies that we should multiply Equation (41) by the proper quantity for further substitution. This is performed in Section 3.3. Here, we choose to express $b^{\prime }$ in terms of ${\psi }^{\prime }$ using Equation (41), without multiplying Equations (40) and (41) by complex conjugates of ${\psi }^{\prime }$ or $b^{\prime }$ immediately.

Setting

$${\psi }^{\prime }=\varphi \left(r\right)exp\left(il(\theta -ct)\right),b^{\prime }=b\left(r\right)exp\left(il(\theta -ct)\right)$$

and using the expression of b with respect to $\varphi$ from Equations (41) and (40), we obtain

$$(\overline{\mathsf{\Omega }}-c)\left[\ddot{\varphi }+{\displaystyle \frac{\dot{\varphi }}{r}}-{\displaystyle \frac{l^2}{r^2}}\varphi -{\displaystyle \frac{\varphi }{R_d^2}}\right]-\varphi {\displaystyle \frac{\overline{\mathsf{\Omega }}\dot{\overline{b}}}{r(\overline{\mathsf{\Omega }}-c)}}-\varphi {\displaystyle \frac{[\dot{\overline{\omega }}-\dot{\overline{b}}]}{r}}=0,$$

(20)

where $\dot{\varphi }\left(r\right)=d\varphi /dr$.

This equation resembles the Taylor–Goldstein equation [42,43]. This can be understood since they both result from a vorticity and a buoyancy equation (in different planes, horizontal or vertical). Thus, it is appropriate to use the change in variable $\varphi \left(r\right)=\sqrt{\overline{\mathsf{\Omega }}-c}\chi \left(r\right)$. Setting $\alpha =\sqrt{\overline{\mathsf{\Omega }}-c}$, some algebra leads to the equation

$${\displaystyle \frac{1}{r}}{\displaystyle \frac{d}{dr}}\left[r(\overline{\mathsf{\Omega }}-c)\dot{\chi }\right]-{\displaystyle \frac{l^2}{r^2}}{\alpha }^2\chi -{\displaystyle \frac{1}{R_d^2}}{\alpha }^2\chi +\chi {\displaystyle \frac{\ddot{\overline{\mathsf{\Omega }}}}{2}}-{\displaystyle \frac{\chi }{r}}(\dot{\overline{\omega }}-\dot{\overline{b}})+{\displaystyle \frac{\dot{\overline{\mathsf{\Omega }}}\chi }{2r}}-{\displaystyle \frac{\chi {\left(\dot{\overline{\mathsf{\Omega }}}\right)}^2}{4{\alpha }^2}}-{\displaystyle \frac{\chi }{r}}{\displaystyle \frac{\overline{\mathsf{\Omega }}\dot{\overline{b}}}{{\alpha }^2}}=0,$$

(21)

where $\dot{\chi }$ is the derivative of $\chi$.

Only now do we multiply this expression by ${\chi }^{*}$ which is the complex conjugate of $\chi$, and we integrate the equation over r as $\int rdr$. This leads to

$$-\int (\overline{\mathsf{\Omega }}-c)[{\left|\dot{\chi }\right|}^2+\left({\displaystyle \frac{l^2}{r^2}}+{\displaystyle \frac{1}{R_d^2}}\right){\left|\chi \right|}^2]rdr+\int {|\chi |}^2\left[{\displaystyle \frac{\ddot{\overline{\mathsf{\Omega }}}}{2}}+{\displaystyle \frac{\dot{\overline{\mathsf{\Omega }}}}{2r}}-{\displaystyle \frac{1}{r}}(\dot{\overline{\omega }}-\dot{\overline{b}})\right]rdr-$$

$$\int {\displaystyle \frac{\frac{{\left(\dot{\overline{\mathsf{\Omega }}}\right)}^2}{4}+\frac{\overline{\mathsf{\Omega }}\dot{\overline{b}}}{r}}{\overline{\mathsf{\Omega }}-c}}{\left|\chi \right|}^{2}rdr=0.$$

(22)

We can take the imaginary part of this expression; the central term will vanish and we will be left with

$$c_i\left[\int [{|\dot{\chi }|}^2+\left({\displaystyle \frac{l^2}{r^2}}+{\displaystyle \frac{1}{R_d^2}}\right){|\chi |}^2]rdr\right]-c_i\left[\int {\displaystyle \frac{\frac{{\left(\dot{\overline{\mathsf{\Omega }}}\right)}^2}{4}+\frac{\overline{\mathsf{\Omega }}\dot{\overline{b}}}{r}}{{|\overline{\mathsf{\Omega }}-c|}^2}}{\left|\chi \right|}^{2}rdr\right]=0.$$

(23)

For $c_i$ to be non-zero, the second integral must be positive. Therefore, we must have

$$C\left(r\right)={\displaystyle \frac{-\overline{\mathsf{\Omega }}d\overline{b}/dr}{{\left(\dot{\overline{\mathsf{\Omega }}}\right)}^{2}r}}<1/4,$$

(24)

at some r, for instability; this is a necessary condition.

Note that this criterion is reminiscent of the Miles–Howard criterion for the Kelvin–Helmholtz instability, which occurs in stratified fluids with a vertical shear of horizontal velocity [44,45].

We can also write this inequality as

$$\overline{\mathsf{\Omega }}d\overline{b}/dr>-r({\dot{\overline{\mathsf{\Omega }})}}^2/4.$$

(25)

Applying this inequality to the case of Section 3.1, we obtain ${\mathsf{\Omega }}_0{B}_0>0$, for instability, which is the condition previously found.

We can generalize this criterion to the presence of bottom topography $h_1\left(r\right)$. Defining ${\overline{\mathsf{\Omega }}}_1\left(r\right)=(1/2r)d{\overline{h}}_1/dr$, we need to have

$$C_1\left(r\right)={\displaystyle \frac{[{\overline{\mathsf{\Omega }}}_1-\overline{\mathsf{\Omega }}]d\overline{b}/dr}{{\dot{\left(\overline{\mathsf{\Omega }}\right)}}^{2}r}}<1/4,$$

(26)

at some r, for instability. Again, we can see that a seamount is stabilizing for positive $d\overline{b}/dr$.

3.3. A Second Instability Criterion

As mentioned in the previous subsection, we can multiply Equation (40) by ${\psi }^{\prime *}$, the complex conjugate of ${\psi }^{\prime }$, and divide it by $(\overline{\mathsf{\Omega }}-c)$, leading to

$${\omega }^{\prime }{\psi }^{\prime *}-{\displaystyle \frac{\overline{\mathsf{\Omega }}}{(\overline{\mathsf{\Omega }}-c)}}{b}^{\prime }{\psi }^{\prime *}-{\displaystyle \frac{|{\psi }^{\prime }{|}^2}{r}}{\displaystyle \frac{1}{(\overline{\mathsf{\Omega }}-c)}}{\displaystyle \frac{d}{dr}}[\overline{\omega }-\overline{b}]=0.$$

(27)

We also multiply the complex conjugate of Equation (41) by $b^{\prime }$ and divide it by $(\overline{\mathsf{\Omega }}-c^{*})$, leading to

$$|b^{\prime }{|}^2-{\displaystyle \frac{d\overline{b}/dr}{(\overline{\mathsf{\Omega }}-c^{*})}}{b}^{\prime }{\psi }^{\prime *}=0.$$

(28)

Finally, we eliminate $b^{\prime }{\psi }^{\prime *}$ between these two equations, and integrate $\int rdr$ to obtain

$$K^{\prime }+P^{\prime }=-\int {\displaystyle \frac{rdr}{(\overline{\mathsf{\Omega }}-c)}}[{\displaystyle \frac{\overline{\mathsf{\Omega }}(\overline{\mathsf{\Omega }}-c^{*})}{d\overline{b}/dr}}|b^{\prime }{|}^2+{\displaystyle \frac{|{\psi }^{\prime }{|}^2}{r}}{\displaystyle \frac{d}{dr}}(\overline{\omega }-\overline{b})],$$

(29)

where

$$(K^{\prime },P^{\prime })=\int rdr(|{\partial }_r{\psi }^{\prime }{|}^2+l^2|{\psi }^{\prime }{|}^2/r^2,|{\psi }^{\prime }{|}^2/R_d^2),$$

are (twice) the kinetic, potential energies of the perturbation.

Let us now take the imaginary part of this equation; it is

$$c_i\int rdr[{\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}{-c|}^2}}{\displaystyle \frac{2\overline{\mathsf{\Omega }}(\overline{\mathsf{\Omega }}-c_r)}{d\overline{b}/dr}}|b^{\prime }{|}^2+{\displaystyle \frac{|{\psi }^{\prime }{|}^2}{r}}{\displaystyle \frac{d}{dr}}(\overline{\omega }-\overline{b})]=0.$$

(30)

For the vortex to be unstable, $c_i$ must be non-zero (positive), and therefore the two terms in the integral must be opposite-signed. Thus, a necessary condition for instability is

$$2\overline{\mathsf{\Omega }}(\overline{\mathsf{\Omega }}-c_r){\displaystyle \frac{d\overline{b}}{dr}}\mathrm{and}{\displaystyle \frac{d}{dr}}[\overline{\omega }-\overline{b}]\mathrm{must}\mathrm{be}\mathrm{opposite}\mathrm{signed}.$$

(31)

Since this criterion involves $c_r$, it is less straightforward to apply.

We have not found how to rigorously substitute $c_r$ by some $\overline{\mathsf{\Omega }}\left(r_c\right)$, as in the Fjortoft criterion. Obtaining $c_r$ exactly requires solving the linear instability problem (numerically), which is not possible for all mean flow and buoyancy distributions. A rough estimate of $c_r$ could be computed from our analytical solution at marginality.

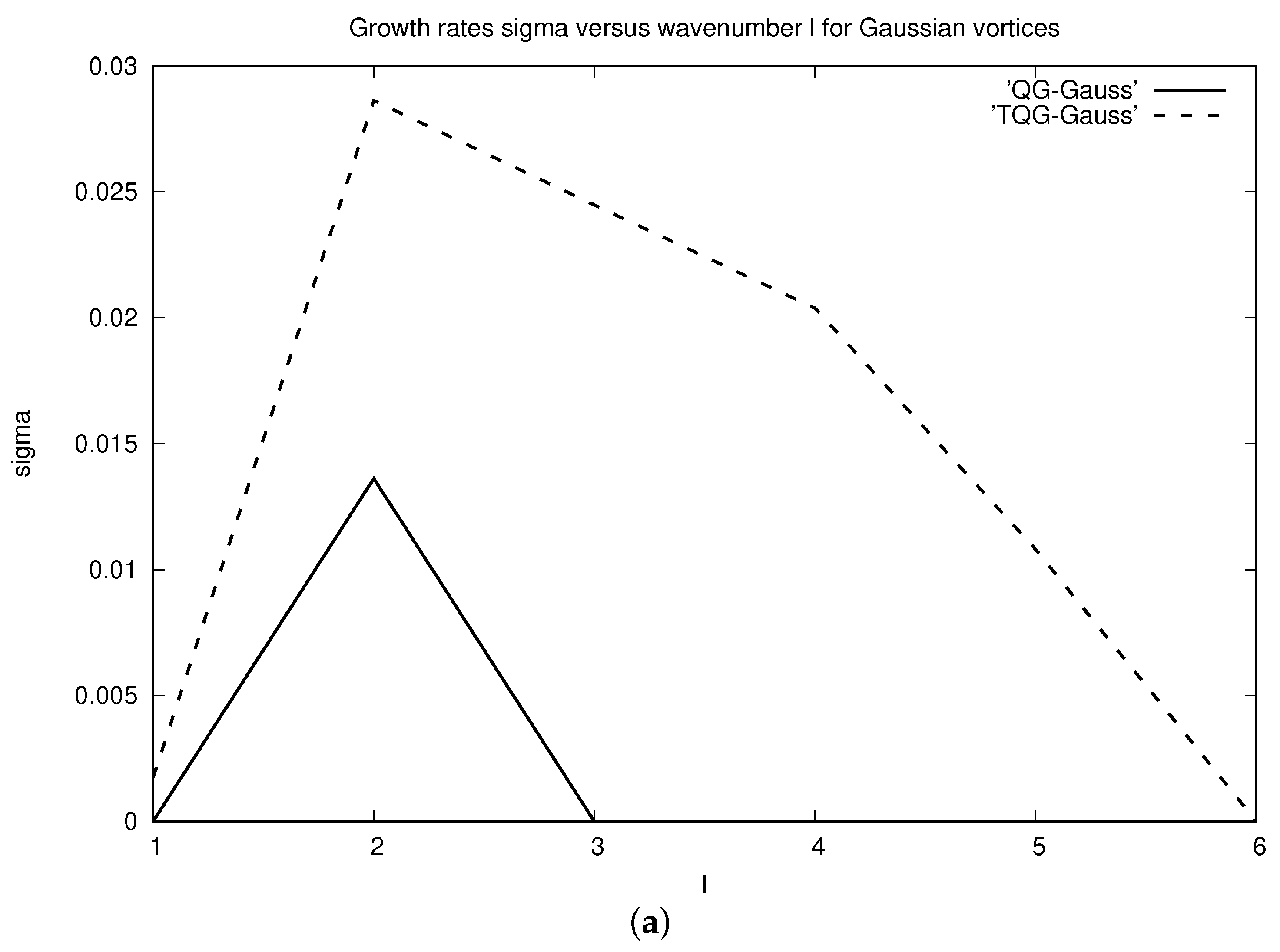
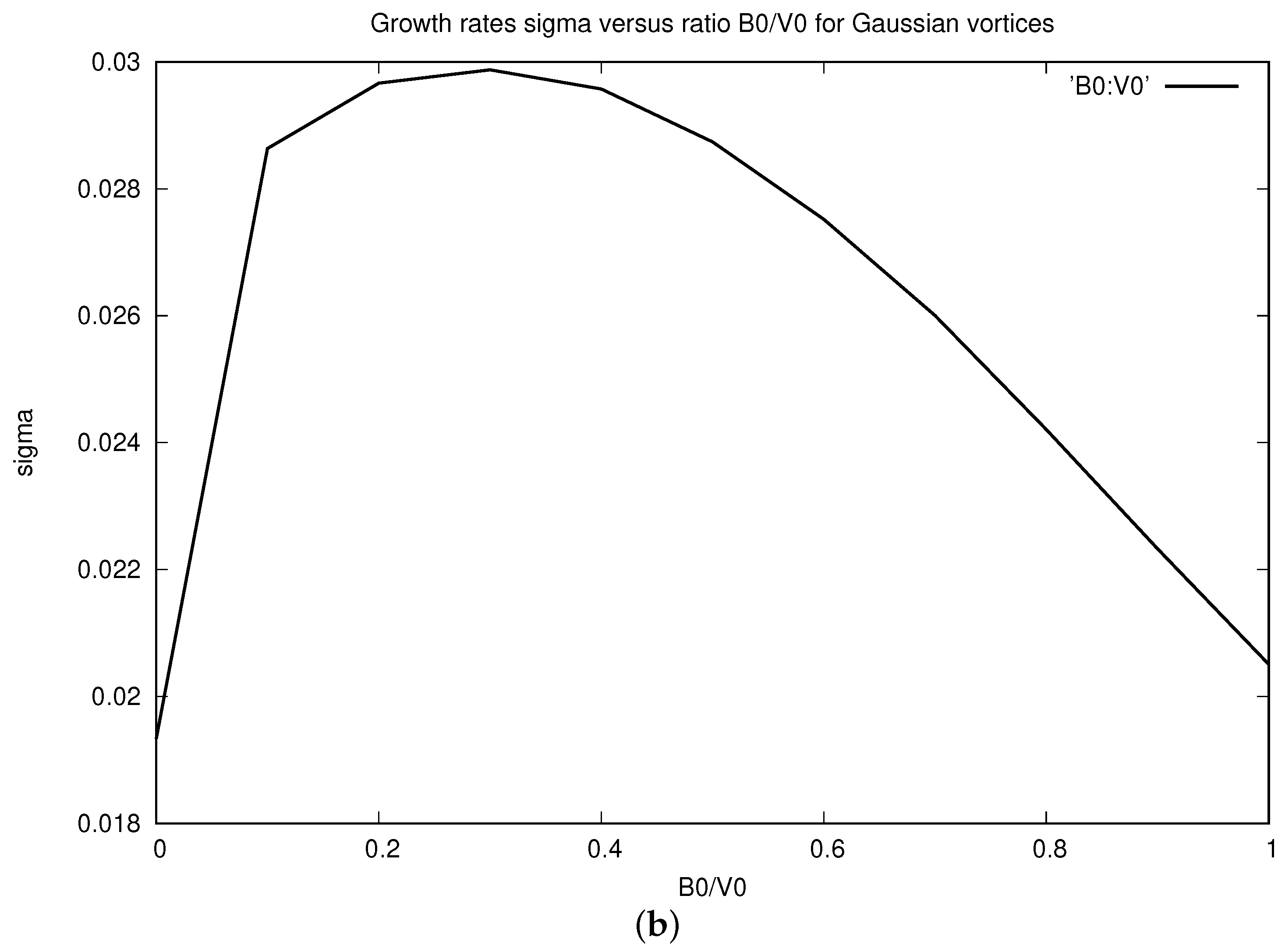
3.4. Numerical Analysis of Linear Stability

Now, we choose a realistic mean distribution of $\overline{V},\overline{b}$ to discretize Equations (40) and (41) over the N steps in r and to solve the linear instability problem numerically. We start with Gaussian mean distributions of streamfunction and of buoyancy:

$$\begin{array}{ccc}\hfill \overline{V}\left(r\right)& =& V_0(r/r_0)exp(-{(r/r_0)}^2),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill \overline{b}\left(r\right)& =& B_{0}exp(-{(r/r_0)}^2).\hfill \end{array}$$

(33)

For simplicity, we set $V_0=1,r_0=1$. This provides a length and a time-scale. We also set $F_1=1/R_d=0$ unless otherwise stated.

As a reference, we solve Equations (40) and (41) with $B_0=0,b^{\prime }=0$; this is the QG case that is well known [46]. For the TQG case, we set $B_0=0.1$.

Figure 1a shows the growth rate $\sigma =l{c}_i$ versus the azimuthal wavenumber l for both cases. In the 2D flow, only $l=2$ is unstable for Gaussian vortices. In the TQG flow, the Gaussian vortex is linearly unstable for all wavenumbers from $l=1$ to $l=5$. In TQG, there is no universally stable solution for $l=1$, contrary to 2D/QG [46]. Furthermore, all growth rates are much larger in TQG than in 2D (twice as large for $l=2$). From this, we can conclude that TQG vortices are not only more unstable than their 2D counterparts, but also that they will develop smaller-scale perturbations. The origin of these differences between the two models can be searched in Equations (40) and (41).

Thus, we conduct a term-by-term analysis of the terms in the two equations for linear instability.

Firstly, it is clear that if we set $d\overline{b}/dr=0$ in both equations, then $b^{\prime }=0$, and Equation (40) becomes the QG linear equation. Indeed, we have the following equations in this case:

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c){\omega }^{\prime }-\overline{\mathsf{\Omega }}{b}^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d}{dr}}\overline{\omega }& =& 0,\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c)b^{\prime }& =& 0,\hfill \end{array}$$

(35)

leading to

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c){\omega }^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d}{dr}}\overline{\omega }& =& 0,\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill b^{\prime }& =& 0.\hfill \end{array}$$

(37)

Therefore, a non-zero mean buoyancy gradient is necessary to account for this difference.

It is also of interest to see that if we cancel the mean buoyancy gradient in the second equation only, the growth rates in this case are comparable to those of QG as long as $B_0/V_0\ll 1$. Then the equations would be

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c){\omega }^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d}{dr}}(\overline{\omega }-\overline{b})& =& 0,\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c)b^{\prime }& =& 0,\hfill \end{array}$$

(39)

We see (in this theoretical approach) that the mean buoyancy gradient is more important in the second equation than in the first one, to account for the difference between QG and TQG dynamics. In this second case, this difference would only be driven by the ratio of $B_0$ to $V_0$ (like-signed $B_0$ and $V_0$ increase the mean vorticity/buoyancy gradient).

More interesting is the cancellation of only the $\overline{\mathsf{\Omega }}{b}^{\prime }$ term in Equation (40); this renders the first equation QG-like (independent from $b^{\prime }$). Equation (41) then only provides $b^{\prime }$ as a function of ${\psi }^{\prime }$ and the growth rates are those of QG, again in the limit $B_0/V_0\ll 1$. In this case, the equations would be

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c){\omega }^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d}{dr}}(\overline{\omega }-\overline{b})& =& 0,\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill (\overline{\mathsf{\Omega }}-c)b^{\prime }-{\displaystyle \frac{{\psi }^{\prime }}{r}}{\displaystyle \frac{d\overline{b}}{dr}}& =& 0,\hfill \end{array}$$

(41)

Therefore, clearly, the term $\overline{\mathsf{\Omega }}{b}^{\prime }$ is chiefly responsible for the difference between the two dynamics: TQG on the one hand, and QG with a passive b tracer on the other.

For the same (Gaussian) flow, we study now the influence of the ratio $B_0/V_0$ on the growth rate $\sigma =l{c}_i$ for $l=2$ (see Figure 1b). Clearly, in the TQG model, the coupling of the vorticity equation with the buoyancy equation destabilizes the flow for small values of this ratio (compared to the QG model). Increasing this ratio to unity then decreases the growth rates. A maximal growth rate is obtained for $B_0/V_0\sim 0.3$.

Again for the Gaussian vortex, with $l=2$ and with $B_0=0.1,V_0=1.0$, we test the sensitivity of growth rates to free surface effects. We call $F_1=1/R{d}^2$ and plot in Figure 2a, the growth rates with respect to $F_1$ both in QG and in TQG. In TQG, the growth rates of horizontal shear instability decrease when $F_1$ increases, as in QG flows [47].

Finally, still for the Gaussian vortex, with $l=2$ and with $B_0=0.1,V_0=1.0$, we test the sensitivity of growth rates to bottom topography. This bottom topography is chosen via ${\mathsf{\Omega }}_1\left(r\right)={\mathsf{\Omega }}_{1}exp(-r^2)$ (see its formal expression in Section 3.2). Figure 2b confirms that a seamount reduces the instability of the flow if $B_0>0$.

Finally, again for the Gaussian vortex, with $l=2$ and with $B_0=0.1,V_0=1.0$, we test the sensitivity of growth rates to bottom topography. This bottom topography is chosen via ${\mathsf{\Omega }}_1\left(r\right)={\mathsf{\Omega }}_{1}exp(-r^2)$ (see its formal expression in Section 3.2). Figure 2b confirms that a seamount reduces the instability of the flow if $B_0>0$.

In 2D flows, it is well known that the growth rates of the perturbation increase with the mean vorticity shear of the vortex. To this aim, we now use the following family of profiles, also known as $\alpha$-exponential profiles [39], for the velocity

$$\begin{array}{ccc}\hfill \overline{V}\left(r\right)& =& V_0(r/r_0)exp(-{(r/r_0)}^{\alpha }),\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill \overline{b}\left(r\right)& =& B_{0}exp(-{(r/r_0)}^{\alpha }).\hfill \end{array}$$

(43)

Figure 3a shows the growth rates versus $\alpha$ in the QG case ($B_0=b^{\prime }=0,F_1=0$), and Figure 3b in the TQG case.

As usual for 2D dynamics, we observe that $\sigma$ increases with $\alpha$ for $l=2,3$; $\alpha$ is not large enough in the chosen range to allow the growth of modes $l=4,5$. We recover the critical value of $\alpha \sim 1.9$ for $l=2$ as mentioned in Ref. [39]. Barotropic instability occurs only for steep-enough vortices, all the more so as the waves are short.

On the contrary, in TQG dynamics, vortices with “flat” vorticity profiles are unstable to both long and short waves. A small growth rate $\sigma \sim 0.03$ exists for $l=1-5$ over a wide range of values of $\alpha$. The $\sigma$ curves for $l=2,3$ emerge from this minimal growth rate; it must be noted that for $\alpha$ that is large enough ($\sim 3–4$), the growth rates in the 2D and TQG are comparable for $l=2,3$.

Physically, one must exert caution for $\alpha \le 1.0$, though the results are mathematically correct. For $\alpha =1.0$, we have $\overline{\omega }=2V_0/r_0[2-r/r_0]exp(-r/r_0)$. Vorticity behaves as $exp(-r)$ near the center and, in a two-dimensional representation, exhibits a cusp at the center. Therefore, it is recommended to consider only cases with $\alpha >1$.

4. Nonlinear Evolution

After the linear analysis of stability, we study numerically the nonlinear regimes of perturbed unstable vortices. Firstly, we study a reference case with Gaussian distributions of buoyancy and streamfunction, with a given ratio between their amplitude, and an elliptical perturbation. Then we will vary all these parameters, and briefly study the influence of a finite deformation radius and of circular topography.

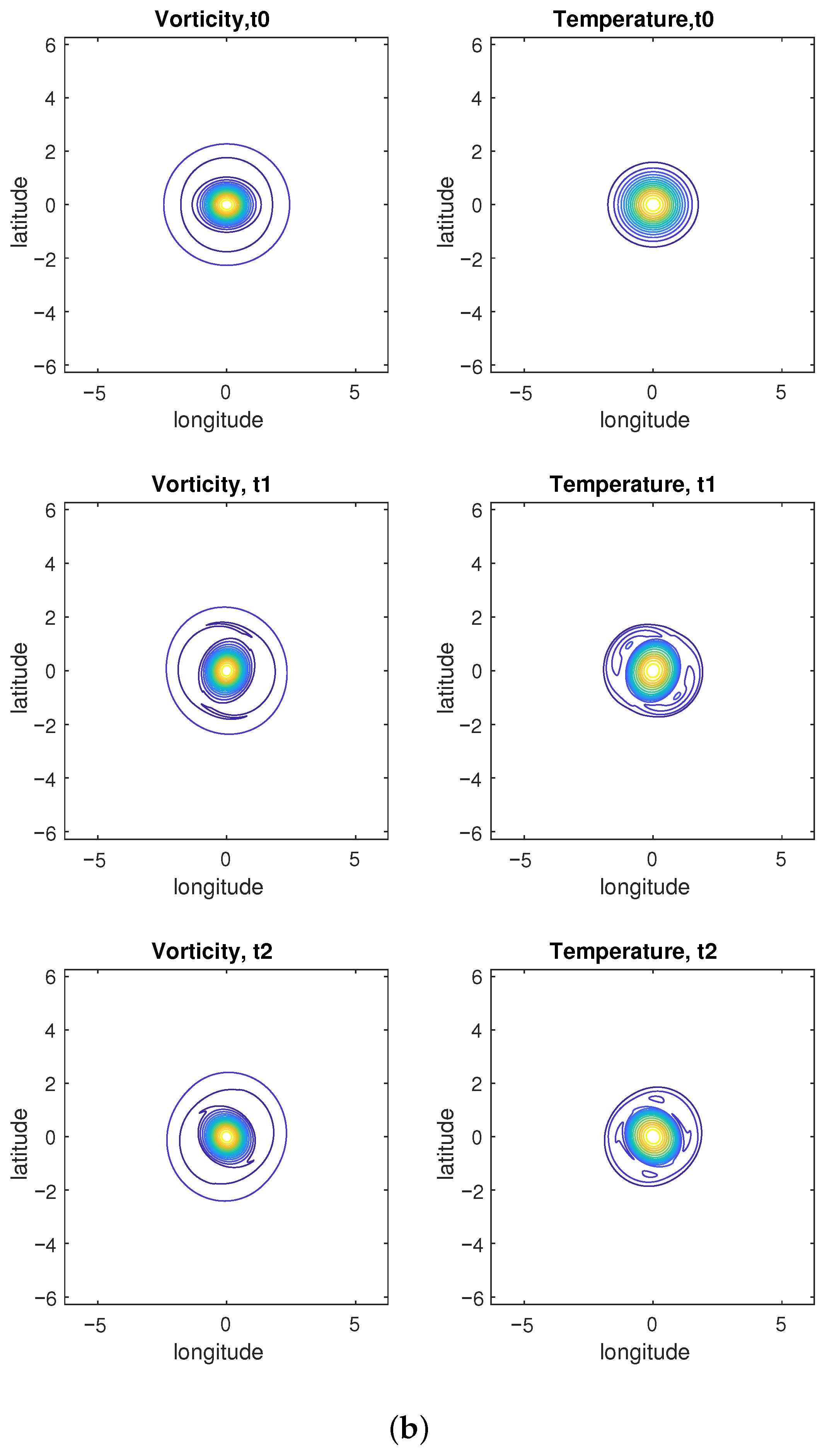
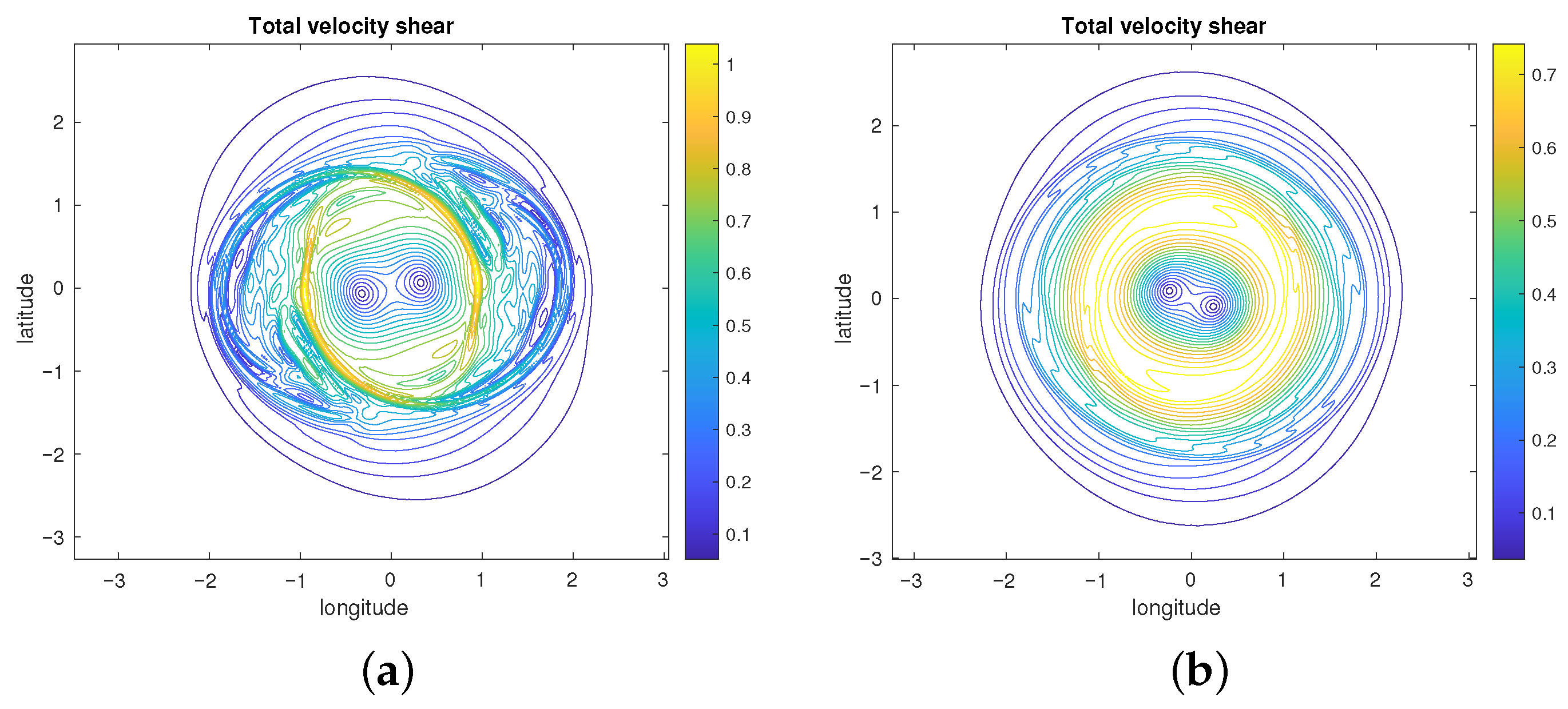
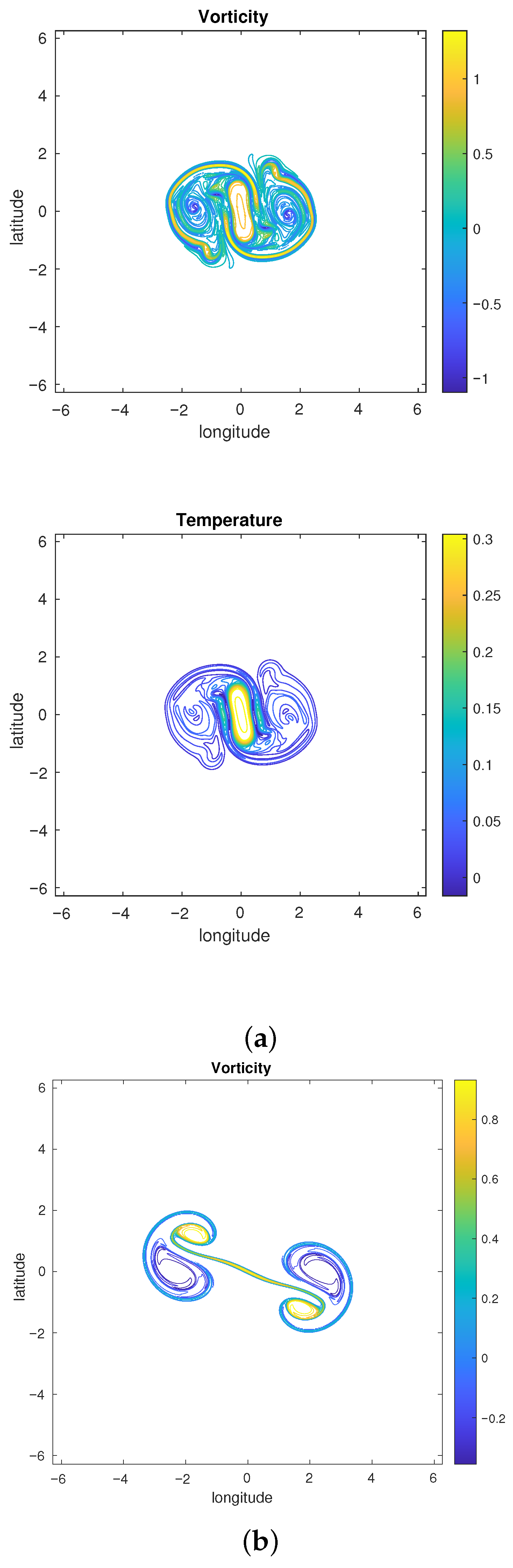
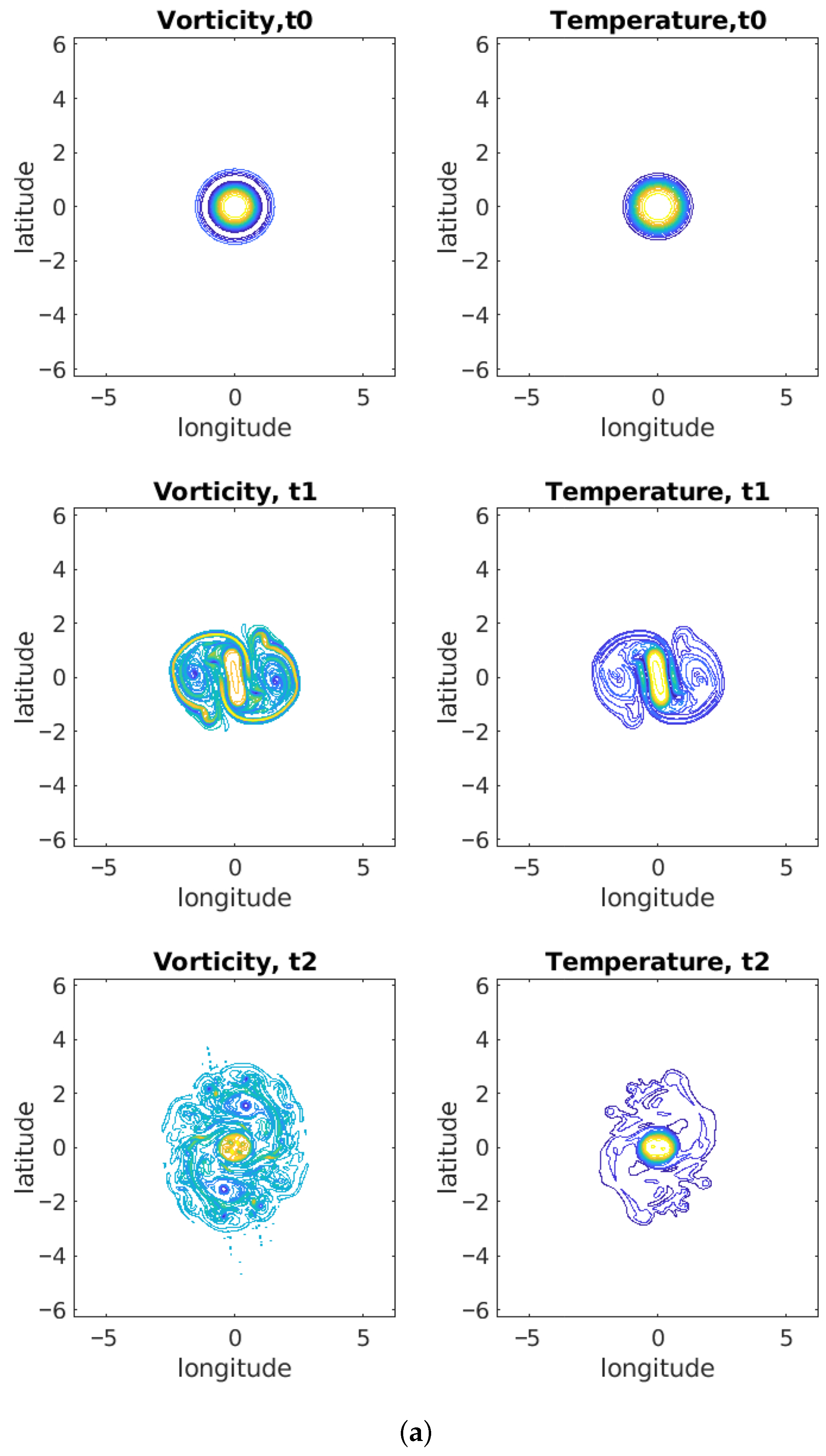
4.1. Reference Case

Our reference case has

$$\psi ={\psi }_{0}exp(-r^2/r_0^2),b=b_{0}exp(-r^2/r_0^2),b_0/{\psi }_0=0.3$$

with only an elliptical perturbation initially (Figure 4a,b at time $t_0=0$). This elliptical perturbation is obtained by stretching the x and y-coordinates initially by a factor $1+ϵ$ and $1-ϵ$, respectively (where $ϵ=0.05$). With these conditions, we ran the TQG model and the decoupled 2D model in parallel. Figure 4 shows the time evolution of vorticity and of buoyancy in the two cases. Initially, the decoupled 2D model dynamics creates filaments during the reorganization of the vortex periphery, yet fewer than the TQG model (see Figure 3a,b at time $t_1=100$). At finite times, the TQG model creates more small-scale features than the decoupled model, in particular radially.

To interpret this appearance of strong vorticity gradients, we note again that the term $\overline{\mathsf{\Omega }}{b}^{\prime }$ plays a key role in the coupling of the vorticity and buoyancy equations. Vorticity and thermal Rossby waves propagate circularly on the radial vorticity and buoyancy gradients. Since these gradients (and the mean flow) are not constant, the buoyancy anomaly of these waves is sheared and forms filaments. Via the coupling, vorticity anomalies are formed; they are also sheared. This is clearly seen in the TQG model vorticity plots (Figure 4a). The vorticity gradients are stronger than those of buoyancy. Filaments are formed around the vortex core. The vorticity anomalies lead to shear flow growth, which increase ${\omega }^{\prime }$ and $b^{\prime }$.

To quantify this process further, we decompose the vorticity anomalies azimuthally in Fourier modes, and radially in Bessel components. This is performed via

$$\begin{array}{ccc}\hfill {\omega }^{\prime }(r,\theta ,t)& =& \sum _l{C}_l(r,t)cos\left(l\theta \right)+S_l(r,t)sin\left(l\theta \right),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill A_l\left(t\right)& =& (2/R^2)\int rdr[C_l^2+S_l^2],\hfill \end{array}$$

(45)

where R is an arbitrary radius (here chosen as $\pi$), large enough to encompass the vortex core and periphery. The modal amplitudes $A_l\left(t\right)$ (of the azimuthal Fourier spectrum) are plotted in Figure 5a,c. On this graph, only the integer values of l have to be considered. Clearly, mode $l=2$ remains the dominant (and nearly sole) mode in the decoupled evolution, while higher modes are much stronger in the TQG model. They correspond, in physical space, to the small-scale features observed in the vorticity field.

Secondly, for $l=2$, we project $C_l(r,t)$ and $S_l(r,t)$ onto a basis of Bessel functions using their orthogonality

$$\begin{array}{ccc}\hfill C_{2k}\left(t\right)& =& \int rdr{C}_2(r,t)J_2({\alpha }_{2k}r/R_0),\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill S_{2k}\left(t\right)& =& \int rdr{S}_2(r,t)J_2({\alpha }_{2k}r/R_0),\hfill \end{array}$$

(47)

and

$$A_{2k}\left(t\right)=\sqrt{C_{2k}^2+S_{2k}^2}\left(t\right),$$

(48)

where $R_0$ is the vortex radius (here equal to unity), and ${\alpha }_{2k}$ is the $k^{th}$ root of the Bessel function $J_2$. It is known that for increasing ${\alpha }_{2k}$, the Bessel function $J_2$ oscillates faster radially (corresponding to thinner structures). Only the integer values of k are physically admissible but for the clarity of representation, the figure interpolates the values of the amplitudes of vorticity anomalies between these integer values of k. Figure 5b,d indicate that radially short perturbations (components $k=3,4,5$) grow initially on the vortex in the decoupled 2D dynamics, but they rapidly decay afterwards. On the contrary, short radial perturbations remain having larger amplitude in the TQG dynamics for the whole duration of the simulation.

Now, we compute the two components of the deformation, the normal strain rate ${\sigma }_n={\partial }_{x}u-{\partial }_{y}v$, the shear strain rate ${\sigma }_s={\partial }_{x}v+{\partial }_{y}u$, and, from them, the total strain rate $\sigma =\sqrt{{\sigma }_n^2+{\sigma }_s^2}$. We plot the latter, for $t=100$ in the simulation, in Figure 6a,b for the TQG and the decoupled models. Clearly, the deformation rate is stronger and more spread out in the TQG simulation. Also, many more small-scale intricate patterns are seen in this simulation compared with the 2D decoupled model one.

Finally, using the Lagrangian conservation of buoyancy in both TQG and 2D equations, one can derive an equation for the evolution of the gradient of buoyancy (equivalently, of buoyancy). In index form, we have

$${\displaystyle \frac{{\partial }_{i}b}{dt}}=-\left({\partial }_i{u}_j\right)\left({\partial }_{j}b\right),$$

(49)

which can be multiplied by the adjoint of the buoyancy gradient to yield

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }_{i}b{\partial }_{i}b}{dt}}=-\left({\partial }_i{u}_j\right)\left({\partial }_{i}b\right)\left({\partial }_{j}b\right)=F.$$

(50)

For the frontogenetic tendency, or frontogenesis function, F indicates where the buoyancy (or buoyancy) gradients will amplify or decay, and thus where filaments will grow or disappear. This function is shown for our TQG simulation in Figure 7. The regions shown correspond to the regions of strong buoyancy gradient in Figure 4a at $t=100$. Clearly, buoyancy gradients are formed in the vicinity of the deformed vortex core; they tend to disappear in the periphery.

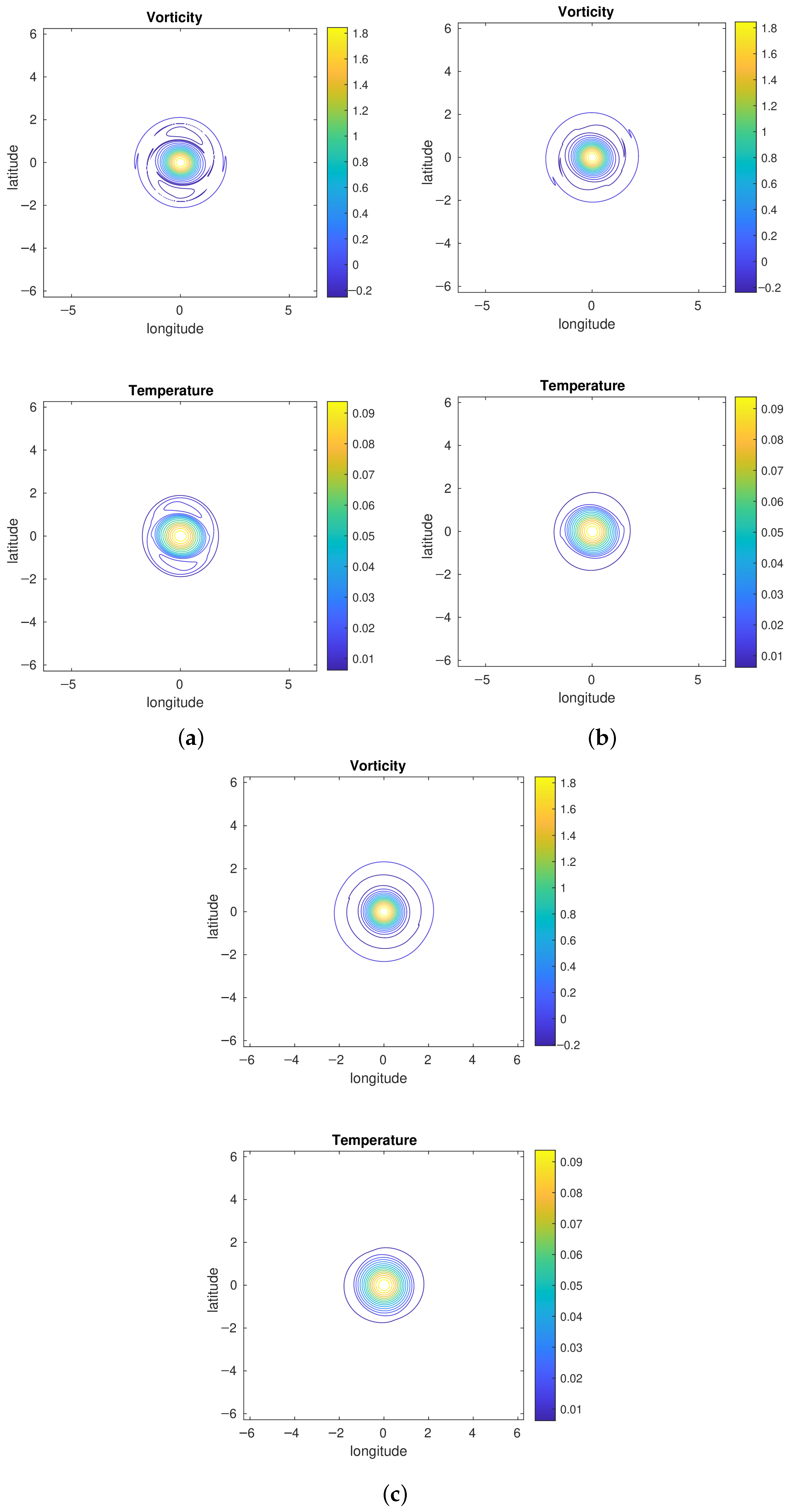
4.2. Parameter Sensitivity

4.2.1. Vorticity Profile Steepness and Relative Intensity of the Mean Buoyancy

Firstly, for an elliptical perturbation ($l=2$), we vary the steepness ($\alpha$) of the mean velocity and buoyancy profiles and the ratio of their intensities ($B_0/V_0$). Here we have

$$\begin{array}{ccc}\hfill \overline{V}\left(r\right)& =& V_0(r/r_0)exp(-{(r/r_0)}^{\alpha }),\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill \overline{b}\left(r\right)& =& B_{0}exp(-{(r/r_0)}^{\alpha }).\hfill \end{array}$$

(52)

Figure 8 indicates that for Gaussian vortices ($\alpha =2$), tripoles are formed by the instability of the circular vortex. Tripole formation is less efficient as $B_0/V_0$ grows. For large values of this ratio, the end-state of the nonlinear simulation is a quasi-axisymmetric vortex. Indeed, as mean buoyancy is larger, the vortex is more prone to small-scale instabilities (as shown by the linear instability theory). This renders the satellites of the tripole less coherent. Thus, their robustness is lesser and the shear that they exert on the vortex core is weaker. For large $B_0/V_0$, the satellites are not coherent any more and the tripolar state is only transient.

For steeper vortices, the presence of filaments in the tripole satellites and around them becomes more prevalent until the whole vortex periphery is completely turbulent (for growing $\alpha$, with constant $B_0/V_0$; see Figure 9a). Also, a mode $l=4$ is observed in the vortex evolution due to both wave–wave interactions (from the fundamental mode $l=2$) and to the growth of small waves in the TQG model (see also Figure 9a). For steep vortices, the radial gradient of mean vorticity is large enough to lead to vortex breaking into two dipoles (the usual irreversible, fully nonlinear, evolution of strongly unstable vortices with $l=2$; see Figure 9b). Then, nonlinear harmonic formation from $l=2$ is more efficient than the growth of small waves via the TQG dynamics. Again, for large $B_0/V_0$, the tripole satellites lose their coherence and are not able to maintain large enough a shear on the vortex core and the whole structure tends towards axisymmetry.

4.2.2. Influence of Stratification and of Bottom Topography

To assess the influence of stratification, we run simulations of the case $B_0/V_0=0.1,\alpha =2,l=2$, increasing $1/R_d^2$ from zero. We have run the model with three values of $1/R_d^2$: 0.25, 1.0, 4.0.

Figure 10 shows the various final states of vorticity and buoyancy (with increasing $1/R_d^2$). Clearly, the vorticity satellites (in the periphery), contributing to the tripolar shape of the vortex, and the small-scale features are progressively erased by the increasing vortex stretching. The vortex core is also more circular. This confirms the linear stability analysis which indicated a decreasing instability with increasing $1/R_d^2$.

To assess the role of bottom topography, we run a simulation with a cubic exponential vortex ($\alpha =3.0$, with $B_0/V_0=0.1$, $1/R_d^2=0$, an elliptical perturbation ($l=2$) and a Gaussian topography $h=h_{0}exp(-{(r/r_0)}^2$, with $h_0=1.0,r_0=1.0$. In Figure 11, we compare the nonlinear evolution of a quartic exponential vortex ($\alpha =4.0$) perturbed elliptically ($l=2$) with $B_0/V_0=0.3$, over a flat bottom (no topography) and over a seamount (positive topography). Over the flat bottom, the unstable vortex transforms first into a tripole with filamentary satellite, an evolution already seen (above). Finally, the vortex periphery becomes turbulent with many small-scale features. On the contrary, over the seamount, the perturbation seems damped and the vortex becomes quasi-circular. This stabilization is in agreement with the linear stability analysis.

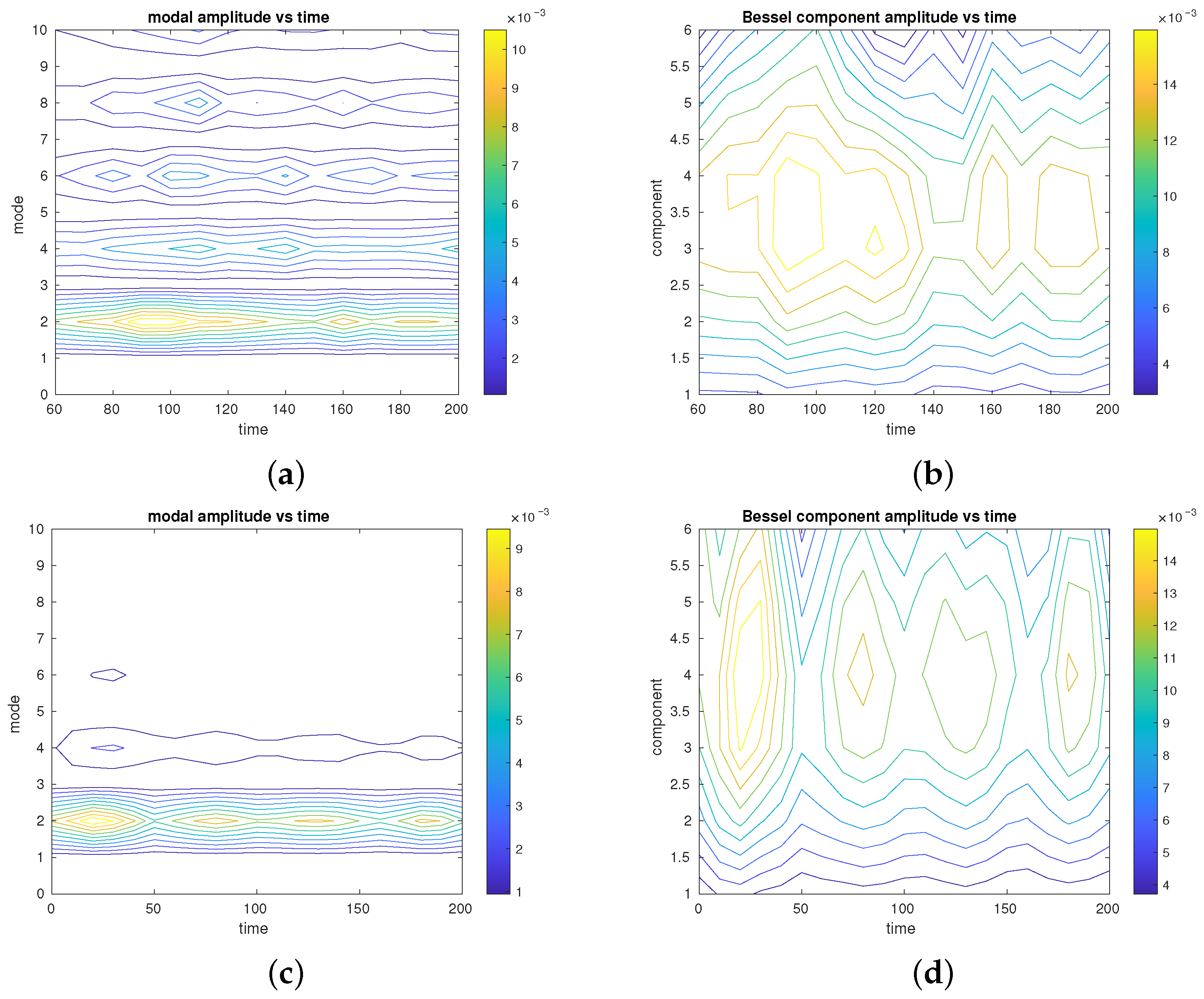
4.2.3. Nonlinear Evolutions with Higher Wavenumber Perturbations

As shown by Refs. [48,49,50], more complex vortex aggregates than tripoles can exist in two-dimensional incompressible flows. Therefore, we study here their possible counterparts in the TQG model. We search quadrupolar vortices formed from the instability of circular vortices, with a mode $l=3$ initial perturbation. The growth of higher-wavenumber perturbations on a power-exponential vortex requires a higher degree of the power (a larger horizontal velocity shear), than that of low-mode perturbations. Here, we consider power-exponential vortices (Equation (3)) with $\alpha \ge 3.5$.

Figure 12a summarizes the various nonlinear evolutions of the unstable vortices when $B_0/V_0=0.1$ or $0.3$. We note that a smaller horizontal shear is needed to stabilize a quadrupole nonlinearly with small $B_0/V_0$, while quadrupoles degenerate into tripoles for larger values of $\alpha$ when $B_0/V_0=0.3$. Again, this shows that the presence of buoyancy in the mean flow weakens the ability of the initial perturbation to grow and (possibly) stabilize nonlinearly at large amplitude.

Figure 12b,c shows two final states of our simulations for unstable TQG vortices with $l=3$ perturbations and $B_0/V_0\le 0.3$. Either the perturbation with $l=3$ decays asymmetrically into a vortex with the superposition of modes $l=2$ and $l=1$, that is, an asymmetric tripole (Figure 12b), or they form a rotating quadrupole (Figure 12c). Note that this latter evolution occurs for lower values of $B_0/V_0$ (that is, 0.1) than for the former evolution (that is, 0.3). This shows that, for large values of $B_0/V_0$, vortices with $l=3$ perturbations are less prone to form quadrupoles. Also, for large $B_0/V_0$, more filaments (short-scale perturbations) develop during the nonlinear evolution of the unstable vortex.

5. Discussion

Our study has, first, provided stability criteria and simple linear solutions to understand the effect of buoyancy coupling with vorticity, on the instability of circular vortices, that is, how vortex instability in the TQG model differs from that in the QG model. The linear stability analysis has shown that the vortices in the TQG model are more unstable than in the QG model, with notably larger growth rates for short waves. Second, the numerical simulations with the nonlinear TQG model have shown that indeed, the short waves grow more on unstable vortices in a TQG model. But paradoxically, this has a rather stabilizing effect on the nonlinear evolution of the linearly unstable vortices, compared with the QG case. This is explained as follows.

During the development of the instability of these vortices, the external annulus of vorticity breaks into l independent vortices. These peripheral vortices can deform and break the vortex core, leading either to rotating multipoles, or to l dipoles [39]. But, in the TQG model, the appearance of filaments and of small vortices render these peripheral vortices less coherent. As a consequence, these latter exert a weaker shear on the vortex core and do not distort it as much. Thus, the vortex is finally less unstable in the nonlinear evolution.

In our study, we have chosen a family of radial vorticity profiles for the mean circular flow; this family is that of alpha-exponential profiles. Note that such profiles are common in observations of vortices at sea [41]. Furthermore, previous studies [46] have shown that the analytical form of the radial profile of vorticity is not essential, as long as it belongs to a family of vortices (e.g., unshielded monopoles, shielded monopoles, unshielded annuli, etc.). Here, our mean flows (the circular flows) correspond to shielded monopoles, that is, opposite-signed vorticity in the vortex core and and in its periphery.

It is of interest to note that during the instability of the circular vortices, elliptical vortices have been observed, as well as dipoles. Therefore, extending our study to the TRSW model will bridge our study and those by Refs. [36,37].

Now, only barotropic (horizontal shear) instability has been studied here and it would be of interest to generalize our results to at least a two-layer TQG model to allow the study of baroclinic instability. Note that the TQG equations are not fully coupled (vorticity is not included in the buoyancy equation), contrary to the two-layer quasi-geostrophic (QG) equations in which each layerwise potential vorticity depends on the other layer streamfunction. Therefore, we can expect new coupling mechanisms between vorticity and buoyancy in a two-layer model.

Also, concerning the equations, the vorticity and buoyancy equations are different in mathematical structure: buoyancy is directly advected (that is, conserved in a Lagrangian manner) while vorticity is advected and modified by the Jacobian of streamfunction and temperature; furthermore, the inversion of vorticity into streamfunction has a widening effect on horizontal fields. The absence of vorticity conservation is another difference between the two-equation TQG model and the two-layer QG model.

Continuing with the analogy and differences between TQG and QG models, we must note that TQG dynamics share with SQG (surface quasi-geostrophy [51]) the ability to generate small-scale features in the nonlinear dynamics. But a major dynamical difference exists between these two models. In the TQG model, the streamfunction derives from the inversion of the vorticity. Therefore, the external velocity field of a vortex decays as $1/r$. In the SQG model, the streamfunction is obtained from the inversion of the buoyancy (a square root of the Laplacian of streamfunction). This leads to a different Green’s function for the inversion and the external velocity field of a buoyancy patch (in SQG) decays in $1/r^2$. Therefore, the small-scale features are dynamically less active in the SQG than in the TQG model. Consequently, vortex instability in the SQG model has much similarity with that in the QG model, contrary to TQG.

One can add that even in the shallow-water (SW) model, where velocity is not geostrophic, vortex instability is comparable to that observed in QG. Therefore, TQG stands apart in this whole range of models (2D, QG, SQG, SW, TQG). It must be remembered that it is an idealized and simplified model. Comparison with oceanic features is difficult, all the more so as the specificity of TQG is the formation of small-scale features, not easily observed via in situ nor satellite sensors.

6. Conclusions

The previous study of vortices in the thermal rotating shallow-water (TRSW) model [38] has yielded features and evolutions quite comparable to those observed in our study. A detailed comparison between TQG and TRSW is now desirable to assess the role of non-geostrophic velocity in vortex evolution in these models. Can our stability criteria be extended, for instance, to weakly non-geostrophic flows?

For oceanographic applications, it could be of interest to compare vortex dynamics in the TQG model to those in a Primitive Equation model with a surface mixed layer. Indeed, such a model would include all physical processes at work in the ocean, in particular, low- and high-frequency dynamics (the latter being excluded in TQG), mechanical and thermohaline forcing by the atmosphere, complete thermodynamics, etc. Realistic ocean models could serve more easily as a testbed for TQG than oceanographic observations (for the reasons mentioned above). A next step in the assessment of TQG models could be the coupling of two such models, one for the ocean surface and one for the atmospheric boundary layer, and the study of vortex and jet dynamics in such coupled models. This research is underway.