Study of Thixotropic Characteristics of a Kerosene Gel Propellant by Bayesian Optimization
Abstract
1. Introduction
2. Results and Discussion
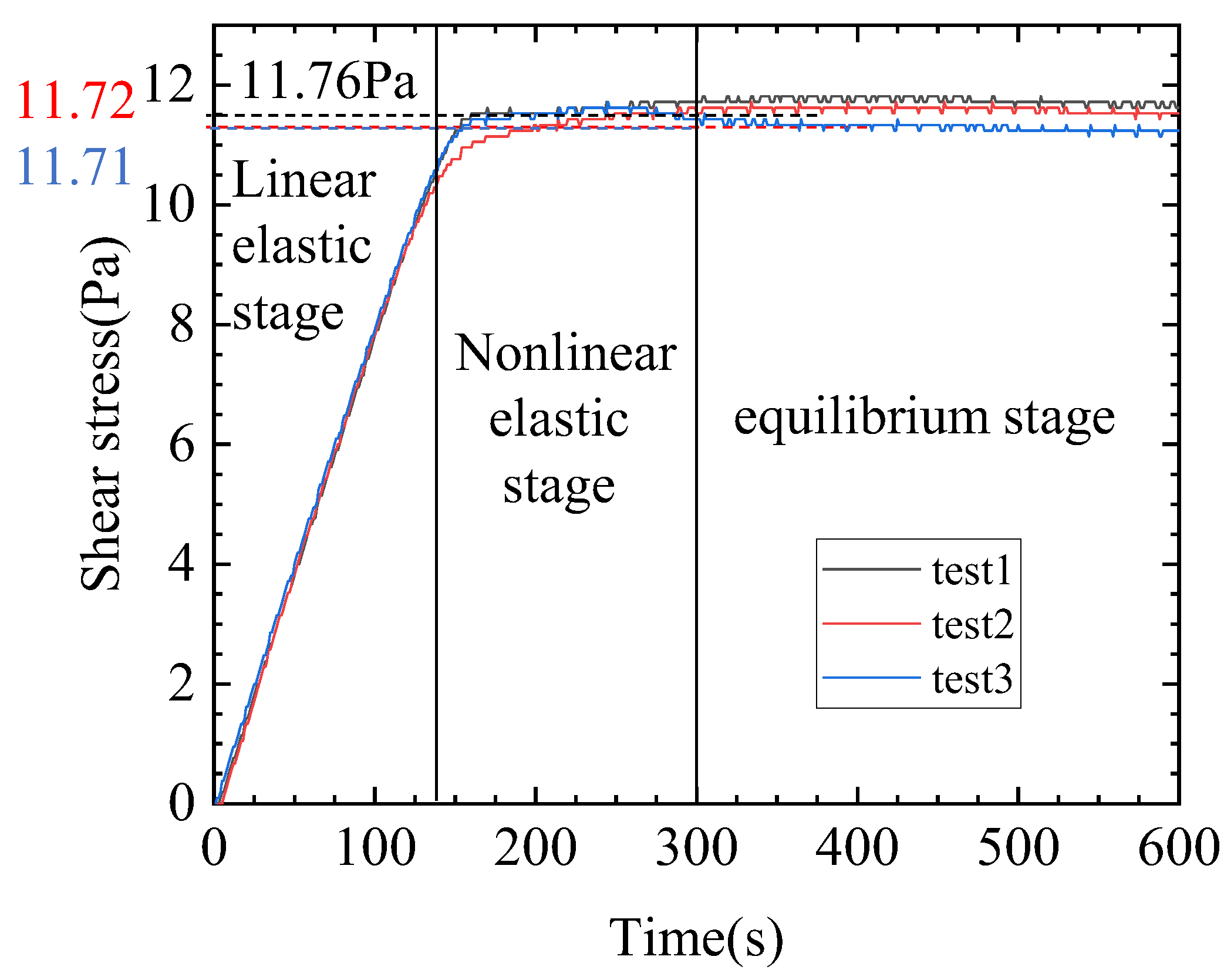
2.1. Experiment and Discussion
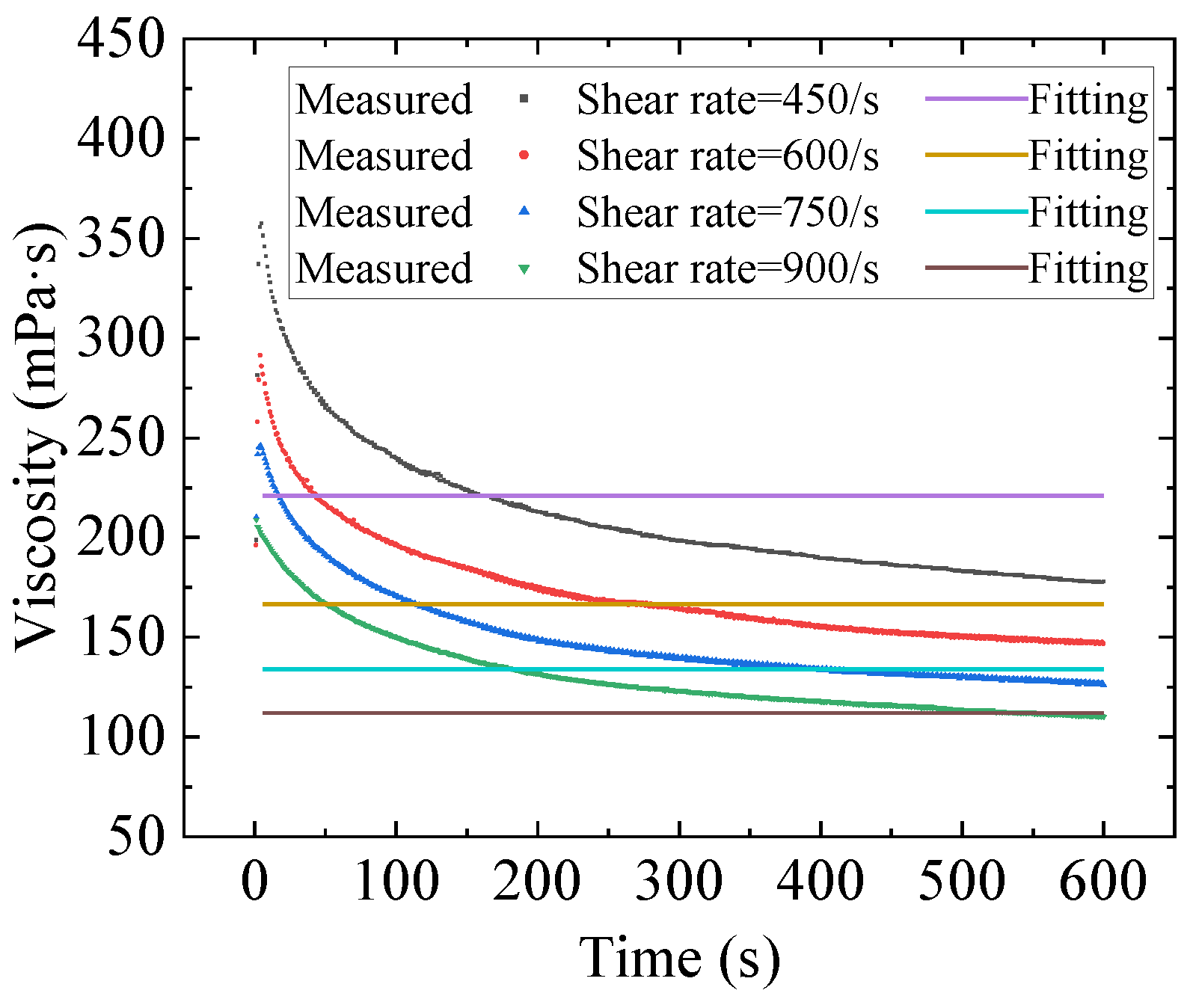
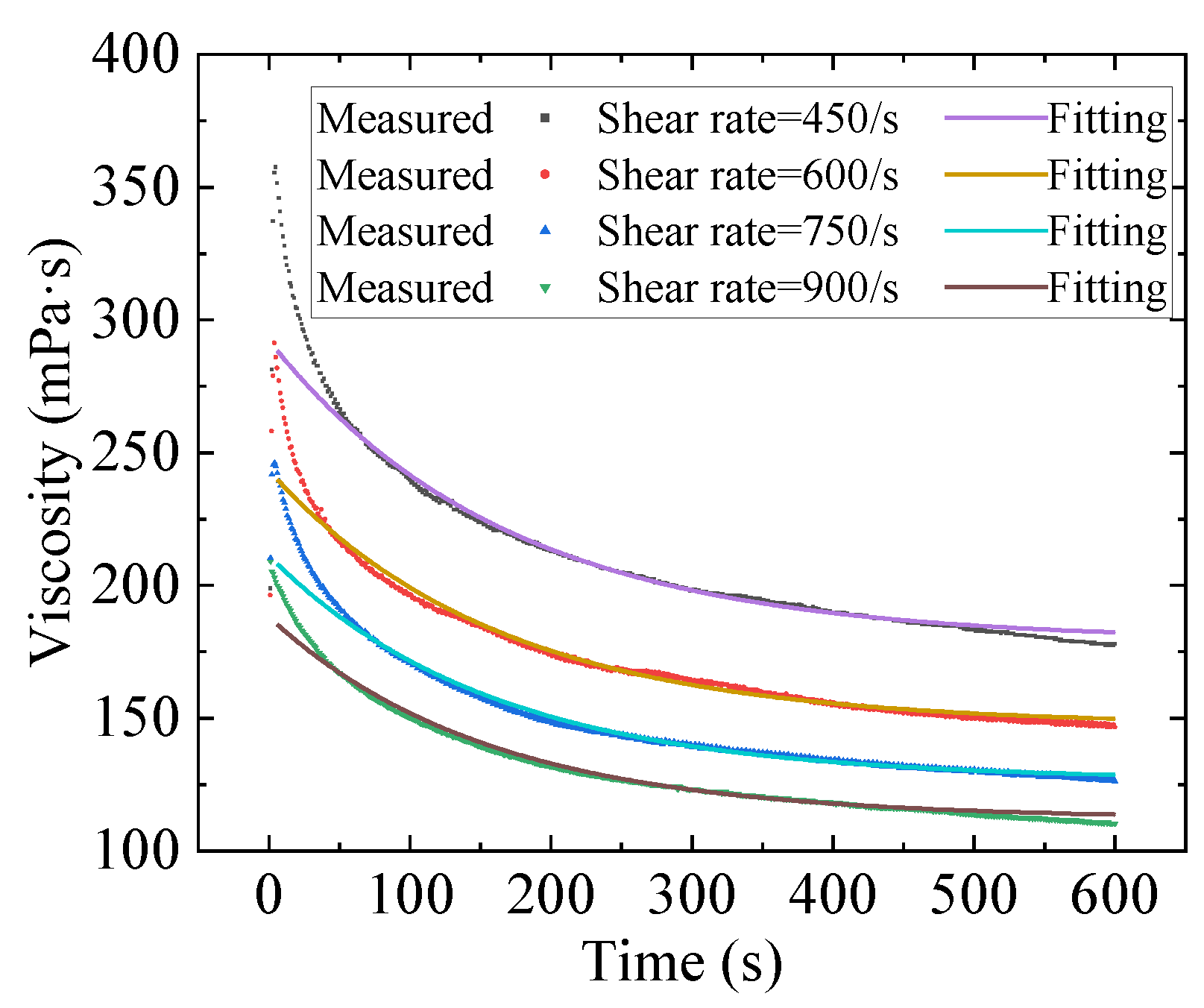
2.2. Numerical Fitting Results and Discussion
3. Conclusions
- (1)
- Using kerosene, Thixatrol ST and absolute ethanol, the kerosene gel system was successfully prepared through water bath heating and high-speed dispersion. The system features yield, shear thinning and thixotropic properties.
- (2)
- The kerosene gel is a plastic fluid with a yield stress of approximately 11.73 Pa. The yield stress was generated by the formation of a network structure through hydrogen bonding between the gelling agents. Upon high-speed shearing, the yield stress disappeared due to the destruction of the network structure.
- (3)
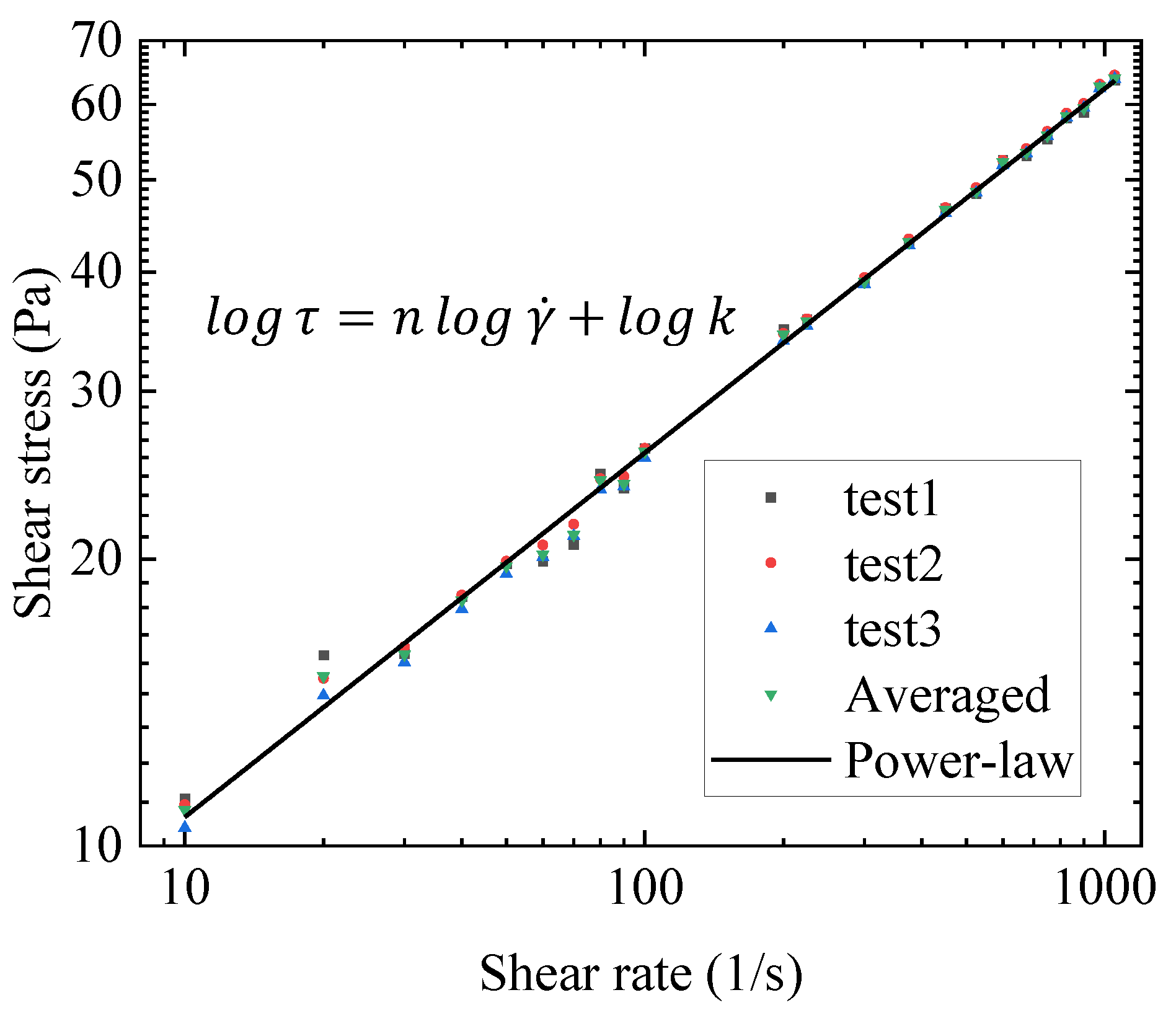
- The gel has shear thinning and thixotropic properties. Hysteresis loop experiments indicated that the apparent viscosity of gels without high-speed pre-shearing decreased with an increasing shear rate. In the rising and falling stages of the shear rate, the gel viscosity showed a prominent time dependence, that is, thixotropy. The high-speed pre-shearing gel exhibited only shear-thinning properties. The power-law model had a good fitting effect on the rheological properties of the gel after high-speed shearing.
- (4)
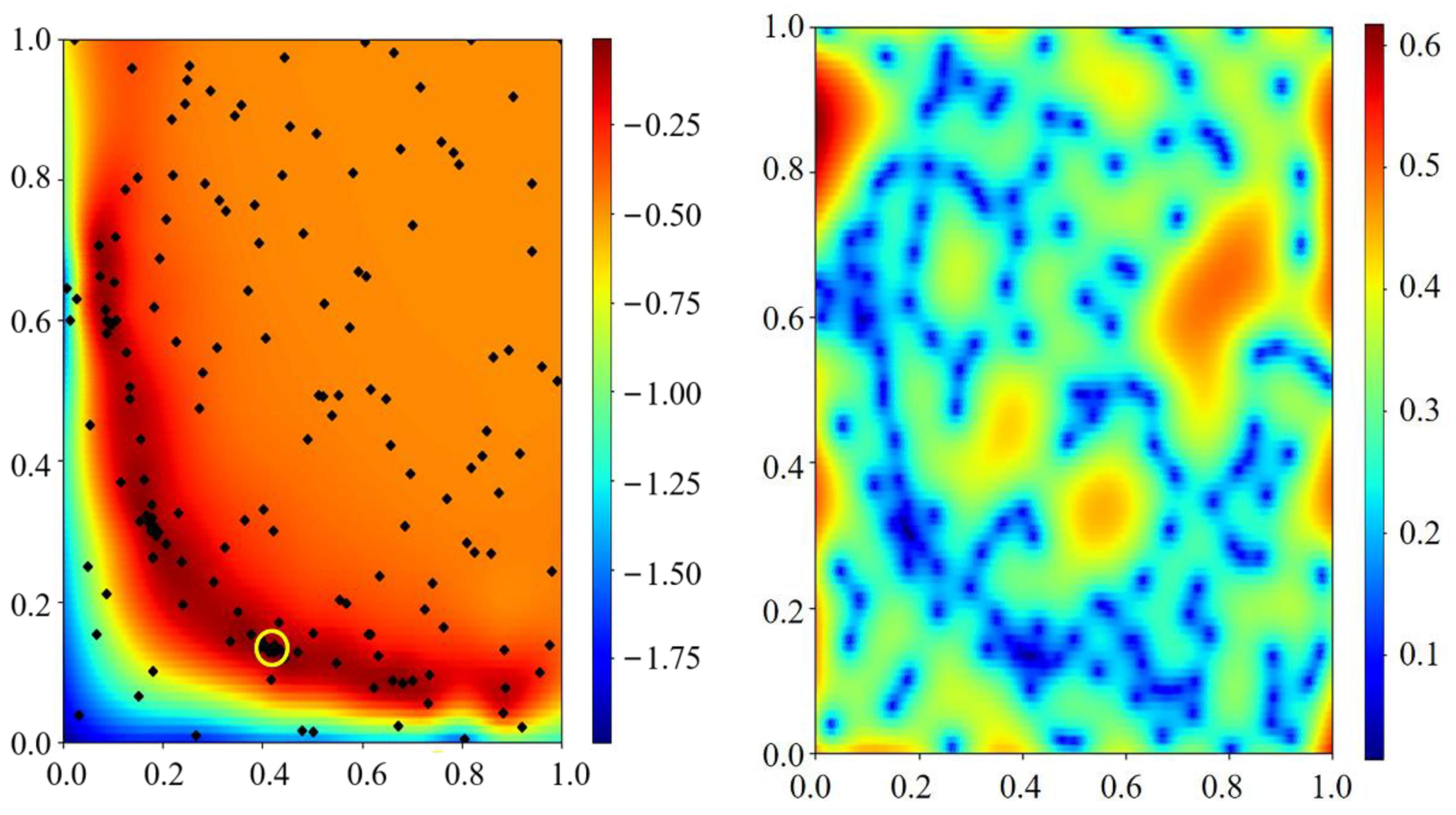
- The Bayesian optimization method can effectively fit multiple parameters at the same time. The method has the ability of global search and local optimization, which can effectively prevent the fitting process from falling into a local optimum.
- (5)
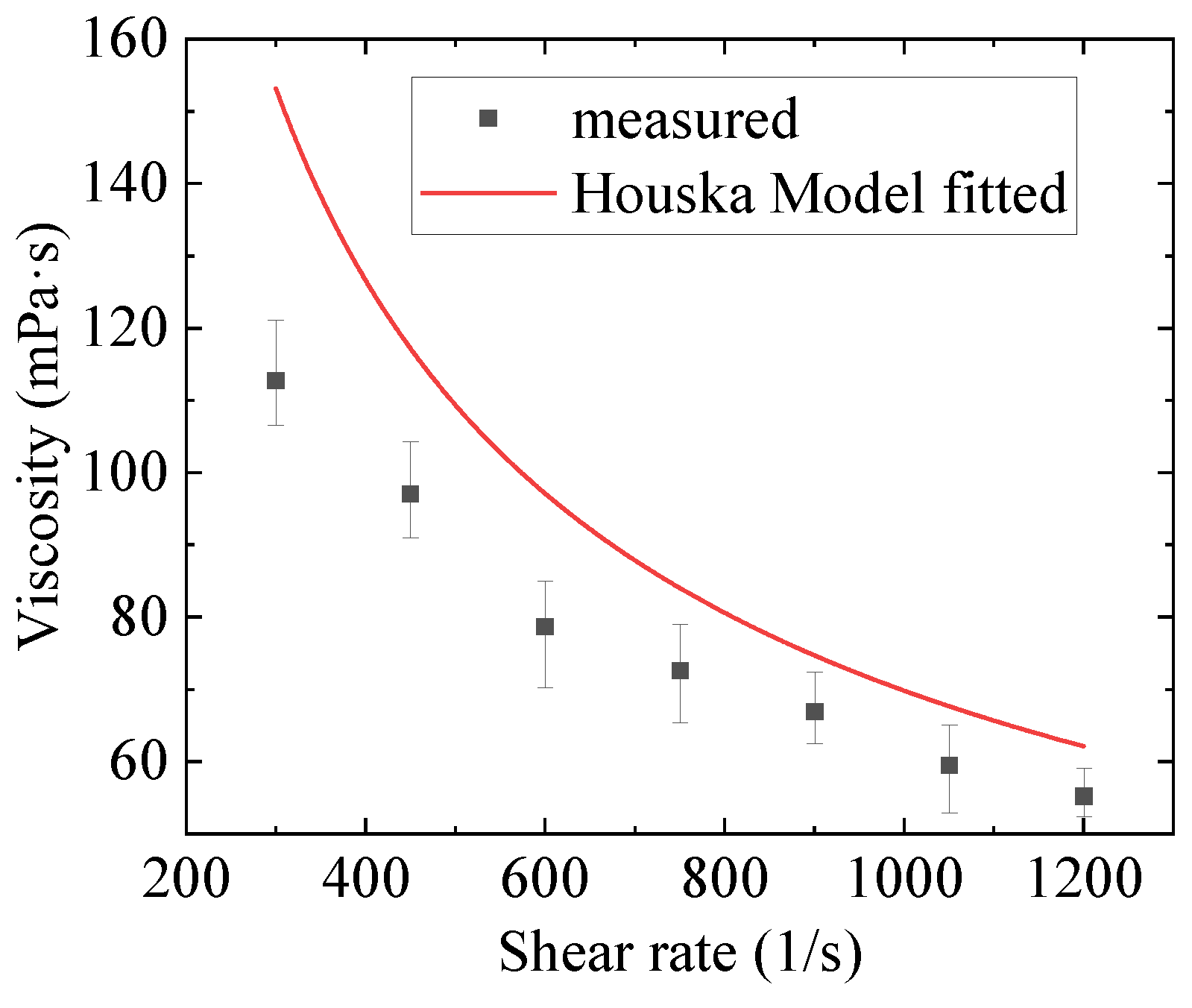
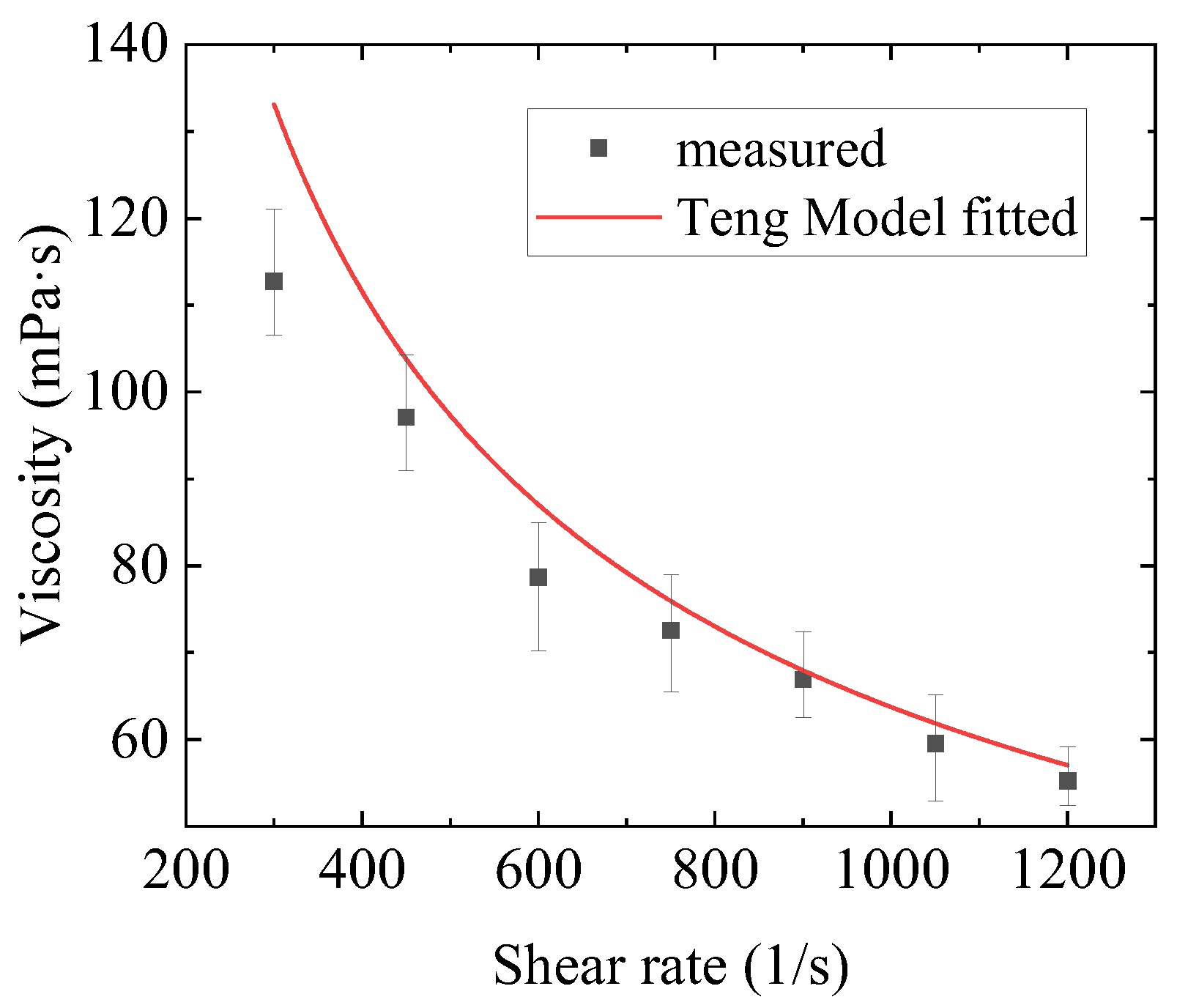
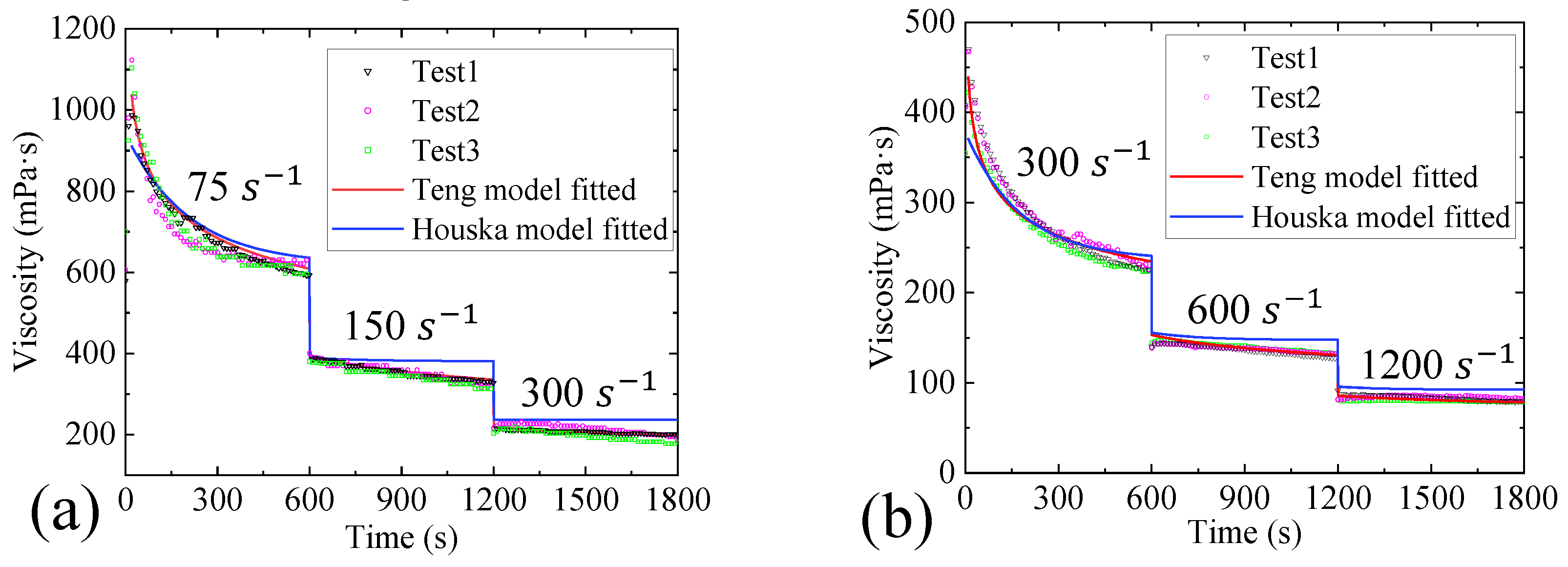
- Three constitutive models were used to fit the rheological properties of the gel by combining with the Bayesian optimization method. The results show that the fitting of the Toorman model failed completely, the Houska model had a certain fitting and predictive ability, and the Teng model performed the best. Moreover, the Teng model effectively modelled the thixotropy of the gel and has a strong predictive ability.
4. Materials and Methods
4.1. Thixotropy Model
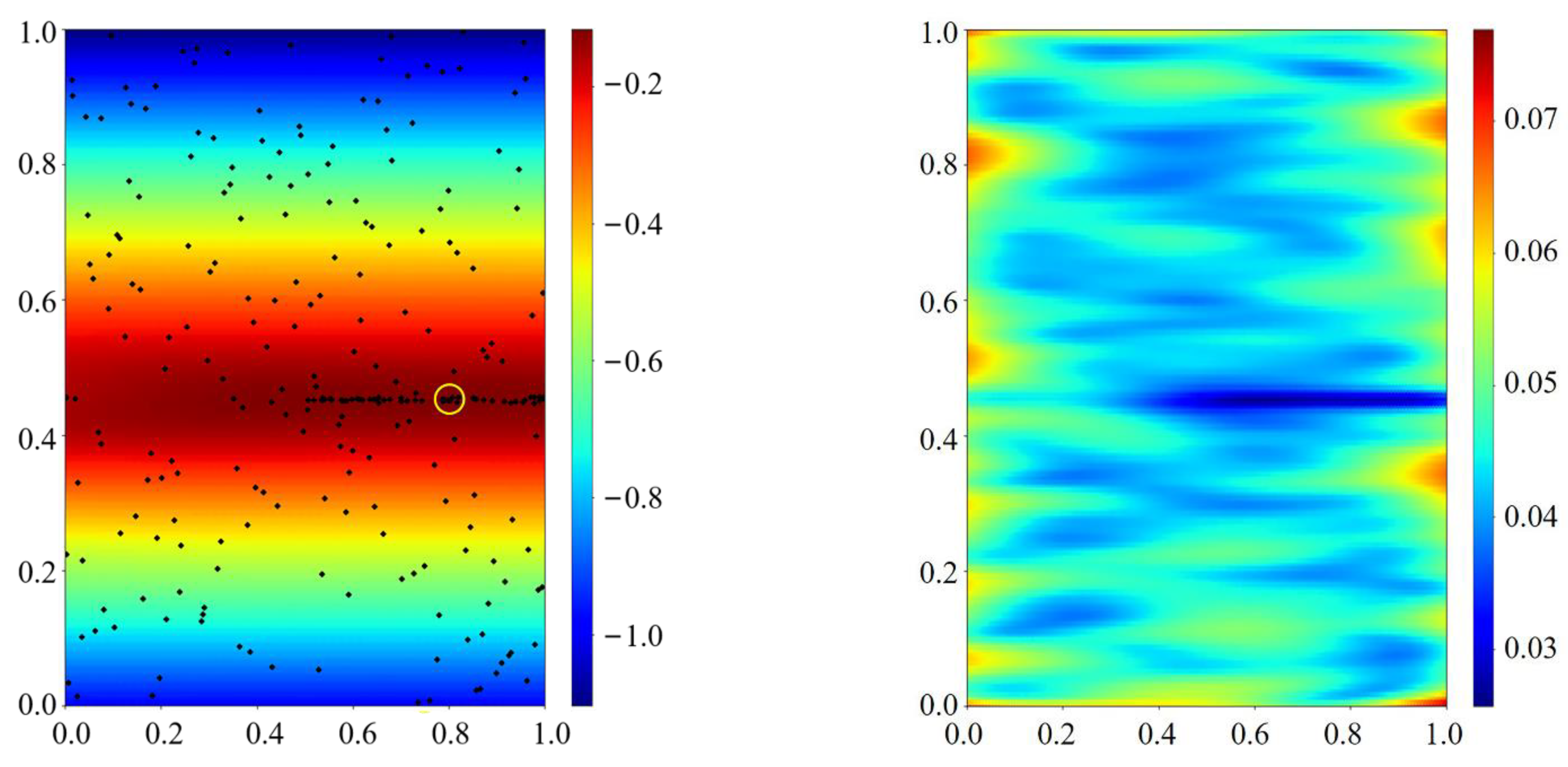
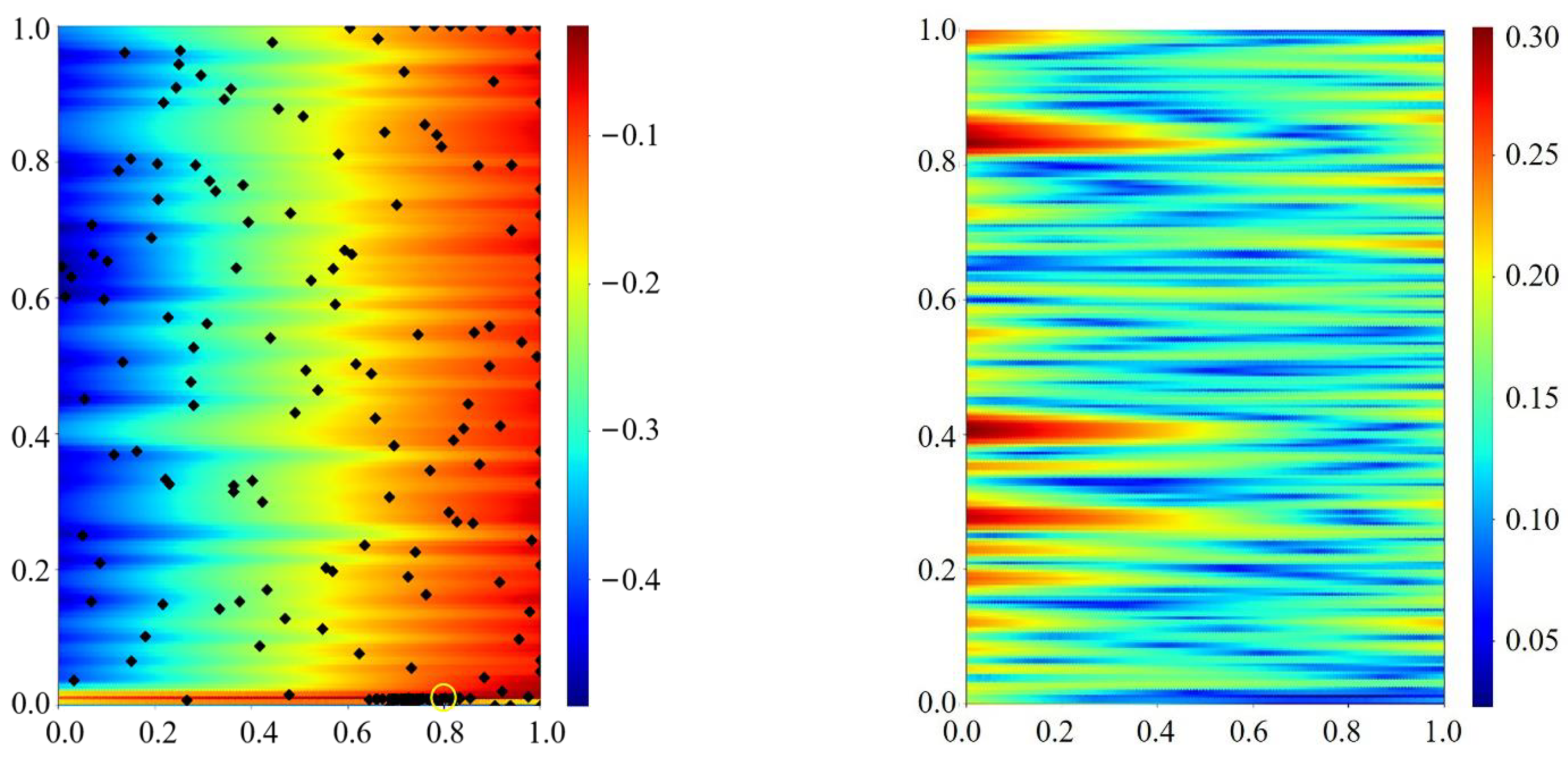
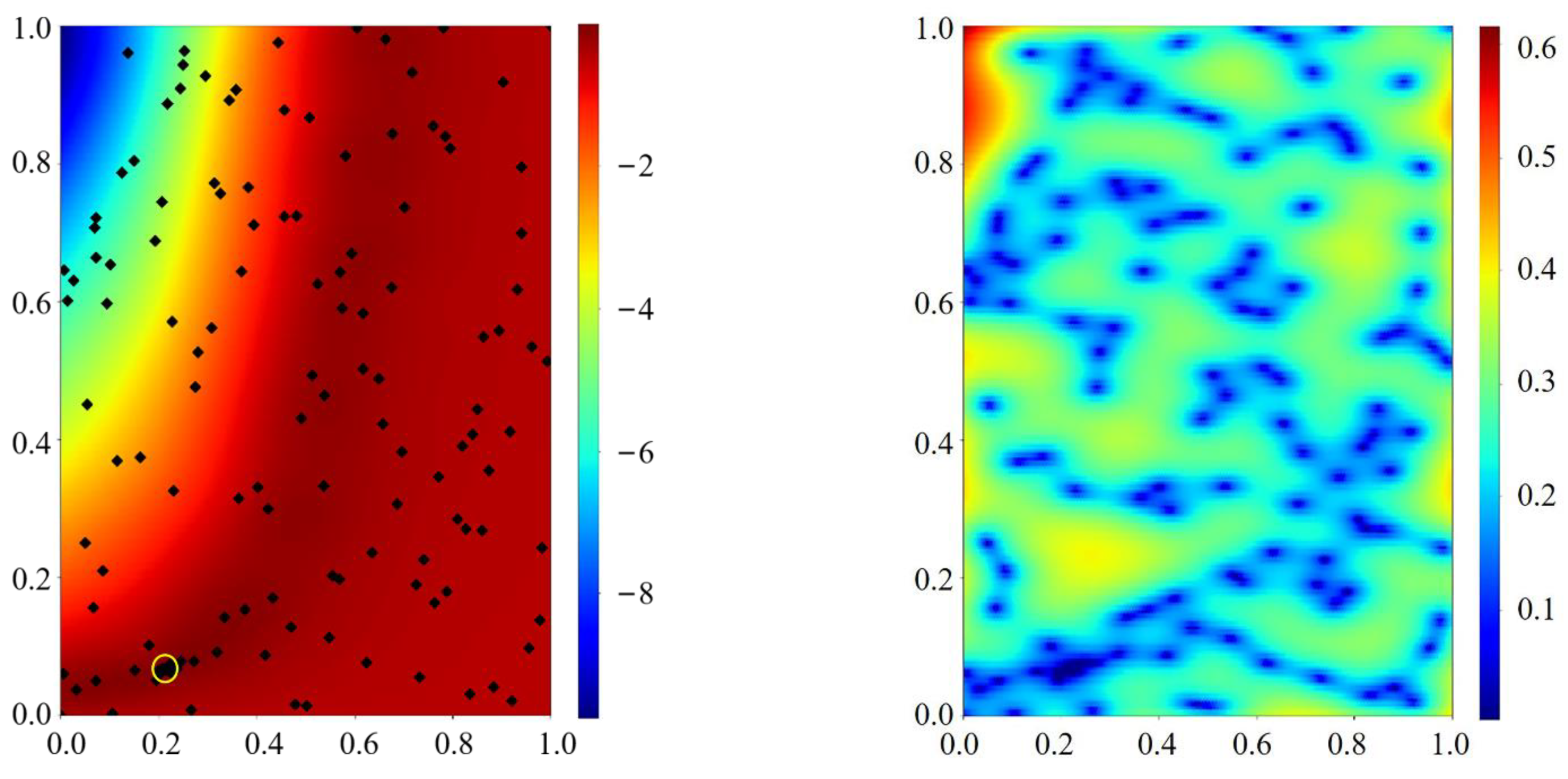
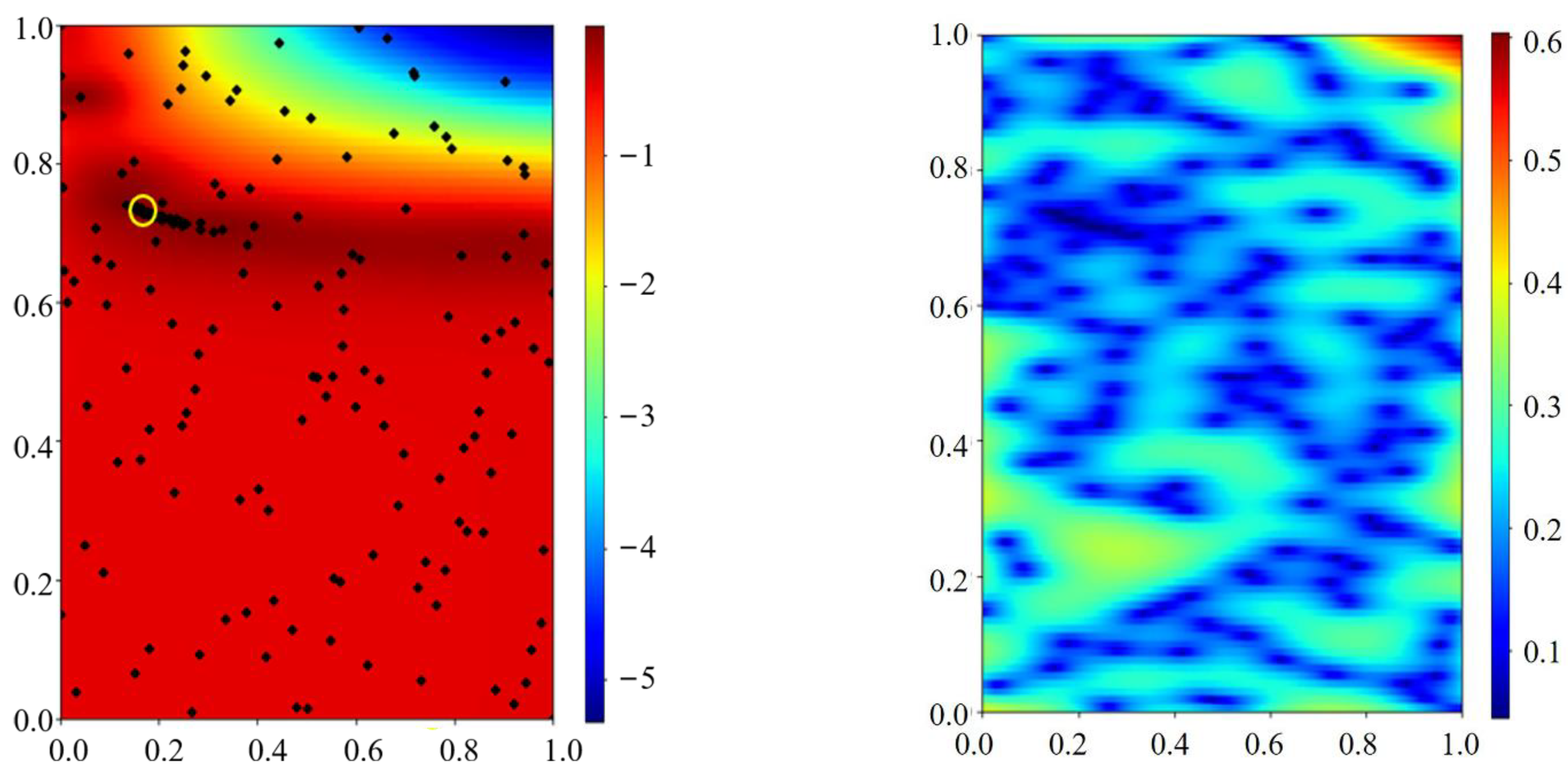
4.2. Numerical Fitting Method
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Composition | Mass Fraction |
|---|---|
| RP-3 kerosene | 90% |
| Gelling agent (thixatrol ST) | 5% |
| Additive (anhydrous ethanol) | 5% |

Appendix B
Appendix C
Appendix C.1. Pseudo-Code of the Bayesian Optimization
| Algorithm A1. Bayesian optimization. |
| 1: Initial sampling |
| 2: Initial statistical model |
| 3: For n = 1,2, do |
| 4: Select new by optimizing acquisition function f |
| 5: Query objective function to obtain |
| 6: Augment data |
| 7: Update statistical model |
| 8: End for |
Appendix C.2. Bayesian Optimization Model
Appendix C.2.1. Gaussian Process Regression (GPR)
Appendix C.2.2. Upper Confidence Bound Acquisition Functions
Appendix C.3. Sampling Theory
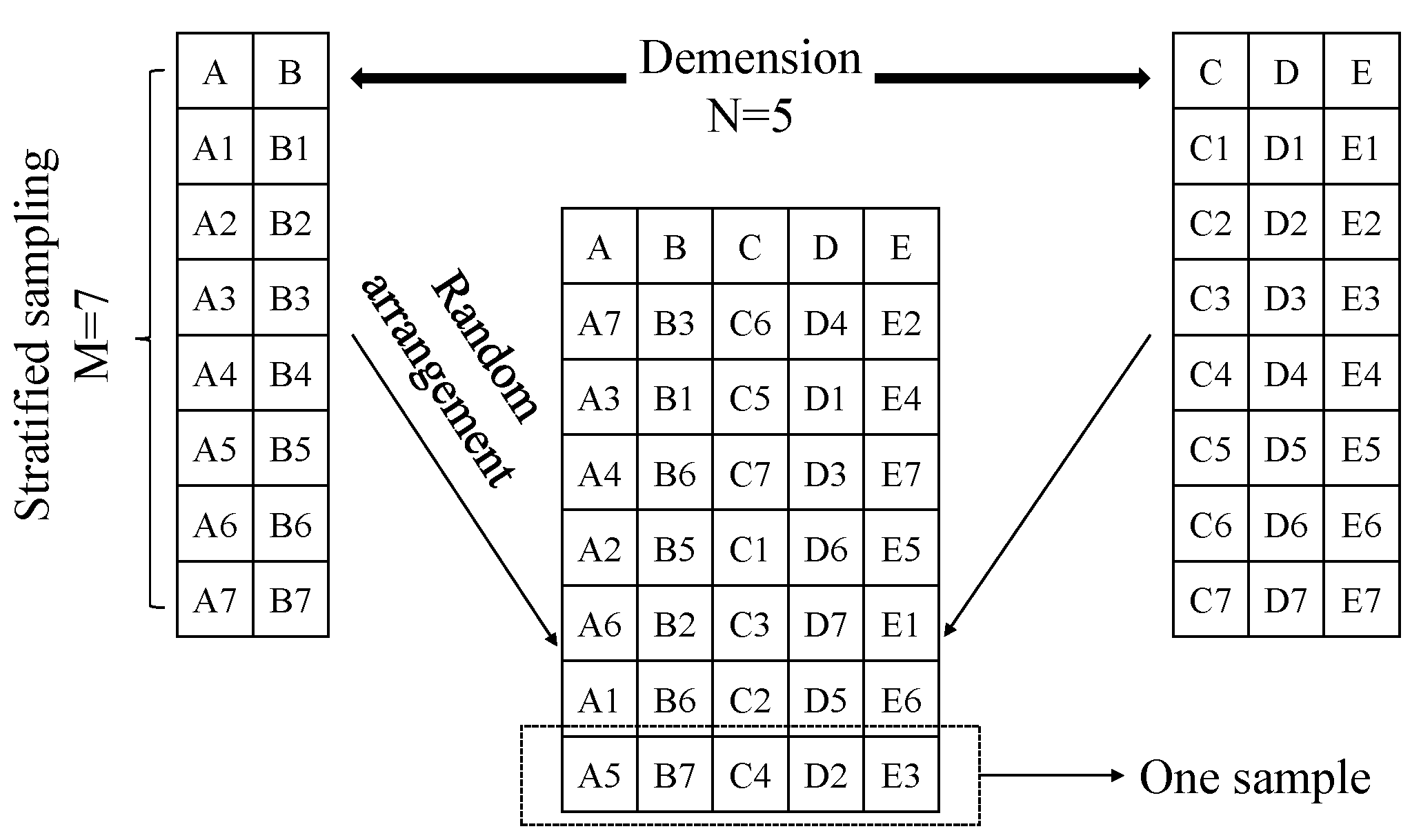
Appendix D

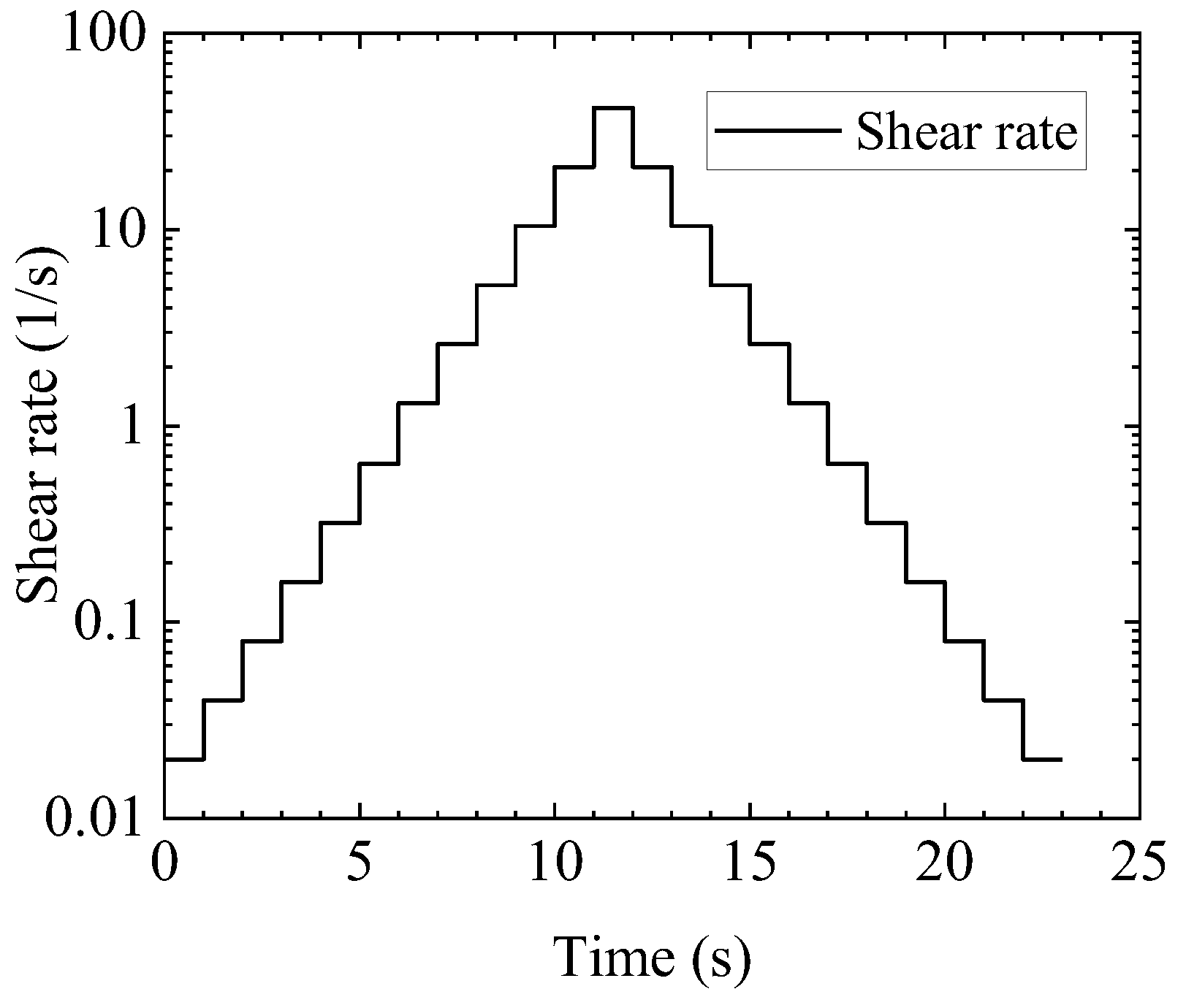
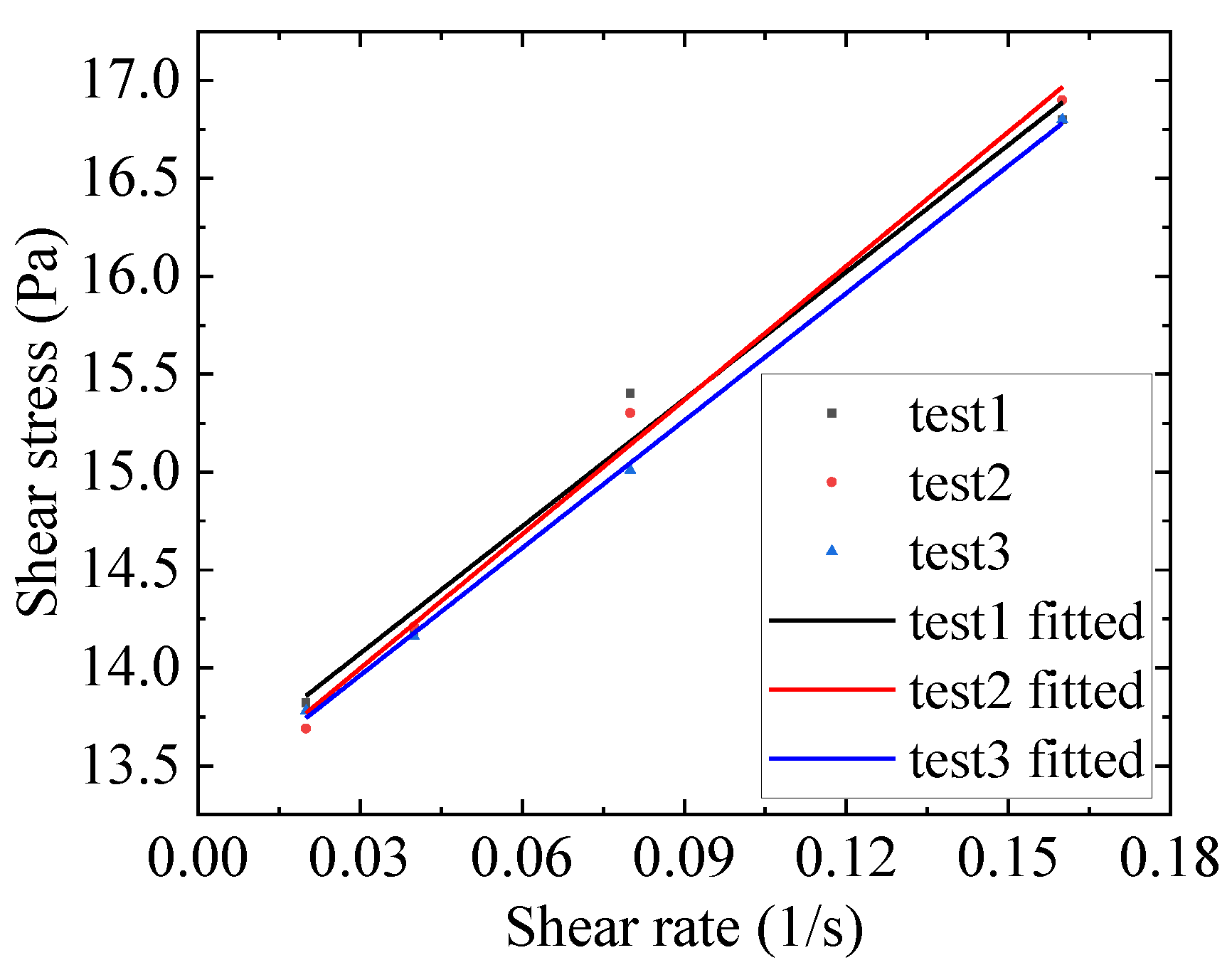
| Case | |||
|---|---|---|---|
| #1 | 21.65 | 13.42 | 0.985 |
| #2 | 22.84 | 13.31 | 0.994 |
| #3 | 21.70 | 13.31 | 0.999 |
Appendix E
| Fluid Processing | Fitted Power-Law Parameters | ||
|---|---|---|---|
| R-Squared | |||
| Kerosene gel processed by high-speed shear | 4.14 | 0.395 | 0.997 |
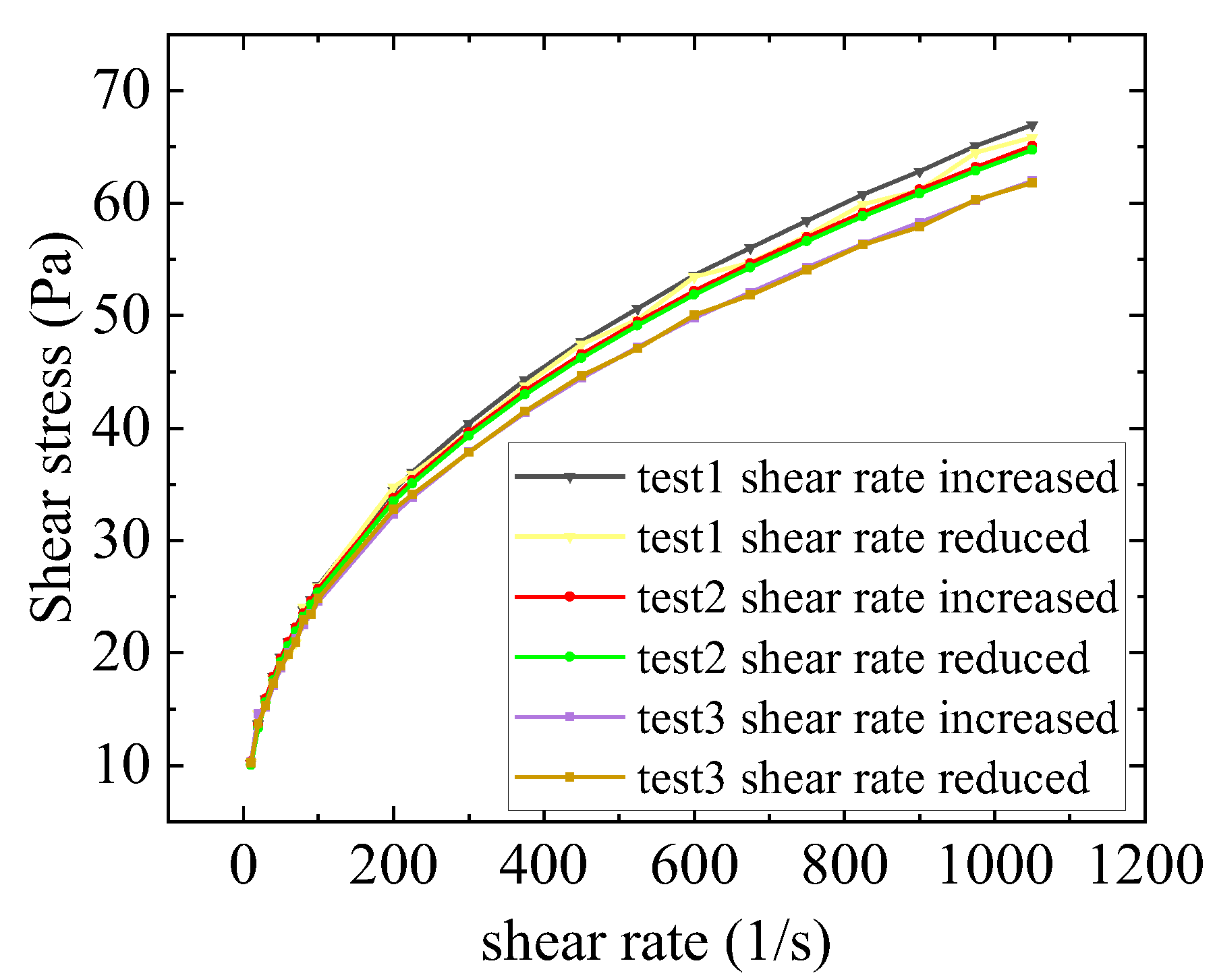
Appendix F

Appendix G
References
- Natan, B.; Rahimi, S. The status of gel propellants in year 2000. Int. J. Energetic Mater. Chem. Propuls. 2002, 5, 172–194. [Google Scholar] [CrossRef]
- Ciezki, H.K.; Hürttlen, J.; Naumann, K.W.; Negri, M.; Ramsel, J.; Weiser, V. Overview of the German gel propulsion technology program. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3794. [Google Scholar]
- Fu, Q.; Ge, F.; Wang, W.; Yang, L. Spray characteristics of gel propellants in an open-end swirl injector. Fuel 2019, 254, 115555. [Google Scholar] [CrossRef]
- Rapp, D.; Zurawski, R. Characterization of aluminum/RP-1 gel propellant properties. In Proceedings of the 24th Joint Propulsion Conference, Boston, MA, USA, 11–13 July 1988. [Google Scholar] [CrossRef]
- Padwal, M.B.; Mishra, D.P. Interactions among synthesis, rheology, and atomization of a gelled propellant. Rheol. Acta 2016, 55, 177–186. [Google Scholar] [CrossRef]
- Hodge, K.; Crofoot, T.; Nelson, S. Gelled propellants for tactical missile applications. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999; p. 2976. [Google Scholar]
- Teipel, U.; Foerter-Barth, U. Mechanical Properties of Gel Propellants with Nanoparticles. J. Energetic Mater. 2004, 22, 69–82. [Google Scholar] [CrossRef]
- Jyoti, B.V.S.; Baek, S.W. Formulation and Comparative Study of Rheological Properties of Loaded and Unloaded Ethanol-Based Gel Propellants. J. Energetic Mater. 2014, 33, 125–139. [Google Scholar] [CrossRef]
- Santos, P.; Arnold, R.; Anderson, W.; Carignano, M.; Campanella, O. Characterization of JP-8/SiO2 and RP-1/SiO2 gels. Eng. Lett. 2010, 18, 41–48. [Google Scholar]
- Barnes, H.A. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Chen, A.; Guan, X.; Li, X.; Zhang, B.; Zhang, B.; Song, J. Preparation and Characterization of Metalized JP-10 Gel Propellants with Excellent Thixotropic Performance. PropellantsExplos. Pyrotech. 2017, 42, 1007–1013. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Thixotropy. Adv. Colloid Interface Sci. 2009, 147–148, 214–227. [Google Scholar] [CrossRef]
- Schalek, E.; Szegvari, A. Die langsame Koagulation konzentrierter Eisenoxydsole zu reversiblen Gallerten. Kolloid-Z. 1923, 33, 326–334. [Google Scholar] [CrossRef]
- Schalek, F.E.; Szegvary, A. Ueber Eisenoxydgallerten. Kolloid-Z. 1923, 32, 318–319. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.; Bonn, D. Viscosity bifurcation in thixotropic, yielding fluids. J. Rheol. 2002, 46, 573–589. [Google Scholar] [CrossRef]
- Pramanik, B. Short Peptide-Based Smart Thixotropic Hydrogels. Gels 2022, 8, 569. [Google Scholar] [CrossRef] [PubMed]
- Zanna, N.; Tomasini, C. Peptide-based physical gels endowed with thixotropic behaviour. Gels 2017, 3, 39. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, S.; Peretz, A.; Natan, B. On Shear Rheology of Gel Propellants. PropellantsExplos. Pyrotech. 2007, 32, 165–174. [Google Scholar] [CrossRef]
- Rahimi, S.; Durban, D.; Khosid, S. Wall friction effects and viscosity reduction of gel propellants in conical extrusion. J. Non-Newton. Fluid Mech. 2010, 165, 782–792. [Google Scholar] [CrossRef]
- Madlener, K.; Ciezki, H. Some aspects of rheological and flow characteristics of gel fuels with regard to propulsion application. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009; p. 5240. [Google Scholar]
- Madlener, K.; Ciezki, H.K. Estimation of Flow Properties of Gelled Fuels with Regard to Propulsion Systems. J. Propuls. Power 2012, 28, 113–121. [Google Scholar] [CrossRef]
- Gupta, B.; Varma, M.; Goel, S. Rheological characterization of fuming nitric acid gel. PropellantsExplos. Pyrotech. 1986, 11, 85–90. [Google Scholar] [CrossRef]
- Dennis, J.D.; Kubal, T.D.; Campanella, O.; Son, S.F.; Pourpoint, T.L. Rheological Characterization of Monomethylhydrazine Gels. J. Propuls. Power 2013, 29, 313–320. [Google Scholar] [CrossRef]
- Arnold, R.; Santos, P.H.S.; Campanella, O.H.; Anderson, W.E. Rheological and Thermal Behavior of Gelled Hydrocarbon Fuels. J. Propuls. Power 2011, 27, 151–161. [Google Scholar] [CrossRef]
- Santos, P.; Carignano, M.; Campanella, O. Qualitative study of thixotropy in gelled hydrocarbon fuels. Eng. Lett. 2011, 19, 13–19. [Google Scholar]
- Negrão, C.O.R.; Franco, A.T.; Rocha, L.L.V. A weakly compressible flow model for the restart of thixotropic drilling fluids. J. Non-Newton. Fluid Mech. 2011, 166, 1369–1381. [Google Scholar] [CrossRef]
- Cheng, D.C.; Evans, F. Phenomenological characterization of the rheological behaviour of inelastic reversible thixotropic and antithixotropic fluids. Br. J. Appl. Phys. 1965, 16, 1599. [Google Scholar] [CrossRef]
- Dullaert, K.; Mewis, J. A structural kinetics model for thixotropy. J. Non-Newton. Fluid Mech. 2006, 139, 21–30. [Google Scholar] [CrossRef]
- Dullaert, K.; Mewis, J. Stress jumps on weakly flocculated dispersions: Steady state and transient results. J Colloid Interface Sci 2005, 287, 542–551. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, S.; Natan, B. Thixotropic Effect of Inorganic Gel Fuels. J. Propuls. Power 2000, 16, 1182–1184. [Google Scholar] [CrossRef]
- Tiu, C.; Boger, D. Complete rheological characterization of time-dependent food products. J. Texture Stud. 1974, 5, 329–338. [Google Scholar] [CrossRef]
- Li, X.; Fang, Y.; Zhang, H.; Nishinari, K.; Al-Assaf, S.; Phillips, G.O. Rheological properties of gum arabic solution: From Newtonianism to thixotropy. Food Hydrocoll. 2011, 25, 293–298. [Google Scholar] [CrossRef]
- De Rooij, R.; Potanin, A.; Van den Ende, D.; Mellema, J. Steady shear viscosity of weakly aggregating polystyrene latex dispersions. J. Chem. Phys. 1993, 99, 9213–9223. [Google Scholar] [CrossRef]
- Toorman, E.A. Modelling the thixotropic behaviour of dense cohesive sediment suspensions. Rheol. Acta 1997, 36, 56–65. [Google Scholar] [CrossRef]
- Houska, M. Engineering Aspects of the Rheology of Thixotropic Liquids. Ph.D. Thesis, Czech Technical University of Prague, Prague, Czech Republic, 1981. [Google Scholar]
- Teng, H.; Zhang, J. A new thixotropic model for waxy crude. Rheol. Acta 2013, 52, 903–911. [Google Scholar] [CrossRef]
- Moller, P.C.F.; Mewis, J.; Bonn, D. Yield stress and thixotropy: On the difficulty of measuring yield stresses in practice. Soft Matter 2006, 2, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Barnes, H.A.; Nguyen, Q.D. Rotating vane rheometry—A review. J. Non-Newton. Fluid Mech. 2001, 98, 1–14. [Google Scholar] [CrossRef]
- Nguyen, Q.; Boger, D. Measuring the flow properties of yield stress fluids. Annu. Rev. Fluid Mech. 1992, 24, 47–88. [Google Scholar] [CrossRef]
- Dzuy, N.Q.; Boger, D.V. Yield stress measurement for concentrated suspensions. J. Rheol. 1983, 27, 321–349. [Google Scholar] [CrossRef]
- Vinogradov, G.V.; Malkin, A.Y. Rheology of Polymers: Viscoelasticity and Flow of Polymers; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Cox, D.D.; John, S. A statistical method for global optimization. In Proceedings of the 1992 IEEE International Conference on Systems, Man, and Cybernetics, Chicago, IL, USA, 18–21 October 1992; pp. 1241–1246. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]

| Model | Steady-State MRE | Transient MRE | ||||||
|---|---|---|---|---|---|---|---|---|
| Toorman | - | - | - | 0.729 | 0.162 | 22.06 | 87.2% | 10.9% |
| Houska | 6.57 | - | 0.20 | 0.0024 | 0.0010 | - | 19.1% | 1.8% |
| Teng | 17.54 | 0.73 | 0.60 | 0.010 | 0.0109 | - | 6.9% | 0.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Chen, C.; Feng, F.; Zhou, C.; Zhang, W.; Wu, W.-T. Study of Thixotropic Characteristics of a Kerosene Gel Propellant by Bayesian Optimization. Gels 2023, 9, 15. https://doi.org/10.3390/gels9010015
Zhou H, Chen C, Feng F, Zhou C, Zhang W, Wu W-T. Study of Thixotropic Characteristics of a Kerosene Gel Propellant by Bayesian Optimization. Gels. 2023; 9(1):15. https://doi.org/10.3390/gels9010015
Chicago/Turabian StyleZhou, Hao, Cai Chen, Feng Feng, Changsheng Zhou, Wenling Zhang, and Wei-Tao Wu. 2023. "Study of Thixotropic Characteristics of a Kerosene Gel Propellant by Bayesian Optimization" Gels 9, no. 1: 15. https://doi.org/10.3390/gels9010015
APA StyleZhou, H., Chen, C., Feng, F., Zhou, C., Zhang, W., & Wu, W.-T. (2023). Study of Thixotropic Characteristics of a Kerosene Gel Propellant by Bayesian Optimization. Gels, 9(1), 15. https://doi.org/10.3390/gels9010015








