On the Determination of Mechanical Properties of Aqueous Microgels—Towards High-Throughput Characterization
Abstract
1. Introduction
2. Fabrication of Microgels
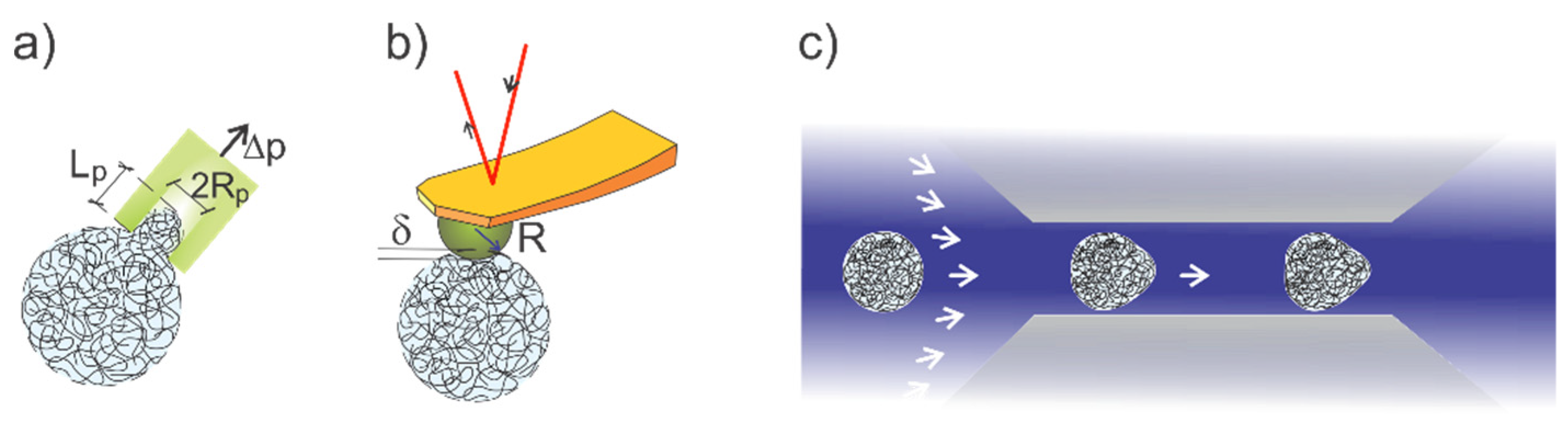
3. Application of AFM to Determine Mechanical Properties of Microgels
4. Micropipette Aspiration for Microgel Mechanical Characterization
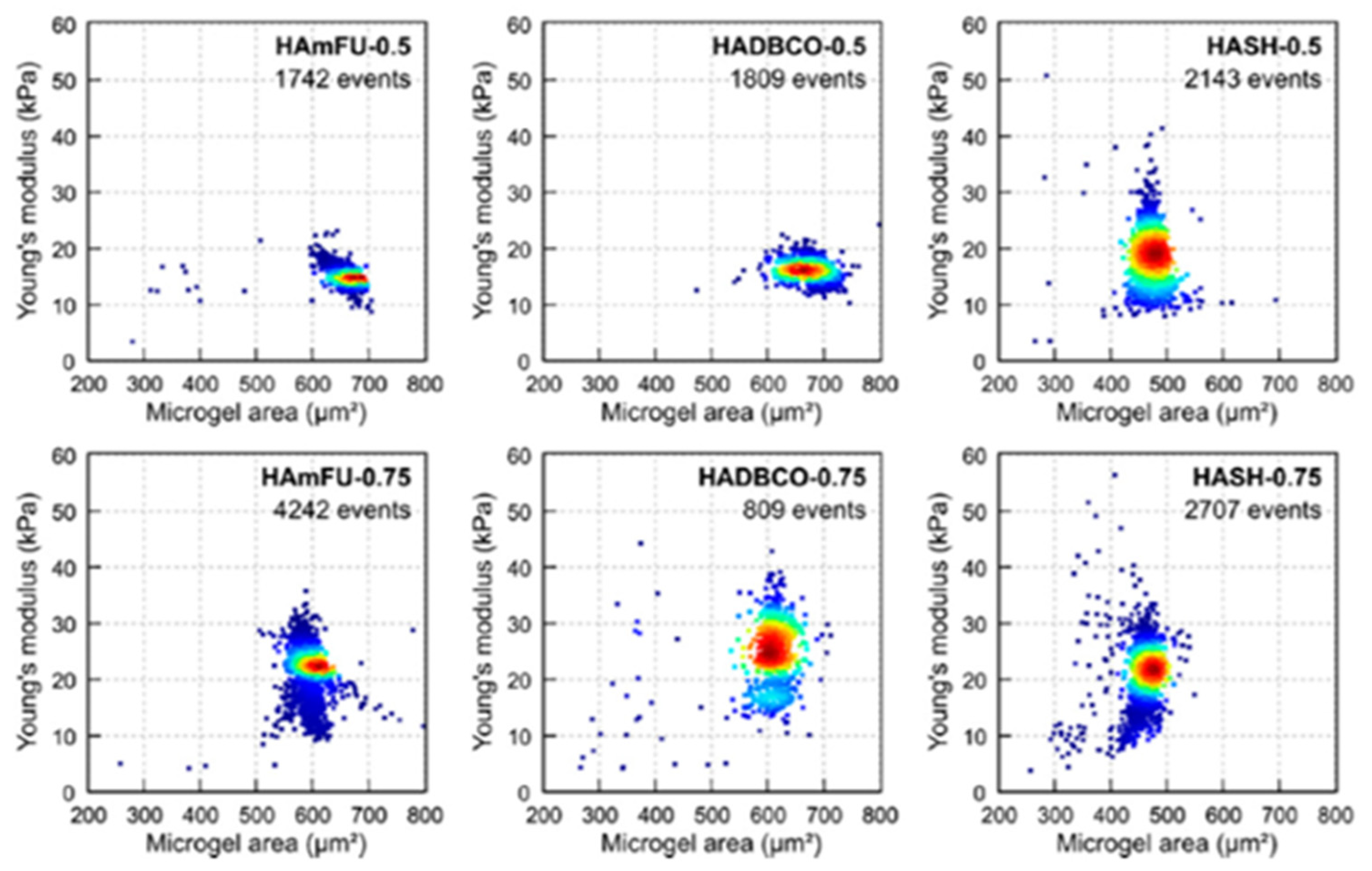
5. High-Throughput Microgel Mechanics’ Determination in Microchannels
6. Local Microgel Deformation by Optical Techniques
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shibayama, M. Spatial inhomogeneity and dynamic fluctuaions of polymer gels. Macromol. Chem. Phys. 1998, 199, 1–30. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, K.; Zhang, H.; Pang, B.; Choi, C.-H.; Mao, A.S.; Liao, H.; Utech, S.; Mooney, D.J.; Wang, H.; et al. Microfluidic Templated Multicompartment Microgels for 3D Encapsulation and Pairing of Single Cells. Small 2018, 14, 1702955. [Google Scholar] [CrossRef] [PubMed]
- Olesen, M.T.J.; Winther, A.K.; Fejerskov, B.; Dagnaes-Hansen, F.; Simonsen, U.; Zelikin, A.N. Bi-Enzymatic Embolization Beads for Two-Armed Enzyme-Prodrug Therapy. Adv. Ther. 2018, 1, 1800023. [Google Scholar] [CrossRef]
- Kamperman, T.; Karperien, M.; Le Gac, S.; Leijten, J. Single-Cell Microgels: Technology, Challenges, and Applications. Trends Biotechnol. 2018, 36, 850–865. [Google Scholar] [CrossRef]
- Fenton, O.S.; Olafson, K.N.; Pillai, P.S.; Mitchell, M.J.; Langer, R. Advances in Biomaterials for Drug Delivery. Adv. Mater. 2018, 30, 1705328. [Google Scholar] [CrossRef] [PubMed]
- Andablo-Reyes, E.; Yerani, D.; Fu, M.; Liamas, E.; Connell, S.; Torres, O.; Sarkar, A. Microgels as viscosity modifiers influence lubrication performance of continuum. Soft Matter 2019, 15, 9614–9624. [Google Scholar] [CrossRef]
- LeBlanc, K.J.; Niemi, S.R.; Bennett, A.I.; Harris, K.L.; Schulze, K.D.; Sawyer, W.G.; Taylor, C.; Angelini, T.E. Stability of High Speed 3D Printing in Liquid-Like Solids. ACS Biomater. Sci. Eng. 2016, 2, 1796–1799. [Google Scholar] [CrossRef] [PubMed]
- O’Bryan, C.S.; Kabb, C.P.; Sumerlin, B.S.; Angelini, T.E. Jammed Polyelectrolyte Microgels for 3D Cell Culture Applications: Rheological Behavior with Added Salts. ACS Appl. Bio Mater. 2019, 2, 1509–1517. [Google Scholar] [CrossRef]
- Isapour, G.; Lattuada, M. Bioinspired Stimuli-Responsive Color-Changing Systems. Adv. Mater. 2018, 30, 1707069. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Pu, W.F. Migration and plugging of polymer microspheres (PMs) in porous media for enhanced oil recovery: Experimental studies and empirical correlations. Colloids Surf. A Physicochem. Eng. Asp. 2020, 597. [Google Scholar] [CrossRef]
- González-Bermúdez, B.; Guinea, G.V.; Plaza, G.R. Advances in Micropipette Aspiration: Applications in Cell Biomechanics, Models, and Extended Studies. Biophys. J. 2019, 116, 587–594. [Google Scholar] [CrossRef]
- Sakai, A.; Murayama, Y.; Yanagisawa, M. Cyclic Micropipette Aspiration Reveals Viscoelastic Change of a Gelatin Microgel Prepared Inside a Lipid Droplet. Langmuir 2020, 36, 5186–5191. [Google Scholar] [CrossRef] [PubMed]
- Guck, J.; Schinkinger, S.; Lincoln, B.; Wottawah, F.; Ebert, S.; Romeyke, M.; Lenz, D.; Erickson, H.M.; Ananthakrishnan, R.; Mitchell, D.; et al. Optical Deformability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence. Biophys. J. 2005, 88, 3689–3698. [Google Scholar] [CrossRef]
- Lekka, M. Discrimination Between Normal and Cancerous Cells Using AFM. Bionanoscience 2016, 6, 65–80. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.Q.; Zhang, B.K.; Tang, G.L.; Yu, X.F.; Galluzzi, M. Cells nanomechanics by atomic force microscopy: Focus on interactions at nanoscale. Adv. Phys. X 2021, 6. [Google Scholar] [CrossRef]
- Krieg, M.; Fläschner, G.; Alsteens, D.; Gaub, B.M.; Roos, W.H.; Wuite, G.J.L.; Gaub, H.E.; Gerber, C.; Dufrêne, Y.F.; Müller, D.J. Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 2019, 1, 41–57. [Google Scholar] [CrossRef]
- Girardo, S.; Träber, N.; Wagner, K.; Cojoc, G.; Herold, C.; Goswami, R.; Schlüßler, R.; Abuhattum, S.; Taubenberger, A.; Reichel, F.; et al. Standardized microgel beads as elastic cell mechanical probes. J. Mater. Chem. B 2018, 6, 6245–6261. [Google Scholar] [CrossRef]
- Heida, T.; Otto, O.; Biedenweg, D.; Hauck, N.; Thiele, J. Microfluidic Fabrication of Click Chemistry-Mediated Hyaluronic Acid Microgels: A Bottom-Up Material Guide to Tailor a Microgel’s Physicochemical and Mechanical Properties. Polymers 2020, 12, 1760. [Google Scholar] [CrossRef]
- Distler, T.; Kretzschmar, L.; Schneidereit, D.; Girardo, S.; Goswami, R.; Friedrich, O.; Detsch, R.; Guck, J.; Boccaccini, A.R.; Budday, S. Mechanical properties of cell- and microgel bead-laden oxidized alginate-gelatin hydrogels. Biomater. Sci. 2021. [Google Scholar] [CrossRef]
- Hauck, N.; Seixas, N.; Centeno, S.P.; Schluelsser, R.; Cojoc, G.; Mueller, P.; Guck, J.; Woell, D.; Wessjohann, L.A.; Thiele, J. Droplet-Assisted Microfluidic Fabrication and Characterization of Multifunctional Polysaccharide Microgels Formed by Multicomponent Reactions. Polymers 2018, 10, 1055. [Google Scholar] [CrossRef]
- Aangenendt, F.J.; Mattsson, J.; Ellenbroek, W.G.; Wyss, H.M. Mechanics from Calorimetry: Probing the Elasticity of Responsive Hydrogels. Phys. Rev. Appl. 2017, 8, 014003. [Google Scholar] [CrossRef]
- Rey, M.; Fernández-Rodríguez, M.Á.; Steinacher, M.; Scheidegger, L.; Geisel, K.; Richtering, W.; Squires, T.M.; Isa, L. Isostructural solid–solid phase transition in monolayers of soft core–shell particles at fluid interfaces: Structure and mechanics. Soft Matter 2016, 12, 3545–3557. [Google Scholar] [CrossRef] [PubMed]
- Mattsson, J.; Wyss, H.M.; Fernandez-Nieves, A.; Miyazaki, K.; Hu, Z.; Reichman, D.R.; Weitz, D.A. Soft colloids make strong glasses. Nature 2009, 462, 83–86. [Google Scholar] [CrossRef]
- Mauri, E.; Giannitelli, S.M.; Trombetta, M.; Rainer, A. Synthesis of Nanogels: Current Trends and Future Outlook. Gels 2021, 7, 36. [Google Scholar] [CrossRef]
- Karg, M.; Pich, A.; Hellweg, T.; Hoare, T.; Lyon, L.A.; Crassous, J.J.; Suzuki, D.; Gumerov, R.A.; Schneider, S.; Potemkin, I.I.; et al. Nanogels and Microgels: From Model Colloids to Applications, Recent Developments, and Future Trends. Langmuir 2019, 35, 6231–6255. [Google Scholar] [CrossRef]
- Nur, H.; Pinkrah, V.T.; Mitchell, J.C.; Benée, L.S.; Snowden, M.J. Synthesis and properties of polyelectrolyte microgel particles. Adv. Colloid Interface Sci. 2010, 158, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.C.; Stabenfeldt, S.E.; Ahn, B.; Hannan, R.T.; Dhada, K.S.; Herman, E.S.; Stefanelli, V.; Guzzetta, N.; Alexeev, A.; Lam, W.A.; et al. Ultrasoft microgels displaying emergent platelet-like behaviours. Nat. Mater. 2014, 13, 1108–1114. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Huang, N.; Grossiord, J.-L.; Moine, L.; Agnely, F.; Vauthier, C. Rheological characterization of mechanical properties of chemically crosslinked microspheres. J. Appl. Polymer Sci. 2013, 128, 3113–3121. [Google Scholar] [CrossRef]
- Merkel, T.J.; Jones, S.W.; Herlihy, K.P.; Kersey, F.R.; Shields, A.R.; Napier, M.; Luft, J.C.; Wu, H.; Zamboni, W.C.; Wang, A.Z.; et al. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc. Natl. Acad. Sci. USA 2011, 108, 586–591. [Google Scholar] [CrossRef] [PubMed]
- Hashmi, S.M.; Dufresne, E.R. Mechanical properties of individual microgel particles through the deswelling transition. Soft Matter 2009, 5, 3682–3688. [Google Scholar] [CrossRef]
- Douglas, A.M.; Fragkopoulos, A.A.; Gaines, M.K.; Lyon, L.A.; Fernandez-Nieves, A.; Barker, T.H. Dynamic assembly of ultrasoft colloidal networks enables cell invasion within restrictive fibrillar polymers. Proc. Natl. Acad. Sci. USA 2017, 114, 885–890. [Google Scholar] [CrossRef]
- Verhulsel, M.; Vignes, M.; Descroix, S.; Malaquin, L.; Vignjevic, D.M.; Viovy, J.-L. A review of microfabrication and hydrogel engineering for micro-organs on chips. Biomaterials 2014, 35, 1816–1832. [Google Scholar] [CrossRef] [PubMed]
- Bai, F.; Yang, X.; Huang, W. Preparation of narrow or monodisperse poly (ethyleneglycol dimethacrylate) microspheres by distillation–precipitation polymerization. Eur. Polymer J. 2006, 42, 2088–2097. [Google Scholar] [CrossRef]
- Goh, E.C.C.; Stöver, H.D.H. Cross-Linked Poly (methacrylic acid-co-poly(ethylene oxide) methyl ether methacrylate) Microspheres and Microgels Prepared by Precipitation Polymerization: A Morphology Study. Macromolecules 2002, 35, 9983–9989. [Google Scholar] [CrossRef]
- Zhou, W.; Stukel, J.M.; Cebull, H.L.; Willits, R.K. Tuning the Mechanical Properties of Poly (Ethylene Glycol) Microgel-Based Scaffolds to Increase 3D Schwann Cell Proliferation. Macromol. Biosci. 2016, 16, 535–544. [Google Scholar] [CrossRef]
- Menut, P.; Seiffert, S.; Sprakel, J.; Weitz, D.A. Does size matter? Elasticity of compressed suspensions of colloidal- and granular-scale microgels. Soft Matter 2012, 8, 156–164. [Google Scholar] [CrossRef]
- Joshi, A.; Nandi, S.; Chester, D.; Brown, A.C.; Muller, M. Study of Poly (N-isopropylacrylamide-co-acrylic acid) (pNIPAM) Microgel Particle Induced Deformations of Tissue-Mimicking Phantom by Ultrasound Stimulation. Langmuir 2018, 34, 1457–1465. [Google Scholar] [CrossRef] [PubMed]
- Milani, A.H.; Freemont, A.J.; Hoyland, J.A.; Adlam, D.J.; Saunders, B.R. Injectable Doubly Cross-Linked Microgels for Improving the Mechanical Properties of Degenerated Intervertebral Discs. Biomacromolecules 2012, 13, 2793–2801. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Nugroho, R.W.N.; Odelius, K.; Edlund, U.; Zhao, C.; Albertsson, A.-C. In Situ Cross-Linking of Stimuli-Responsive Hemicellulose Microgels during Spray Drying. ACS Appl. Mater. Interfaces 2015, 7, 4202–4215. [Google Scholar] [CrossRef]
- Lorenzo-Lamosa, M.L.; Remuñán-López, C.; Vila-Jato, J.L.; Alonso, M.J. Design of microencapsulated chitosan microspheres for colonic drug delivery. J. Controll. Release 1998, 52, 109–118. [Google Scholar] [CrossRef]
- Wang, L.-Y.; Ma, G.-H.; Su, Z.-G. Preparation of uniform sized chitosan microspheres by membrane emulsification technique and application as a carrier of protein drug. J. Controll. Release 2005, 106, 62–75. [Google Scholar] [CrossRef] [PubMed]
- Shintaku, H.; Kuwabara, T.; Kawano, S.; Suzuki, T.; Kanno, I.; Kotera, H. Micro cell encapsulation and its hydrogel-beads production using microfluidic device. Microsyst. Technol. 2007, 13, 951–958. [Google Scholar] [CrossRef]
- Liu, K.; Deng, Y.; Zhang, N.; Li, S.; Ding, H.; Guo, F.; Liu, W.; Guo, S.; Zhao, X.-Z. Generation of disk-like hydrogel beads for cell encapsulation and manipulation using a droplet-based microfluidic device. Microfluid. Nanofluid. 2012, 13, 761–767. [Google Scholar] [CrossRef]
- Tumarkin, E.; Kumacheva, E. Microfluidic generation of microgels from synthetic and natural polymers. Chem. Soc. Rev. 2009, 38, 2161–2168. [Google Scholar] [CrossRef]
- Park, J.I.; Saffari, A.; Kumar, S.; Günther, A.; Kumacheva, E. Microfluidic Synthesis of Polymer and Inorganic Particulate Materials. Ann. Rev. Mater. Res. 2010, 40, 415–443. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Conrad, J.C.; Rhodes, S.K.; Link, D.R.; Marquez, M.; Weitz, D.A.; Lewis, J.A. Microfluidic Assembly of Homogeneous and Janus Colloid-Filled Hydrogel Granules. Langmuir 2006, 22, 8618–8622. [Google Scholar] [CrossRef]
- Bong, K.W.; Bong, K.T.; Pregibon, D.C.; Doyle, P.S. Hydrodynamic Focusing Lithography. Angew. Chem. Int. Ed. 2010, 49, 87–90. [Google Scholar] [CrossRef]
- Kim, C.; Park, K.-S.; Kim, J.; Jeong, S.-G.; Lee, C.-S. Microfluidic synthesis of monodisperse pectin hydrogel microspheres based on in situ gelation and settling collection. J. Chem. Technol. Biotechnol. 2017, 92, 201–209. [Google Scholar] [CrossRef]
- Hati, A.G.; Bassett, D.C.; Ribe, J.M.; Sikorski, P.; Weitz, D.A.; Stokke, B.T. Versatile, cell and chip friendly method to gel alginate in microfluidic devices. Lab Chip 2016, 16, 3718–3727. [Google Scholar] [CrossRef]
- Utech, S.; Prodanovic, R.; Mao, A.S.; Ostafe, R.; Mooney, D.J.; Weitz, D.A. Microfluidic Generation of Monodisperse, Structurally Homogeneous Alginate Microgels for Cell Encapsulation and 3D Cell Culture. Adv. Healthcare Mater. 2015, 4, 1628–1633. [Google Scholar] [CrossRef]
- Zhang, H.; Tumarkin, E.; Sullan, R.M.A.; Walker, G.C.; Kumacheva, E. Exploring Microfluidic Routes to Microgels of Biological Polymers. Macromol. Rapid Commun. 2007, 28, 527–538. [Google Scholar] [CrossRef]
- Marquis, M.; Renard, D.; Cathala, B. Microfluidic Generation and Selective Degradation of Biopolymer-Based Janus Microbeads. Biomacromolecules 2012, 13, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Tumarkin, E.; Peerani, R.; Nie, Z.; Sullan, R.M.A.; Walker, G.C.; Kumacheva, E. Microfluidic Production of Bi-opolymer Microcapsules with Controlled Morphology. J. Am. Chem. Soc. 2006, 128, 12205–12210. [Google Scholar] [CrossRef] [PubMed]
- Iwamoto, S.; Nakagawa, K.; Sugiura, S.; Nakajima, M. Preparation of gelatin microbeads with a narrow size distribution using microchannel emulsification. AAPS PharmSciTech 2002, 3, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.B.; Hashimoto, M.; Dang, T.T.; Hoare, T.; Kohane, D.S.; Whitesides, G.M.; Langer, R.; Anderson, D.G. Preparation of Monodisperse Biodegradable Polymer Microparticles Using a Microfluidic Flow-Focusing Device for Controlled Drug Delivery. Small 2009, 5, 1575–1581. [Google Scholar] [CrossRef]
- Hati, A.G.; Szymborski, T.R.; Steinacher, M.; Amstad, E. Production of monodisperse drops from viscous fluids. Lab Chip 2018. [CrossRef]
- Visser, C.W.; Kamperman, T.; Karbaat, L.P.; Lohse, D.; Karperien, M. In-air microfluidics enables rapid fabrication of emulsions, suspensions, and 3D modular (bio) materials. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef]
- Kamperman, T.; Trikalitis, V.D.; Karperien, M.; Visser, C.W.; Leijten, J. Ultrahigh-Throughput Production of Monodisperse and Multifunctional Janus Microparticles Using in-Air Microfluidics. ACS Appl. Mater. Interfaces 2018, 10, 23433–23438. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.T.; Zhang, X.X.; Shang, L.R.; Zhao, Y.J. Thriving microfluidic technology. Sci. Bull. 2021, 66, 9–12. [Google Scholar] [CrossRef]
- Lai, Y.; He, D.; Hu, Y. Indentation adhesion of hydrogels over a wide range of length and time scales. Extreme Mech. Lett. 2019, 31, 100540. [Google Scholar] [CrossRef]
- Aufderhorst-Roberts, A.; Baker, D.; Foster, R.J.; Cayre, O.; Mattsson, J.; Connell, S.D. Nanoscale mechanics of microgel particles. Nanoscale 2018, 10, 16050–16061. [Google Scholar] [CrossRef] [PubMed]
- Kwon, S.; Yang, W.; Moon, D.; Kim, K.S. Comparison of Cancer Cell Elasticity by Cell Type. J. Cancer 2020, 11, 5403–5412. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.C.; Horkay, F. Nanomechanics of polymer gels and biological tissues: A critical review of analytical approaches in the Hertzian regime and beyond. Soft Matter 2008, 4, 669–682. [Google Scholar] [CrossRef]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef]
- Lekka, M.; Sainz-Serp, D.; Kulik, A.J.; Wandrey, C. Hydrogel Microspheres: Influence of Chemical Composition on Surface Morphology, Local Elastic Properties, and Bulk Mechanical Characteristics. Langmuir 2004, 20, 9968–9977. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, E.S.; Ramakrishna, S.N.; Spencer, N.D.; Benetti, E.M. Controlled Crosslinking Is a Tool To Precisely Modulate the Nanomechanical and Nanotribological Properties of Polymer Brushes. Macromolecules 2017, 50, 2932–2941. [Google Scholar] [CrossRef]
- Shiratori, S.S.; Rubner, M.F. pH-dependent thickness behaviour of sequentially adsorbed layers of weak polyelectrolytes. Macromolecules 2000, 33, 4213–4219. [Google Scholar] [CrossRef]
- Zavgorodnya, O.; Serpe, M.J. Assembly of poly(N-isopropylacrylamide)-co-acrylic acid microgel thin films on polyelectrolyte multilayers: Effects of polyelectrolyte layer thickness, surface charge, and microgel solution pH. Colloid Polym. Sci. 2011, 289, 591–602. [Google Scholar] [CrossRef]
- Scheffold, F. Pathways and challenges towards a complete characterization of microgels. Nat. Commun. 2020, 11, 4315. [Google Scholar] [CrossRef]
- Maza, E.; von Bilderling, C.; Cortez, M.L.; Díaz, G.; Bianchi, M.; Pietrasanta, L.I.; Giussi, J.M.; Azzaroni, O. Layer-by-Layer Assembled Microgels Can Combine Conflicting Properties: Switchable Stiffness and Wettability without Affecting Permeability. Langmuir 2018, 34, 3711–3719. [Google Scholar] [CrossRef]
- Zhu, P.-W.; Chen, L. Effects of cosolvent partitioning on conformational transitions and chain flexibility of thermoresponsive microgels. Phys. Rev. E 2019, 99, 022501. [Google Scholar] [CrossRef]
- Backes, S.; Krause, P.; Tabaka, W.; Witt, M.U.; von Klitzing, R. Combined Cononsolvency and Temperature Effects on Ad-sorbed PNIPAM Microgels. Langmuir 2017, 33, 14269–14277. [Google Scholar] [CrossRef]
- Backes, S.; Von Klitzing, R. Nanomechanics and Nanorheology of Microgels at Interfaces. Polymers 2018, 10, 978. [Google Scholar] [CrossRef] [PubMed]
- Burmistrova, A.; Richter, M.; Uzum, C.; Klitzing, R.V. Effect of cross-linker density of P (NIPAM-co-AAc) microgels at solid surfaces on the swelling/shrinking behaviour and the Young’s modulus. Colloid Polymer Sci. 2011, 289, 613–624. [Google Scholar] [CrossRef]
- Nyström, L.; Álvarez-Asencio, R.; Frenning, G.; Saunders, B.R.; Rutland, M.W.; Malmsten, M. Electrostatic Swelling Transitions in Surface-Bound Microgels. ACS Appl. Mater. Interfaces 2016, 8, 27129–27139. [Google Scholar] [CrossRef]
- Virumbrales-Muñoz, M.; Santos-Vizcaino, E.; Paz, L.; Gallardo-Moreno, A.M.; Orive, G.; Hernandez, R.M.; Doblaré, M.; Gonzalez-Martin, M.L.; Fernández, L.J.; Pedraz, J.L.; et al. Force spectroscopy-based simultaneous topographical and me-chanical characterization to study polymer-to-polymer interactions in coated alginate microspheres. Sci. Rep. 2019, 9, 20112. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Varga, I.; Kardos, A.; Dobryden, I.; Claesson, P.M. Temperature-Dependent Nanomechanical Properties of Adsorbed Poly-NIPAm Microgel Particles Immersed in Water. Langmuir 2021, 37, 1902–1912. [Google Scholar] [CrossRef]
- Mohapatra, H.; Kruger, T.M.; Lansakara, T.I.; Tivanski, A.V.; Stevens, L.L. Core and surface microgel mechanics are differ-entially sensitive to alternative crosslinking concentrations. Soft Matter 2017, 13, 5684–5695. [Google Scholar] [CrossRef] [PubMed]
- Bachman, H.; Brown, A.C.; Clarke, K.C.; Dhada, K.S.; Douglas, A.; Hansen, C.E.; Herman, E.; Hyatt, J.S.; Kodlekere, P.; Meng, Z.; et al. Ultrasoft, highly deformable microgels. Soft Matter 2015, 11, 2018–2028. [Google Scholar] [CrossRef]
- Matsui, S.; Kureha, T.; Hiroshige, S.; Shibata, M.; Uchihashi, T.; Suzuki, D. Fast Adsorption of Soft Hydrogel Microspheres on Solid Surfaces in Aqueous Solution. Angew. Chem. Int. Ed. 2017, 56, 12146–12149. [Google Scholar] [CrossRef]
- Theret, D.P.; Levesque, M.J.; Sato, M.; Nerem, R.M.; Wheeler, L.T. The Application of a Homogeneous Half-Space Model in the Analysis of Endothelial Cell Micropipette Measurements. J. Biomech. Eng. 1988, 110, 190–199. [Google Scholar] [CrossRef]
- Daza, R.; Gonzalez-Bermudez, B.; Cruces, J.; De la Fuente, M.; Plaza, G.R.; Arroyo-Hernandez, M.; Elices, M.; Perez-Rigueiro, J.; Guinea, G.V. Comparison of cell mechanical measurements provided by Atomic Force Microscopy (AFM) and Micropipette Aspiration (MPA). J. Mech. Behav. Biomed. Mater. 2019, 95, 103–115. [Google Scholar] [CrossRef] [PubMed]
- Zhou, E.H.; Lim, C.T.; Quek, S.T. Finite element simulation of the micropipette aspiration of a living cell undergoing large viscoelastic deformation. Mech. Adv. Mater. Struct. 2005, 12, 501–512. [Google Scholar] [CrossRef]
- Sakai, A.; Murayama, Y.; Fujiwara, K.; Fujisawa, T.; Sasaki, S.; Kidoaki, S.; Yanagisawa, M. Increasing Elasticity through Changes in the Secondary Structure of Gelatin by Gelation in a Microsized Lipid Space. ACS Cent. Sci. 2018, 4, 477–483. [Google Scholar] [CrossRef]
- Kleinberger, R.M.; Burke, N.A.D.; Dalnoki-Veress, K.; Stover, H.D.H. Systematic study of alginate-based microcapsules by micropipette aspiration and confocal fluorescence microscopy. Mater. Sci. Eng. C Mater. Biol. Appl. 2013, 33, 4295–4304. [Google Scholar] [CrossRef]
- Li, Y.; Sarıyer, O.S.; Ramachandran, A.; Panyukov, S.; Rubinstein, M.; Kumacheva, E. Universal behavior of hydrogels confined to narrow capillaries. Sci. Rep. 2015, 5, 17017. [Google Scholar] [CrossRef]
- Wyss, H.M.; Franke, T.; Mele, E.; Weitz, D.A. Capillary micromechanics: Measuring the elasticity of microscopic soft objects. Soft Matter 2010, 6, 4550–4555. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.; Li, T.-D.; Chen, Z.; Deng, W.; Anbari, A.; Fan, J. Understanding transport of an elastic, spherical particle through a confining channel. Appl. Phys. Lett. 2020, 116, 103705. [Google Scholar] [CrossRef]
- Byun, S.; Son, S.; Amodei, D.; Cermak, N.; Shaw, J.; Kang, J.H.; Hecht, V.C.; Winslow, M.M.; Jacks, T.; Mallick, P.; et al. Characterizing deformability and surface friction of cancer cells. Proc. Natl. Acad. Sci. USA 2013, 110, 7580–7585. [Google Scholar] [CrossRef] [PubMed]
- Adamo, A.; Sharei, A.; Adamo, L.; Lee, B.; Mao, S.; Jensen, K.F. Microfluidics-Based Assessment of Cell Deformability. Anal. Chem. 2012, 84, 6438–6443. [Google Scholar] [CrossRef]
- Nyberg, K.D.; Scott, M.B.; Bruce, S.L.; Gopinath, A.B.; Bikos, D.; Mason, T.G.; Kim, J.W.; Choi, H.S.; Rowat, A.C. The physical origins of transit time measurements for rapid, single cell mechanotyping. Lab Chip 2016, 16, 3330–3339. [Google Scholar] [CrossRef]
- Gossett, D.R.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Di Carlo, D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef]
- Mietke, A.; Otto, O.; Girardo, S.; Rosendahl, P.; Taubenberger, A.; Golfier, S.; Ulbricht, E.; Aland, S.; Guck, J.; Fischer-Friedrich, E. Extracting Cell Stiffness from Real-Time Deformability Cytometry: Theory and Experiment. Biophys. J. 2015, 109, 2023–2036. [Google Scholar] [CrossRef] [PubMed]
- Urbanska, M.; Muñoz, H.E.; Shaw Bagnall, J.; Otto, O.; Manalis, S.R.; Di Carlo, D.; Guck, J. A comparison of microfluidic methods for high-throughput cell deformability measurements. Nat. Methods 2020, 17, 587–593. [Google Scholar] [CrossRef]
- Fregin, B.; Czerwinski, F.; Biedenweg, D.; Girardo, S.; Gross, S.; Aurich, K.; Otto, O. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun. 2019, 10, 415. [Google Scholar] [CrossRef] [PubMed]
- Belotti, Y.; Tolomeo, S.; Conneely, M.J.; Huang, T.; McKenna, S.J.; Nabi, G.; McGloin, D. High-Throughput, Time-Resolved Mechanical Phenotyping of Prostate Cancer Cells. Sci. Rep. 2019, 9, 9. [Google Scholar] [CrossRef]
- Saadat, A.; Huyke, D.A.; Oyarzun, D.I.; Escobar, P.V.; Øvreeide, I.H.; Shaqfeh, E.S.G.; Santiago, J.G. A system for the high-throughput measurement of the shear modulus distribution of human red blood cells. Lab Chip 2020, 20, 2927–2936. [Google Scholar] [CrossRef]
- Mokbel, M.; Mokbel, D.; Mietke, A.; Träber, N.; Girardo, S.; Otto, O.; Guck, J.; Aland, S. Numerical Simulation of Real-Time Deformability Cytometry To Extract Cell Mechanical Properties. ACS Biomater. Sci. Eng. 2017, 3, 2962–2973. [Google Scholar] [CrossRef]
- Witkowski, T.; Ling, S.; Praetorius, S.; Voigt, A. Software concepts and numerical algorithms for a scalable adaptive parallel finite element method. Adv. Comput. Math. 2015, 41, 1145–1177. [Google Scholar] [CrossRef]
- Ahmmed, S.M.; Bithi, S.S.; Pore, A.A.; Mubtasim, N.; Schuster, C.; Gollahon, L.S.; Vanapalli, S.A. Multi-sample deformability cytometry of cancer cells. APL Bioeng. 2018, 2, 032002. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Galior, K.; Ma, V.P.-Y.; Salaita, K. Molecular Tension Probes for Imaging Forces at the Cell Surface. Acc. Chem. Res. 2017, 50, 2915–2924. [Google Scholar] [CrossRef]
- Neubauer, J.W.; Hauck, N.; Männel, M.J.; Seuss, M.; Fery, A.; Thiele, J. Mechanoresponsive Hydrogel Particles as a Platform for Three-Dimensional Force Sensing. ACS Appl. Mater. Interfaces 2019, 11, 26307–26313. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Yun, S.H. Confocal Brillouin microscopy for three-dimensional mechanical imaging. Nat. Photon. 2008, 2, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.-J.; Kabakova, I.V.; Ruberti, J.W.; Sherwood, J.M.; Dunlop, I.E.; Paterson, C.; Török, P.; Overby, D.R. Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials. Nat. Methods 2018, 15, 561–562. [Google Scholar] [CrossRef]
- Scarcelli, G.; Yun, S.H. Reply to ‘Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials’. Nat. Methods 2018, 15, 562–563. [Google Scholar] [CrossRef] [PubMed]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Lekka, M.; Laidler, P.; Gil, D.; Lekki, J.; Stachura, Z.; Hrynkiewicz, A.Z. Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur. Biophys. J. 1999, 28, 312–316. [Google Scholar] [CrossRef]
- Targosz-Korecka, M.; Brzezinka, G.D.; Malek, K.E.; Stȩpień, E.; Szymonski, M. Stiffness memory of EA.hy926 endothelial cells in response to chronic hyperglycemia. Cardiovasc. Diabetol. 2013, 12, 96. [Google Scholar] [CrossRef]
- Szymonski, M.; Targosz-Korecka, M.; Malek-Zietek, K.E. Nano-mechanical model of endothelial dysfunction for AFM-based diagnostics at the cellular level. Pharmacol. Rep. 2015, 67, 728–735. [Google Scholar] [CrossRef]
- Mokrozub, V.V.; Lazarenko, L.M.; Sichel, L.M.; Babenko, L.P.; Lytvyn, P.M.; Demchenko, O.M.; Melnichenko, Y.O.; Boyko, N.V.; Biavati, B.; DiGioia, D.; et al. The role of beneficial bacteria wall elasticity in regulating innate immune response. EPMA J. 2015, 6, 13. [Google Scholar] [CrossRef]
| Monomer and Crosslinker | Microgel Properties | Ref. |
|---|---|---|
| Precipitation polymerization | ||
| EGDMA-PolyEGDMA Co-polymerization of Divinylbenzene-PolyEGDMA-co-DVB | Size: PolyEGDMA: 1.18–2.27 µm (PDI = 1.006–1.035). PolyEGDMA-co-DVB: 1.93-2–45 µm (PDI = 1.006–1.019). | [33] |
| Co-polymerization MAA-PEGMM, EDMA crosslinker | Size: 0.45–3.25 µm depending on reactant conc. 0.77 µm (0.44%)–2.79 µm (20.3%) depending on solvent. | [34] |
| PEG-DA, crosslinked using Tetra-thiol + UV light | Size: 1.76 ± 0.26 µm. PDI = 1.26 (n < 200). | [35] |
| Co-polymerization N-isopropylacrylamide (NIPPAm) and acrylic acid (Acc), crosslinked using BIS (0.1,1 and 10 wt%) | Size: 2 ± 0.5 µm. | [36] |
| Co-polymerization PVA -PEGMMA, crosslinked using PEGDMA (1–11%) and HEMA4L46 (3%) | Size after sieving between 315 and 500 µm: PEGDMA: 376 ± 1 µm to 462 ± 2 µm. HEMA4L46: 379 ± 2 µm. Elastic modulus (G’): PEGDMA: 17±1 kPa to 1.1 ± 0.1 kPa. HEMA4L46: 4.8 ± 0.2 kPa. | [28] |
| Surfactant-free emulsion polymerization | ||
| N-isopropylacrylamide, crosslinked using N,N’-methylenebisacrylamide | Size: 700 nm (room temp), 300 nm (310 K), PDI = 7%. Young‘s modulus (E): 8 ± 1–4 kPa (300 K), 86 ± 22 kPa (313 K). | [30] |
| Co-polymerization N-isopropylacrylamide (NIPPAm) and acrylic acid (Acc) crosslinked using BIS (0, 2, 4 and 7%) | Size: 760.3 ± 14.7 nm to 821.8 ± 47.0 nm depending on BIS concentration. | [37] |
| Seed-feed | ||
| Co-polymerization MMA, MAA, EGD and GM Microgels: M-EGD, GM-E-EGD and DX microgels | Size: GM-M-EGD:102 nm (C.V 16) and M-EGD:107 nm (C.V 18). Storage modulus (G’): DX microgel storage modulus: 72.9–134 kPa. | [38] |
| Spray drying | ||
| AcGGM Microgel: Hemicellulose | Size: 2.0 ± 1.0 µm (pure), 1.3 ± 0.3 µm, 2.7 ± 2.2 µm depending on added functional material. | [39] |
| Chitosan core and Eudragit coat | Core size: 1.8 ± 1.1 µm to 2.9 ± 1.7 µm depending on solvent and chitosan type. Core-coat size: 152 ± 4 µm to 223 ± 6 µm. Depending on Eudragit type and core/coat ratio. | [40] |
| Membrane emulsification | ||
| Chitosan | Size: 12.92 (C.V 19.70%)–17.40 µm (C.V 21.94%) depending on monomer concentration. 13.81 (13.35%)–13.83µm (22.85%) depending on oil phase. | [41] |
| Particle replication in nonwetting templates (PRINT®) | ||
| HEA PEGDA (1–10%) | Disc size: 5.2–5.9 µm d + 1.22-1.54 µm tall. Elastic modulus: 1% PEGDA: 7.8 ± 1 kPa 10% PEGDA: 63.9 ± 15.7 kPa. | [29] |
| Polymer | Microfluidic Device | Sample Properties | Crosslinking | Properties of Microgels; | Ref |
|---|---|---|---|---|---|
| Alginate | Flow focusing for alginate emulsification, T-junction of Ca emulsification | η = 48 mPas at cp = 1.5% | Ca induced. Coalescence between emulsified alginate and Ca droplets. Constant pH. | Non-spherical microgels with size in the range 150–100 µm Ø depending on flow rates. CV of size: 6.4%. Disc-like hydrogels. | [42,43] |
| Flow focusing | Pronova UP MVG, Novamatrix cp = 2.0% | Ca induced. Emulsified alginate with Ca-EDTA, Ca released from EDTA by acetic acid diffusing from oil phase after emulsification. | Spherical microgels with size in the range 17–50 µm Ø depending on flow rates. pH 5 in microgels. | [50] | |
| Flow focusing | Alginate, cp = 2% | Ca induced. Emulsfied alginate with CaCO3; increasing Ca solubility from the carbonate by acetic acid diffusing from the continuous phase. pH reduced | Nearly spherical microgels with size in the range 54–72 µm Ø obtained by varying flow rates. | [51,52] | |
| Flow focusing of dual inlet aqueous solutions | Mw = 268 kDa FG = 0.68; used at cp = 0.8% | Ca induced by competitive ligand exchange from different chelators at constant pH (user controlled in the range from 8 to 5). | Spherical micgrogels with size 50 µm Ø | [49] | |
| κ-carra-geenan | Flow focusing | Mw = 1000 kDa, Copenhagen Hercules cp = 0.8%; | Ca induced by including CaCl2 in the continuous phase (0.25% CaCl2 in undecanol). | Spherical microgels with size about 65 µm Ø obtained at given flow rates. | [53] |
| Pectin | Flow focusing | M = (239.5 ± 10.5) kDa; 24% amidation, 23% esterification; cp = 1–10% | Ca induced; 4M CaCl2 dispersed at ratio 1:3 in mineral oil with 2 wt% span 80. | Spherical microgels with Ø~70µm and CV of 3.5% obtained under some conditions. | [48] |
| Gelatin | Calf bone gelatin, 300 Bloom; cp of 5% in water at pH 7.4 | Thermosetting: Emulsified by extrusion through microchannel plate, at 40 °C and collected in continuous phase as 25 °C, subsequently cooled to 5 °C. | Spherical microgels with diameter 31.6 µm, relative S.D. of 7.3%. | [54] | |
| Hyaluronic acid derivatives | Flow focusing for initial emulsification of aqueous pregel, crosslinking initiator added in downstream junction | Hyaluronic acid derivatives. HA base polymer Mw 40–65 kDa | Passerini type X-linking using PEG dialdehyde initiated by compound added in the second junction; diffusing initiator from continous phase. | Spherical microgels wih tunable size, the range 70–90 µm diameter shown explicitly. | [20] |
| Microgel Properties | Immobilization | Cantilever | AFM Mode | Shear or Young’s Modulus | Ref. |
|---|---|---|---|---|---|
| PNIPAm at cp 18.2 mg/mL–21.8 mg/mL crosslinked with BIS | Adsorption on silicon substrate | MLCT-Bio-DC 0.01 N/m 0.03 N/m pyramid | FV; PF-QNM | 3–32 kPa 17–48 kPa | [61] |
| Sodium alginate at cp 0.9–1.7%, crosslinked with Ca or Ba ions; size range 425–870 µm | Micropatterned grid | MLCT 0.03 N/m–0.1 N/m pyramid | FV | 0.4–14.4 kPa | [65] |
| (PNIPAM-co-PMAA/PDADMAC)9/PNIPAM-co-PMAAb at cp = 12 mmol, crosslinked with BIS. Size range 200–1400 nm | Adsorption: APTES coated silicon | SNML 0.07 N/m pyramid | PF-QNM | 75 kPa at 25 °C 450 kPa at 40 °C | [70] |
| PNIPAm-co-Aac at cp 3.7% and 5.4%, crosslinked with BIS, size range 280–480 nm | Adsorption on Au coated silicon | HQ:CSC38/NO AL 0.05 N/m cone | Microrheology | 100 kPa–800 kPa | [72] |
| PNIPAm at cp 1.14% crosslinked either with 2.5 or 10 mol% BIS. Size of microgels ~1000 nm | Adsorption on Au coated silicon | AR-iDrive-N01 0.09 N/m pyramid | FV | 1–4 kPa (for 2% BIS) 6–40 kPa (for 10% BIS) | [74] |
| MMA; size of the order ~100 nm | GOPS coated borosilicate | ScanAsyst-Fluid 0.4–0.7 N/m pyramid | PF-QNM | qualitative-deformation images | [75] |
| Alginate microspheres (UPLVG, FMC) at cp = 1.5% crosslinked with Ca. Size larger than 100 µm | Deposition on nylon mesh; 330 µm holes; glued to Petri dish | PNP- TR 0.32 N/m pyramid | QI, scan size 3µm × 3µm | up to 8.75 MPa | [76] |
| Alginate microspheres (UPLVG, FMC) at cp = 1.5% crosslinked with genipin. Size larger than 100 µm | Deposition on nylon mesh; 330 µm holes; glued to Petri dish | PNP-TR 0.32 N/m pyramid | QI, scan size 3µm × 3µm | up to 3.67 MPa | [76] |
| PNIPAm crosslinked with BIS; size of microgels 150–350 nm | Adsorption: APTES coated silicon | MLCT-BIO-DC 0.03 N/m pyramid | QI | 16–140 N/m | [8,77] |
| Polyacrylamide (PAAm) 5.9% to 11.8% Crosslinked with BIS; size of microgels 13.3–18.0 µm | Plasma cleaned silicon | MLCT 0.03 N/m pyramid | FV | 0.09–11 kPa | [17][ |
| PAAm functionalized with NHS (N-succinimidyl ester) 7.9%, crosslinked with BIS– | Plasma cleaned silicon | MLCT 0.03 N/m pyramid | FV | 1.6 kPa | [17] |
| pS-co-NIPAM, 50% to 70%; crosslinked with BIS (0–3 mol%); size of microgels 220–627 nm; | Not specified | silicon nitride 0.2–0.8 N/m | FV | 0.24–0.99 GPa | [78] |
| ULC microgels—PNIPAm 146 mM Crosslinked with BIS; size range of microgels 1.1 ± 0.1 µm | Adsorption on APTES coated glass | silicon nitride 0.09 N/m sphere | FV | ~10 kPa | [12,79] |
| Covalently crosslinked hyaluronic acid-based microgels fabricated using microfluidics. Size: 73–91 µm depending on crosslinker and cp | Adsorption on PEI imine coated, plasma cleaned glass | CSC38 0.09 N/m tipless | Force-distance | E from 11 to 34 kPa depending on sample | [20] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oevreeide, I.H.; Szydlak, R.; Luty, M.; Ahmed, H.; Prot, V.; Skallerud, B.H.; Zemła, J.; Lekka, M.; Stokke, B.T. On the Determination of Mechanical Properties of Aqueous Microgels—Towards High-Throughput Characterization. Gels 2021, 7, 64. https://doi.org/10.3390/gels7020064
Oevreeide IH, Szydlak R, Luty M, Ahmed H, Prot V, Skallerud BH, Zemła J, Lekka M, Stokke BT. On the Determination of Mechanical Properties of Aqueous Microgels—Towards High-Throughput Characterization. Gels. 2021; 7(2):64. https://doi.org/10.3390/gels7020064
Chicago/Turabian StyleOevreeide, Ingrid Haga, Renata Szydlak, Marcin Luty, Husnain Ahmed, Victorien Prot, Bjørn Helge Skallerud, Joanna Zemła, Małgorzata Lekka, and Bjørn Torger Stokke. 2021. "On the Determination of Mechanical Properties of Aqueous Microgels—Towards High-Throughput Characterization" Gels 7, no. 2: 64. https://doi.org/10.3390/gels7020064
APA StyleOevreeide, I. H., Szydlak, R., Luty, M., Ahmed, H., Prot, V., Skallerud, B. H., Zemła, J., Lekka, M., & Stokke, B. T. (2021). On the Determination of Mechanical Properties of Aqueous Microgels—Towards High-Throughput Characterization. Gels, 7(2), 64. https://doi.org/10.3390/gels7020064







