1. Introduction
Commonly used gels are prepared using chemical reagents while mixing, by lowering the temperature and by the irradiation of high-energy electromagnetic waves, such as an electron beam and UV, where the cross-linking sites of polymer networks are dispersed randomly in gels, resulting in a macroscopically isotropic and homogeneous structure. This is because the maximum entropy of easily deformed polymer segments between cross-linking sites is obtained when the number of conformational states is maximum. Therefore, to prepare anisotropic gels some asymmetry, such as an asymmetric external force on the gel, should be required. To date, most studies performed on gelation have been on homogeneous systems [
1,
2,
3]. In industry, however, gels are frequently prepared at an interface between two phases. Following the classification of chemical reactions into homogeneous and heterogeneous reactions, we refer to the gelation occurring in a homogeneous phase as homogeneous gelation and the gelation involving reactions at interfaces between different phases as heterogeneous gelation. In 1954, Thiele reported the fabrication of anisotropic beads by dripping an alginate solution in a bath of calcium chloride aqueous solution [
4]. Thiele and coworkers prepared anisotropic channel-like alginate gels induced by diffusion of various multivalent cations [
5]. These are among the first examples of heterogeneous gelation, on which many studies have now been reported [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. The most important gels yielded by heterogeneous gelation are gels in parts of the human body. They are anisotropic, with the anisotropy often having a gradient, such as blood vessel walls [
18]. Although the mechanism of biosynthesis is rather complex, most biotissues are yielded from a surface or a point and the growth is directional [
19]. Therefore, understanding heterogeneous gelation is important from both industrial and biological viewpoints.
Among the systems that undergo heterogeneous gelation, polymer solutions in contact with solutions containing gelators such as cross-linkers have many promising applications. As a typical example of an anisotropic gel whose structure has been studied is a cylindrical gel prepared by the dialysis of sodium alginate aqueous solution in calcium chloride aqueous solution [
4,
5,
6,
7,
8,
9,
10,
20]. Maki et al., performed a small-angle X-ray scattering study on the structure of the alginate gel and showed that the polymer orientation is perpendicular to the flow of the gelators [
20]. They showed that the gel is highly anisotropic near the surface (dialysis tube) but becomes isotropic toward the center. It has been shown for many combinations of polymers and gelators that the orientation is always similar to that observed for the alginate [
14,
15,
21]. By changing the boundary conditions, we can prepare anisotropic gels with various shapes such as spherical gels and fiber-like gels [
8]. The birefringence distribution of the gels is consistent with the orientation of polymer molecules perpendicular to the flow of the gelators [
8]. In these systems, polymer molecules cannot permeate into the gel and the gelators selectively diffuse into the already yielded gel, resulting in the cross-linking of polymers at the reaction front. Since the polymers should have a high affinity with the gelators, they are in contact with the interface over a large contact area, which results in molecular orientation. Study of the microrheological events occurring on polymer molecules in the boundary layer at the sol-gel interface is challenging, although such studies should be performed in the near future.
For applications, the present approach to yielding anisotropy has an advantage of gelation in a self-organized manner under mild conditions. Several elaborate gels having unique properties have been developed. Gong’s group at Hokkaido University used a double network gelation involving the contact of synthetic polymer solutions with gelator solutions to prepare a variety of tough anisotropic artificial substitutes such as artificial cartilage [
22,
23]. Furusawa et al. prepared epithelial lumen-like engineered tissues by the contact of collagen solutions with buffer solutions having a high pH due to spinodal decomposition [
24]. Konno et al., prepared a multilayer cylindrical gel consisting of an inner isotropic gel layer and an outer highly anisotropic gel layer [
25,
26]. The release of drugs from gel particles having such multilayers may exhibit different behavior from the common exponential behavior observed for homogeneous particles and used for stepwise or constant drug release, similarly to capsules or spheres having layer-by-layer wall membranes [
27].
On the other hand, the results of studies on the dynamics of heterogeneous gelation have not been organized and almost no applications of such gelation dynamics have been reported, although basic data on the gelation dynamics for simple polymer systems that undergo gelation in contact with gelator solutions have been accumulated [
28,
29,
30,
31,
32,
33]. Measurable physical quantities characterizing the gelation process are the gel fraction and the molecular weight distribution in the sol fraction in homogeneous gelation [
1], whereas they are the gel volume and the degree of orientation of the gel in heterogeneous gelation [
8]. In most cases, gel layers are formed at the interface between the polymer solution and the gelator solution and extended into the polymer solution while keeping the sol-gel interface clear [
8]. Yamamoto et al., developed an irreversible thermodynamic theory focusing on the motion of the sol-gel boundary (moving boundary (MB) picture) [
28,
29].
In this article, we attempt to reorganize the experimental results on the basis of the MB picture, focusing on the role of the gelator. Then we propose a way of classifying the previously reported systems into several types as a first step toward understanding the characteristics of heterogeneous gelation dynamics. The gelation dynamics are expressed using universal scaling equations corresponding to the gelation mechanism, such as gelation induced by the inflow of cross-linkers (Case 1), by solvent exchange (Case 2), by the inflow of catalysts (Case 3), by the exchange of solutes having very different diffusion constants (Case 4) and by nucleation at low supersaturation (Case 5) (see
Section 2.3 for details). In
Section 3, we discuss the physical meaning of isotropic and anisotropic gelation from the standpoint of phase separation. By fitting data for gelation dynamics whose gelation mechanism is unknown to the universal scaling equation for Cases 1–5, we can identify the type of the gelation of the system. Furthermore, we can determine kinetic coefficients from the fitting parameters. The second aim of this article is to apply the analytical method to one of the most important biomedical processes, blood coagulation. Although some properties of the blood of patients can be obtained from conventional biochemical tests and the time required for blood coagulation, we have few means of estimating kinetic properties in blood coagulation, which is part of the missing link between blood properties and disorder in blood coagulation. Analysis of the dynamics of blood coagulation by fitting the data to the universal scaling equation enables us to extract information on kinetic coefficients in the process that cannot be obtained by static measurements. In
Section 4, we describe the application of the analytical method for gelation dynamics to two model systems of blood coagulation to determine several key kinetic coefficients relating to blood coagulation.
2. Experimental Results on Gelation Dynamics and Classification of Systems by Moving Boundary Picture
We propose a generalized model of heterogeneous gelation and show the observed gelation dynamics of chitosan solution [
30] as a typical example in
Section 2.1. Then we demonstrate a theoretical analysis of the dynamics based on the MB picture in
Section 2.2. In
Section 2.3 we discuss the factors which determine the characteristics of the dynamics in
Section 2.2 and propose a way of classifying of various systems according to the key factors.
2.1. Gelation Dynamics of Chitosan Solution in Contact with Solutions with High pH
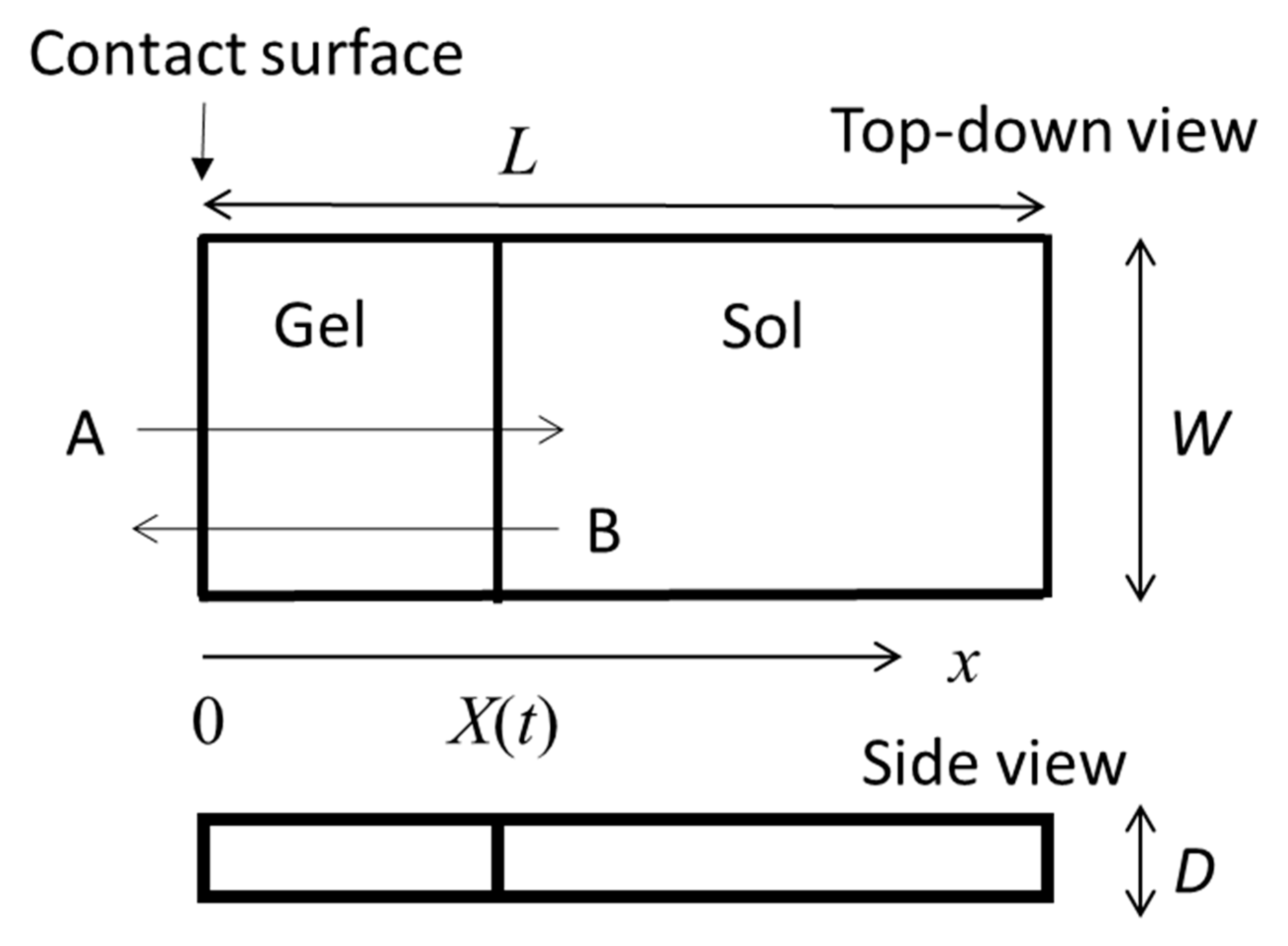
The gel growth behaviors from the interface of polymer solutions with various types of gelator solutions have been observed. In
Figure 1 we show an illustration of one of the simplest cases, the one-dimensional growth of a gel in a polymer solution cell in contact with a gelator solution bath (left-hand side of the cell). This model was proposed for the analysis of gelation dynamics of chitosan solution induced by a change of pH.
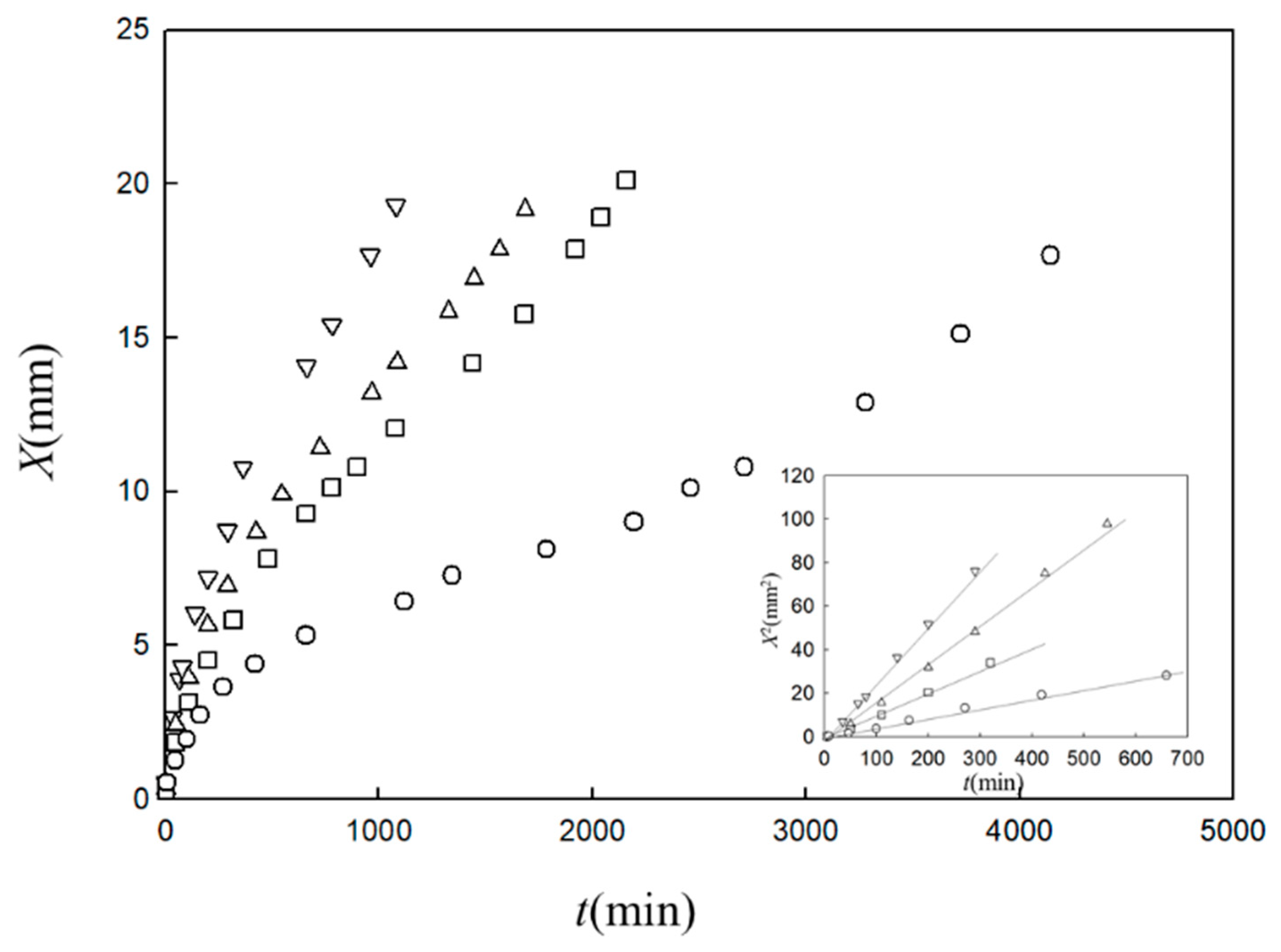
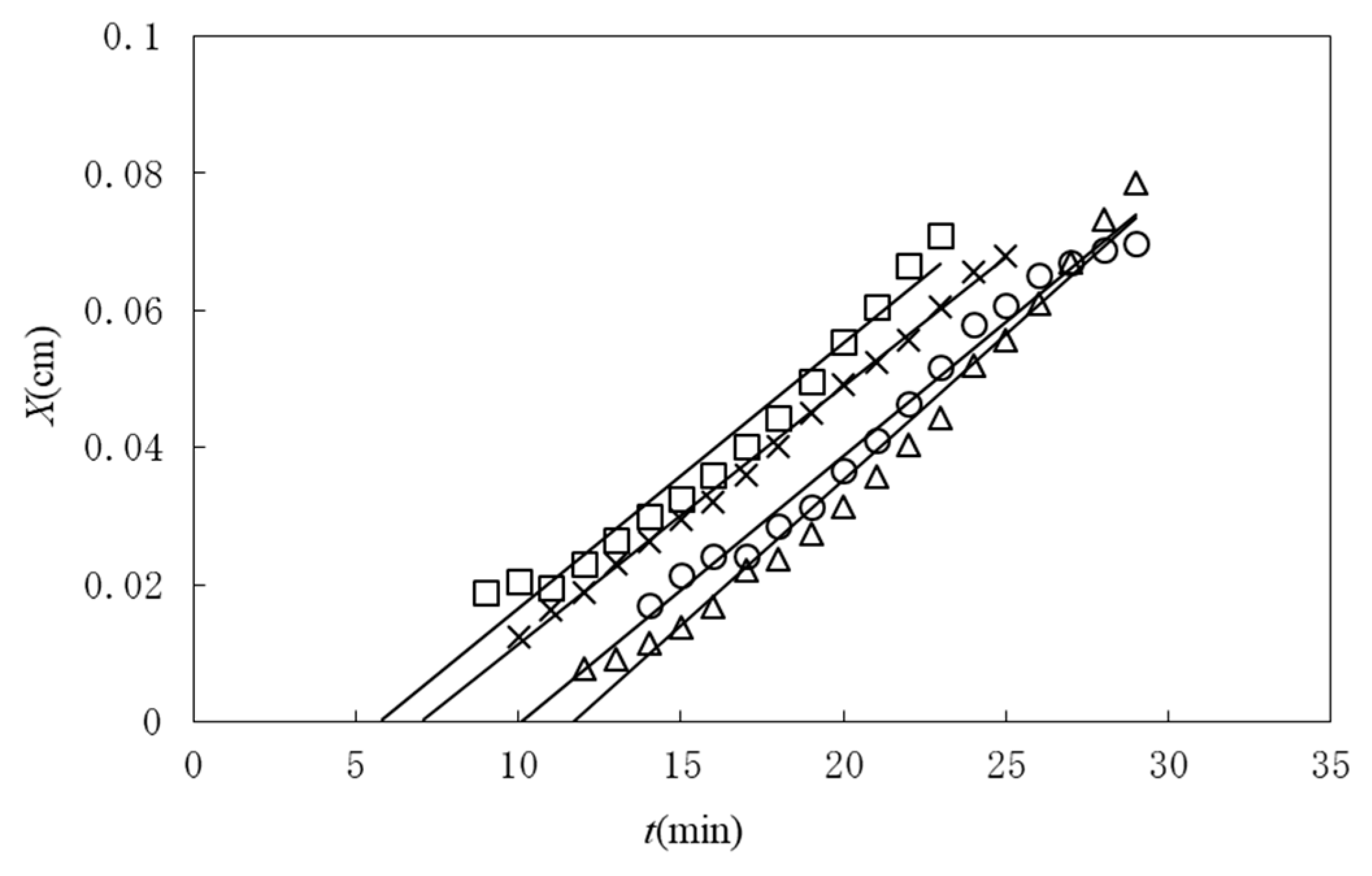
Figure 2 shows a typical observed time course of the gel layer thickness
X(
t) induced at the interface of chitosan solution with NaOH solution [
25]. Chitosan solution is soluble at a low pH and forms a gel at a neutral pH by hydrogen bonding. Under the geometry shown in
Figure 1, the part of the chitosan solution where the pH changes from a low pH to a neutral pH is transformed to a gel. The initial process appears to be expressed by square-root behavior
, as shown in the inset of
Figure 2, suggesting diffusion-limited dynamics. Here we modify the model shown in
Figure 1 and generalize it by including various cases in which A and B have different roles other than those of NaOH solution and chitosan solution, respectively. For example, the outflow of B may or may not be involved in gelation and gelation can occur with or without the consumption of A in the generalized model. Similar initial behaviors have, however, been observed for different types of gelator solutions under various geometries, whereas the late-stage behaviors were different from each other [
28,
29,
30].
2.2. Moving Boundary Picture for Gelation Dynamics
The MB picture proposed by Yamamoto et al. [
28,
29] describes the gelation dynamics in terms of the sol-gel interface motion caused by the inflow of the gelator. The idea of the MB picture will be briefly explained through the gelation dynamics of chitosan solution. The dynamics introduced in
Section 2.1 is analyzed as follows. In the system, the chitosan solution is enclosed in an
(length) ×
(width) ×
(depth) rectangular-solid space as shown in
Figure 1 and is immersed in NaOH solution. The chitosan solution is in contact with the NaOH solution at a
side surface (the contact surface) [
30].
The motion of the boundary is derived from the following assumptions.
(A) The sodium ions flow into the sol part and the acetate ions flow out from the sol part to the NaOH solution through the gel layer. The neutralization caused by the flows instantly results in the cross-linking of the inner chitosan solution to produce a new gel layer.
(B) The gel layer does not capture the inflow sodium-ions and the outflow acetate-ions by acting as a sink and the flows change so slowly that they can be considered to be in a steady state; all the gelators inflowing from the gelator solution arrive at the inner polymer solution through the gel layer to realize a steady state.
(C) The NaOH solution, gel and inner sol are in local thermodynamic equilibrium at the boundaries.
The concentrations of sodium ions in the NaOH solution, in the inner sol, in the gel layer, at the interface between the gel and the NaOH solution at the position in the gel layer and at the interface between the gel and the inner sol in the gel layer are respectively denoted by , , , and . The concentrations of acetate ions at the corresponding positions are respectively denoted by , , , and . The chemical potentials of the sodium ion in the NaOH solution, in the inner sol and in the gel layer are respectively denoted by , and and those of the acetate ion are denoted by , and .
The flux of the inflow sodium-ion in the gel layer is expressed as
where
is the sodium ion flux density and is expressed in terms of the concentration
and velocity
of the sodium ion as
. The unit vector along the
-axis is denoted by
. According to Fick’s law, the velocity of the sodium ion at
is given by
where
is the mobility of the sodium ion. Therefore, we have
In a similar way, we have the flux of the outflow acetate-ion as
with
In the above, is the mobility of the acetate-ion.
Let a new gel layer thickness
be produced during period
by neutralization caused by the sodium ion inflow. Assumption (A) gives the following relationship:
where
is the number of sodium ions required to neutralize a unit volume of the inner chitosan solution with acetate ion concentration
and is reasonably assumed to be proportional to
,
where
is a positive constant. Note that
is a function of the immersion time
. Hence, we have the time development equation for the gel thickness:
Assumption (B) requires the following relationships:
Integrating the differential Equations (9) and (10), we have the steady-state flows of sodium ions and acetate ions:
where
and
are the pressures of sodium ions and acetate ions respectively given by
Here, the free energies and per unit volume satisfy the relationships and .
Assumption (C) gives the chemical potential balance
Since the concentration of acetic acid is not so large, the chemical potential balance can be rewritten by assuming continuity of the concentration,
and
. In the immersion solution, the concentration of acetic acid is very small,
, because the volume of the immersion solution is very large. Hence,
. Therefore, the flux of the acetate-ion flow is given by
In the dilute limit of acetate ions in the gel, the pressure is expressed by
and the flux is given by
where
. The acetate ion concentration in the sol part
decreases with increasing immersion time
since acetate ions flow out from the sol part and the time development of the acetate ion concentration is given by
where
is the volume of the sol part. Using Equations (15) and (16), we have
Treating the sodium ion flow in the same manner as the acetate ion flow, we have
where
.
Solving the simultaneous equations, Equations (8), (19) and (20), with the initial condition
and
and introducing the scaled variables
and
, we have the scaled equation
with
and
From the expansion
around
, we derive the initial-stage (
) behavior as
This equation indicates square-root behavior in which the gel thickness increases proportionally to the square of the immersion time,
The square-root behavior is a characteristic feature of the diffusion-limited dynamics.
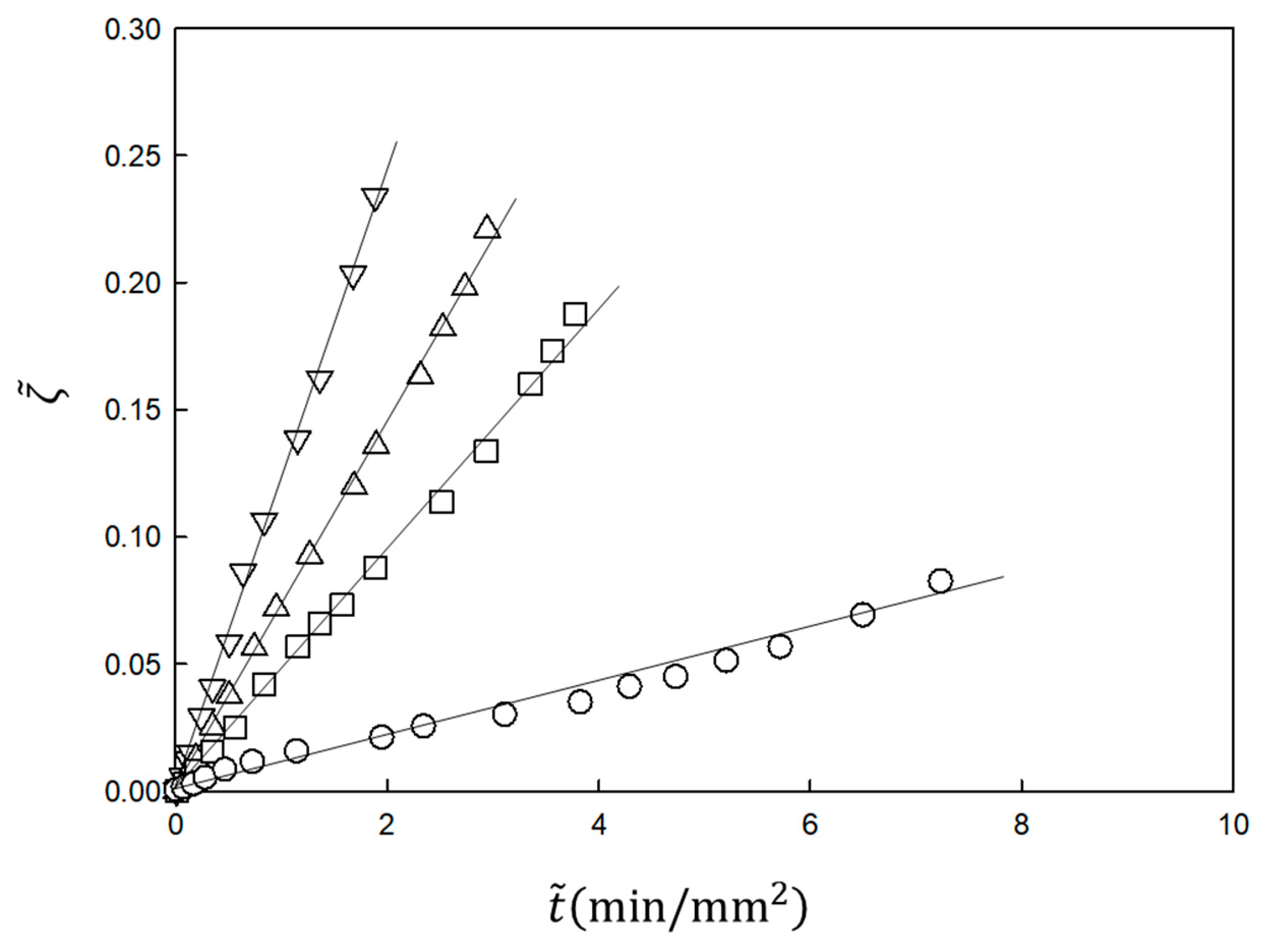
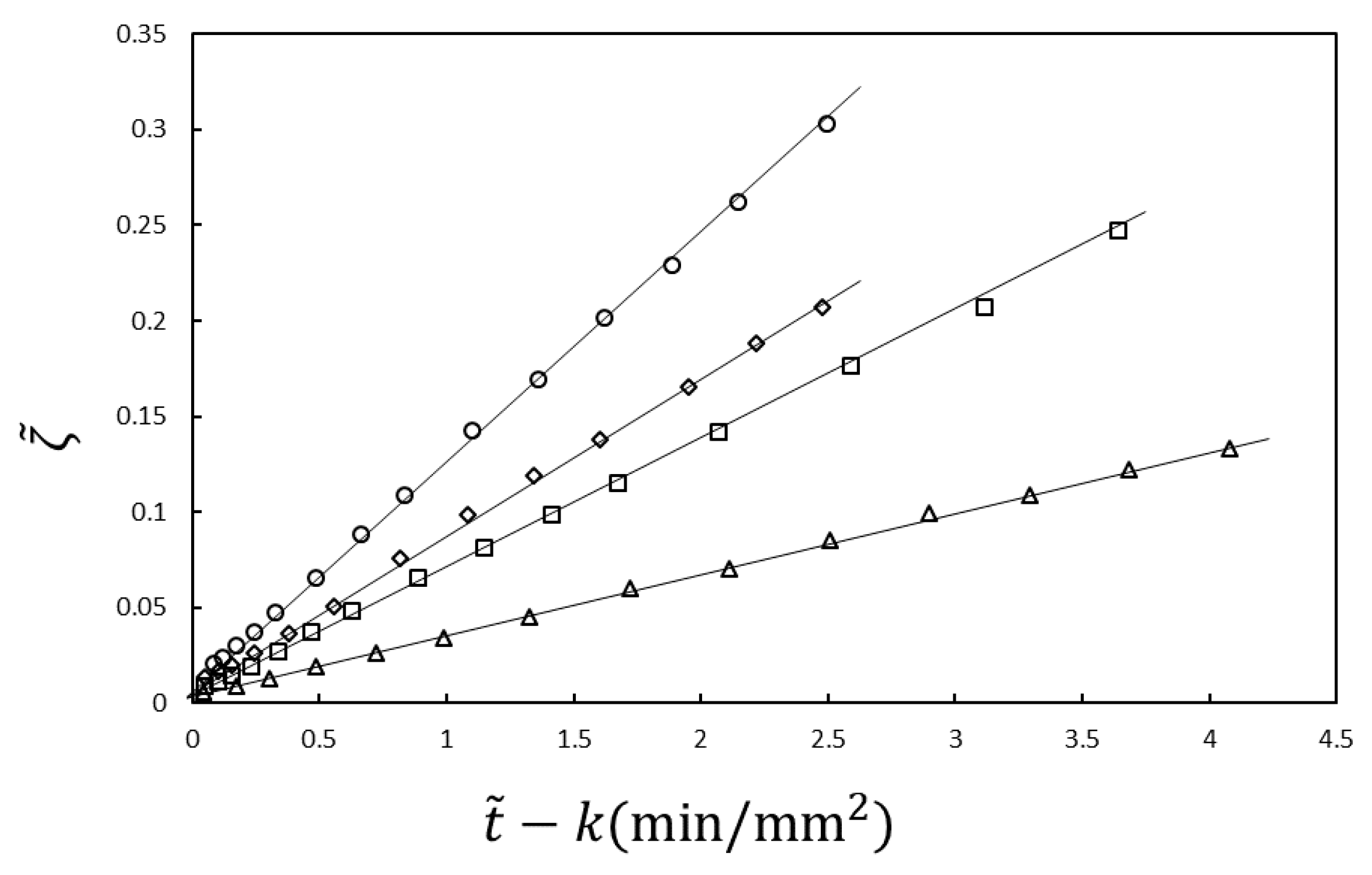
The experimental results shown in
Figure 2 are analyzed using Equations (21) and (22). In the analysis,
and
are the fitting parameters. The results are plotted according to the equations in
Figure 3. The slope
Kin is proportional to the NaOH concentration in the immersion solution, inversely proportional to the acetic acid concentration in the chitosan solution and independent of the chitosan concentration, as predicted by Equation (23) [
30] (not shown). Therefore, the time course of the gel thickness is fully explained by the MB picture. The observed gelation behavior is expressed by the scaled Equation (21) with system-dependent coefficients
and
. Thus, we can obtain information on the kinetic coefficients
γ and
kAc of the system from the fitting parameters
and
by comparing the experimental data with the theoretical equation.
2.3. Classification of Gelation Dynamics
In the gelation of chitosan solution, there are three types of characters having different roles. The first character is chitosan molecules, which are the element polymers constituting the gel. The second character is sodium ions, which are the gelator and are consumed to produce a gel layer. The third character is acetate ions, which are the gelation inhibitor.
Focusing on the gelator and the gelation inhibitor, we classify the gelation system into several types depending on the gelation mechanism. The simplest case is Case 1, in which cross-linking occurs simply by the inflow of cross-linkers as gelators; the gelation inhibitors are absent and the gelators are consumed to produce a gel layer. In
Figure 1, the gelator A is involved in gelation whereas B is not involved in gelation. An example of Case 1 is a system where sodium alginate aqueous solution is in contact with calcium chloride aqueous solution (alginate/Ca
2+ system) [
4,
5,
6,
7,
8,
9,
10,
20], in which calcium ions are the gelators. In Case 2, gelators flow into the element polymer solution and the gelation inhibitors flow out. Examples of Case 2 are polymers such as chitosan and collagen that undergo gelation via the formation of hydrogen bonds induced by a change in pH resulting from contact with a high pH solution. When chitosan or collagen in acetic acid solution with a low pH comes in contact with an aqueous solution of NaOH with a high or medium pH, anisotropic gels are prepared [
15,
30]. The gelator may be a catalyst, as in Case 3, making it necessary to consider the repeated use of the catalyst. In Case 3, although the inhibitors are absent, as in Case 1, the gelators are
not consumed in the gelation. An example of Case 3 is the system where gelatin aqueous solution is in contact with transglutaminase aqueous solution [
34].
Note that transient viscoelastic change occurs without any reactions when both solutes in liquid phases have very different diffusion constants [
35]. We define this case as Case 4. In Case 4, the inhibitors are absent, as in Case 1. However, the gelator makes
no links between the polymers. An example of Case 4 is the system where a high-molecular-weight DNA aqueous solution sandwiched between a pair of cover glasses is immersed in a low-molecular-weight DNA aqueous solution. In this case, the initial inflow of low-molecular-weight DNA causes the high-molecular-weight DNA solution to transiently form an anisotropic gel-like substance owning to the excluded volume effect and then the high-molecular-weight DNA diffuses to the immersion solution, finally resulting in a homogeneous solution. The gelation dynamics of the above-mentioned typical diffusion-limited systems were derived in
Section 2.2 and are summarized in
Table 1.
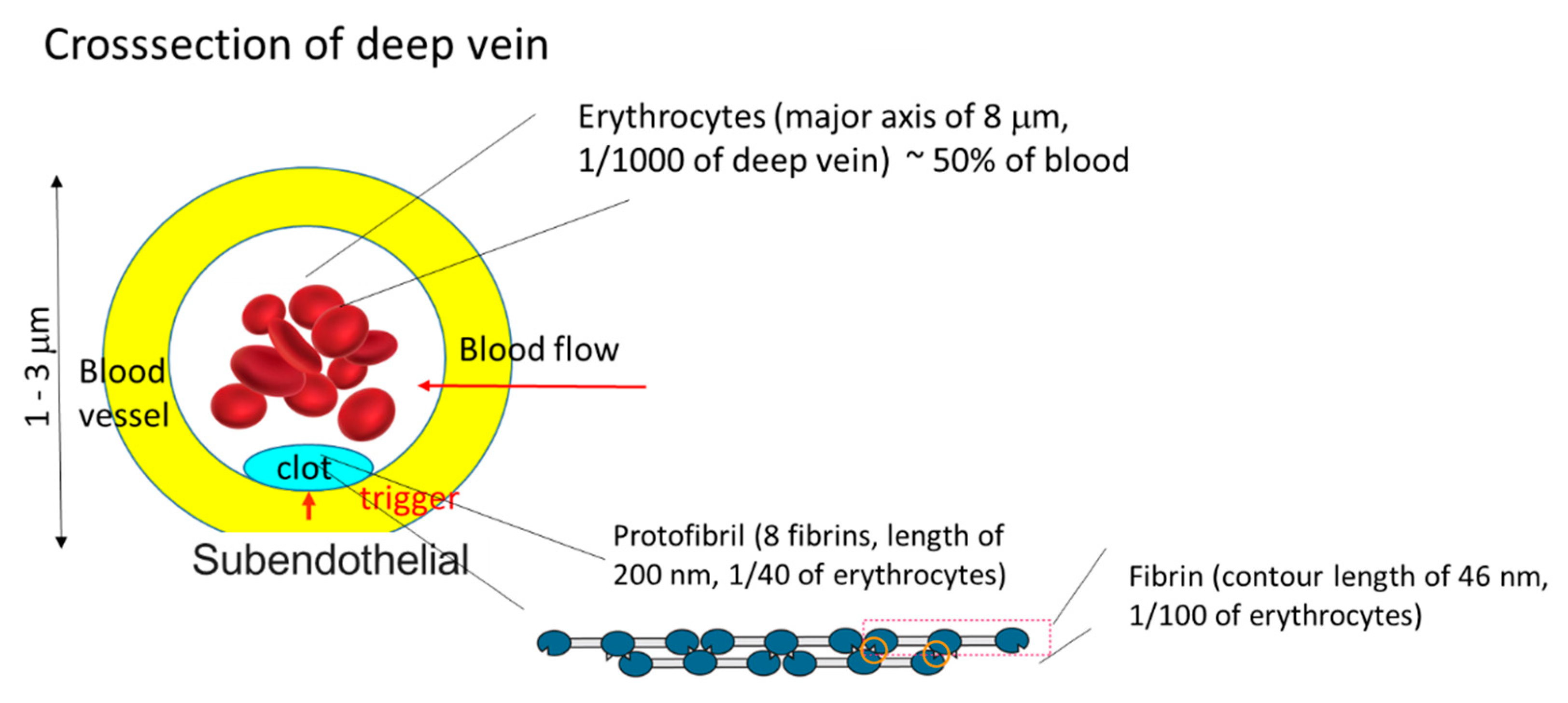
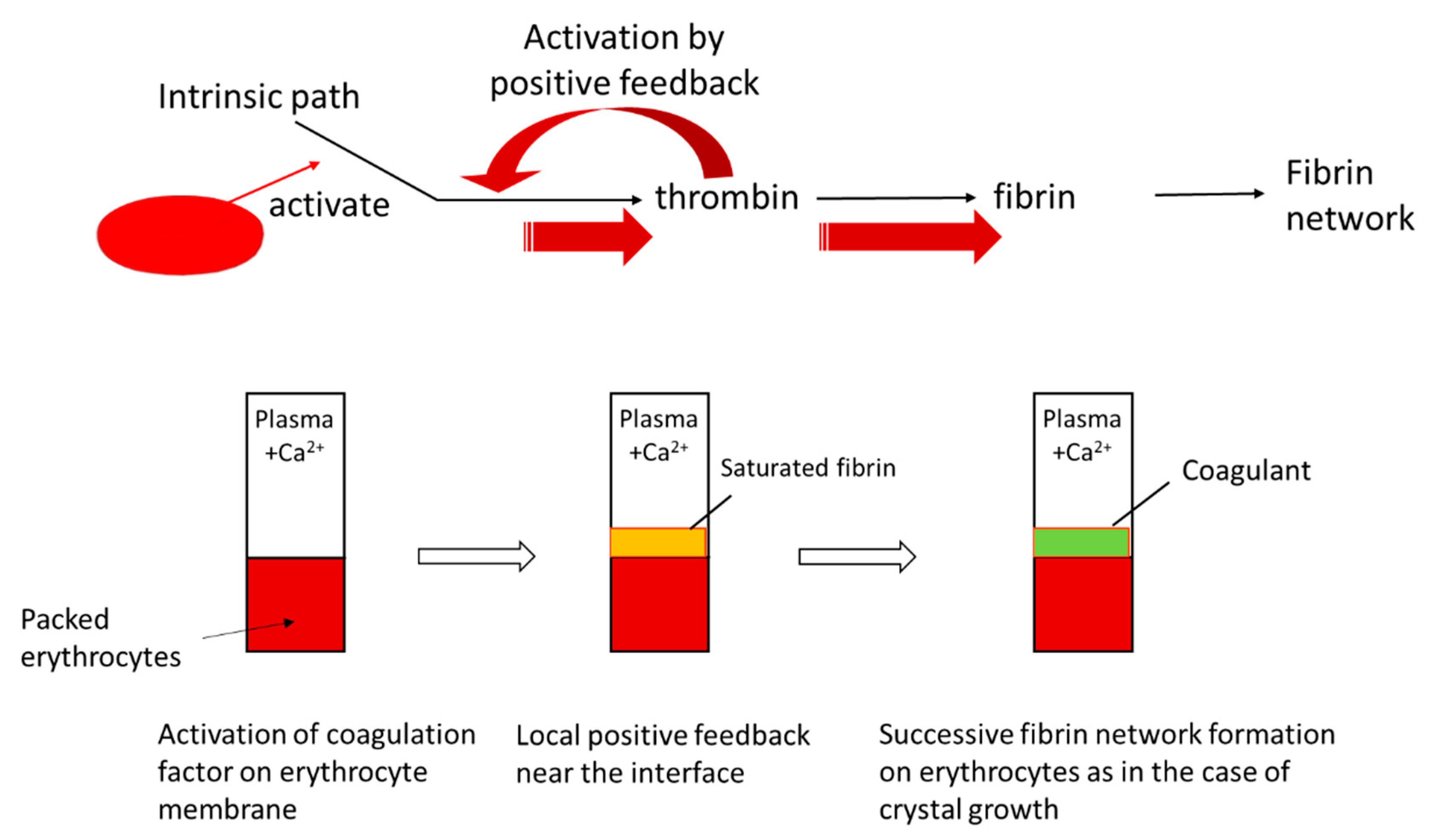
Case 5 is similar to the crystal growth from solutions at low supersaturation. Assume that the free energy of a polymer solution has a double minimum with different values. The lower and higher values correspond to gel phase and sol phase, respectively. If a gel region is nucleated by contact with a solid phase, then the polymer solution gels and the front line of the gel moves forward. In Case 5, neither gelators nor gelation inhibitors are present. The gelation is not diffusion-limited in this case. An example of Case 5 is the system where plasma is in contact with packed erythrocytes, which is discussed in detail in
Section 4.2. The cases given above are not exhaustive but are those for which examples are reported [
28,
29,
30,
31,
32,
33,
34,
35].
3. Theoretical View of Heterogeneous Gelation from the Standpoint of Phase Transition Dynamics
Here we regard gelation as a phase transition and discuss the gelation dynamics in the context of the phase transition dynamics [
36,
37,
38] for the polymer solution in contact with the gelator solution. Let us discuss the gelation system corresponding to Case 1 as the simplest case. The state of the polymer solution depends on the concentration
of gelators in the polymer solution. The state of the polymer solution is described in terms of the
order parameter , which expresses the degree of gelation;
when the polymer solution is in the gel state and
when it is in the sol state. Then, the
local free energy of the polymer solution is a function of
and
,
Let us consider a one-dimensional gel growth system, as shown in
Figure 1. The free-energy functional expressing the whole of the polymer solution is given by
where the positive constants
and
express the increase in free energy with respect to the space inhomogeneity of the gelator concentration and the degree of gelation, respectively. Since the concentration of gelators is a conserved quantity, the time development equation for the gelator is given by
where
denotes the elapsed time and
is the kinetic coefficient for
. Since
is an order parameter and is not a conserved quantity, the time development equation for
is given by
where
is the kinetic coefficient for
. The boundary conditions
is imposed, where
and
are, respectively, the chemical potential of the gelator in the polymer solution at the liquid-liquid contact interface and that in the gelator solution. In terms of
,
is generally given by
One of the most characteristic features of the heterogeneous gelation process is that the boundary between the sol phase and gel phase is macroscopically clear. Thus, the gel growth dynamics can be visualized by the MB picture. The dynamics shown in
Table 1 was derived by means of the MB picture.
Assumptions (A)–(C) in
Section 2.2 for the gelation of chitosan solution (Case 2) is modified for Case 1 as follows [
28] since the outflow ions are not involved in gelation in Case 1.
(A’) All the inflow gelators arriving at the inner polymer solution instantly cross-link the polymers to produce a new gel layer.
(B’) The gel layer does not capture the inflow gelators by acting as a sink and the gelator flow changes so slowly that it can be considered to be in a steady state; all the gelators inflowing from the gelator solution arrive at the inner polymer solution through the gel layer to realize a steady state.
(C’) The gelator solution, gel and inner polymer solution are in local thermodynamic equilibrium at the boundary.
According to the above three assumptions, in terms of the concentration
and chemical potential
) of the gelator in the gel layer, the gelator flow density
is given by
where
is the mobility of the gelator and we modify Equations (8), (19) and (20) governing the time development equations for the sol-gel boundary
as [
22]
where
is the number of gelators required to produce a unit volume of gel. Note that
is constant and the equation corresponding to Equation (18) is absent in Case 1 since gelation inhibitors are absent.
Using the initial condition
, we obtain the solution of Equation (33) as
where
. For Case 1, the square root behavior occurs during the entire period, although the behavior only occurs during the initial stage for Case 2.
Let us compare the above results with the phase transition dynamics given by Equations (28) and (29). The MB picture does not refer to the time development of the degree of gelation. Assumption (A’), however, requires that the time development of
is very rapid and an equilibrium value that depends on the gelator density
is quickly achieved. Thus, the degree of gelation
is expressed as
where for simplicity we let the “level function”
be given by the step function defined by
and
is a positive constant satisfying the equation
The gelator concentration in the MB picture indicates the concentration
of the gelator dissolved in the solvent, which is given by
Therefore, in the context of phase transition dynamics, Equation (32) should be rewritten as
Equation (39) requires the relationship
for the kinetic coefficient
. Assumption (B’) requires that the gelator flow can be regarded as a steady flow. The time dependence of the gelator concentration
is very weak and appears only through the time dependence of the boundary
; the boundary condition, that is, Assumption (C’), determines the weak time dependence. Hence, the gelator concentration is given by
The chemical potential
in Equations (32) and (39) is given by
To effectively use the description of the phase transition dynamics given by Equations (28) and (29), it is necessary to clarify the function forms of
and
and the value of the kinetic constant
statistical-mechanically and/or experimentally. This requirement will be discussed as a future issue. Here, we discuss a problem independent of the details of
and
. Equation (33), expressing the gelation dynamics, is valid when the dynamics of
is very fast compared with the gelator diffusion. What kind of dynamics is obtained in the opposite case, in which the dynamics of
is very slow? The answer is obtained from the common phase transition dynamics. In this case, Equations (28) and (29) are rewritten as
with
The boundary condition is given by
where the equilibrium value of the degree of gelation
is obtained from the equation
The dynamics described by Equation (44) is limited by the free energy and is regarded as the relaxation from an unstable state to a stable state minimizing the free energy.
When
is a double-well-type function (both the sol phase (
) and the gel phase (
) locally minimize the local free energy
) and the constant
is small, the solution of Equation (44) is approximately [
37,
39]
In this case, the gelation dynamics is also visualized by the motion of the sol-gel boundary. Therefore, to pay attention to the motion of the sol-gel boundary is valid. We could call the moving boundary picture the analysis method in which we pay attention to the sol-gel boundary motion even in the case of the energy-limited dynamics. The time dependence of , however, differs from the square-root behavior. The dynamics is expected to effectively visualize the gelation dynamics for Case 5.
Finally, we discuss how the anisotropy is taken into account. The presence of a gelator concentration gradient
during gelation is one of the characteristics of heterogeneous gelation. Therefore, we assume that the local free energy depends on the concentration gradient and introduce the order parameter
expressing the degree of anisotropy of the polymer solution, where
when the polymer solution is anisotropic and
when it is isotropic. The local free energy is given by
The free-energy functional is given by
where the positive constant
expresses the increase in free energy with respect to the space inhomogeneity of the anisotropy. In addition to Equations (28) and (29), we introduce the time development equation for
as
where
is the kinetic coefficient for
.
Let us discuss the diffusion-limited gelation dynamics with the anisotropy expressed by the MB picture. The gelation dynamics of curdlan solution [
28] is in this category. In this case, the time development of the anisotropy is expressed as
where
Equation (53) requires the local free energy to reach a local minimum at a finite value of the degree of anisotropy. Note that global minimization of the local free energy at a finite is not required. At a concentration gradient larger than a threshold value, the local free energy is expected to have such a local minimum. The increase in the degree of gelation roughly coincides with the increase in anisotropy. The kinetic coefficient rapidly drops to zero with increasing since the gelation significantly interferes with the polymer motion in the polymer solution. Thus, the degree of anisotropy is fixed at a finite value .