Propagation of Fatigue Cracks in Friction of Brittle Hydrogels
Abstract
1. Introduction
2. Results and Discussion
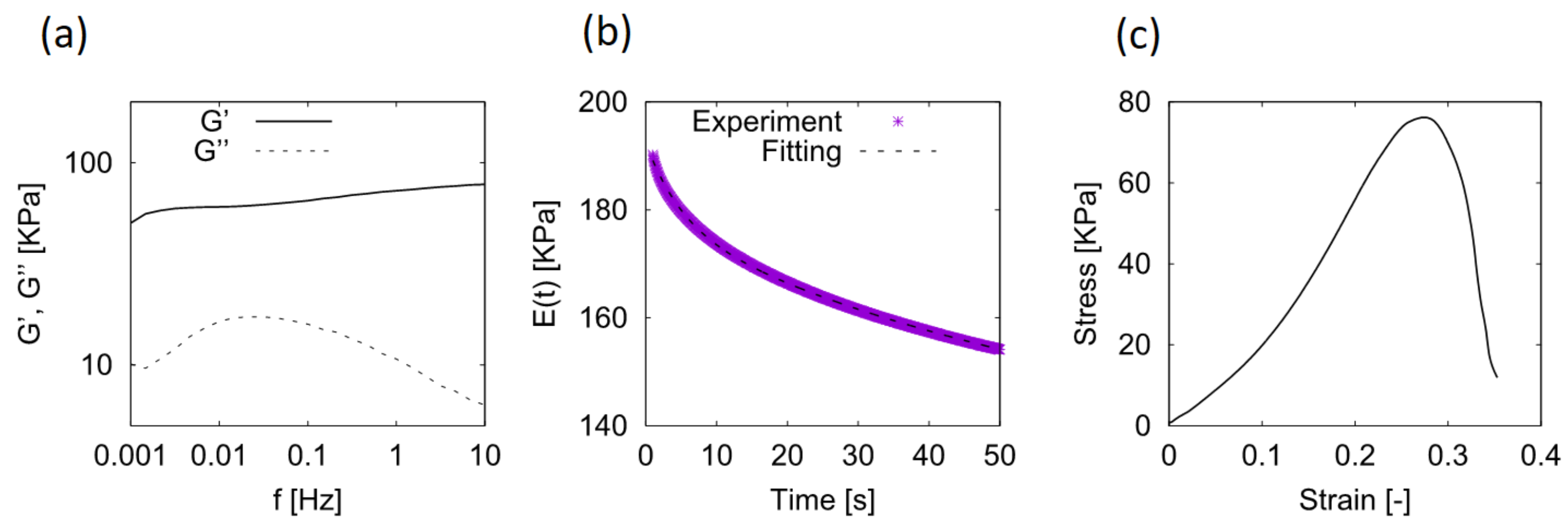
2.1. Stress-Relaxation Behavior
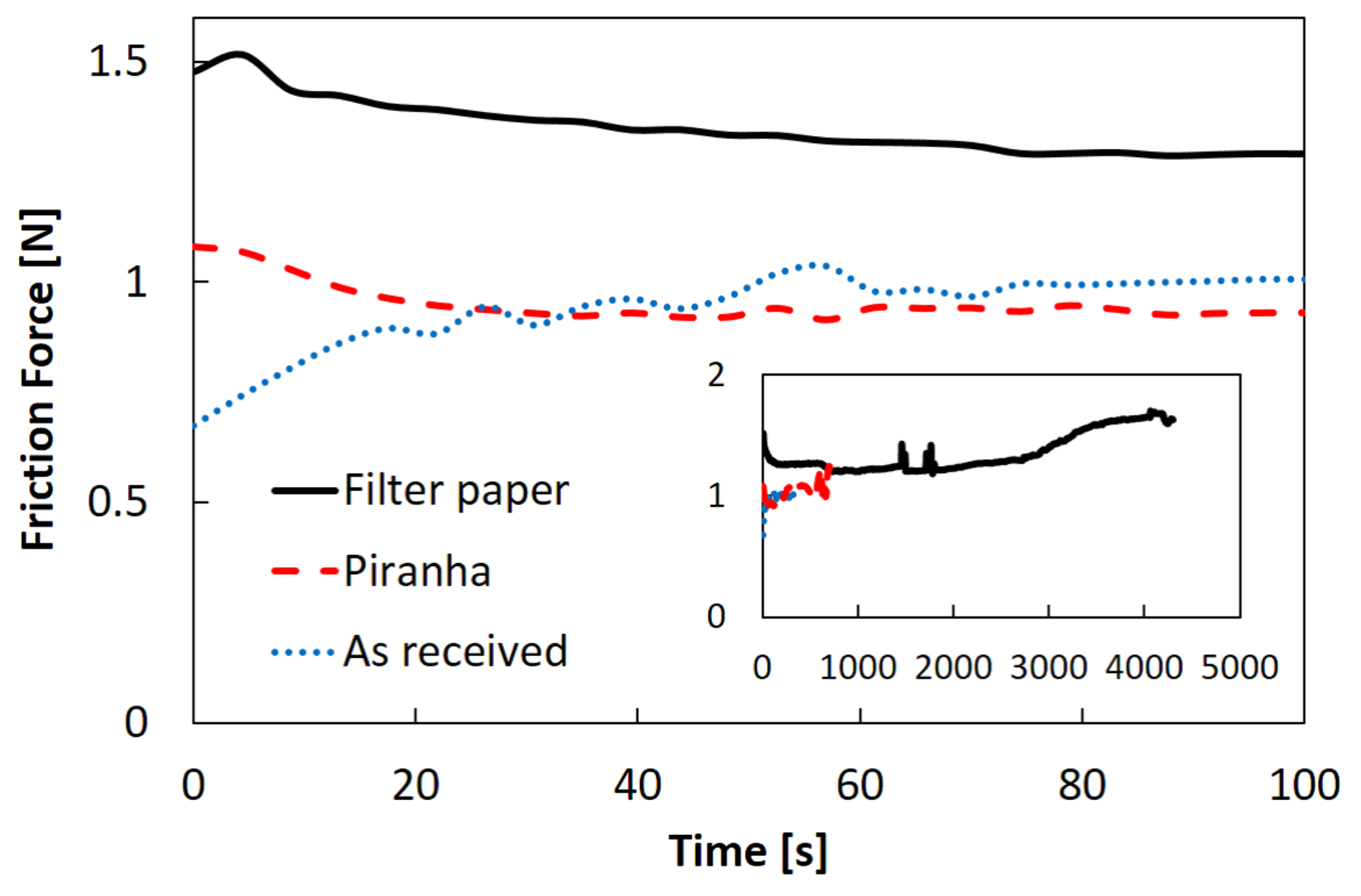
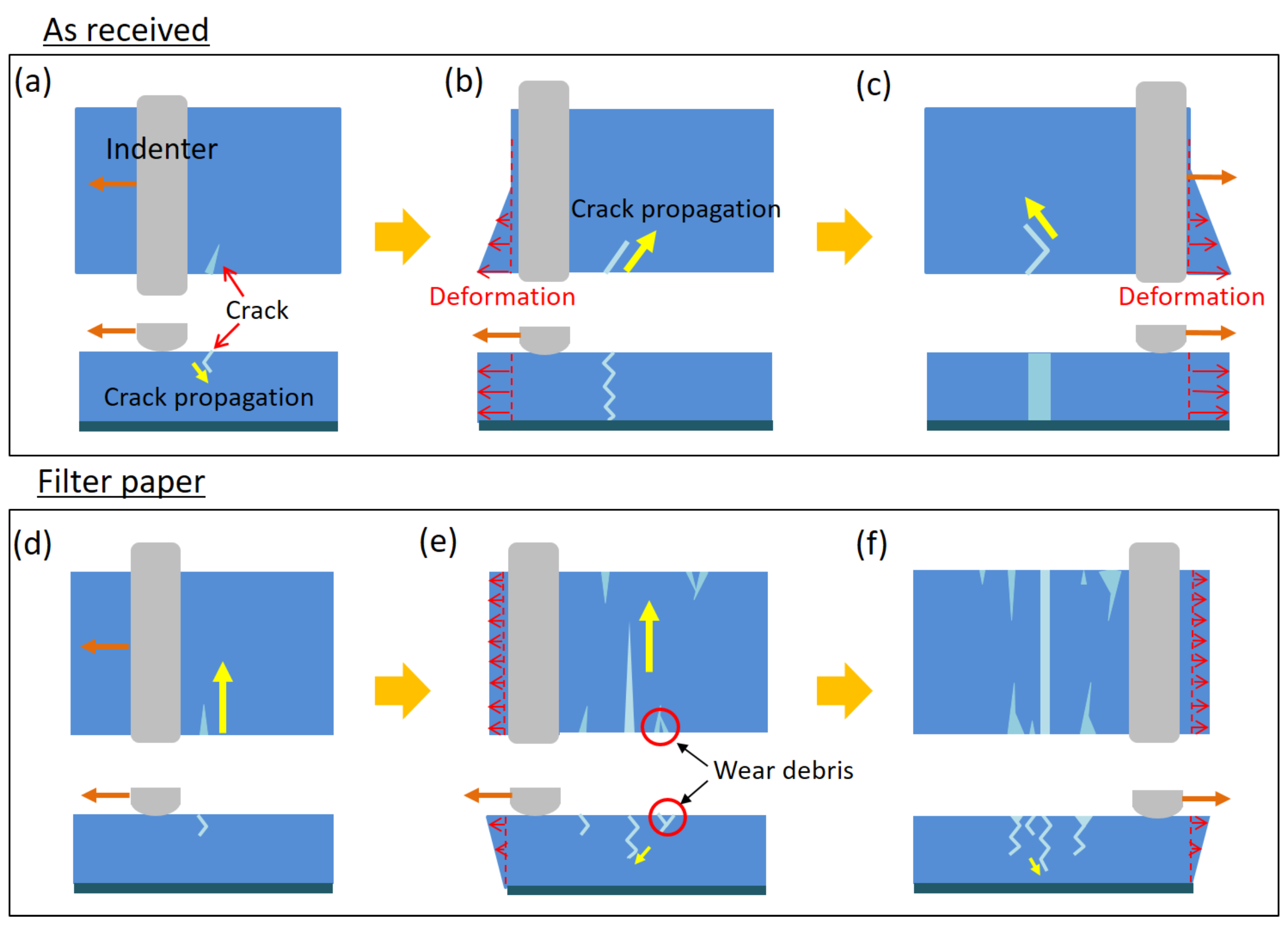
2.2. Effects of Adhesion Strength between Gel and Bottom Glass Slide
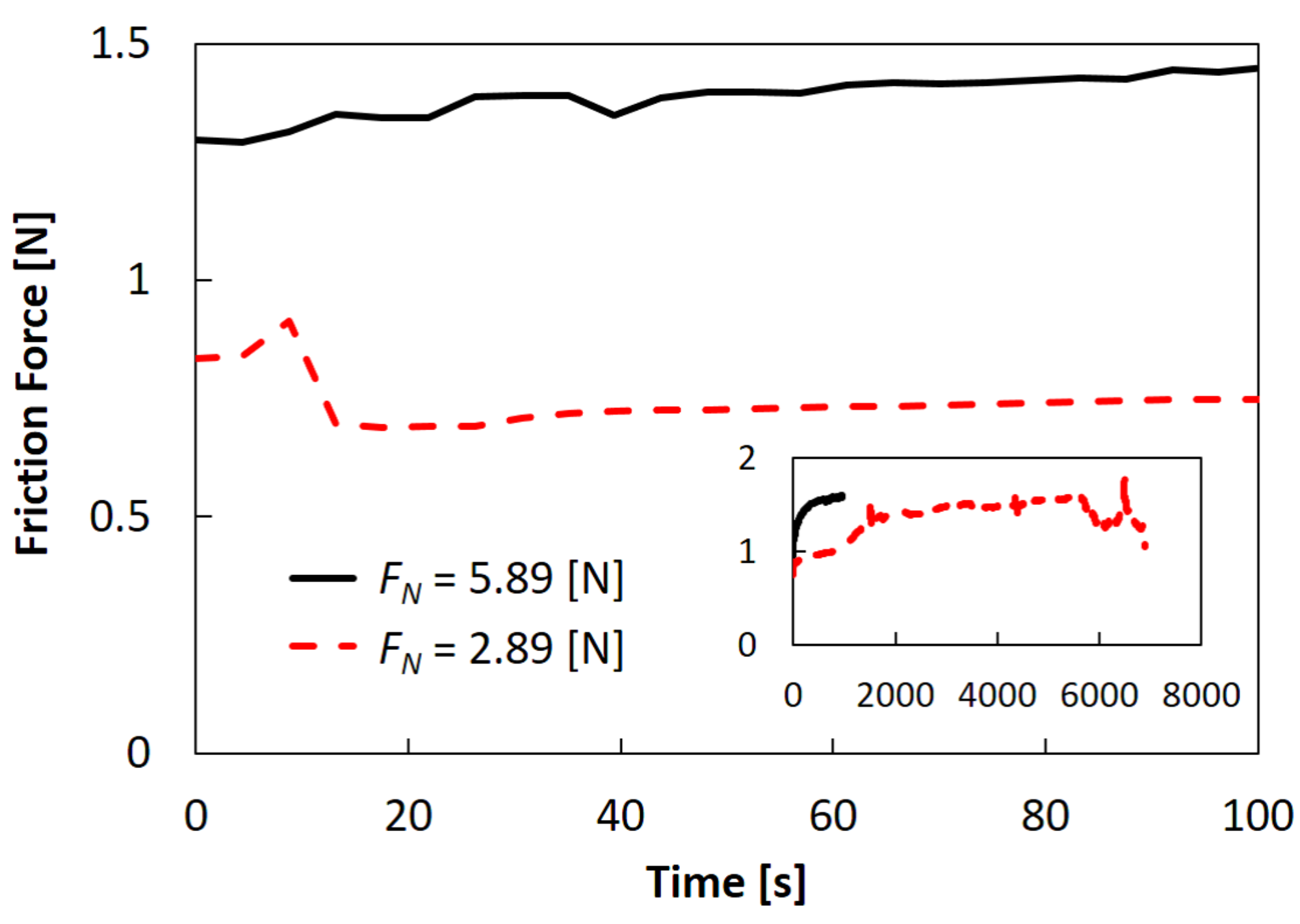
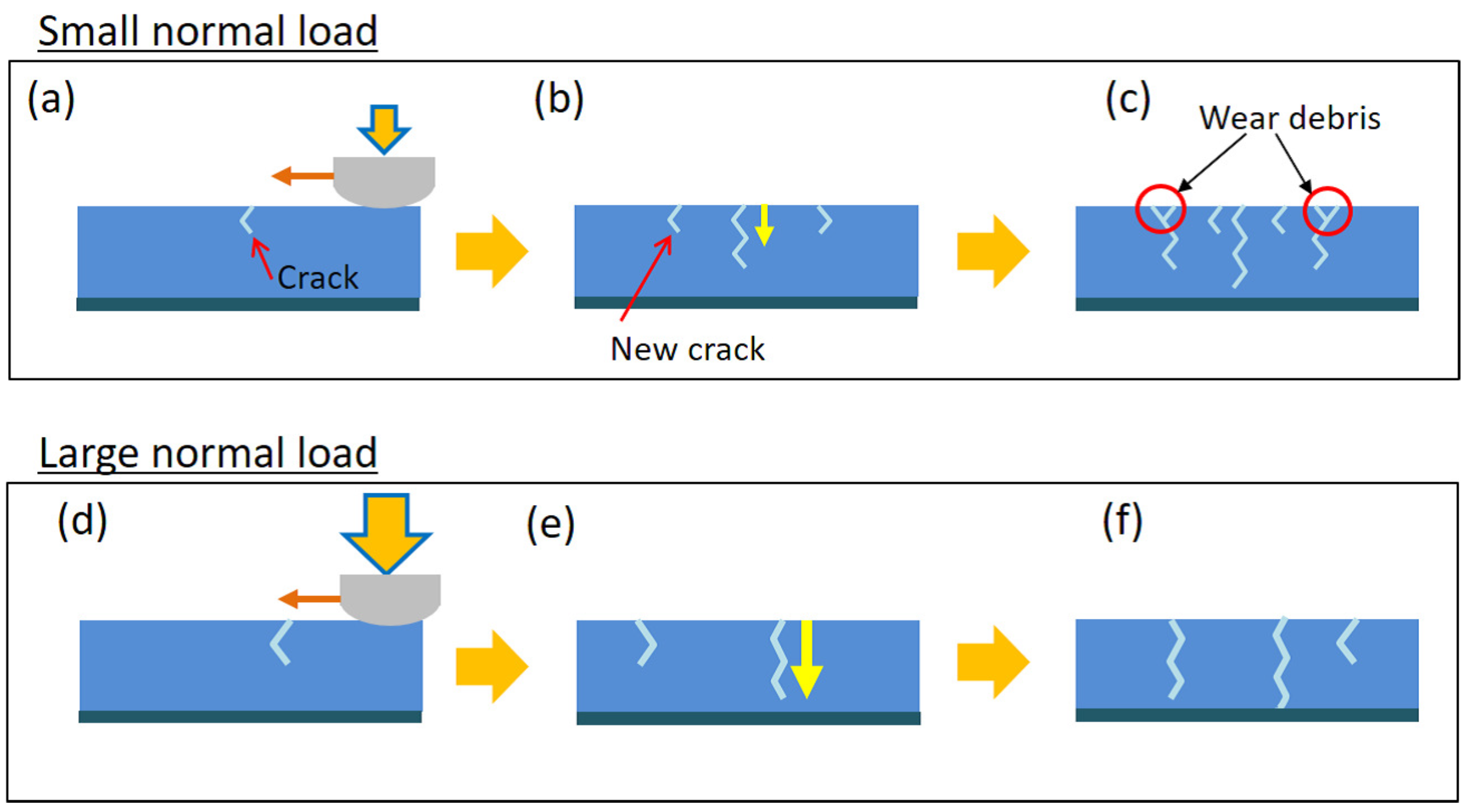
2.3. Effects of Normal Load
2.4. Toward the Toughening of Hydrogels
3. Conclusions
4. Experiment
4.1. Sample
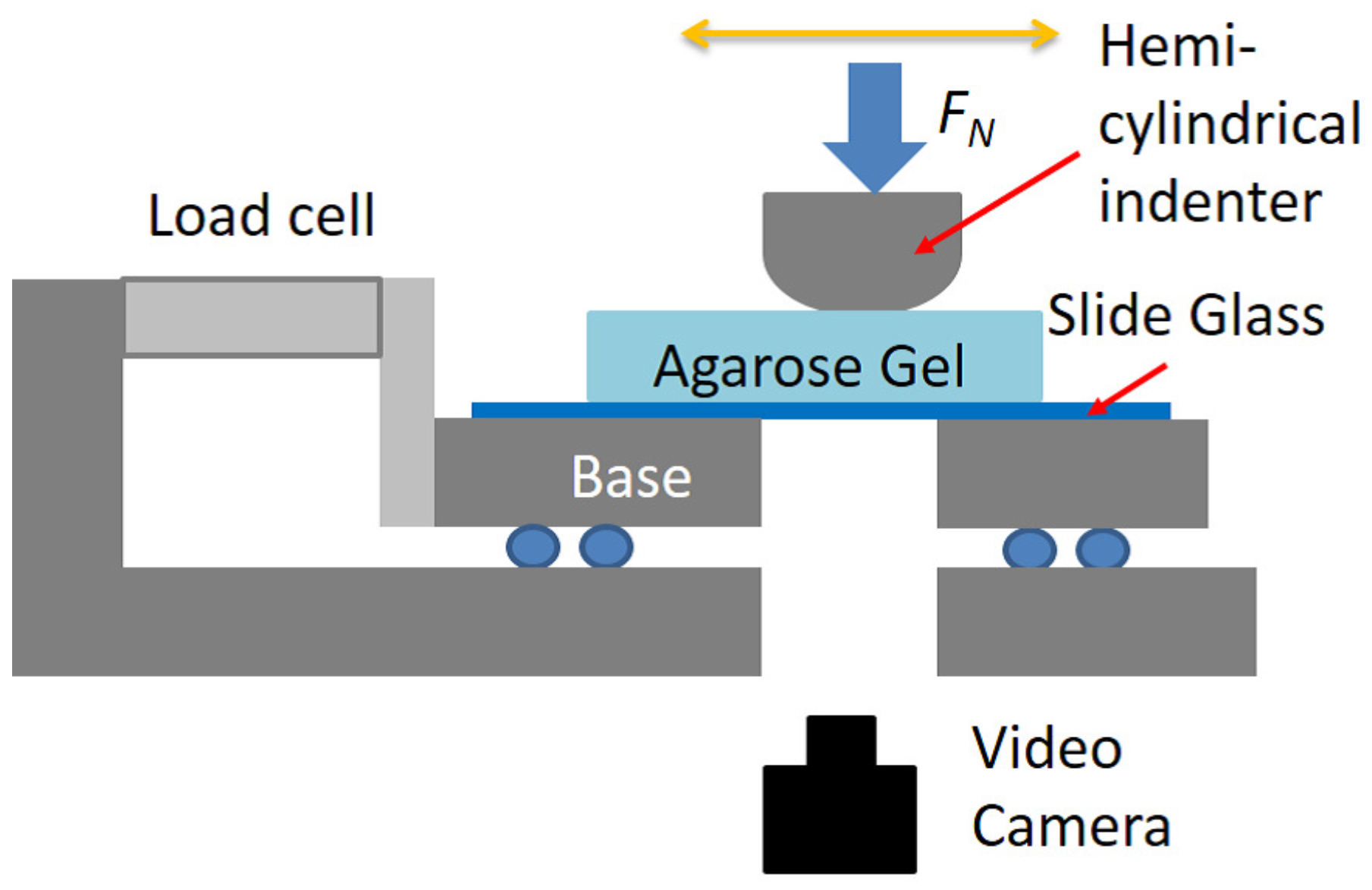
4.2. Friction Experiment
4.3. Visualization
4.4. Characterization of Mechanical Properties
4.5. Evaluation of Adhesion Strength between Gel and Bottom Slide Glass
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gong, J.P. Friction and lubrication of hydrogels—Its richness and complexity. Soft Matter 2006, 2, 544–552. [Google Scholar] [CrossRef]
- Kaneko, D.; Tada, T.; Kurokawa, T.; Gong, J.P.; Osada, Y. Mechanically Strong Hydrogels with Ultra-Low Frictional Coefficients. Adv. Mater. 2005, 17, 535–538. [Google Scholar] [CrossRef]
- Gong, J.P.; Kurokawa, T.; Narita, T.; Kagata, G.; Osada, Y.; Nishimura, G.; Kinjo, M. Synthesis of Hydrogels with Extremely Low Surface Friction. J. Am. Chem. Soc. 2001, 123, 5582–5583. [Google Scholar] [CrossRef] [PubMed]
- Takata, M.; Yamaguchi, T.; Doi, M. Electric Field Effect on the Sliding Friction of a Charged Gel. J. Phys. Soc. Jpn. 2009, 78, 084602. [Google Scholar] [CrossRef]
- Takata, M.; Yamaguchi, T.; Doi, M. Friction Control of a Gel by Electric Field in Ionic Surfactant Solution. J. Phys. Soc. Jpn. 2010, 79, 063602. [Google Scholar] [CrossRef]
- Suzuki, R.; Yamaguchi, T.; Doi, M. Frictional Property of Hydrogels Prepared under Electric Fields. J. Phys. Soc. Jpn. 2013, 82, 124803. [Google Scholar] [CrossRef]
- Jin, Z.; Dowson, D. Bio-friction. Friction 2013, 1, 100–113. [Google Scholar] [CrossRef]
- Murakami, T.; Higaki, H.; Sawae, Y.; Ohtsuki, N.; Moriyama, S.; Nakanishi, Y. Adaptive multimode lubrication in natural synovial joints and artificial joints. Proc. IMechE H J. Eng. Med. 1998, 212, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Freeman, M.E.; Furey, M.J.; Love, B.J.; Hampton, J.M. Friction, wear, and lubrication of hydrogels as synthetic articular cartilage. Wear 2000, 241, 129–135. [Google Scholar] [CrossRef]
- Murakami, T.; Yarimitsu, S.; Nakashima, K.; Yamaguchi, T.; Sawae, Y.; Sakai, N.; Suzuki, A. Superior lubricity in articular cartilage and artificial hydrogel cartilage. Proc. IMechE J J. Eng. Tribol. 2014, 228, 1099–1111. [Google Scholar] [CrossRef]
- Murakami, T.; Sakai, N.; Yamaguchi, T.; Yarimitsu, S.; Nakashima, K.; Sawae, Y.; Suzuki, A. Evaluation of a superior lubrication mechanism with biphasic hydrogels for artificial cartilage. Tribol. Int. 2015, 89, 19–26. [Google Scholar] [CrossRef]
- Bray, J.C.; Merrill, E.W. Poly(vinyl alcohol) hydrogels for synthetic articular cartilage material. J. Biomed. Mat. Res. 1973, 7, 431–443. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.Q.; Xiao, J.M.; Zhang, X.H. The development of artificial articular cartilage—PVA-hydrogel. Bio-Med Mater. Eng. 1998, 8, 75–81. [Google Scholar]
- Stammen, J.A.; Williams, S.; Ku, D.N.; Guldberg, R.E. Mechanical properties of a novel PVA hydrogel in shear and unconfined compression. Biomaterials 2001, 22, 799–806. [Google Scholar] [CrossRef]
- Pan, Y.; Xiong, D. Friction properties of nano-hydroxyapatite reinforced poly(vinyl alcohol) gel composites as an articular cartilage. Wear 2009, 266, 699–703. [Google Scholar] [CrossRef]
- Murakami, T.; Yarimitsu, S.; Nakashima, K.; Sakai, N.; Yamaguchi, T.; Sawae, Y.; Suzuki, A. Biphasic and boundary lubrication mechanisms in artificial hydrogel cartilage: A review. Proc. IMechE H J. Eng. Med. 2015, 229, 864–878. [Google Scholar] [CrossRef] [PubMed]
- Murakami, T.; Yarimitsu, S.; Sakai, N.; Nakashima, N.; Yamaguchi, T.; Sawae, Y. Importance of adaptive multimode lubrication mechanism in natural synovial joints. Tribol. Int. 2017, 113, 306–315. [Google Scholar] [CrossRef]
- Murakami, T.; Yarimitsu, S.; Sakai, N.; Nakashima, K.; Yamaguchi, T.; Sawae, Y.; Suzuki, A. Superior lubrication mechanism in poly (vinyl alcohol) hybrid gel as artificial cartilage. Proc. IMechE J J. Eng. Tribol. 2017, 231, 1160–1170. [Google Scholar] [CrossRef]
- Gong, J.P.; Katsuyama, Y.; Kurokawa, T.; Osada, Y. Double-Network Hydrogels with Extremely High Mechanical Strength. Adv. Mater. 2003, 15, 1155–1158. [Google Scholar] [CrossRef]
- Yasuda, K.; Gong, J.P.; Katsuyama, Y.; Nakayama, A.; Tanabe, Y.; Kondo, E.; Ueno, M.; Osada, Y. Biomechanical properties of high-toughness double network hydrogels. Biomaterials 2005, 26, 4468–4475. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.A.; Kurokawa, T.; Kamita, G.; Gong, J.P. Lamellar Bilayers as Reversible Sacrificial Bonds To Toughen Hydrogel: Hysteresis, Self-Recovery, Fatigue Resistance, and Crack Blunting. Macromolecules 2011, 44, 8916–8924. [Google Scholar] [CrossRef]
- Kundu, S.; Crosby, A.J. Cavitation and fracture behavior of polyacrylamide hydrogels. Soft Matter 2009, 5, 3963–3968. [Google Scholar] [CrossRef]
- Boue, T.G.; Harpaz, R.; Fineberg, J.; Bouchbinder, E. Failing softly: A fracture theory of highly-deformable materials. Soft Matter 2015, 11, 3812–3821. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X. Multi-scale multi-mechanism design of tough hydrogels: Building dissipation into stretchy networks. Soft Matter 2014, 10, 672–687. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Long, R.; Hui, C.-Y. The energy release rate of a pressurized crack in soft elastic materials: Effects of surface tension and large deformation. Soft Matter 2014, 10, 7723–7729. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Jagota, A.; Hui, C.-Y. Adhesive contact of a rigid circular cylinder to a soft elastic substrate—The role of surface tension. Soft Matter 2015, 11, 3844–3851. [Google Scholar] [CrossRef] [PubMed]
- Baumberger, T.; Caroli, C.; Martina, D.; Ronsin, O. Magic angles and cross-hatching instability in hydrogel fracture. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Shimazaki, R.; Yano, S.; Yoshida, G.; Yamaguchi, T. Solvent effects on the fracture of chemically crosslinked gels. Soft Matter 2016, 12, 8135–8142. [Google Scholar] [CrossRef] [PubMed]
- Suciu, A.N.; Iwatsubo, T.; Matsuda, M.; Nishino, T. A Study upon Durability of the Artificial Knee Joint with PVA Hydrogel Cartilage. JSME Int. J. C 2004, 47, 199–208. [Google Scholar] [CrossRef]
- Doi, M. Soft Matter Physics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Ateshian, G.A.; Lai, W.M.; Zhu, W.B.; Mow, V.C. An asymptotic solution for the contact of two biphasic cartilage layers. J. Biomech. 1994, 27, 1347–1360. [Google Scholar] [CrossRef]
- Ateshian, G.A. The Role of Interstitial Fluid Pressurization in Articular Cartilage Lubrication. J. Biomech. 2009, 42, 1163–1176. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Fillmore, D.J. Kinetics of swelling of gels. J. Chem. Phys. 1979, 70, 1214. [Google Scholar] [CrossRef]
- Gu, W.Y.; Yao, H.; Huang, C.Y.; Cheung, H.S. New insight into deformation-dependent hydraulic permeability of gels and cartilage, and dynamic behavior of agarose gels in confined compression. J. Biomech. 2003, 36, 593–598. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Cotterell, B.; Rice, J.R. Slightly curved or kinked cracks. Int. J. Fract. 1980, 16, 155–169. [Google Scholar] [CrossRef]
- Sakai, N.; Hashimoto, C.; Yarimitsu, S.; Sawae, Y.; Komori, M.; Murakami, T. A functional effect of the superficial mechanical properties of articular cartilage as a load bearing system in a sliding condition. Biosurf. Biotribol. 2016, 2, 26–39. [Google Scholar] [CrossRef]
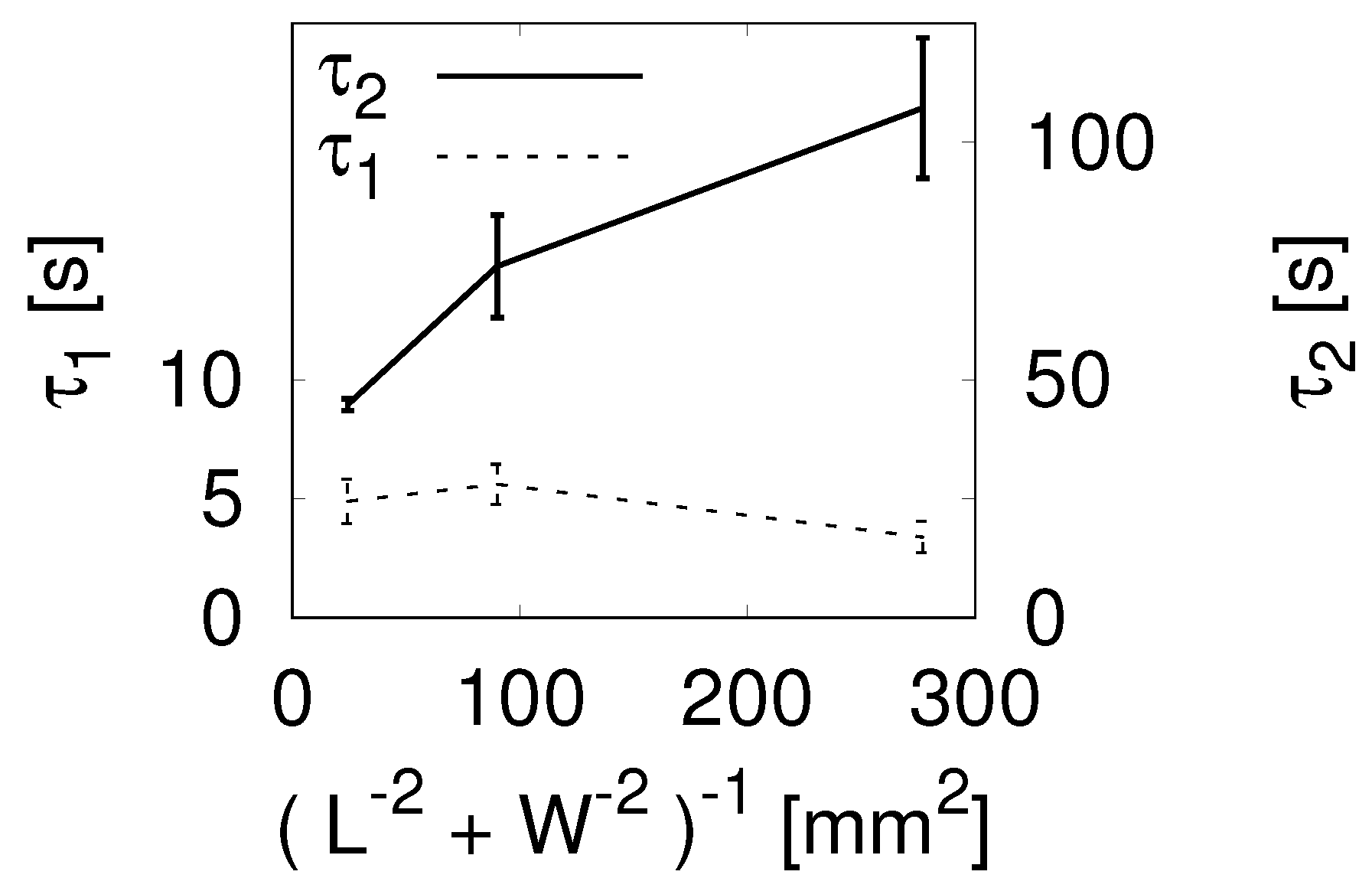


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, T.; Sato, R.; Sawae, Y. Propagation of Fatigue Cracks in Friction of Brittle Hydrogels. Gels 2018, 4, 53. https://doi.org/10.3390/gels4020053
Yamaguchi T, Sato R, Sawae Y. Propagation of Fatigue Cracks in Friction of Brittle Hydrogels. Gels. 2018; 4(2):53. https://doi.org/10.3390/gels4020053
Chicago/Turabian StyleYamaguchi, Tetsuo, Ryuichiro Sato, and Yoshinori Sawae. 2018. "Propagation of Fatigue Cracks in Friction of Brittle Hydrogels" Gels 4, no. 2: 53. https://doi.org/10.3390/gels4020053
APA StyleYamaguchi, T., Sato, R., & Sawae, Y. (2018). Propagation of Fatigue Cracks in Friction of Brittle Hydrogels. Gels, 4(2), 53. https://doi.org/10.3390/gels4020053





