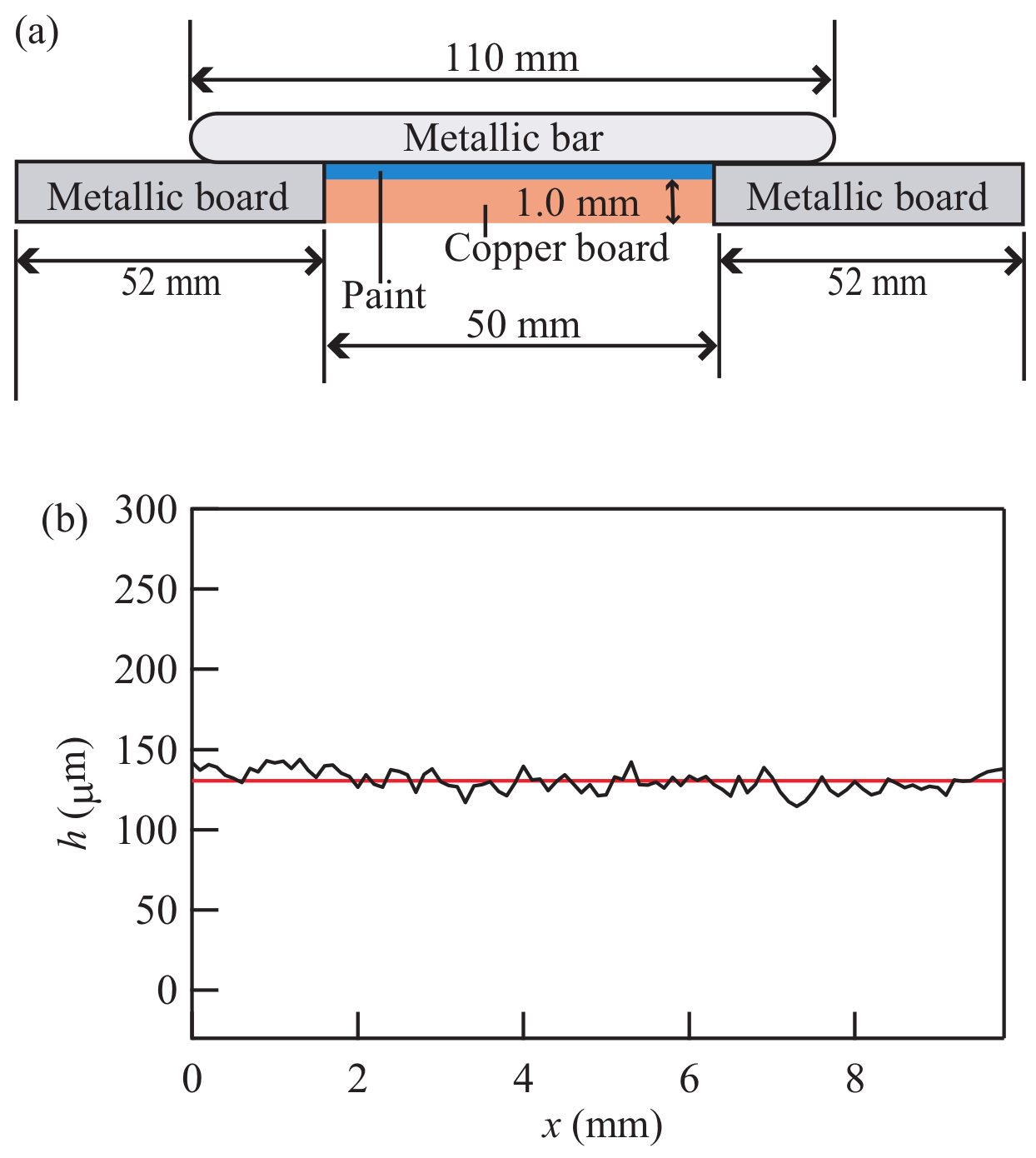
2.2. Model
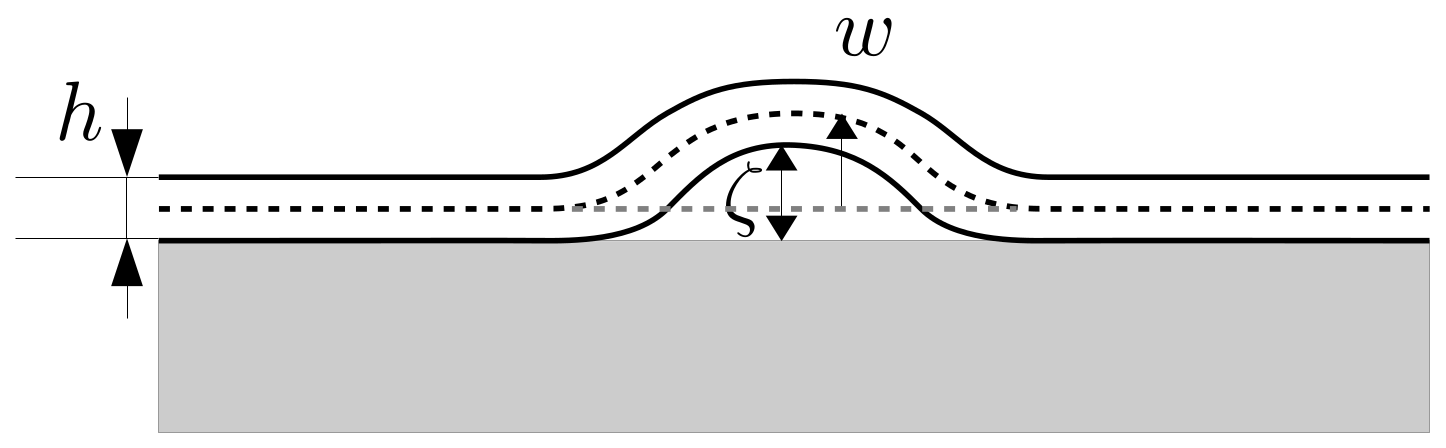
We next introduce a simple model for the buckling that is observed in our experiments. Consider the coating of paint to be an elastic thin film that is attached adhesively to a solid substrate (
Figure 5). Because of the absorption of the organic solvent, the elastic film swells, producing compression stress. Suppose that the elastic film exists on a flat substrate, whose surface corresponds to the
-
plane, and let the
axis be normal to the surface of the substrate. The total energy
of this system consists of the elastic strain energy in the film and the interfacial traction energy between the film and substrate:
where
and
are the energies per unit area of the film and the interface, respectively.
According to the Föppl–von Kármán plate theory, the elastic energy per unit area in a film of thickness
h is given by [
8,
9,
10,
11,
12]
Greek subscripts refer to in-plane coordinates
or
, and repeated Greek subscripts indicate summation over indices 1 and 2. The parameters
and
are the shear modulus and Poisson ratio of the film, respectively. Mid-plane displacements in the in-plane and
directions are denoted by
and
w, respectively. Supposing the film to be under equibiaxial stress, we take the initial in-plane strain to be
. Then,
To express the interfacial traction energy between the film and substrate, we use the cohesive zone model [
13,
14,
15]. The interfacial energy per unit area is then
where
is the distance between the substrate and film, and
is the normal traction. When the film thickness is constant,
. We represent the normal traction as
where
. The parameters
and
are the normal interfacial toughness and the characteristic length of a normal displacement jump, respectively.
The total energy
is thus expressed in terms of the displacements
and
w. Equilibrium states must satisfy
and
. However, instead of solving
, we employ the time-dependent Ginzburg–Landau equation, which is often used in dynamical systems,
where
is a constant related to the characteristic relaxation time. Scaling all lengths by
h, times by
, the nondimensional equation and
by
in Equation (
10), we obtain
where the variables are dimensionless,
is the nondimensional form of Equation (
9), and
The in-plane displacements
included in
are obtained from the equation
.
2.3. Linear Stability Analysis
A linear stability analysis of Equation (
11) provides some insight into the condition of buckling. Linearizing Equation (
11) around
, and taking the Fourier transform of the linearized equation, we obtain
where
is the Fourier transform of
w, and
k is the wavenumber. The linear growth rate
g is given by
Unstable modes, which cause deformations in the layer, appear when
; in other words,
This equation shows that wrinkles emerge above a certain threshold of stress. The existence of the threshold is consistent with the experimental results shown in
Figure 2, which indicate that buckles emerge under an upper limit of
T, since
and
depend on
T. Equation (
15) shows that the wavenumber of the fastest-growing mode is
The growth rate of the fastest-growing mode is inversely proportional to the timescale,
2.4. Numerical Simulations
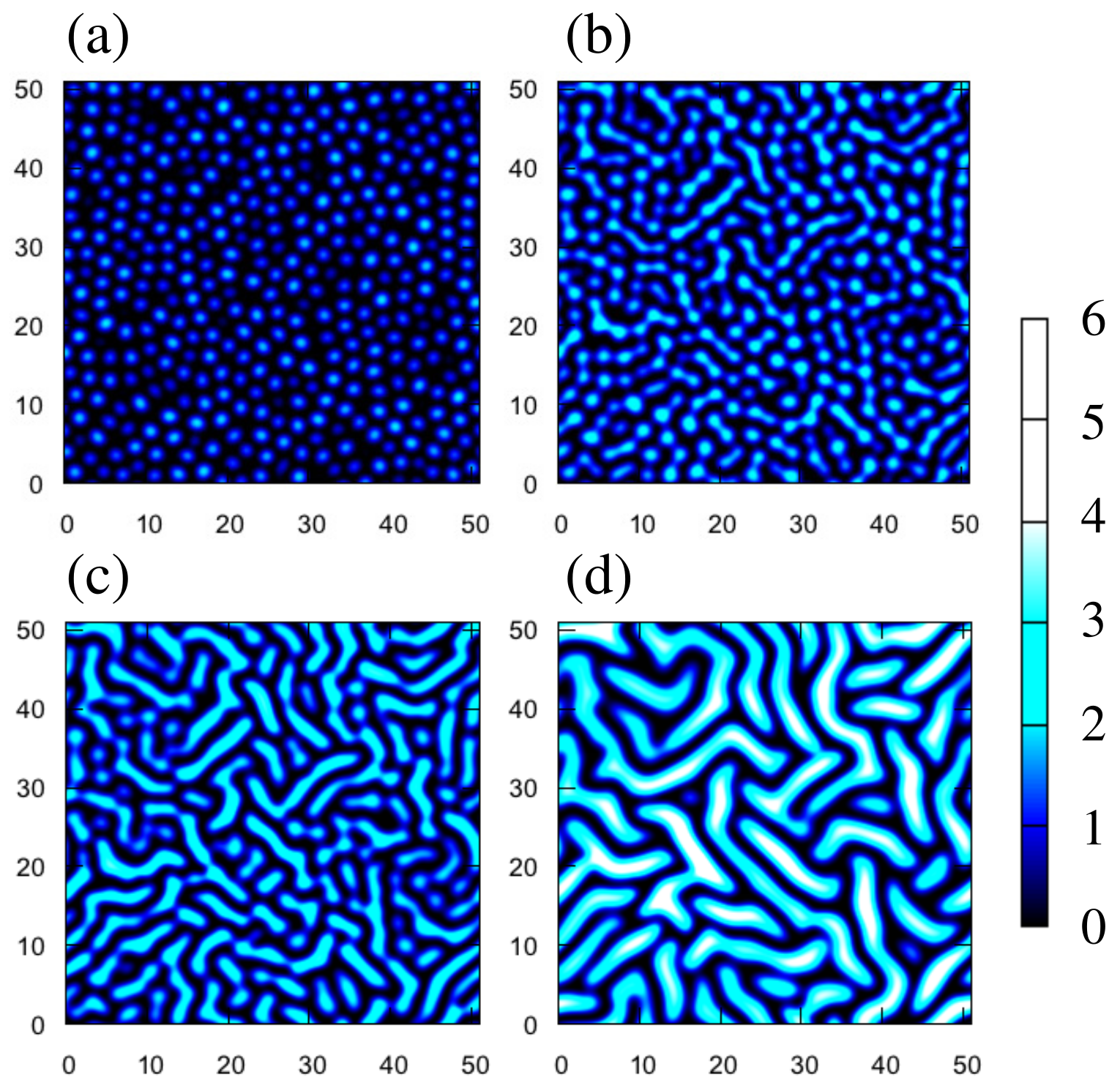
Numerical simulation is useful for demonstrating that our simple model does reproduce buckling of the film. Simulated patterns of the displacement
w are shown in
Figure 6. In the initial states, we take
plus a small amount of noise, and we impose periodic boundary conditions on a
grid system. The length of a side corresponds to about 6.8 mm for
mm. The values of the side length and
h are close to experimental ones. In
Figure 6, we take
,
. The other parameters used in the following simulations are
and
.
Some characteristics of the snapshots in
Figure 6 look similar to those of the experiments in
Figure 1c–f. Small bumps appear at an early stage (
Figure 6a). The amplitudes of the bumps grow with time, and some bumps coalesce with others (
Figure 6b,c). However, the amplitudes continue to grow in the simulations (
Figure 6d), which is significantly different from the experiments. This indicates that our model is not yet adequate to explain the nonlinear effects in the actual experiments.
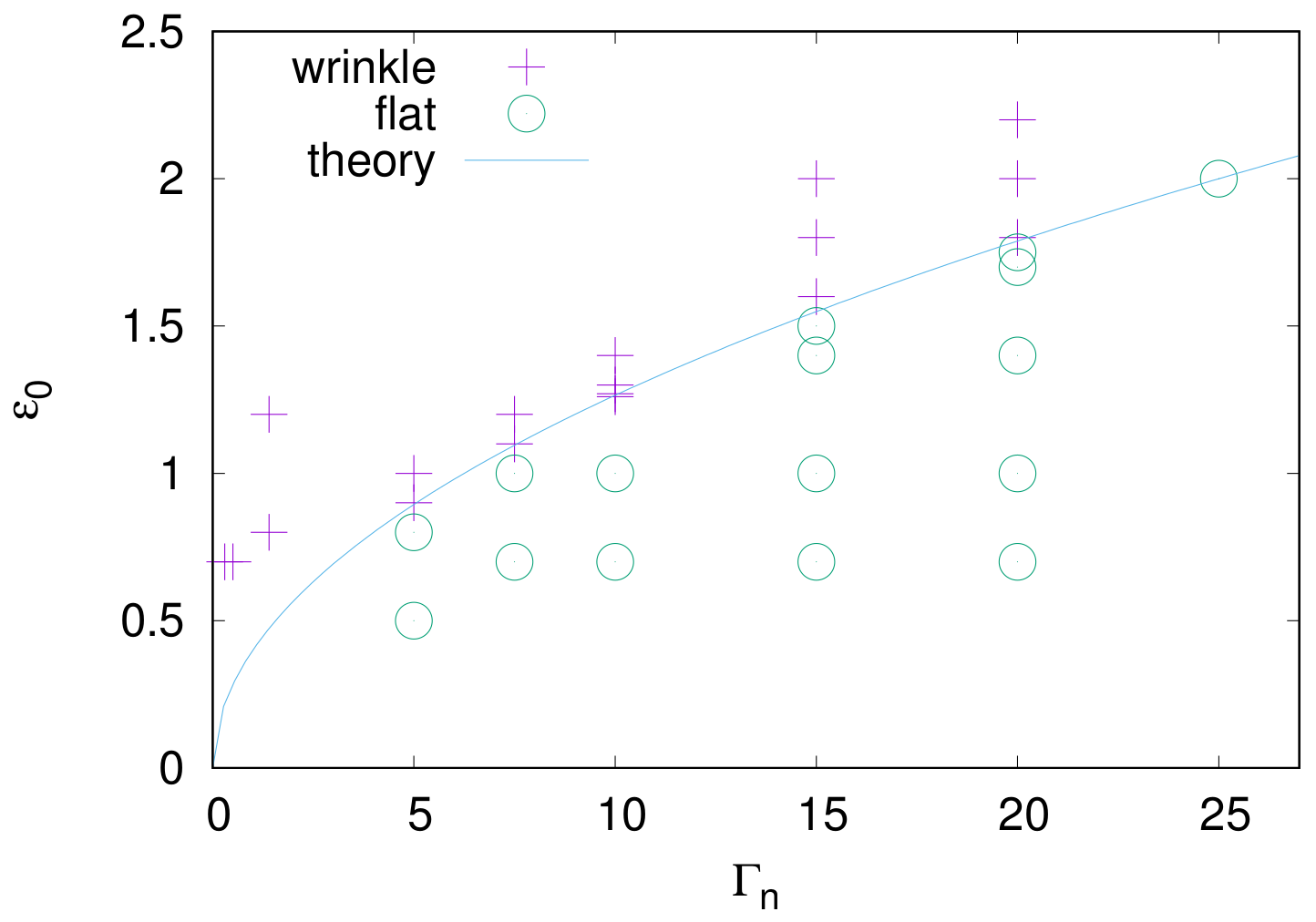
The phase diagram shown in
Figure 7 illustrates the numerical verification of the wrinkle-emerging condition. The linear stability analysis suggests that wrinkles should appear above the solid curve, which is given by Equation (
16). Numerical data shown as symbols demonstrate that the analysis is sufficiently valid.
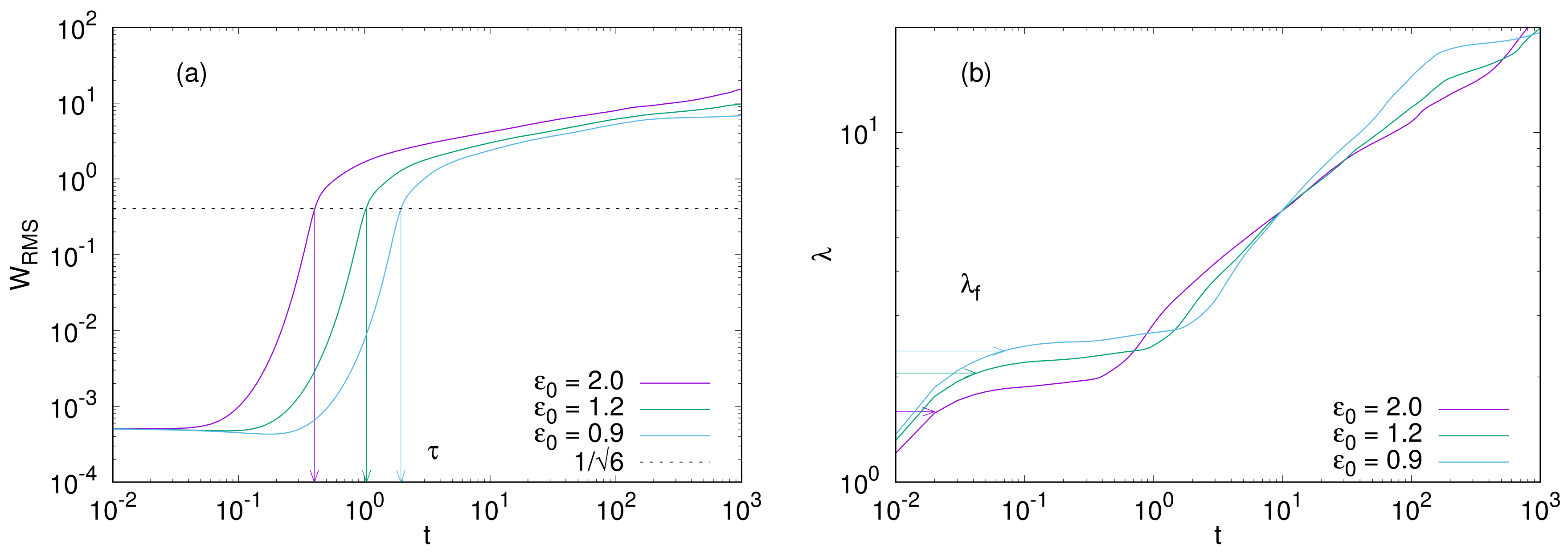
Figure 8a shows the time evolution of the root-mean-square (RMS) of
w,
where
L is the system size. The parameter values except for
are taken as the same as
Figure 6. This is also interpreted as the time evolution of the average amplitude
A of wrinkles, since
, where we suppose a stripe form of
. The arrows in
Figure 8a indicate the initial-growth time
which is the transition time from the initial-growth regime to the coarsening one. Let us here estimate the amplitude at the initial-growth time. In the coarsening regime, we can assume that the interfacial energy becomes negligible and that the time evolution slows down significantly. Thus, setting
in Equation (
11), we have
On the other hand, calculating the spacial average of
given by Equation (13) leads to
Equating Equtaions (
20) and (
21), we have
. The initial-growth time
is determined as the time when
, and thus,
.
The average wavelength of wrinkles is
, where
Here,
is the Fourier transform of
, where
is the spacial average of
w. The time evolution of the average wavelength is shown in
Figure 8b. In the initial-growth regime, the average wavelength is approximately equal to (or slightly larger than) that of the fastest-growing mode, which is indicated by the arrows in
Figure 8b. The wavelength
of the fastest-growing mode is estimated from the linear stability analysis and evaluated as
, where
is given by Equation (
17).
2.5. Correspondence between Experimental and Numerical Results
We here rewrite the time scale
in other forms to examine experimental and numerical results by means of the linear stability analysis. Suppose that the growth rate of a certain unstable mode
is
, where
C is a positive constant. Using Equations (
15), (
17) and (
18), we have
where
. Equation (
23) leads to
where
,
, and
is a constant. For the minimum wavenumber
with a non-negative growing rate,
, and thus,
. Then, Equtaions (
23) and (
24) turn to be
where
Equations (
24) and (
25) are useful to examine experimental and numerical results, respectively.
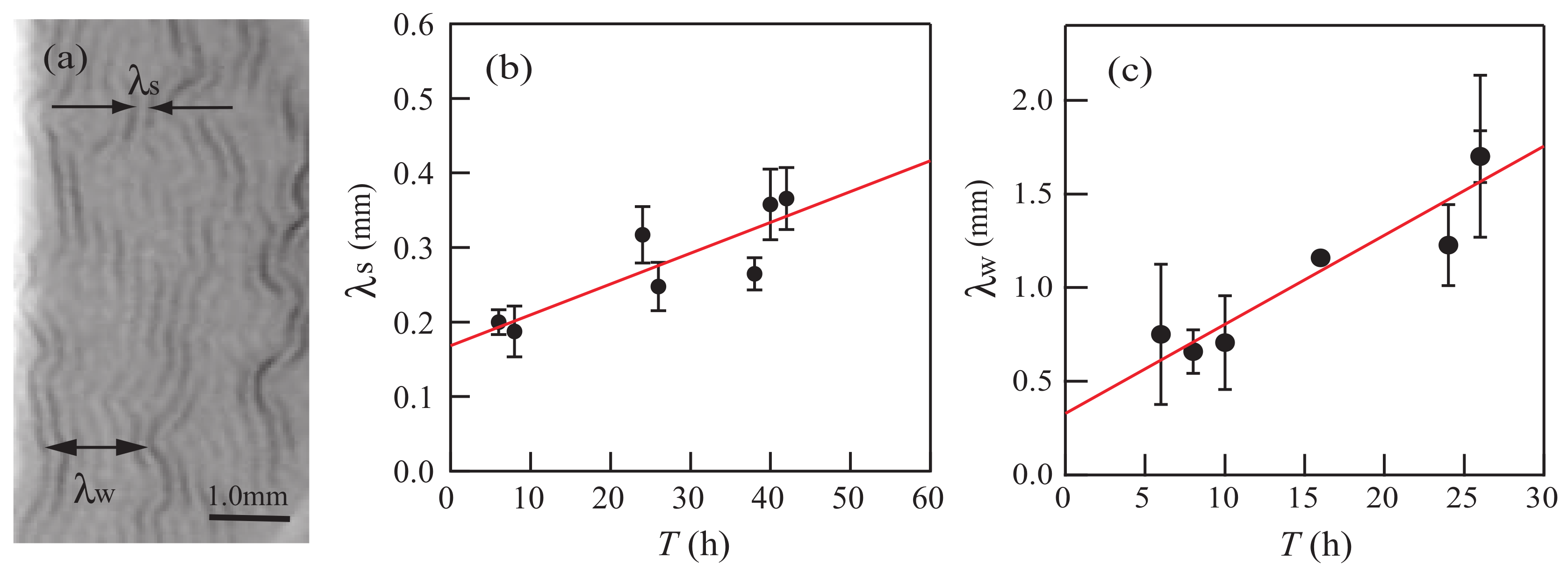
We first examine experimental results, using Equation (
24). We assume that
and
in Equation (
24) correspond to
and
in
Figure 3, respectively. This assumption implies that structures with wavelengths
and
appear in the linear-instability region and that
and
correspond to unstable modes of pattern formation. We also assume that
[
8].
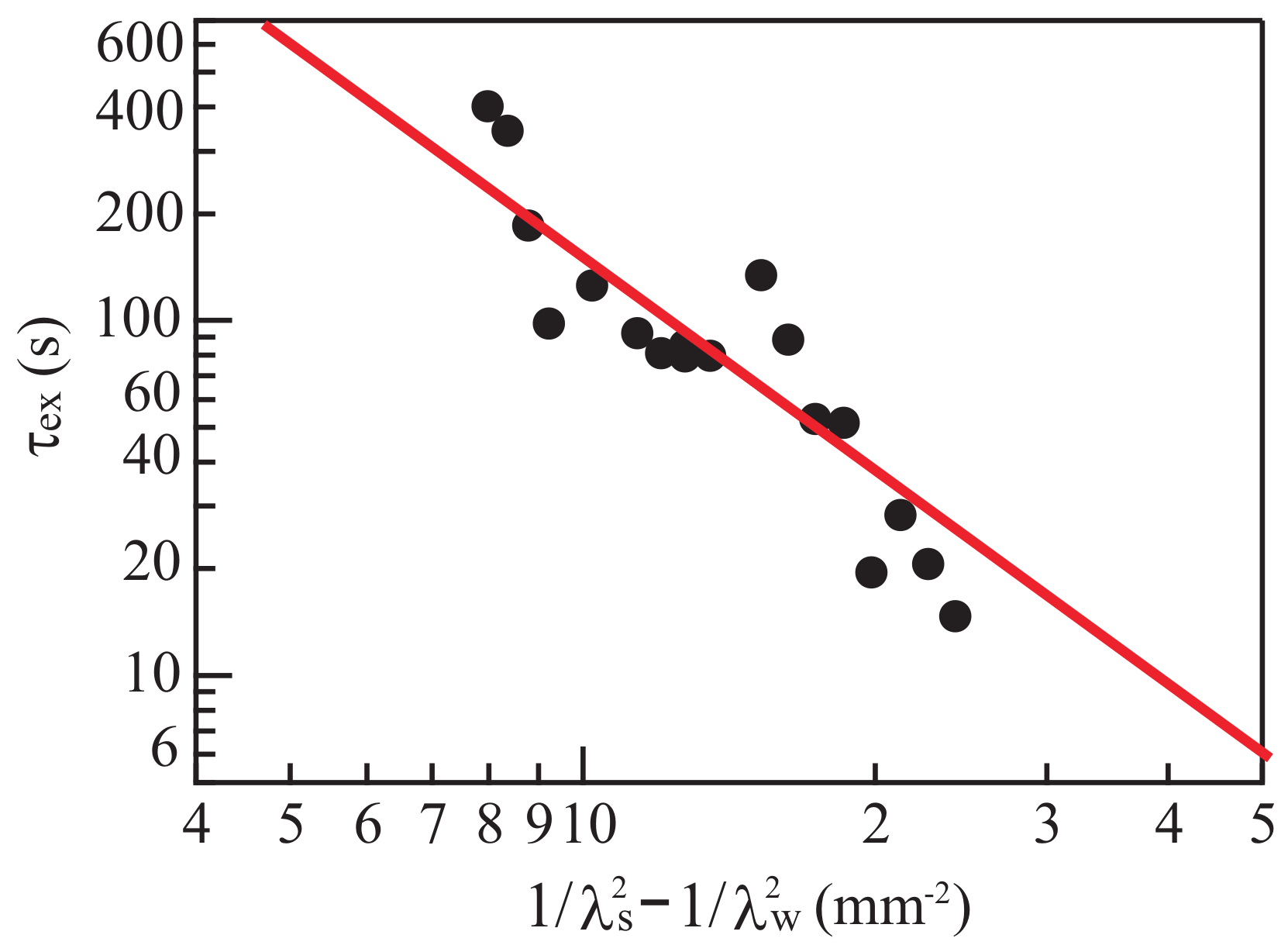
The closed circles in
Figure 9 show experimental data about the relation between
and
. Values of
and
are obtained using Equations (
1) and (
2). The experimental data agree reasonably closely with the line given by Equation (
24), which is shown as a solid line. The exponent of the fitted line is
, and
of Equation (
24) nearly vanishes for the fitted line.
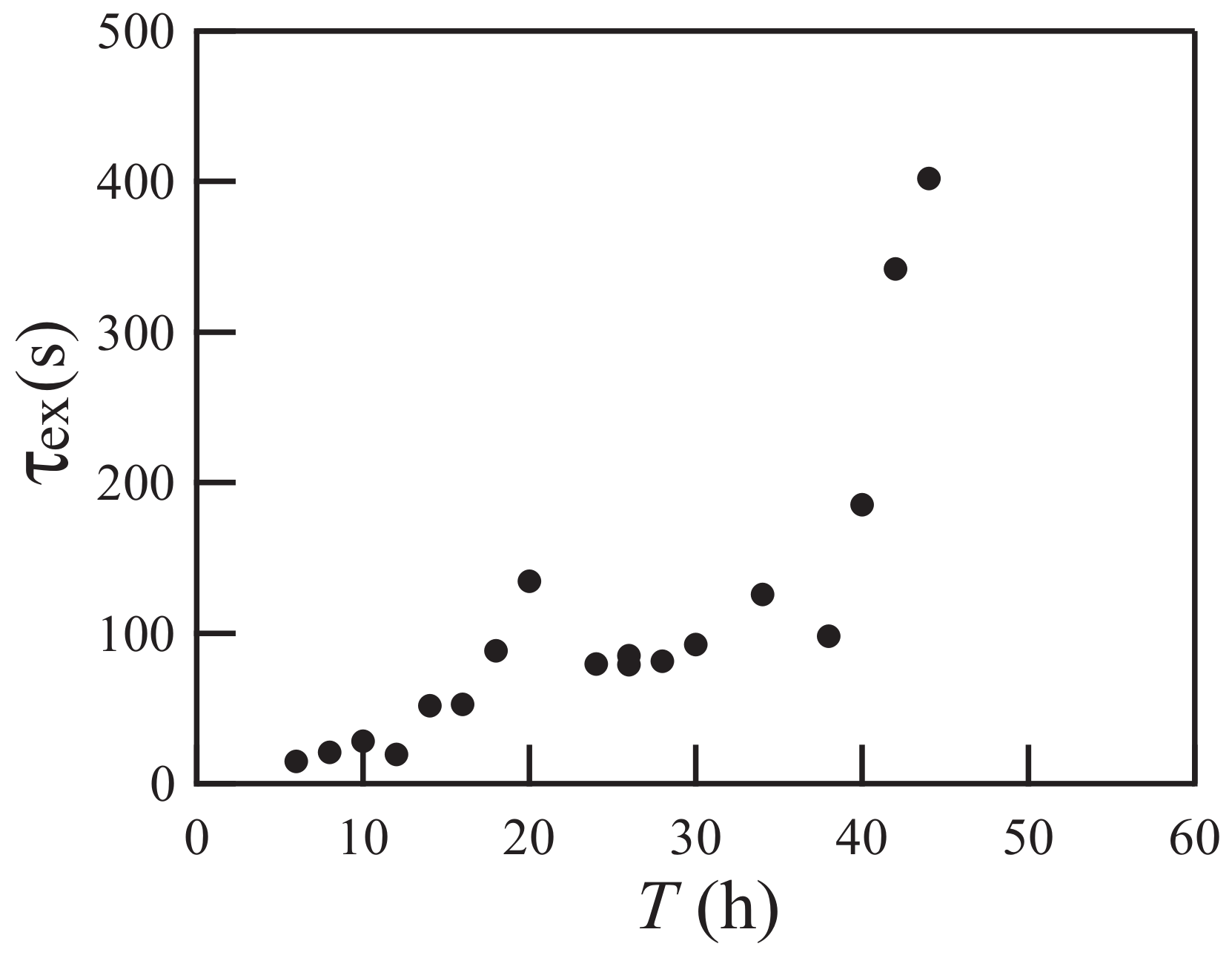
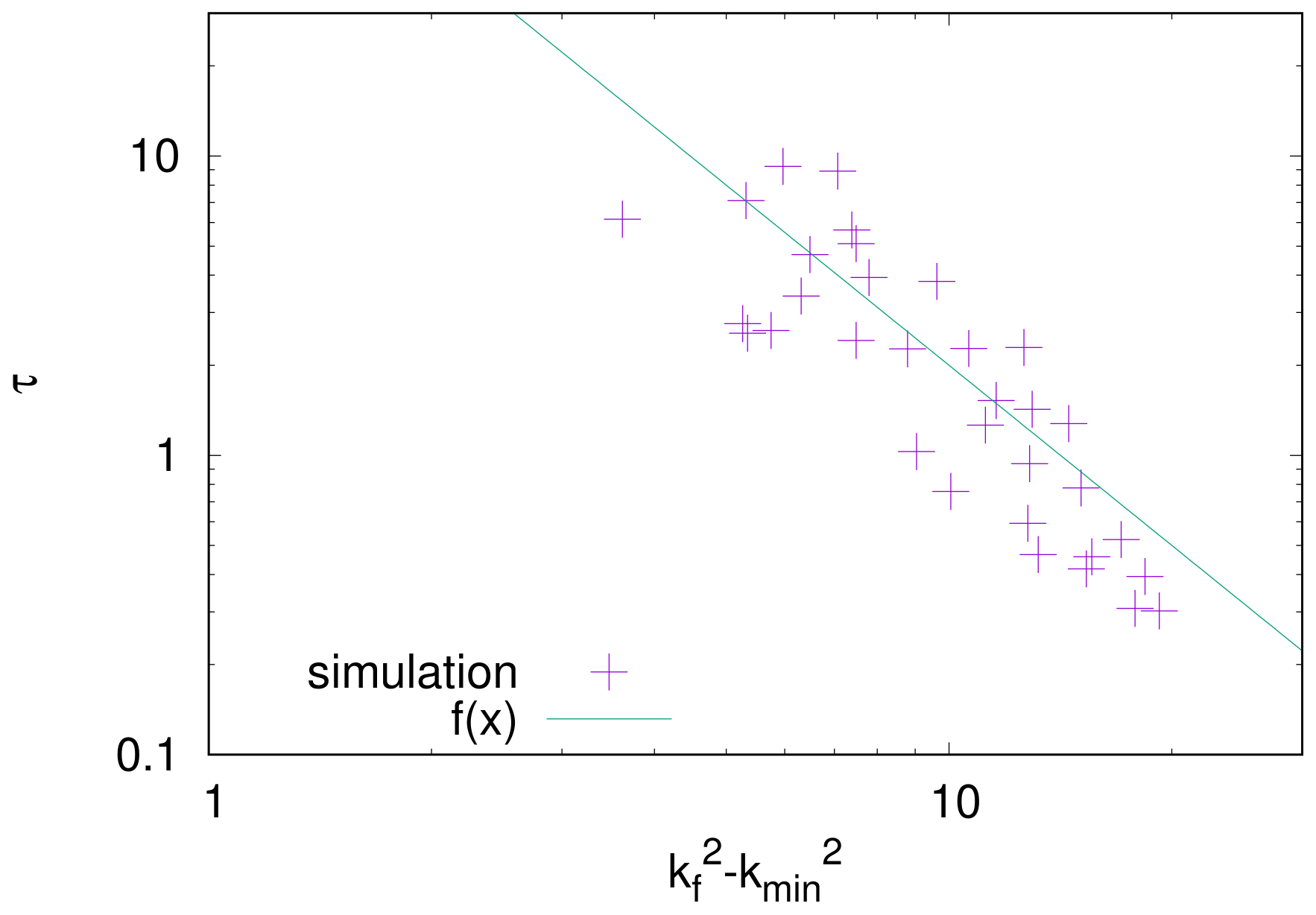
Figure 10 shows the numerical counterparts. The initial-growth time
is plotted as a function of
. The initial-growth time is defined as the time when
reaches
(See
Figure 8), and its value is obtained from numerical simulations with different combinations of
and
. The parameters used in the simulation gives
through Equation (
26). Assuming that the initial-growth time
is proportional to
of Equation (
25), we fit the line given by Equation (
25) to the numerical data. The fitted line reasonably agrees with the numerical data.