Preparation and Mechano-Functional Characterization of PEGylated Fibrin Hydrogels: Impact of Thrombin Concentration
Abstract
1. Introduction
2. Results and Discussion
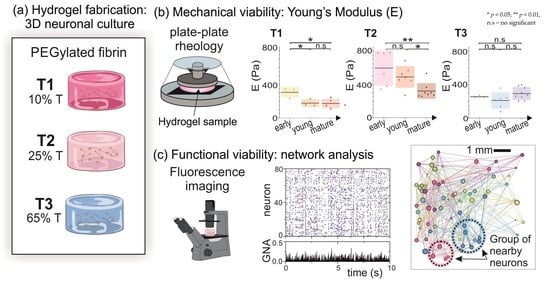
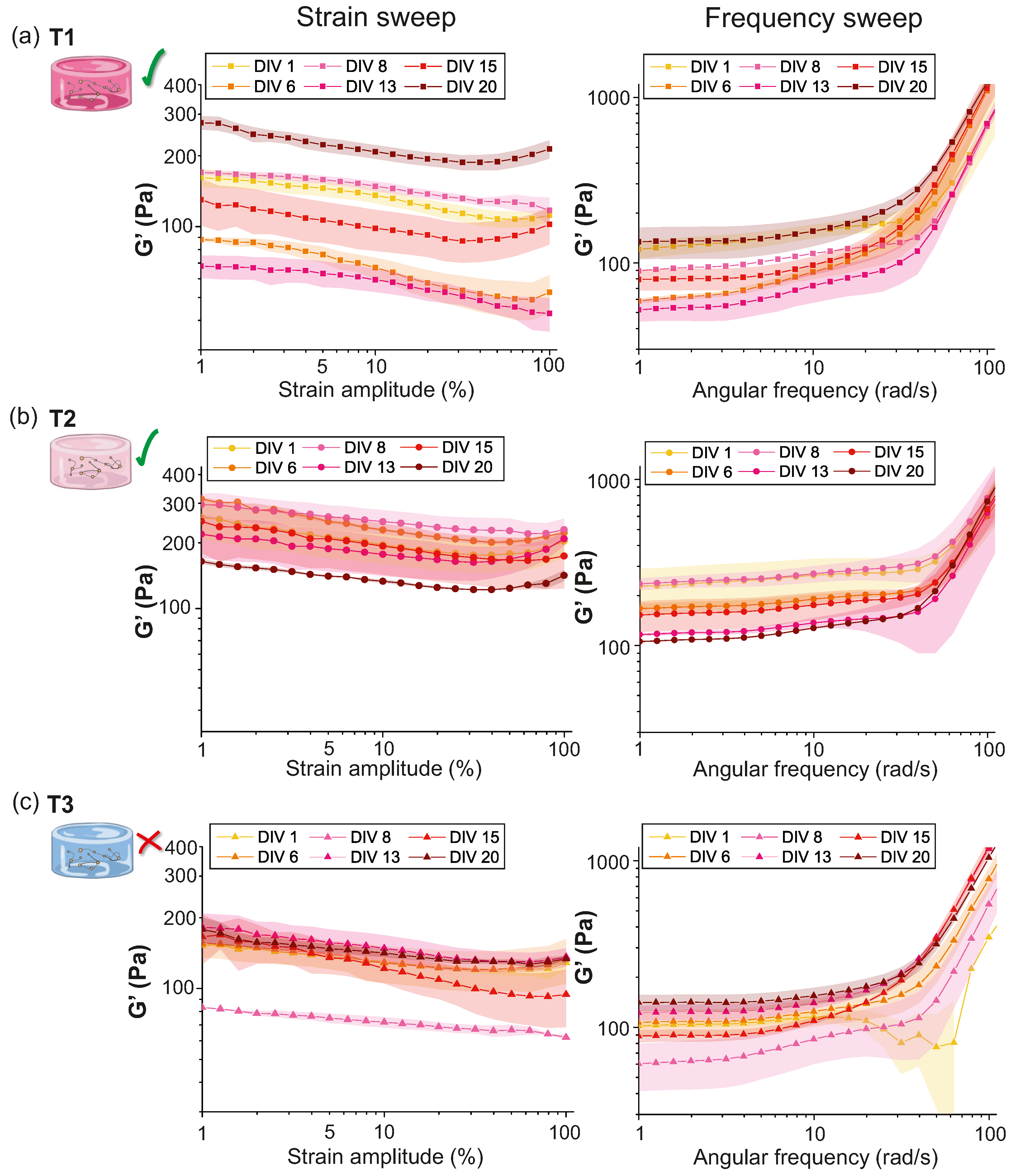
2.1. Rheological Characterization of Hydrogels
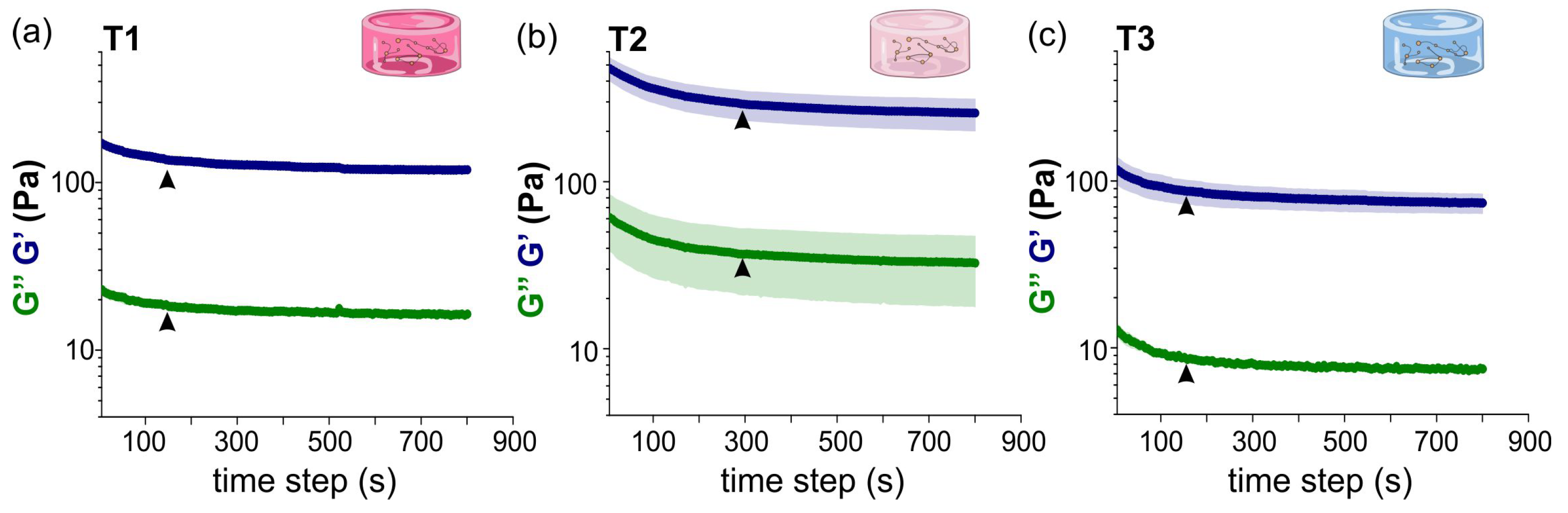
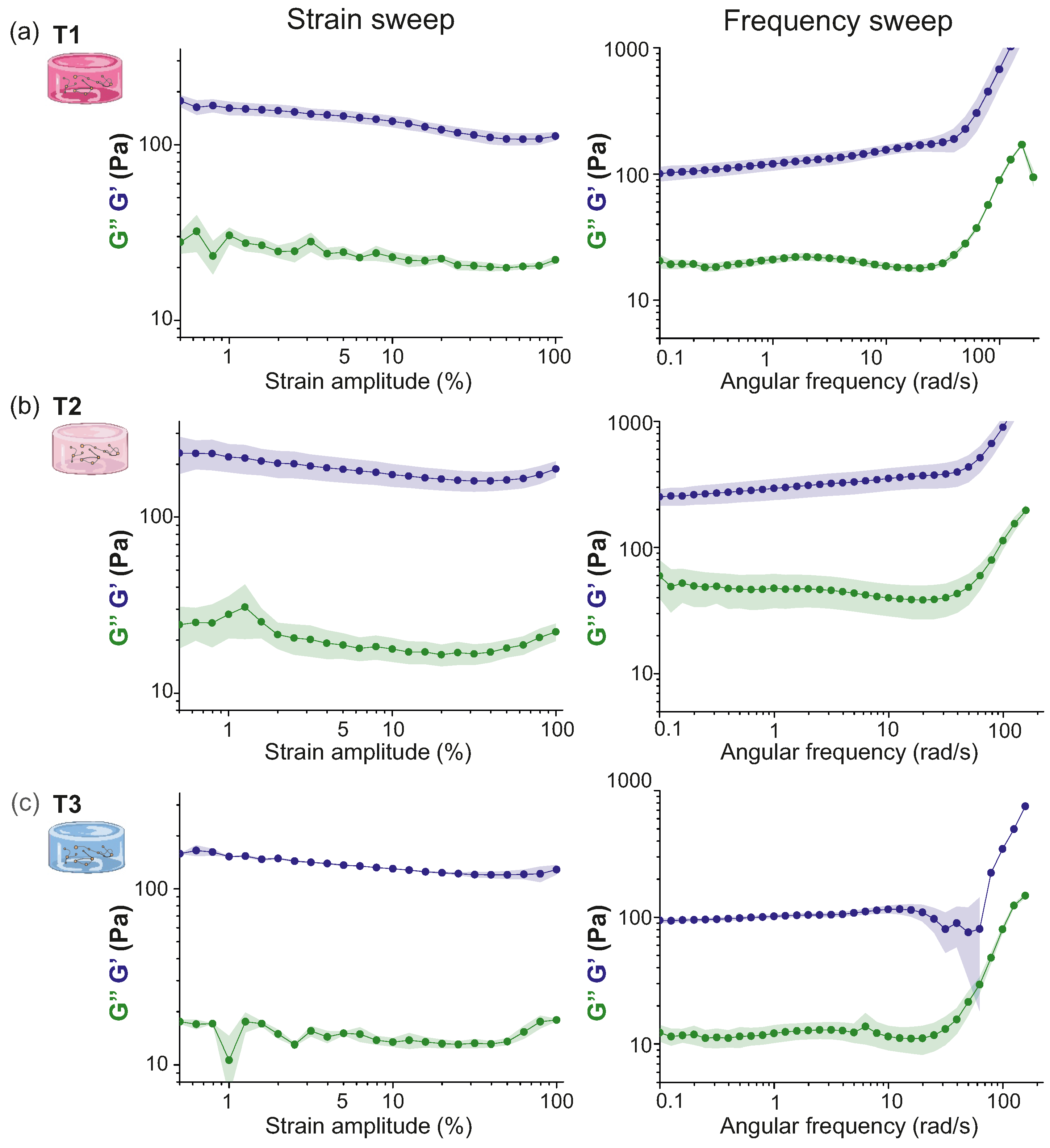
2.1.1. Characterization of Hydrogels Viscoelastic Behavior
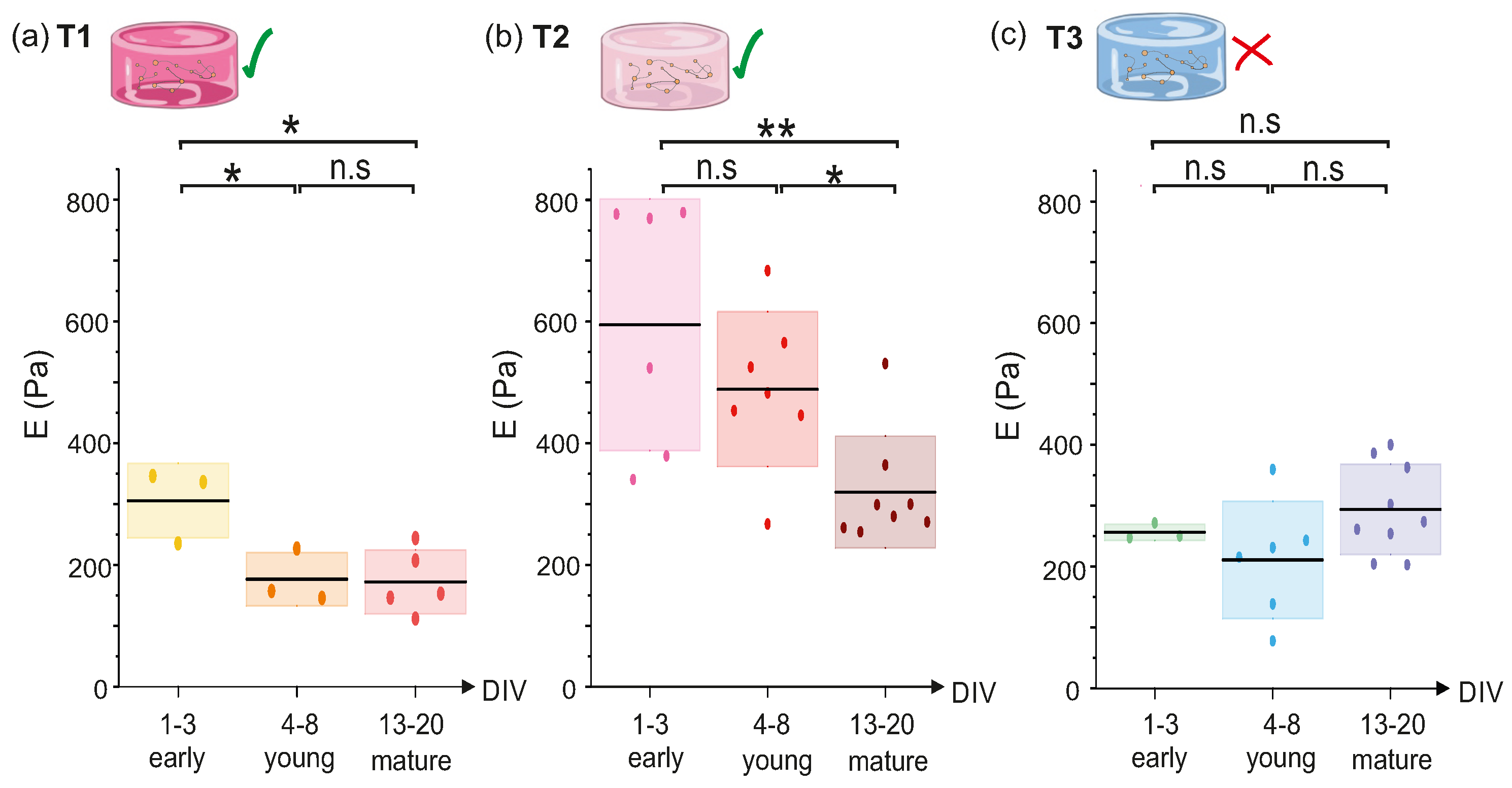
2.1.2. Evolution of T1, T2 and T3 Hydrogels during Development
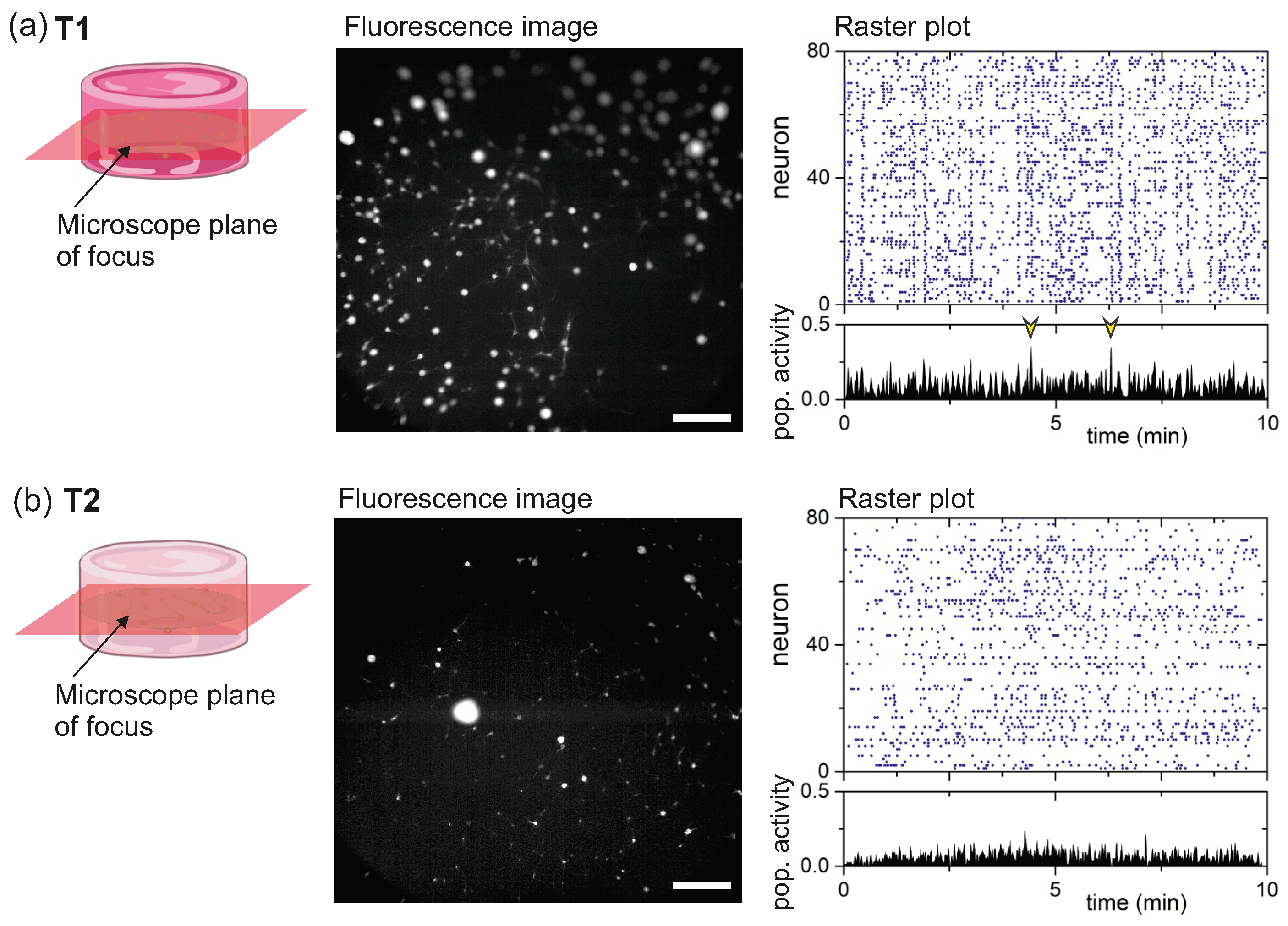
2.2. Functional Characterization of Hydrogels’ Neuronal Networks
2.3. Discussion: Influence of Hydrogel Composition and Microstructure on Young’s Modulus
2.4. Discussion: Hydrogel Stability and Network Formation
3. Conclusions
4. Materials and Methods
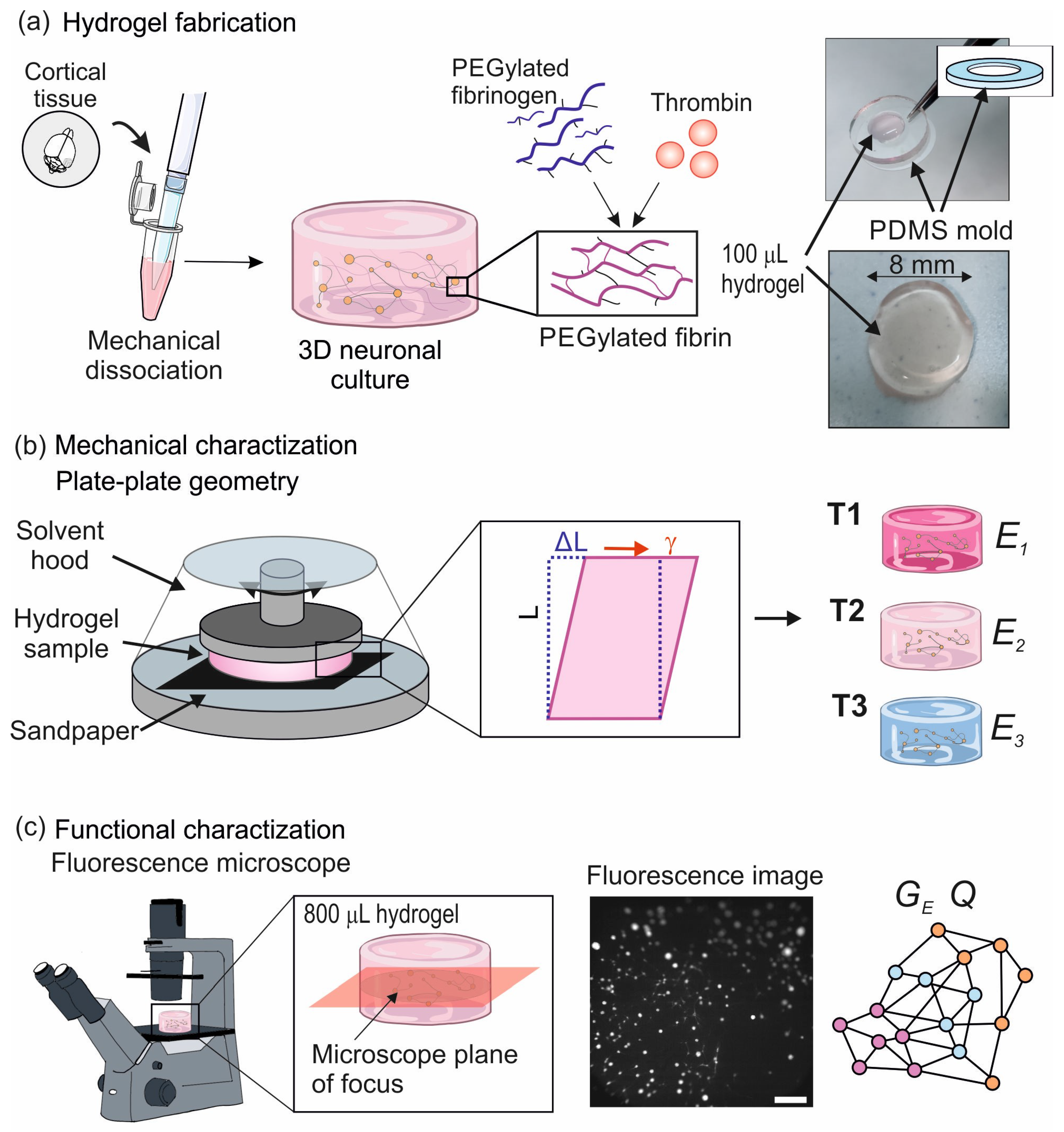
4.1. Preparation of Hydrogels and 3D Neuronal Cultures
- Fibrinogen stock solution: A 25 mg/mL fibrinogen solution was prepared in warm PBS. To prevent the formation of bubbles, small amounts of fibrinogen fibers were gently poured onto the warm PBS surface until complete dissolution, and stored in an incubator at 37 °C for stabilization. This process was repeated as needed until the desired fibrinogen concentration was achieved.
- Thrombin stock solution: It was prepared with a base concentration of 5 U/mL by diluting it in warm PBS.
- PEGylated fibrinogen solution: It was prepared by mixing L of a 6 mg/mL PEG–NHS solution in PBS with 1 mL of fibrinogen solution to obtain a 5:1 molar ratio. The resulting mixture was incubated at 37 °C for 2 h to promote crosslinking between fibrinogen and PEG strains.
- PDMS molds: They were prepared by mixing a volume ratio of 90% base and 10% curing agent of PDMS. The solution was poured on a flat plastic Petri dish and cured in an oven for 2 h at 90 °C. PDMS was then gently removed and pierced using stainless steel punchers. For the L hydrogels, 8 mm diameter, 1 mm thick hollow cylinders were prepared and placed on a 24-well plate for subsequent culturing.
- Cell suspension: Cortical tissue from CD1 mouse embryos at day 16 of development was dissected in L-15 medium previously enriched with 4% glucose 1 M, 1% glutamax and % gentamicin. The tissue was then transferred to plaiting medium (see Table 1) for mechanical dissociation through repeated pipetting, firstly on a L micro-pipette, and secondly on flame-polished glass Pasteur pipette tailored with a diameter tip of m for perfect dissociation. Dissociated tissue contained neural progenitors that later differentiated into neurons and glia, with an approximate ratio of 80% neurons and 20% glia cells as estimated from 2D cultures immunostaining analyses [28]. Progenitors were mixed with plaiting medium to a final concentration of cells/mL. The preparation of the primary neuronal cultures was carried out in accordance with the regulations of the University of Barcelona and governmental laws for animal experimentation.
- Cell transduction with a calcium indicator: To monitor spontaneous neuronal activity on the prepared cultures, the genetically encoded fluorescent calcium indicator GCaMP6s was incorporated into the cell solution via viral transduction through adeno-associated viruses (AAVs), which expressed the calcium indicator under the synapsin-I promoter and therefore only mature neurons exhibited fluorescence. Viruses were incorporated into the cell suspension at a 1:1000 ratio shortly before preparation of the final neuronal network.
- Final 3D neuronal cultures: PEGylated fibrinogen solution was combined with the neural progenitors cell suspension to have a final concentration of ∼200,000 cells/mL and placed into the corresponding containers (8 mm PDMS cavities for L samples or 13 mm plastic wells the L ones). Thrombin solution was next incorporated, cleaving specific bonds in fibrinogen and giving rise to fibrin monomers. These monomers then polymerized through covalent bonds, forming a 3D network. Since the whole process took place within 1 min, the mixture of fibrinogen, cell suspension and thrombin was carried out all at once to ensure a homogeneous distribution of neurons within the hydrogel. All the considered T1–T3 variants (with gradually higher concentration of thrombin) contained the same amount of fibrinogen and cell suspension. Thus, the observed differences across hydrogels were only caused by changes in the thrombin levels. Table 2 and Table 3 summarize the materials used for the preparation of the hydrogels.
- Cell culture maintenance and excitatory-inhibitory balance: Hydrogels were incubated at 37 °C, 5% CO2, and 95% humidity. At DIV 5, ‘plating medium’ was replaced by ‘changing medium’ to limit glial growth, and thereafter at DIV 7 to ‘final medium’. From here onward, ‘final medium’ was refreshed every two days. All hydrogels, independently of its volume and thrombin concentration, were treated identically, i.e., they experienced the same manipulations and media changes. Cultures contained both glia and neurons, with the latter comprising 80% excitatory neurons and 20% inhibitory ones in the mature stage [58]. Both neuronal types expressed GCaMP6s.
4.2. Hydrogels Rheological Characterization
4.2.1. Determination of Rheological Properties: Data Analysis
4.2.2. Rheological Tests
- Time sweep test. This rheological test was used for tracking the evolution of the structure of the hydrogel along time and procured key information such as degradation, gelation or solvent evaporation. The sample was subjected to a constant oscillation frequency and strain amplitude , set to rad/s and , respectively, (see Table 4).
- Strain sweep test. It was carried out to determine the linear viscoelastic region (LVR) of the hydrogel or the range in strain amplitudes in which the gel remains undamaged. The amplitude of the strain oscillation was progressively increased from to , while the frequency remained constant at rad/s.
- Frequency sweep test. It provided information about the rheological response of the hydrogel at different timescales, and revealed whether the sample softened or thickened at faster deformations. The oscillation frequency was progressively increased (from to 600 rad/s) at constant strain amplitude %. In the experiments presented here, even though rheological quantities slightly changed with in this range of strain, this value of % was used for the strain amplitude to characterize the dependence in frequency.
4.2.3. Experimental Details in Rheological Measurements
- A bulk rheometer HR-2 Discovery (TA instrument) was used for the experiments. A 8 mm plate–plate geometry was used with a fixed gap of m, chosen to ensure the integrity of the samples in preliminary tests [17]. The instrument has a lower measurable limit of 2 nN·m of the oscillation torque, as illustrated in Figure 1.
- To preserve the physiological temperature of living neurons during the test, the rheometer was equipped with a Peltier thermoelectric device that maintained a constant temperature of 37 °C.
- To prevent the hydrogel from slipping during measurements, sandpaper was attached to both surfaces of the plate-plate geometry [63].
- To avoid evaporation in the sample during the tests, a custom-made solvent hood was employed to encase the samples, and the surrounding environment was subsequently saturated with humidity by introducing a small quantity of culture medium around the hydrogel.
4.3. Characterization of Functional Traits
4.3.1. Neuronal Activity Recordings
4.3.2. Effective Connectivity and Network Traits
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| AAV | Adeno-associated virus |
| DIV | Day in vitro |
| E | Young’s modulus |
| ECM | Extracellular matrix |
| FUDR | (5-fluoro-deoxy-uridine) |
| Complex shear modulus | |
| Storage modulus | |
| Loss modulus | |
| Global Efficiency | |
| Generalized Transfer Entropy | |
| LVR | Linear viscoelastic regime |
| Average connectivity | |
| MEM | Modified Eagle Medium |
| PEG | Polyethylene glycol |
| PEG-NHS | Mono-Methyl polyethylene glycol succinate N-succinimidyl ester |
| PDMS | Polydimethylsiloxane |
| PBS | Phosphate-buffered saline |
| Q | Modularity statistic |
| ROIs | Regions of Interest |
| RPM | Revolutions per minute |
| SAOS | Small Amplitude Oscillatory Shearing |
| TE | Transfer Entropy |
| tPA | plasminogen activator |
| uPA | urokinase plasminogen activator |
| Strain amplitude | |
| Oscillation frequency | |
| Poisson’s ratio |
References
- Villanueva-Flores, F.; Garcia-Atutxa, I.; Santos, A.; Armendariz-Borunda, J. Toward a New Generation of Bio-Scaffolds for Neural Tissue Engineering: Challenges and Perspectives. Pharmaceutics 2023, 15, 1750. [Google Scholar] [CrossRef]
- Ozgun, A.; Lomboni, D.; Arnott, H.; Staines, W.A.; Woulfe, J.; Variola, F. Biomaterials-based strategies for in vitro neural models. Biomater. Sci. 2022, 10, 1134–1165. [Google Scholar] [CrossRef]
- Murphy, A.R.; Laslett, A.; O’Brien, C.M.; Cameron, N.R. Scaffolds for 3D in vitro culture of neural lineage cells. Acta Biomater. 2017, 54, 1–20. [Google Scholar] [CrossRef]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef]
- Caliari, S.R.; Burdick, J.A. A practical guide to hydrogels for cell culture. Nat. Methods 2016, 13, 405–414. [Google Scholar] [CrossRef]
- Weisel, J.W.; Nagaswami, C.; Makowski, L. Twisting of fibrin fibers limits their radial growth. Proc. Natl. Acad. Sci. USA 1987, 84, 8991–8995. [Google Scholar] [CrossRef]
- Ryan, E.A.; Mockros, L.F.; Weisel, J.W.; Lorand, L. Structural origins of fibrin clot rheology. Biophys. J. 1999, 77, 2813–2826. [Google Scholar] [CrossRef] [PubMed]
- Wolberg, A.S. Thrombin generation and fibrin clot structure. Blood Rev. 2007, 21, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Weisel, J.W.; Litvinov, R.I. Mechanisms of fibrin polymerization and clinical implications. Blood J. Am. Soc. Hematol. 2013, 121, 1712–1719. [Google Scholar] [CrossRef]
- Brown, A.C.; Barker, T.H. Fibrin-based biomaterials: Modulation of macroscopic properties through rational design at the molecular level. Acta Biomater. 2014, 10, 1502–1514. [Google Scholar] [CrossRef] [PubMed]
- Balgude, A.; Yu, X.; Szymanski, A.; Bellamkonda, R. Agarose gel stiffness determines rate of DRG neurite extension in 3D cultures. Biomaterials 2001, 22, 1077–1084. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, L.A.; Ju, Y.E.; Marg, B.; Osterfield, M.; Janmey, P.A. Neurite branching on deformable substrates. Neuroreport 2002, 13, 2411. [Google Scholar] [CrossRef]
- Jiang, F.X.; Yurke, B.; Schloss, R.S.; Firestein, B.L.; Langrana, N.A. Effect of dynamic stiffness of the substrates on neurite outgrowth by using a DNA-crosslinked hydrogel. Tissue Eng. Part A 2010, 16, 1873–1889. [Google Scholar] [CrossRef] [PubMed]
- Koser, D.E.; Thompson, A.J.; Foster, S.K.; Dwivedy, A.; Pillai, E.K.; Sheridan, G.K.; Svoboda, H.; Viana, M.; da F. Costa, L.; Guck, J.; et al. Mechanosensing is critical for axon growth in the developing brain. Nat. Neurosci. 2016, 19, 1592–1598. [Google Scholar] [CrossRef]
- O’Connor, S.M.; Stenger, D.A.; Shaffer, K.M.; Ma, W. Survival and neurite outgrowth of rat cortical neurons in three-dimensional agarose and collagen gel matrices. Neurosci. Lett. 2001, 304, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Johansson, F.; Kanje, M.; Eriksson, C.; Wallman, L. Guidance of neurons on porous patterned silicon: Is pore size important? Phys. Status Solidi C 2005, 2, 3258–3262. [Google Scholar] [CrossRef]
- López-León, C.F.; Soriano, J.; Planet, R. Rheological Characterization of Three-Dimensional Neuronal Cultures Embedded in PEGylated Fibrin Hydrogels. Gels 2023, 9, 642. [Google Scholar] [CrossRef]
- Yan, C.; Pochan, D.J. Rheological properties of peptide-based hydrogels for biomedical and other applications. Chem. Soc. Rev. 2010, 39, 3528–3540. [Google Scholar] [CrossRef]
- Stojkov, G.; Niyazov, Z.; Picchioni, F.; Bose, R.K. Relationship between structure and rheology of hydrogels for various applications. Gels 2021, 7, 255. [Google Scholar] [CrossRef]
- Zhang, G.; Drinnan, C.T.; Geuss, L.R.; Suggs, L.J. Vascular differentiation of bone marrow stem cells is directed by a tunable three-dimensional matrix. Acta Biomater. 2010, 6, 3395–3403. [Google Scholar] [CrossRef]
- Weisel, J.W. Structure of fibrin: Impact on clot stability. J. Thromb. Haemost. 2007, 5, 116–124. [Google Scholar] [CrossRef]
- Ghosh, K.; Shu, X.Z.; Mou, R.; Lombardi, J.; Prestwich, G.D.; Rafailovich, M.H.; Clark, R.A.F. Rheological Characterization of in Situ Cross-Linkable Hyaluronan Hydrogels. Biomacromolecules 2005, 6, 2857–2865. [Google Scholar] [CrossRef]
- Krieger, I.M. Bingham Award Lecture—1989: The role of instrument inertia in controlled-stress rheometers. J. Rheol. 1990, 34, 471–483. [Google Scholar] [CrossRef]
- Ewoldt, R.; Johnston, M.; Caretta, L. Experimental challenges of shear rheology: How to avoid bad data. In Complex Fluids in Biological Systems; Spagnolie, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Lai, V.K.; Lake, S.P.; Frey, C.R.; Tranquillo, R.T.; Barocas, V.H. Mechanical behavior of collagen-fibrin co-gels reflects transition from series to parallel interactions with increasing collagen content. J. Biomech. Eng. 2012, 134, 011004. [Google Scholar] [CrossRef] [PubMed]
- Carola, G.; Malagarriga, D.; Calatayud, C.; Pons-Espinal, M.; Blasco-Agell, L.; Richaud-Patin, Y.; Fernandez-Carasa, I.; Baruffi, V.; Beltramone, S.; Molina, E.; et al. Parkinson’s disease patient-specific neuronal networks carrying the LRRK2 G2019S mutation unveil early functional alterations that predate neurodegeneration. Npj Park. Dis. 2021, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Montalà-Flaquer, M.; López-León, C.F.; Tornero, D.; Houben, A.M.; Fardet, T.; Monceau, P.; Bottani, S.; Soriano, J. Rich dynamics and functional organization on topographically designed neuronal networks in vitro. Iscience 2022, 25, 105680. [Google Scholar] [CrossRef] [PubMed]
- Estévez-Priego, E.; Moreno-Fina, M.; Monni, E.; Kokaia, Z.; Soriano, J.; Tornero, D. Long-term calcium imaging reveals functional development in hiPSC-derived cultures comparable to human but not rat primary cultures. Stem Cell Rep. 2023, 18, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, P.; Fotiadis, P.; Parkes, L.; Bassett, D.S. The expanding horizons of network neuroscience: From description to prediction and control. NeuroImage 2022, 258, 119250. [Google Scholar] [CrossRef]
- Spedden, E.; White, J.D.; Naumova, E.N.; Kaplan, D.L.; Staii, C. Elasticity maps of living neurons measured by combined fluorescence and atomic force microscopy. Biophys. J. 2012, 103, 868–877. [Google Scholar] [CrossRef]
- Berkovitch, Y.; Seliktar, D. Semi-synthetic hydrogel composition and stiffness regulate neuronal morphogenesis. Int. J. Pharm. 2017, 523, 545–555. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, D.A.; Muga, K.; Boothroyd, E.M. The effect of fibrin structure on fibrinolysis. J. Biol. Chem. 1992, 267, 24259–24263. [Google Scholar] [CrossRef] [PubMed]
- Carr, M., Jr.; Alving, B. Effect of fibrin structure on plasmin-mediated dissolution of plasma clots. Blood Coagul. Fibrinolysis Int. J. Haemost. Thromb. 1995, 6, 567–573. [Google Scholar] [CrossRef]
- Lord, S.T. Molecular mechanisms affecting fibrin structure and stability. Arterioscler. Thromb. Vasc. Biol. 2011, 31, 494–499. [Google Scholar] [CrossRef]
- Collet, J.; Park, D.; Lesty, C.; Soria, J.; Soria, C.; Montalescot, G.; Weisel, J. Influence of fibrin network conformation and fibrin fiber diameter on fibrinolysis speed: Dynamic and structural approaches by confocal microscopy. Arterioscler. Thromb. Vasc. Biol. 2000, 20, 1354–1361. [Google Scholar] [CrossRef]
- Qian, Z.; Gilbert, M.E.; Colicos, M.A.; Kandel, E.R.; Kuhl, D. Tissue-plasminogen activator is induced as an immediate–early gene during seizure, kindling and long-term potentiation. Nature 1993, 361, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Seeds, N.W.; Williams, B.L.; Bickford, P.C. Tissue plasminogen activator induction in Purkinje neurons after cerebellar motor learning. Science 1995, 270, 1992–1994. [Google Scholar] [CrossRef] [PubMed]
- Yepes, M.; Sandkvist, M.; Coleman, T.A.; Moore, E.; Wu, J.Y.; Mitola, D.; Bugge, T.H.; Lawrence, D.A. Regulation of seizure spreading by neuroserpin and tissue-type plasminogen activator is plasminogen-independent. J. Clin. Investig. 2002, 109, 1571–1578. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Yang, B.; Liu, Q.; Jin, L.; Shao, Y.; Yuan, T.; Zhang, Y.N.; Wang, C.; Shi, Z.; Li, X.; et al. Effects of Univariate Stiffness and Degradation of DNA Hydrogels on the Transcriptomics of Neural Progenitor Cells. J. Am. Chem. Soc. 2023, 145, 8954–8964. [Google Scholar] [CrossRef] [PubMed]
- Long, K.R.; Huttner, W.B. How the extracellular matrix shapes neural development. R. Soc. Open Biol. 2019, 9, 180216. [Google Scholar] [CrossRef] [PubMed]
- Lam, D.; Enright, H.A.; Cadena, J.; Peters, S.K.; Sales, A.P.; Osburn, J.J.; Soscia, D.A.; Kulp, K.S.; Wheeler, E.K.; Fischer, N.O. Tissue-specific extracellular matrix accelerates the formation of neural networks and communities in a neuron-glia co-culture on a multi-electrode array. Sci. Rep. 2019, 9, 4159. [Google Scholar] [CrossRef]
- Si, W.; Gong, J.; Yang, X. Substrate stiffness in nerve cells. Brain Sci. Adv. 2023, 9, 24–34. [Google Scholar] [CrossRef]
- Orlandi, J.G.; Soriano, J.; Alvarez-Lacalle, E.; Teller, S.; Casademunt, J. Noise focusing and the emergence of coherent activity in neuronal cultures. Nat. Phys. 2013, 9, 582–590. [Google Scholar] [CrossRef]
- Plachez, C.; Richards, L.J. Mechanisms of axon guidance in the developing nervous system. Curr. Top. Dev. Biol. 2005, 69, 267–346. [Google Scholar]
- Stoeckli, E.T. Understanding axon guidance: Are we nearly there yet? Development 2018, 145, dev151415. [Google Scholar] [CrossRef]
- López-Mengual, A.; Segura-Feliu, M.; Sunyer, R.; Sanz-Fraile, H.; Otero, J.; Mesquida-Veny, F.; Gil, V.; Hervera, A.; Ferrer, I.; Soriano, J.; et al. Involvement of mechanical cues in the migration of Cajal-Retzius cells in the marginal zone during neocortical development. Front. Cell Dev. Biol. 2022, 10, 886110. [Google Scholar] [CrossRef]
- Huang, G.Y.; Zhou, L.H.; Zhang, Q.C.; Chen, Y.M.; Sun, W.; Xu, F.; Lu, T.J. Microfluidic hydrogels for tissue engineering. Biofabrication 2011, 3, 012001. [Google Scholar] [CrossRef] [PubMed]
- Yamada, M.; Sugaya, S.; Naganuma, Y.; Seki, M. Microfluidic synthesis of chemically and physically anisotropic hydrogel microfibers for guided cell growth and networking. Soft Matter 2012, 8, 3122–3130. [Google Scholar] [CrossRef]
- Geraili, A.; Jafari, P.; Hassani, M.S.; Araghi, B.H.; Mohammadi, M.H.; Ghafari, A.M.; Tamrin, S.H.; Modarres, H.P.; Kolahchi, A.R.; Ahadian, S.; et al. Controlling differentiation of stem cells for developing personalized organ-on-chip platforms. Adv. Healthc. Mater. 2018, 7, 1700426. [Google Scholar] [CrossRef] [PubMed]
- Sirkkunan, D.; Pingguan-Murphy, B.; Muhamad, F. Directing axonal growth: A review on the fabrication of fibrous scaffolds that promotes the orientation of axons. Gels 2021, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Cosson, S.; Lutolf, M. Hydrogel microfluidics for the patterning of pluripotent stem cells. Sci. Rep. 2014, 4, 4462. [Google Scholar] [CrossRef]
- Luo, L. Architectures of neuronal circuits. Science 2021, 373, eabg7285. [Google Scholar] [CrossRef] [PubMed]
- Mantha, S.; Pillai, S.; Khayambashi, P.; Upadhyay, A.; Zhang, Y.; Tao, O.; Pham, H.M.; Tran, S.D. Smart hydrogels in tissue engineering and regenerative medicine. Materials 2019, 12, 3323. [Google Scholar] [CrossRef] [PubMed]
- Catoira, M.C.; Fusaro, L.; Di Francesco, D.; Ramella, M.; Boccafoschi, F. Overview of natural hydrogels for regenerative medicine applications. J. Mater. Sci. Mater. Med. 2019, 30, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Tayler, I.M.; Stowers, R.S. Engineering hydrogels for personalized disease modeling and regenerative medicine. Acta Biomater. 2021, 132, 4–22. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, H.; Moriya, S.; Ide, K.; Hayakawa, T.; Akima, H.; Sato, S.; Kubota, S.; Tanii, T.; Niwano, M.; Teller, S.; et al. Impact of modular organization on dynamical richness in cortical networks. Sci. Adv. 2018, 4, eaau4914. [Google Scholar] [CrossRef]
- Soriano, J.; Rodríguez Martínez, M.; Tlusty, T.; Moses, E. Development of input connections in neural cultures. Proc. Natl. Acad. Sci. USA 2008, 105, 13758–13763. [Google Scholar] [CrossRef] [PubMed]
- Oswald, P. Rheophysics: The Deformation and Flow of Matter; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Patel, P.N.; Smith, C.K.; Patrick, C.W., Jr. Rheological and recovery properties of poly (ethylene glycol) diacrylate hydrogels and human adipose tissue. J. Biomed. Mater. Res. Part A Off. J. Soc. Biomater. Jpn. Soc. Biomater. Aust. Soc. Biomater. Korean Soc. Biomater. 2005, 73, 313–319. [Google Scholar] [CrossRef]
- Oyen, M. Mechanical characterisation of hydrogel materials. Int. Mater. Rev. 2014, 59, 44–59. [Google Scholar] [CrossRef]
- Duong, H.; Wu, B.; Tawil, B. Modulation of 3D fibrin matrix stiffness by intrinsic fibrinogen–thrombin compositions and by extrinsic cellular activity. Tissue Eng. Part A 2009, 15, 1865–1876. [Google Scholar] [CrossRef]
- Divoux, T.; Barentin, C.; Manneville, S. From stress-induced fluidization processes to Herschel-Bulkley behaviour in simple yield stress fluids. Soft Matter 2011, 7, 8409–8418. [Google Scholar] [CrossRef]
- Orlandi, J.G.; Fernández-García, S.; Comella-Bolla, A.; Masana, M.; Barriga, G.G.D.; Yaghoubi, M.; Kipp, A.; Canals, J.M.; Colicos, M.A.; Davidsen, J.; et al. NETCAL: An Interactive Platform for Large-Scale, NETwork and Population Dynamics Analysis of CALcium Imaging Recordings. Zenodo, Version 7.0.0 Open Beta, 2017. Available online: https://zenodo.org/records/1119026 (accessed on 2 January 2024).
- Grewe, B.F.; Langer, D.; Kasper, H.; Kampa, B.M.; Helmchen, F. High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nat. Methods 2010, 7, 399–405. [Google Scholar] [CrossRef]
- Soriano, J. Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish. Biophysica 2023, 3, 181–202. [Google Scholar] [CrossRef]
- Stetter, O.; Battaglia, D.; Soriano, J.; Geisel, T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012, 8, e1002653. [Google Scholar] [CrossRef] [PubMed]
- Ludl, A.A.; Soriano, J. Impact of physical obstacles on the structural and effective connectivity of in silico neuronal circuits. Front. Comput. Neurosci. 2020, 14, 77. [Google Scholar] [CrossRef] [PubMed]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the International AAAI Conference on Web and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 3, pp. 361–362. [Google Scholar]
- Latora, V.; Marchiori, M. Economic small-world behavior in weighted networks. Eur. Phys. J. B Condens. Matter Complex Syst. 2003, 32, 249–263. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]

| Medium | Composition |
|---|---|
| MEM+3G | Eagle’s MEM-enriched with % glucose, 1% 100× glutamax, |
| and g/mL gentamicin | |
| Plaiting Medium | 90% MEM + 3G, g/mL gentamicin, 5% horse serum, |
| 5% fetal calf serum and L/mL B27 | |
| Changing Medium | 90% MEM, 10% horse serum and % FUDR |
| Final Medium | 90% MEM and 10% horse serum |
| Hydrogel | Cell Medium (L) | PEGylated Fibrinogen (L) | Thrombin (L) |
|---|---|---|---|
| T1 (10%) | 65 | 25 | 10 |
| T2 (25%) | 50 | 25 | 25 |
| T3 (65%) | 10 | 25 | 65 |
| Hydrogel | Cell Medium (L) | PEGylated Fibrinogen (L) | Thrombin (L) |
|---|---|---|---|
| T1 (10%) | 520 | 200 | 80 |
| T2 (25%) | 400 | 200 | 200 |
| T3 (65%) | 80 | 200 | 520 |
| Parameter | Time Sweep | Strain Test | Frequency Sweep |
|---|---|---|---|
| Frequency (rad/s) | 0.6–600 | ||
| Strain amp. (%) | 5 | 0.1–100 | 5 |
| Product | References |
|---|---|
| PDMS | 184 SIL ELAST KIT, Dow, Corning, Midland, Michigan, USA |
| PBS | 15374875, ThermoFisher Sci., Waltham, MA, USA |
| L-15 | Gibco, 15188319, ThermoFisher Sci., Waltham, MA, USA |
| Glutamax | 35050038, ThermoFisher Sci., Waltham, MA, USA |
| Gentamicin | G1272, Sigma-Aldrich, St. Louis, MO, USA |
| PEG–NHS | 713783, Sigma-Aldrich, St. Louis, MO, USA |
| Fibrinogen | F8630-1G, Sigma-Aldrich, St. Louis, MO, USA |
| Thrombin | T4648-IKU, Sigma-Aldrich, St. Louis, MO, USA |
| MEM | 21090022, ThermoFisher Sci., Waltham, MA, USA |
| D-(+)-Glucose | G5400-1KG, Sigma-Aldrich, St. Louis, MO, USA |
| Horse serum | 11435045, ThermoFisher Sci., Waltham, MA, USA |
| Fetal calf serum | 15343681, ThermoFisher Sci., Waltham, MA, USA |
| B27 | 17504001, ThermoFisher Sci., Waltham, MA, USA |
| FUDR | F0503, Sigma-Aldrich, St. Louis, MO, USA |
| Calcium indicator GCaMP6s | AAV9.Syn.GCaMP6s.WPRE.SV40, |
| Addgene, Watertown, MA, USA | |
| CD1 mouse | Charles River Laboratories, Wilmington, MA, USA |
| Stainless steel punchers | Bahco 400.003.020, SNA Europe, Vitoria-Gasteiz, Spain |
| Glass coverslips | #1 Marienfeld-Superior, Lauda-Königshofen, Germany |
| Four-well plates | Nunc 179830, ThermoFisher Sci., Waltham, MA, USA |
| Autoclave | Selecta 4002515, Spain |
| Inverted microscope | Carl-Zeiss-Stiftung, Oberkochen, Germany |
| High-speed CMOS camera | Hamamatsu Photonics, Hamamatsu City, Shizuoka, Japan |
| Bulk rheometer HR-2 Discovery | TA instruments, New Castle, DE, USA |
| Sandpaper (grit P600-BF08) | Wurth, Künzelsau, Germany |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-León, C.F.; Planet, R.; Soriano, J. Preparation and Mechano-Functional Characterization of PEGylated Fibrin Hydrogels: Impact of Thrombin Concentration. Gels 2024, 10, 116. https://doi.org/10.3390/gels10020116
López-León CF, Planet R, Soriano J. Preparation and Mechano-Functional Characterization of PEGylated Fibrin Hydrogels: Impact of Thrombin Concentration. Gels. 2024; 10(2):116. https://doi.org/10.3390/gels10020116
Chicago/Turabian StyleLópez-León, Clara F., Ramon Planet, and Jordi Soriano. 2024. "Preparation and Mechano-Functional Characterization of PEGylated Fibrin Hydrogels: Impact of Thrombin Concentration" Gels 10, no. 2: 116. https://doi.org/10.3390/gels10020116
APA StyleLópez-León, C. F., Planet, R., & Soriano, J. (2024). Preparation and Mechano-Functional Characterization of PEGylated Fibrin Hydrogels: Impact of Thrombin Concentration. Gels, 10(2), 116. https://doi.org/10.3390/gels10020116