Automated Nuclear Morphometry: A Deep Learning Approach for Prognostication in Canine Pulmonary Carcinoma to Enhance Reproducibility
Abstract
Simple Summary
Abstract
1. Introduction
- Inter-observer reproducibility of nuclear pleomorphism estimates between pathologists is low in cPC, justifying the investigation of nuclear morphometry.
- Algorithmic morphometry is able to accurately measure nuclear size and shape parameters.
- Algorithmic morphometry is at least equivalent to manual morphometry nuclear pleomorphism estimates (which is impractical for a routine diagnostic test) and other established prognostic tests with regard to prognostic ability.
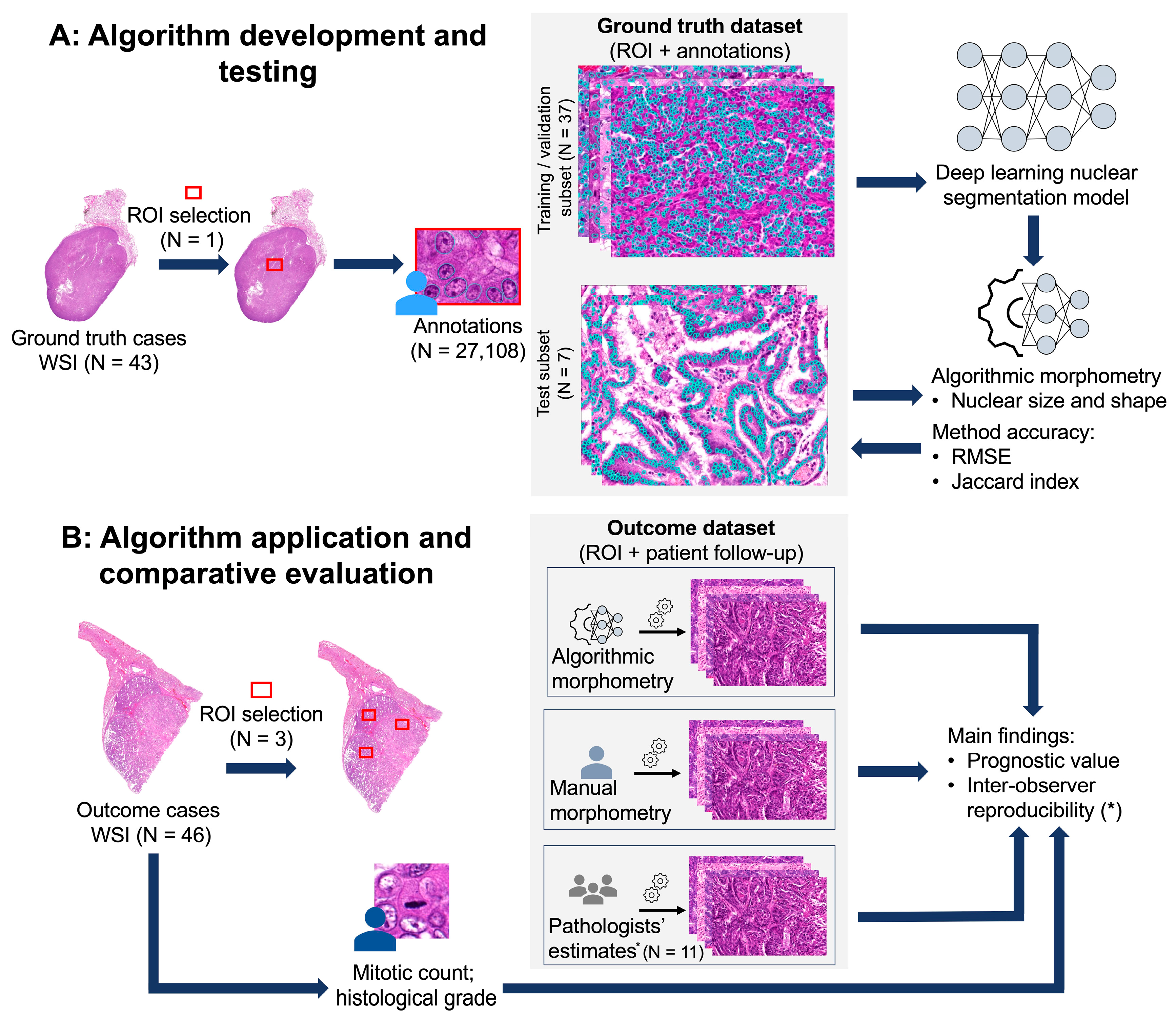
2. Materials and Methods
2.1. Material (Study Cases and Datasets)
2.1.1. Outcome Dataset
2.1.2. Ground Truth Dataset
2.2. Methods
2.2.1. Pathologists’ Estimates of Nuclear Pleomorphism
- Mild: an overall uniform nuclear size.
- Moderate: some variation in the nuclear size but with less than a two-fold difference.
- High: variation in the nuclear size with a greater than two-fold difference.
- Absent: regular (all or most round-to-oval nuclei with smooth contours).
- Present: irregular (numerous nuclei with uneven contours).
2.2.2. Supervised Deep Learning-Based Algorithm (Fully Automated Morphometry)
Deep Learning Segmentation Model
Algorithmic Morphometry
2.2.3. Benchmark Prognostic Tests
Manual Morphometry
Mitotic Count (MC)
Histological Grade
Clinical Staging System
2.2.4. Statistical Analysis
Inter-Observer Reproducibility
Test Accuracy of Algorithmic Morphometry
Prognostic Value
3. Results
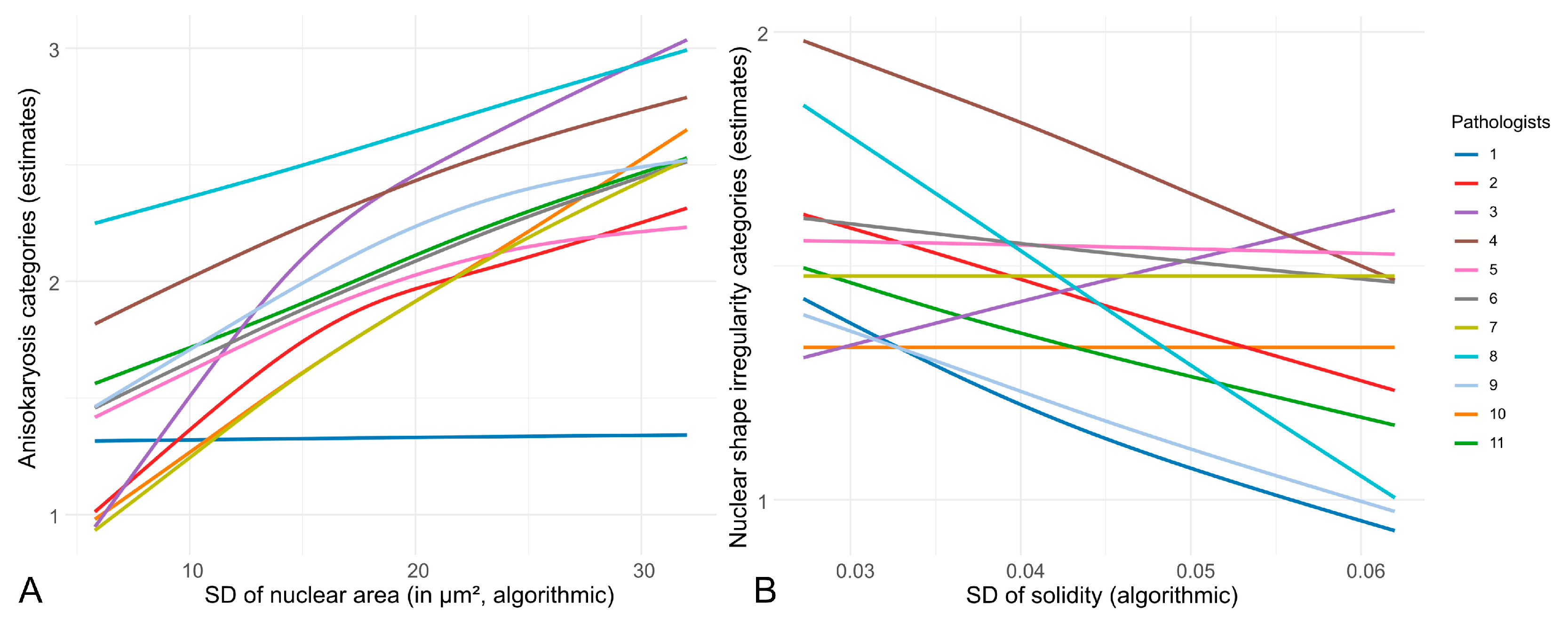
3.1. Inter-Observer Reproducibility of Nuclear Pleomorphism Estimates
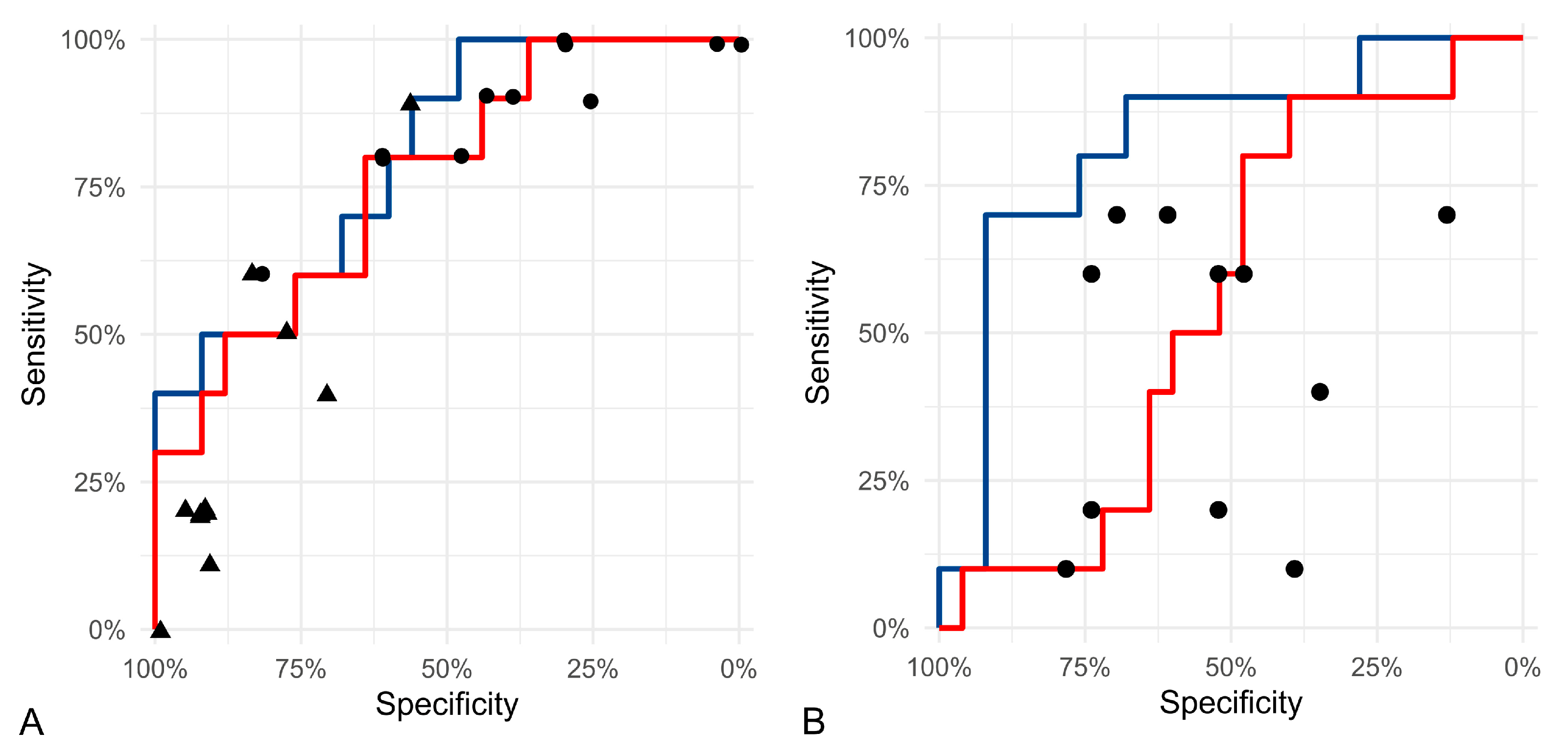
3.2. Test Accuracy of Algorithmic Morphometry
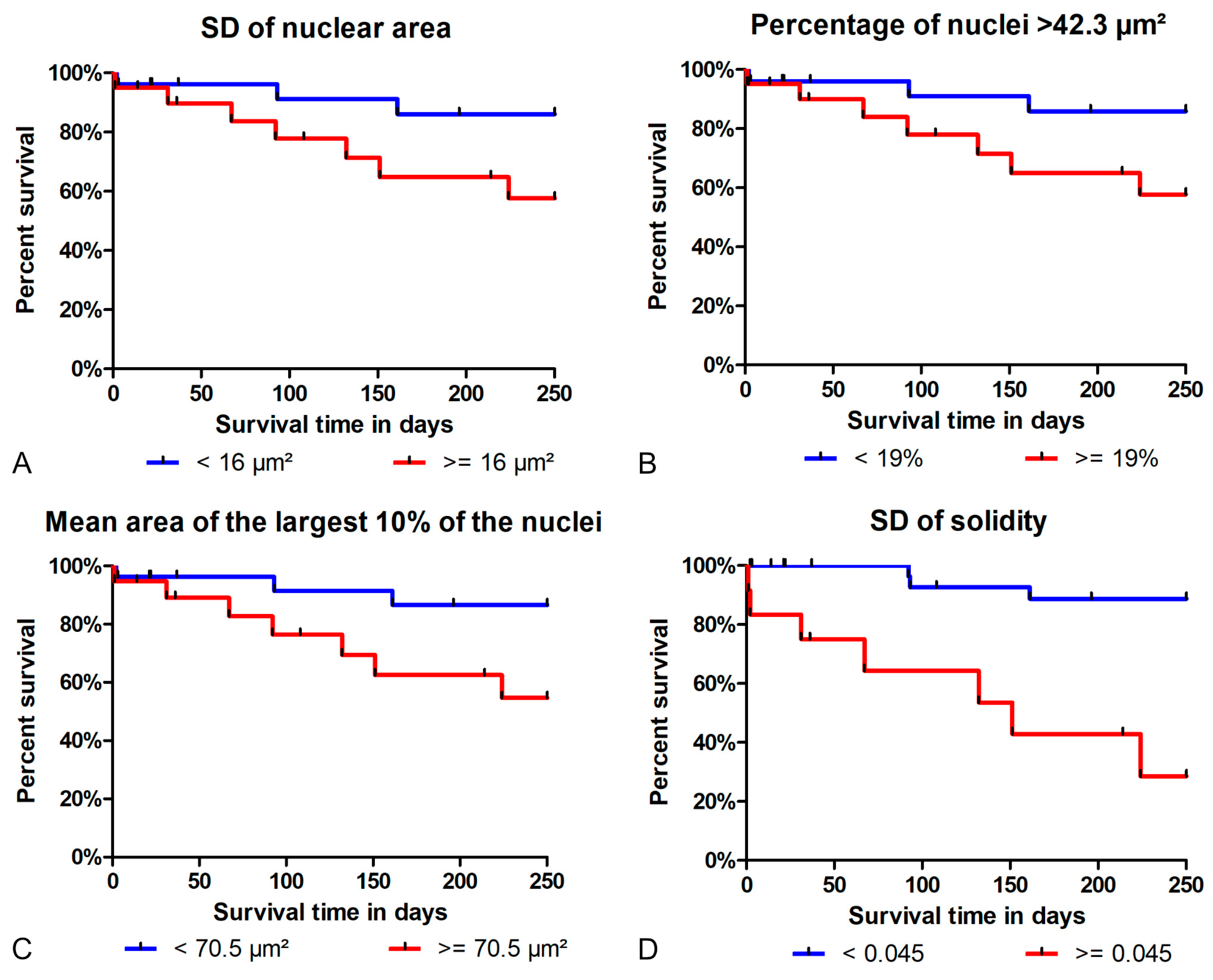
3.3. Prognostic Value
4. Discussion
- We have demonstrated the low inter-observer reproducibility of nuclear pleomorphism estimates among pathologists in cPC. Nuclear morphometry presents a reasonable approach to overcome this limitation.
- The algorithm’s segmentation ability was good for nuclear size parameters and acceptable for shape parameters. Future studies may benefit from implementing filters and/or optimizing the algorithm to improve the model’s accuracy.
- Regarding tumor-specific survival, the prognostic ability of the algorithmic morphometry was similar to manual morphometry for most parameters, with the exception of SD of solidity, and other established prognostic tests (histological grade, mitotic count, and clinical staging). The algorithm has the advantage of efficiency as a large number of nuclei can be measured within a few seconds and thus makes morphometry feasible for routine diagnostic service.
4.1. Inter-Observer Reproducibility
4.2. Test Accuracy of Algorithmic Morphometry
4.3. Inter-Algorithmic Reproducibility
4.4. Two-Dimensional vs. Stereological Approach
4.5. Prognostic Value
4.6. Diagnostic Applications and Considerations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehlhaff, C.J.; Leifer, C.E.; Patnaik, A.K.; Schwarz, P.D. Surgical Treatment of Primary Pulmonary Neoplasia in 15 Dogs. J. Am. Anim. Hosp. Assoc. 1984, 20, 1061–1067. [Google Scholar]
- Moulton, J.E.; Von Tscharner, C.; Schneider, R. Classification of Lung Carcinomas in the Dog and Cat. Vet. Pathol. 1981, 18, 513–528. [Google Scholar] [CrossRef] [PubMed]
- Hahn, F.F.; Muggenburg, B.A.; Griffith, W.C. Primary Lung Neoplasia in a Beagle Colony. Vet. Pathol. 1996, 33, 633–638. [Google Scholar] [CrossRef] [PubMed]
- Able, H.; Wolf-Ringwall, A.; Rendahl, A.; Ober, C.P.; Seelig, D.M.; Wilke, C.T.; Lawrence, J. Computed Tomography Radiomic Features Hold Prognostic Utility for Canine Lung Tumors: An Analytical Study. PLoS ONE 2021, 16, e0256139. [Google Scholar] [CrossRef]
- Deberry, J.D.; Norris, C.R.; Griffey, S.M.; Almy, F.S. Correlation between Fine-Needle Aspiration Cytopathology and Histopathology of the Lung in Dogs and Cats. J. Am. Anim. Hosp. Assoc. 2002, 38, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Griffey, S.M.; Kraegel, S.A.; Madewell, B.R. Rapid Detection of K-Ras Gene Mutations in Canine Lung Cancer Using Single-Strand Conformational Polymorphism Analysis. Carcinogenesis 1998, 19, 959–963. [Google Scholar] [CrossRef] [PubMed]
- McNiel, E.A.; Ogilvie, G.K.; Powers, B.E.; Hutchison, J.M.; Salman, M.D.; Withrow, S.J. Evaluation of Prognostic Factors for Dogs with Primary Lung Tumors: 67 cases (1985–1992). J. Am. Vet. Med Assoc. 1997, 211, 1422–1427. [Google Scholar] [CrossRef] [PubMed]
- Plavec, T.; Žagar, Ž.; Kessler, M. Klinisch-Pathologische Befunde, Postoperative Überlebenszeiten Und Prognostische Faktoren Bei Hunden Mit Primären Lungenkarzinomen. Tierärztliche Prax. Ausg. Kleintiere Heimtiere 2022, 50, 317–328. [Google Scholar] [CrossRef]
- Ogilvie, G.K.; Haschek, W.M.; Withrow, S.J.; Richardson, R.C.; Harvey, H.J.; Henderson, R.A.; Fowler, J.D.; Norris, A.M.; Tomlinson, J.; McCaw, D. Classification of Primary Lung Tumors in Dogs: 210 Cases (1975–1985). J. Am. Vet. Med. Assoc. 1989, 195, 106–108. [Google Scholar]
- Polton, G.A.; Brearley, M.J.; Powell, S.M.; Burton, C.A. Impact of Primary Tumour Stage on Survival in Dogs with Solitary Lung Tumours. J. Small Anim. Pract. 2008, 49, 66–71. [Google Scholar] [CrossRef]
- Ogilvie, G.K.; Weigel, R.M.; Haschek, W.M.; Withrow, S.J.; Richardson, R.C.; Harvey, H.J.; Henderson, R.A.; Fowler, J.D.; Norris, A.M.; Tomlinson, J. Prognostic Factors for Tumor Remission and Survival in Dogs after Surgery for Primary Lung Tumor: 76 Cases (1975–1985). J. Am. Vet. Med. Assoc. 1989, 195, 109–112. [Google Scholar] [PubMed]
- Plavec, T.; Bolliger, C. Kleintieronkologie, 4th ed.; Kessler, M., Ed.; Thieme: Stuttgart, Germany, 2022; pp. 489–497. ISBN 9783132419254. [Google Scholar]
- Wilson, D.W. Tumors in Domestic Animals, 5th ed.; Meuten, D.J., Ed.; Tumors of the Respiratory Tract; Wiley-Blackwell: Raleigh, NC, USA, 2016; pp. 467–498. ISBN 9780813821795. [Google Scholar]
- Lee, B.M.; Clarke, D.; Watson, M.; Laver, T. Retrospective Evaluation of a Modified Human Lung Cancer Stage Classification in Dogs with Surgically Excised Primary Pulmonary Carcinomas. Vet. Comp. Oncol. 2020, 18, 590–598. [Google Scholar] [CrossRef] [PubMed]
- McPhetridge, J.B.; Scharf, V.F.; Regier, P.J.; Toth, D.; Lorange, M.; Tremolada, G.; Dornbusch, J.A.; Selmic, L.E.; Bae, S.; Townsend, K.L.; et al. Distribution of Histopathologic Types of Primary Pulmonary Neoplasia in Dogs and Outcome of Affected Dogs: 340 Cases (2010–2019). J. Am. Vet. Med. Assoc. 2022, 260, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Ichimata, M.; Kagawa, Y.; Namiki, K.; Toshima, A.; Nakano, Y.; Matsuyama, F.; Fukazawa, E.; Harada, K.; Katayama, R.; Kobayashi, T. Prognosis of Primary Pulmonary Adenocarcinoma after Surgical Resection in Small-Breed Dogs: 52 Cases (2005–2021). J. Vet. Intern. Med. 2023, 37, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Paoloni, M.C.; Adams, W.M.; Dubielzig, R.R.; Kurzman, I.; Vail, D.M.; Hardie, R.J. Comparison of Results of Computed Tomography and Radiography with Histopathologic Findings in Tracheobronchial Lymph Nodes in Dogs with Primary Lung Tumors: 14 Cases (1999–2002). J. Am. Vet. Med. Assoc. 2006, 228, 1718–1722. [Google Scholar] [CrossRef]
- Dagher, E.; Abadie, J.; Loussouarn, D.; Campone, M.; Nguyen, F. Feline Invasive Mammary Carcinomas: Prognostic Value of Histological Grading. Vet. Pathol. 2019, 56, 660–670. [Google Scholar] [CrossRef] [PubMed]
- Mills, S.W.; Musil, K.M.; Davies, J.L.; Hendrick, S.; Duncan, C.; Jackson, M.L.; Kidney, B.; Philibert, H.; Wobeser, B.K.; Simko, E. Prognostic Value of Histologic Grading for Feline Mammary Carcinoma: A Retrospective Survival Analysis. Vet. Pathol. 2015, 52, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Pradel, J.; Berlato, D.; Dobromylskyj, M.; Rasotto, R. Prognostic Significance of Histopathology in Canine Anal Sac Gland Adenocarcinomas: Preliminary Results in a Retrospective Study of 39 Cases. Vet. Comp. Oncol. 2018, 16, 518–528. [Google Scholar] [CrossRef] [PubMed]
- Sabattini, S.; Bettini, G. Grading Cutaneous Mast Cell Tumors in Cats. Vet. Pathol. 2019, 56, 43–49. [Google Scholar] [CrossRef]
- Santos, M.; Correia-Gomes, C.; Santos, A.; de Matos, A.; Dias-Pereira, P.; Lopes, C. Interobserver Reproducibility of Histological Grading of Canine Simple Mammary Carcinomas. J. Comp. Pathol. 2015, 153, 22–27. [Google Scholar] [CrossRef]
- Santos, M.; Correia-Gomes, C.; Santos, A.; de Matos, A.; Rocha, E.; Lopes, C.; Pereira, P.D. Nuclear Pleomorphism: Role in Grading and Prognosis of Canine Mammary Carcinomas. Vet. J. 2014, 200, 426–433. [Google Scholar] [CrossRef] [PubMed]
- Fragoso-Garcia, M.; Wilm, F.; Bertram, C.A.; Merz, S.; Schmidt, A.; Donovan, T.; Fuchs-Baumgartinger, A.; Bartel, A.; Marzahl, C.; Diehl, L.; et al. Automated Diagnosis of 7 Canine Skin Tumors Using Machine Learning on H&E-Stained Whole Slide Images. Vet. Pathol. 2023, 60, 865–875. [Google Scholar] [CrossRef]
- Alsubaie, N.M.; Snead, D.; Rajpoot, N.M. Tumour Nuclear Morphometrics Predict Survival in Lung Adenocarcinoma. IEEE Access 2021, 9, 12322–12331. [Google Scholar] [CrossRef]
- Chuang, W.Y.; Yu, W.H.; Lee, Y.C.; Zhang, Q.Y.; Chang, H.; Shih, L.Y.; Yeh, C.J.; Lin, S.M.T.; Chang, S.H.; Ueng, S.H.; et al. Deep Learning–Based Nuclear Morphometry Reveals an Independent Prognostic Factor in Mantle Cell Lymphoma. Am. J. Pathol. 2022, 192, 1763–1778. [Google Scholar] [CrossRef]
- Casanova, M.; Branco, S.; Veiga, I.B.; Barros, A.; Faísca, P. Stereology in Grading and Prognosis of Canine Cutaneous Mast Cell Tumors. Vet. Pathol. 2021, 58, 483–490. [Google Scholar] [CrossRef] [PubMed]
- Meuten, D.J.; Moore, F.M.; Donovan, T.A.; Bertram, C.A.; Klopfleisch, R.; Foster, R.A.; Smedley, R.C.; Dark, M.J.; Milovancev, M.; Stromberg, P.; et al. International Guidelines for Veterinary Tumor Pathology: A Call to Action. Vet. Pathol. 2021, 58, 766–794. [Google Scholar] [CrossRef]
- Aubreville, M.; Bertram, C.; Klopfleisch, R.; Maier, A. SlideRunner: A Tool for Massive Cell Annotations in Whole Slide Images. In Proceedings of the Bildverarbeitung für die Medizin 2018, Erlangen, Germany, 13 March 2018; Informatik Aktuell. Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hyndman, P.S.; Kennedy, K.; Donovan, T.A. Histological Risk Factors for Survival in Dogs with Primary Epithelial Pulmonary Tumors Following Lung Lobectomy.
- Van Der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-Image: Image Processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Proceedings 4; Springer: Cham, Switzerland, 2018; Volume 11045, pp. 3–11. [Google Scholar] [CrossRef]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing Network Design Spaces. In Proceedings of the Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Pavel, I. Segmentation Models Pytorch. 2019. Available online: https://github.com/qubvel/segmentation_models.pytorch (accessed on 27 January 2024).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: Glasgow, UK, 2019; pp. 8024–8035. Available online: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf (accessed on 27 January 2024).
- William, F. PyTorch Lightning. 2019. Available online: https://lightning.ai/docs/pytorch/stable/ (accessed on 27 January 2024).
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; MICCAI 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9351. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Haghofer, A.; Parlak, E.; Bartel, A.; Donovan, T.A.; Assenmacher, C.-A.; Bolfa, P.; Dark, M.J.; Fuchs-Baumgartinger, A.; Klang, A.; Jäger, K.; et al. Nuclear Pleomorphism in Canine Cutaneous Mast Cell Tumors-Comparison of Reproducibility and Prognostic Relevance between Estimates, Manual Morphometry and Algorithmic Morphometry. arXiv 2023, arXiv:2309.15031. [Google Scholar]
- Bertram, C.A.; Aubreville, M.; Donovan, T.A.; Bartel, A.; Wilm, F.; Marzahl, C.; Assenmacher, C.A.; Becker, K.; Bennett, M.; Corner, S.; et al. Computer-Assisted Mitotic Count Using a Deep Learning–Based Algorithm Improves Interobserver Reproducibility and Accuracy. Vet. Pathol. 2022, 59, 211–226. [Google Scholar] [CrossRef]
- Donovan, T.A.; Moore, F.M.; Bertram, C.A.; Luong, R.; Bolfa, P.; Klopfleisch, R.; Tvedten, H.; Salas, E.N.; Whitley, D.B.; Aubreville, M.; et al. Mitotic Figures—Normal, Atypical, and Imposters: A Guide to Identification. Vet. Pathol. 2021, 58, 243–257. [Google Scholar] [CrossRef] [PubMed]
- Owen, L.N.; World Health Organization; Veterinary Public Health U; Oncology WHOCCfC. TNM Classification of Tumours in Domestic Animals; Owen, L.N., Ed.; World Health Organization: Geneva, Switzerland, 1980. [Google Scholar]
- Hallgren, K.A. Computing Inter-Rater Reliability for Observational Data: An Overview and Tutorial. Tutor. Quant. Methods Psychol. 2012, 8, 23–24. [Google Scholar] [CrossRef] [PubMed]
- Valli, V.E.; Myint, M.; Barthel, A.; Bienzle, D.; Caswell, J.; Colbatzky, F.; Durham, A.; Ehrhart, E.J.; Johnson, Y.; Jones, C.; et al. Classification of Canine Malignant Lymphomas According to the World Health Organization Criteria. Vet. Pathol. 2011, 48, 198–211. [Google Scholar] [CrossRef]
- Brown, D.L. Practical Stereology Applications for the Pathologist. Vet. Pathol. 2017, 54, 358–368. [Google Scholar] [CrossRef] [PubMed]
- Chuang, W.Y.; Chang, S.H.; Yu, W.H.; Yang, C.K.; Yeh, C.J.; Ueng, S.H.; Liu, Y.J.; Chen, T.D.; Chen, K.H.; Hsieh, Y.Y.; et al. Successful Identification of Nasopharyngeal Carcinoma in Nasopharyngeal Biopsies Using Deep Learning. Cancers 2020, 12, 507. [Google Scholar] [CrossRef] [PubMed]
- Chuang, W.Y.; Chen, C.C.; Yu, W.H.; Yeh, C.J.; Chang, S.H.; Ueng, S.H.; Wang, T.H.; Hsueh, C.; Kuo, C.F.; Yeh, C.Y. Identification of Nodal Micrometastasis in Colorectal Cancer Using Deep Learning on Annotation-Free Whole-Slide Images. Mod. Pathol. 2021, 34, 1901–1911. [Google Scholar] [CrossRef]
- Chen, C.L.; Chen, C.C.; Yu, W.H.; Chen, S.H.; Chang, Y.C.; Hsu, T.I.; Hsiao, M.; Yeh, C.Y.; Chen, C.Y. An Annotation-Free Whole-Slide Training Approach to Pathological Classification of Lung Cancer Types Using Deep Learning. Nat. Commun. 2021, 12, 1193. [Google Scholar] [CrossRef] [PubMed]
- Steinbuss, G.; Kriegsmann, M.; Zgorzelski, C.; Brobeil, A.; Goeppert, B.; Dietrich, S.; Mechtersheimer, G.; Kriegsmann, K. Deep Learning for the Classification of Non-Hodgkin Lymphoma on Histopathological Images. Cancers 2021, 13, 2419. [Google Scholar] [CrossRef] [PubMed]
- Haghofer, A.; Fuchs-Baumgartinger, A.; Lipnik, K.; Klopfleisch, R.; Aubreville, M.; Scharinger, J.; Weissenböck, H.; Winkler, S.M.; Bertram, C.A. Histological Classification of Canine and Feline Lymphoma Using a Modular Approach Based on Deep Learning and Advanced Image Processing. Sci. Rep. 2023, 13, 19436. [Google Scholar] [CrossRef]
- Ström, P.; Kartasalo, K.; Olsson, H.; Solorzano, L.; Delahunt, B.; Berney, D.M.; Bostwick, D.G.; Evans, A.J.; Grignon, D.J.; Humphrey, P.A.; et al. Artificial Intelligence for Diagnosis and Grading of Prostate Cancer in Biopsies: A Population-Based, Diagnostic Study. Lancet Oncol. 2020, 21, 222–232. [Google Scholar] [CrossRef]
- Bulten, W.; Pinckaers, H.; van Boven, H.; Vink, R.; de Bel, T.; van Ginneken, B.; van der Laak, J.; Hulsbergen-van de Kaa, C.; Litjens, G. Automated Deep-Learning System for Gleason Grading of Prostate Cancer Using Biopsies: A Diagnostic Study. Lancet Oncol. 2020, 21, 233–241. [Google Scholar] [CrossRef] [PubMed]


| Feature | Measurement | Parameters |
|---|---|---|
| Size | Area (in µm2) | Mean, median, standard deviation (SD), skewness, mean and median of the largest 10% of the nuclei, 90th percentile (90th P), percentage of large nuclei (>42.3 µm2 or >50.5 µm2) |
| Shape | Eccentricity | Mean, median, SD, skewness |
| Solidity | Mean, median, SD, skewness |
| Model | Binary Segmentation | Object Localization | ||
|---|---|---|---|---|
| Dice | F1 | Precision | Recall | |
| 1 | 0.8073 | 0.8615 | 0.8877 | 0.8369 |
| 2 | 0.7761 | 0.8397 | 0.8726 | 0.8091 |
| 3 | 0.7801 | 0.8649 | 0.8470 | 0.8835 |
| Morphometric Parameter | Method | Threshold Value | Sensitivity | Specificity | Precision |
|---|---|---|---|---|---|
| SD of area | Algorithmic | 16 µm2 | 70.0% | 68.0% | 46.7% |
| Manual | 10 µm2 | 70.0% | 64.0% | 43.8% | |
| Mean area of largest 10% of the nuclei | Algorithmic | 70.5 µm2 | 70.0% | 72.0% | 50.0% |
| Manual | 53.03 µm2 | 70.0% | 64.0% | 43.8% | |
| 50 µm2 | 90.0% | 64.0% | 50.0% | ||
| Percentage of nuclei above 42.3 µm2 | Algorithmic | 19% | 70.0% | 68.0% | 46.7% |
| Manual | 26% | 70.0% | 76.0% | 53.8% | |
| SD of solidity | Algorithmic | 0.045 | 70.0% | 92.0% | 77.8% |
| Manual | 0.0204 | 70.0% | 48.0% | 35.0% |
| Prognostic Test | Algorithm | Pathologists | |||
|---|---|---|---|---|---|
| Threshold | HR (95%CI) | Threshold/Categories | HR (95%CI) | ||
| Morphometry | SD of area | 16 µm2 | 3.38 (0.87–13.1) | 10 µm2 | 3.32 (0.85–12.9) |
| Mean area of largest 10% of nuclei | 70.5 µm2 | 3.85 (0.99–15.0) | 50 µm2 | 9.83 (1.24–78.1) | |
| % nuclei above 42.3 µm2 | 19% | 3.32 (0.85–12.9) | 26% | 4.34 (1.12–16.9) | |
| SD of solidity | 0.045 | 9.88 (2.52–38.7) | 0.0204 | 1.94 (0.50–7.52) | |
| Other | Grade | NA | NA | 1 vs. 2, 3 | 1.01 (0.12–7.98) |
| NA | NA | 1, 2 vs. 3 | 1.75 (0.36–8.36) | ||
| MC, pathologist 1 | NA | NA | 1, 2 vs. 3, 4 | 0.79 (0.20–3.08) | |
| MC, pathologist 2 | NA | NA | 1, 2 vs. 3, 4 | 0.41 (0.10–1.61) | |
| Stage | NA | NA | 1 vs. 2, 3, 4 | 1.42 (0.36–5.49) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glahn, I.; Haghofer, A.; Donovan, T.A.; Degasperi, B.; Bartel, A.; Kreilmeier-Berger, T.; Hyndman, P.S.; Janout, H.; Assenmacher, C.-A.; Bartenschlager, F.; et al. Automated Nuclear Morphometry: A Deep Learning Approach for Prognostication in Canine Pulmonary Carcinoma to Enhance Reproducibility. Vet. Sci. 2024, 11, 278. https://doi.org/10.3390/vetsci11060278
Glahn I, Haghofer A, Donovan TA, Degasperi B, Bartel A, Kreilmeier-Berger T, Hyndman PS, Janout H, Assenmacher C-A, Bartenschlager F, et al. Automated Nuclear Morphometry: A Deep Learning Approach for Prognostication in Canine Pulmonary Carcinoma to Enhance Reproducibility. Veterinary Sciences. 2024; 11(6):278. https://doi.org/10.3390/vetsci11060278
Chicago/Turabian StyleGlahn, Imaine, Andreas Haghofer, Taryn A. Donovan, Brigitte Degasperi, Alexander Bartel, Theresa Kreilmeier-Berger, Philip S. Hyndman, Hannah Janout, Charles-Antoine Assenmacher, Florian Bartenschlager, and et al. 2024. "Automated Nuclear Morphometry: A Deep Learning Approach for Prognostication in Canine Pulmonary Carcinoma to Enhance Reproducibility" Veterinary Sciences 11, no. 6: 278. https://doi.org/10.3390/vetsci11060278
APA StyleGlahn, I., Haghofer, A., Donovan, T. A., Degasperi, B., Bartel, A., Kreilmeier-Berger, T., Hyndman, P. S., Janout, H., Assenmacher, C.-A., Bartenschlager, F., Bolfa, P., Dark, M. J., Klang, A., Klopfleisch, R., Merz, S., Richter, B., Schulman, F. Y., Ganz, J., Scharinger, J., ... Bertram, C. A. (2024). Automated Nuclear Morphometry: A Deep Learning Approach for Prognostication in Canine Pulmonary Carcinoma to Enhance Reproducibility. Veterinary Sciences, 11(6), 278. https://doi.org/10.3390/vetsci11060278







