1. Introduction
Ill-posed inverse problems represent a major challenge to research in many disciplines. They arise, e.g., when one wishes to reconstruct the shape of an astronomical object after its light has passed through a turbulent atmosphere and an imperfect telescope or when we image the interior of a patients skull during a computer tomography scan. In a more theoretical setting, extracting spectral functions from numerical simulations of strongly correlated quantum fields constitutes another example. The common difficulty among these tasks lies in the fact that we do not have direct access to the quantity of interest (from here on referred to as ) but instead only to a distorted representation of it, measured in our experiment (from here on denoted by D). Extracting from D, in general, requires us to solve an inherently nonlinear optimization problem, which we construct and discuss in detail below.
Let us consider the common class of inverse problems, where the quantity of interest
and the measured data
D are related via an integral convolution
with a kernel function
. For the sake of simplicity let us assume (as is often the case in practice) that the function
K is exactly known. The task at hand is to estimate the function
that underlies the observed
D. The ill-posedness (and ill-conditioning) of this task is readily spotted if we acknowledge that our data comes in the form of
discrete estimates
of the true function
, where
denotes a source of noise. In addition, we need to approximate the integral in some form for numerical treatment. In its simplest form, writing it as a sum over
bins we obtain
At this point, we are asked to estimate optimal parameters from data points, which themselves carry uncertainty. A naive fit of the ’s is of no use, since it would produce an infinite number of degenerate solutions, which all reproduce the set of ’s within their error bars. Only if we introduce an appropriate regularization can the problem be made well-posed, and it is this regularization which in general introduces nonlinearities.
Bayesian inference represents one way to regularize the inversion task. It provides a systematic procedure for how additional (so called prior) knowledge can be incorporated to that effect. Bayes theorem
states that the
posterior probability
for some set of parameters
to be the true solution of the inversion problem is given by the product of the
likelihood probability
and the
prior probability
. The
independent normalization
is often referred to as the
evidence. Assuming that the noise
is Gaussian, we may write the likelihood as
where
is the unbiased covariance matrix of the measured data with respect to the true mean and
refers to the synthetic data that one obtains by inserting the current set of
parameters into (
2). A
fit would simply return one of the many degenerate extrema of
, hence being referred to as a maximum likelihood fit.
The important ingredient of Bayes theorem is the presence of the prior probability, often expressed in terms of a regulator functional
It is here where pertinent domain knowledge can be encoded. For the study of intensity profiles of astronomical objects and hadronic spectral functions for example, it is a-priori known that the values of must be positive. Depending on which type of information one wishes to incorporate, the explicit form of will be different. It is customary to parameterize the shape of the prior distribution by two types of hyperparameters, the default model and a confidence function . The discretized represents the maximum of the prior for each parameter and each its corresponding spread.
Once both the likelihood and prior probability are set, we may search for the maximum a posteriori (MAP) point estimate of the
’s via
constitutes the most probable parameters given our data and prior knowledge. (In the case that no data is provided, the Bayesian reconstruction will simply reproduce the default model
m.) Note that since the exponential function is monotonous, instead of finding the extremum of
, in practice, one often considers the extremum of
directly.
The idea of introducing a regularization in order to meaningfully estimate the most probable set of parameters underlying observed data has a long history. As early as 1919 [
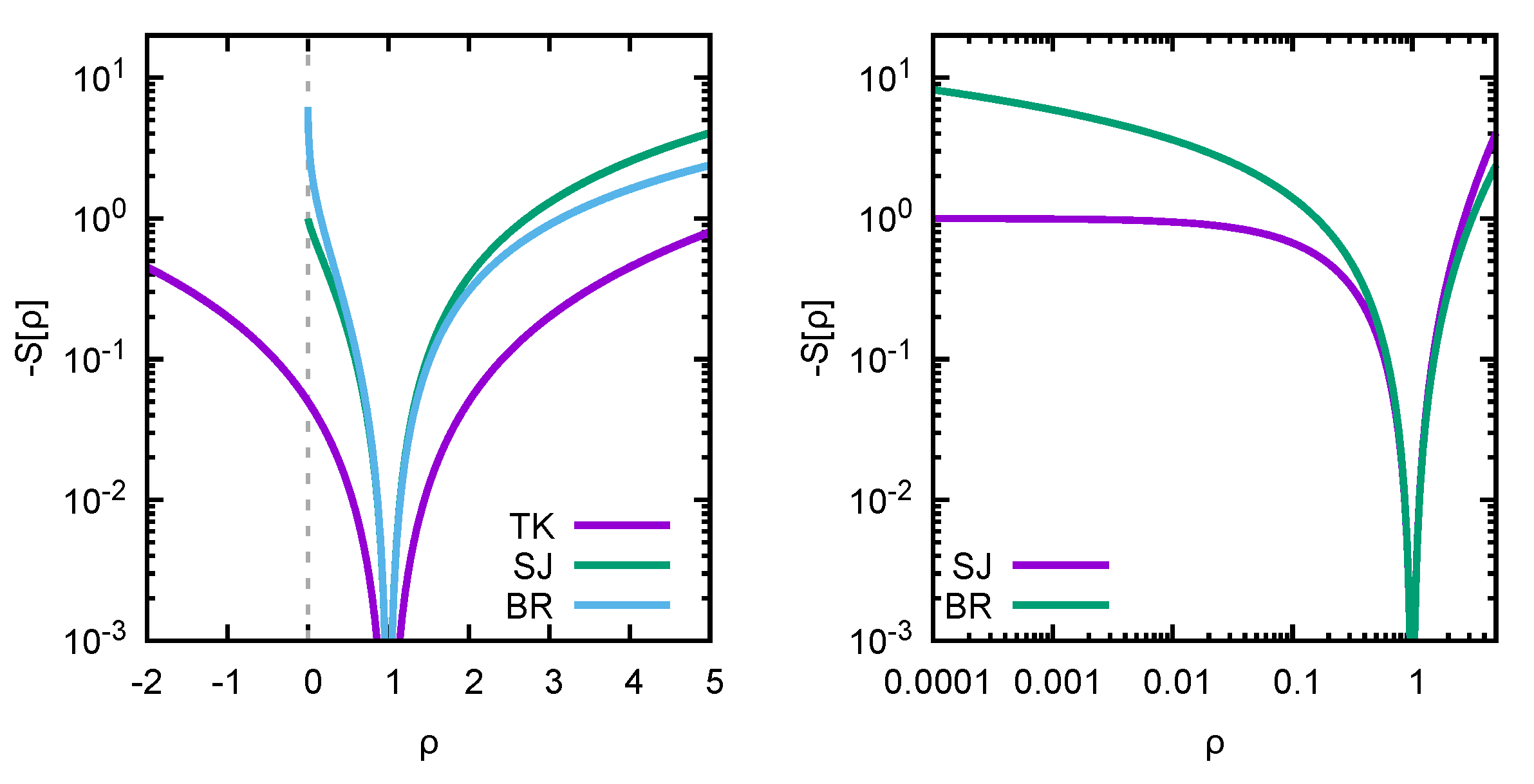
1], it was proposed to combine what we here call the likelihood with a smoothing regulator. Let us have a look at three choices of regulators from the literature: the historic Tikhonov (TK) regulator [
2] (1943–), the Shannon–Jaynes entropy deployed in the Maximum Entropy Method (MEM) [
3,
4] (1986–), and the more recent Bayesian Reconstruction (BR) method [
5] regulator (2013–), respectively,
Both
and
are axiomatically constructed, incorporating the assumption of positivity of the function
. The assumption manifests itself via the presence of a logarithmic term that forces
to be positive-semidefinite in the former and positive-definite in the latter case. It is this logarithm that is responsible for the numerical optimization problem (
6) to become genuinely nonlinear.
Note that all three functions are concave, which (as proven for example in [
6]) guarantees that if an extremum of
exists, it is unique—i.e., within the
dimensional solution space spanned by the discretized parameters
, in the case that a Bayesian solution exists, we will be able to locate it with standard numerical methods in a straightforward fashion.
2. Diagnosis of the Problem in Bryan’s MEM
In this section, we investigate the consequences of the choice of regularization on the determination of the most probable spectrum. Starting point is the fully linear Tikhonov regularization, on which a lot of the intuition in the treatment of inverse problems is built. We then continue to the Maximum Entropy Method, which amounts to a genuinely nonlinear regularization and point out how arguments, which were valid in the linear case, fail in the nonlinear context.
2.1. Tikhonov Regularization
The Tikhonov choice amounts to a Gaussian prior probability, which allows to take on both positive and negative values. The default model denotes the value for , which was most probable before the arrival of the measured data D (e.g., from a previous experiment), and represents our confidence into the prior knowledge (e.g., the uncertainty of the previous experiment).
Since both (
4) and (
7) are at most quadratic in
, taking the derivative in (
6) leads to a set of linear equations that need to be solved to compute the Bayesian optimal solution
. It is this fully linear scenario from which most intuition is derived when it comes to the solution space of the inversion task. Indeed, we are led to the following relations
which can be written solely in terms of linear vector-matrix operations. Note that in this case
contains the vector
in a linear fashion. (
10) invites us to parameterize the function
via its deviation from the default model
and to look for the optimal set of parameters
. Here, we may safely follow Bryan [
7] and investigate the singular values of
with
U being an
special orthogonal matrix,
an
matrix with
nonvanishing diagonal entries, corresponding to the singular values of
and
being an
special orthogonal matrix. We are led to the expression
which tells us that in this case, the solution of the Tikhonov inversion lies in a functional space spanned by the first
columns of the matrix
(usually referred to as the SVD or singular subspace) around the default model
—i.e., we can parameterize
as
The point here is that if we add to this SVD space parametrization any further column of the matrix
, it directly projects into the null space of
K via
. In turn, such a column does not contribute to computing synthetic data via (
2). As was pointed out in [
8], in such a linear scenario, the SVD subspace is indeed all there is. If we add extra columns of
to the parametrization of
, these do not change the likelihood. Thus, the corresponding parameter
of that column is not constrained by data and will come out as zero in the optimization procedure of (
6), as it encodes a deviation from the default model, which is minimized by
.
2.2. Maximum Entropy Method
Now that we have established that in a fully linear context the arguments based on the SVD subspace are indeed justified, let us continue to the Maximum Entropy Method, which deploys the Shannon–Jaynes entropy as regulator.
encodes as prior information, e.g., the positivity of the function
, which manifests itself in the presence of the logarithm in (
8). This logarithm however also entails that we are now dealing with an inherently nonlinear optimization problem in (
6). Carrying out the functional derivative with respect to
on
, we are led to the following relation
As suggested by Bryan [
7], let us introduce the completely general (since
) and nonlinear redefinition of the parameters
Inserting (
15) into (
14), we are led to an expression that is formally quite similar to the result obtained in the Tikhonov case
While at first sight this relation is also amenable to be written as a linear relation for
, it is actually fundamentally different from (
10), since due to its nonlinear nature,
enters
via componentwise exponentiation. It is here, when attempting to make a statement about such a nonlinear relation with the tools of linear algebra, that we run into difficulties. What do I mean by that? Let us push ahead and introduce the SVD decomposition of the transpose Kernel as before,
At first sight, this relation seems to imply that the vector
—which encodes the deviation from the default model (this time multiplicatively)—is restricted to the SVD subspace, spanned by the first
entries of the matrix
. My claim (as put forward most recently in [
9]) is that this conclusion is false, since this linear-algebra argument is not applicable when working with (
16). Let us continue to setup the corresponding SVD parametrization advocated, e.g., in [
8]
In contrast to (
13), the SVD space is not all there is to (
18) (see explicit computations in
Appendix A). This we can see by taking the
column of the matrix
, exponentiating it componentwise, and applying it to the matrix
K. In general, we get
This means that if we add additional columns of the matrix
to the parametrization in (
18), they do not automatically project into the null-space of the Kernel (see the explicit example in
Appendix A of this manuscript) and thus will contribute to the likelihood. In turn, the corresponding parameter
related to that column will not automatically come out to be zero in the minimization procedure (
6). Hence, we cannot a priori disregard its contribution and thus, the contribution of this direction of the search space, which is not part of the SVD subspace. We thus conclude that limiting the solution space in the MEM to the singular subspace amounts to an ad-hoc procedure, motivated by an incorrect application of linear-algebra arguments to a fully nonlinear optimization problem.
A representative example from the literature, where the nonlinear character of the parametrization of
is not taken into account, is the recent [
8] (see Equations (7) and (12) in that manuscript). We emphasize that one does not apply a column of the matrix
itself to the matrix K but the componentwise exponentiation of this column. This operation does not project into the null-space.
In those cases where we have only few pieces of reliable prior information and our datasets are limited, restricting to the SVD subspace may lead to significantly distorted results (as shown explicitly in [
10]). On the other hand, its effect may be mild if the default model already encodes most of the relevant features of the final result and the number of datapoints is large, so that the SVD subspace is large enough to (accidentally) encompass the true Bayesian solution sought after in (
6). Independent of the severity of the problem, the artificial restriction to the SVD subspace in Bryan’s MEM is a source of systematic error, which needs to be accounted for when the MEM is deployed as precision tool for inverse problems.
Being liberated from the SVD subspace does not lead to any conceptual problems either. We have brought to the table
points of data, as well as
points of prior information in the form of the default model
m (as well as its uncertainty
). This is enough information to determine the
parameters
uniquely, as proven in [
6].
Recognizing that linear-algebra arguments fail in the MEM setup also helps us to understand some of the otherwise perplexing results found in the literature. If the singular subspace were all there is to the parametrization of
in (
18), then it would not matter whether we use the first
columns of
or just use the
columns of
directly. Both encode the same target space, the difference being only that the columns of
are orthonormal. However, as was clearly seen in Figure 28 of [
11], using the SVD parametrization or the columns of
leads to significantly different results in the reconstructed features of
. If the MEM were a truly linear problem, these two parameterizations gave exactly the same result. The finding that the results do not agree emphasizes that the MEM inversion is genuinely nonlinear and the restriction to the SVD subspace is ad hoc.
2.3. Numerical Evidence for the Inadequacy of the SVD Subspace
Let us construct an explicit example to illustrate the fact that the solution of the MEM reconstruction may lie outside of the SVD search space. Since Bryan’s derivation of the SVD subspace proceeds independently of the particular form of the kernel K, the provided data D, and the choice of the default model m, we are free to choose them at will. For our example, we consider a transform often encountered among inverse problems related to the physics of strongly correlated quantum systems.
One then has
and we may set
. With
entering simply as scaling factor in (
16), we do not consider it further in the following. Let me emphasize again that the arguments leading to (
16) did not make any reference to the data we wish to reconstruct. Here, we will consider three datapoints that encode a single delta peak at
, embedded in a flat background.
Now, let us discretize the frequency domain between
and
with
points. Together with the choice of
,
, and
, this fully determines the kernel matrix
in (
2). Three different mock functions
are considered, with
,
, and
, the background is assigned the magnitude
(see
Figure 1 left).
Bryan’s argument states that in the presence of three datapoints (see
Figure 1 right), irrespective of the data encoded in those datapoints, the extremum of the posterior must lie in the space spanned by the exponentiation of the three first columns of the matrix
, obtained from the SVD of the transpose kernel
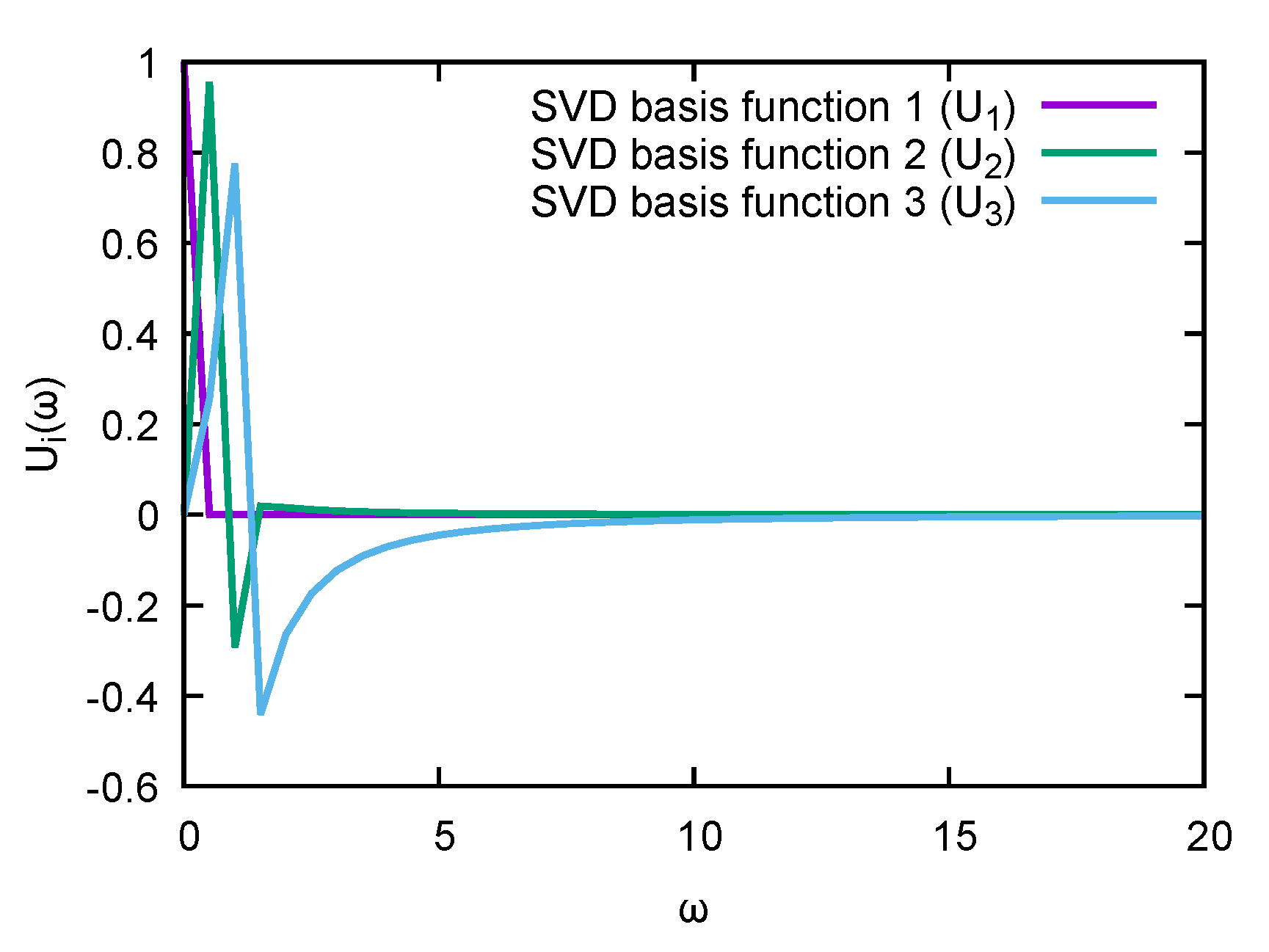
. In
Figure 2, its first three columns are explicitly plotted. Note that while they do show some peaked behavior around the origin, they quickly flatten off above
. From this inspection by eye, it already follows that it will be very difficult to linearly combine
,
, and
into a sharply peaked function, especially for a peak located at
.
Assuming that the data comes with constant relative error
, let us find out how well we can reproduce it within Bryan’s search space. A minimization carried out by Mathematica (see the explicit code in
Appendix B) tells us that
,
, and
—i.e., we clearly see that we are not able to reproduce the provided datapoints well (i.e.,
) and that as the deviation becomes more and more pronounced, the higher the delta peak is positioned along
. In the full search space on the other hand, we can always find a set of
’s which bring the likelihood as close to zero as desired.
Minimizing the likelihood of course is not the whole story in a Bayesian analysis, which is why we have to take a look at the contributions from the regulator term . Remember that by definition, it is negative. We find that for all three mock functions , Bryan’s best fit of the likelihood leads to values of . On the other hand, a value of is obtained in the full search space for the parameter set which contains only one entry that is unity and all other entries being set to the background at .
From the above inspection of the extremum of and the associated value of inside and outside of Bryan’s search space, we arrive at the following: Due to the very limited structure present in the SVD basis functions , , and , it is in general not possible to obtain a good reconstruction of the input data. This in turn leads to a large minimal value of accessible within the SVD subspace. Due to the fact that cannot compensate for a large value of , we have constructed an explicit example where at least one set of ’s (the one that brings close to zero in the full search space) leads to a smaller value of and thus to a larger posterior probability than any of the ’s within the SVD subspace.
In other words, we have constructed a concrete example in which the MEM solution, given by the global extremum of the posterior, is not contained in the SVD subspace.
4. Summary and Conclusions
We have critically assessed in this paper the arguments underlying Bryan’s MEM, which we show to be flawed as they resort to methods of linear algebra when treating an inherently nonlinear optimization problem. Therefore, we conclude that even though the individual steps in the derivation of the SVD subspace are all correct, they do not apply to the problem at hand and their conclusions can be disproved with a direct counterexample. The counterexample we provided utilizes the fact that the componentwise exponentiated columns of the matrix do not project into the null-space of the Kernel when computing synthetic data. After establishing the fact that the restriction to the SVD subspace is an ad-hoc procedure, we discussed possible ways to overcome it, suggesting either to systematically extend the search space within the MEM or abandon the MEM in favor of one of the many modern Bayesian approaches developed over the past two decades.
In our ongoing work to improve methods for the Bayesian treatment of inverse problems, we focus on the development of more specific regulators. So far, the methods described above only make reference to very generic properties of the quantity , such as smoothness and positivity. As a specific example, in the study of spectral functions in strongly-correlated quantum systems, the underlying first principles theory provides extra domain knowledge about admissible structures in that so far is not systematically exploited. A further focus of our work is the extension of the separable regulators discussed in this work to fully correlated prior distributions that exploit cross-correlation between the individual parameters .