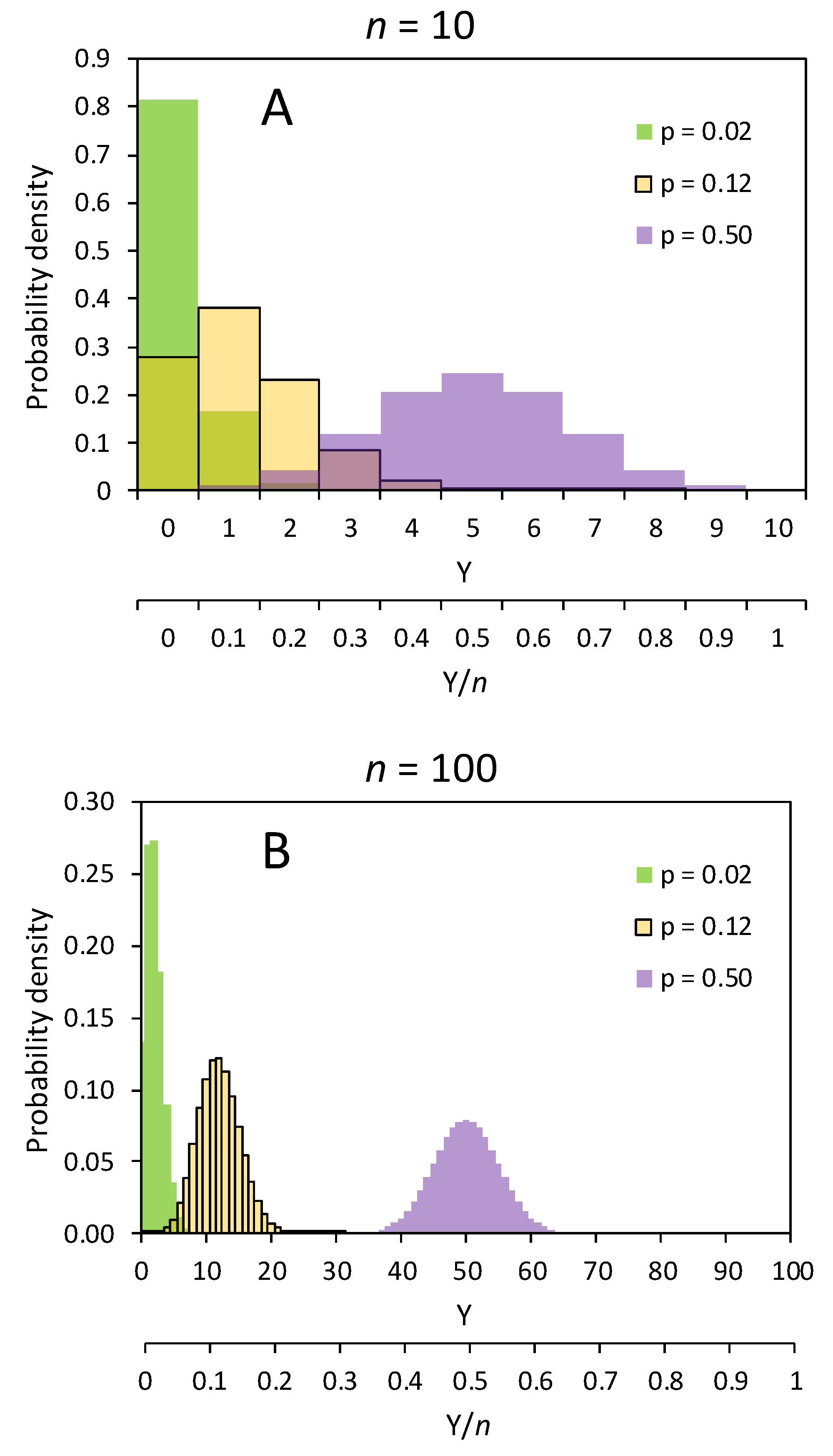2.1. Example 1: Hierarchical Design with Two-Level Nesting for FGP
In this first example, FGP data from Gianinetti et al. [
37] showing the protective effect of a red coat (enriched in reddish flavonoid compounds) on rice kernels, as measured in terms of germination, are analyzed. The original dataset is given in
Annex SI, and the detailed statistical analysis is commented on in
Annex SII.
Figure 2A displays the distribution of the data according to the combination of two fixed factors, each with two levels: Red/white kernel color (a genetic trait characterizing the grain type), and presence/absence of
Epicoccum nigrum in the plate, as pre-established infecting agent. Each of the two kernel colors was represented by three cultivars; hence, the cultivar effect was nested within kernel color. At a hierarchically lower level, plates were nested within each combination of the two experimental factors: Cultivar and presence/absence of
E. nigrum. In mixed models the variances are estimated hierarchically [
6], separating the processes that generate between-groups variation in means (i.e., representing the effects occurring among the combinations of the levels of the fixed factors) from variation within groups (i.e., within-group variances of random factors). Plates are a random factor whose levels, i.e., the individual plates, are always nested within the combination of all the other factors. In this sense, they are different from typical blocks for which both between-block and within-block factors are commonly envisioned (although within-plate effects are envisaged for repeated measures studies). Thus, germination tests typically have a hierarchical design with plates as the lowest-rank nested random factor.
In this example, the cultivar could be considered either a fixed or random factor. Although in the crop sciences the cultivar is an established genotype and is, therefore, usually considered a fixed factor, in the present case the effect that is under investigation is the genetically determined color of the caryopsis, a chief genetic trait that is modeled as fixed factor, whereas the diverse genotypes studied within each grain type (red versus white) were considered as a random genetic difference around the chief color effect. This allows one to make generalizations about the findings since, when a factor is considered random, its levels in the experiment are considered a random sample drawn from a theoretical population of levels [
6]. Thereby, conclusions about any one specific level are not the main concern, but inference about the whole population can be drawn; that is, the conclusions based on a sample of random levels can be extended to the whole theoretical population of levels [
5]. The comparison between the studied red and white kernelled cultivars is, thus, meant to be a general expectation for the response of red and white kernelled cultivars. In
Annex SII, it is shown that changing from considering the cultivar as a fixed factor to a random factor causes a noticeable plunge in the significance of the effect of kernel color, thus, the generalization has a price. In fact, the cultivar variance is then used in the
F test of grain type (red or white). For proper inference, the significance of fixed effects must indeed be tested at the right level of hierarchical models, the one that really affects the results [
5,
6].
The experimental design, thus, is hierarchical, with two levels of nesting corresponding to the two random factors. The variances of the data within each of the four combinations of the two grain colors and the presence/absence of
E. nigrum are largely unequal (
Figure 2A), and, in fact, these data are heteroskedastic and non-Gaussian (
Annex SII). The GLIMMIX procedure accounts for these features of binomial data, and it provides fit statistics that can be used for comparisons among models (at least under some conditions), as well as the over-dispersion parameter, which is useful to evaluate the fit of the model to the data [
22]. As previously seen, over-dispersion measures the presence of additional variance with respect to the binomial one. In fact, over-dispersion occurs when data appear more dispersed than is expected for distributions that have mean-variance relationship, like the binomial [
3,
35]. This might happen because the observed distribution is a mixture of different distributions, where the binomial sampling distribution is superimposed on another variance distribution, typically Gaussian, due to some unmodeled variable [
22]. For germination data, over-dispersion can be due to a mis-specified, or incomplete, model, a case that includes an incorrect specification of the covariance structure [
3]; or to heterogeneity of seeds beyond the random variability expected for a single seed population [
7]. In the first case, often some source of random variation is not accounted for, or an insufficient account of a positive correlation among some observations is provided. Indeed, if clustering of seeds into plates is not considered in the model, noticeable over-dispersion is observed (
Annex SII). It is worth noting that, in binomial and Poisson GzLMMs (which do not have a residual dispersion parameter), type I errors can be inflated when over-dispersion is due to omitting essential random factors that should be used in correct
F tests [
16,
22] (
Annex SII).
Although the natural link function for binomial data is the logit [
9,
35], use of the probit link function to linearize the germination response (which is the inverse of the cumulative distribution function of the standard normal distribution) is advocated here. In fact, probit models are best suited for threshold processes, where the linear response (on the linked scale) represents an unobservable normally distributed random variable such that, when it is above or below some threshold, we observe either a 0 (“failure”) or 1 (“success”), thereby resulting in a binomially distributed observed response [
3,
16]. This is exactly what happens in the transition from dormancy to germination [
27].
A relevant problem of using GzLMMs is that, when a random effect is present, a pseudo-likelihood is used as default estimation technique, but, unfortunately, pseudo-likelihoods cannot be compared across different models [
22]. This means that we cannot rely on fit statistics to compare different models, and that in several cases even statistical tests aimed at evaluating the G-side and R-side structures are not exact [
22], though they provide rough tests that can give some useful hint when large differences, or highly significant effects, are found (
Annex SII) [
35]. As previously mentioned, when only G-side random factors are present, integral approximations to true likelihood can be employed to overcome the limitations of pseudo-likelihood [
22]. However, only small differences were found for inference from these germination data whether the Laplace integral approximation was used or not (
Annex SII). Hence, though advisable, an integral approximation is not advocated here above the default pseudo-likelihood; at least if the data are FGP not too close to 0 or 1, the experiment design is well defined, and no comparison of different models is necessary. It is immediately evident that this holds true chiefly for germination tests, but not for observational studies, where model comparison is typically used to select relevant factors. The Laplace integral approximation is, thus, almost always mandatory in the latter case.
Modeling of the R-side structure prevents application of the integral approximations [
22]. This holds true both for marginal models, where only the R-side structure is considered, as well as for quasi-marginal models, in which both G-side an R-side effects are modeled [
22]. Nonetheless, a quasi-marginal model for FGP leads to very close inference with respect to a conditional model, notwithstanding two-levels nesting of random factors (
Annex SII). This is because the between-plates variance is small, and therefore, it does not alter the binomial distribution very much, whereas a large random variance due to the cultivar effect (nested within grain color type) is separately modeled as a random factor, so that the quasi-marginal distribution is conditional to this non-negligible Gaussian effect.
It, thus, appears that FGP data from germination tests can be analyzed with default pseudo-likelihoods, provided that any random factor contributing a large variance component is modeled on the G-side (
Annex SII) so that the marginal, or quasi-marginal, distribution is still approximately binomial [
16,
22] and that the statistical model correctly reflects the experimental design [
9]. Although either the conditional or quasi-marginal model can be used for these data, in general, directly modeling the plate effect on the G-side may be a sensible choice. In this example, the cultivar effect must be modeled as a random factor also to ensure the correct
F test. For FGP data, a conditional model is probably the first choice as it exploits the basic features of GzLMMs.
Figure 2B displays the expected means and their confidence interval for the conditional model, as well as their comparison (at
p ≤ 0.05).
It should be noted that the comparison between cell means is of interest here, not the comparison between the means of the main effects, since the interaction between main effects is significant and nonnegligible (
Annex SII). In fact, in the presence of significant and nonnegligible interaction, main effects ought not to be of interest [
3,
15]. That the interaction also needs to be nonnegligible is because statistically significant interactions of little practical consequence can and do happen, but they do not preclude assessing main effects [
3]. To obtain an unbiased estimate of the interaction effect, the interaction should always be assessed first; for this reason, the type III test of fixed effects is usually preferred [
3].
It also worth mentioning that, for multiple comparisons of means, plots showing differences between mean pairs (and the statistical significance for their values being different from zero) are sometimes preferred to plots showing means (and using letters to show significant and non-significant differences among them) because the latter might induce to consider significance as a black-or-white concept [
38]. In fact, confidence intervals for the former kind of plot can be directly interpreted as showing the range within which the real effect size (i.e., the supposedly true difference) is likely to lie, and therefore, displaying the magnitude of the significance of the difference in response between treatment levels [
38]. Thus, in place of showing a plot with group means and their 95% confidence intervals (like in
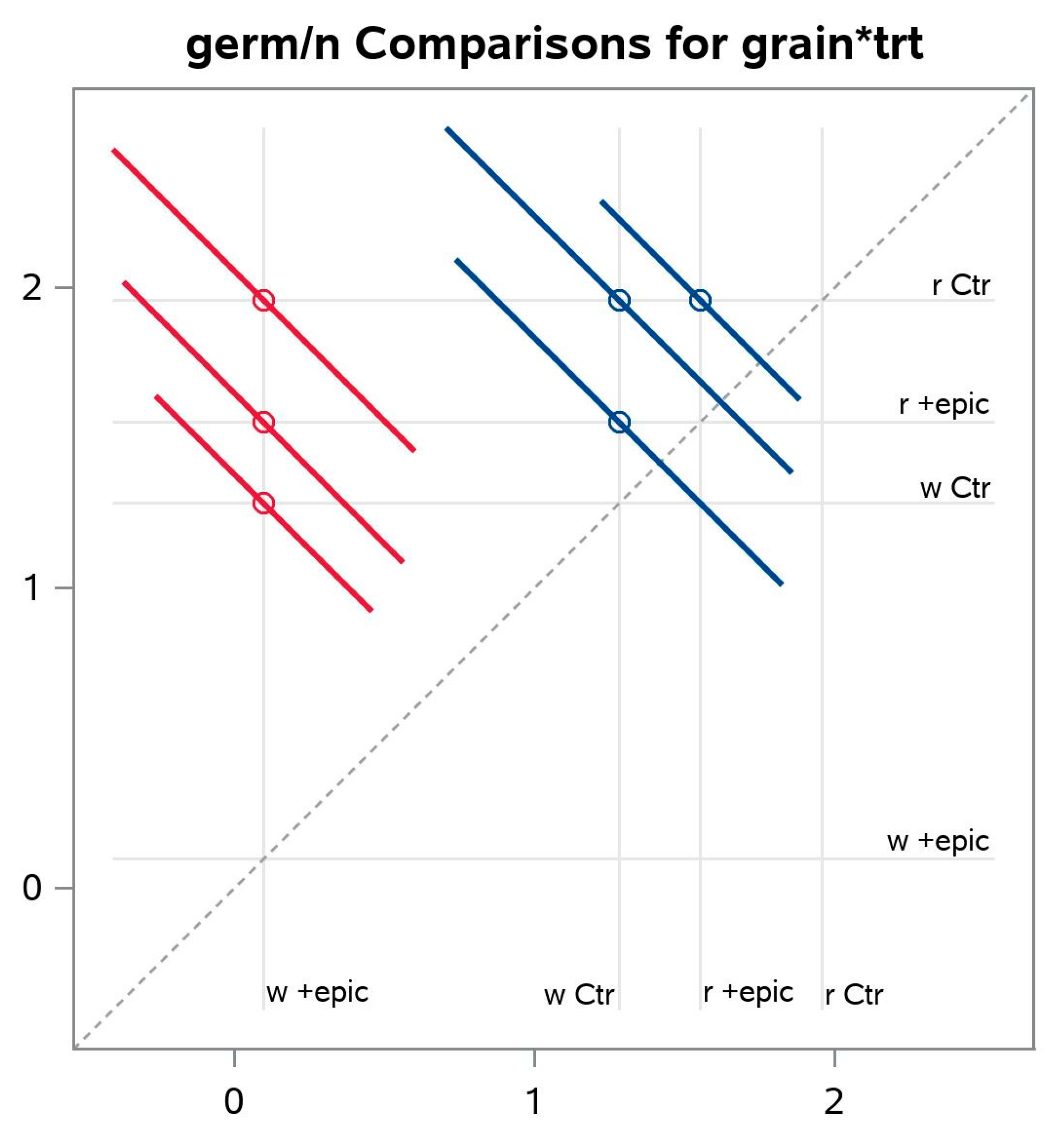
Figure 2B), and then using letters (or asterisks) to show significant and non-significant differences, a diffogram (also called a pairwise difference plot or mean-mean scatter diagram), or a similar plot, can be used to directly, and quantitatively, indicate whether the pairwise differences between means of groups are statistically significant (
Figure 3) [
39]. In a diffogram, the horizontal and vertical axes of the plot are equal and are drawn in least squares means units (on the linear scale; that is, in probit units in the present case). Horizontal and vertical reference lines are placed in correspondence of the means of the groups. Whenever a mean is compared with itself, the corresponding horizontal and vertical grid lines cross along a diagonal reference line that has unit slope. For each comparison, apart from self-matching crosses, a colored line segment, centered at the intersection of horizontal and vertical reference lines for the least square means in the pair, is drawn (by SAS default, only those above the diagonal reference line are considered). They correspond to the
m(
m–1)/2 pairwise comparisons of means for
m groups and display their significance. The length of each segment (as projected on one or the other axis, since it has a 45-degree inclination) corresponds to the width of a confidence interval for the least squares mean difference between the means (the 95% confidence interval is represented by default). The confidence interval for the difference crosses the line of equality when the interval contains 0 (corresponding to the reference diagonal). In this way, if a line segment intersects the diagonal reference line, then the corresponding group means are not significantly different. Segments that fail to cross the diagonal reference line with unit slope correspond to significant least squares mean differences. The wider the distance between the confidence interval of the difference (the line segment) and the diagonal, the stronger the significance. Although a diffogram offers a better statistical representation for pairwise comparisons of means, as it illustrates how significance is conventionally translated into a categorical yes-or-no decision though it really represents a graded evidence for the falsification (i.e., disproval) of the null hypothesis [
38], mean plots may be easier to understand, particularly in the case of longitudinal data.
Finally, diagnostic plots can be used to evaluate fitting problems of the statistical model, but judgments based on these plots need to consider the peculiarities of binomial data (
Annex SII).
2.2. Example 2: A Longitudinal Study of Rice Germination Progress
Longitudinal (through time) data for rice germination following seed soaking at three temperatures (
Figure 4A) [
40] were analyzed. The original dataset is given in
Annex SIII, and the detailed statistical analysis is commented on in
Annex SIV. These data can be analyzed with MANOVA (
Annex SIV), but GzLMMs are more informative and are not restricted by assumptions of multivariate normality and homogeneity of variances and covariances [
3,
5,
9]. The two analyses also require different arrangements of the data (
Annex SIII). GzLMMs consider plates as subjects of repeated measures through time and, thus, separately estimate the between-plates effects (which can be either fixed or random, like in the analysis of FGP), and the within-plate effect (which includes the fixed effect of time, as well as the random effect of serial correlation [
5]).
Even in this example, as observed for FGP data, the effect of plates is small (almost negligible for longitudinal data because of stronger BLUP shrinkage;
Annex SIV). Thence, the conditional model solutions approximately match with estimates obtained by the marginal model, and thus, when properly outlined, the conditional and marginal models provide closely similar inference (
Annex SIV). The marginal model appears slightly better than the quasi-marginal model only because the germination curves are very similar, and therefore, they suit a longitudinal covariance structure, the first-order ante-dependence structure (ANTE(1)), that may give convergence problems in quasi-marginal models and is, therefore, better modeled with a marginal model [
22], though it converges to a congruent solution even for the quasi-marginal model in this instance. Agreement of solutions between conditional and marginal, or quasi-marginal, approaches is expected to be a general feature of usual germination tests (chiefly because of a tiny plate effect), which is very interesting because it makes these different GzLMM approaches practically inter-exchangeable.
For longitudinal (aka repeated measure) data, the use of an integral approximation, like the Laplace method [
22], that approximates the marginal log likelihood of the GzLMM by integrating out the random effects from the joint distribution, is of much greater concern than it is for end-of-test (FGP) data because it can improve convergence of estimates (
Annex SIV). Furthermore, an integral approximation is recommended for the initial evaluation of the model since it allows the use of true likelihood, and thus, it provides unbiased estimations for over-dispersion and diagnostic tests of the variance/covariance structure [
22].
As general advice, indeed, conditional models (aka subject-specific models, where plates are the subjects) are recommended for testing diverse variance/covariance structures on the G-side with Laplace approximation and then choosing the best structure based on the smaller value of the Akaike Information Criterion with small-sample Correction (AICC) goodness-of-fit statistic [
16]. Thereafter, the best fitting model should be run without the integral approximation to allow for the use of the Kenward–Roger method for the adjustment of degrees of freedoms in
F tests and of confidence intervals, available with pseudo-likelihood only [
22]. This improves the statistical robustness of statistical inference, especially for small experiments [
16,
22], such as germination tests.
Unfortunately, owing to the hierarchical structure typical of the experimental designs of germination tests, where plates represent subjects nested within a fixed-effects framework, computational problems can arise because nesting corresponds to an entirely unbalanced interaction and the nested plate effect is thus completely confounded with its plate x treatment interaction [
5]. As this interaction is embedded into the covariance structure on the G-side, troubles can occur for estimation convergence when modeling the longitudinal structure on the G-side too (
Annex SIV).
Thus, marginal (that is, with R-side random effects only) and quasi-marginal (with both G-side and R-side random effects) models ensure better convergence since, on the R-side, the plate × treatment interaction is not embedded into typical covariance structures like ANTE(1) and the first-order autoregressive structure (AR(1)) [
22], and serial correlation is thereby modeled separately from random factors (
Annex SIV). The R matrix could also account for the between-plates random effect, although only indirectly [
22]. However, as the exact covariance structure of the data is not known, it is recommended that marginal models use an ‘empirical’ procedure, or sandwich estimator, which is more robust to misspecifications of the covariance structure; the Morel–Bokossa–Neerchal (MBN) correction is advised, specifically for small experiments [
22]. The ‘empirical’ option is the preferred alternative to the use of Kenward–Roger degrees of freedom in R-side modeling [
22].
On the other hand, plates represent a random factor, which can be directly modeled by the G matrix. Thus, serial correlation and the plate random factor can be separately accounted for by the R and G matrices, respectively, in a quasi-marginal model [
22]. In the present example, however, the marginal model performs slightly better than the quasi-marginal model because, as already mentioned, the ANTE(1) structure better suits the similar germination time-courses, and it is preferentially adopted for marginal rather than quasi-marginal models. The least square means with interval confidence and inference about means comparison are displayed in
Figure 4B for the marginal model. Similar inference was obtained with the corresponding conditional model as well as with MANOVA (
Annex SIV).
The fact that, when each one is properly formulated, the three kinds of GzLMM provide matching inferences (
Annex SIV), indicates that the specific issues and restrictions that apply to each one do not affect germination tests. As the experimental designs of germination tests are quite easy to identify, the lack of fit statistics is usually not a problem. Besides, although analysis of the repeated measures GzLMM requires determining which of the plausible covariance structures best fits the data, and this is typically done by computing fit criteria, like the AICC [
9,
16], the vast majority of data fit the split-plot-in-time, AR(1), or ANTE(1) structures [
9]. In
Annex SIV it is shown that a marginal model with ANTE(1) structure should be used when the progress curves are not sharply different (
Figure 4B) since it better suits if germination curves display an overall similar shape. A quasi-marginal model with AR(1) (with groups) + random intercept structure [
3,
35] ought instead to be preferred when the progress curves are of widely different shapes, like when seed samples with diverse dormancy intensities, or different speed of germination, are compared, because of greater flexibility with respect to the widely different shapes of the germination time-courses. In this example, the former model is indeed preferred because of the similar curves, and it provides close inference to the conditional model (
Annex SIV) since both the between-plates effect and serial correlation are small.
Germination time-courses are commonly characterized by an initial lag stage followed by a burst of germination that, more or less quickly, finally approaches a plateau [
4]. Since, in GzLMMs, means are analyzed on the linear scale, where a mean of zero cannot be defined, zero means recorded during the lag stage are a problem (
Annex SIV). As the initial lag time represents the time required for seed imbibition and metabolism re-activation during which the seeds cannot yet achieve visible germination [
1,
2], this initial stage is evidently distinct from the actual germination progress that is under statistical examination. Thus, removing these data from the dataset, or just excluding this non-germinative stage from the analysis, solves this trouble (
Annex SIV;
Figure 4B).
Notice that, in GzLMMs, though means are modeled on the linked scale, where means of zero are not allowed, the single observations are modeled on the data scale, where zeros are not a problem, at least when true likelihood is used. When pseudo-likelihood is used, shrinkage of BLUPs of random effects toward their non-zero mean [
22,
35] can still allow model optimization in the presence of some zero data, though an integral approximation provides much better estimations of the standard errors (
Annex SIV). This is particularly evident for germination tests that utilize a small number of plates because the paucity of within-group information to estimate the mean is counteracted by the model using data from other groups (that is, levels of the random factor, i.e., plates, from other combinations of fixed factors) to improve the precision of the estimate [
6], at least for groups modeled as having the same variance. This further supports the use of the Laplace approximation for longitudinal data when some zero values are present. In general, however, models with correlated errors and crossed random effects, for which the joint distribution is difficult to ascertain, are more easily optimized by means of linearization methods based on pseudo-likelihood [
16,
22].
Although time is a continuous variable, it is usually dealt with as a categorical variable, as the germination progress is not linear to time, even on the linked scale (
Annex SIV). Time can be modeled as a continuous variable by, for example, introducing one, or more, suitable polynomial/logarithmic/reciprocal term(s) that linearize(s) the relationship. A possible solution in this sense is the use of splines (
Annex SIV). However, no advantage was apparent when the germination time-courses were modeled with splines (
Annex SIV). Moreover, as splines are based on empirical polynomials, the risk of unwanted oscillations exists if a time-course shows stairsteps. There is, thus, not much reason to advise the use of splines in this context.
2.3. Example 3: A Longitudinal Study of the Germination Progress for Three Herbs
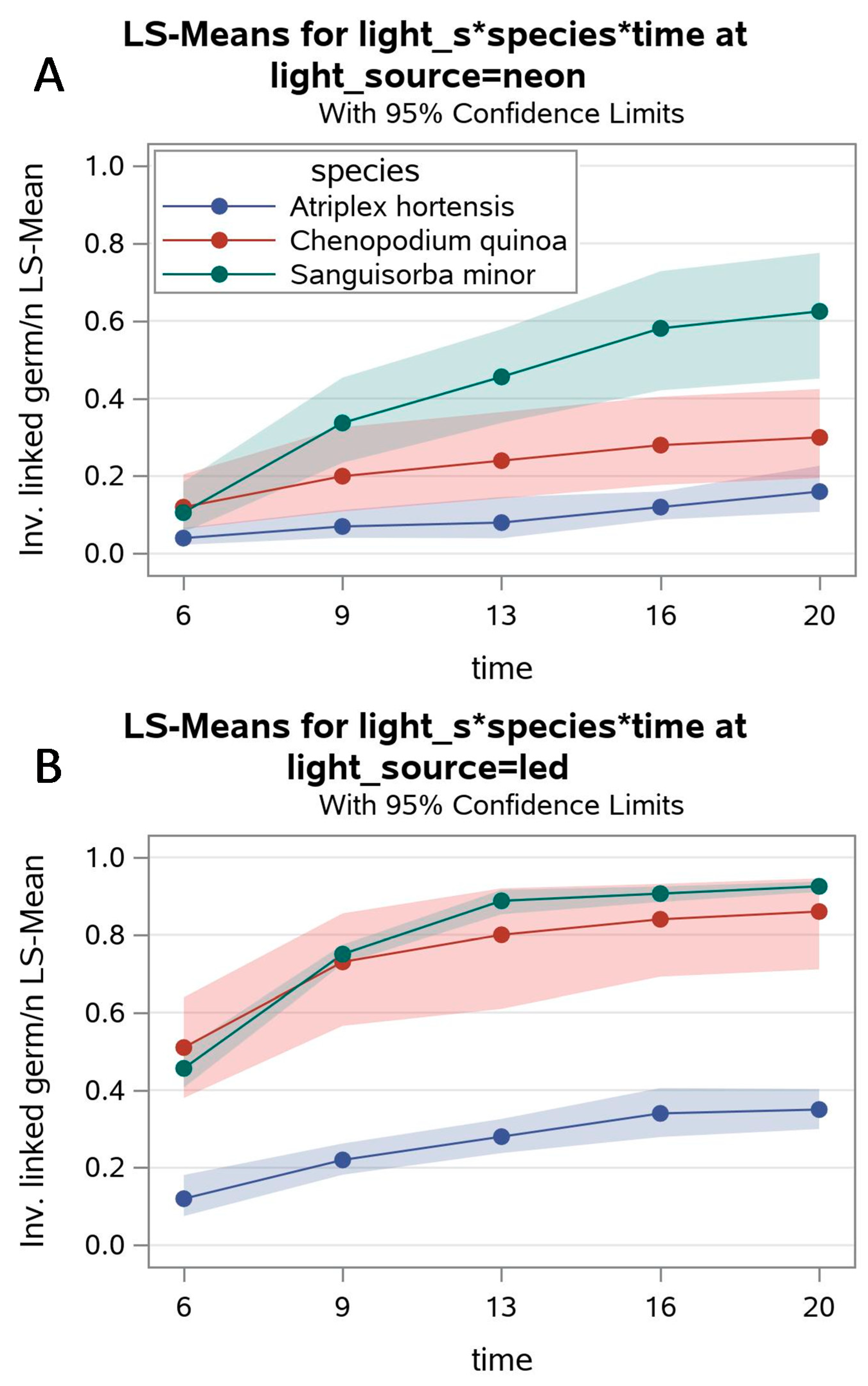
The cumulative germination of three herb species through time in response to two diverse light sources (
Figure 5) [
41] was analyzed. The dataset is given in
Annex SV, and the statistical analysis is commented on in
Annex SVI. Although only part of the germination progress was recorded (
Figure 5) the time-courses can still be properly analyzed for inference; in fact, as little as two timepoints might be enough for some specific testing applications if the observations are carefully chosen as representative of the time-course [
42]. Inference can then be obtained about the significance of the effects of the factors (
Annex SVI). Means and confidence intervals are shown in
Figure 6. Results of the overall (i.e., across the two light sources) mean separation test (with SMM multiple comparison adjustment) are not shown.
Notice that a small separation between the confidence interval bands, as shown in
Figure 6, does not guarantee that the corresponding means are significantly different [
43]. In fact, in the present instance, the mean separation test is more restrictive (i.e., less prone to declare a difference to be significant) than such an empirical criterion (and the former is, indeed, the correct way to infer statistically significant differences). Analogously, overlapping of the confidence interval bands (
Figure 6) is not, in general, a correct way to infer that statistical differences are not significant [
43], even though it contingently holds true in the present instance.
These germination time-courses are widely divergent (
Figure 5), and thus, the quasi-marginal model with AR(1) covariance structure was used to analyze these data (
Annex SVI). When the germination time-courses are largely diverse, indeed, the ANTE(1) structure can even lead to convergence failure. Although the AR(1) covariance structure assumes a constant correlation between adjacent within-subject errors, which is usually intended as requiring equal time spacings [
35], longitudinal changes in germination percentage are not linear through time, even on the linked scale, and time intervals are often chosen (and should always be chosen) to match with the expected intensity of changes, roughly favoring the adoption of a single autocorrelation parameter throughout the whole germination time-course (
Annex SIV). The empirical ‘sandwich’ MBN estimator helps increasing the robustness of this structure for small-size experiments [
22]. If geometric spacing is used (e.g., time 1, 2, 4, 8, and so on), the logarithm of time can be used to make these observations appear to be equally spaced [
3].
Although there are only two replicate plates, the standard errors are relatively small because of a very small variance of the random plate effect, as usual (
Annex SVI). Indeed, plates are just clusters of seeds and, therefore, represent binomial samples rather than individual subjects that are expected to diverge even noticeably in the studied response, in terms of both random deviations from the intercept (i.e., base differences) as well as of slopes (i.e., real subjects can display individual divergences in the linear response, modeled as subject x treatment random interactions [
3,
22]). It can also be worth noticing that in longitudinal studies the plate effect is typically smaller with respect to FGP data. This is because of greater BLUP shrinkage due to the detection of the within-plate longitudinal stochastic variance component that is consequently removed from the overall observed variability among plates for the computation of the between-plates variance (
Annex SIV) [
35].
Quasi-marginal GzLMMs appear to be particularly suitable for longitudinal germination tests because of quick and usually smooth estimation convergence (
Annexes IV and VI). As previously mentioned, serial correlation among the observations from the same subject (here, plate) is a form of data clustering that extends through time the effect of clustering seeds into plates, and as such, reduces the observed within-plate variance of the repeated measures, with respect to independent measurements, correspondingly incrementing the apparent between-plates variability, and thereby increasing over-dispersion. Thus, between-plates random differences (additional to the binomial sampling variance) and serial correlation of observations on the same plate represent two forms of over-dispersion that can be interchangeably dealt with either as a random factor (on the G-side) or in terms of the variance/covariance structure of the error terms (on the R-side). Keeping them separate in quasi-marginal models allows one to deal with each random effect with its own most suitable matrix, thereby avoiding potential convergence issues due to stochastic preponderance of one or the other effect when both are computed in the same matrix, which can lead to boundary estimation troubles and failure of model optimization (see
Annex SIV). Thus, for germination data, the G matrix ought to be typically used to model the variance of the between-subjects factors, whereas the covariance structure of the repeated measures model, i.e., the serial correlation of the within-subject error terms, is more easily modeled with the R matrix. Quasi-marginal models can, therefore, be preferred for the analysis of longitudinal data in germination tests.
2.4. Example 4: Germination Indices from the Longitudinal Study of Rice Germination Progress
Germination indices were computed from data in
Annex SIII (reported from [
40]) for cumulative germination of rice following seed soaking at three temperatures. Three indices were calculated [
1]: the MGT, the MGR, and the coefficient of uniformity of germination (CUG). The dataset is given in
Annex SVII, and the statistical analysis is commented on in
Annex SVIII. Germination indices do not have a binomial distribution, but they can have heterogeneous variances, and this can be managed by the GzLMM procedure using the default Gaussian distribution. Although a test for heteroskedasticity supports homogeneity of variances in this instance (as is expected, since the three germination curves in
Figure 2 are quite similar) so that statistical analysis with GLMs is adequate (
Annex SVIII), further analysis is considered for the CUG to illustrate the use of the GLIMMIX procedure in case of heteroskedastic data with a Gaussian distribution. The CUG also seems more sensitive to stochastic variations of the germination progress data than the MGT and the MGR (
Annex SVIII;
Figure 7A).
In
Annex SVIII, it is shown that using a conditional model can cause some trouble because of the hierarchical structure of germination tests, where plates are a random factor nested within combinations of fixed effects. As already said, nesting confounds the effect of the nested factor with the effect of its interaction with the fixed factor (temperature, in this case). For a Gaussian response, however, the random interaction cannot appear in the model because it is confounded with the residual variance [
16]. Under the assumption of data normality, in fact, the variance of the interaction between the random and fixed factors represents the residual variance that is used in the denominator of the
F test for the fixed factor [
5]. Hence, modeling the plate effect as a random factor may be problematic because it is nested, and the response is Gaussian; thus, the test of significance can incur problems. Although the integral approximation (which is anyway not recommended for Gaussian data [
3]) allows using the BLUP shrinkage to provide a residual variance that allows analysis, a conditional model is indeed at the boundaries of estimability for these Gaussian data owing to over-specification (
Annex SVIII).
On the other hand, using a marginal model, that is, modeling the plate effect indirectly in terms of correlation of residuals, overcomes this over-specification trouble since the residual variance is left out from the default variance/covariance structure in the R-side model (
Annex SVIII). Thus, marginal models can be preferred for the analysis of germination indices because a conditional model can incur over-specification for Gaussian data, a consequence of the fact that plates are replicates nested within combinations of treatments rather than true blocks (which are replicates of the whole set of experimental contrasts).
Figure 7B shows the results of the statistical analysis based on the marginal model. It is immediately apparent that the means at 30 and 40 °C are statistically different even though their 95% confidence intervals overlap. In fact, it is the confidence interval of the difference between the means of two groups that dictates whether the means are significantly different or not (not the overlap, or lack thereof, between the confidence intervals of the two means), depending on whether or not it spans over zero (that is, the difference cannot be declared to be significantly different from zero). Although not necessary, at least in this case, a diffogram would provide a clearer representation of this statistical issue.