Database for Research Projects to Solve the Inverse Heat Conduction Problem
Abstract
1. Summary
- It is necessary to construct a model for building potential HTC series.
- The temperature history for a given HTC can be generated by a cooling simulation process, which is very time consuming in the case of millions of inputs.
2. Data Description
2.1. Heat Transfer Coefficient File
- All values are encoded as floats, even though some of them are integers (number of control points).
- The number of control points is always 5.
- The value of is 10 °C. Therefore, the number of HTC values is 86, according to temperatures 0 °C, 10 °C, 20 °C, …, 850 °C.
- The size of one header record is 64 bytes.
- The size of one data record is 344 bytes.
- Training set: The training database, containing 1,000,000 record pairs
- –
- “train_htc_header.bin”: The header part of the training dataset ( megabytes)
- –
- “train_htc_data.bin”: The data part of the training dataset ( megabytes)
- Validation set: The validation database, containing 100,000 record pairs
- –
- “valid_htc_header.bin”: The header part of the validation dataset ( megabytes)
- –
- “valid_htc_data.bin”: The data part of the validation dataset ( megabytes)
- Test set: The test database, containing 100,000 record pairs
- –
- “test_htc_header.bin”: The header part of the test dataset ( megabytes)
- –
- “test_htc_data.bin”: The data part of the test dataset ( megabytes)
2.2. Temperature File
- The value of is s. Therefore, the number of temperature values is 121, according to time s, 1 s, …, 60 s.
- The size of one data record is 480 bytes.
- Training set: The training database, containing 1,000,000 records
- –
- “train_temp_data.bin”: The temperature data of the training dataset
- Validation set: The validation database, containing 100,000 records
- –
- “valid_temp_data.bin”: The temperature data of the validation dataset
- Test set: The test database, containing 100,000 records
- –
- “test_temp_data.bin”: The temperature data of the test dataset
3. Methods
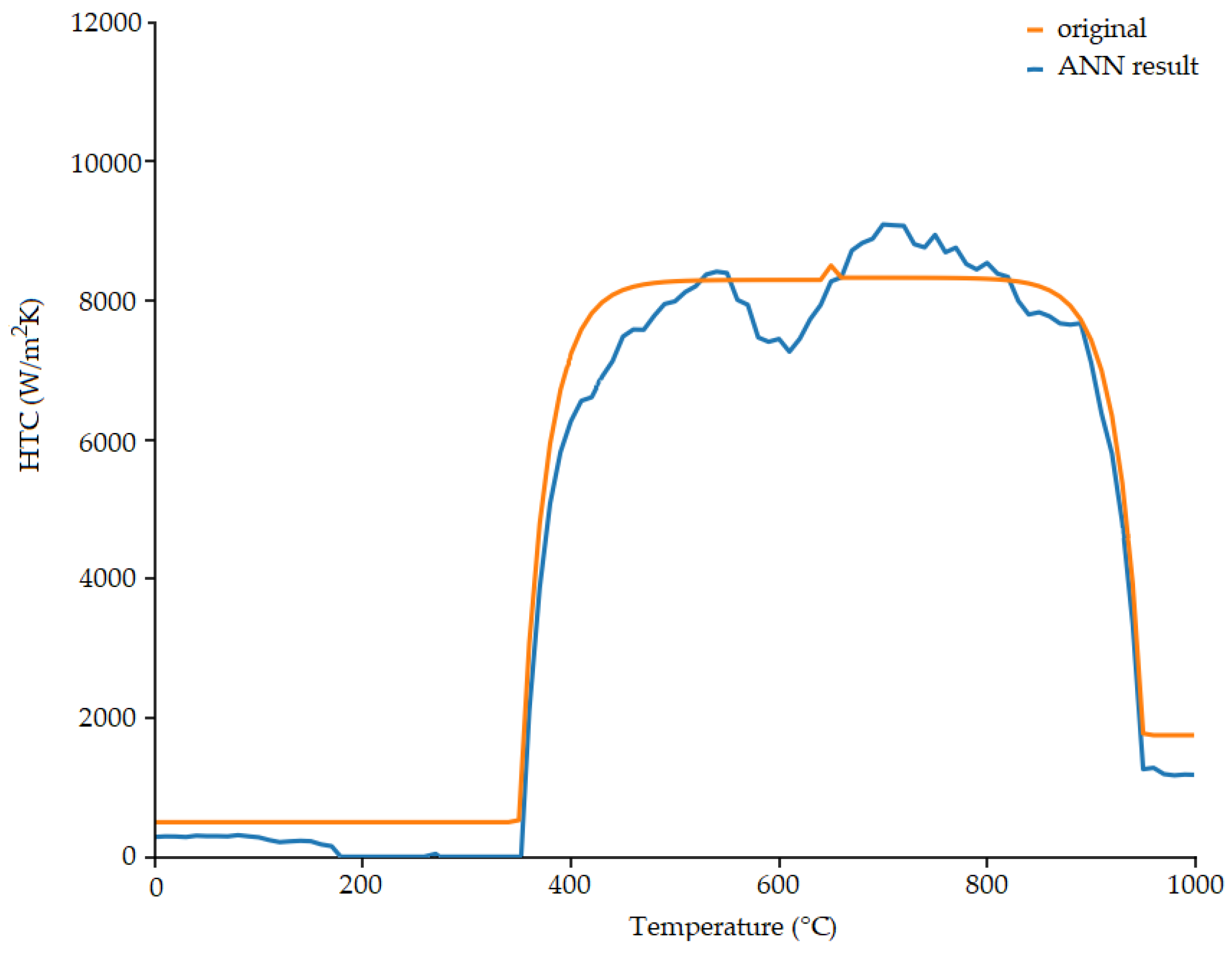
3.1. Model for HTC Generation
3.2. Temperature History Generation
4. Usage Notes
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mackenzie, D.S. Advances in Quenching A Discussion of Present and Future Technologies. In Proceedings of the 22nd Heat Treating Society Conference and the 2nd International Suface Engineering Congress, Indianapolis, Indiana, 12–17 September 2003; pp. 21–28. [Google Scholar]
- Alifanov, O.M. Inverse Heat Transfer Problems; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Das, R. A simplex search method for a conductive–convective fin with variable conductivity. Int. J. Heat Mass Transf. 2011, 54, 5001–5009. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Colaço, M.J.; Orlande, H.R.B.; Dulikravich, G.S. Inverse and optimization problems in heat transfer. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 1–24. [Google Scholar] [CrossRef]
- Özisik, M.N.; Orlande, H.R.B. Inverse Heat Transfer: Fundamentals and Applications; Taylor & Francis: Didcot, UK, 2000. [Google Scholar]
- Vakili, S.; Gadala, M.S. Effectiveness and Efficiency of Particle Swarm Optimization Technique in Inverse Heat Conduction Analysis. Numer. Heat Transf. Part B-Fundam. 2009, 56, 119–141. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J.; Liu, J.; Yang, Z.; Chen, X. An enhanced sparse regularization method for impact force identification. Mech. Syst. Signal Process. 2019, 126, 341–367. [Google Scholar] [CrossRef]
- Guan, J.S.; Lin, L.Y.; Ji, G.L.; Lin, C.M.; Le, T.L.; Rudas, I.J. Breast tumor computer-aided diagnosis using self-validating cerebellar model neural networks. Acta Polytech. Hung. 2016, 13, 39–52. [Google Scholar] [CrossRef]
- Sumelka, W.; Łodygowski, T. Reduction of the number of material parameters by ANN approximation. Comput. Mech. 2013, 52, 287–300. [Google Scholar] [CrossRef][Green Version]
- Felde, I.; Szénási, S. Estimation of temporospatial boundary conditions using a particle swarm optimisation technique. Int. J. Microstruct. Mater. Prop. 2016, 11, 288–300. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.B.; Sun, Y.; Xu, C.B.; Chen, X.F. Wave propagation of laminated composite plates via GPU-based wavelet finite element method. Sci. China Technol. Sci. 2017, 60, 832–843. [Google Scholar] [CrossRef]
- Aciu, R.M.; Ciocarlie, H. Runtime Translation of the Java Bytecode to OpenCL and GPU Execution of the Resulted Code. Acta Polytech. Hung. 2016, 13, 25–44. [Google Scholar]
- Cotronis, Y.; Konstantinidis, E.; Louka, M.A.; Missirlis, N.M. A comparison of CPU and GPU implementations for solving the Convection Diffusion equation using the local Modified SOR method. Parallel Comput. 2014, 40, 173–185. [Google Scholar] [CrossRef]
- Szénási, S. Solving the Inverse Heat Conduction Problem using NVLink capable Power architecture. PeerJ Comput. Sci. 2017, 3, 1–20. [Google Scholar] [CrossRef]
- Szénási, S.; Felde, I. Using Multiple Graphics Accelerators to Solve the Two-dimensional Inverse Heat Conduction Problem. Comput. Methods Appl. Mech. Eng. 2018, 336, 286–303. [Google Scholar] [CrossRef]
- Szénási, S.; Felde, I. Configuring Genetic Algorithm to Solve the Inverse Heat Conduction Problem. In Proceedings of the 5th International Symposium on Applied Machine Intelligence and Informatics (SAMI2017), Herl’any, Slovakia, 26–28 January 2017; pp. 387–391. [Google Scholar]
- Szénási, S.; Felde, I. Configuring Genetic Algorithm to Solve the Inverse Heat Conduction Problem. Acta Polytech. Hung. 2017, 14, 133–152. [Google Scholar] [CrossRef]
- Felde, I.; Fried, Z.; Szénási, S. Solution of 2-D Inverse Heat Conduction Problem with Graphic Accelerator. Mater. Perform. Charact. 2017, 6, 882–893. [Google Scholar] [CrossRef]
- Szénási, S.; Felde, I. Modified Particle Swarm Optimization Method to Solve One-dimensional IHCP. In Proceedings of the 16th IEEE International Symposium on Computational Intelligence and Informatics (CINTI2015), Budapest, Hungary, 19–21 November 2015; pp. 85–88. [Google Scholar] [CrossRef]
- Szénási, S.; Felde, I.; Kovács, I. Solving One-dimensional IHCP with Particle Swarm Optimization using Graphics Accelerators. In Proceedings of the 10th Jubilee IEEE International Symposium on Applied Computational Intelligence and Informatics (SACI2015), Timisoara, Romania, 21–23 May 2015; pp. 365–369. [Google Scholar]
- Fried, Z.; Pintér, G.; Szénási, S.; Felde, I.; Szél, K.; Sáfár, A.; Sousa, R.; Deus, A. On the Nature-Inspired Algorithms Applied to Characterize Heat Transfer Coefficients. In Proceedings of the Thermal Processing in Motion 2018, Spartanburg, SC, USA, 5–7 June 2018; pp. 47–51. [Google Scholar]
- Szénási, S.; Felde, I. Estimating the Heat Transfer Coefficient using Universal Function Approximator Neural Network. In Proceedings of the 12th International Symposium on Applied Computational Intelligence and Informatics (SACI2018), Timisoara, Romania, 17–19 May 2018; pp. 401–404. [Google Scholar] [CrossRef]
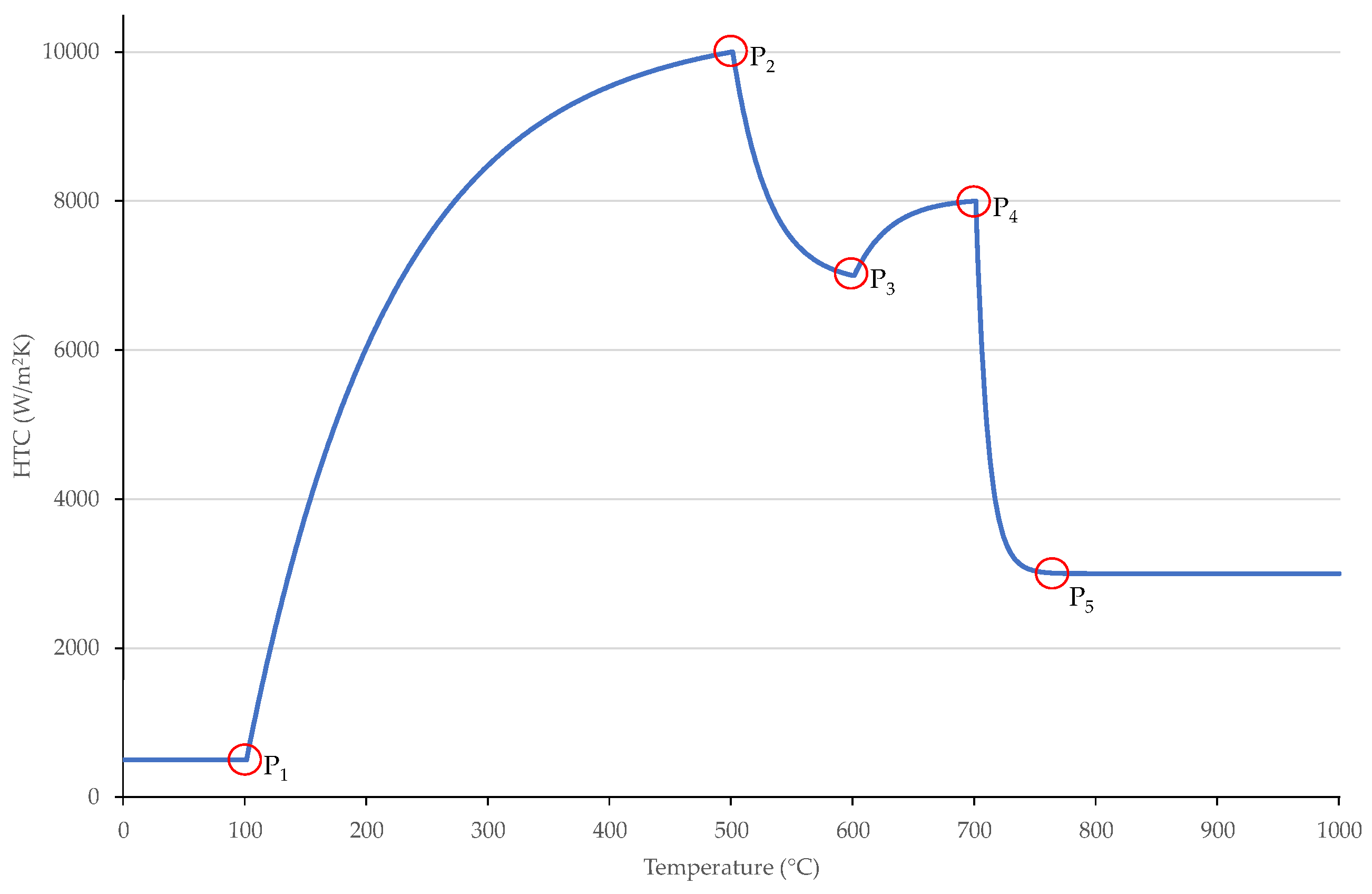
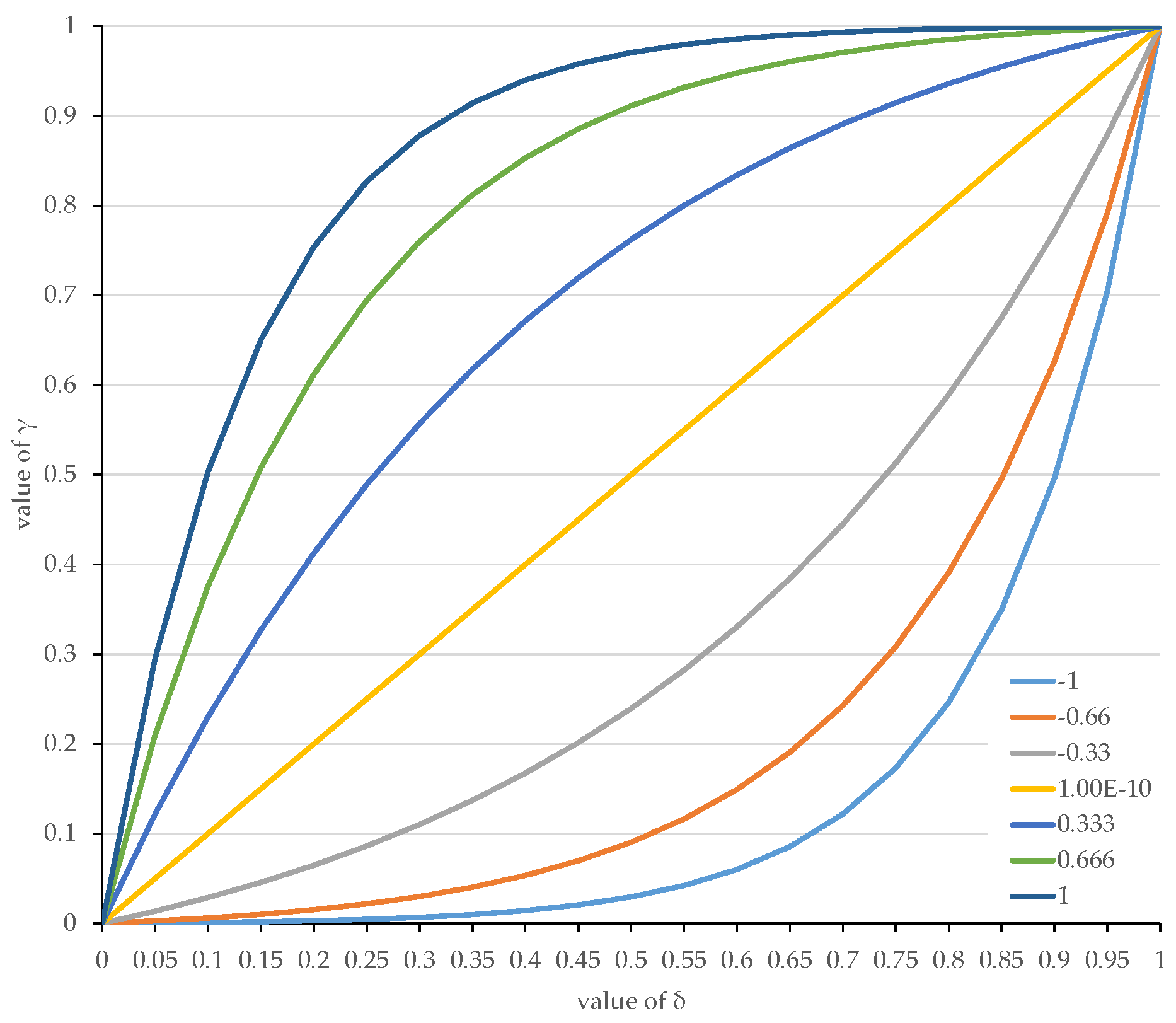
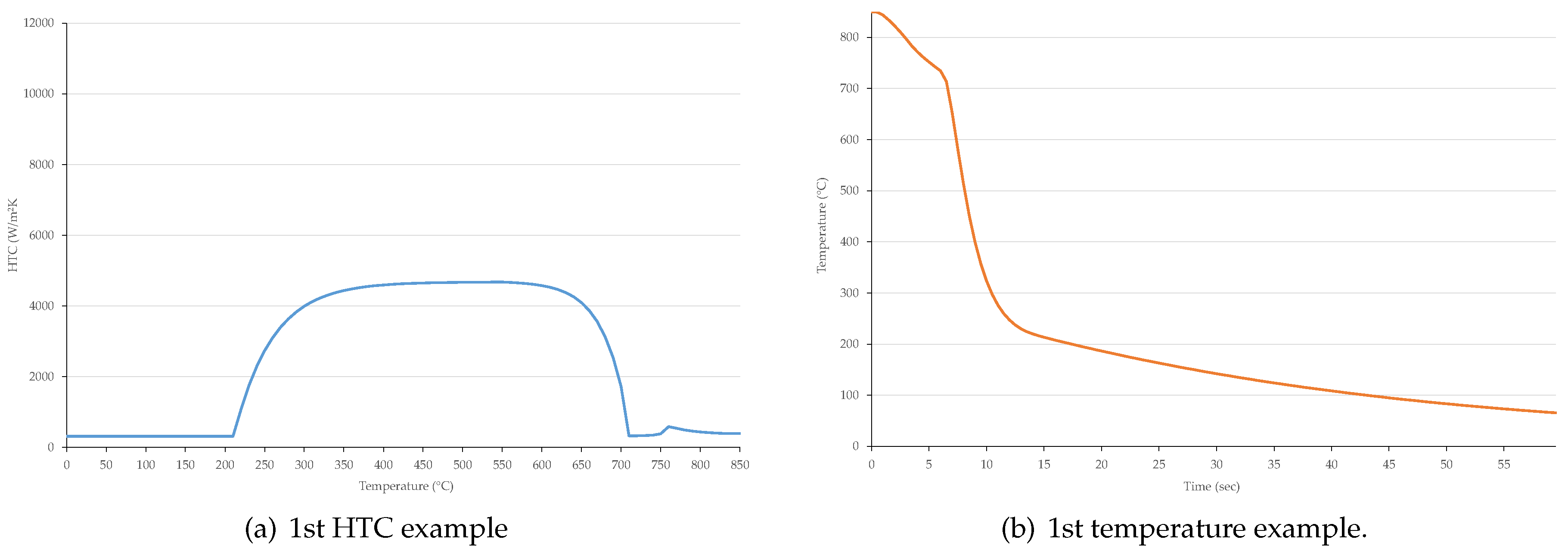
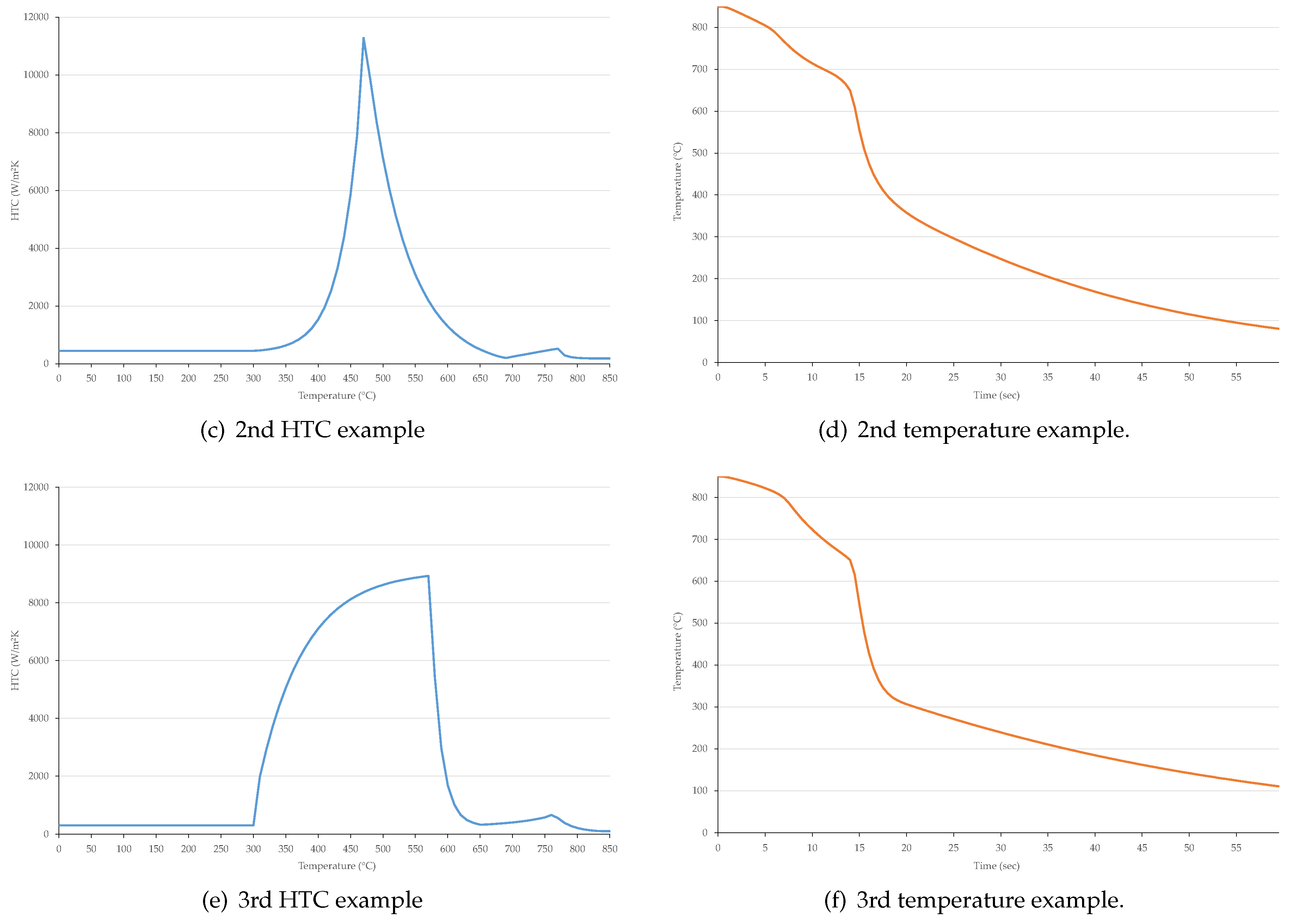
| Count | Size | Type | Description | Unit | Min Value | Max Value |
|---|---|---|---|---|---|---|
| 1 | 4 byte | float | Number of control points | 0 | ||
| Number of control points | 4 byte | float | ith control point temperature | °C | 0 | 850 |
| 4 byte | float | ith control point HTC | 0 | 12,000 | ||
| 4 byte | float | ith control point |
| Count | Size | Type | Description | Unit | Min Value | Max Value |
|---|---|---|---|---|---|---|
| 4 byte | float | HTC value for temperature | 0 | 12,000 |
| Count | Size | Type | Description | Unit | Min Value | Max Value |
|---|---|---|---|---|---|---|
| 4 byte | float | Temperature value for time | °C | 0 | 850 |
| Temperature (°C) | HTC () | |||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| 200 | 400 | 200 | 500 | |
| 401 | 650 | 2000 | 12,000 | |
| 651 | 750 | 200 | 500 | |
| 751 | 820 | 500 | 800 | |
| 821 | 850 | 100 | 400 | |
| Temperature T (°C) | Heat Conductivity k (W/mK) |
|---|---|
| 27.00 | 14.8 |
| 95.45 | 15.8 |
| 195.95 | 17.4 |
| 205.15 | 17.5 |
| 346.75 | 19.8 |
| 554.15 | 23.1 |
| 596.15 | 23.8 |
| 662.15 | 24.9 |
| 796.45 | 27.1 |
| Temperature T (°C) | Specific Heat Cp (kJ/kgK) |
|---|---|
| 27.00 | 0.4440 |
| 95.45 | 0.4801 |
| 195.95 | 0.5038 |
| 205.15 | 0.5038 |
| 346.75 | 0.5041 |
| 554.15 | 0.5453 |
| 596.15 | 0.5536 |
| 662.15 | 0.5958 |
| 796.45 | 0.6817 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szénási, S.; Felde, I. Database for Research Projects to Solve the Inverse Heat Conduction Problem. Data 2019, 4, 90. https://doi.org/10.3390/data4030090
Szénási S, Felde I. Database for Research Projects to Solve the Inverse Heat Conduction Problem. Data. 2019; 4(3):90. https://doi.org/10.3390/data4030090
Chicago/Turabian StyleSzénási, Sándor, and Imre Felde. 2019. "Database for Research Projects to Solve the Inverse Heat Conduction Problem" Data 4, no. 3: 90. https://doi.org/10.3390/data4030090
APA StyleSzénási, S., & Felde, I. (2019). Database for Research Projects to Solve the Inverse Heat Conduction Problem. Data, 4(3), 90. https://doi.org/10.3390/data4030090





